基于混合简化粒子群算法的贝叶斯网络结构学习研究
2024-03-20刘浩然崔少鹏王念太蔡炎滨时倩蕊张力悦
刘浩然, 李 晟, 崔少鹏, 王念太, 蔡炎滨, 时倩蕊, 张力悦
(1.燕山大学 信息科学与工程学院,河北 秦皇岛 066004;2.河北省特种光纤与光纤传感重点实验室,河北 秦皇岛 066004)
1 引 言
贝叶斯网络(Bayesian network, BN)是表示随机变量之间相互依赖或独立关系的概率图模型。网络结构表示为有向无环图,用来定性地表示变量之间的依赖关系[1],参数为节点间条件概率分布,用来定量地描述变量之间的依赖程度[2]。由于BN结构在表示和推理方面的强大能力[3],使其在生物医学[4]、故障诊断[5]、状态监测[6]等领域得到了广泛的应用。
BN学习可以分为结构学习和参数学习[7],参数学习需要在结构已知的基础上进行,所以贝叶斯网络结构学习(BN structure learning,BNSL)是基础。BNSL可分为精确学习算法[8]和近似学习算法[9]。精确学习算法是遍历整个搜索空间,然后找到全局最优解,但是通常算法效率不高,大型网络结构甚至不可实现;近似学习算法通常采用启发式策略对结构空间搜索以获得最优解,其计算效率较高,所以近似学习算法得到广泛研究和应用。
近似学习算法一般分为3类:基于约束[10]、基于评分搜索[11]和基于混合搜索[12]。除以上方法外,结合仿生学算法的BNSL发展迅速,许多优质算法被提出,如遗传算法(genetic algorithm, GA)[13]、狼群算法[14]、蚁群算法[15]、鲸鱼群算法[16]、粒子群优化(particle swarm optimization, PSO)[17]等。
PSO算法因为其编码方式简单、全局搜索能力强、收敛速度快而被广泛地应用到BNSL中。文献[18]提出一种基于二进制粒子群算法的贝叶斯网络学习算法;文献[19]运用混沌粒子群算法得到最优位置,即最优初始网络结构,以此获得节点排序,并带入K2算法,从而获得最优网络结构;文献[20]将PSO算法和GA算法相结合,利用GA的交叉和变异重新定义粒子的更新规则,并利用马尔科夫链定理证明了该算法的全局收敛性。以上3个算法都是对PSO算法进行了改进,但是其初始结构都是随机生成的,这导致算法的随机性过大,结果和效率都不太好。文献[21]提出了一种基于进化策略的BNSL算法,并设计了一种新的初始结构编码方法,以避免生成非法结构循环图。然而,由于编码相对复杂,后续计算需要较高的计算机性能,并且不容易实现。文献[22]提出PC算法构建初始结构,用带有突变算子的双速度离散粒子群优化BN结构,该文的优化策略是利用突变算子更新粒子的位置,从而使粒子向最优解的位置不断搜索,但是生成的初始解太随机化并且双速度离散化过程太发散,所以最终寻找到的最优粒子并不好。文献[23]首先用PC算法构建出定向网络结构,将结构转化为一个基因组,然后利用随机数控制基因组的每一个基因进行均匀变异和均匀交叉操作。实验证明,在相同数据集的小网络中,能够学习到评分较高的网络并具有较好的收敛性,但其更新规则中的交叉和变异概率的选择过于随机,失去了GA算法的优势。
本文提出的混合简化粒子群算法优化贝叶斯网络结构学习算法(hybrid simplified particle swarm algorithm-Bayesian network structure learning,BNs-HsPSO)通过最大支撑树策略生成无向结构,然后利用V-结构和条件相对平均熵(conditional relative average entropy,CRAE)共同确定初始结构的方向,此方式有效减少了后期多次循环迭代寻优的时间,提高了搜索效率。由于粒子群算法常用于解决连续性问题,为了更好地用于解决本文BNSL离散型问题,根据文献[24]提出的不含速度项的简化粒子群算法公式,然后结合GA算法的交叉和变异策略,生成了新的改进粒子群算法迭代公式,由此可实现BNSL的优化。在更新过程中,本文自定义变异和交叉概率,从而避免迭代过程的冗余;增加副粒子增缓策略优化未迭代更新的粒子进而增加种群多样性,避免算法陷入局部最优。因此最终搜索到含有更多正确边的BN结构并增强了算法的学习效率。
2 BNs-HsPSO算法研究
2.1 BNs-HsPSO算法初始种群构建
设节点集合为X={x1,x2,…,xn},利用互信息公式(1)计算任意两节点xi和xj的互信息I(xi,xj),并对集合X中所有的节点关系进行计算,最后得到X的互信息矩阵XI={I(xi,xj)}n×n。
(1)
式中:P(xi,xj)表示xi和xj的联合概率;P(xi)表示xi的边缘概率;P(xj)表示xj的边缘概率。互信息具有非负对称性,即I(xi,xj)=I(xj,xi)。I(xi,xj)>0说明两节点xi和xj之间存在相互影响,I(xi,xj)=0表示两节点是相互独立的。
令T=XI,从集合X中选择任意节点xi作为起始点,并令集合V={xi},同时从集合X-V中寻找另一个节点xj,使得互信息值在XI中为最大,同时用无向边连接xj,xp。并将节点xj也加入到集合V中;重复以上步骤,直到V=X时,此时,便可得到最大支撑树结构矩阵T。
此时T中两节点间只有无向边,本篇采用V-结构[25]和CRAE[2]共同确定无向边的方向,具体过程如下。
V-结构:对于无遮挡元组
(2)
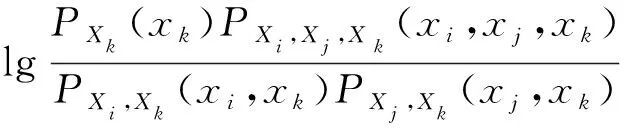
(3)
式中:PXi,Xj,Xk(xi,xj,xk)表示节点xi,xj,xk的联合概率;PXi,Xk(xi,xk)表示节点xi,xk的联合概率。PXk(xk)表示xk的先验概率。
通过V-结构确定了部分无向边的方向,对于剩余的无向边通过CRAE策略来确定方向。CRAE策略简洁且高效,具体计算公式如下:
(4)
(5)
(6)
式中:|xi|为变量xi的取值个数;H(xi)为离散随机变量xi的熵;H(xi|xj)是离散变量xi在已知xj条件下的不确定性。如果CRAE(xi→xj)≥CRAE(xj→xi),则两节点方向为xi→xj,否则两节点方向为xj→xi。
经过对初始结构定向,表示无向图的矩阵XM转化为表示有向图的矩阵XG。在XG矩阵中,若XG(xi,xj)=1表示在网络结构中的指定方向为xi→xj,即表明xi是xj的父节点。以矩阵XG为原始矩阵,对XG随机的增加一条边或者反转一条边,从而形成一个新的矩阵,重复生成多个这样的新矩阵,直到加边或转边不会生成新的矩阵为止。存储这些矩阵的集合为G,G={XG1,XG2,…,XGm},m为矩阵个数。
2.2 BNs-HsPSO算法寻优
将G中的m个结构看作m个粒子的位置,m为初始的粒子群中个体数目,个体最优粒子的位置即为当前待优化的结构矩阵,全局最优粒子的位置是评分值最大的结构矩阵。变异操作的目的是避免陷入局部最优,当需更新粒子的评分值和整个粒子群的平均评分值差异性在阈值范围内时变异;交叉操作是增加种群多样性,此时交叉操作是优化粒子的当前位置。G中第i个粒子的位置更新过程如式(7)所示:
XGi(t+1)=(((XGi(t)⊕w)⊗c1)⊗c2)
(7)
式中:⊕为变异操作;w为变异概率;⊗代表与个体最优粒子或全局最优粒子交叉操作;c1、c2为交叉概率;i=1,2,…,m。
XGi(t)→XGi(t+1)的实现分为3个步骤,即变异操作、与个体最优粒子交叉操作、与全局最优粒子交叉操作等步骤。变异操作的具体过程如式(8):
(8)
式中:A表示条件变异操作;t表示当前的第t次迭代;M表示在当前条件下变异;|w-1|代表变异条件(a=0.05);w=score(i)/favg,score(i)表示当前结构XGi(t)的BIC评分值,favg表示所有参与迭代粒子的平均评分值。
与个体最优粒子交叉操作如式(9)所示:
(9)
式中:B表示与个体最优粒子的条件交叉操作;S表示当前条件下与全局最优粒子交叉;c1=score(i)/fpbest表示与个体最优粒子的交叉概率;fpbest表示个体最优粒子的评分值。
与全局最优粒子交叉操作如式(10)所示:
(10)
式中:XGi(t+1)表示与全局最优粒子的条件交叉操作;S表示当前条件下与个体最优粒子交叉;c2=score(i)/fgbest表示与全局最优粒子交叉概率;fgbest表示全局最优粒子的评分值。
当迭代粒子完成变异操作后,利用BIC评分判断此结构的优劣,未优化的粒子选择副粒子增缓策略(见2.3节)来增强优化效果。在迭代过程中可能会出现环状结构,增加去环操作(见2.4节)去除环状粒子,提高粒子的准确性。
2.3 副粒子增缓策略
由于迭代后期粒子位置趋于集中化且评分值不再增加,此时整体粒子群的优化极易陷入局部最优。为增强种群多样性,避免陷入局部最优,从而提出副粒子增缓策略。
副粒子的选择:同第2.1节所示得到互信息矩阵XI={I(xi,xj)}n×n,并且确定阈值大小,当I(xi,xj)值大于阈值时,将XI中对应的(xi,xj)元素坐标i、j保留在L空数组中。由于XI是对称矩阵,则仅保留对称矩阵中上三角或下三角的元素对应坐标值。并将L排列成二维稀疏矩阵,按互信息I(xa,xb)>I(xc,xd)>…>I(xl,xo)(a,b,c,l,o∈{1,2,…,n})的顺序排列,最终形成l×2维的L,l的大小等于在阈值设定下,筛选出的最大矩阵元素个数。副粒子如式(11)所示:
(11)
增缓策略:在2.2节的算法寻优过程之后,因为评分值不增加而无迭代寻优的粒子选择在副粒子的作用下优化,即寻得新的粒子位置,避免全部粒子向局部最优粒子的位置移动。未优化的粒子的改变主要在于增加边的操作,未优化的粒子群为G′(G′∈G),G′={XG′1,XG′2,……,XG′n},n为未优化粒子群个数。当选择副粒子中某一维的元素(a,b)时,判断XG′i中对应位置XG′i(a,b)的元素值,若XG′i(a,b)=0时,对XG′i粒子加边操作,即XG′i(a,b)=1,否则不变。
副粒子增缓策略后的粒子通过适应度函数值判断粒子的优化程度,并和原粒子群合并; 然后进行去除环状操作,以确保最终的网络结构无异常环状。
2.4 去除环状操作
在变异操作和交叉操作中可能会产生非法环状结构,因此为了保证变异后的贝叶斯网络结构不含有异常的环状结构,需要对贝叶斯网络进行修正。修正方法如下:
重复第1步至第4步的操作,直到最终并无任何环状结构。
2.5 BNs-HsPSO算法流程图
BNs-HsPSO算法流程图如图1所示。
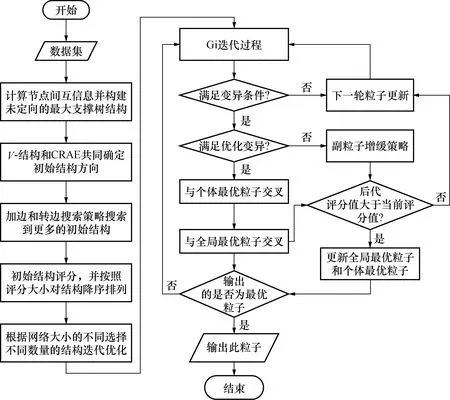
图1 算法整体流程图Fig.1 Overall algorithm flowchart
3 实验分析
实验运行环境:Inter(R)Core(TM)i5-8250U CPU,主频1.60 GHz,内存4 GB,Windows10 64bit操作系统。在MATLAB2020a平台中基于bnt-master工具箱进行实验。为了验证本文算法的性能优势,使用常用的且具有代表性的贝叶斯网络中的ASIA、CAR、CHILD、ALARM网络进行实验对比。其中ASIA网络包含8个节点、8条边;CAR网络包括12个节点、9条边;CHILD网络包括20个节点、25条边;ALARM网络包括37个节点、46条边。在如上个网络中随机生成训练数据集作为实验数据,其中4个网络分别随机生成了1 000、2 000、3 000、5 000组数据。
3.1 参数设置
不同阈值参数的设置影响迭代的效率和准确性,副粒子中阈值的设置影响评分值的大小、收敛速度和正确边及多边的个数。由于在ASIA、CAR网络中取不同阈值时评分值及收敛速度相差不大,所以在CHILD和ALARM中做阈值对评分值及收敛速度的对比实验。图2是在不同阈值下,CHILD、ALARM网络所达到的最高评分值所需迭代次数。图3是在不同阈值下,ASIA、CAR、CHILD、ALARM网络与标准网络相比正确边及多边的个数。此两组实验分别是在5 000组数据且20次迭代结果所得的平均值。
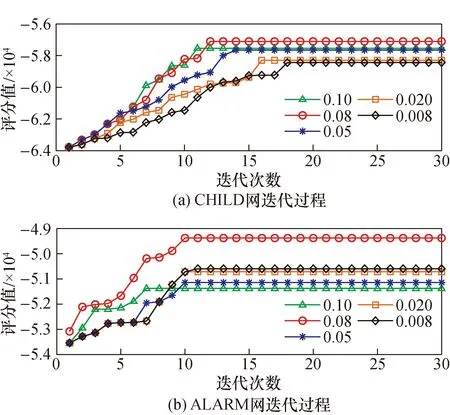
图2 不同网络下的迭代过程Fig.2 Iterative processes under different networks
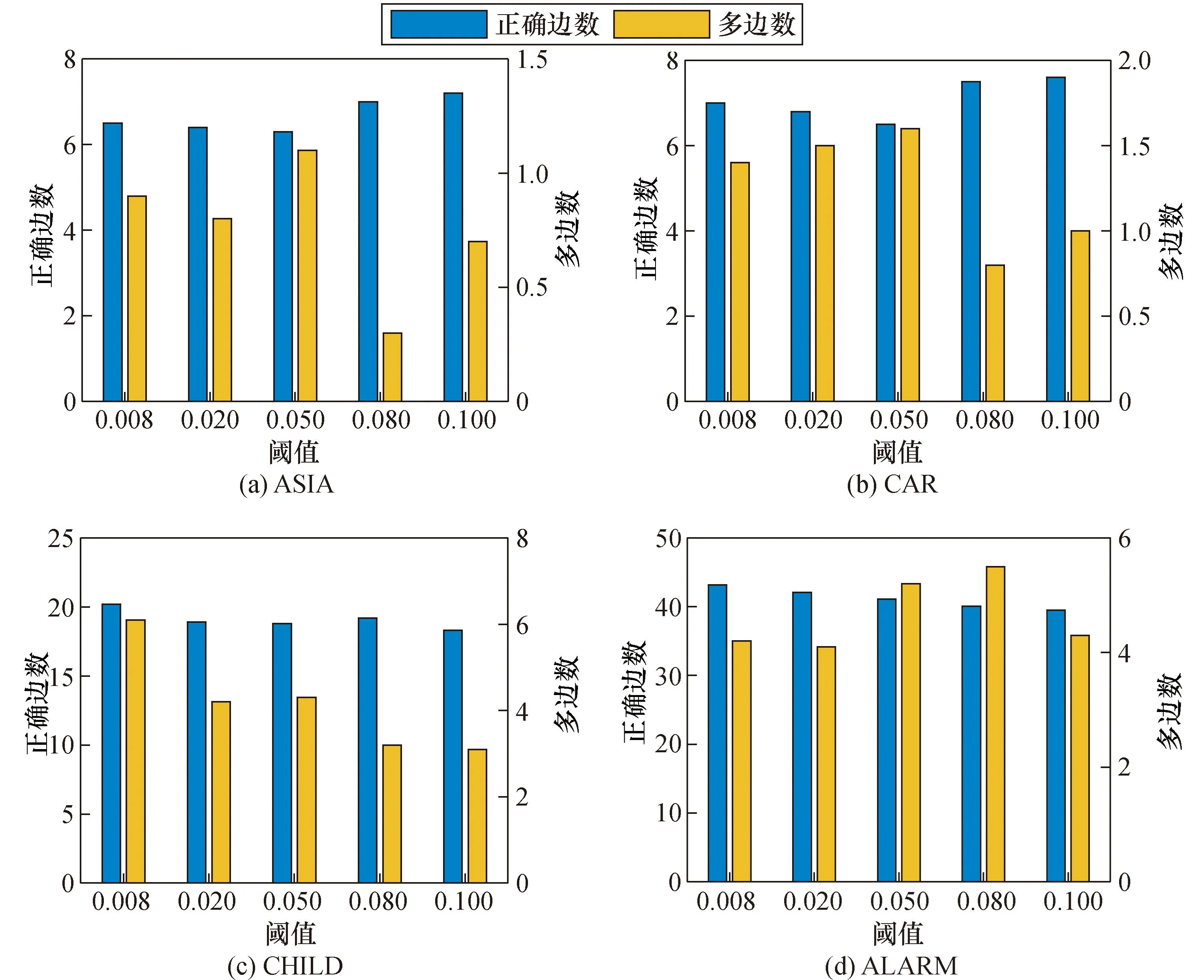
图3 不同网络下的边数对比结果Fig.3 Comparison results of the number of edges under different networks
由图2可知,当阈值为0.08时评分值的绝对值最大,且迭代次数最小,并在之后一直维持最大评分值的绝对值。由图3可知,在ASIA、CAR、CHILD中,当阈值为0.08时,正确边数是最大的且多边数是最小的。而在ALARM网络中,将阈值设为0.08并无优势,但是结合4个网络中正确边数的数量及评分值等指标,最终副粒子增缓策略中的阈值设置为0.08。
3.2 与其他算法的对比实验
为了验证所提算法的有效性,将本文的算法与BNC-PSO[20]和PC-PSO[23]以及常用的经典的BN结构学习算法MMHC[26]算法和贪婪算法[27](Greedy Search, GS)进行对比实验。实验次数为50次,并在标准网络随机生成的相同数据样本中对比了以上算法在各网络中取得的最佳BIC评分平均值如表1到表4所示。

表1 ASIA网络中平均BIC评分的对比Tab.1 Comparison of average BIC scores in ASIA networks

表2 CAR网络中平均BIC评分的对比Tab.2 Comparison of average BIC scores in CAR networks

表3 CHILD网络中平均BIC评分的对比Tab.3 Comparison of average BIC scores in CHILD networks

表4 ALARM网络中平均BIC评分的对比Tab.4 Comparison of average BIC scores in ALARM networks
BIC评分用来评价学习到的网络和真实网络的匹配程度。
由表1~表4数据结果可知,在1 000、2 000、3 000、5 000组数据下,平均评分值的对比结果:在ASIA网络中,本文算法的评分值比MMHC算法增长5.8%,比GS算法增长6.4%,比BNC-PSO增长5.4%,比PC-PSO算法增长5.5%;在CAR网络的数据结果显示,本文算法的评分值比MMHC增长9.3%,比GS算法增长9.6%,比BNC-PSO增长3.2%,比PC-PSO算法增长1.1%;在CHILD网络中,本文算法的评分值比MMHC算法增长0.4%,比GS算法增长0.3%,比BNC-PSO增长1.1%,比PC-PSO算法增长0.1%;在ALARM网络中,本文算法评分值比MMHC算法增长2.2%,比GS算法增长2.5%,比BNC-PSO算法增长3.3%,比PC-PSO算法增长3.0%。
上述评分值对比结果表明,在相同数据量下,本文的算法在评分值上比其他算法均有优势。GS在某种意义上容易陷入局部最优解,这是由于GS算法不考虑各种可能的情况,总是在寻找当前状态下最优的解,所以本文算法评分值大于GS算法。MMHC算法在进行评分禁忌搜索后仍有陷入局部最优的趋势,所以本算法比MMHC算法增长率较高。BNC-PSO算法它的初始结构是随机生成的,后期迭代过程可以增加部分评分值,但其评分值和本文算法评分值仍有差距。
PC-PSO算法在初始结构构建中使用了PC算法确定初始结构,但PC算法无法在不完整数据下找到完整数据的因果关系,即无法寻找到更多的正确边数,从而降低了一定的评分值。但从4个网络的评分对比值中发现,在CHILD网络中,本文算法比其他算法的评分值增长率并不明显,这是由于本文算法在CHILD网寻优过程中会出现比其他网络更多的多边,这些边是标准网络中所没有的边,即副粒子增缓策略阈值的约束在CHILD网络中略差。
为了对本文算法学习到的贝叶斯网络结构准确性有更深入的检测,本文选取了评价算法性能中常用具有代表性的指标[28]来验证该算法的性能,部分指标的物理意义如表5所示。

表5 评价算法性能指标Tab.5 Evaluate algorithm performance indicators
其中,HD、ACC值的计算公式如式(12)和(13)所示:
HD=FP+FN
(12)
(13)
通过表5所示,本实验选用TP、HD、ACC指标作为实验对比项,各个算法的对比结果如图4到图6所示。

图4 4个网络中不同算法的TP值Fig.4 TP values for different algorithms in four networks
图4为4个网络中不同的算法TP值的对比结果。
由图4可知,在CHILD网络中,本文的BNs-HsPSO算法的TP值差于GS算法和MMHC算法,但在ASIA、CAR、ALARM网络TP值具有明显优势。因为本文BNs-HsPSO算法在初始结构中使用最大支撑树搜索策略构建初始结构,所以在CHILD网络中存在少边情况,而副粒子增缓策略会增加部分多边,所以在CHILD网络中本文BNs-HsPSO算法与GS和MMHC算法相比略差。同时,本文算法与PC-PSO算法相比的优势在于副粒子增缓策略的约束使得本算法的TP值比PC-PSO算法在ASIA和CAR网络中更高。
图5为4个网络中不同的算法HD值的对比结果。当HD值越小时,整体算法的学习效果更好。同时在ASIA、CAR、ALARM网络中,本文BNs-HsPSO算法的HD值明显较小,而在CHILD网络中,本文算法的HD值略差,这是由于本算法的阈值约束不得当造成的多边情况。BNs-HsPSO算法增加了初始结构的约束及迭代过程的优化,其搜索性能较强,所以无论数据量的大小,其HD值均会增大。但整体来看,本文算法的HD值更低,与标准网络更接近。
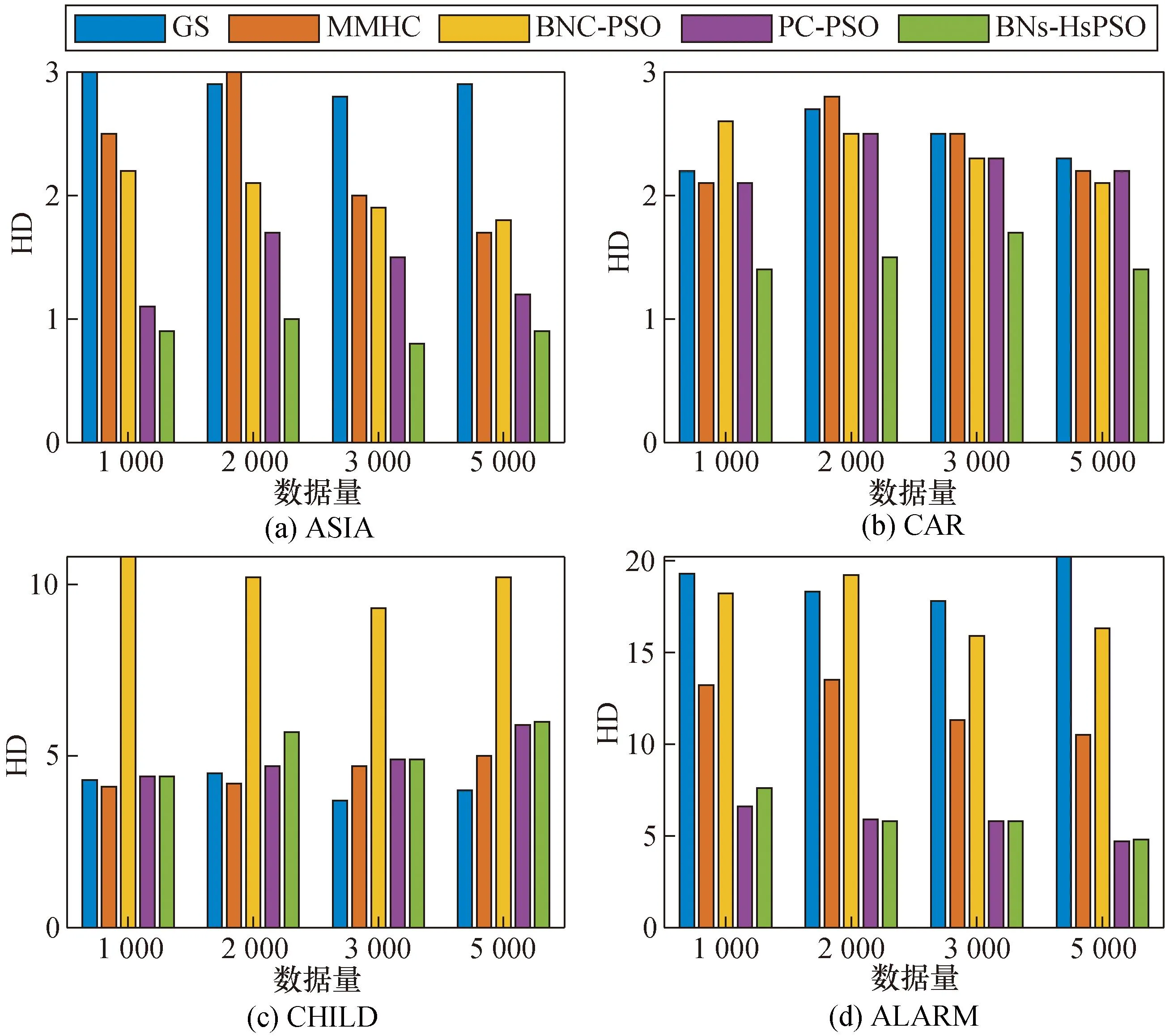
图5 4个网络中不同算法的HD值Fig.5 HD values for different algorithms in four network
图6为4个网络中不同的算法ACC值的对比结果。
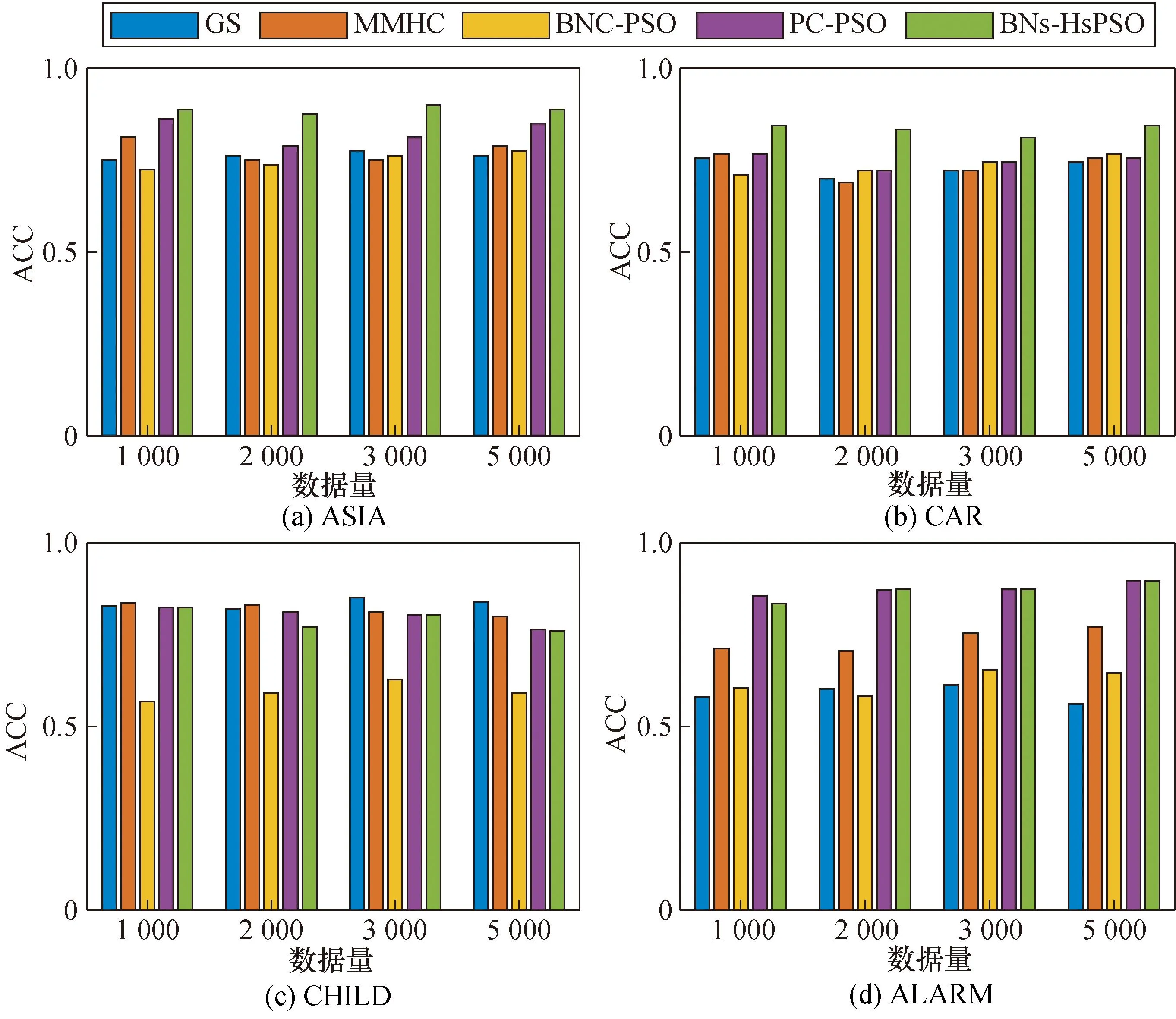
图6 4个网络中不同算法的ACC值Fig.6 ACC values for different algorithms in four networks
由图6可知,在ASIA网络中,本文的BNs-HsPSO算法相比于其他算法有较高的ACC值,而在数据量增大时,BNs-HsPSO算法的ACC值也在提高。这是由于数据量增大时,所选择的数据范围较广,所以得到的网络结构更趋近于正确的网络结构,ACC值就有所提高。
在CHILD网络中,BNs-HsPSO算法与GS、MMHC算法相比不具有优势。由于BNs-HsPSO算法的初始结构中使用最大支撑树来连接两节点,而最大支撑树算法只是保留最大互信息相连的边,此时会出现少边的情况。同时在搜索过程中的副粒子增缓策略会增加边,但由于增加了错误边时式(13)的分母变大,从而导致ACC值偏低。在GS算法和MMHC算法中充分搜索到了最多的正确边数,这两个算法的ACC值在CHILD网络中则较高。在ALARM网络中,随着数据量的增加,对比算法中大多数算法的正确率都会逐步提高,但在GS算法中,当数据量增加时,不可避免地陷入局部最优,会导致搜索过程中搜索到的错误边更多,最终ACC值反而下降了。可以看出,本文BNs-HsPSO算法的ACC值最高。
综上,结合BIC评分值和部分指标的对比,可以明显地看出本文BNs-HsPSO算法的学习效果优于其他算法,这是由于在初始结构构建的时候增加了V-结构和CRAE的定向策略,后期迭代过程引入自定义迭代概率和副粒子增缓策略,使得算法学习过程能搜索到更多的正确边并能获得更优的评分值,减少了随机搜索和随机迭代概率导致的陷入局部最优的可能性。
4 结 论
本文提出混合粒子群优化贝叶斯网络结构的学习算法BNs-HsPSO,该算法首先通过互信息确定2节点的依赖强度,然后构建非定向最大支撑树结构,利用V-结构、CRAE确定结构方向,即可得到初始网络结构;以此结构为基础并利用爬山算法产生众多的结构模型,在粒子群中表现为较优的初代种群。交叉、变异条件概率策略的提出优化了粒子群位置变化,同时提出的副粒子策略针对未优化粒子进行更新,最终搜索到最优的网络结构。实验结果表明,BNs-HsPSO算法能够学习到更好的贝叶斯网络结构模型。不同网络下的学习结果表明,本文算法在评分结果和学习到的正确边数等评价指标中优于其他算法,且在小型网络中具有更高的准确率。
