一种多雷达机动目标探测高阶运动特征估计方法 *

窦凇耀，陈映，陈燕，刘政玮

（北京无线电测量研究所，北京 100854）

0 引言

在现代防御当中，只有获得目标高阶运动特征的高精度估计才能有效提高对目标拦截的概率。但是非合作目标机动性的增强对目标高阶运动特征（加速度）的估计带来了严峻挑战［1-2］。传统的单站雷达通过选择合适的目标运动模型和滤波估计方法来提升对目标加速度的估计精度。常用的机动目标跟踪模型可以分为两类，一类是单模型，另一类是多模型。单模型有CA（constant acceleration）模型、CT（coordinated turning）模型、Singer 模型、“当前”统计模型以及将目标机动加加速度描述为一阶时间相关过程的Jerk 模型等［3-6］。多模型算法的模型集合由单模型构成，交互多模型算法（interactive multiple model，IMM）被认为是目前机动目标跟踪最有效的方法之一［7-8］。由于传统IMM 算法的模型集合是固定不变的，为了有效提升模型集合对目标真实运动模式的匹配度，出现了模型集合可以自适应调整的变结构交互多模算法［9-12］。

由于雷达获得的量测信息一般是在球坐标系中进行描述的，所以需要用到非线性的滤波方法。常用的非线性滤波估计方法有扩展卡尔曼滤波（extended Kalman filter，EKF）、无敏卡尔曼滤波（unscented Kalman filter，UKF）等［13-14］。除此之外，还有适用于非高斯情形的容积卡尔曼滤波（cubature Kalman filter，CKF）和在线调整状态预测误差协方差矩阵的强跟踪滤波器（strong tracking filter，STF）等［4，15］。

单站雷达对目标高阶运动特征的估计精度较差，因为单雷达机动目标跟踪方法都是对上述常规目标运动模型的修正，但是对于非合作目标而言，通过运动模型修正的方式始终是有缺陷的，因为始终不知道目标对象如何机动。本文侧重从多雷达探测结合径向速度增广量测的角度来研究目标高阶运动特征估计精度的提升［16］。

1 集中式雷达组网目标跟踪算法

假设在集中式的雷达组网中有N个雷达节点，这N个雷达节点分别位于不同的位置，共同组成一个探测网络，每个雷达节点将量测信息直接发送到融合中心［17］。本文假设雷达的数据采集速率相同但开机时刻不同，在忽略通信时延的情况下，由融合中心采用序贯无迹卡尔曼滤波算法进行信息融合［18-19］。

1.1 序贯无迹卡尔曼滤波

在直角坐标系下将目标的运动方程定义为

式中：F为CA 模型的状态转移函数；Wk为过程噪声。

目标的状态向量为

式中：xk，yk，zk分别为目标在X，Y，Z方向上的位置；˙ 分别为目标在X，Y，Z方向上的速度分别为目标在X，Y，Z方向上的加速度。

式中：T为雷达采样间隔；⊗为矩阵直积的运算符号。

在雷达坐标系下将量测方程定义为

式中：Pr为雷达的位置坐标；Vk为量测噪声；h(·)为目标的非线性量测函数，具体表示如下：

假设已知k时刻系统的融合估计值为，对应的融合协方差阵为。根据目标的运动方程和量测方程可以得到系统对目标的一步预测为

式中：k1为第1 个量测到达的时刻，各个传感器之间在不同时刻的量测噪声互不相关。在融合中心按照量测到达的时刻，利用UKF 对目标的运动状态进行序贯滤波更新，第1 个到达的量测对融合中心状态估计值的更新为

后续到达的第i个量测(1 ＜i≤N)对融合中心的状态估计值的更新为

k+1 时刻系统的融合估计值，对应的协方差阵

1.2 带径向速度的目标状态估计CRLB（Cramer-Rao lower bound）

量测函数中的径向速度表达式［20］为

一般雷达的量测为距离，方位角和俯仰角，为了提升机动目标加速度的跟踪精度，增加径向速度维量测，构造量测向量为Zk= (rk，ak，ek，vrk)T，其中rk为距离，ak是方位角，ek是俯仰角，vrk是径向速度。

由式（9）得到新的量测函数为

带径向速度的目标状态估计CRLB 为

从式（11）中可以看出，想要求出J-1的解析式需要对一个9×9 的矩阵求逆，较为困难，但是从式（11）可以看出

速度估计CRLB 取J-1的速度项对应的部分，引入径向速度维之后速度估计CRLB 的增加项为可以看出速度估计CRLB 的精度提升为。增加径向速度维量测有效地提升了速度估计的精度，进一步提升了目标加速度的估计精度。

1.3 双传感器的几何精度因子（geometry dilution of precision，GDOP）

根据每个传感器的Fisher 矩阵Ji可以得到双传感器状态估计的CRLB 为

为了讨论的方便，只考虑目标的距离信息rk和方位角信息ak，则

取位置估计CRLB 的迹作为双传感器的GDOP［21］，双传感器的GDOP 图见图1。

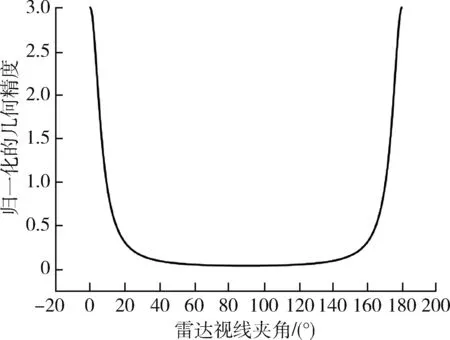
图1 双传感器的GDOP 图Fig. 1 Dual sensor GDOP diagram

图1 中雷达视线夹角是雷达与目标之间视线的夹角，从图1 中可以看出雷达视线夹角在60°～120°，目标的GDOP 值较小，GDOP 值越小代表着估计的精度也就越高，因此雷达与目标之间视线的夹角应尽可能地保持在60°～120°。

2 仿真校验

本文模拟一段目标机动的三维场景，然后采用3 部相同的雷达在不同位置以集中式的方法进行组网，采用序贯无迹卡尔曼滤波算法对3 部雷达的跟踪结果进行融合。

分3 个方向对目标运动建模为X= 3 000t+500 000；Y= 20 000 sin (wt) + 700 000（w= π/120）；Z= 9 000 000，t从0 到540 s。

假设有3 个雷达同时跟踪该运动目标。3 部雷达的量测误差均相同，雷达 1 的位置为(200 000，700 000，0)； 雷 达 2 的 位 置 为[650 000，900 000，0]； 雷 达 3 的 位 置 为[1 200 000，500 000，0]（单位均为m）。3 部雷达量测周期都是0.6 s，但是3 部雷达的开机时间不同，之间相差0.2 s。雷达1，2，3 依次开机。目标的实际运动轨迹如图2 所示。图2 中目标运动轨迹上的三角代表目标的运动方向，圆圈代表结束跟踪时刻目标的位置。运动轨迹下方的三角代表雷达。目标真实的加速度如图3 所示。

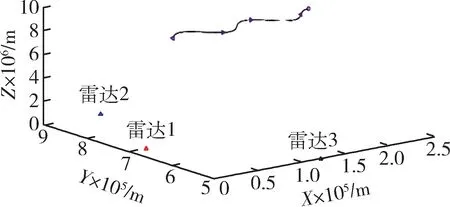
图2 目标真实运动轨迹Fig. 2 True trajectory of the target

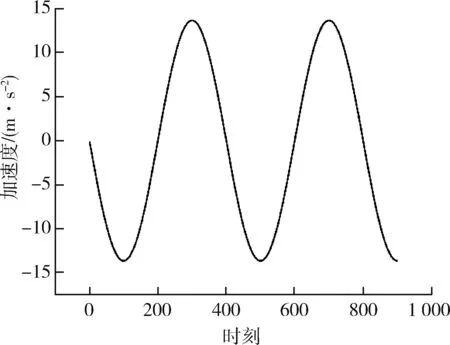
图3 目标真实加速度Fig. 3 True target acceleration

2.1 量测精度对机动目标加速度估计影响

2.1.1 测距精度对机动目标加速度估计的影响

在固定测角精度为0.3°的情况下，研究测距精度对机动目标加速度估计的影响。

3 部雷达均采用三维的CA 模型对目标进行跟踪。3 部雷达属于同一型号雷达，量测误差均相等，单个雷达对目标加速度的估计误差和融合后的加速度估计误差如图4 所示。

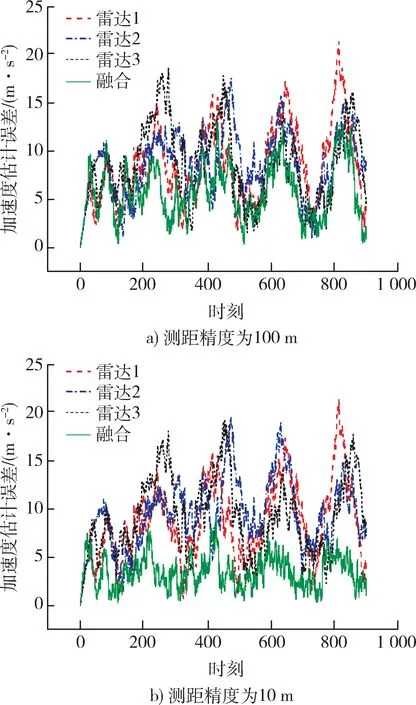
图4 不同测距精度下雷达的加速度误差对比Fig. 4 Comparison of radar acceleration error under different ranging accuracy

从图4 可以看出，测距精度从100 m 增加到10 m，增加了10 倍，对单个雷达的加速度估计误差的影响不是很明显。但是测距精度增大10 倍以后，融合估计的加速度项误差明显增加。通过以上的仿真实验可以说明机动目标的融合估计加速度精度对距离量测精度敏感，下面继续研究机动目标加速度精度对测角精度的敏感性。

2.1.2 测角精度对机动目标的加速度估计影响

在固定距离量测精度为10 m 的情况下，对比测角精度为0.3°和0.03°对机动目标加速度估计的影响。仿真结果见图5。

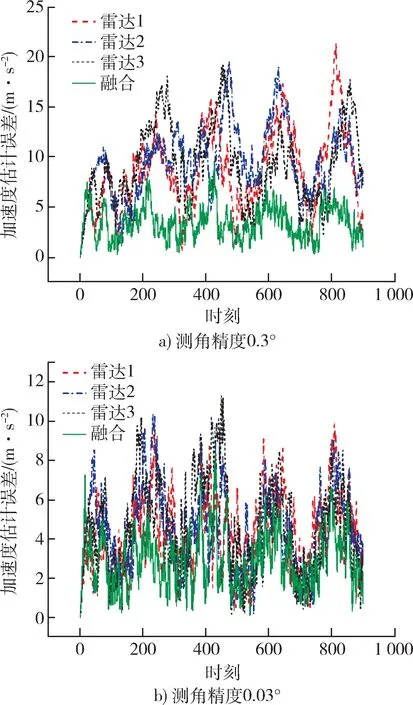
图5 不同测角精度下雷达加速度项误差对比Fig. 5 Comparison of radar acceleration error under different angle measurement accuracy

从图5 中看出，测角精度从0.3°提升到0.03°，精度提升了10 倍，单个雷达加速度项估计均得到了明显提升。但是经过融合估计之后，加速度误差在测角精度变化前后，变化并不明显。这样的仿真实验结果说明该雷达网络的机动目标加速度估计精度对于测角误差并不敏感，改进雷达的测角精度无法进一步有效提升机动目标的加速度估计精度。

2.2 径向速度辅助的机动目标加速度估计

从2.1 节的仿真可以看出，采用雷达组网具有很强的抗干扰性能，即使单个雷达的跟踪误差很大，融合后的跟踪精度依旧很高，但是机动目标加速度对雷达的测角精度并不敏感。为了进一步提升机动目标的加速度估计精度，在量测中增加径向速度维。

在固定测角精度为0.03°，测距精度为10 m 的情况下，研究径向速度对机动目标加速度估计的影响，径向速度的误差为0.5 m/s。

在有无径向速度辅助跟踪的情况下，对比加速度项估计误差，如图6 所示。

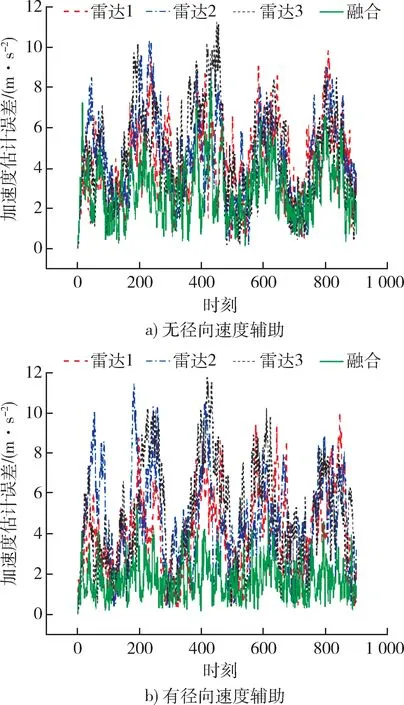
图6 有无径向速度量测下雷达的加速度误差对比Fig. 6 Comparion of radar acceleration error with or without radial velocity measurement

从图6 可以看出，增加了径向速度维以后，对机动目标的加速度项估计精度明显提升了，在无径向速度维时，加速度估计误差的均值为3 m/s2。在加入径向速度量测之后，加速度估计误差的均值下降到了1.7 m/s2。这说明增加了量测维度使得机动目标的加速度估计精度得到了明显的提升。为了进一步提升对机动目标加速度的估计精度，对雷达站的布局进行优化。

2.3 雷达布站对机动目标加速度估计的影响

雷达组网中，除了数据融合算法、雷达探测性能会对目标的状态估计产生影响之外，雷达站与跟踪目标之间的几何位置也会对目标的加速度估计产生影响，为了进一步提升机动目标加速度的估计精度，将雷达布站进行优化如图7，雷达布站优化以后的加速度估计结果见图8。优化之后的雷达站点：雷达1 的位置为(-300 000，-1600 000，0)；雷达2的位置为(1 300 000，3 000 000，0)；雷达3 的位置为(2 900 000，-1 600 000，0)。

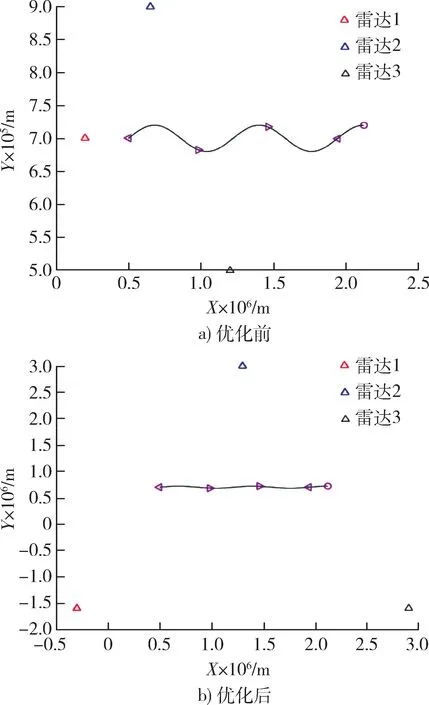
图7 雷达布站俯视图Fig. 7 Top view of radar stations

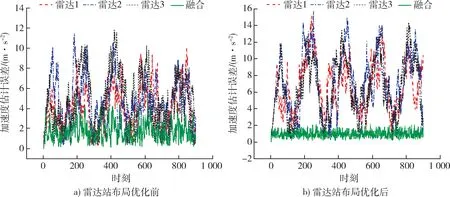
图8 雷达布站优化前后加速度估计的误差对比Fig. 8 Error comparison of acceleraion estimation before and after radar station optimization

从图7 中可以看出优化前雷达1 和雷达3、雷达2 的视线夹角在不断地减小至40°以下，雷达2 和雷达3 的视线夹角一直在140°～180°，3 部雷达的视线范围始终没有达到最优。但是优化后可以保证雷达1 和雷达3 的视线夹角在90°～120°，满足60°～120°的最优位置范围。从图8 可以看出经过雷达布站的优化过后，机动目标加速度的融合估计精度得到了明显的提高，误差的均值达到了0.9 m/s2。图8的仿真结果充分证明了雷达站布局对目标加速度的估计有着十分重要的影响。

将不同实验条件下，雷达组网对机动目标加速度的估计结果汇总到表1。从表1 可以看出测距精度对目标加速度估计误差的影响最大，其次是径向速度和雷达站的布局，最后是测角精度。由于测角精度对目标加速度估计精度的影响较小，在忽略角度量测后，目标加速度的估计精度几乎不变。

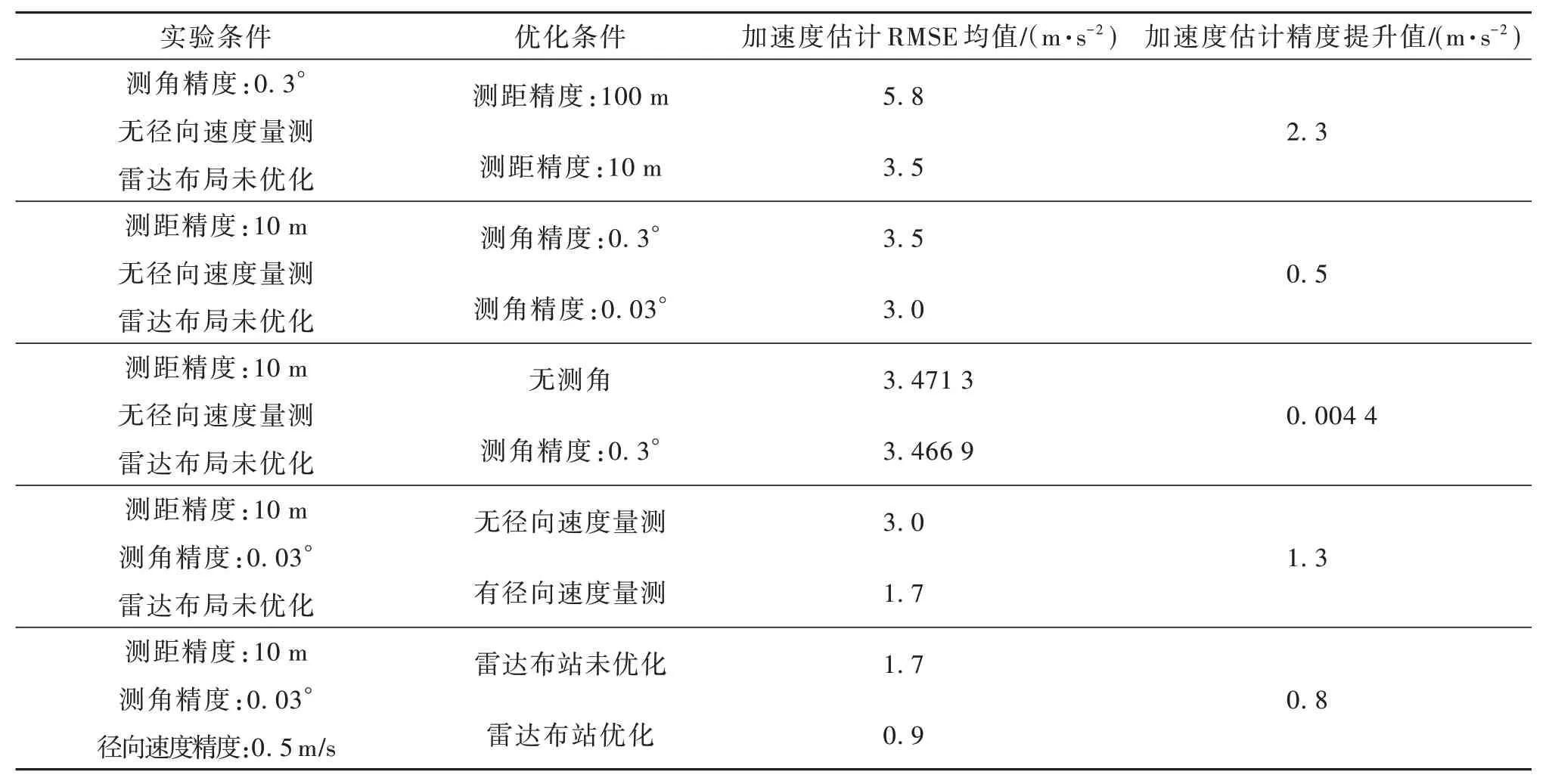
表1 不同优化条件下机动目标加速度估计精度Table 1 Acceleration estimation accuracy of maneuvering target under different optimation conditions

3 结束语

雷达组网可以有效克服单个雷达的缺陷，提升目标跟踪的精度和稳定性，这是因为在多雷达探测的情况下采用序贯无迹卡尔曼滤波的方式进行信息融合，相当于增加了雷达对目标的数据采集速率，因此加速度的估计精度得到了提升。在本文的仿真实验中，距离量测精度对机动目标加速度融合估计精度的影响比角度量测精度更大。为了进一步提升对机动目标加速度的估计精度，除了进一步提升测距精度以外，还可以引入径向速度作为新的一维量测。增加一维量测相当于增加了一维对目标的观测视角，自然可以增加对目标状态估计的信息量，进而提升估计精度。可以看出，在径向速度辅助下，机动目标加速度估计精度得到了很大的提升。除此之外，雷达站的布局和目标之间的相对几何关系也会对观测精度造成影响，对雷达站的布局进行优化之后，加速度的估计精度可以再一次得到明显提升。雷达组网结合径向速度增广量测有效获得了目标高阶运动特征的高精度估计。