不同厚度航行器高速入水冲击载荷及壳体变形特性

赵海瑞，施 瑶，*，潘 光，黄桥高，刘晓娅

(1. 西北工业大学 航海学院，西安 710072；2. 无人水下运载技术工信部重点实验室，西安 710072)

0 引言

为适应海洋强国战略的不断推进，水下航行器在尺寸和投送方式上进行了升级。采用空投或火箭助飞的大尺度水下航行器具备投送距离远、突防能力强和装载能力大等优势，可显著提高综合性能。大尺度航行器在投放的最后阶段，将高速跨越水气交界面，该过程为典型的流固耦合作用过程。航行器撞水阶段受到的瞬时强冲击载荷将使壳体产生严重的变形，并对内部仪器造成不可逆的破坏。

入水冲击的研究始于Von Karman[1]，他在研究水上飞机迫降时，基于动量守恒定理建立了结构物入水理论模型。Wagner[2]发展了Von Karman的理论，提出了小斜升角模型的近似平板理论，得到了结构物入水冲击压力与速度平方成正比的结论。刚体假设并不适用于所有研究，Wilkinson等[3]对比了刚性和弹性回转壳体的入水冲击载荷，发现刚性体假设得到的入水冲击载荷与实际情况相比偏小。在计算方法方面，Hirt等[4]提出了任意朗格朗日-欧拉（arbitrary Lagrange-Euler, ALE）法，实现了流固耦合问题中结构大变形和液面移动的求解。汪振等[5]采用ALE方法对直径300 mm实心弹体以150～190 m/s速度入水的冲击载荷进行了研究，发现实心弹体的径向载荷在达到峰值后逐渐收敛于零。施红辉等[6]研究了连发射弹出入水问题，获得了超空泡演化过程对射弹速度衰减和阻力系数的影响。Xia等[7]研究了半密封和全密封圆柱壳体入水问题，结果表明，进入半密封圆柱壳的流体将对入水弹道、空泡和结构特征产生较大影响。Liu等[8]采用新型浸入式边界法对直径100 mm的不同头型细长体高速入水问题开展了研究，获取了小角度入水时载荷及弯矩的变化规律。邹田春等[9]开展了直径160 mm圆柱体垂直低速入水的数值模拟，并得到了不同速度、质量和长度下的冲击响应特性。孙志明等[10]对直径324 mm的航行器开展了速度、角度及攻角等入水参数下的亚声速入水研究，并分析了流体动力、运动姿态及空泡形态。Zhang等[11]建立了新的振荡气泡动力学理论，该理论统一了不同的经典气泡方程，可对各种复杂现象下的空化和气泡现象进行理论预报。Liu等[12]研究了直径60 mm超空泡构型航行器高速斜入水后的转弯特性，并对该过程中的冲击载荷及尾拍震荡现象进行了分析。

在航行器壳体变形方面，现有研究主要关注变形量的大小。黄志刚等[13]研究了直径120 mm的钢材料回转体在不同壁厚下的入水载荷特性，得到了回转体头部厚度对结构强度有显著影响的结论。潘光课题组研究了不同尺寸的航行器高速入水时的壳体变形：针对小尺度航行器，研究了直径324 mm航行器低速入水时的壳体变形，结果表明，形变量随壳体厚度减小而增大[14]；针对大尺度航行器，研究了直径533 mm大质量航行体带缓冲头帽时的壳体变形，结果表明，缓冲头帽可有效降低壳体头部变形量[15-16]；此外，还结合模态分析和冲击响应谱研究了直径大于500 mm的大尺度航行器带头帽高速入水时的动力特性，结果表明，航行器入水阶段，壳体主要变形模式为压缩和弯曲[17]。

综上，在入水冲击载荷方面，研究对象多为直径小于500 mm的模型。高速入水时，尺寸的增加将使航行器面临更加恶劣的冲击环境。一方面质量的增加使航行器惯性增大，撞水面积增大使冲击载荷增大。另一方面，大尺度航行器的厚径比（壳厚与直径的比值）减小，壳体受载荷影响将产生更大的变形，并产生独特的变形模式。已有研究关心不同入水初始条件下的变形量，对变形模式和载荷与变形的内在关联等问题则缺乏深入研究。因此本文采用结构化任意拉格朗日-欧拉（structured arbitrary Lagrange-Euler, S-ALE）方法对大尺度航行器高速入水撞水阶段的载荷及变形进行研究，分析二者之间的内在关联性、壳体的变形模式及变形机理，以及壳体厚度对变形的影响。

1 模型介绍

1.1 几何模型

大尺度航行器如图1所示，最大直径D为533.4 mm，总长L为7738 mm，总质量1840 kg，壳体厚度分别为5、8、10 mm。

图1 大尺度航行器示意图Fig. 1 Schematic diagram of a large-scale vehicle

1.2 数值模型

ALE方法结合了Lagrange方法和Euler方法的优点，可看作是Euler方法加网格的移动。该方法允许多种介质在网格中运动，同时可移动的网格将大量减少计算所需网格数量，因此非常适合带有结构大变形过程的流固耦合计算。S-ALE方法在传统ALE方法的基础上，通过设置节点信息将流场网格参数化，并将材料属性与网格信息分离存储，简化了网格生成过程，可显著提高求解效率并将K文件大小减小90%以上。本文使用LS-DYNA软件开展仿真计算，并基于S-ALE方法提出了一种适用航行器高速入水的数值计算方法。S-ALE算法的控制方程由质量守恒方程、动量守恒方程和能量守恒方程组成：

式中：ρ是流体密度；xi是欧拉坐标系中的坐标；v是材料的速度，vij的下标表示对i和j的微分；w是由w = v-u给出的相对速度，u是网格的速度；E是内能；σij是应力张量，σij,j的下标表示对j的微分；b是作用在流体上的体积力。

航行器使用拉格朗日网格，采用Solid单元，材料为铝合金。使用*MAT_PLASTIC_KINEMATIC材料模型获取载荷及变形数据，材料参数如表1所示。水和空气使用*MAT_NULL本构模型，状态方程分别由*EOS_GRUNEISEN和*EOS_LINEAR_POLYNOMIAL描述，施瑶等[18]对航行体带开槽包裹式缓冲头帽入水时的降载性能开展了研究，本文水和空气的状态方程参数沿用了其中的数值。使用*ALE_STRUCTURED_MESH_CONTROL_POINTS控制流体网格参数化节点信息，使用*ALE_STRUCTURED_MESH控制参数化网格生成。使用罚函数法实现流固耦合过程中结构响应信息的捕捉，通过*ALE_STRUCTURED_FSI实现流固耦合过程。

表1 航行器材料参数Table 1 Material parameters of the vehicle

计算域尺寸如图2所示，将四个竖直边界面和底面均设置为无反射边界面，并固定底面。定义如图3所示的坐标系，图中O0-x0y0z0为地面坐标系，O-xyz为局部坐标系，O-x1y1z1为速度坐标系，本文不考虑攻角、侧滑角等入水姿态角，因此局部坐标系与速度坐标系重合。定义x方向为轴向，y方向为法向，由右手法则得到的垂直于xOy平面的z方向为侧向。入水角θ为水面与x轴的夹角。

图2 计算域尺寸Fig. 2 Computational domain size

图3 计算坐标系Fig. 3 Coordinate system

1.3 模型验证

为了验证所建立的数值方法的正确性，在无人水下运载技术工信部重点实验室的综合水池开展了入水试验。试验时使用作者参与设计的高速入水发射装置对模型进行加速[13]，在空中和水下布置了两台1000帧/s高速相机以捕捉模型入水姿态及入水空泡形态，水下相机位于水面下0.5 m，使用水下照明灯拍摄补光，4630 A三轴式压阻加速度传感器采集冲击加速度数据。

使用建立的数值方法对实验模型开展了相同入水初始条件下的仿真，入水速度68.5 m/s，入水角60°。实验模型和简化后的仿真模型如图4所示，模型直径200 mm，总长483 mm。

图4 实验及仿真模型Fig. 4 Experimental and simulation models

从仿真和试验的结果对比来看，空泡轮廓吻合度较好（图5），轴向加速度峰值相对误差3.4%，法向加速度峰值相对误差10.5%（图6），表明所建立的数值模型具有较高的精度。

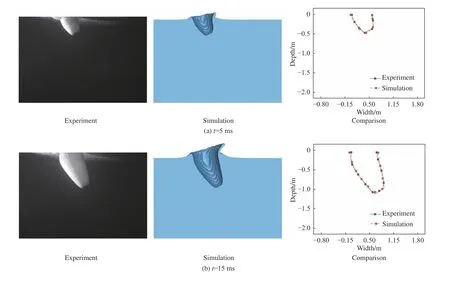
图5 不同时刻实验及仿真空泡对比Fig. 5 Comparison of cavitation at different time instances between experimental and simulation results

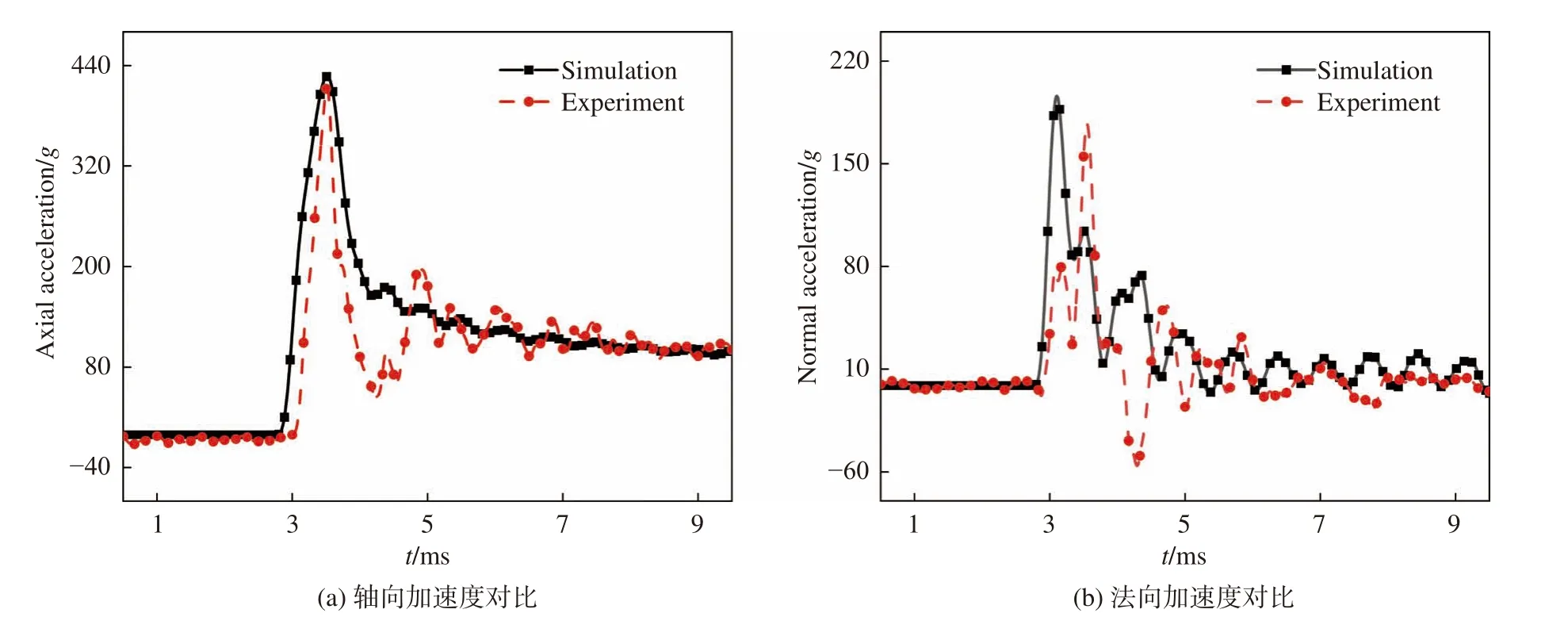
图6 实验及仿真加速度对比Fig. 6 Comparison of acceleration between experimental and simulation results

为了在保证计算精度的前提下减小计算时间，在航行器入水速度150 m/s、入水角90°条件下进行了网格无关性验证工作。使用无量纲参数R定义流体和固体的网格尺寸比，如公式（4）所示：

式中，LFluid为流体网格尺寸，LSolid为固体网格尺寸。

固定冲击区域流体网格尺寸LFluid为15 mm，采用局部加密策略以减少网格数量，对非冲击区域网格进行等比放大（30.0 mm）。分别取R为0.50、0.75、1.00、1.25、1.50、1.75、2.00，即分别使用30.0、20.0、15.0、12.0、10.0、8.5、7.5 mm大小的网格对航行器进行网格划分。不同R取值下网格数量见表2。使用无量纲系数ac定义航行器的入水冲击加速度，如公式（5）所示：

表2 R值与网格数量对应关系Table 2 Correspondence between the R value and the grid quantity

式中，m为航行器的质量，F为航行器受到的入水冲击力，a为航行器加速度，ρ为水的密度，r为航行器的最大半径，v为航行器的入水速度。不同网格下的加速度系数时程曲线如图7所示，R取不同值时，曲线变化趋势相同。峰值系数和峰值脉宽对比如图8所示，加速度峰值随R增加呈现先增大后收敛的趋势，在R大于1.00时趋于收敛。而峰值脉宽随R增加呈现先减小后收敛的趋势，在R大于0.75时趋于收敛。综合考虑峰值和峰值脉宽的收敛趋势，取R为1.25，LFluid为15 mm（冲击区域），LSolid为12 mm，最终网格如图9所示。

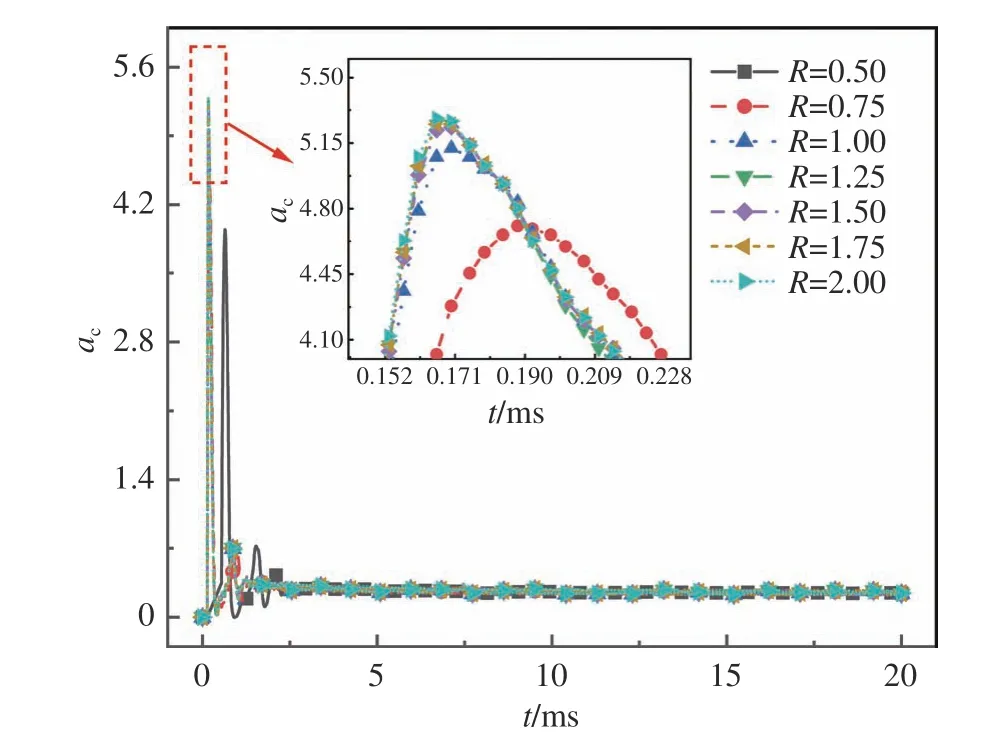
图7 不同R值的加速度系数时程曲线Fig. 7 Time history curves of the acceleration coefficients for different R values

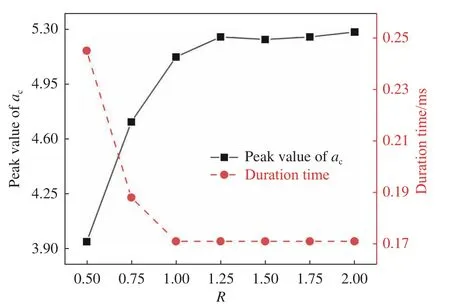
图8 不同R值的加速度峰值系数和峰值脉宽Fig. 8 Peak value and peak pulse widths of acceleration coefficient for different R values

图9 最终网格图Fig. 9 Final grid diagram

进一步地，开展了采样无关性验证工作。在有限元分析中，采样频率fs决定着数据的密度。航行器高速入水是一个短暂且力学环境剧烈变化的过程，其中的冲击载荷、应力及应变等一系列动力学物理量均具有峰值大而脉宽短的特点。过低的采样频率将无法准确捕获峰值信息，过高的采样频率会浪费计算资源。取5组采样频率分别为1×104、1×105、1×106、1×107、1×108，得到不同采样频率下的加速度系数时程曲线如图10所示，fs大于1×104时，曲线基本重合。不同fs下的加速度峰值系数和峰值脉宽对比如图11所示，加速度峰值随fs增加呈现先增大后收敛的趋势，在fs大于1×104时趋于收敛；而峰值脉宽随fs增加呈现先减小后收敛的趋势，在fs大于1×105时趋于收敛。综合考虑峰值和峰值脉宽的收敛趋势，最终取fs为1×106。

图10 不同采样频率的加速度系数时程曲线Fig. 10 Time history curves of the acceleration coefficient at different sampling frequencies

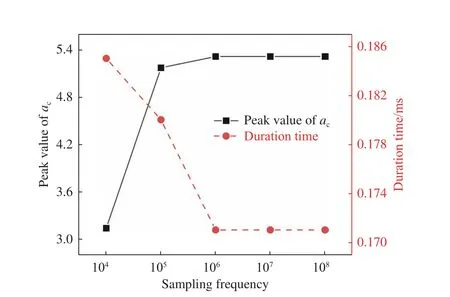
图11 不同采样频率的加速度峰值系数和峰值脉宽Fig. 11 Peak value and peak pulse widths of acceleration coefficient at different sampling frequencies

2 结果与分析

本文通过S-ALE方法对大尺度航行器高速入水撞水阶段的载荷及变形进行了研究，对壳厚、入水角度、入水速度等参数变化影响进行了分析。参数范围如表3所示。

表3 计算工况Table 3 Calculation condition

2.1 载荷与变形关联性分析

在航行器入水过程中，壳体受入水冲击载荷作用将发生变形，而壳体变形后将改变流固耦合力的作用面积和方向，因此首先以壳体厚度8 mm为例，分析航行器入水冲击载荷与壳体变形之间的关联。如图图12所示，入水角60°，入水速度150 m/s。航行器撞水瞬间，轴向和法向载荷出现一次峰值，峰值大小接近，峰值时刻（t= 0.8 ms）壳体尚无明显变形，得出载荷的一次峰值主要由入水速度、角度和航行器头型等初始状态决定。此后航行器头部受流体持续挤压出现明显内凹变形（t= 1.4 ms），轴向载荷最终稳定在30g左右振荡，而法向载荷持续升高并超过一次峰值（t= 7.6 ms），此时壳体头部出现较大内凹变形。理论上入水过程航行器动能持续降低，后续载荷应小于撞水瞬间的一次峰值，但法向载荷的变化说明，结构大变形将显著影响航行器受力状态，使航行器斜入水所受法向载荷急剧增大。本文没有考虑侧滑角等入水姿态角的影响，因此径向载荷几乎为零。

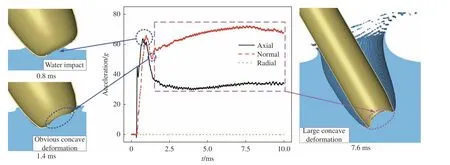
图12 冲击载荷与变形关联图（θ = 60°，v = 150 m/s）Fig. 12 Correlation diagram between the impact load and the deformation (θ = 60°，v = 150 m/s)

由图12可知，载荷的一次冲击波具有峰值高而脉宽短的特点，一次波形的脉宽时间对应了壳体的初期变形状态，下面将从峰值和脉宽的角度分析一次冲击波对于壳体变形的影响，计算工况见表3。

图13为壳厚8 mm、入水角60°时的轴向和法向载荷一次峰值及脉宽随入水速度的变化规律，图14显示了脉宽作用时间内一次波形对壳体变形的影响。峰值脉宽随入水速度增加而下降，同时壳体变形随入水速度升高而明显增大。结合图13和图14分析可知，当入水速度较小时（50 m/s），轴向和法向的峰值及脉宽较为接近，因此轴向和法向峰值脉宽时间内的壳体变形量基本相同，当入水速度较大时（300 m/s），轴向载荷峰值和脉宽明显大于法向，此时轴向峰值脉宽时间内的变形远大于法向。说明载荷峰值和脉宽共同影响着壳体的变形程度，其分别对应了航行器高速入水的强冲击和高应变环境。当入水速度为150 m/s时，轴向和法向的载荷峰值几乎相等，但轴向峰值脉宽明显大于法向，此时轴向峰值脉宽时间内的变形明显大于法向。得出结论，脉宽对壳体变形具有较大影响，相对于载荷峰值，脉宽的“毫秒级”特性使其易被忽视。

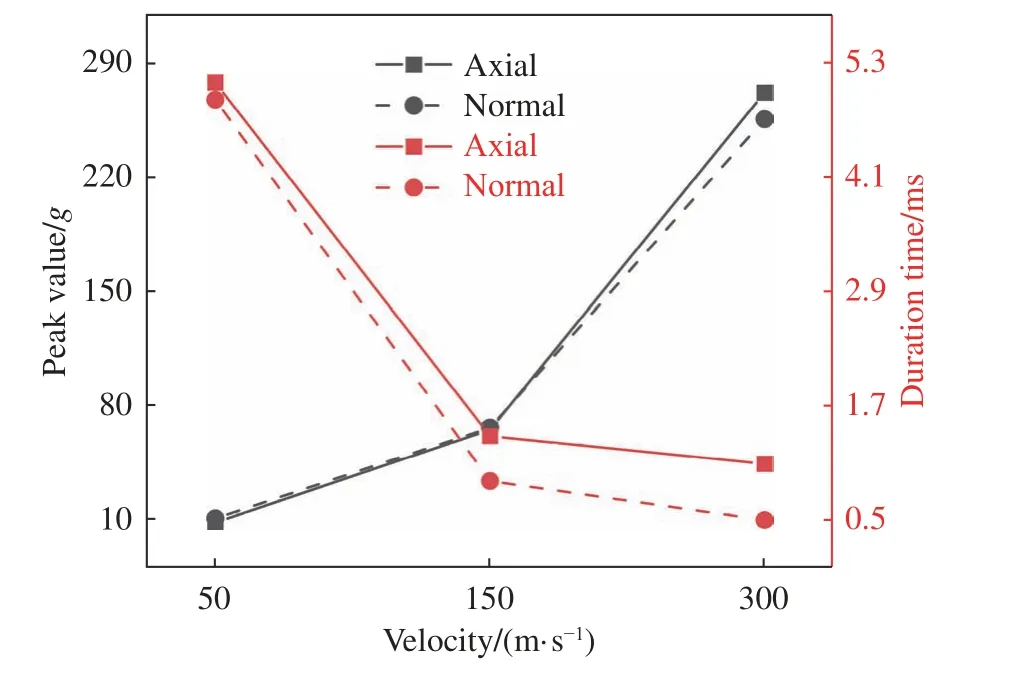
图13 不同速度下轴向和法向载荷峰值及脉宽Fig. 13 Peak values and pulse widths of the axial and normal loads at different speeds

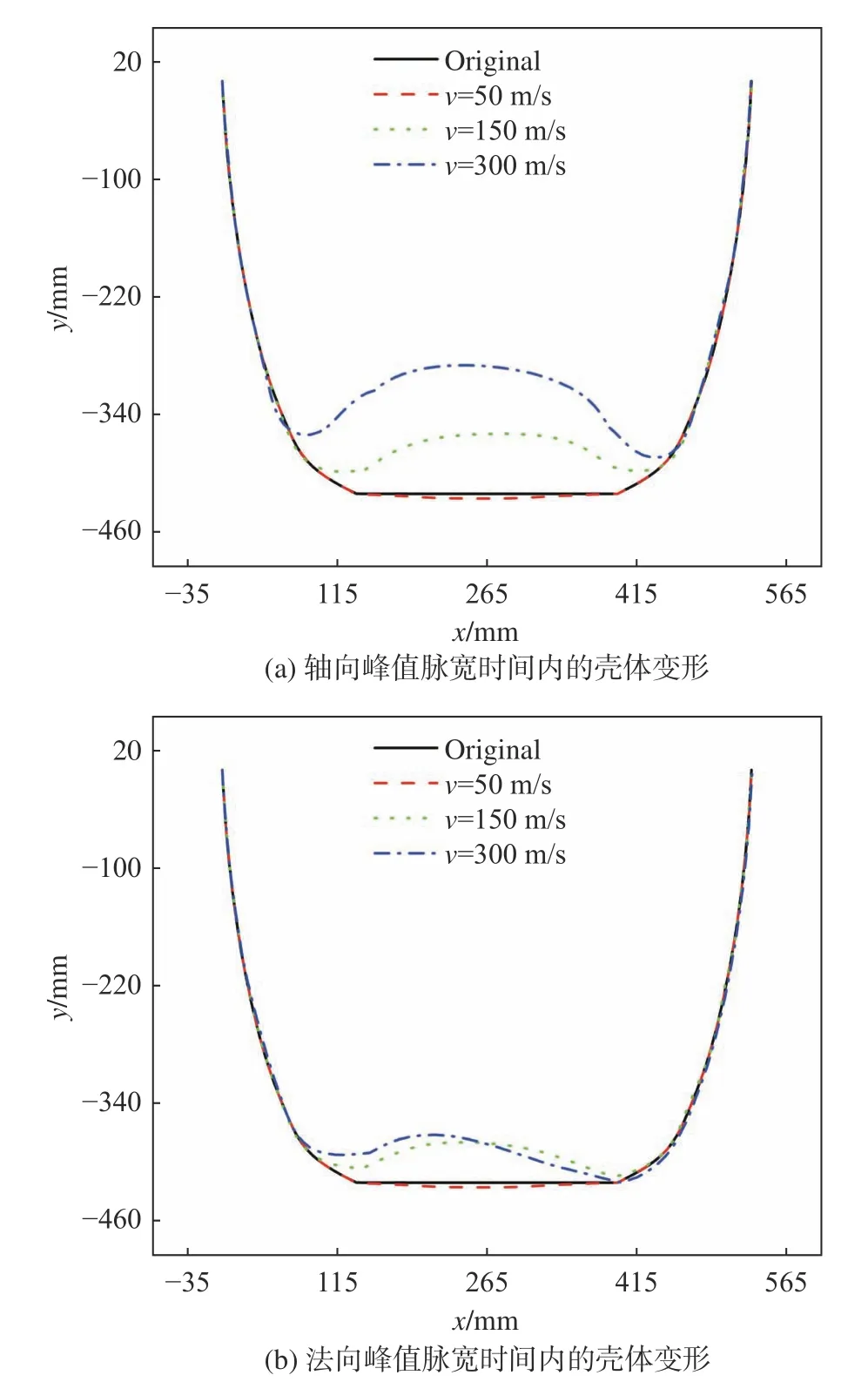
图14 轴向和法向脉宽作用时间内一次波形对壳体变形的影响Fig. 14 Influence of the first wave on the shell deformation under the axial and normal pulses

进一步地，从一次冲击波峰值和脉宽的角度分析壳体厚度对于变形的影响。图15～图17显示了不同入水速度下壳体厚度对于载荷及变形的影响，其中壳体变形为轴向峰值脉宽时间内的变形量。易见3个速度下壳体变形均随壳厚增加而减小。由图15可知，当入水速度较低时（50 m/s），轴向和法向载荷峰值随壳厚增加而增大，轴向和法向脉宽随壳厚增加而减小。当壳厚从5 mm增大到10 mm时，法向峰值增大了1.689g，轴向脉宽减小了2.01 ms，脉宽的变化比峰值更加明显。可得出低速时，当增大壳厚，结构主要通过减小脉宽来抑制变形。

图15 入水速度50 m/s时壳厚对载荷及变形的影响Fig. 15 Influence of shell thickness on the load and deformation at the velocity of 50 m/s

由图16可知，当入水速度为150 m/s时，轴向和法向载荷峰值均随壳厚增加而减小。当壳厚从5 mm增大到10 mm时，轴向峰值减小了7.107g，轴向脉宽增大了0.39 ms，壳厚对于峰值的影响大于脉宽，且可得出随入水速度升高，增大壳厚时，结构主要通过减小峰值来抑制变形。

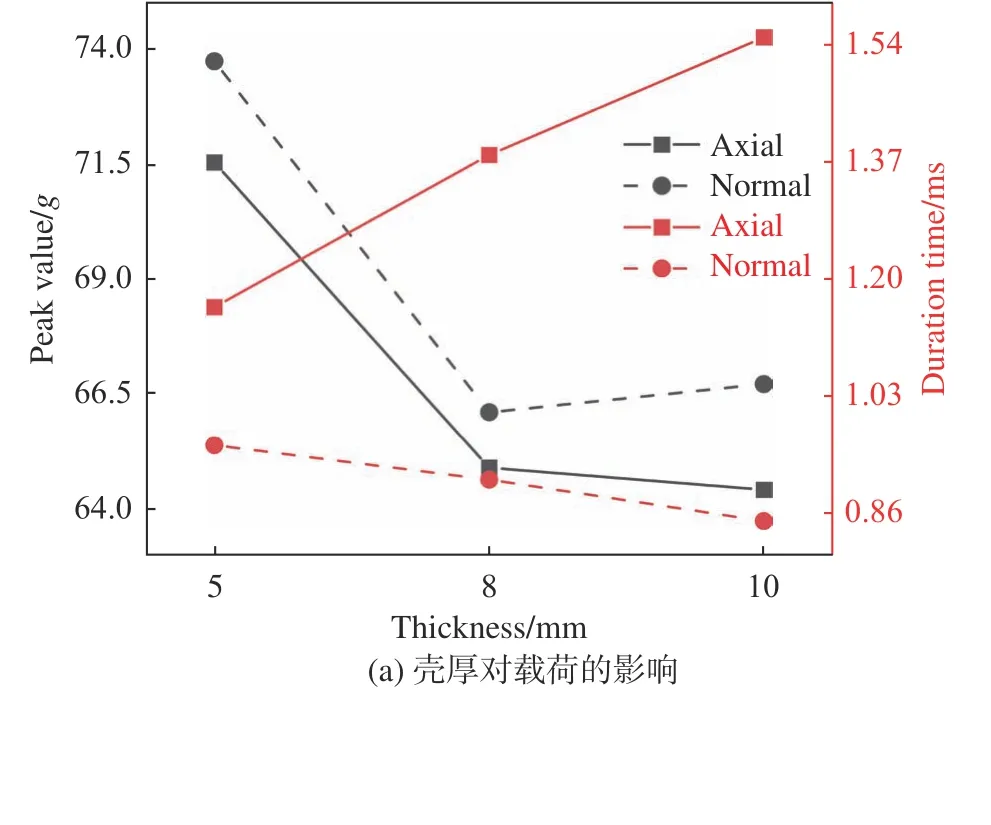
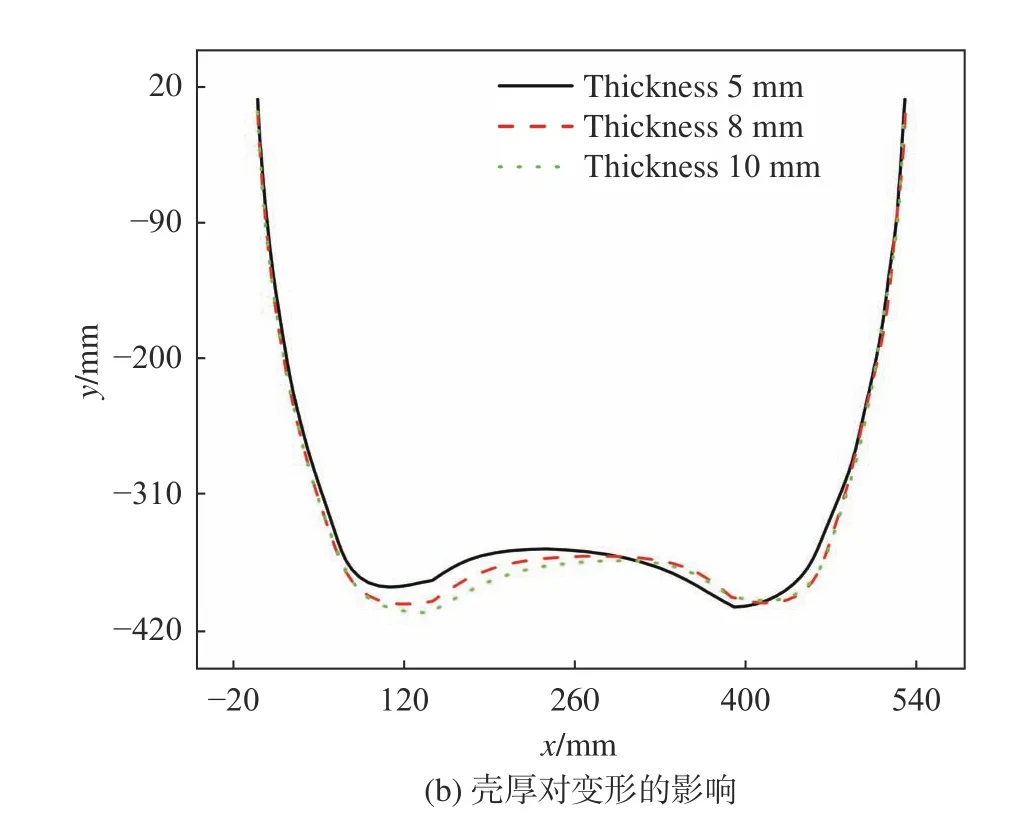
图16 入水速度150 m/s时壳厚对载荷及变形的影响Fig. 16 Influence of shell thickness on the load and deformation at the velocity of 150 m/s

由图17可知，当入水速度较高时（300 m/s），壳厚从5 mm增大到10 mm，轴向峰值减小了22.858g，轴向脉宽减小了0.2 ms，壳厚对于峰值的影响远大于脉宽。增大壳厚可有效减小变形量，但8 mm和10 mm壳厚对变形的抑制效果较为接近。说明航行器以较高速入水时，单纯增加壳厚已不足以抑制撞水初期（一次峰值脉宽时间内）的壳体变形。

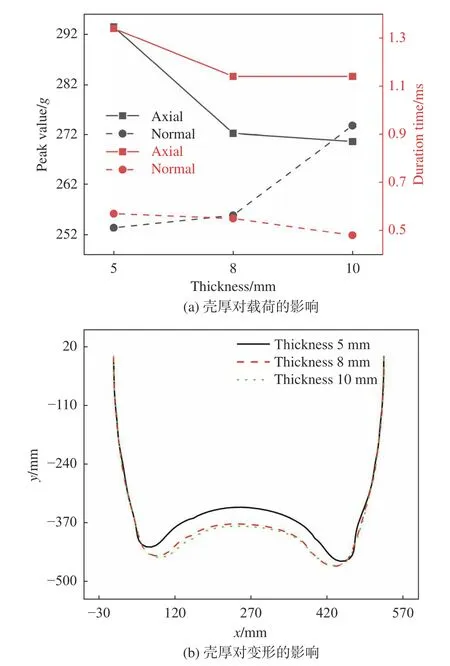
图17 入水速度300 m/s时壳厚对载荷及变形的影响Fig. 17 Influence of shell thickness on the load and deformation at the velocity of 300 m/s

为了分析入水角度对于载荷和变形的影响，图18对比了入水速度150 m/s下不同入水角下的轴向和法向载荷峰值及脉宽。当入水角增大，轴向载荷峰值逐渐增大，而轴向峰值脉宽逐渐减小，法向载荷峰值及脉宽均逐渐减小。由图18（a）可知，入水角60°时，壳体厚度对于轴向脉宽的影响大于载荷峰值；入水角90°时，壳体厚度对于轴向载荷峰值的影响大于脉宽。由图18（b）可知，当入水角增大时，法向分量逐渐减小，因此壳厚对于法向分量的影响也逐渐下降。图19对比了3种壳厚下，入水角度对于壳体变形的影响，其中入水速度均为150 m/s，壳体变形均为轴向载荷峰值脉宽时间内的变形量。随着入水角增大，变形量逐渐减小，且变形不对称性逐渐降低。壳厚为5 mm时，入水角60°和70°的变形量较为接近，入水角80°和90°的变形量较为接近。壳厚为8 mm和10 mm时的变形结果较为接近，入水角60°的变形量较大，增大入水角后，变形量较为接近。可得出，增大壳体厚度可改善入水角度对于变形的影响。

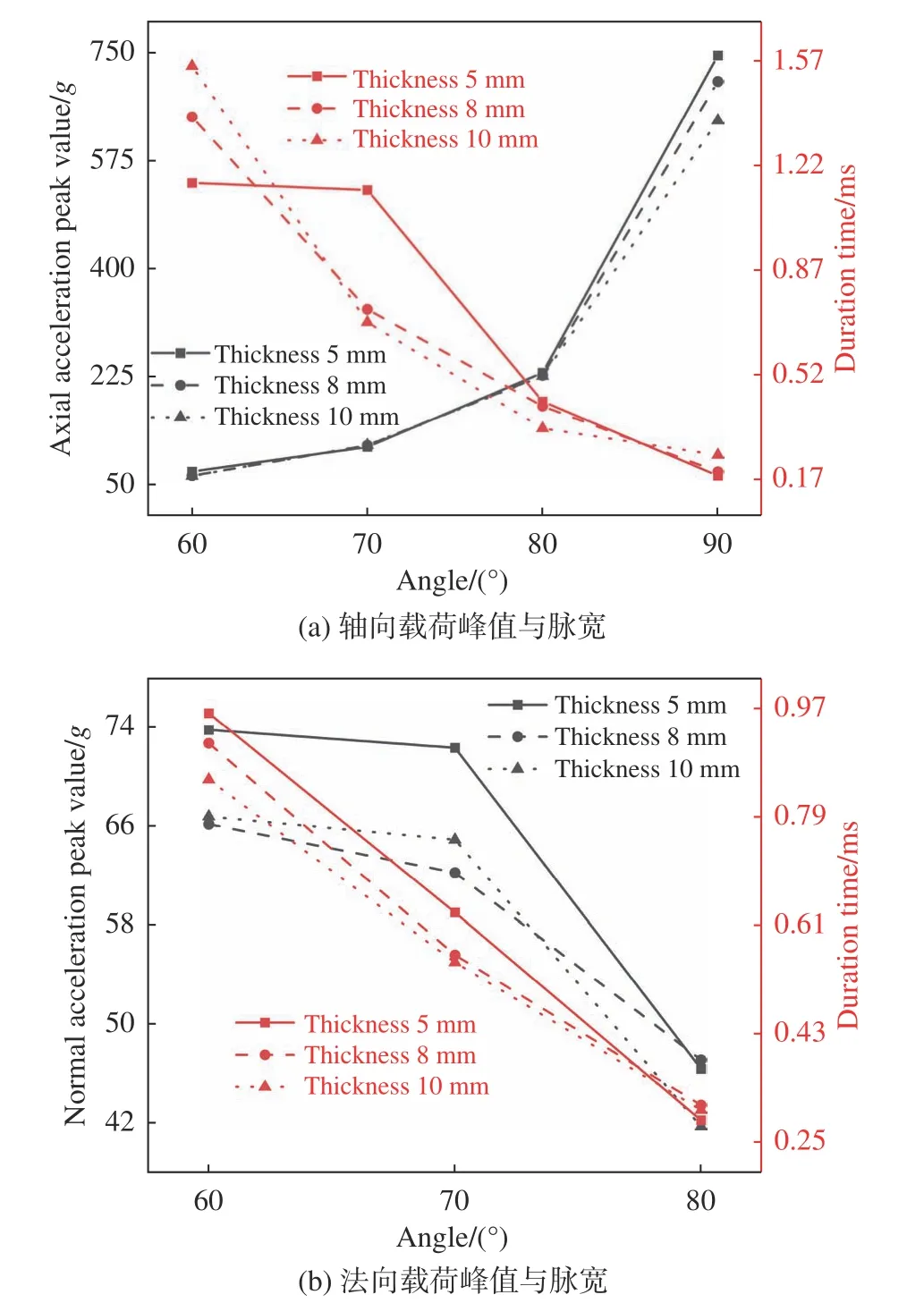
图18 不同壳厚下入水角度对载荷峰值及脉宽的影响Fig. 18 Influence of incident angle on the peak load and pulse width under different shell thickness

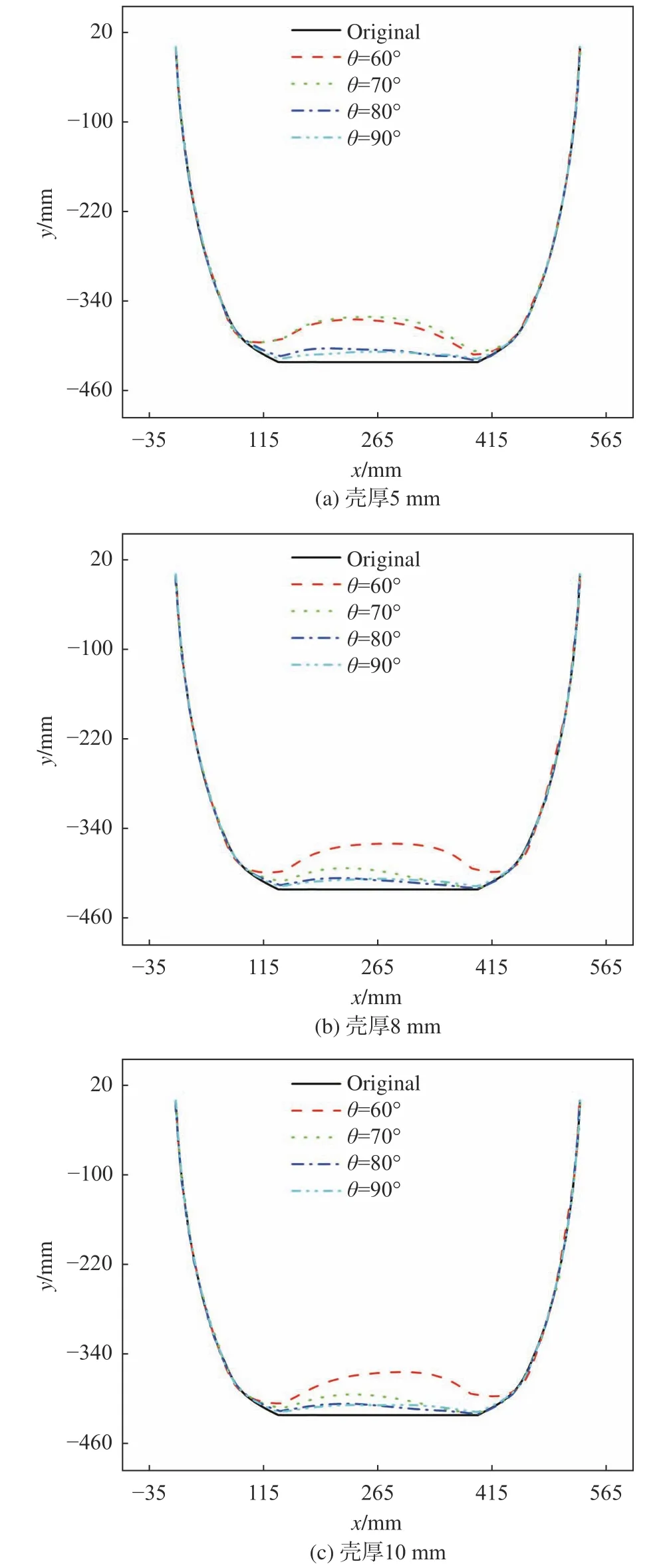
图19 不同壳厚下入水角度对壳体变形的影响Fig. 19 Influence of incident angle on the shell deformation under different shell thickness

2.2 变形模式分析

观察图15～图17可知，壳体存在多种变形形状，下面将通过对变形区域压强、应力及应变的分析，获取航行器高速撞水阶段的壳体变形模式。

图20显示了航行器头部内侧的压强云图及对应时刻的壳体变形模式，其中入水角60°，入水速度150 m/s，壳体厚度8 mm。将壳体头段变形的内凹中心范围记为区域A，将内凹的边缘处记为区域B，将位于变形区边缘的卷曲范围记为区域C。

图20 不同时刻头部内侧压强云图及变形模式图Fig. 20 Pressure contours on the head inner side and the deformation modes at different time instances

观察云图可知，压强相对于纵平面（xOy平面）对称。在整个变形区域中，区域C因受弯矩和挤压的双重作用表现为卷曲压缩，因此压强最大。而内凹区（区域A和区域B）压强为负值，分析为航行器撞水后，壳体前端面受水的冲击作用开始内凹，此时外表面受压缩而内表面受到拉伸作用，因此内凹区的内表面压强为负值。同时，受斜入水影响，区域B的y＋方向的压强绝对值大于y－方向，使得壳体内凹变形向y＋方向偏斜。

在航行器撞水过程中，壳体首先出现内凹变形，即区域A；然后在流体的持续冲击和挤压下，区域B壳体由初始弯曲状态被拉伸，使内凹区域逐渐扩张；在内凹区扩张的同时，区域C的壳体将受到卷曲压缩作用，并逐渐向区域B过渡，转为受拉伸作用，先后经历压缩与拉伸两个相反方向力的作用使得此处的结构更加脆弱。结合图17（b）分析可知，当壳体厚度过小（5 mm）时，卷曲变形将来不及过渡到拉伸区域从而在原卷曲区域x－方向附近形成另一个反向卷曲区域，最终区域C将出现一对方向相反的卷曲对，呈S形，如图21所示。

图21 区域C卷曲对Fig. 21 Curl pairs in area C

为了进一步对内凹区域的变形状态进行分析，在内侧平面布置了如图22所示的7个监测单元（E1～E7）。

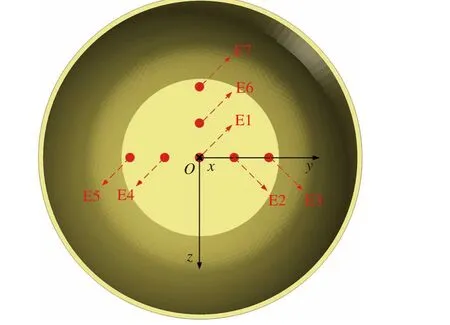
图22 监测单元位置Fig. 22 Locations of the monitoring elements

监测单元的压强时域变化如图23所示，监测单元在撞水瞬间受到外侧单元挤压，出现短暂正向压力值，然后因壳体内凹而受拉伸作用，表现为负值，并在1.5 ms左右达到负峰值后迅速趋于稳定。图23（a～c）分别对比了y＋方向、y－方向和z－方向的单元压强，可发现区域A边缘处的压强绝对值明显大于内侧。图23（d、e）对比了区域A中部和边缘处的单元压强，可发现区域A的y－半区的压强绝对值大于y＋半区。可得出，区域A边缘及y－半区为高压区。

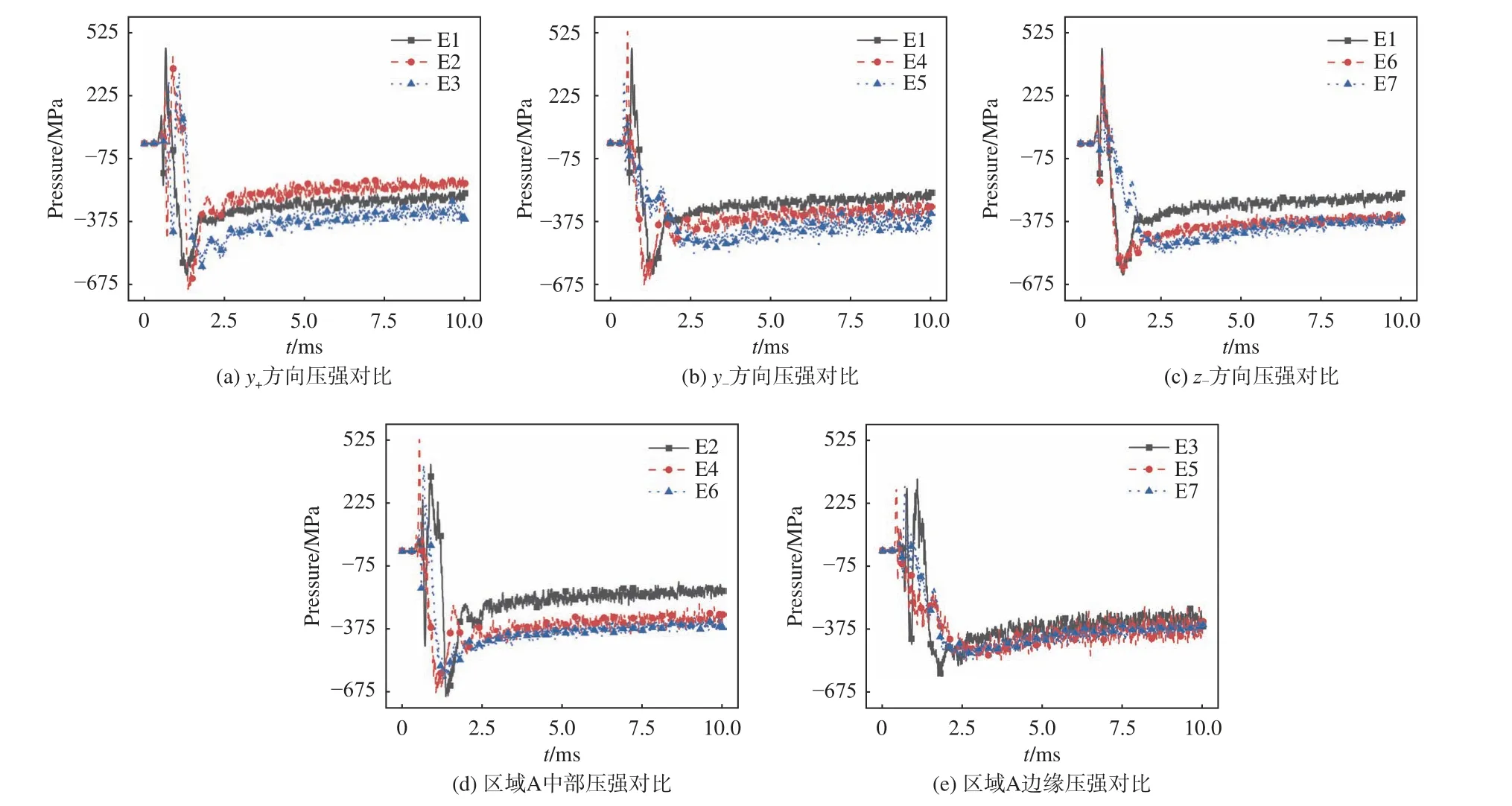
图23 不同方向和区域单元压强对比Fig. 23 Comparison of pressure on elements in different directions and regions

监测单元的应力时域变化如图24所示，应力在撞水瞬间产生波动后迅速趋于稳定，并可得到与压强类似的结论，即区域A的y－半区的应力大于y＋半区，并且区域A边缘处的应力值明显大于内侧，说明区域A边缘处为应力集中区域，且y－半区为高应力区域。上文对压强和应力的分析揭示了变形的潜在方向，高压与高应力反映了该位置变形需要更高的能量，即同等能量下y－半区变形小于y＋半区。通过压强和应力得到了区域A的变形趋势，还需进一步开展应变分析以确定该变形趋势的内因。

图24 单元有效应力对比Fig. 24 Comparison of effective stress on the elements

有效应变反映变形的弹塑性状态，而有效塑性应变显示变形的塑性应变累积。从图25和图26可发现区域A从中心到边缘处，应变值逐渐增大，塑性应变在应变中占据了主导，但弹性应变也起到了一定的作用。位于y－方向上的E4单元的弹性应变抑制了总应变的增长，而位于y＋方向上的E2单元的弹性应变加剧了总应变的增长，导致了y＋方向的变形略大于y－方向，这是航行器斜入水内凹变形非对称性的内在原因。

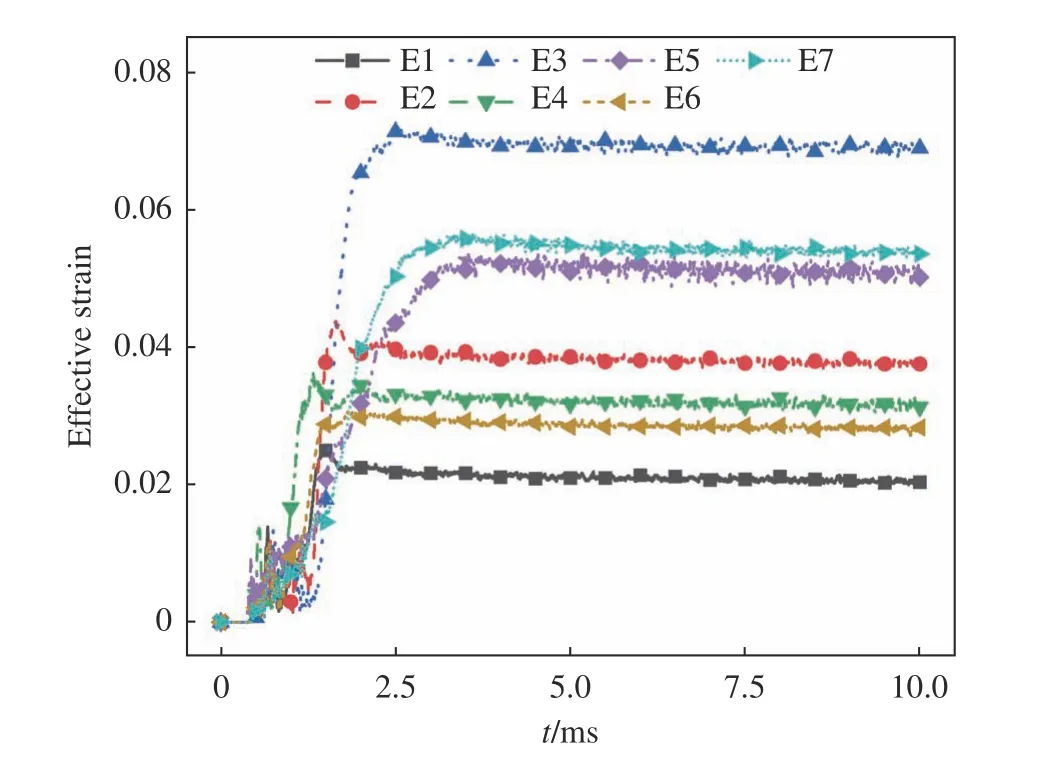
图25 单元有效应变对比Fig. 25 Comparison of effective strain on the elements

图26 单元有效塑性应变对比Fig. 26 Comparison of effective plastic strain on the elements

取位于y＋方向的单元E3进行入水速度与壳体厚度对变形模式的影响分析。图27为v= 50 m/s时壳厚对于E3单元应变的影响。壳厚5 mm时结构同时存在弹性和塑性应变，增大壳厚后，结构只存在弹性应变，此时变形模式如图28所示。壳体区域A在上凹和下凸间不断转换，由于区域A一直受到水的冲击作用，下凸幅值远小于上凹幅值，这也对图15（b）中出现的下凸变形进行了解释。

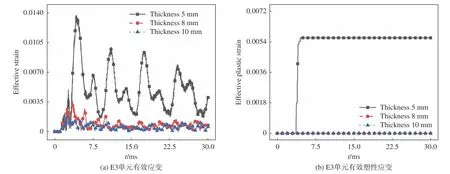
图27 入水速度50 m/s时壳厚对E3单元应变的影响Fig. 27 The influence of shell thickness on the strain of element E3 at velocity of 50 m/s

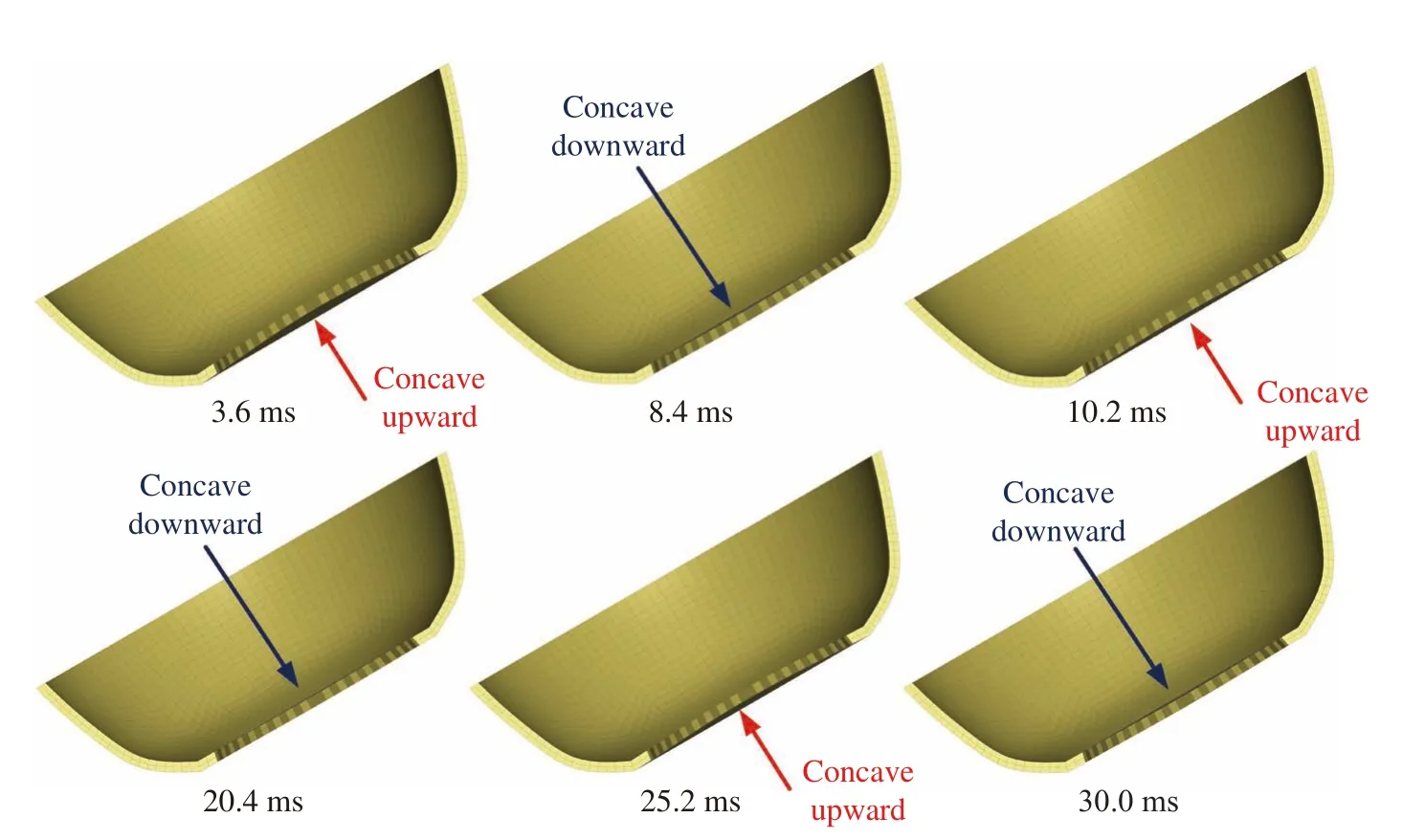
图28 弹性变形下壳体头部变形模式Fig. 28 Deformation mode of the shell head under elastic deformation

图29和图30分别为入水速度150 m/s和300 m/s时壳厚对E3单元应变的影响。观察可发现，入水速度升高后，有效塑性应变与有效应变接近，此时塑性变形占据主导。此外，应变值随壳体厚度增加而增大，这说明增加壳厚可有效提升该位置的变形能力，而变形为壳体吸收冲击能量的一种形式，因此可得出，增加壳厚可提升区域A壳体对入水冲击能量的吸收能力。在上文对壳体变形模式的分析中，区域A、B和C分别具有各自的变形模式且变形依次出现，因此当区域A因增加壳厚吸收了更多的入水冲击能量，而总冲击能量不变时，则必将导致区域B和C的变形量减小。这是增加壳厚而总变形量减小的内在原因。

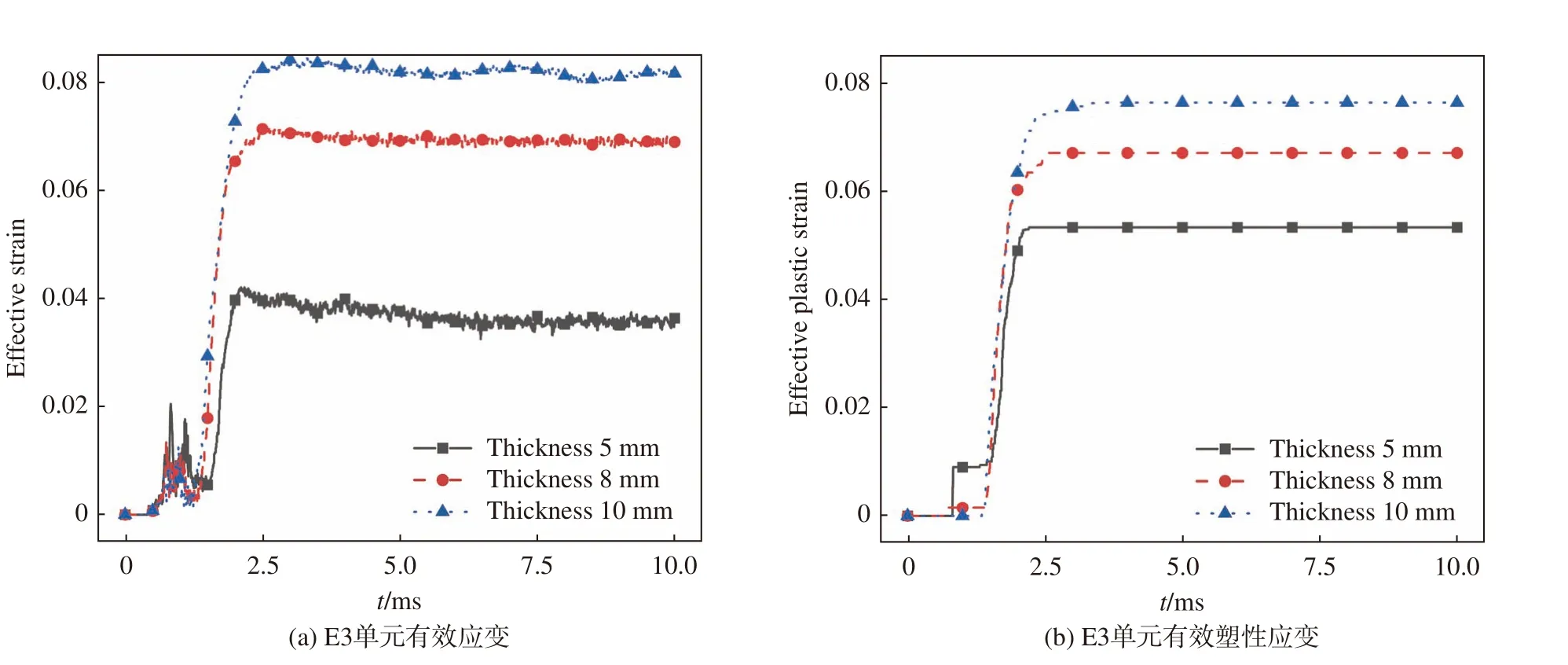
图29 入水速度150 m/s时壳厚对E3单元应变的影响Fig. 29 Influence of shell thickness on the strain of element E3 at the velocity of 150 m/s

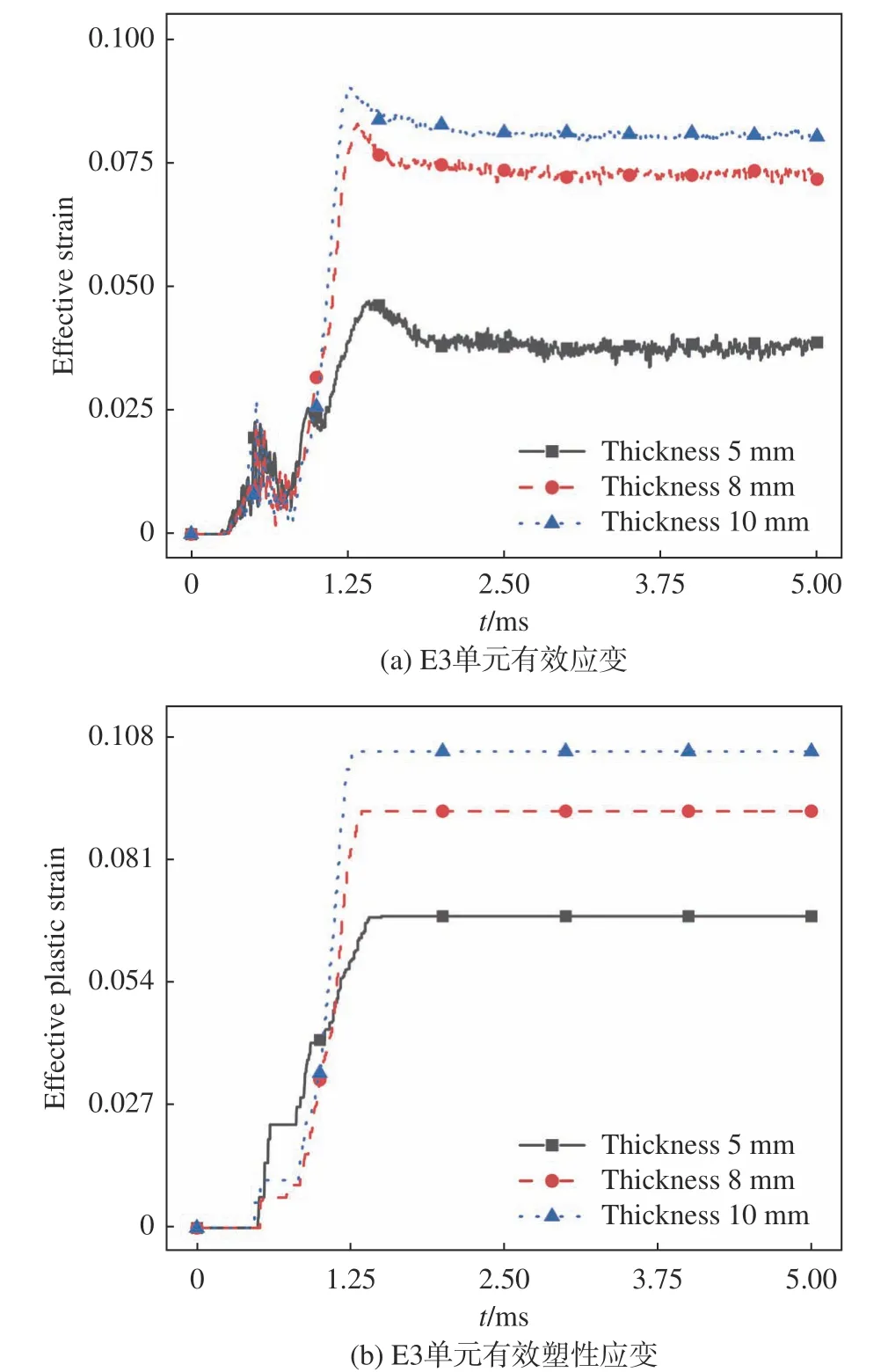
图30 入水速度300 m/s时壳厚对应变的影响Fig. 30 Influence of shell thickness on the strain of element E3 at the velocity of 300 m/s

3 结论

本文使用S-ALE方法开展了航行器高速入水撞水阶段壳体所受冲击载荷及变形相关研究，分析了载荷与变形的关联性，获取了壳体变形模式及变形机理，并分析了壳厚对壳体变形的影响规律，主要得到了以下结论：

1） 航行器斜入水时，法向载荷受结构内凹大变形影响将急剧增大，载荷峰值和脉宽共同影响着壳体的变形程度，其中“毫秒级”的脉宽对壳体变形也具有较大贡。

2） 入水速度较低时，当增大壳厚，结构主要通过减小脉宽来抑制变形；入水速度较高时，当增大壳厚，结构主要通过减小峰值来抑制变形。高速时壳厚对于变形的抑制效应减弱，增加壳厚可减小入水角度对于变形的影响。

3） 入水速度较低时，变形模式以弹性变形为主，呈现上凹和下凸的不断转换，且壳厚大于 5 mm时只存在弹性变形；入水速度较高时，变形模式以塑性变形为主，依次出现内凹变形区域A、拉伸区域B和卷曲压缩区域C，区域C逐渐向区域B过渡，且区域C在小壳厚时将出现S形卷曲对。

4） 航行器斜入水时内凹变形向y＋方向偏斜，导致变形非对称的内在机理为弹性应变与塑性应变的叠加效应。增加壳厚可提升区域A壳体对入水冲击能量的吸收能力，当总冲击能量不变时，区域B和C的变形量减小，此为增加壳厚而总变形量减小的内在机理。

本文得到的冲击载荷及壳体变形相关结论，适用于直径大于500 mm的薄壁回转体航行器，以入水角度60°～90°、入水速度50～300 m/s入水时撞水阶段的力学过程分析，可为其他条件下的相关研究提供参考。