基于CFD的并列超空泡射弹高速斜入水流体动力特性研究

韩可新，刘海晓，漆 超，陈志宏，吕续舰，*

(1. 南京理工大学 能源与动力工程学院，南京 210094；2. 海军研究院，北京 100061)

0 引言

单运动体以一定速度从空气进入水中，整个多相流动过程包括入水冲击，开空泡，空泡扩张、闭合以及溃灭，表现出明显的不稳定性、非线性特征[1]，易导致运动体失稳。针对单运动体入水问题的研究，早期学者多关注球体低速垂直入水现象的演化过程。在19世纪末Worthington等[2]基于闪光摄像技术研究了球体入水空泡发展规律，Truscott等[3-4]基于高速摄像系统，给出了在不同转速和入水速度下球体的空泡形态演化规律。此外，还研究了球体自身物性（质量、直径和表面粗糙度等）的改变对其入水过程受力特性的变化影响。如Speirs等[5]通过试验方法研究了邦德数、韦伯数以及球的接触角对球体入水特性的影响，发现球体的空泡形态与接触角密接相关。随着研究不断深入，数值计算方法逐步成为研究入水空泡流动的重要手段。Abraham等[6]采用数值仿真方法研究了球体入水过程的受力特性，发现球体的阻力系数与球的速度、表面张力以及雷诺数等参数无关。魏英杰等[7]采用试验与数值模拟结合的方法，发现超弹性球体在入水后具有独特的球体变形行为和空泡形态。对于球体的研究有利于深入了解入水过程中的流动演化机理，但实际海战中的武器外形是复杂多样的，因此针对圆柱体[8-9]、细长体[10-11]、楔形体[12]等几何模型的研究对于推动超空泡武器的发展具有重要意义。

上述研究主要围绕单运动体入水展开，而近些年为提高武器的打击能力，集群作战的新型手段愈发重要，多体入水研究相继展开。多体跨介质入水过程中，不可避免地存在多体间相互干扰作用，使得运动体入水过程的流体动力特性更加复杂。因此，对多体跨介质过程中流场、受力以及多体间扰动特性开展研究具有重要意义。多运动体连续入水依据时空效应可分为串行入水和并行入水。针对串行入水问题的研究，Rabbi等[13]发现尾球入水冲击加速度取决于第一个球入水产生的空泡状态，同时也受到两球入水时间间隔的影响。Lyu等[14-15]分析了不同时序差下串行球体连续入水过程的空泡闭合形式及受力特性，研究发现串行入水过程中后序物体的流体动力特性主要受前序物体产生空泡流的影响。

针对多运动体并行入水问题研究，Shademani等[16]通过对比不同楔角和入水角，给出了每种工况下楔形体的受力特性。Hasheminasab等[17]通过试验方法发现非对称楔形体的垂直面受空气夹带的影响，其压力显著低于非垂直方向的压力。Lu等[18]通过数值仿真方法研究了时间间隔对双弹异步并行入水过程空泡形态特征和减阻性能变化的影响。王旭和吕续舰[19-20]针对不同横向间距的球体开展了同步并行入水试验，详细描述了不同间距下入水空泡演化、尾迹以及飞溅形态。Wang等[21]利用高速摄像系统和CFD数值仿真技术开展了不同时间间隔和横向距离下双球并联垂直入水试验和数值研究。张鹤[22]基于CFD方法对并行圆柱体高速入水过程进行仿真研究，详细分析了多相流场的分布规律，同时开展并行射弹入水试验研究，进一步揭示了射弹同步和异步入水的空泡演化和弹道特性。研究发现，横向间距是影响并行入水过程的重要因素。卢佳兴等[23-24]基于高速摄像技术的光学测量方法，对低速圆柱体并联入水过程中空泡演化特性开展试验研究，分析了不同弗劳德数、轴线间距对圆柱体同步并联入水的影响。路丽睿等[25]基于高速摄像方法开展圆柱体低速并联入水试验研究，分析了入水速度对并联入水过程圆柱体运动特性的影响以及空泡演化过程对圆柱体运动的影响机理。闫雪璞等[26]基于CFD方法对超空泡射弹异步并联入水过程展开研究，分析不同纵向间距对异步射弹的流场特性与运动特性。

综上所述，目前针对入水问题和多体干扰研究主要集中于楔形体、球体和圆柱体入水，同时多数研究主要聚焦于运动体低速垂直入水问题。而涉及高速超空泡射弹并行入水问题的研究相对较少，且较于异步并行入水，弹间干扰对同步并行入水过程中的空泡演化规律和受力特性的影响更为显著。因此，本文基于CFD方法对并行射弹高速斜入水过程进行数值仿真，采用VOF模型、6DOF模型和重叠网格技术等建立并列弹高速入水模型，重点分析并列弹跨介质过程的空泡演化规律和受力特性。同时，通过与相同工况下单个弹体的流体动力特性对比分析，探究不同射弹间距下并列弹跨介质入水过程的干扰机理。

1 数值方法及验证

1.1 基本控制方程

基于Navier-Stokes方程，采用均质平衡多相流方法，引入VOF多相流模型描述水、水蒸气和非凝结性气体等混合物组成的多相流场效应。通过求解质量守恒方程和动量方程分析流场结构。质量守恒方程为：

式中：t表示时间；xi为笛卡尔坐标分量，ui为笛卡尔坐标下的速度分量，其中i= 1、2、3；ρm为混合介质密度。

动量守恒方程为：

式中，µm为动力黏度，µt为湍流黏性系数。

1.2 湍流模型

SSTk-ω模型能够有效将近壁面区域和远场区域的无关流动形式融合，具有更大的非线性程度。同时SSTk-ω模型在大逆压梯度和分离流动的模拟中表现良好，可以很好地显示近壁面自由流动情况。鉴于此，本文采用SSTk-ω模型模拟并列弹高速入水的运动状态及流场结构特征。

湍动能黏度与湍动能k和比耗散率ω有关，方程如下：

式中，ω=ε/(Cµk)；γ=min[a*,a1ω/(SF)]，其中S、F分别代表用户定义源项和混合函数，a*为低雷诺数修正系数，经验系数。

湍动能输运方程和比耗散率输运方程为：

1.3 空化模型

本文采用Z-Wart空化模型进行数值计算，该模型适用于计算空泡流动的非定常过程。Z-Wart空化模型用修正的Rayleigh-Plesset（R-P）方程描述空泡的生长和溃灭时空泡体积变化情况，广义的R-P气泡动力学方程表达为：

式中，RB和pB分别为气泡的半径和泡内压力；ρl和τ分别为液体的密度和液体的表面张力系数；p为远场压力。

1.4 计算模型及网格划分

本文模型如图1所示，该模型由弹头、弹身和弹尾三部分组成，弹体最大直径Dm= 12 mm，全弹长L= 142 mm，头部空化器直径Dc= 4.25 mm，弹体质量m=63.58 g，其中弹尾部对称布置八片尾翼。

图1 用于计算的弹体模型Fig. 1 Projectile model for simulation

两射弹轴线间距为S，使用Dm对其无量纲化，即G=S/Dm。以G= 4为例给出并列弹跨介质入水的计算域模型，如图2所示。沿自由液面水平方向为x方向，法向为y方向，z方向为两弹中心连线方向，原点在两并列弹头中心连线中点处。沿x方向设置计算域长度为10L，沿y方向设置计算域高度为40D，沿z方向设置弹两侧宽为22D。

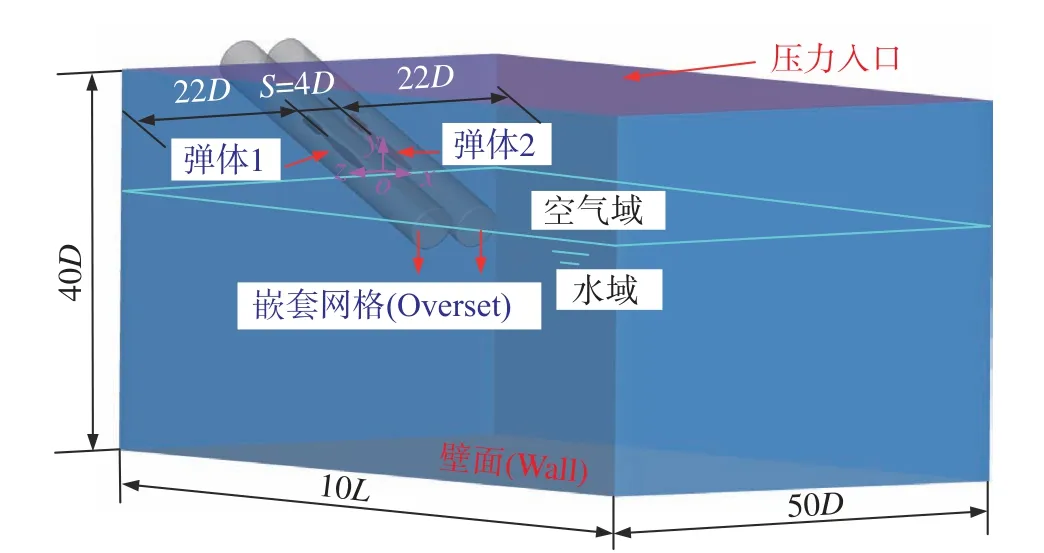
图2 并列弹入水计算域Fig. 2 Calculation domain of parallel-projectile water entries

计算域顶部采用压力入口边界条件，其余壁面均采用无滑移壁面边界条件。求解方法采用非稳态法，时间步长设定为1×10-5s，空间离散格式采用二阶迎风格式，压力与速度耦合采用Coupled耦合求解算法，与Wang等[21]采用的数值计算方法相同。

采用重叠网格方法对射弹和背景域进行网格划分，弹体子网格和背景域网格均采用三维六面体网格。对流动梯度较大的区域以及近壁面进行局部加密，且在弹体表面设置边界层网格。对两弹采用相同的网格划分方法，弹体表面网格如图3所示。图4所示为并列弹高速跨介质入水背景域网格示意图。为满足计算精度需求，对自由液面和弹体运动区域进行局部加密。同时为提高网格质量，背景域网格采用O型网格进行划分。

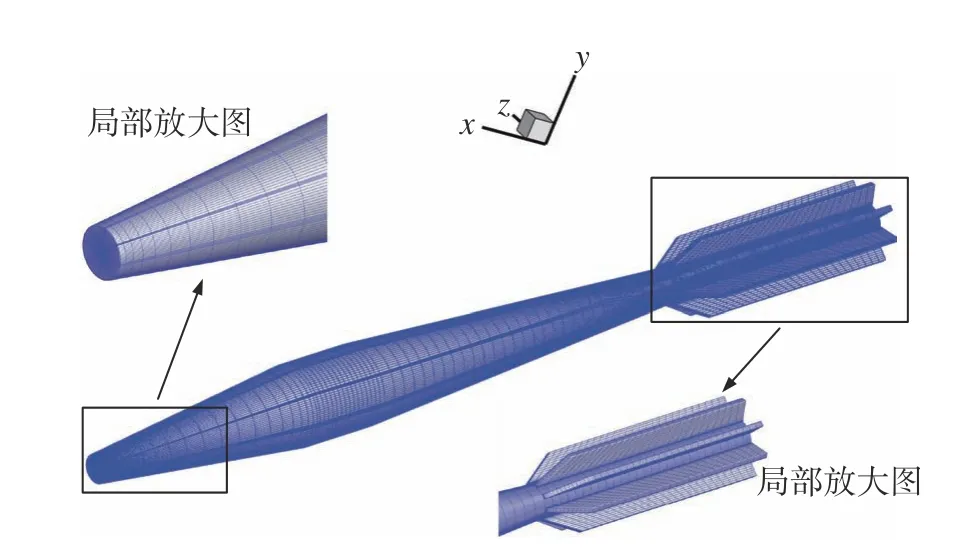
图3 弹体模型网格示意图Fig. 3 Schematic diagram of detailed projectile mesh

图4 背景域及重叠网格Fig. 4 Background domain and overset mesh

1.5 数值方法确认和验证

为确保数值计算模型的稳定性和准确性，开展计算网格收敛性分析，并通过高速斜入水试验和文献[22]多弹水中运动空泡干扰数据对计算模型进行验证。

1.5.1 网格无关性验证

在入水速度U= 450 m/s、入水角θ= 25°和轴线间距G= 4的工况下，开展网格无关性验证。图5为用三套不同稀疏程度的子网格360万（Mesh A）、450万（Mesh B）和520万（Mesh C）计算得到的弹体轴向力系数CA结果。坐标定义为沿弹体轴线方向为轴向，垂直于弹体轴线方向为法向，垂直于轴向、法向方向为侧向。图5显示三套网格下的CA差异主要体现在入水冲击峰值点的不同，采用Mesh A网格计算得到的峰值点较小，且出现的时间较早，而Mesh B与Mesh C网格计算得到的结果基本一致。综合考虑计算精度与计算效率，选择Mesh B网格进行后续并列弹高速入水数值仿真。

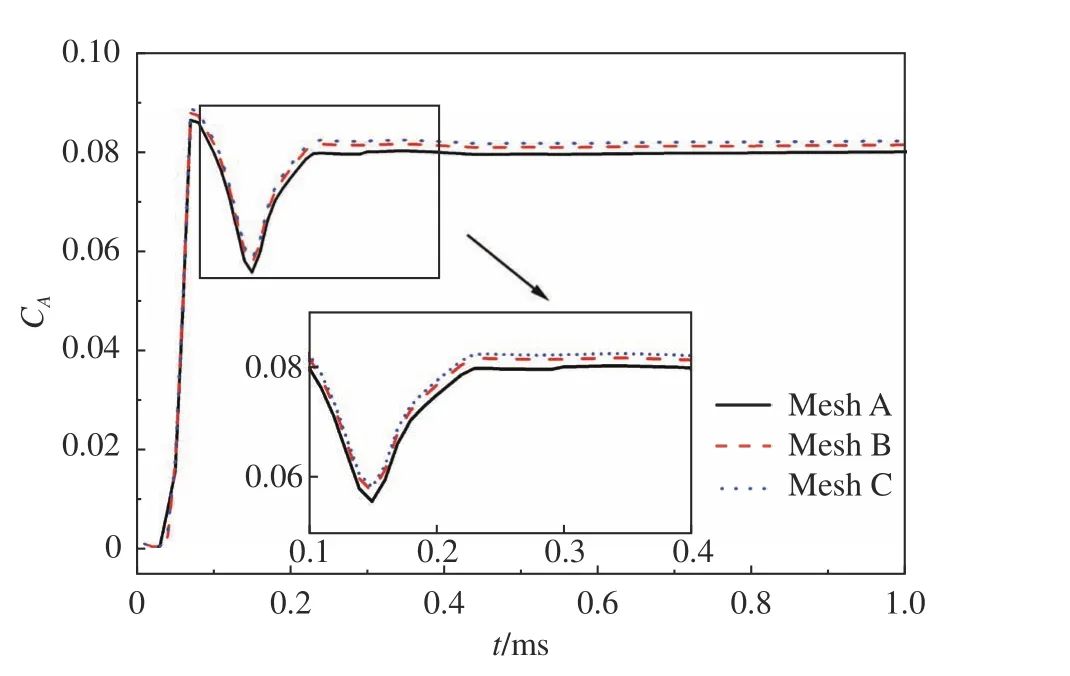
图5 网格无关性验证Fig. 5 Mesh independence verification

1.5.2 高速斜入水数值方法验证

为验证高速入水计算模型，本文开展高速射弹跨介质入水试验。试验系统示意图如图6所示，主要由水箱、高速相机系统、发射系统以及数据采集系统组成，其中水箱尺寸为2000 mm × 3000 mm × 2000 mm。为防止射弹入水后对水箱玻璃侧面产生破坏，在水箱侧部铺设缓冲钢板。试验发射系统由发射架、枪架、12.7 mm弹道枪、激发电磁装置以及触发装置组成，通过声控触发装置控制高速相机的采集，高速相机拍摄帧率为6400帧/s。

所采用的数值计算模型和网格划分情况如图7所示。单个弹的初始速度和入水角分别为270 m/s和20°。图8为单个弹空泡形态仿真与试验结果对比情况，可以看出试验结果和仿真结果基本吻合。再由图9不同时刻弹尾处空泡直径的仿真值、文献[27]经验公式值和试验值的对比情况，可以得出仿真值相对于经验公式值和试验值结果误差分别为2.42%～3.98%和1.76%～2.21%。

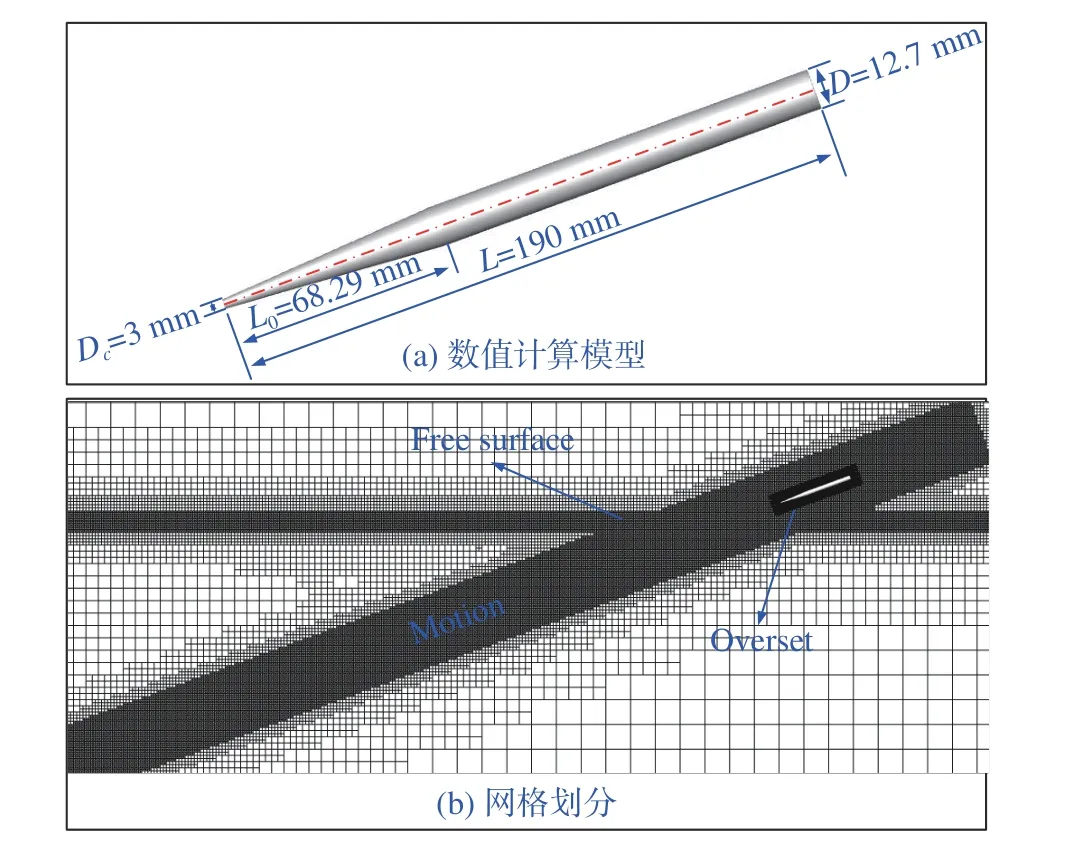
图7 单个弹入水计算模型及网格划分Fig. 7 Computational model and grid details for single-projectile entering water

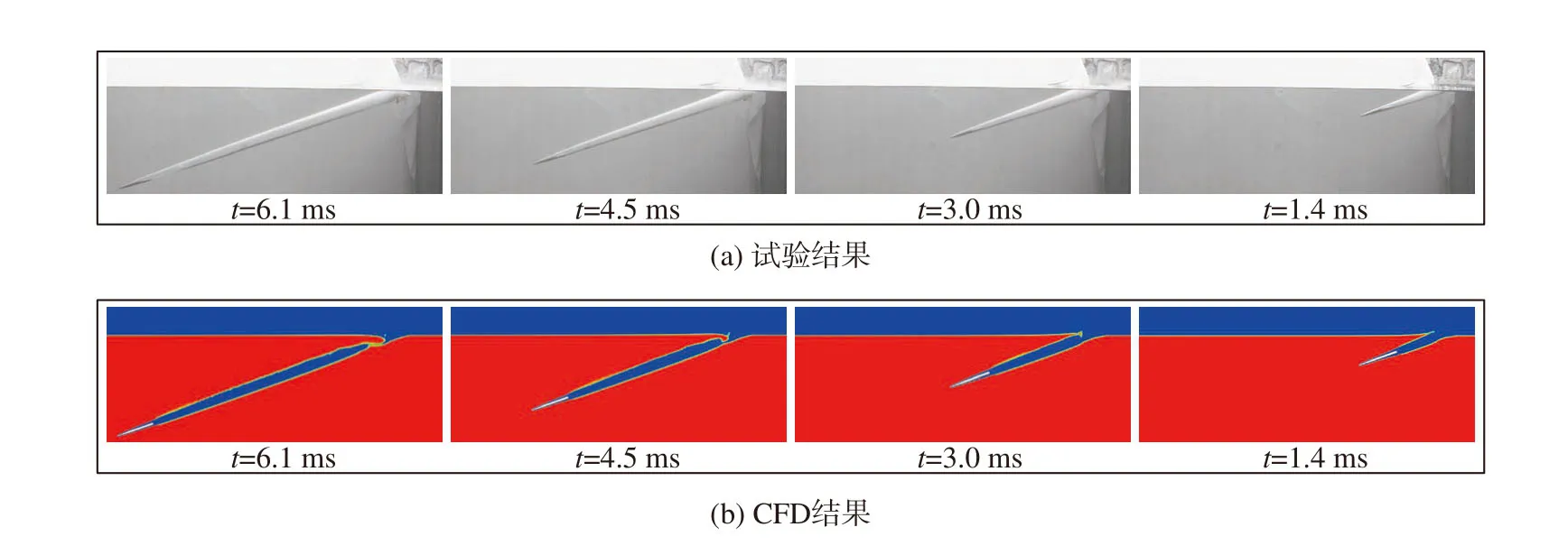
图8 单个弹空泡形态试验与仿真结果对比Fig. 8 Comparisons between experimental and simulated results of single-projectile cavity shape

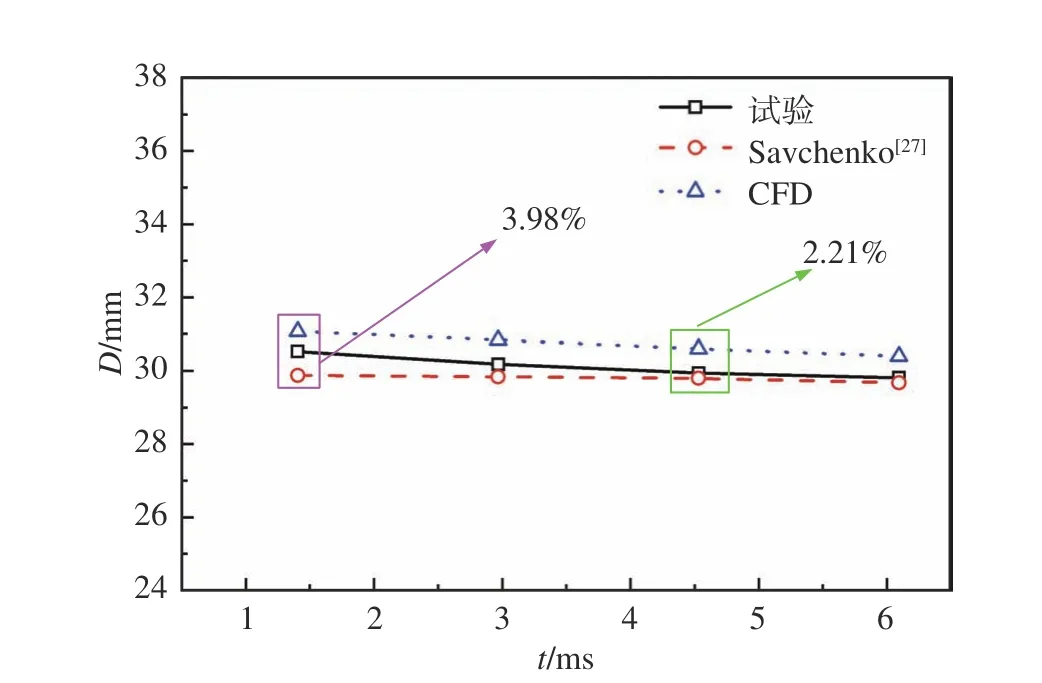
图9 单个弹尾处空泡直径的试验、仿真和经验公式结果对比Fig. 9 Comparison of experimental, simulated and empirical formulae results for the cavity diameter at projectile tail

用本文数值方法对单个弹的速度和位移进行计算，所得的仿真结果与试验结果进行了对比，结果见图10。从图中可看到单个弹的速度仿真值相对于试验结果的误差约为0.07%～0.19%，位移的仿真值相对于试验结果误差约为0.73%～1.37%，表明用该数值方法模拟高速射弹入水过程的流体动力结果与试验相接近，进而验证了该数值模型的准确性和可行性。

图10 单个弹的速度、位移仿真结果与试验值的对比Fig. 10 Comparison of simulated and experimental results for single projectile velocities and displacements

1.5.3 并列弹水下运动流动干扰数值方法验证

为进一步验证射弹并联运动计算模型，开展并列弹运动仿真研究，对网格划分如图11所示，并与文献[22]中的试验结果对比。图12为多弹空泡形态仿真与试验结果对比情况，可以看出试验结果和仿真结果基本吻合。图13给出了不同时刻弹尾处空泡直径的试验、仿真和文献[27]经验公式计算结果对比情况，可以得出仿真值相对于经验公式计算值和试验结果误差分别为4.51%～6.24%和0.84%～2.22%。基于上述研究，可以看出采用文中所建立数值模型模拟并列弹间相互干扰是可行的。

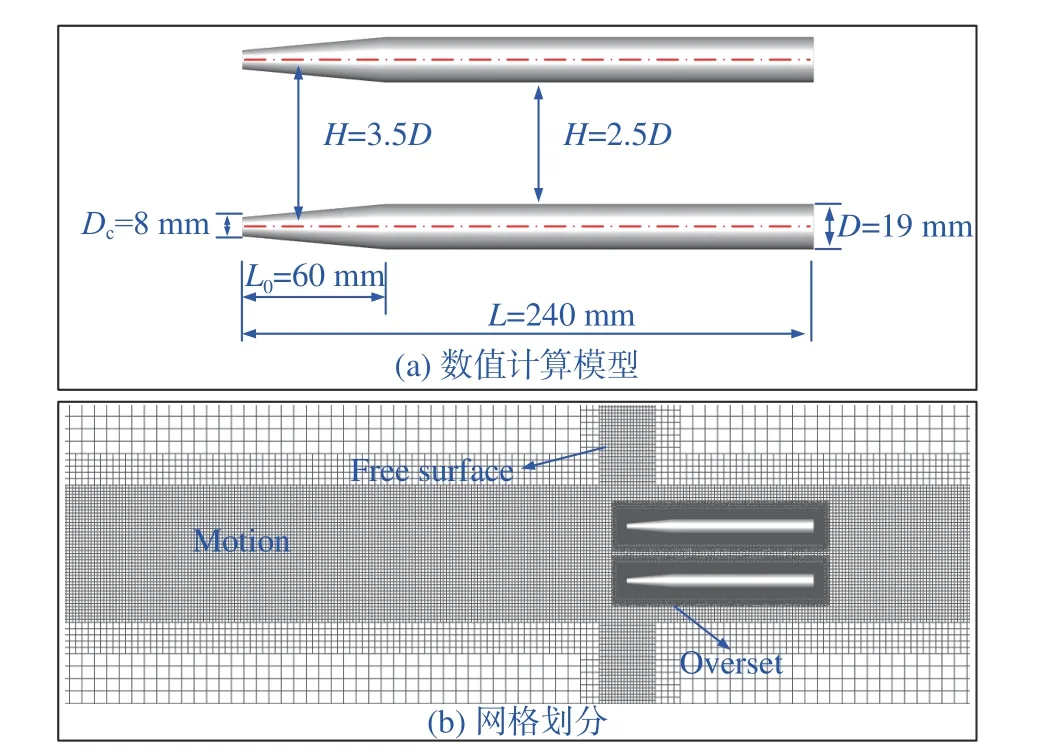
图11 并列弹计算模型及网格划分Fig. 11 Parallel-projectile computational model and mesh

图12 并列弹空泡形态试验与仿真结果对比Fig. 12 Comparison of experimental and simulated results for parallel-projectile cavity shape

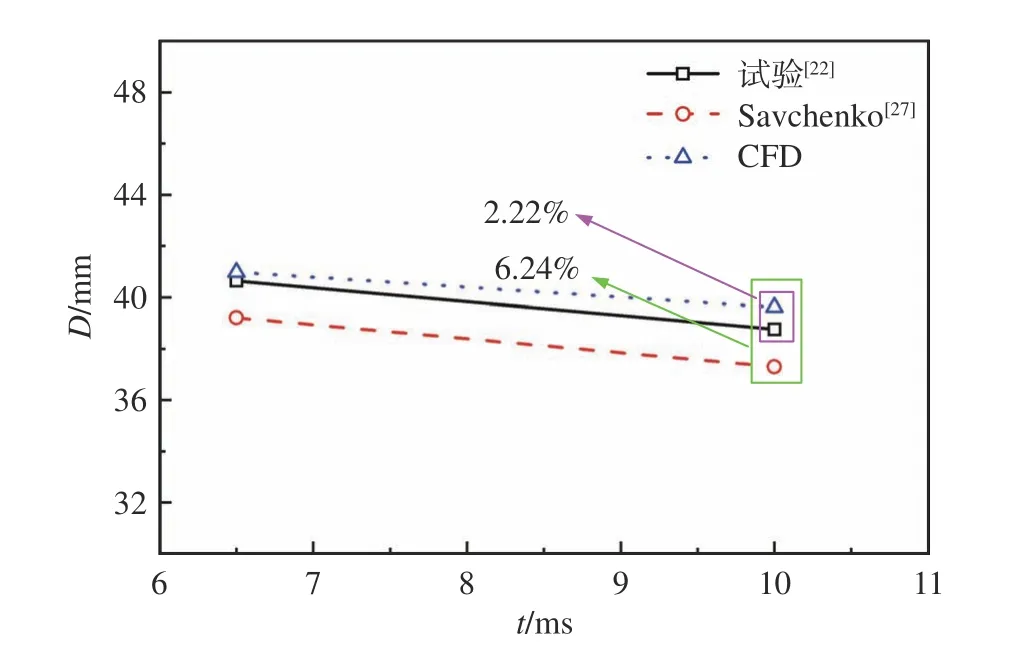
图13 并列弹尾处空泡直径的试验、仿真和经验公式结果对比Fig. 13 Comparison of experimental, simulated and empirical formulae results for the cavity diameter at parallel-projectile tail

2 数值计算结果及分析

并列跨介质射弹高速入水过程中涉及弹间干扰和空泡耦合等问题，导致并列射弹入水过程的流动特性更加复杂。本节通过CFD方法开展入水速度U= =450 m/s，入水角θ= 25°，在轴线间距G= 1.5、2.0、2.5、3.0、4.0等工况下的并列射弹跨介质入水过程研究。重点分析并列弹入水过程的受力特性、流场演化规律和空泡耦合特性，并结合单个弹的情况进行对比分析，明确轴线间距对并列弹跨介质入水过程流体动力特性变化的影响。

2.1 并列弹高速入水空泡演化特性

图14展示了入水过程中空泡形态演化特性， 从图14（a）可以发现在入水初期，单个弹头部高速入水撞击自由液面时，受到从空气相到水相间介质突变产生的巨大冲击载荷，同时与大气压作用下使周围流体获得动能向四周移动。当t= 0.4 ms时，随时间推移单个弹浸没水中，直至被空泡完全包裹。随着射弹入水深度增加，空泡在流体的惯性力、表面张力等相互作用下，其长度、直径处于增大阶段，空泡轮廓呈扩张状态。当t= 1 ms时单个弹入水过程经历了入水冲击阶段、流动形成阶段以及空泡敞开阶段，单个弹空泡形态呈轴对称分布，弹身无沾湿现象发生。与单个弹入水过程相比，在G= 2.0时并列弹入水过程中的空泡形态，较并列弹初始位置呈现出较好的镜面对称，如图14（b）所示。与单个弹入水过程相比，并列弹运动姿态随着入水深度增大发生显著变化，呈现出头部排开，尾部靠拢现象。在开空泡阶段，多弹外侧空泡自由扩张，形成了和单个弹入水过程较为接近的空泡壁面，而多弹内侧空泡由于相互挤压影响导致其发展受限，呈现出非对称性。由于多弹表面内外侧的压差使射弹产生偏转，射弹肩部、尾部和内侧空泡壁面在向对称线方向扩张过程中挤压内侧流体，受压流体在空泡边界附近形成了相对流动，其动能逐渐转变为势能，表现为并列弹间内侧区域发生空泡融合。两弹内侧空泡相互挤压而贴近弹体。随着入水过程的进行，弹体的偏转幅度逐渐增大。由于弹体质心位置更靠近弹头，偏转过程中引起射弹肩部局部沾湿，弹尾撞击空泡内壁，因此会对射弹的运动稳定性产生影响。在G= 2.0时，并列弹入水过程空泡呈对称演化，但在弹间扰动的作用下，并列弹的运动姿态发生显著变化。

图15展示了不同轴线间距下空泡形态，从图15（a）中可以看出，当t= 0.4 ms时入水空泡完全裹弹体，射弹姿态产生显著变化。在G= 1.5时，并列弹肩部和尾部水花之间碰撞较为剧烈，空泡内侧的发展受到限制，外侧空泡仅与周围流体相互作用，导致空泡轮廓沿弹体轴线呈非对称分布。在G= 2.0时，并列弹仍表现出尾部靠拢的姿态变化。随着轴线间距增大至G= 3.0时，并列弹的姿态变化不再显著，并列弹之间干扰作用逐渐减弱，包裹射弹的空泡两侧周围流体发展，沿弹体轴线逐渐呈对称分布，接近单个弹的空泡轮廓。

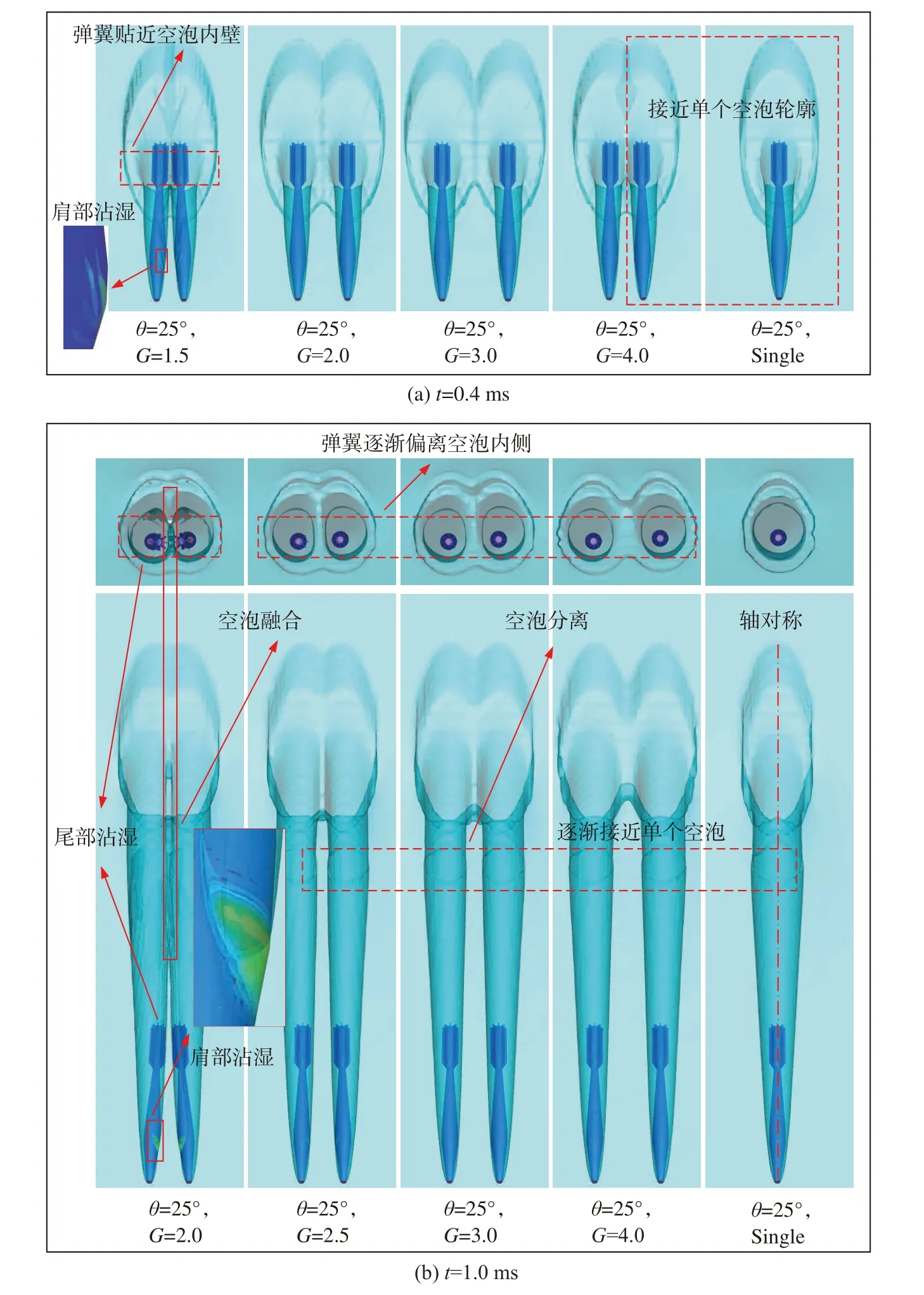
图15 不同轴线间距下空泡形态Fig. 15 Bubble morphology at different axial distance

进一步对射弹水下空泡形态进行分析，当t= 1 ms时并列弹入水空泡处于敞开阶段，如图15（b）所示。当轴线间距G= 1.5时，并列弹产生剧烈碰撞且偏转幅度很大，导致空泡轮廓出现断裂现象。在G= 2.0时，可以看到射弹肩部、尾部受到空泡两侧不对称的水动力作用，撞击空泡内侧壁面，内侧壁面变得粗糙，并列弹肩部、尾部均出现明显沾湿。同时，并列弹头部发生显著分离且内侧空泡上端出现融合现象，存在复杂的空泡耦合作用。

在G= 2.5时，并列弹肩部、尾部偏离内侧空泡壁面。当轴线间距增大至G= 4.0时，由于并列弹之间干扰作用逐渐减弱，空泡轮廓以及姿态变化与单个弹入水相接近。因此，并列弹入水过程中轴线间距会影响空泡间的相互干扰，轴线间距越小，干扰越大。在轴线间距小于一定值时，产生的入水空泡内侧壁面会相互碰撞融合；当轴线间距大于一定值时，并列弹间干扰作用消失，与单个弹入水基本相同。

为定量分析高速射弹入水空泡演化，对空泡轮廓尺寸进行无量纲化处理。其中Lc表示空泡长度，L表示弹长，Rc表示空泡半径，R表示弹体最大半径。Dt表示在弹长L处的空泡直径，Dh表示在弹身过渡段Lh=42mm处的空泡直径。图16给出了弹体完全入水（t= 0.4 ms）时不同轴线间距下空泡轮廓。从图中可以看出，在G= 1.5时，并列弹受到相邻弹的影响较大，空泡直径（内外侧空泡半径之和）仅为2.5，且内侧空泡半径小于外侧空泡半径。在G= 2.0时，外侧空泡较G= 1.5时变化更大，Rc/R最大值从1.25增加到1.75，内侧空泡受到相邻弹的影响，Rc/R最大值仅从1.25增加到1.4。随着轴线间距的增加，内侧空泡逐渐扩张，直至接近单个弹体空泡轮廓，而外侧轮廓在G= 2.0时已接近单个弹体情况。在G= 4.0时，并列弹之间相互干扰较弱，此时内外侧空泡轮廓趋近于对称。

图17给出了不同间隙比下在1 ms时刻下空泡轮廓曲线。可以看出，在t= 1 ms、G= 2.0时，弹体呈现头部分开，尾部靠拢的现象，空泡无量纲直径达到3.6，内侧空泡受弹轴倾斜挤压的影响，内侧空泡最大半径达到2，外侧空泡最大半径达到1.6。在G= 2.5时，弹轴倾斜较小，对内侧空泡的挤压作用减弱，内侧空泡最大半径减弱到1.6，外侧空泡最大半径达到2。在G= 3.0时，受并列弹相互干扰作用的减弱，弹轴倾斜效应不再显著，此时，内外侧空泡轮廓呈对称分布，内侧空泡最大半径达到1.3，外侧空泡最大半径达到1.5，内侧空泡受到邻弹挤压作用，相比外侧略小。在G= 4.0时，内外侧空泡轮廓呈现对称分布，外侧空泡轮廓相比单个弹体较宽，内侧空泡轮廓相比单个弹体较窄。因此，并列弹入水过程中轴线间距会对空泡轮廓有一定的影响，轴线间距越小，对内外侧空泡半径、长度干扰作用越大。

图17 不同轴线间距下空泡轮廓变化规律（t = 1 ms）Fig. 17 The variation of cavity profile at different axis distance(t = 1 ms)

2.2 并列弹运动及受力特性分析

图18为不同轴线间距的并列弹和单个弹入水时的速度随时间的衰减特性，可以看出，在不同轴线间距下，并列弹体入水时速度衰减特性变化较小，衰减趋势和单个弹体相似。在t= 0.05～0.2 ms内，当G=1.5时，并列弹姿态变化显著，导致两弹发生碰撞后无速度衰减变化；当G= 2.0～3.0时，并列弹完全浸没水中，此时并列弹速度衰减较单个弹体略微增大。随着轴线间距的增加，速度衰减特性减弱，当G= 4.0时，并列弹的速度衰减特性接近单个弹体。

图18 并列弹速度变化特性Fig. 18 The variation of parapllel-projectile velocity

从图19中的并列弹位移特性可得，同一时刻下，并列弹体的轴向位移SA随着轴线间距的增加而逐渐增加，而并列弹的法向位移SN随着轴线间距的增加而逐渐减小，在G= 4.0时，并列弹的轴向位移和法向位移特性逐渐接近单个弹体。

图19 不同轴线间距下并列弹位移特性Fig. 19 Displacement characteristics of parallels projectile with different axial distance

为明确两弹的相互作用引起的侧向运动规律，图20给出了不同轴线间距下的侧向位移变化曲线。从图中可以看出，并列弹体的侧向位移随轴线间距的增加而减小，最后趋近于单个弹体变化情况，且并列弹的侧向位移受轴线间距影响变化显著。当G= 1.5时，并列弹姿态变化显著导致两弹发生碰撞，因此在0.8 ms以后无位移变化。当G= 2.0～2.5时，并列弹弹间干扰作用依然很大，随轴线间距增大至G=4.0时，并列弹侧向位移变化幅度很小且与单个弹入水基本相同。

图20 不同轴线间距下并列弹侧向位移特性Fig. 20 Lateral displacement characteristics of parallel projectiles with different axial distance

结合并列弹的受力特性，对并列弹的运动特性进一步开展分析。图21给出了不同轴线间距下并列弹轴向力系数CA和法向力系数CN随时间的变化过程。从图中可以看出，不同轴线间距下，弹体抨击水面引起的CA峰值基本相同，但随着入水深度的增加，CA随着轴线间距的增加而减小，直至趋近于单个弹的情况。与CA变化趋势不同，CN的峰值点随轴线间距增大而减小，直至近似于单个弹体。随着入水深度的增加，CN也表现出随轴线间距的增加而降低的规律。结合图19可以得出，随着轴间距减小，并列弹间相互干扰作用越大，其受到的法向力引起的弹道法向偏移量越大，易造成并列弹失稳的运动状态。

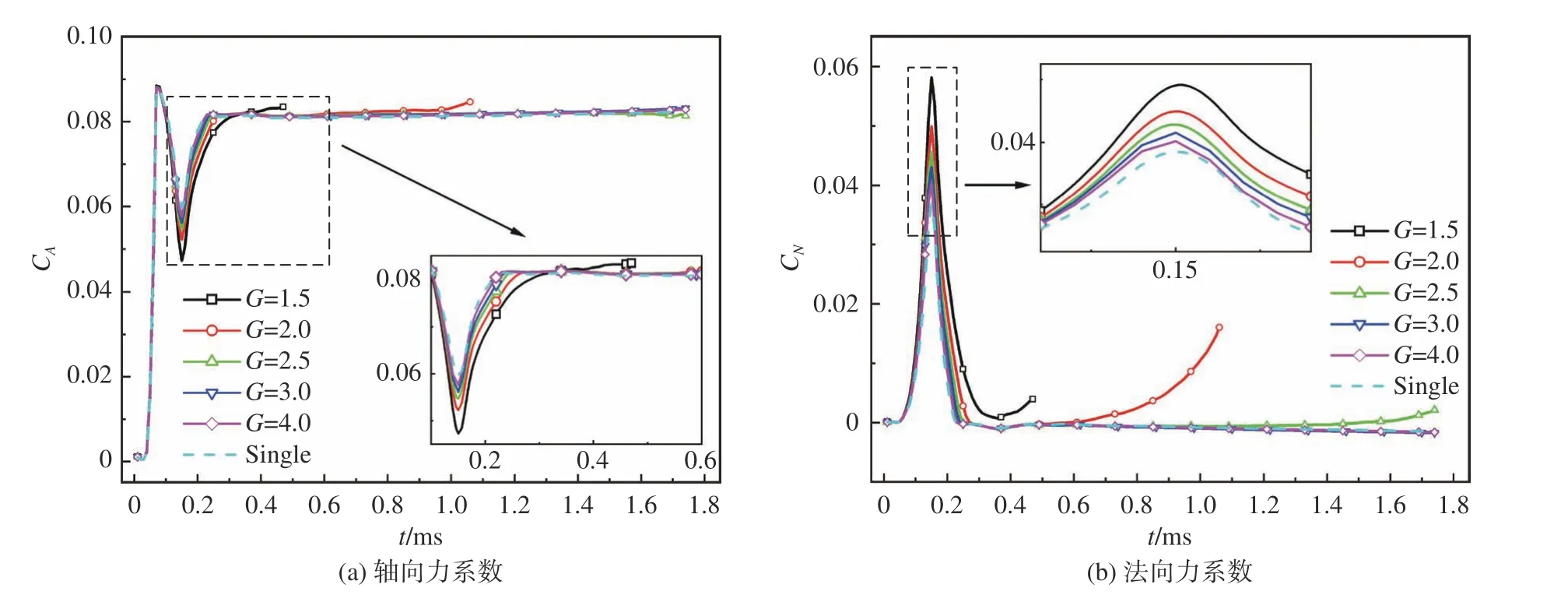
图21 不同轴线间距下并列弹流体动力系数Fig. 21 Hydrodynamic coefficients of parallel projectiles with different axis distances

图22给出了不同轴线间距下侧向力系数随时间的变化关系，用|CZ|表示两并列弹体相互吸引和排斥力的相互作用，吸力为正，斥力为负。从图中可以看出，不同轴线间距下，并列弹入水过程均表现出相互排斥的作用，且斥力均表现为先增加后减小最后稳定增加的趋势。随着轴线间距的增加，并列弹体斥力逐渐减小，直至和单个弹体类似。这是由于并列弹入水后，在低轴线间距下，射弹肩部沾湿，射弹内外侧表面的压差使射弹头部受到排斥的作用力，头部相互远离，尾部靠拢。当射弹尾部撞击空泡壁时，尾部沾湿使射弹的排斥作用减弱，但是射弹的质心靠近头部，因此头部的作用力相较于尾部更显著，最终使射弹头部分离，尾部靠拢，直至弹体失稳，该现象随轴线间距的增大而减弱。

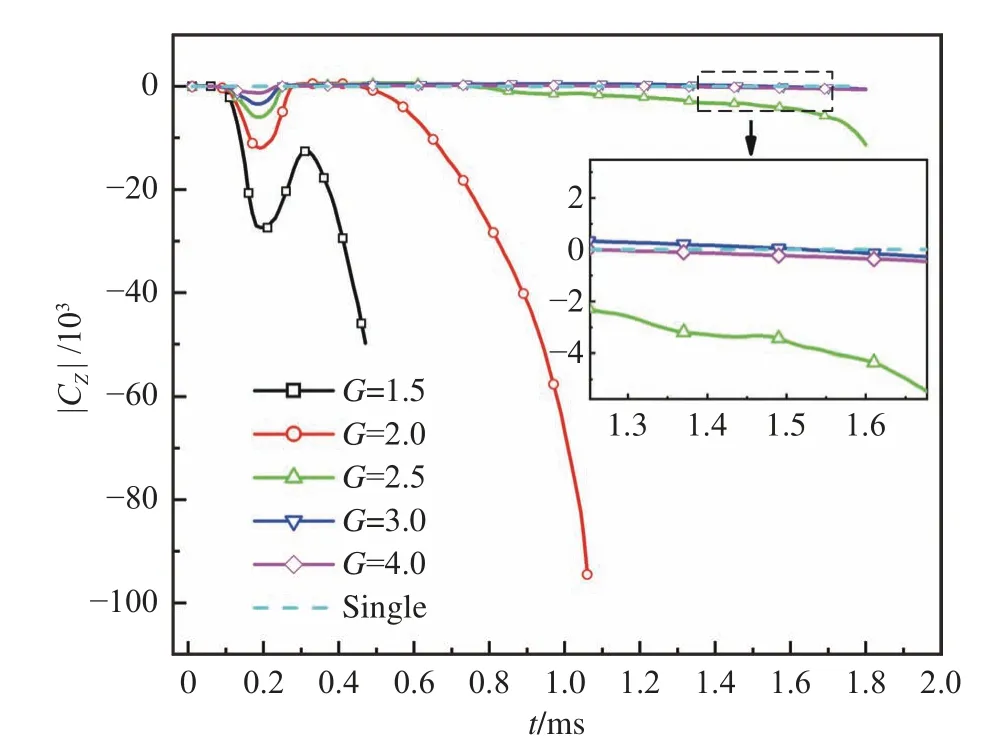
图22 不同轴线间距下并列弹侧向力系数特性Fig. 22 Characteristics of lateral force coefficient of parallel projectiles with different axis distance

2.3 并列弹高速入水流场分布规律

结合并列弹受力特性对高速并列弹入水流场分布规律进行分析，图23给出了在G= 2.0、θ=25°时并列弹入水流场压力变化云图。可以看出，在t= 0.1 ms时刻，弹头形成局部高压区，但高压区域范围较小。在t= 0.3 ms时刻，头部高压区范围增大，头部高压区产生叠加现象。压力向周围流场传递，压力梯度逐渐减小。随着入水深度的增加，在t= 0.6 ms时刻，并列弹姿态产生显著变化，表现出射弹头部分开，尾部靠拢的现象，内侧流体靠近弹身处开始出现局部高压区。随着入水深度的增加，并列弹的姿态变化更显著，引起内侧流体高压区范围扩大，直至t= 1 ms时刻，并列弹尾部发生碰撞。

图23 轴线间距G = 2.0时压力变化云图Fig. 23 Pressure distribution at the case of G = 2.0

图24所示为射弹完全入水时不同轴线间距下的压力云图，从图24（a）可以发现，并列弹头部形成对称高压区域，空泡内部形成局部低压区。在G= 1.5时，并列弹呈现出头部分离、尾部靠近的现象。内侧流体受到挤压，弹体内侧的高压区向头部偏移，并列弹头部形成叠加对称高压区域，肩部受并列弹相互干扰形成局部高压区。在G= 2.0时，并列弹头部重叠高压区减小，并列弹内侧局部高压区效应减弱。在G=3.0时，并列弹姿态变化不再显著。随着轴线间距增大至G= 4.0，压力场分布趋近于单个弹的压力场分布。随入水深度进一步增大，在t= 1 ms时刻不同轴线间距下的压力场分布云图如图24（b）所示。在G= 1.5时，并列弹已发生剧烈碰撞，导致压力场分布紊乱。G= 2.0时，并列弹内侧低压导致射弹姿态发生显著变化，并列弹头部产生偏转，此时弹体头部重叠高压区分离，肩部、尾部受弹间相互干扰作用形成局部高压区。当轴线间距的增加至G= 4.0时，并列弹压力分布与单个弹体相似。

图24 完全入水时并列弹不同轴线间距下的压力云图Fig. 24 Pressure distribution at different axis distance when parallel projectiles fully submerged in water

图25所示为在t= 1 ms时不同轴线间距下并列弹中心线处的压力分布规律。结合图24可以看出，随着轴线间距减小，内侧空泡压力分布对空泡演化的影响程度在深度较深位置更为明显。其主要原因是在深度较小区域（接近自由液面区域），当并列弹高速入水时，流体将动能转化为势能所克服的环境压力较小。在轴线间距较小的工况下（空泡敞开阶段），并列弹相互干扰作用明显，在内侧区域流体的动能转化为势能，包裹射弹内侧空泡周围压力场分布高于外侧；在轴线间距较大的工况下，并列弹相互干扰作用减弱，内侧区域流体主要向外排开，流场获得的能量主要为动能，其分布规律逐渐接近单个弹入水压力分布。

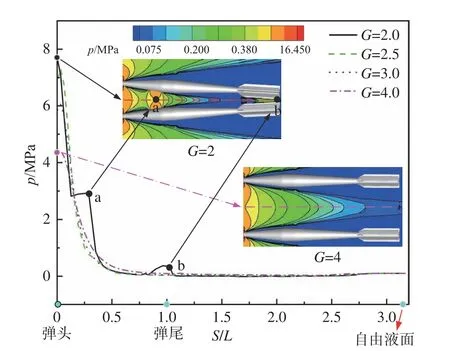
图25 不同轴线间距下并列弹中心线处压力分布(t = 1 ms)Fig. 25 Pressure distribution at the centerline of parallel projectiles under different axle distance (t = 1 ms)

但在水深较深处，流体动能向势能转化需要克服的环境压力较大，使得该区域环境静压成为了影响空泡发展的核心因素，而相同水深处环境静压相近，并列弹随着轴线间距减小对压力场造成的扰动相较于环境静压更大，因此在水深较深处，距并列弹头部1倍弹长范围内，包裹并列弹空泡的周围压力分布差异较大。

图26给出了G= 2.0、θ=25°时并列弹入水流场速度云图和流线变化图。可以看出，在t= 0.1 ms时刻，弹体头部触水，排开周围流体，在压力梯度力、黏性力和表面张力共同作用下形成流动。在t= 0.3 ms时刻，在弹身外侧形成反向对称涡，随着并列弹进入水中，包裹射弹的空泡内存在被卷吸进入的空气以及因空化数较低而产生的水蒸气，使射弹周围速度场变化剧烈，但尾涡不随并列弹一起运动。在t= 0.4 ms时刻，并列弹内侧形成和外侧反向对称涡。t= 0.8 ms时刻，并列弹头部分离，尾部靠近，并列弹内侧流线出现复杂运动。在t= 1 ms时刻，弹头内侧前端流线朝向运动前方，并列弹尾部流线在并列弹中心处汇合形成朝向后方的流线束，同时在射弹头部存在动能耗散，产生显著低速区域。

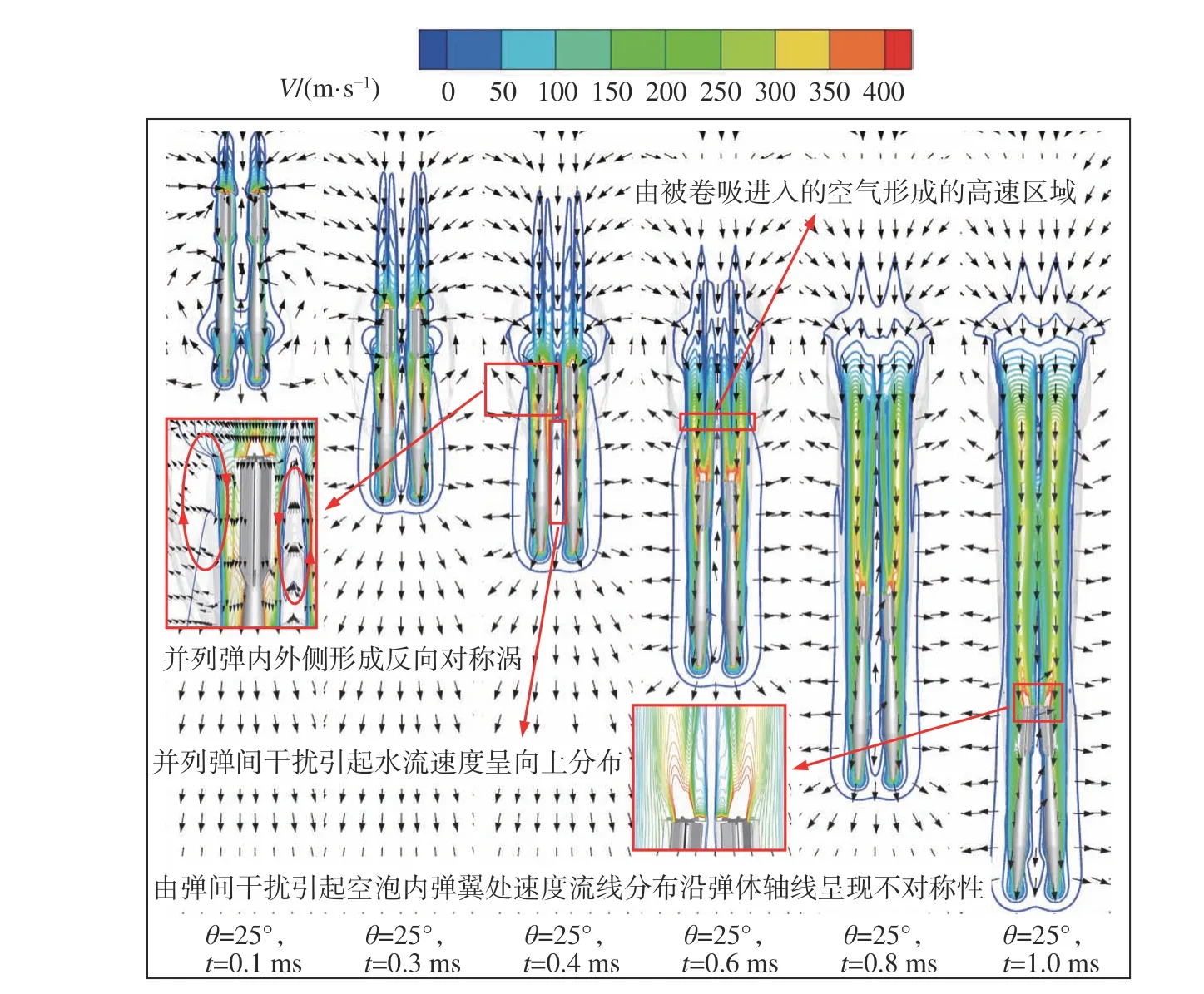
图26 轴线间距G = 2.0时并列弹入水流场速度云图Fig. 26 Flow field velocity distribution of parallel projectiles entering water at the case of G = 2.0

进一步对射弹入水一定深度后的速度云图进行分析，如图27所示。结合图28所示不同轴线间距下并列弹中心线处速度分布规律，可以发现高速区域主要集中在弹体头部和弹体后方空泡内，外侧流场在弹身周围呈现出均匀对称分布，在弹体后方形成对称反向流体涡，流体涡主要在空泡尾端与液面交界处。在G= 2.0时，弹间相互干扰作用使内侧弹翼附近流线变化剧烈。在距离射弹头部1.5倍弹长左右，发生空泡融合且并列弹中心线处于空泡内的低压区，使流线速度大小呈现先增大后减小趋势。随着轴线间距增加至G= 4.0时，并列弹间干扰作用减弱，内侧空泡周围的流线沿两弹体中轴线呈轴对称分布。因此，根据并列弹高速入水流场分布特性，可以发现随轴线间距减小，并列弹入水过程中的空泡干扰越大。同时受弹间干扰的影响，内侧空泡压力、速度分布规律对空泡演化的影响程度在深度较深位置更为明显。

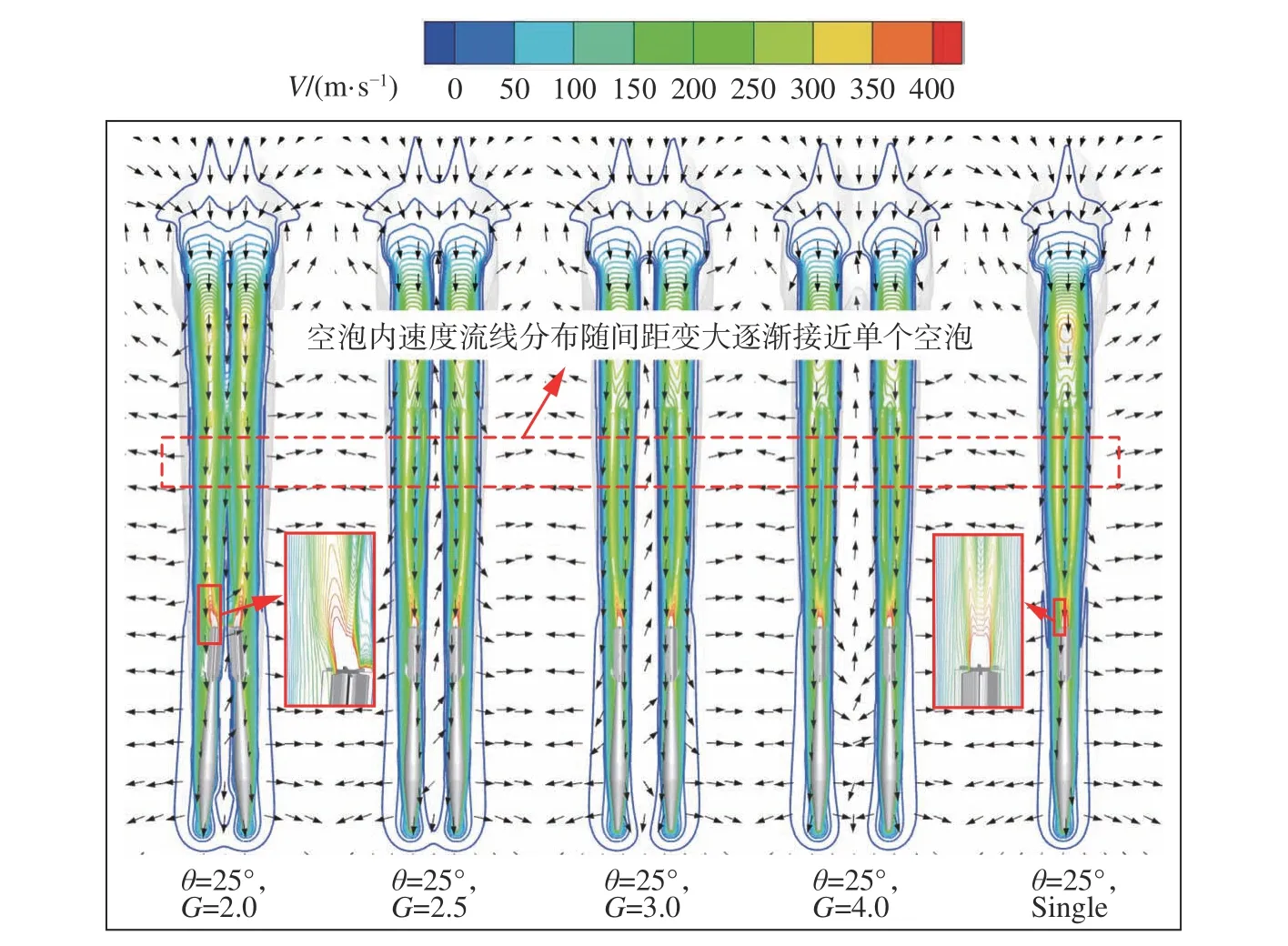
图27 射弹入水一定深度后不同间隙下速度云图，t = 1 msFig. 27 The velocity cloud map of parallel projectiles at different axis distance after entering water at a certain depth when t = 1 ms

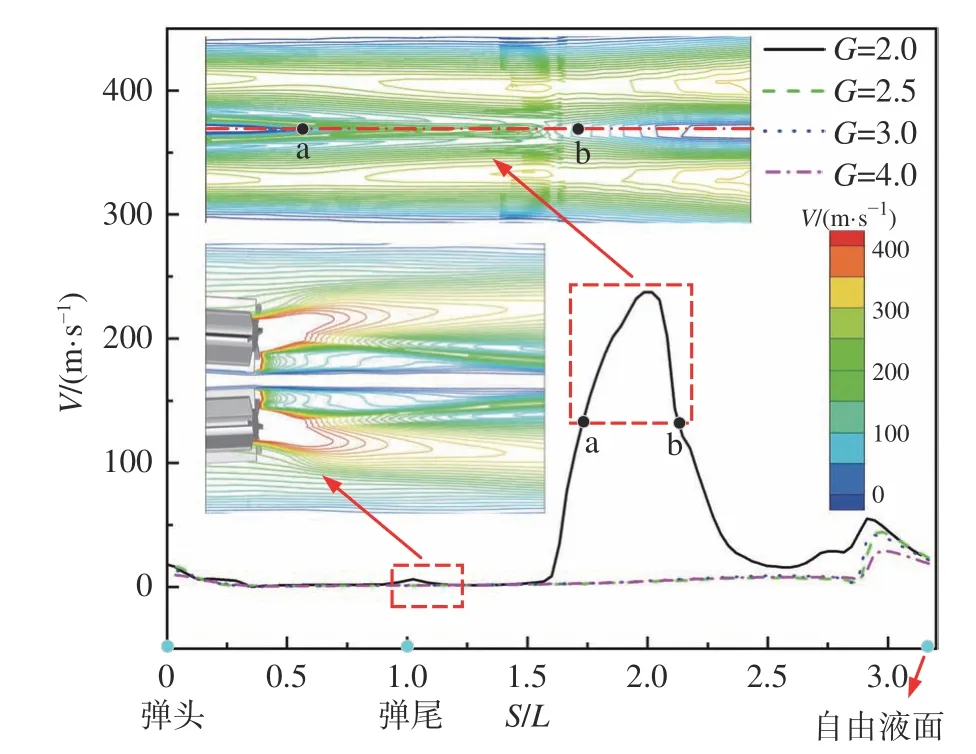
图28 t = 1 ms时不同轴线间距下并列弹中心线处速度分布Fig. 28 The velocity distribution at the centerline of parallel projectiles varies with different axial distance at t = 1 ms

3 结论

本文基于RANS方法，针对轴线间距G= 1.5、2.0、2.5、3.0、4.0的同步并列射弹，在入水速度为U=450 m/s、入水角θ= 25°工况下开展数值模拟，通过仿真和实验结果对比完成了数值方法的验证，并用该方法研究了并列射弹跨介质入水过程的空泡耦合演化特性、三维流场结构和流体动力特性，通过与单个弹结果的对比分析，主要得到以下结论：

1） 与单个弹入水过程相比，并列弹高速入水过程空泡演化规律与轴线间距密切相关。随着轴线间距的减小，双空泡相互干扰产生变形， 会形成一对非对称空泡，但双空泡整体关于中心轴呈现出良好的镜面对称。

2） 相较于入水初期，在入水深度较深位置时，轴线间距越小，弹间相互干扰越大，并列弹侧向位移增大，引起射弹的弹道轨迹发生偏转，表现出显著的头部分离和尾部靠拢的现象， 易造成并列弹失稳。

3） 随着轴线间距增大，并列弹间相互干扰作用减弱，并列弹侧向位移曲线与单个弹逐渐吻合，双空泡入水过程的流体动力特性逐渐趋近于单个弹入水空泡。

后续可通过实验与仿真相结合方法，进一步开展多体间不同排列方式下轴线间距对多体串/并行入水过程的流体动力特性的研究，为密集发射的跨介质飞行器研制提供有益的参考。