Investigation on the roles of equilibrium toroidal rotation during edge-localized mode mitigated by resonant magnetic perturbations

Liangkang DONG (董良康) ,Shaoyong CHEN (陈少永),* ,Maolin MOU (牟茂淋) ,Yang LUO (罗杨) ,Chenchen QIN (秦晨晨) and Changjian TANG (唐昌建)

1 College of Physics,Sichuan University,Chengdu 610064,People’s Republic of China

2 Key Laboratory of High Energy Density Physics and Technology of Ministry of Education,Sichuan University,Chengdu 610064,People’s Republic of China

3 Institute of Fusion Science,School of Physical Science and Technology,Southwest Jiaotong University,Chengdu 610031,People’s Republic of China

Abstract The effects of equilibrium toroidal rotation during edge-localized mode (ELM) mitigated by resonant magnetic perturbation (RMP) are studied with the experimental equilibria of the EAST tokamak based on the four-field model in the BOUT++code.As the two main parameters to determine the toroidal rotation profiles,the rotation shear and magnitudes were separately scanned to investigate their roles in the impact of RMPs on peeling-ballooning (P-B) modes.On one hand,the results show that strong toroidal rotation shear is favorable for the enhancement of the self-generated E × B shearing rate 〈ωE×B〉 with RMPs,leading to significant ELM mitigation with RMP in the stronger toroidal rotation shear region.On the other hand,toroidal rotation magnitudes may affect ELM mitigation by changing the penetration of the RMPs,more precisely the resonant components.RMPs can lead to a reduction in the pedestal energy loss by enhancing the multimode coupling in the turbulence transport phase.The shielding effects on RMPs increase with the toroidal rotation magnitude,leading to the enhancement of the multimode coupling with RMPs to be significantly weakened.Hence,the reduction in pedestal energy loss by RMPs decreased with the rotation magnitude.In brief,the results show that toroidal rotation plays a dual role in ELM mitigation with RMP by changing the shielding effects of plasma by rotation magnitude and affecting 〈ωE×B〉 by rotation shear.In the high toroidal rotation region,toroidal rotation shear is usually strong and hence plays a dominant role in the influence of RMP on P-B modes,whereas in the low rotation region,toroidal rotation shear is weak and has negligible impact on P-B modes,and the rotation magnitude plays a dominant role in the influence of RMPs on the P-B modes by changing the field penetration.Therefore,the dual role of toroidal rotation leads to stronger ELM mitigation with RMP,which may be achieved both in the low toroidal rotation region and the relatively high rotation region that has strong rotational shear.

Keywords: edge-localized mode,peeling-ballooning modes,resonant magnetic perturbation,toroidal rotation,plasma response,tokamak

1.Introduction

In tokamaks,the high-confinement mode (H-mode)improves the plasma energy confinement time to approximately twice that of the low-confinement mode (L-mode),and it is characterized by the formation of an edge transport barrier (ETB) [1].However,the steep edge gradient of pressure and strong bootstrap current can drive the ballooning and peeling modes,respectively,resulting in the coupling peeling-ballooning mode (P-B mode) in the pedestal region[2,3].The P-B mode instability may cause pedestal crash,and a large amount of energy and particles are periodically expelled from the plasma edge,forming a type I edge-localized mode (ELM) [1,3].The enormous thermal flux of uncontrolled type I ELM can potentially damage the plasmafacing components.One of the promising active methods of ELM control is the application of external resonant magnetic perturbation (RMP) coils to mitigate or suppress type I ELM[4,5].This method has been proven to be effective for several tokamaks,such as DIII-D [5,6],JET [7,8],EAST[9-11],ASDEX-Upgrade [12,13],MAST [14,15],KSTAR[16,17],and HL-2A [18],in recent years.

Despite effective ELM crash controls,the physical mechanisms behind some interesting phenomena that are closely related to ELM control are not yet fully understood.Recent results from DIII-D [19-21] revealed an apparent toroidal rotation threshold for ELM suppression with RMP,and ELM suppression is lost (or achieved) when toroidal rotation is below (or above) the threshold.Similarly,ELMs were also suppressed in experiments with a high toroidal rotation,Vtor,ped＞ 40 km s-1,in KSTAR,but the rotation threshold remains unclear [22,23],whereas a lower plasma rotation was found to be favorable to access ELM suppression in EAST [11].Extensive efforts [11,19-21] in ELM control have found that an electron perpendicular rotation near the pedestal top close to zero is very critical for achieving strong ELM mitigation or suppression.In addition,the results from MAST [14,15,24,25] found that ELM mitigation increases with the size of the lobe structure near the X point,and the lobe length decreases with toroidal rotation,which suggests that better ELM mitigation may be achieved with low toroidal rotation.This indicates that ELM mitigation is closely relevant to the shielding effect,which partly depends on the toroidal rotation.A large number of experiments have shown that both high and low toroidal rotations may be favorable for ELM control,and the roles of toroidal rotation in ELM control with RMP are incompletely understood.

As mentioned previously,extensive experiments on ELM control with RMP have revealed that it does not consistently depend on toroidal rotation,which suggests that the roles of toroidal rotation may be multiple in the influence of RMP on ELM.On one hand,toroidal rotation shear has important effects on the instability of P-B modes[26-28].On the other hand,the magnitude of toroidal rotation can significantly change the strength of the resonant components of RMP through plasma response,especially shielding effects [29-31].Therefore,toroidal rotation may play multiple roles in ELM mitigation by affecting the plasma response and instability of P-B modes.However,the roles of toroidal rotation in ELM mitigation by RMP are not completely understood.It is of interest to investigate the roles of toroidal rotation in ELM mitigation with RMP to provide a reference for relevant experiments to achieve better ELM control.This work is devoted to studying the roles of toroidal rotation in ELM mitigation with RMP.

In this study,the roles of toroidal rotation in the influence on P-B modes with RMP have been studied based on the BOUT++four-field model.Initially,we attempt to investigate the impact of toroidal rotation shear on the influence of RMP on P-B modes.Subsequently,we take into account the influence of toroidal rotation magnitude,which mainly plays a crucial role in the plasma response.The remainder of this paper is organized as follows.The BOUT++four-field model that couples the RMP field to the P-B mode and the adopted equilibria from shot 52340 in the EAST device are presented in section 2.Section 3 presents the roles of toroidal rotation shear in the influence of the P-B modes with RMP.The additional effects of the toroidal rotation magnitude are presented in section 4,followed by a summary and a conclusion in section 5.

2.Physical model and equilibria

There are two main steps to study the roles of equilibrium toroidal rotation in the impact of RMP on the P-B modes.First,different toroidal rotation profiles are adopted in MARS-F code [31] to calculate the RMP fields with the plasma response.Second,the RMP fields calculated from MARS-F are coupled to the P-B modes in the BOUT++fourfield model [32] to analyze the linear instability and nonlinear evolution of the P-B modes.In this section,we briefly introduce the BOUT++four-field model and the adopted equilibria.

2.1.Physical model

MARS-F is a robust linear response code that has been widely used to calculate RMP fields in tokamaks,such as EAST [33],MAST [34],ASDEX-Upgrade [35,36],JET [37],and HL-2A [30].The results indicate that MARS-F is capable of providing relatively accurate descriptions of the linear plasma response in tokamaks.Therefore,it was also adopted in this study to calculate the RMP fields with plasma response.

Subsequently,the RMP fields obtained from MARS-F are coupled to P-B modes based on the BOUT++four-field model [32],which is a reduced MHD two-fluid code that can describe the P-B mode evolution and pedestal crash process in the tokamak boundary region.As presented in equations(1)-(8),four important and crucial fields (vorticity U,magnetic potential A‖,parallel velocity v‖,and pressure P)are solved to describe the evolution process of the P-B modes.It contains some non-ideal effects,including ion diamagnetic drift,E × B drift,finite resistivity,and hyperresistivity (known as anomalous electron viscosity).is equilibrium toroidal rotaion.

Based on the BOUT++four-field model,we coupled the RMP fields to the P-B mode by adding RMP into the equilibrium magnetic field,and the basic equations can be written as

In this study,the equilibrium toroidal rotation was considered in the four-field model.It is known that the force from the toroidal rotation has an impact on the equilibrium force balance.As the ion force balance equation (9) shows,the equilibrium profiles should satisfy the basic equilibrium force balance

To satisfy the equilibrium force balance,· ∇V0should be very small in comparison with ∇Pi0,namely,· ∇V0/∇Pi0≪ 1.Here,.Therefore,is the precondition of the equilibrium force balance.In this study,all the toroidal rotation profiles can satisfy the precondition of equilibrium force balance,.In conclusion,the forces of toroidal rotations have little impact on the equilibrium force balance.

The field-aligned flux coordinate system (x,y,z) [38]adopted in this modeling work was derived from an orthogonal toroidal coordinate system (ψ,θ,ζ),where ψ is the poloidal flux,θ is the poloidal angle,and ζ is the toroidal angle.The relationship between the coordinate systems(x,y,z) and (ψ,θ,ζ) is shown in equation (13).In addition,ν is the local field-line pitch given by ν(ψ,θ)=B · ∇ζ/B · ∇θ=Bζhθ/BθR,and hθ=1/|∇θ| is the scale factor for θ.As the simulation region is symmetric in the toroidal,only one-third of the torus is calculated to economize the computing resources.The grid-point space size of the simulation region ψ=0.6 -1.0 is set to be (Nx,Ny,Nz)=(132,128,128) in the linear simulation and (Nx,Ny,Nz)=(260,128,128) in the nonlinear simulation.

2.2.Equilibria

The safety factor,equilibrium toroidal rotation,and Spitzer resistivity determined by the electron temperature play crucial roles in the plasma response.Therefore,the crucial profiles adopted in the modeling work are from the diagnostic data at 3.15 s of shot 52340 in EAST [9],as shown in figures 1(a) and (b).To investigate the roles of toroidal rotation in the impact of RMP on P-B modes,a series of equilibrium toroidal rotation profiles were generated from the typical hyperbolic tangent function,which will be introduced in detail in the following sections.

To study the effect of RMP on P-B modes,some important parameter profiles adopted in BOUT++were obtained from the experimental diagnostic data at 3.15 s of shot 52340 in EAST,and the equilibria were reconstructed by CORSICA [39].The safety factor,pressure,and parallel current density profiles are shown in figures 1(a),(c),and(d),respectively.The density is set as a constant n0=3 × 1019m-3for improving the computational efficiency,and it is close to the electron density in shot 52340 [9].It is worth noting that the same equilibrium safety factor,toroidal rotation,and resistivity profiles were used in both MARS-F and BOUT++for self-consistency.

3.Role of toroidal rotation shear in the influence of RMP on P-B modes

Rotation shear and magnitude are the two main parameters that determine the toroidal rotation profiles,and they may play important roles in ELM mitigation with RMP.In this section,we investigate the role of toroidal rotation shear in the influence of RMP on P-B modes.A classical hyperbolic tangent function,as in equation (14),is used to generate a series of rotation shear profiles.

where V0and C are used to adjust the magnitude of rotation,ψ0is the shear peak position,Dsis used to adjust the rotation shear,and Amis the amplification factor.In tokamaks,changing the shear of toroidal rotation usually means that the rotation magnitude changes simultaneously.As presented in figure 2(a),we merely varied Ds=6,12,18,...,36 to increase the toroidal rotation shear while fixing ψ0=0.97,C=-3900,V0=20050,and Am=1 to keep the rotation magnitude unchanged as much as possible.Figure 2(a)shows the toroidal rotation profiles with significantly different shear,and figure 2(b) shows the rotation shear profiles.The rotation profiles in figure 2(a) were adopted in the MARS-F code to calculate the n=3 response RMP with current Icoil=10 kAt.The n=3 RMP coil phase was selected as Δϕ=120° for the following reason.Both modeling and experiments show that ELM mitigation is significantly influenced by the RMP coil phase Δϕ,and the best Δϕ also varies with plasma parameters,such as Q95.In a previous study [40],the influence of Δϕ on RMP-ELM mitigation was systematically studied.The relevant results show that RMP can reduce the ELM amplitude by enhancing the multimode coupling of P-B modes,and the reduction intensity of the ELM amplitude is closely associated with the strength of the resonant components.Therefore,the configuration of the RMP coils,such as the coil phase Δϕ,can influence the reduction in ELM amplitude by changing the strength of the resonant components.In other words,the multimode coupling increases with the strength of the resonant components;therefore,the RMP poloidal spectrum can be changed by adjusting the phase difference Δϕ between the upper and lower RMP coils from 0° to 360°,and hence obtain the optimal coil phase difference that causes the strongest reduction in the ELM amplitude by maximizing the strength of the resonant components.In this study,we mainly focused on the role of toroidal rotation in RMP-ELM mitigation.By scanning the RMP coil phase from 0° to 360°,the strength of the resonant components of n=3 RMP reaches a peak value when Δϕ=120°,that is,Δϕ=120° is approximately the best Δϕ to maximize the strength of the resonant components.Therefore,if not otherwise specified,we adopted the best phase (Δϕ=120°) in this study to maximize the strength of the resonant components.In this way,the response RMP with the best phase would help us make the reduction in ELM amplitude reduction more obvious and make the physical phenomena clearer.

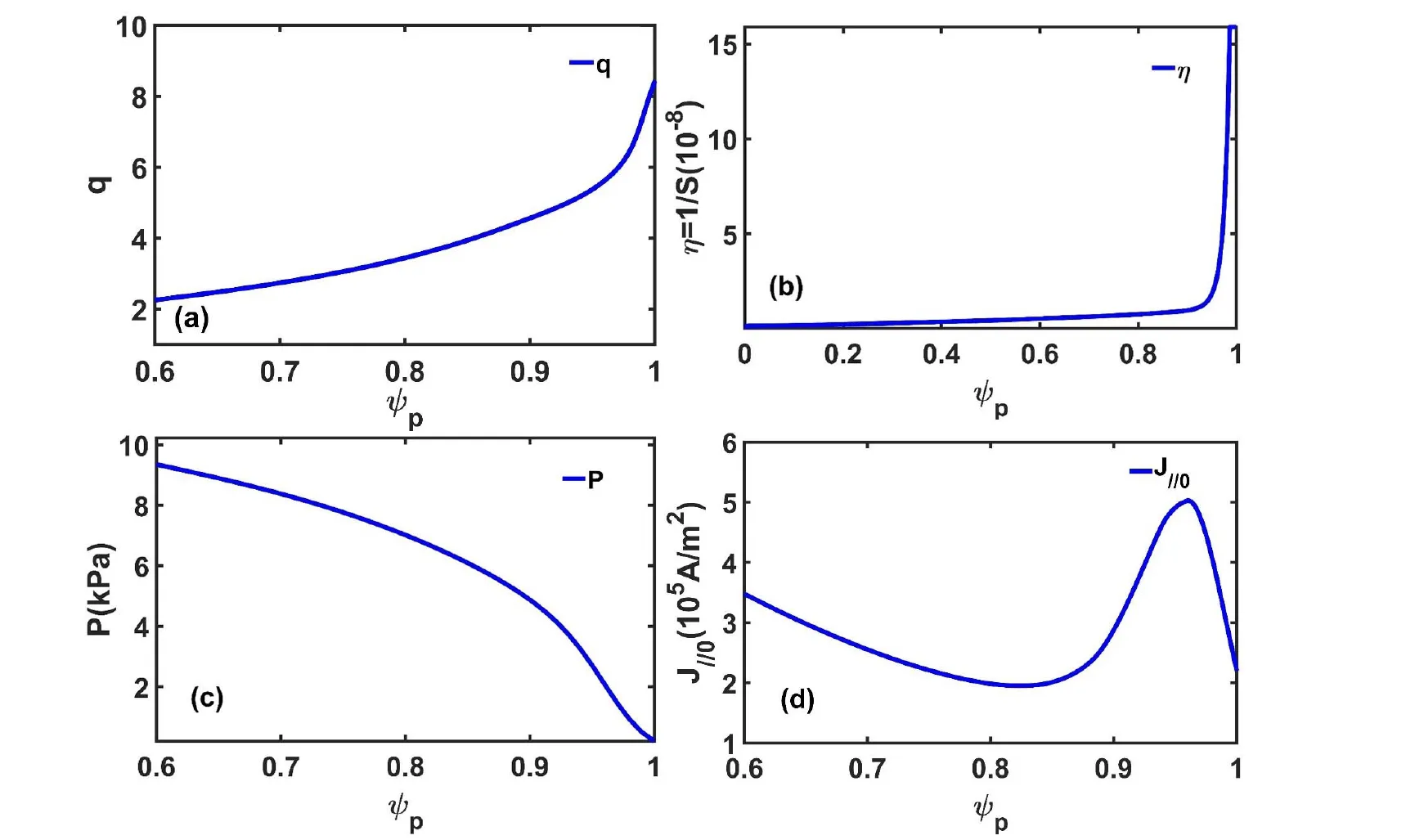
Figure 1.(a) Safety factor,(b) Spitzer resistivity (normalized to Lundquist number),(c) equilibrium pressure,and (d) parallel current profiles at 3.15 s and of shot 52340 in EAST;ψp is the normalized poloidal flux.

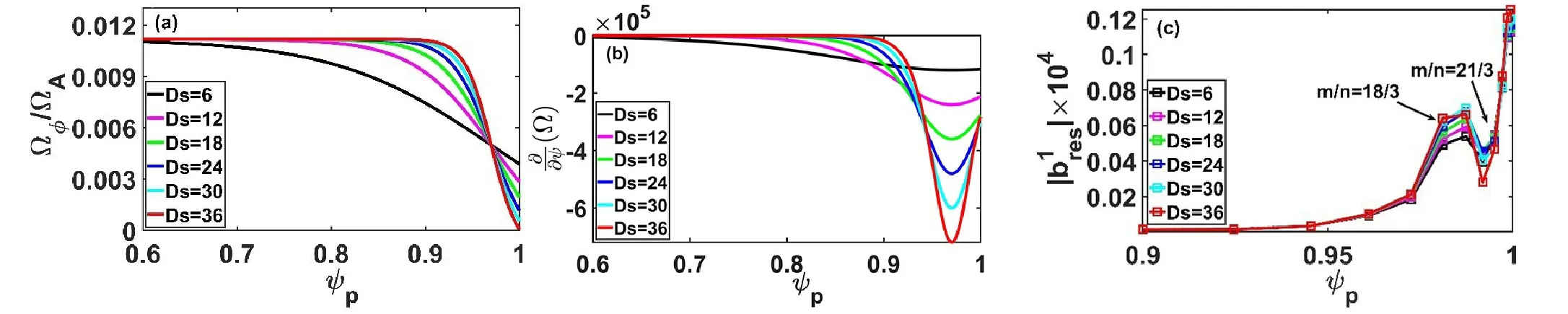
Figure 2.(a) Equilibrium toroidal rotation (normalized to the Alfvén frequency ΩA=3.24013315 × 106);(b) corresponding rotation shear;and (c) amplitudes of the resonant radial field of various components for Icoil=10 kAt,Δϕ=120° and response RMP fields with corresponding toroidal rotation shear profiles;ψp is the normalized poloidal flux.

The amplitudes of the various resonant radial field components of Icoil=10 kAt,Δϕ=120°,and n=3 response RMP are shown in figure 2(c).It is evident from the figure that the amplitudes of the resonant radial field components remain largely unchanged.As shown in figures 2(a)-(c),the rotation shear increased significantly,whereas the rotation magnitudes did not change too much,which kept the shielding effect of the plasma changing slightly.Through the rotation profiles,we can focus on the role of toroidal rotation shear in the influence of RMP on P-B modes and exclude the interference caused by the shielding effects due to rotation magnitudes.

Figure 3.(a) Linear growth rates of P-B modes versus toroidal mode numbers (n) with different toroidal rotation shear profiles.The dashed and solid lines are without and with the Icoil=10 kAt,Δϕ=120° and n=3 response RMP fields,respectively.(b) Changes in the linear growth rates of the P-B modes with different toroidal rotation shear profiles after adding the Icoil=10 kAt,Δϕ=120°,and n=3 response RMP fields.The diamagnetic effect is not included.

The rotation profiles in figure 2 and the corresponding Icoil=10 kAt,n=3,and Δϕ=120° response RMP,which were calculated from the MARS-F code,were adopted in the BOUT++four-field model.Note that the response RMP fields contain all the components,including resonant and non-resonant MPs.In a previous study [40],the effects of RMP with plasma response on P-B modes and ELM crash were systematically studied,and the results showed that RMP can cause ELM amplitude reductions by enhancing the multimode coupling of the P-B modes,which is closely related to the strength of the resonant components of RMP.However,the impact of non-resonant MPs on ELM amplitude reduction was not observed in the multimode coupling study.It is widely recognized that toroidal rotation can significantly influence the plasma shielding effect on RMP,particularly the resonant components of RMP.Hence,it may play an important role in RMP-ELM mitigation by changing the shielding effect on resonant components.Therefore,in this study,we mainly focused on the strength of resonant MPs.In all simulations,non-ideal effects,including ion diamagnetic drift,E × B drift,finite resistivity,and hyperresistivity,were considered if not otherwise specified.Initially,the role of rotation shear in the influence of RMP on the linear growth of the P-B modes is studied.The value of the hyper-Lundquist parameter is αH≃ 10-4-10-6in typical tokamaks [41] and was set to αH=1.0 × 10-4in our linear simulation.To make the conclusion clearer,the linear instability of the P-B modes was simulated without considering the diamagnetic effect.In figure 3(a),the dashed and solid lines represent the linear growth rates of the P-B modes without/with n=3,Δϕ=120° response RMP,respectively.The change in the growth rate Δγ is defined as Δγ=γrmp-γwo-rmp.Here,γrmpand γwo-rmprepresent the linear growth rates of the P-B modes with and without the response RMP fields,respectively.Therefore,Δγ ＜ 0 indicates that the growth rates are reduced when the RMP fields are coupled with the P-B modes.Figure 3(b) presents the change in the growth rate Δγ caused by RMP with different toroidal rotation shear profiles.It was found that the growth rates of the P-B modes significantly decreased with rotation shear,which is consistent with previous modeling results [26,28].The growth rates of the P-B modes were reduced when RMP was added,and the reductions in growth rates increased with toroidal rotation shear.In particular,for highn modes,the reductions in growth rates increased significantly with toroidal rotation shear.

The linear growth rates of the P-B modes with diamagnetic effects were also studied.Figures 4(a) and (b) present the linear growth rates without and with RMP,respectively.Figure 4(c) shows the change in the growth rate Δγ caused by RMP with different toroidal rotation shear profiles.The reductions in the growth rates of the P-B modes,especially high-n modes,increased with the toroidal rotation shear when RMP was added.It is worth noting that because of the problem of numerical instability,some linear growth rates of the P-B modes (such as n=6,24,and 36) with RMP fields cannot be obtained accurately when Ds=36.Therefore,the linear growth rates of the P-B modes when Ds=36 are not shown in figure 4.The incomplete results of Ds=36 still show that the reductions in the growth rates of the P-B modes,especially high-n modes,increased with the toroidal rotation shear when RMP was added.This did not influence the physical conclusion of this study.In summary,the linear results suggest that RMP may lead to stronger reductions in the linear growth rates of the P-B modes with stronger toroidal rotation shear.

Figure 4.Diamagnetic effect is considered.The linear growth rates of P-B modes versus toroidal mode numbers (n) with different toroidal rotation shear profiles (a) without and (b) with the Icoil=10 kAt,Δϕ=120°,and n=3 response RMP fields.(c) Changes in the linear growth rates of the P-B modes with different toroidal rotation shear profiles after adding the Icoil=10 kAt,Δϕ=120°,and n=3 response RMP fields.

We investigate the role of toroidal rotation shear in the influence of RMP on the nonlinear process of an ELM crash.Non-ideal effects,including ion diamagnetic drift,E × B drift,finite resistivity,and hyper-resistivity,were considered in all nonlinear simulations.The hyper-Lundquist parameter is αH=1.6 × 10-4,which is slightly larger than αH=1.0 × 10-4in the linear simulation,to improve numerical stability.In the modeling study,a small initial vorticity perturbation with toroidal number n=21,which is the most unstable mode in the linear growth rate spectrum,was set to U1=1.0 × 10-4in the simulation.The P-B modes developed progressively under the influence of the pressure gradient and parallel current in the pedestal region,leading to pedestal crash and energy release.To characterize the pedestal energy loss during ELM crash,‘ELM_size’ is defined as the ratio of energy loss to pedestal stored energy[41].This is represented as

Here,ψin=0.6 is the inner boundary in the simulation,and ψoutis the radial position of the peak pressure gradient.The symbol 〈 〉ζpresents the average over bi-normal periodic coordinate.J is Jacobian.

The role of toroidal rotation shear in the influence of RMP on ELM_size evolution is presented in figure 5.The ELM_size evolution during the nonlinear process can be usually divided into three phases.First,the perturbation grows quietly,and the pedestal would not crash because the initial most unstable mode is not large enough to break the equilibrium in the linear growing phase (approximately t ＜ 50τAin figure 5(a)).Second,a large amount of energy is released from the pedestal in the rapid initial crash phase,which corresponds to the sharp increase in ELM_size(t ≈ (50 -90) τAin figure 5(a)).The third is the nonlinear turbulence transport phase of P-B modes,in which pedestal energy is further transported out slowly and ELM_size reaches saturation gradually (about t ＞ 90τA).Next,we discuss the influence of toroidal rotation shear on ELM_size without/with RMP in the phases.

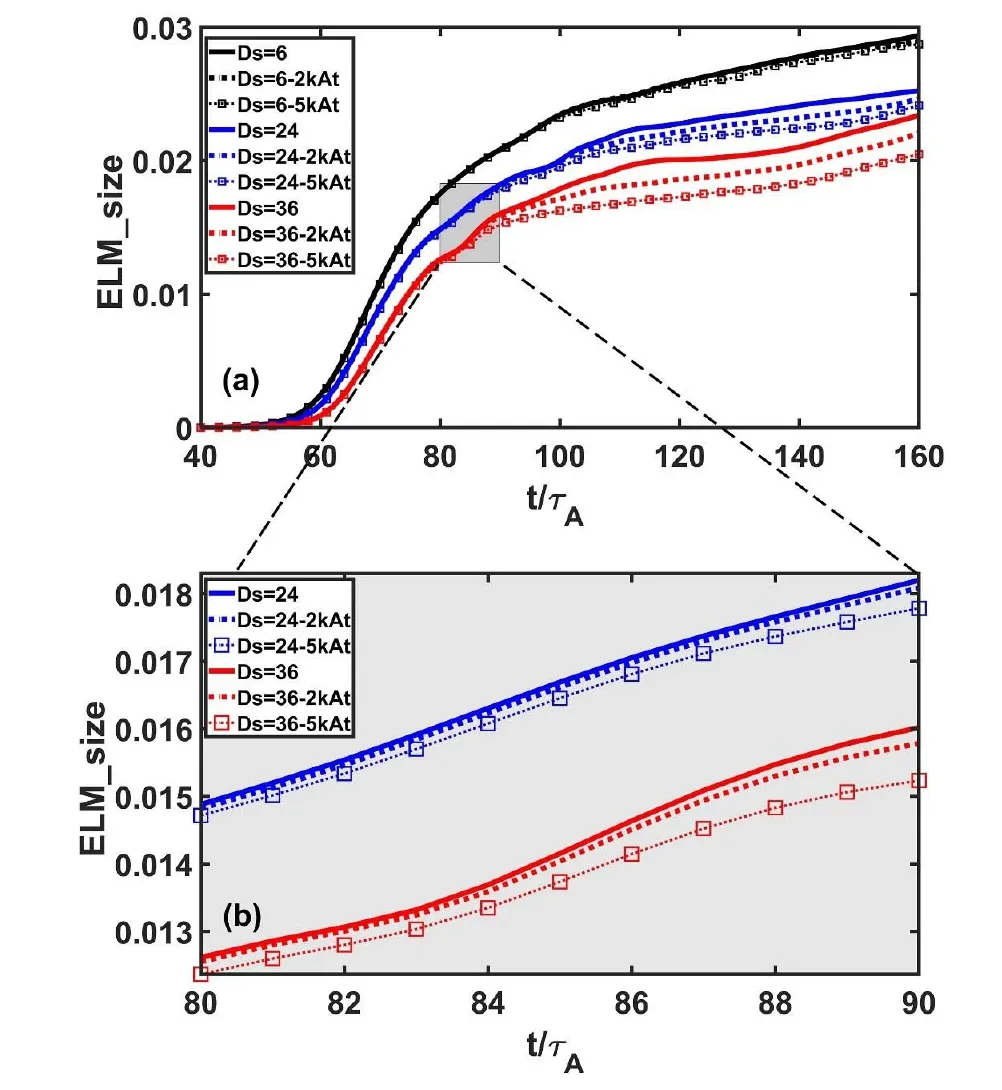
Figure 5.(a) Time evolution of ELM_size without RMP (solid lines),with Icoil=2 kAt (dashed lines) and Icoil=5 kAt (square dashed lines) Δϕ=120° and n=3 response RMP fields when different toroidal rotation shear profiles were adopted.(b) Enlarged view of the ELM_size evolution in the initial pedestal crash phase of (a).

The initial crash (t ≈ (50 -90) τA) is the link from the linear growth phase to the nonlinear turbulence transport phase;hence,its feature is closely related to linear growth.The intensity of the initial crash depends mainly on the amplitude peak value of the dominant mode,which is usually the most unstable mode n=21 in the linear growth rate spectrum,and its amplitude peak value is related in part to the linear growth rate.Figures 3 and 4 show that the toroidal rotation shear can stabilize the P-B modes,resulting in the delay of the initial pedestal crash as Dsincreases.The reduction in growth rates caused by RMP increased with Ds,as shown in figures 3 and 4,but the change in the growth rate Δγ was relatively small.Therefore,the influence of RMP on the initial pedestal crash is negligible despite the different toroidal rotation shear,as shown in figure 5(b).However,RMP has a significantly distinct influence on ELM_size with different toroidal rotation shear in the turbulence transport phase (approximately t ＞ 90τA).When the toroidal rotation shear is relatively weak,that is,Ds=6,the reduction in ELM_size caused by RMP is very small despite the increase in RMP coil current,as shown in figure 5(a).The reductions in ELM_size will increase significantly with Dswhen the toroidal rotation shear is relatively stronger,such as Ds=24 and 36,and ELM_size reductions also increase with the RMP coil current Icoil=2 and 5 kAt.

More systematic studies on the roles of toroidal rotation shear in the influence of RMP on ELM_size are shown in figure 6.ΔELM_size is the change in ELM_size,and it is defined as ΔELM_size=ELM_sizermp-ELM_sizewo-rmp.Here,ELM_sizermpand ELM_sizewo-rmprepresent the pedestal energy loss with and without RMP,respectively.Therefore,ΔELM_size ＜ 0 indicates that ELM_size is reduced when RMP is coupled to the P-B modes.It was found that ELM_size decreased with the shear parameter Ds,as shown in figures 6(a) and (b).The addition of RMP resulted in a substantial reduction in ELM_size,especially during the turbulence transport phase (approximately t ＞ 90τA).This reduction was further amplified by the toroidal rotation shear.ELM_size was further reduced when the RMP coil current Icoilincreased from 2 kAt to 5 kAt.

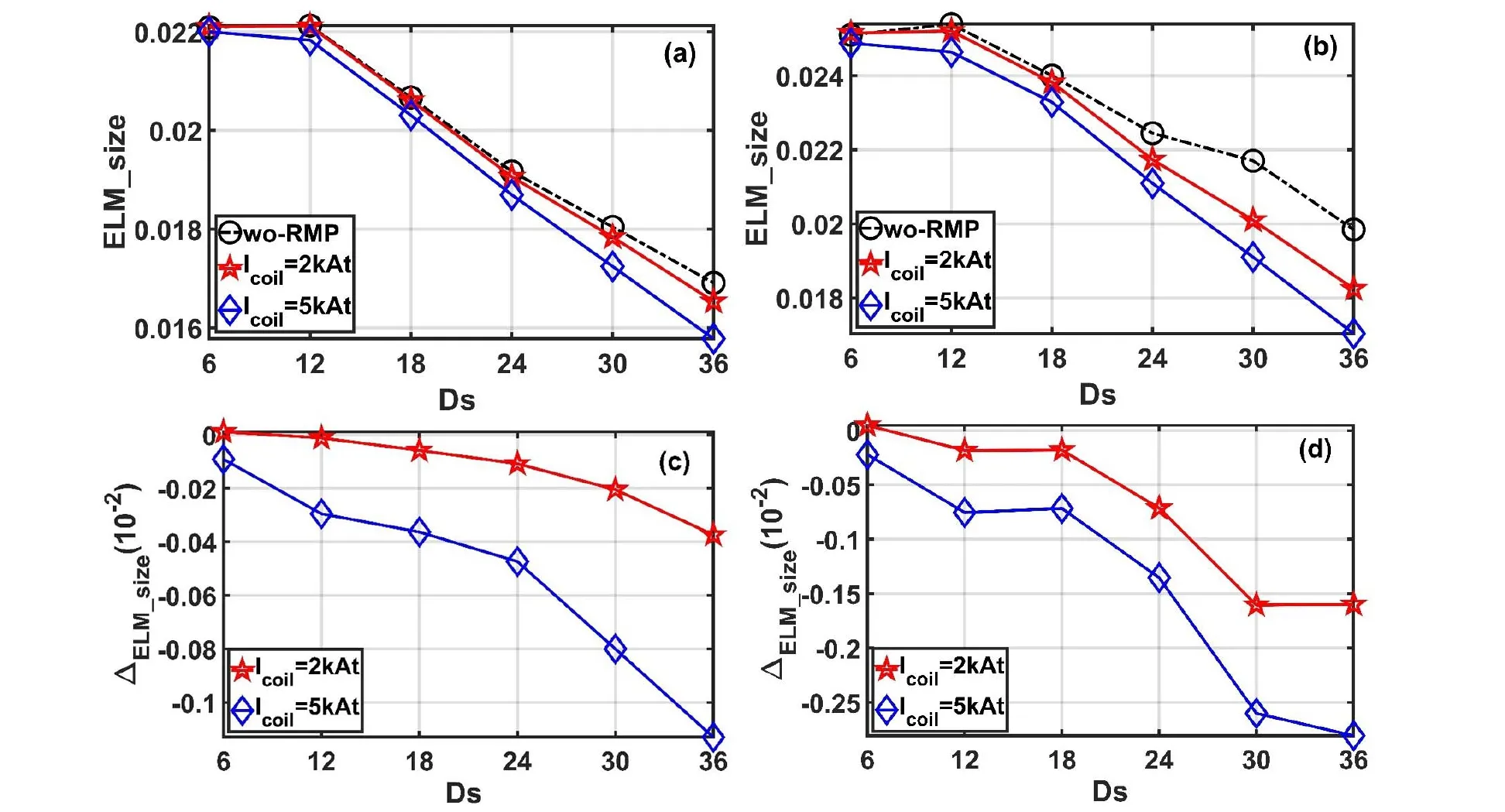
Figure 6.ELM_size at (a) t=90τA and (b) t=120τA with different toroidal rotation shear profiles.Reductions of ELM_size at (c)t=90τA and (d) t=120τA .The black dashed lines represent the case without RMP;the red and blue lines represent the case with Icoil=2 kAt and Icoil=5 kAt,Δϕ=120°,and n=3 response RMP fields,respectively.

Figure 7.Time evolution of the pressure perturbation with various toroidal mode numbers.(a) Ds=6 and (b) Ds=36 without RMP;(c)Ds=6 and (d) Ds=36 with Icoil=5 kAt,Δϕ=120°,and n=3 response RMP fields.

The reductions in ELM_size led by RMP increased with the toroidal rotation shear.To investigate the physical mechanisms,we analyzed the nonlinear evolution of the P-B modes in the turbulence transport phase,as presented in figures 7(a)-(d).As shown in figures 7(a) and (b),other modes,such as n=18,24,...,gradually developed due to the slow multimode coupling,whereas the initial most unstable mode n=21 dominated the nonlinear process.After adding Icoil=5 kAt,n=3,and Δϕ=120° RMP,other modes,such as n=18,24,...,rapidly developed,and the initial most unstable mode n=21 lost its dominant role quickly in the nonlinear process,as shown in figures 7(c) and (d).This suggests that the multimode coupling of the P-B modes is significantly enhanced by RMP.However,it is worth noting that RMP can obviously enhance the multimode coupling of P-B modes in both weak and strong rotation shear regions,that is,Ds=6 and 36,respectively.Rotational shear does not seem to have a significant impact on the enhancement of multimode coupling caused by RMP.

To further visually determine whether toroidal rotation shear has an impact on the enhancement of multimode coupling with RMP,Δp1was used to characterize the energy change of the initial most unstable mode n=21.Here,Δp1=p1,rmp-p1,wo-rmpand p1,rmp,p1,wo-rmpare the amplitudes of n=21 with and without RMP,respectively.Therefore,Δp1＜ 0 indicates that the energy of n=21 reduces more quickly when RMP is coupled to the P-B modes,which means that multimode coupling is enhanced by RMP.The impact of the toroidal rotation shear on the evolution of n=21 during the multimode coupling process is shown in figures 8(a) and (b).It is known that the transfer of energy from the initial most unstable mode n=21 to other modes,such as n=18 and 24,occurs due to the multimode coupling in the turbulence transport phase (approximately t ＞ 90τA).As shown in figure 8(a),the amplitude of n=21 gradually decreased in the turbulence transport phase without RMP.On the other hand,the rapid reduction in the amplitude of n=21 with RMP indicates that the multimode coupling was significantly enhanced by RMP,resulting in a more rapid energy transfer to other modes.Rotation shear had no significant impact on the enhanced multimode with RMP.Figure 8(b) shows the reduction in the amplitude of n=21 during the multimode coupling process,as influenced by various toroidal rotation shear.It was found that the amplitude reduction of n=21 significantly decreased in both the weak and strong rotation shear regions.

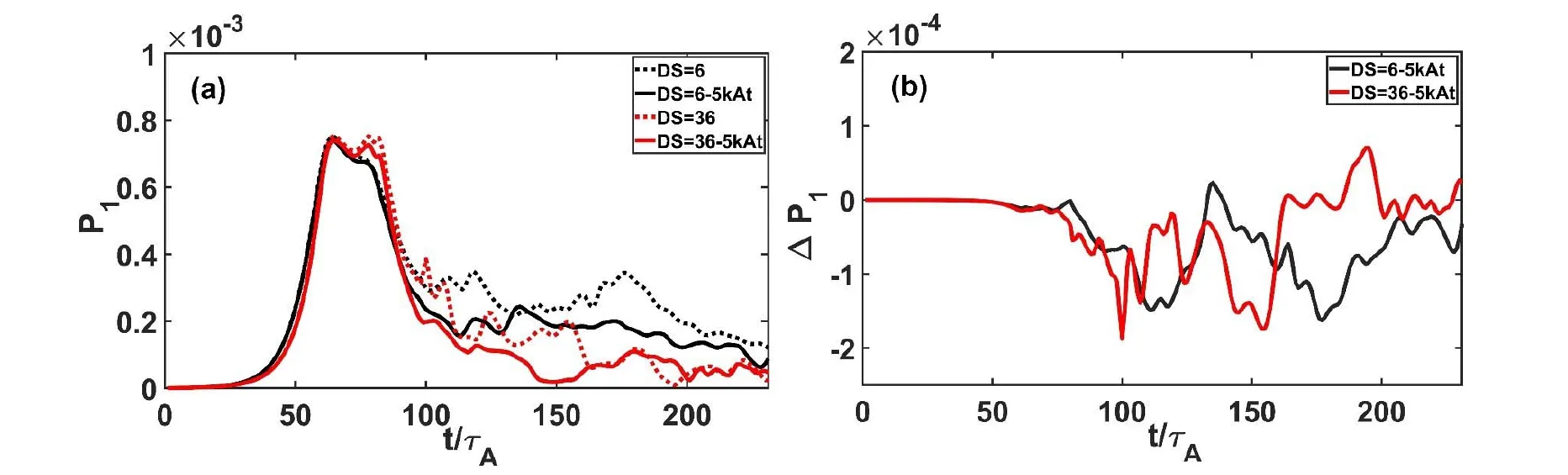
Figure 8.(a) Time evolution of the initial most unstable modes n=21;the dashed and solid lines are without and with Icoil=5 kAt,Δϕ=120°,and n=3 response RMP fields,respectively.(b) Changes in the amplitudes of n=21 after adding Icoil=5 kAt,Δϕ=120°,and n=3 response RMP fields.

The intermediate shear region (Ds=24) is the link between the weak and strong shear regions;hence,the characteristics of the multimode coupling in the link region (or intermediate shear region) are closely related to the weak and strong shear regions.An analysis of the multimode coupling with Ds=24 found that RMP can clearly enhance the multimode coupling of the P-B modes in the intermediate shear region.In summary,regardless of whether it is in a weak or strong rotation shear region,including the intermediate shear region,RMP can significantly improve the multimode coupling.However,there is no obvious dependence between the rotation shear and the enhancement of the multimode coupling induced by RMP.This suggests that rotation shear has no significant impact on the enhancement of multimode coupling that is brought about by RMP.

To further investigate why the reduction in ELM_size brought about by RMP increases with toroidal rotation shear,the E × B shearing rate was analyzed.It is widely known that the development of turbulence can be suppressed by a self-generated E × B shear,and the E × B shearing rate is defined as [42,43]

To have a clear physical cognition of the roles of toroidal rotation shear in the influence of RMP on ELM_size,the average E × B shearing rate 〈ωE×B〉 in the turbulence transport phase was analyzed.The average E × B shearing rate〈ωE×B〉 is defined as

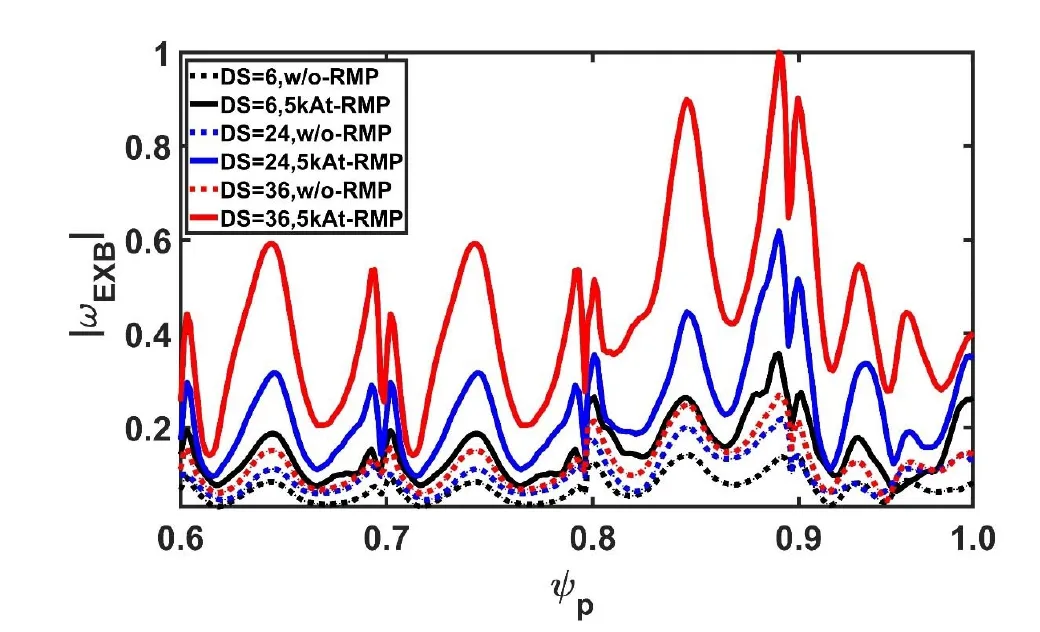
Figure 9.Average E × B shearing rate 〈ωE×B〉 between 100τA and 160τA,normalized to the maximum value.The black,blue,and red dashed lines represent Ds=6,24,and 36 without RMP,respectively.The solid lines correspond to the Icoil=5 kAt,Δϕ=120°,and n=3 response RMP fields.

Here,t1=100τAand t2=160τA.The average of the E × B shearing rate 〈ωE×B〉 is shown in figure 9.The dashed and solid lines represent without and with RMP,respectively.The results show that the E × B shearing rate was enhanced after the addition of RMP.When the equilibrium toroidal rotation shear is stronger,the enhancement of 〈ωE×B〉 with RMP also gets stronger during the turbulence transport phase.The E × B shear can reduce the turbulence transport and ELM_size;hence,RMP may lead to greater reductions in ELM_size with stronger toroidal rotation shear.

In summary,toroidal rotation shear plays an important role in the influence of RMPs on P-B modes and hence significantly affects the pedestal energy loss with RMP during ELM crashes.It is known that pedestal crashes partly depend on the multimode coupling in the turbulence transport phase.Extensive studies have shown that a moderate pedestal crash resulting from a significantly enhanced multimode coupling can replace the dramatic energy loss caused by the domination of a single mode in a nonlinear process[44-47],which may be responsible for the decrease in ELM_size.However,a detailed analysis of the enhanced multimode coupling with RMP did not reveal that the rotation shear has a significant impact on the enhancement of multimode coupling.Interestingly,RMP may lead to stronger 〈ωE×B〉,and the enhancement of 〈ωE×B〉 increases with toroidal rotation shear.Therefore,RMP may lead to greater reductions in ELM_size in the stronger toroidal rotation shear region.

4.Role of toroidal rotation with different magnitudes in the influence of RMP on P-B modes

Figure 10.(a) Equilibrium toroidal rotation (normalized to Alfvén frequency ΩA=3.24013315 × 106) with Am=0.1 -1 and (b) corresponding rotation shear.(c) Amplitudes of the resonant radial field of various components for Icoil=10 kAt,Δϕ=120°,and n=3 RMP fields with plasma response in the Am=0.1 -1 toroidal rotation profiles;ψp is the normalized poloidal flux.

The role of toroidal rotation shear is examined in detail in section 3.The focus will now shift toward examining the roles of rotation magnitudes,which mainly determine the shielding effects of plasma,on the influence of RMP on the P-B modes.It is known that changing the shear of toroidal rotation usually means that the rotation magnitude also changes simultaneously in tokamaks.Therefore,the rotation shear and magnitudes change significantly at the same time in this section.Equation (14) is used to calculate the toroidal rotation profiles.We set ψ0=0.97,C=-8955,V0=46900,and Ds=24,and vary the amplification factor Am=0.1,0.2,...1 to increase the toroidal rotation shear and magnitude at the same time,as shown in figure 10(a).Figure 10(a) shows the toroidal rotation profiles with different rotation shear and magnitudes,and figure 10(b) shows the rotation shear profiles.The rotation profiles in figure 10(a) were adopted in the MARS-F code to calculate the n=3 response RMP with current Icoil=10 kAt.The amplitudes of the various resonant radial field components with plasma response are shown in figure 10(c),and they significantly decrease with the toroidal rotation magnitudes due to the increasing shielding effects of plasma.Therefore,as shown in figures 10(a)-(c),the rotation shear increased and the rotation magnitudes changed significantly,which changed the shielding effect of plasma.Through the rotation profiles,we can simultaneously study the role of the shielding effect,which is closely related to the toroidal rotation magnitude and rotation shear in the influence of RMP on the P-B modes.

The rotation profiles in figure 10 and the corresponding Icoil=10 kAt,n=3,and Δϕ=120° response RMP calculated from the MARS-F code were adopted into the BOUT++four-field model.First,the roles of rotation shear and magnitude in the influence of RMP on the linear growth of the P-B modes are studied.The value of the hyper-Lundquist parameter is αH=1.0 × 10-4in the linear simulation.The linear growth rates of the P-B modes with different toroidal rotation profiles Am=0.1,0.2,...1 are presented in figure 11.Figures 11(a) and (b) show the without and with RMP cases,respectively.The changes in the linear growth rates of the P-B modes ‘Δγ’ with different toroidal rotation profiles are shown in figures 11(c) and (d).The linear growth rates decrease with Am,which means that the toroidal rotation shear can stabilize the P-B modes,especially the high-n modes,as shown in figure 11(a).The roles of toroidal rotation in the influence of RMP on the P-B modes are as follows.

(1) Am＜ 0.4.The rotation shear and magnitude are both low when Am＜ 0.4.In the low rotation region,the rotation shear is too weak,and hence has no obvious impact on ELM mitigation with RMP.However,a low rotation magnitude allows the resonant components to penetrate into the plasma.Therefore,the shielding effect,which is closely related to the toroidal rotation magnitudes,plays a dominant role in the influence of RMP on the P-B modes in the low rotation region,and it weakens the impact of RMP on the linear growth of the P-B modes.As shown in figure 10(c),the amplitudes of the various resonant radial field components with plasma response significantly decrease with Am,which means that the shielding effect of plasma rapidly increases with the toroidal rotation magnitude.Hence,the reductions in the linear growth rates ‘Δγ’ caused by RMP decrease with Amdue to the increasing shielding effects,as shown in figure 11(c).

(2) Am＞ 0.6.Am＞ 0.6 is the high rotation region,in which both toroidal rotation shear and magnitude are very strong.In the high rotation region,the rotation magnitude is too high to allow the resonant component to penetrate into the plasma.The shielding effect changes slightly when Amis increased in the high rotation region,as shown in figure 10(c).In the high rotation region,the rotation shear is relatively strong,and its effect on the P-B modes is significant.Hence,the rotation shear plays a dominant role in the influence of RMP on the P-B modes.As shown in figure 11(d),the reductions in the growth rates of the P-B modes,especially the high-n modes,clearly increase with the toroidal rotation shear when RMP is added.This suggests that RMP may lead to stronger reductions in the linear growth rates of the P-B modes with stronger toroidal rotation shear,which is consistent with the conclusion in section 3.

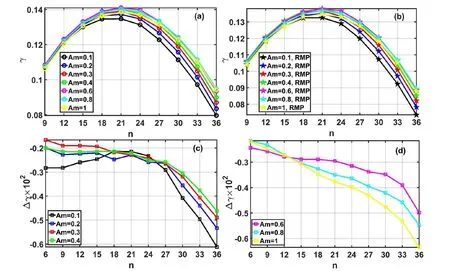
Figure 11.(a) Linear growth rates of the P-B modes versus toroidal mode numbers (n) with Am=0.1 -1 toroidal rotation profiles (a) without and (b) with Icoil=10 kAt,Δϕ=120°,and n=3 response RMP fields.(c) Changes in the linear growth rates of the P-B modes with (c)Am=0.1 -0.4 and (d) Am=0.6 -1 toroidal rotation profiles after adding Icoil=10 kAt,Δϕ=120°,and n=3 response RMP fields.

Next,we investigate the nonlinear process of an ELM crash.The parameters and non-ideal effects adopted here are the same as those in the nonlinear simulation in section 3.The evolution of the pedestal energy loss ‘ELM_size’ with different toroidal rotation profiles is presented in figure 12.The effects of toroidal rotation on ELM_size reduction are as follows.

(1) Am＜ 0.4.As shown in the area marked by the blue dashed ellipse in figures 12(a) and (d),the toroidal rotation shear is relatively weak when Am＜ 0.4.By comparing figures 12(a) and (d),we can observe that the ELM_size reductions caused by RMP decrease with Amin the low rotation region.

(2) Am＞ 0.6.The toroidal rotation shear is strong when Am＞ 0.6,as shown in the area marked by the red dashed ellipse in figures 12(a) and (d).In the high rotation region,the ELM_size reductions caused by RMP increase with Amdue to the increase in the strong rotation shear.Additionally,the ELM_size reductions increase with the RMP coil current Icoil=2 kAt,4 kAt,6 kAt.

As indicated earlier,toroidal rotation has a significant impact on ELM_size reduction with RMP.To explore the physical mechanisms behind this interesting phenomenon,the nonlinear evolution of the P-B modes in the turbulence transport phase was analyzed.

The evolution of the P-B modes in the low toroidal rotation region (Am=0.1 and 0.2) is shown in figure 13.In the linear phase (approximately t ＜ 50τAin figures 13(a)-(d)),RMP had little impact on the evolution of the P-B modes because the changes in the linear growth rates were very small.In the nonlinear turbulence transport phase (approximately t ＞ 80τA),as shown in figure 13(a),the energy slowly transferred from n=21 to other modes,such as n=18,24,...because of the slow multimode coupling without RMP;hence,n=18,24,...gradually increased.Tremendous energy was released from the pedestal because the single dominant mode n=21 was very strong in the nonlinear phase and manifested as a large ELM_size.However,as shown in figure 13(c),the initial most unstable mode,n=21,decreased significantly,and multimodes grew very rapidly in the transport turbulence phase when RMP was coupled to the P-B modes,which means that the multimode coupling was enhanced by RMP.The enhanced multimode coupling process may cause the initial most unstable mode n=21 to lose its dominant role very quickly during a pedestal crash,and multimodes grew rapidly.In other words,a moderate pedestal crash resulting from multimode coupling significantly enhanced by RMP replaces the dramatic energy loss due to the domination of a single mode in the nonlinear process [44-47],which is responsible for the reduction in ELM_size.Interestingly,the enhancement of multimode coupling caused by RMP significantly decreased with Amin the low toroidal rotation region.As shown in figures 13(c)and (d),when Am=0.1 increased to 0.2,the decrease in the dominant mode n=21 became slower.It could be that toroidal rotation magnitude increased with Am,and the shielding effect was significantly enhanced,thereby weakening the enhancement of the multimode coupling caused by RMP.

Figure 12.Distribution of pedestal energy loss ELM_size in the Am versus time plane.(a) Without RMP,with (b) Icoil=2 kAt,(c) 4 kAt,and (d) 6 kAt,Δϕ=120°,and n=3 response RMP fields.

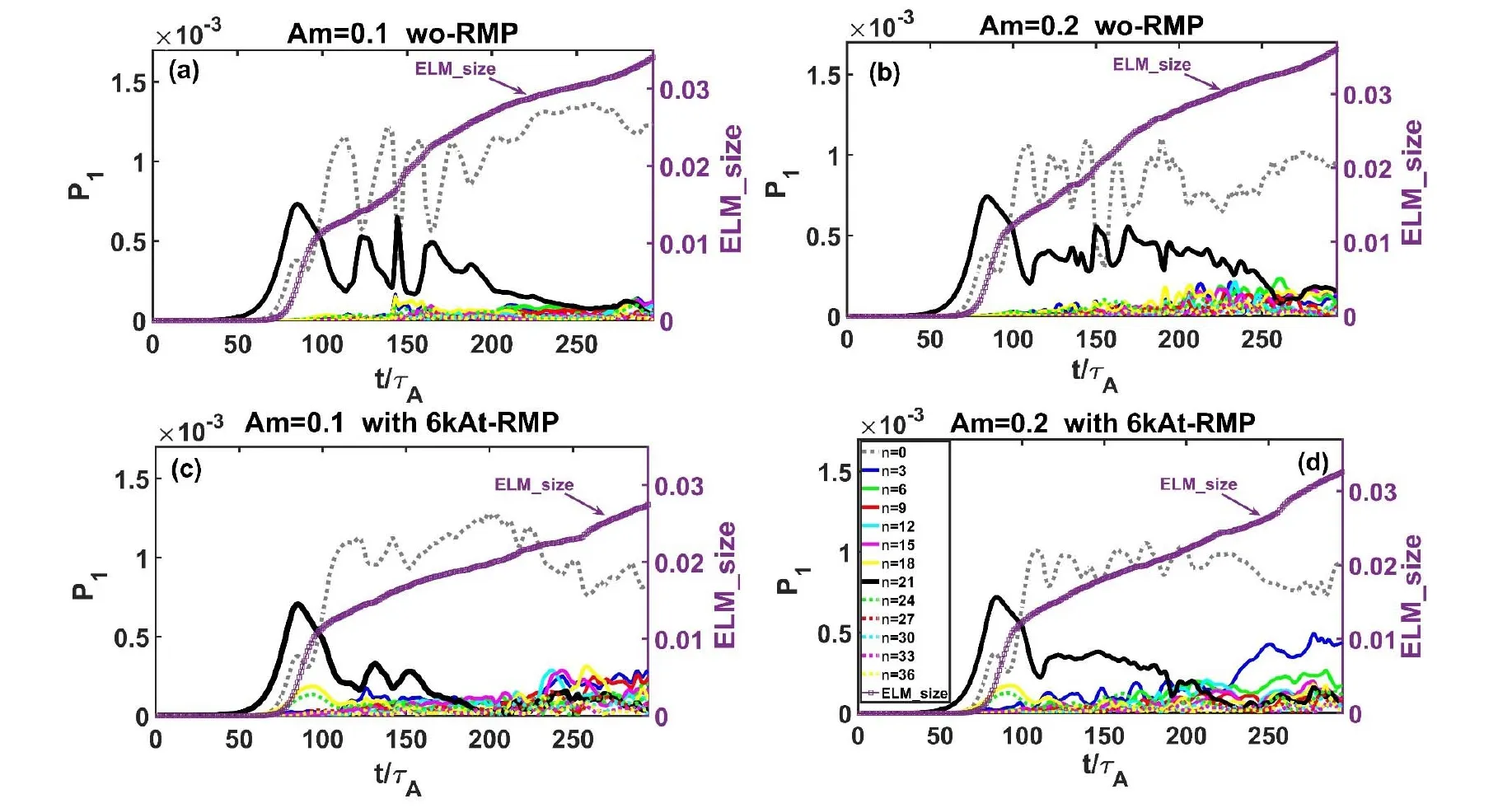
Figure 13.Time evolution of various toroidal modes of pressure perturbation.(a) Am=0.1 and (b) 0.2 without RMP;(c) Am=0.1 and (d)0.2 with Icoil=6 kAt,Δϕ=120°,and n=3 response RMP fields.

To visually present the roles of toroidal rotation magnitudes in the influence of RMP on multimode coupling,Δp1and Δp1/p1were used to characterize the energy change of the initial most unstable mode n=21.Here,Δp1/p1=Δp1/p1,wo-rmpand p1,wo-rmpwere the amplitudes of n=21 without RMP.Therefore,Δp1and Δp1/p1＜ 0 indicate that the energy of n=21 reduced more quickly when RMP was coupled to the P-B modes,which means that multimode coupling is enhanced by RMP.The impact of the toroidal rotation magnitudes on the evolution of n=21 during the multimode coupling process is shown in figures 14(a)-(c).The energy transferred from the initial most unstable mode n=21 to other modes n=18,24,...because of the slow multimode coupling.Hence,the amplitudes of n=21 gradually decreased in the turbulence transport phase without RMP,as shown in figure 14(a).However,the amplitudes of n=21 were rapidly reduced with RMP,which means that the multimode coupling was enhanced with RMP,and the energy transferred to other modes more quickly.Figures 14(b) and (c) show the reductions in the amplitudes of n=21 with different toroidal rotation magnitudes.It was found that the amplitude reductions of n=21 significantly decreased with the toroidal rotation magnitudes when Am＜ 0.4,and the time to start reducing the amplitude of n=21 was also delayed longer when Amincreased.Both the lower-amplitude reductions of n=21 and the longer delay time suggest that the enhancement of the multimode coupling with RMP was significantly weakened.This was mainly because the shielding effects of plasma on RMP—more precisely the resonant components—clearly increased with the toroidal rotation magnitude,as shown in figure 10(c).

Figure 15.Time evolution of various toroidal mode spectra of pressure perturbation.(a) Am=0.1 and (b) 0.2 without RMP;(c) Am=0.1 and (d) 0.2 with Icoil=6 kAt,Δϕ=120°,and n=3 response RMP fields.The multimode coupling is enhanced by RMP in the nonlinear phase,especially between the red and black vertical dashed lines,and the enhancement of multimode coupling induced by RMP is significantly weakened by increasing the toroidal rotation magnitudes.

We further show the roles of toroidal rotation magnitudes in the influence of RMP on the multimode coupling of the P-B modes.The toroidal mode spectrum evolution of the pressure fluctuation at the peak gradient location at the outer midplane is shown in figures 15(a)-(d).The mode spectrum strength was normalized by the maximum value at each time step.The n=0 part is not included here.As shown in figure 15(a),the initial most unstable mode n=21 dominated in the nonlinear process because of the slow multimode coupling;hence,the mode spectrum was very narrow without RMP.After adding Icoil=6 kAt,n=3,and Δϕ=120° response RMP,the initial most unstable mode n=21 lost its dominant role rapidly in the nonlinear process due to the quick multimode coupling.Hence,the mode spectrum significantly broadened,as shown in figure 15(c).This suggests that the multimode coupling of the P-B modes was enhanced by RMP in the nonlinear phase,especially between the red and black vertical dashed lines.As shown in figures 10(a) and (c),with the increase in toroidal rotation magnitude,the screening on RMP—more precisely the resonant components—became stronger.The enhancement of multimode coupling induced by RMP was significantly weakened by the increasing shielding effects of the plasma when the toroidal rotation magnitude increased,as shown in figures 15(c) and (d).Therefore,RMP led to stronger reductions in ELM_size with lower rotation magnitudes,such as Am=0.1.In brief,RMP can lead to reductions in ELM_size by enhancing the multimode coupling in the turbulence transport phase.The toroidal rotation shear was relatively weak and had little impact on the P-B modes with RMP when Am＜ 0.4.The shielding effects on RMP increased with the toroidal rotation magnitude,leading to a significant weakening of the enhancement of multimode coupling with RMP.Therefore,the reductions in ELM_size caused by RMP decreased with Amin the weak toroidal rotation shear region (Am＜ 0.4).

As shown in figure 12,contrary to the results in the low toroidal rotation region (Am＜ 0.4),the reduction in ELM_size caused by RMP increased with Amin the high toroidal rotation region (Am＞ 0.6).The toroidal rotation shear was relatively strong and played a dominant role in the influence of RMP on the P-B modes when Am＞ 0.6.The average E × B shearing rate 〈ωE×B〉 in the turbulence transport phase is shown in figure 16.The dashed and solid lines represent without and with RMP,respectively.It was found that the E × B shearing rate is stronger when RMP was added,and the enhancement of 〈ωE×B〉 caused by RMP increased with the equilibrium toroidal rotation shear during the turbulence transport phase.It is widely known that the development of turbulence can be suppressed by the selfgenerated E × B shear,leading to the reduction in turbulence transport and ELM_size.Hence,RMP could lead to higher reductions in ELM_size with stronger toroidal rotation shear.This is consistent with the conclusion in section 3.In addition,it is worth noting that all the 〈ωE×B〉 were significantly enhanced by RMP when Am=0.1,0.2,…,0.8,1.0.However,toroidal rotation had no impact on the enhancement of the 〈ωE×B〉 induced by RMP when Am＜ 0.4,because the toroidal rotation shear was too weak in the low rotation region.

Figure 16.Average E × B shearing rate 〈ωE×B〉 between 120τA and 220τA,which is normalized to the maximum value.The red and green dashed lines represent Am=0.8 and 1 without RMP,respectively.The solid lines represent the Icoil=6 kAt,Δϕ=120°,and n=3 response RMP fields.

5.Conclusion and discussion

Toroidal rotation shear and magnitude are the two main parameters that determine the toroidal rotation profiles.Toroidal flow may play a dual role in the influence of RMP on P-B modes and their subsequently triggered ELM crashes.On one hand,the rotation shear can impact the evolution of P-B modes [26-28];hence,it would play an important role in the influence of RMP on the P-B modes.On the other hand,the magnitude of toroidal rotation can significantly change the strength of the resonant components of RMP through the shielding effects of plasma [29,31],which may influence the direct coupling between RMP and the P-B modes.In this study,the roles of toroidal rotation in ELM mitigation by RMP have been investigated by separately studying the impact of the two parameters on ELM mitigation with RMP.

First,we adopted the toroidal rotation profiles with significantly different shear.Meanwhile,the rotation magnitudes were kept as unchanged as possible to ensure that the amplitudes of the resonant components of the RMP changed slightly.Thus,we excluded the interference caused by the changing shielding effects due to the varying rotation magnitudes.It was found that both the reductions in the linear growth rates and ELM_size increase with the toroidal rotation shear.The analysis shows that the E × B shearing rate is significantly stronger when RMP is added.When the equilibrium toroidal rotation shear is stronger,the enhancement of 〈ωE×B〉 that is caused by RMP also becomes stronger during the turbulence transport phase.The E × B shear can reduce the turbulence transport and ELM_size;hence,RMP may lead to higher reductions in ELM_size with stronger toroidal rotation shear.

Second,the role of the toroidal rotation magnitude in the RMP-ELM mitigation was studied.The results show that RMP can lead to reductions in ELM_size by enhancing the multimode coupling in the turbulence transport phase.The shielding effects on RMP increase with toroidal rotation magnitude,causing the enhancement of multimode coupling induced by RMP to be significantly weakened.Therefore,the reductions in ELM_size caused by RMP decrease with rotation magnitude.It is worth noting that changing the toroidal rotation shear usually means that the rotation magnitude also changes at the same time in tokamak devices.Therefore,the varying rotation shear and magnitudes were simultaneously considered in the simulation by scanning the amplification factor Am.The modeling results suggest that ELM_size reductions with RMP nonmonotonically depend on the toroidal rotation in tokamaks.In the low rotation region,Am＜ 0.4 because the rotation shear is very weak,the impact of toroidal rotation shear on the ELM_size reduction is small,and the shielding effect that is closely related to the rotation magnitude plays a dominant role in the ELM_size reductions with RMP.The screening on RMP increases with the rotation magnitude,and hence weakens the reduction in ELM_size caused by RMP.Therefore,the ELM_size reductions caused by RMP decrease with Amin the low rotation region.However,in the high toroidal rotation region Am＞ 0.6,the rotation shear is relatively strong and plays a dominant role in the ELM_size reduction caused by RMP.The E × B shearing rate is significantly enhanced when RMP is added,and the enhancement of 〈ωE×B〉 caused by RMP also increases with the toroidal rotation shear in the turbulence transport phase,leading to the ELM_size reduction increase with Amin the high rotation region.

As presented in figures 5 and 6,the reduction in ELM size is relatively weak.In a previous study [40],the impact of RMP on ELM crashes was found to be multiple.On one hand,RMP can reduce ELM_size in the nonlinear process by enhancing the multimode coupling of P-B modes.The plasma response can weaken the impact of RMP on ELM by partially screening the applied RMP fields,and more precisely,the resonant components.On other hand,RMP can also further reduce the ELM_size by changing the equilibrium pressure profiles by the transport response.Although the impact of multimode coupling on ELM_size is relatively weaker than the latter,studying the impact of multimode coupling can still help us understand the role of toroidal rotation in RMP-ELM mitigation.In addition,the same results regarding the impact of RMP on multimode coupling have been reported in the JOREK code [44,45].It is significant that the same effects of enhanced multimode coupling were further observed using a different code,BOUT++.In this study,the role of toroidal rotation in multimode coupling was systematically investigated.On one hand,by exploring the role of toroidal rotation in multimode coupling and RMPELM mitigation,this study may provide further information for understanding the physical mechanism of RMP-ELM mitigation.On the other hand,it is also expected to help understand the influence of toroidal rotation on RMP-ELM mitigation and provide guidance for optimization of plasma parameters,such as toroidal rotation,to achieve better ELM control in experiments.

The simulation region is symmetric in toroidal direction;therefore,only one nth of the torus is calculated,where n depends on the RMP toroidal number to economize the computing resources.This is a common method used in BOUT++simulations to improve computing efficiency.In our study,to improve computing efficiency,only one-third of the torus region was calculated in the BOUT++simulation;hence,the RMP toroidal number is n=3,which is distinct from the n=1 RMP adopted in shot 52340.However,the relevant physical mechanism behind the RMPELM mitigation would be the same.For example,there are some imperfections because the nonlinear calculations only consider a fraction of the domain;hence,the simulations missed two-thirds of the spectrum.To check whether ignoring these primary nonlinear channels is justified,the Appendix presents the nonlinear calculations with the whole domain,in which the toroidal number of P-B modes includes n=0,1,2,3,4,5,6,….Correspondingly,the toroidal number of RMP is n=1.The conclusion of n=1 RMP is consistent with that of n=3 RMPs.This justified the nonlinear coupling simulation using only a fraction of the domain.In conclusion,both n=1 and n=3 RMPs can lead to reductions in ELM_size by enhancing the multimode coupling in the turbulence transport phase,and the toroidal rotation magnitude plays an important role in ELM mitigation by influencing the enhancement of multimode coupling induced by RMP.With the increase in toroidal rotation magnitude,the shielding effect of plasma on RMP—more precisely the resonant components—becomes stronger,which leads to the significant weakening of the enhancement of the multimode coupling induced by RMP;hence,the ELM_size reduction decreases.Although there are some differences between the impact of n=1 and n=3 RMP fields on the multimode coupling of P-B modes,the relevant physical conclusions and mechanisms of n=1 and n=3 RMP in the multimode coupling of P-B modes during ELM crashes are the same.

The presented results are preliminary discussions on the role of equilibrium toroidal rotation in the reduction of pedestal energy loss with RMP.Some aspects are expected to be discussed and improved in our next study.In this study,we only examined the impact of the equilibrium toroidal rotation on ELM_size reduction.MARS-F is a linear response model.The RMP fields have a significant influence on toroidal rotation by braking [48,49].In turn,toroidal rotation would affect the penetration of the resonant component via the shielding effect.This is a complex nonlinear response process,which is a challenge for us in the calculation of plasma response in the future.

It is well known that some equilibrium profiles,such as density profile,safety factor,equilibrium toroidal rotation,and Spitzer resistivity determined by the electron temperature,have an important influence on the plasma response.Therefore,to calculate the response RMP fields more accurately,this study adopted real profiles,including real density profiles,real safety factor,and Spitzer resistivity determined by real electron temperature,in MARS-F simulation,and the same equilibrium safety factor,toroidal rotation,and resistivity profiles were used in both MARS-F and BOUT++for self-consistency.However,to improve the computational efficiency of the BOUT++simulation,the density was set as a constant n0=3 × 1019m-3in the BOUT++simulation,which is close to the electron density in shot 52340.Although we adopted a constant density in the BOUT++simulation,the main physical conclusion that involved the role of toroidal rotation in RMP-ELM mitigation remained unchanged.Of course,the density profile itself would influence the P-B modes and subsequent ELM crash,which has been widely examined in previous studies [43,50].Therefore,more physical phenomena would be observed in the RMP-ELM mitigation if the effect of the real density profile is considered.The influence of the density profile on the instability of P-B modes during RMP-ELM mitigation will be explored in a future study.

It was found that ELM control with RMP nonmonotonically depends on the toroidal rotation.Both the low toroidal rotation and the relatively high rotation with a strong rotation shear are favorable for ELM mitigation with RMP.The results from MAST [14,24,25] found that ELM mitigation increases with the size of the lobe structure near the X-point,and the lobe length decreases with toroidal rotation,which suggests that the better ELM mitigation can be achieved with low toroidal rotation.This indicates that ELM mitigation is closely related to the shielding effect,which partly depends on the toroidal rotation,and lower plasma rotation was also found to be favorable to access strong ELM mitigation and ELM suppression in EAST [9,11].In our study,the screening effect on RMP—more precisely the resonant components—was also found to play dominant roles in the low rotation region,and the relevant results suggest that the reduction in ELM amplitude decreases with toroidal rotation.

Additionally,recent results from DIII-D [19-21]revealed an apparent toroidal rotation threshold for ELM suppression with RMP,and ELM suppression is lost (or achieved) when the toroidal rotation is below (or above) the threshold.Similarly,ELM suppression was achieved with a high toroidal rotation,Vtor,ped＞ 40 km s-1,in KSTAR [22,23].These experiments indicate that a high toroidal rotation may be beneficial for ELM control with RMP.Some further studies [19,20] on DIII-D focused on resolving the cause of this rotation threshold.The relevant results show that field penetration,which is closely related to the changes in the E × B flow or perpendicular electron flow near the pedestal top,plays a crucial role in ELM suppression with RMP.This can be explained by the inward motion of the zero-crossing point of the perpendicular electron flow,which moves the region of field penetration too far from the pedestal top when the rotation is too low.In our study,the relatively high rotation was also found to be favorable for ELM mitigation with RMP,although only in the strong rotation shear region.In a previous study [40],the results for toroidal flow also showed that the resonant components of RMPs,whose corresponding rational surface is located at the pedestal top,can lead to stronger reductions in ELM_size in the nonlinear phase.This suggests that the penetration of resonant components,whose corresponding rational surface is located at the pedestal top,may play a major role in ELM mitigation.However,this previous study only partially discussed the role of toroidal rotation in RMP-ELM mitigation.In this study,we systematically investigated the influence of toroidal rotation on RMPELM mitigation.However,the field penetration related to the changes in the perpendicular electron flow is a complex nonlinear response process,and our model does not include the perpendicular electron flow mode.Future work will consider a more self-consistent work frame and include more flow models,such as toroidal rotation evolution and perpendicular electron flow.In particular,a relevant model for perpendicular electron flow is under active investigation.In the future,comparing relevant modeling results and experiments may yield more interesting physical phenomena and conclusions.Further investigation of the effects of E × B flow or perpendicular electron flow on field penetration in ELM suppression/mitigation will be reported in a future study.

Acknowledgments

The authors thank Xueqiao Xu and Tianyang Xia for their contributions to the BOUT++framework,Yueqiang Liu for his help on the MARS-F code,and Youwen Sun and Manni Jia for providing the equilibrium data on EAST tokamaks.This work was supported by the National MCF Energy R&D Program of China (Nos.2019YFE03090400 and 2019YFE03030004),National Natural Science Foundation of China (Nos.12375222 and 11775154),and National Key R&D Program of China (Nos.2017YFE0301203 and 2017YFE0301101).

Appendix.Results of n=1 RMP

The simulation calculated the nonlinear coupling process with the whole domain instead of considering only a fraction of the domain.Correspondingly,the toroidal number of RMP is n=1.The grid-point space size of the simulation region was increased to (Nx,Ny,Nz)=(260,128,256) to achieve basic computing accuracy for the nonlinear simulation.Here,the parameter profiles are the same as in the n=3 RMP cases if not otherwise specified,and the detailed simulation work is as follows.

For step 1,we still calculated the n=1 response RMP fields under Am=0.1 and 0.3 toroidal rotation profiles based on MARS-F.The Am=0.1 and 0.3 rotation profiles are shown in figure A1(a) and are the same as figure 10(a).The coil current of n=1 RMP is Icoil=6 kAt and Δϕ=0°.The amplitudes of the various resonant radial field components with plasma response are shown in figure A1(b),and they significantly decreased with the toroidal rotation magnitudes due to the increasing shielding effects of plasma when Am=0.1 increased to Am=0.3.

For the second step,the Am=0.1 and 0.3 rotation profiles and the corresponding Icoil=6 kAt,n=1,Δϕ=0°response RMP calculated from the MARS-F code were adopted in the BOUT++four-field model.A small initial vorticity perturbation with toroidal number n=21 was set to U1=1.0 × 10-4in the simulation.The nonlinear processes of the ELM crash were calculated,and ELM_size is presented in figure A2.It was found that n=1 RMP can reduce ELM_size,and the reductions in ELM_size due to RMP are significantly influenced by toroidal rotation.The ELM_size reduction due to RMP decreased with toroidal rotation magnitudes when Am=0.1 increased to Am=0.3.The results are consistent with those for n=3 RMP.

Now,we explore the impact of n=1 RMP on nonlinear multimode coupling.Figure A3(a) presents the time evolution of the initial most unstable modes n=21,and the dashed and solid lines are without and with Icoil=6 kAt,Δϕ=0°,and n=1 response RMP fields,respectively.As shown in figure A3(b),Δp1is used to characterize the energy change of the initial most unstable mode (n=21),and Δp1＜ 0 indicates that the energy of n=21 reduces more quickly when RMP is coupled to P-B modes,which means that multimode coupling is enhanced by RMP.

Figure A2.(a) Time evolution of ELM_size without RMP (solid lines),with Icoil=6 kAt (dashed lines),Icoil=6 kAt,Δϕ=0°,n=1 response RMP fields when adopted Am=0.1 and 0.3 toroidal rotation profiles.

The impact of the toroidal rotation magnitudes on the evolution of n=21 during the multimode coupling process is shown in figures A3(a) and (b).As shown in figure A3(a),the amplitudes of n=21 gradually decreased in the turbulence transport phase without RMP.However,the amplitudes of n=21 rapidly decreased with RMP,which means that the multimode coupling is enhanced by RMP,energy transfers to other modes more quickly,and toroidal rotation magnitudes have a significant impact on the enhancement of the multimode coupling.When the rotation magnitude increases from Am=0.1 to 0.3,the value of Δp1decreases and the time to start reducing the amplitude of n=21 is delayed for a longer period,as presented in figure A3(b).Both the lower-amplitude reductions of n=21 and the longer delay time suggest that the enhancement of the multimode coupling with RMP is significantly weakened when the toroidal rotation magnitude increases.This is mainly because the shielding effects of plasma on RMP—more precisely the resonant components—clearly increase with the toroidal rotation magnitude.

Figure A1.(a) Equilibrium toroidal rotation (normalized to Alfvén frequency) with Am=0.1 and 0.3.(b) The amplitudes of the resonant radial field of various components for Icoil=6 kAt,Δϕ=0°,and n=1 RMP fields with plasma response in the Am=0.1 and 0.3 toroidal rotation profiles;ψp is the normalized poloidal flux.

Figure A3.(a) Time evolution of the initial most unstable mode n=21;the dashed and solid lines represent without and with Icoil=6 kAt,Δϕ=0°,and n=1 response RMP fields,respectively.(b) Changes in the amplitudes of n=21 after adding Icoil=6 kAt,Δϕ=0°,and n=1 response RMP fields.

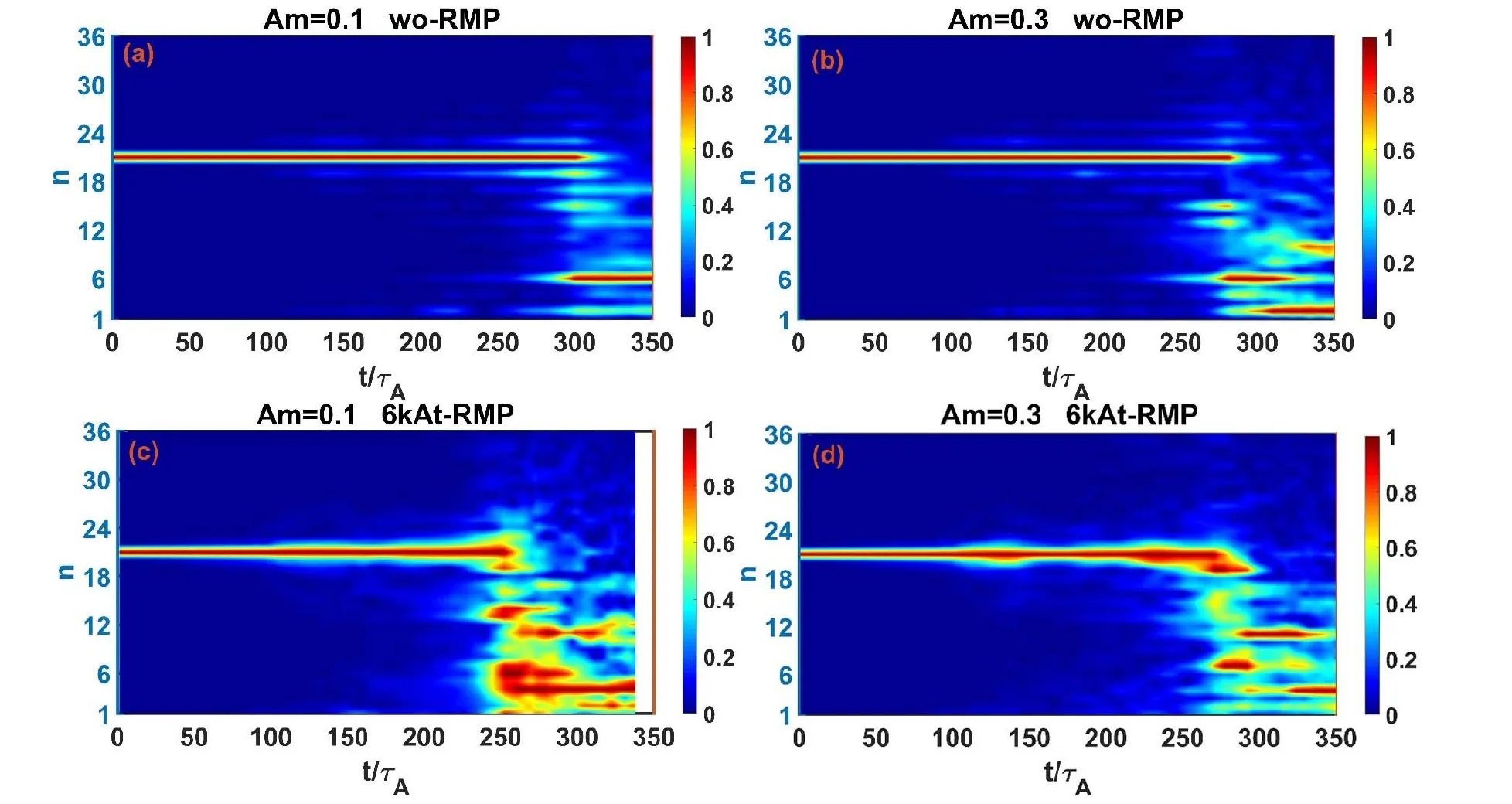
Figure A4.Time evolution of various toroidal mode spectra of pressure perturbation: (a) and (b) Am=0.1 and 0.3 without RMP,respectively;(c) and (d) Am=0.1 and 0.3 with Icoil=6 kAt,Δϕ=0°,and n=1 response RMP fields,respectively.The multimode coupling is enhanced by RMP in the nonlinear phase,and the enhancement of the multimode coupling induced by RMP is significantly weakened by an increase in toroidal rotation magnitudes.

To further show the roles of toroidal rotation magnitudes in the influence of RMP on the multimode coupling of P-B modes,the toroidal mode spectrum evolution of the pressure fluctuation at the peak gradient location at the outer midplane is shown in figures A4(a)-(d).The mode spectrum strength is normalized by the maximum value at each time step.The n=0 part is not presented here.As shown in figure A4(a),the initial most unstable mode n=21 dominates in the nonlinear process due to the slow multimode coupling;hence,the mode spectrum is very narrow without RMP.After adding the Icoil=6 kAt,n=1,and Δϕ=0° response RMP,the initial most unstable mode n=21 loses its dominant role rapidly in the nonlinear process due to the quick multimode coupling;hence,the mode spectrum significantly broadens,as shown in figure A4(c).This suggests that the multimode coupling of P-B modes is enhanced by RMP in the nonlinear phase.Compared with figure A4(c),the enhancement of multimode coupling induced by RMP is significantly weaker when the toroidal rotation magnitude increases to Am=0.3,as shown in figure A4(d).

In summary,RMP can lead to reductions in ELM_size by enhancing the multimode coupling in the turbulence transport phase,and the toroidal rotation magnitude plays an important role in ELM mitigation by influencing the enhancement of multimode coupling.With the increase in toroidal rotation magnitude,the shielding effect of plasma on RMP—more precisely the resonant components—becomes stronger,which leads to a significant weakening of the enhancement of the multimode coupling;hence,the ELM_size reduction decreases.The conclusion for n=1 RMP is consistent with that for n=3 RMPs.This justifies the nonlinear coupling simulation with only a fraction of the domain.