基于最小二乘法和BP神经网络的磁流变阻尼器H-B模型参数辨识方法

张忠奎，张晗，闫洋洋

(1.潍坊科技学院山东省高校设施园艺实验室，山东潍坊 262700；2.深圳迈瑞生物医疗电子股份有限公司，广东深圳 518055)

0 前言

磁流变液是一种新型智能材料，由可磁化粒子和基液组成，磁流变液的剪切屈服应力随不同的磁感应强度发生变化[1-2]。磁流变液阻尼器是以磁流变液为工作介质的智能控制装置，借助于磁流变液剪切屈服应力随磁感应强度的变化而变化的性质，在不同的电流下，输出的阻尼力连续可调。因此磁流变液阻尼器在建筑物减震、转子抑振、斜拉索桥梁振动控制、车辆悬架抑振、机械减振及光整加工等领域得到了广泛的应用[3-8]。

建立准确的阻尼力输出模型是磁流变阻尼器应用的前提。阻尼特性建模主要有理论建模和实验建模2种。GRACZYKOWSKI、PAWOWSKI[9]考虑磁流变液的压缩性和通过腔室的流动影响，提出了一种新的阻尼器理论建模方法。实验中的建模主要是利用实验数据对经典模型的参数进行辨识。Bingham模型是目前常见且实用的磁流变阻尼器参数化动力模型，但是磁流变液的剪切稀化现象导致的非线性滞回特性使得该模型在参数辨识时存在误差[10]。孔祥东等[11]通过改进Bingham模型提高了模型精度，解决了高阶曲线的Runge振荡现象。目前，磁流变阻尼器常见的参数化动力模型包括双黏性滞回模型[12]、Bouc-Wen模型[13]、双曲正切模型[14]、修正Dahl模型[15]、正弦曲线模型[16]等。

H-B(Herschel-Bulkley)模型能够较好地模拟磁流变阻尼器由于剪切稀化现象导致的非线性滞回特性[17-18]。但是采用H-B模型辨识时，参数值通常随试验条件而变化，导致阻尼力辨识误差较大。因此本文作者从磁流变阻尼器H-B模型出发，在理论和仿真的基础上，提出一种最小二乘法和BP神经网络相结合的磁流变阻尼器H-B模型参数辨识方法。通过最小二乘法和BP神经网络获得各参数与电流的函数关系，从而对磁流变阻尼器的阻尼力进行准确计算。最后通过磁流变阻尼器阻尼特性实验对参数辨识结果的通用性与准确性进行实验验证。

1 磁流变阻尼器设计及仿真

1.1 磁流变阻尼器结构设计

图1所示为设计的磁流变液阻尼器，结构参数为：阻尼通道长度70 mm，通道间隙2 mm，缸筒内径38 mm，活塞杆径10 mm。在外力的作用下，活塞杆推动活塞沿缸筒左右移动，迫使磁流变液流过阻尼通道。由流体纳维斯托克斯方程可知，在磁流变液的流动过程中，阻尼器阻尼通道两端产生压力差，从而产生阻尼力。

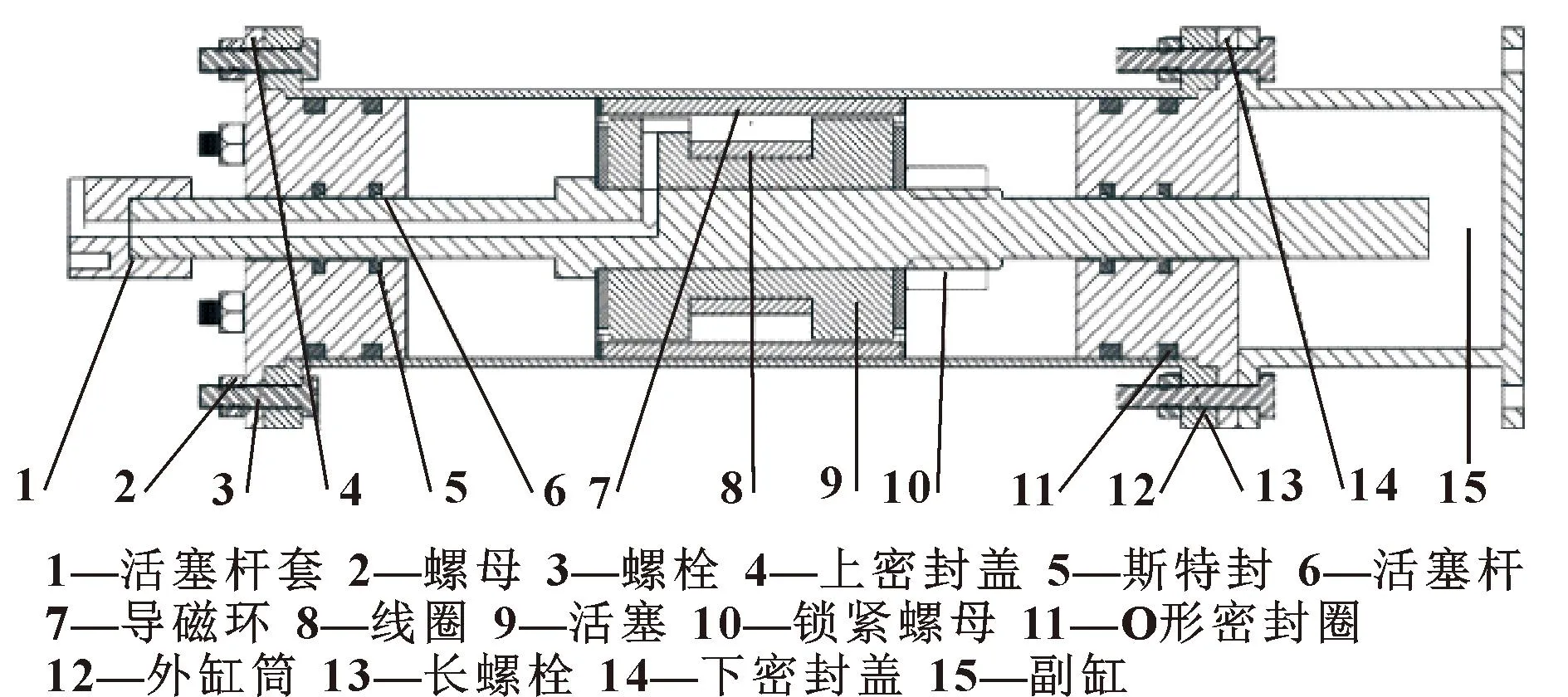
图1 磁流变液阻尼器结构设计

根据磁流变阻尼器的结构，输出阻尼力表达式[19]为

F=cev+FI

(1)

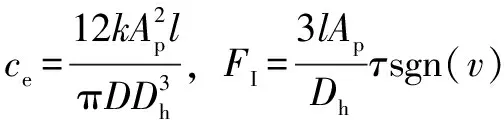
其中：ce为磁流变液的阻尼系数；FI为库仑阻尼力；k为黏度系数；v为活塞相对缸体的速度；l为阻尼器阻尼通道有效长度；D为缸体内径；Ap为活塞有效面积；Dh为活塞阻尼孔直径。

1.2 磁流变阻尼器磁场仿真

对磁流变阻尼器输出阻尼力进行理论计算时，只描述了剪切应力与阻尼力的关系，电流与剪切屈服应力的关系未知。通过研究磁流变液特性可知：磁场的变化直接影响磁流变液的剪切屈服应力，因此首先对阻尼器磁场进行仿真分析，计算电流与剪切应力之间的关系，从而计算阻尼器输出阻尼力。在磁场作用下计算磁流变液流过阻尼通道所产生的阻尼力，首先要明确磁流变液的本构方程，磁场作用下的磁流变液是一种典型的非牛顿流体，即其切应力和剪切应变速率之间的关系不是线性的。工程实际中采用Bingham模型的较多，但是磁流变液的剪切稀化现象导致的非线性滞回特性使得该模型在参数辨识时存在误差。文中将采用H-B模型对磁流变阻尼器进行分析。H-B模型的本构方程为

(2)

剪切屈服应力和磁感应强度的关系可以从所使用的磁流变液的性质得到，而磁感应强度和电流的关系则与多个因素相关，如线圈匝数、导线直径、活塞直径等结构参数，因此设计磁流变液阻尼器时，需要对其进行磁场仿真。

增热型吸收式热泵是以消耗高温热能为代价，通过向系统中输入高温热源，进而从低温热源中回收一部分热能，提高其温度，以中温热能供给用户。将热泵技术应用于回收油页岩干馏污水的余热，以炼油厂瓦斯尾气锅炉产生的蒸汽(0.8 MPa)为动力，以干馏污水为低温热源，回收干馏污水的热量用于冬季采暖。干馏污水处理及热量回收的工艺流程图见图4。

磁场作用下，材料的磁感应强度受其磁化特性的影响很大。一般铁磁性材料的磁化曲线呈非线性。在磁场强度较小时，磁感应强度增加很快，当磁场强度上升到一定程度时，磁感应强度几乎不再增加，达到磁饱和状态。仿真中采用的导磁材料为纯铁，磁化曲线如图2所示，在磁导率大的地方将磁化曲线点数设置得密集一些，当达到磁饱和后，也即越过工作点之后的曲线点数设置稀疏一些，由此提高计算精度和效率。

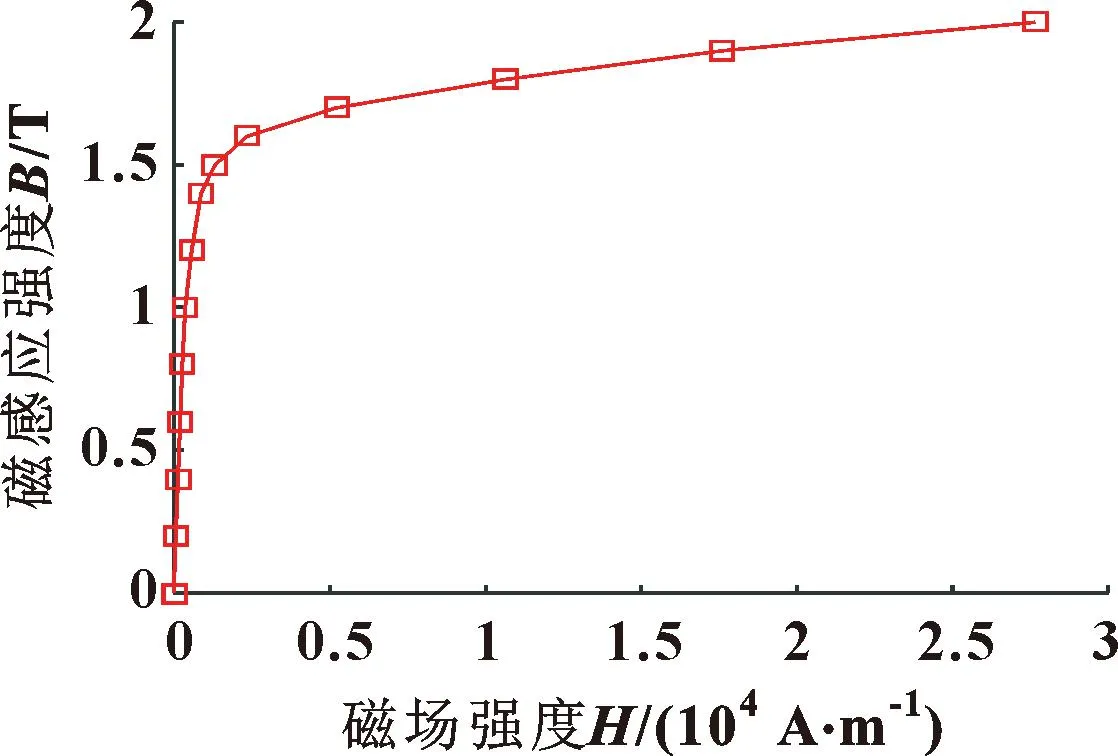
图2 纯铁磁感应强度与磁场强度关系曲线

为了探究阻尼通道处磁感应强度的变化规律，在磁流变液阻尼器流体域上给定3个测点A、B、C，如图3所示。电流分别设置为0、0.5、1.0、1.5、2.0、2.5、3.0、3.5 A，通过仿真得到了点A、B、C在不同电流下的磁感应强度如图4所示。仿真得到的阻尼器磁场磁感线分布如图5所示。

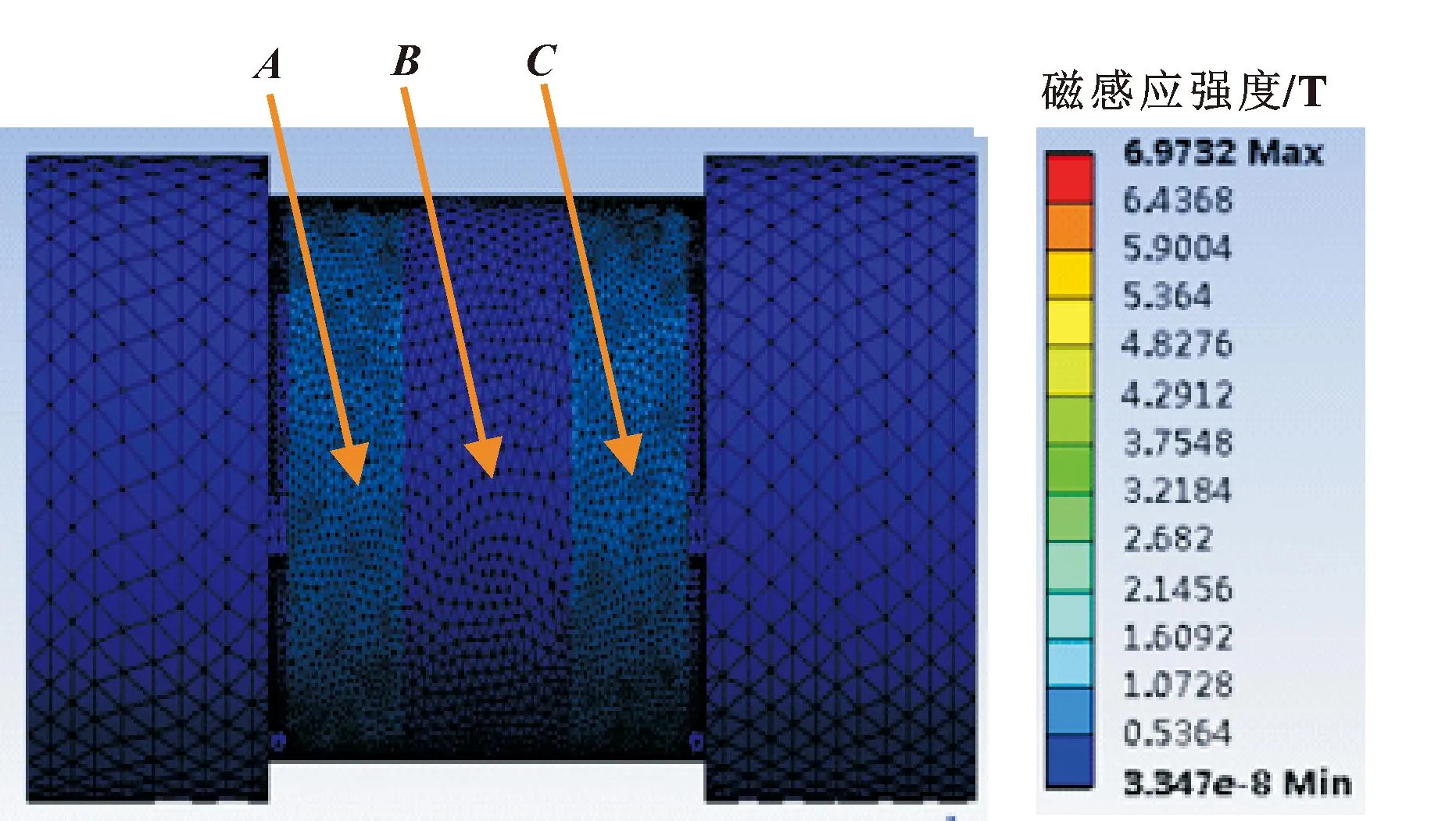
图3 磁流变液测点分布

图4 不同电流下的磁感应强度

图5 磁流变液阻尼器磁感线分布

由图4可知：点A、C的磁感应强度变化趋势基本一致，随着电流的增加，磁感应强度先快速上升后保持稳定。点A、C磁感应强度约为2.5×10-1T，点B磁感应强度约为3.1×10-3T。与点A、C相比，点B磁感应强度非常小。由图5可知：点B处包裹有线圈，通过的磁感线较少。根据点A、C处的磁感应强度数据可计算出电流与磁感应强度间的关系。

文中所采用的磁流变液的性质如图6所示。根据图6中的数据可计算出磁流变液剪切屈服应力与磁感应强度关系曲线，从而计算出电流与剪切屈服应力之间的关系。

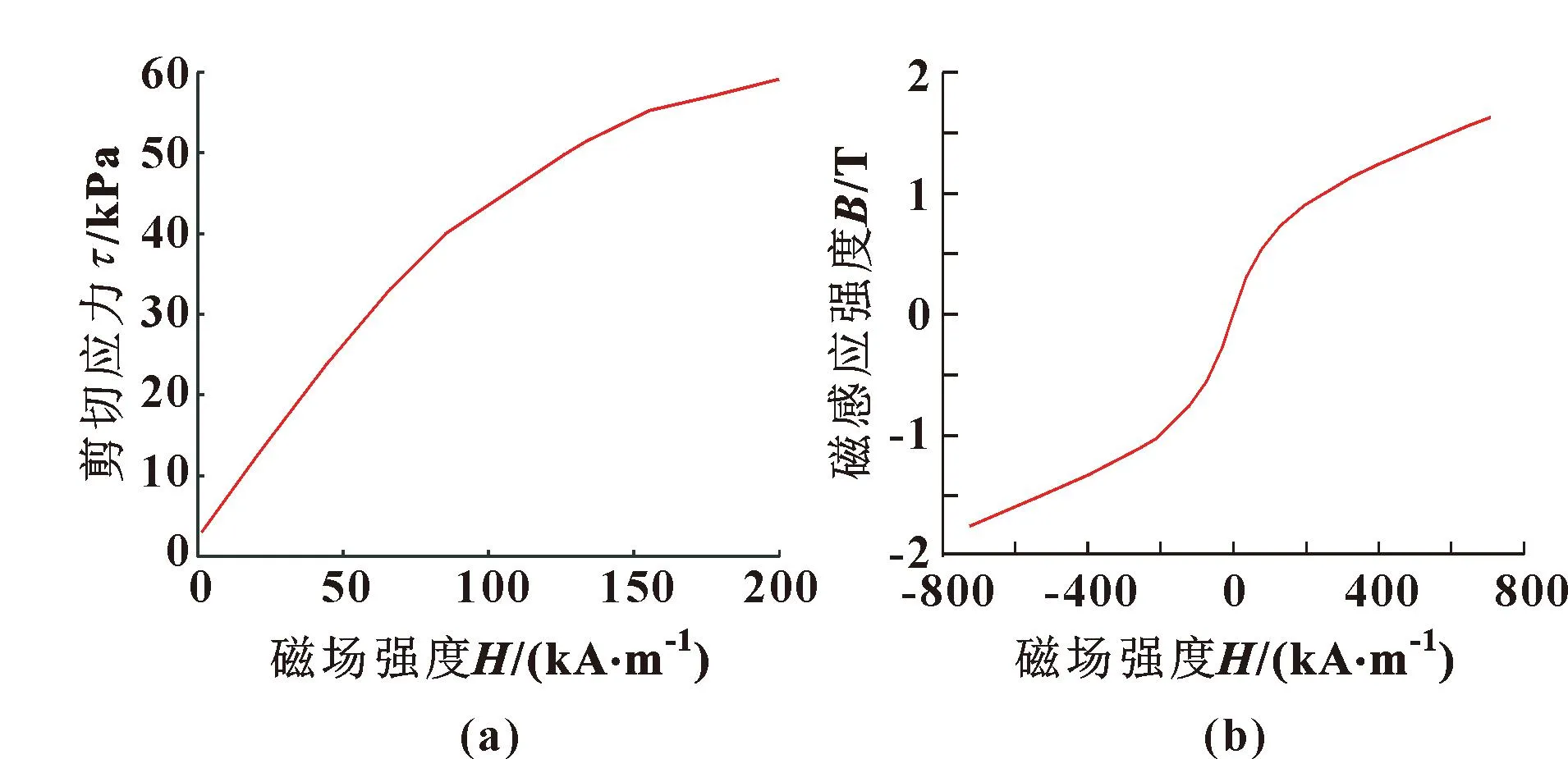
图6 磁流变剪切屈服应力(a)和液磁感应强度(b)曲线

1.3 磁流变阻尼器阻尼力计算

通过Fluent仿真可以得到阻尼器流体域的压力分布，如图7所示，磁流变液在阻尼器内部的流速分布如图8所示。对活塞端面上的压力分布进行积分，得到端面阻尼力。

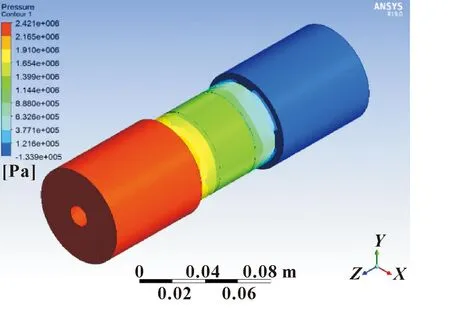
图7 磁流变液阻尼器压力分布云图

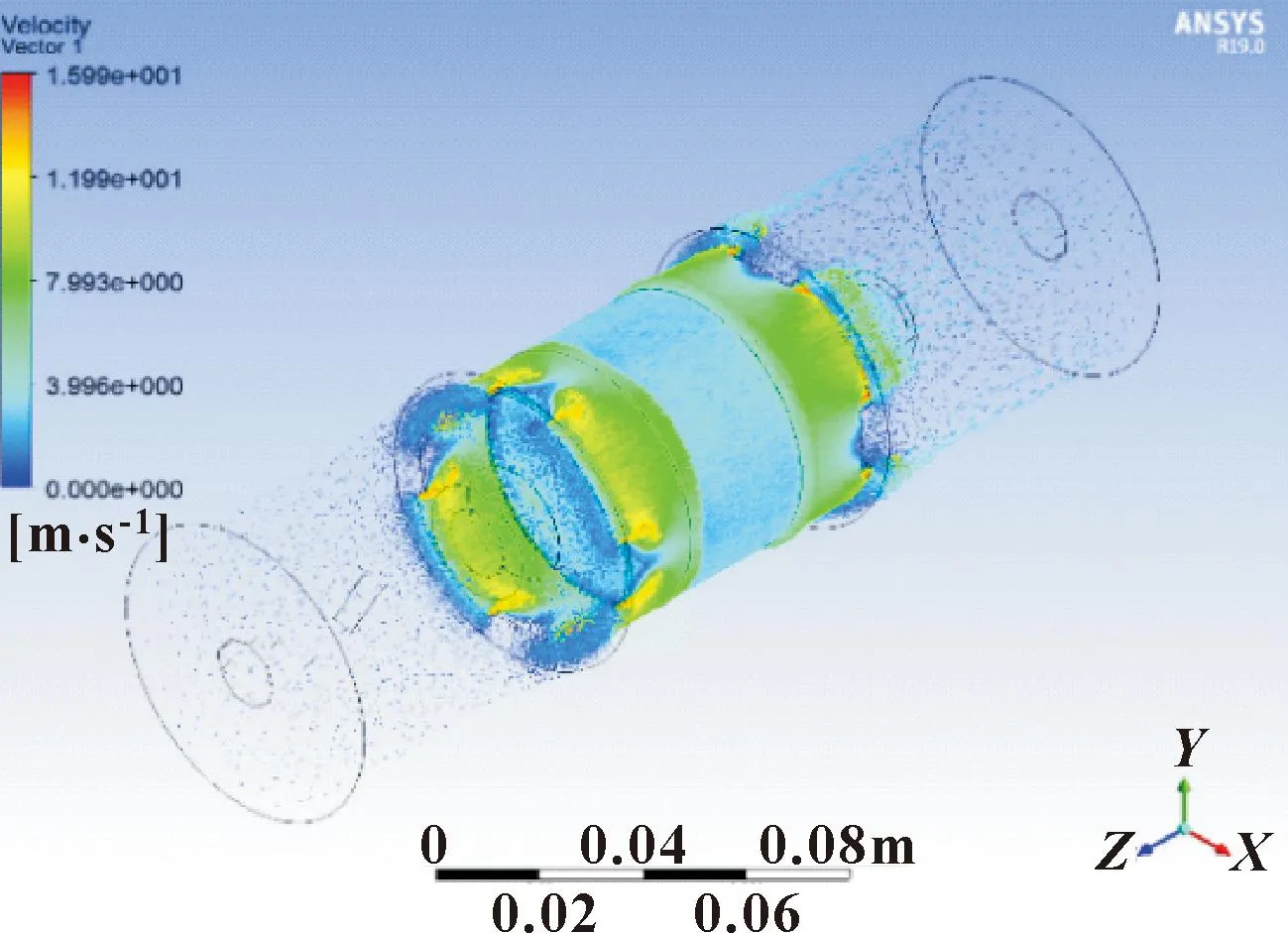
图8 磁流变液阻尼器速度分布云图

电流分别设置为0、0.2、0.4、0.6、0.8、1.0 A，根据仿真数据得到图9所示的磁流变阻尼器阻尼力-电流-速度曲线。

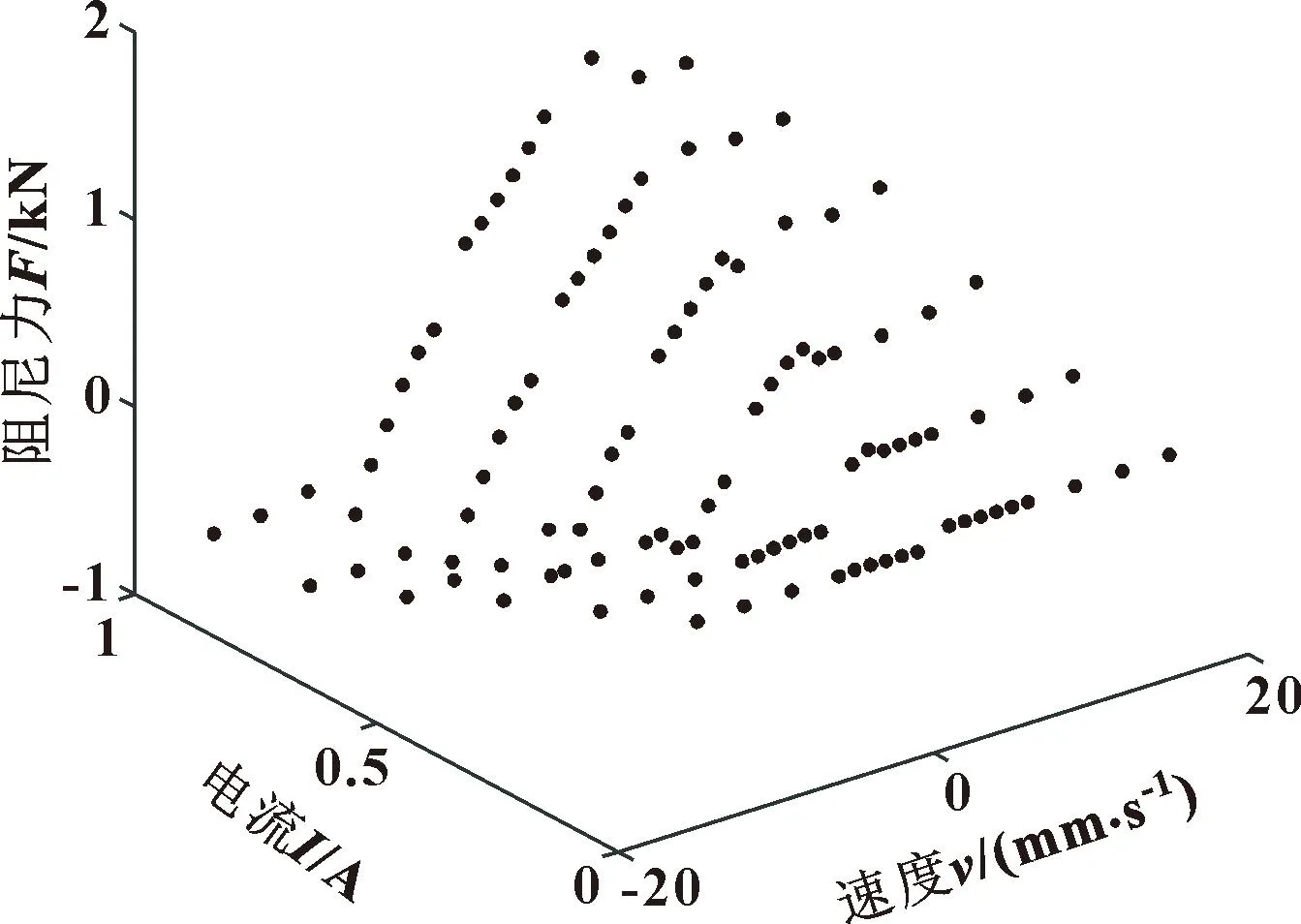
图9 磁流变液阻尼器阻尼力-电流-速度曲线

2 磁流变阻尼器H-B模型参数辨识

根据仿真试验测得的磁流变阻尼器数据，采用Herschel-Bulkley(H-B)黏塑性模型及非线性最小二乘法进行拟合，辨识磁流变阻尼器H-B黏塑性模型中未知的参数。取电流为0～1.0 A的试验数据。设所辨识的模型的数学表达式为

Fd(vj)=f(vj,a)

(3)

非线性模型残差平方和的目标函数E为

(4)

式中：Fdj(vj)表示试验测阻尼力数据。

采用最小二乘法进行参数识别，即以残差平方和最小作为最小二乘准则，从而求得目标函数的最佳值。采用高斯-牛顿迭代法(Gauss-Newton Iteration Method)求解式(4)的极小值。磁流变阻尼器H-B黏塑性模型中的参数辨识结果如表1所示。

表1 Herschel-Bulkley模型参数辨识

最小二乘法求得的最优解与所选择的初始值存在较大的关系，所以若初始值选择不合适，即使获得了最优解，也可能导致错误的辨识值[20]。因此为了避免因为初始值的选择而导致的辨识误差，文中采用BP神经网络对辨识后的数据进行验证，防止因为初始值的选择而导致误差。BP神经网络基本结构如图10所示，包括输入层、隐含层和输出层。如图11所示，仿真试验数据通过输入层输入，经激励函数处理及隐含层学习训练，结果通过输出层输出，其中隐含层采用2层网络，分别使用10个节点。BP神经网络采用梯度下降误差反向传递算法，当误差未达要求时，继续将误差值反向输入，持续训练。经过神经网络训练后的数据和仿真试验对比数据如图12所示。可知：拟合数据和仿真试验数据基本上吻合，拟合精度高，参数辨识结果满足要求。

图10 BP神经网络结构

图11 BP神经网络数据训练

图12 阻尼力数据对比

3 磁流变液阻尼器阻尼特性试验

为了验证基于最小二乘法和BP神经网络相结合的阻尼器参数辨识方法对磁流变阻尼器H-B模型参数辨识的准确性，测试磁流变阻尼器的阻尼力与速度和电流之间的关系，试验装置如图13所示。

图13 磁流变阻尼器试验装置

图14所示为速度为15 mm/s时，不同输入电流条件下磁流变阻尼器试验输出阻尼与参数辨识计算阻尼的对比曲线。参数辨识计算结果与试验结果趋势基本一致，最大误差约2.16%，验证了参数辨识结果的准确性。

图14 阻尼力对比曲线

4 结论

文中针对Bingham模型磁流变阻尼器由于剪切稀化效应引起的阻尼力计算误差问题，在理论和仿真分析的基础上，提出一种最小二乘法和BP神经网络相结合的磁流变阻尼器H-B模型参数辨识方法，对磁流变阻尼器的阻尼力进行了准确计算，最后通过磁流变阻尼器试验对理论方法进行了验证。结果表明：文中所采用的磁流变阻尼器H-B模型参数辨识方法精确度高、吻合性好，验证了参数辨识结果的通用性及准确性。