五轴测量复杂曲面粗糙度及其无干涉方法
2024-03-13何金明姚宇峰常智勇
陈 鹏,何金明,袁 圆,姚宇峰,常智勇+,万 能
(1.西北工业大学 机电学院,陕西 西安 710072;2.陕西省“四主体一联合”航空发动机智能装配工程技术中心,陕西 西安 710072;3.中国航发湖南动力机械研究所,湖南 株洲 412000)
0 引言
表面粗糙度是衡量零件加工质量的重要指标,其大小直接决定零件的工作性能和疲劳寿命[1]。航空复杂件多数都是长时间处于交变应力的恶劣工况下,粗糙度控制不合格时,极易发生疲劳断裂[2-3]。因此,关键零部件的粗糙度控制对航空飞行器整机的安全性至关重要。然而,目前针对复杂零件曲面粗糙度的检测一直是个瓶颈。现有的粗糙度检测方式主要分为非接触式测量和接触式测量两类[4-5],其中非接触式主要以光学测量为主,包括白光干涉测量[6]、共聚焦测量[7]、激光衍射法[8]等。尼启良等[9]用自行研制的软X射线反射率计测量超光滑表面,直观反映出了表面形貌特征;易怀安等[10]提出基于图像清晰度评价的粗糙度测量方法,并论证了该方法的可行性。虽然非接触式粗糙度检测效率高,但是由于光学检测结构的限制,对待测零件的开阔性要求较高,难以有效测量复杂零件及微小区域的粗糙度[11],而且应用成本较高。接触式测量主要采用机械式测头在待测表面上取相应的采样段,通过一定滤波处理得到待测区域的表面粗糙度值[12-13]。KOCHETKOV等[14]考虑机械滤波效应,提出基于解析几何的测针与表面接触数学模型,研究测尖直径对表面粗糙度参数的影响;SOUZA等[15]采用不同测尖的粗糙度传感器测量不同加工方式下的表面粗糙度,评估不同大小测尖对表面粗糙度参数的影响;STEINMEYER等[16]利用粗糙度测头测量渐开线齿面轮廓的粗糙度,实现了粗糙度测量系统与齿轮测量系统之间的转换。虽然接触式粗糙度测量精度高,对零件的表面反射性要求低,但是测量速度慢,自动化程度低,需要人为对探针进行免干涉判断等。
传统的非接触式和接触式测量方式只能测量形状比较开阔区域的表面粗糙度,国内外很少有针对复杂零件曲面粗糙度接触式检测的研究,目前大都采用样板比对法、样膏法、手持式粗糙度测量仪等方法来测量。样板比对测量虽然有样板作为参考,但是测量结果依赖检验员的经验,且结果为范围值,缺乏量化标准[17];样膏法虽然可以测量具体结果,但是打样周期长,最终成型的效果直接影响粗糙度的测量结果;手持式粗糙度测量仪虽然自由度高,可以检测到部分难以测量的区域,但是测量过程极其不稳定,结果的可信度较低[18]。现代加工技术的进步也为检测技术的发展提出了挑战,亟需寻找一种高精、高效的自动化粗糙度检测方法,来满足复杂零件粗糙度检测的需求。
粗糙度五轴测量是一种基于五轴测量机的新型接触式粗糙度测量方法。凭借五轴测量机自由度高、可达域广等特点[19-20],搭载粗糙度测量传感器,可以对复杂零件关键位置进行自动化粗糙度检测。五轴技术测量粗糙度具有测量过程稳定性好、测量精度高等优点,然而五轴测量机自由度高,在测量复杂零件时,传感器干涉判断比较复杂[21]。国内外学者对五轴加工过程中刀具的干涉判断进行了大量研究,南长峰等[22]针对五轴加工中的刀具干涉问题,提出基于临界约束和临界位置精细化的干涉判断方法,达到快速确定干涉范围、生成无干涉刀轨的目的;王国勋等[23]通过计算曲面上的点与刀具位置的关系来判断刀具的干涉情况;WU等[24]对曲面上的任意一点构造可视锥,根据可视锥判断刀具的干涉情况,解决了五轴加工过程中曲面与刀具的干涉问题;DING等[25]将刀具用包围盒建模,表面采用八叉数近似,在刀具包围盒与曲面八叉树的灰度八分位之间进行干涉检查,实现了对五轴加工过程中全局干涉的精确检查。
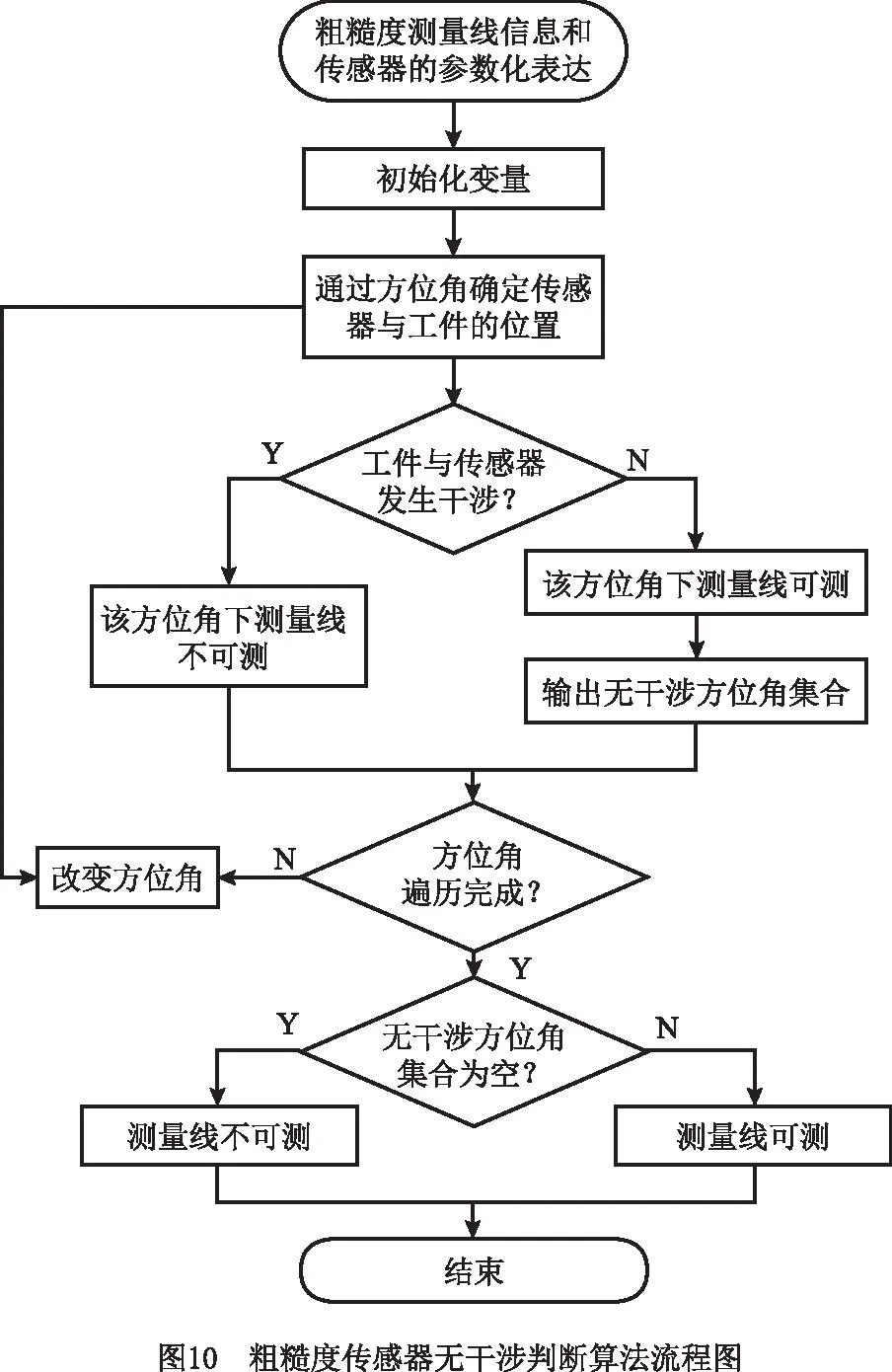
虽然五轴加工中对刀具的干涉检查已有很深入的研究,但是与刀具结构不同的是,粗糙度传感器结构复杂,并非单一的回转体或轴对称结构,这对传感器的精确建模分析和干涉判断提出了更高的要求,特别是在微小区域粗糙度测量时。另外,粗糙度五轴测量操作过程也相当复杂,只能手动在线操作,不能实现自动化检测,极大地降低了测量机的使用价值和测量效率。手动编程时,极易出现原本粗糙度可测的区域,因手动调整难以找到合适的测杆方位而被误判为不可测,这种情况在狭小区域或相互遮挡严重的区域尤为显著。因此,传感器的干涉检查是粗糙度五轴测量中需要解决的关键问题。针对粗糙度五轴测量的不足,分析粗糙度传感器运动方式,本文提出一种基于五轴的粗糙度检测无干涉方法,以实现对复杂曲面粗糙度测量区域的预测和无干涉自动化检测。
1 粗糙度五轴测量原理
粗糙度五轴测量由五坐标测量机搭载粗糙度传感器实现。如图1所示,五轴测量机由X-Y-Z轴加上两个旋转轴A轴和B轴构成,可以实现五轴联动[26]。粗糙度传感器由测尖、滑台、测根、测杆、数据接收处理器、金属保护壳等组成,其自身轴线为C轴,传感器可以绕C轴旋转。传感器被安装到五轴测量机上,由测座驱动,经A,B旋转轴将传感器设置为空间任意方位,配合坐标测量机移动轴和C轴运动,将传感器送达坐标测量机内任意位置进行测量。

进行传统粗糙度测量时,测杆的轴线与粗糙度测量线平行,而五轴测量机则通过五轴联动使测杆轴线与粗糙度测量线成一定角度。测量时,需要在待测表面上给出粗糙度测量线L,测量线的长度根据国标确定,记测量线起点为Vs,终点为Ve。五轴测量机通过A,B,C旋转轴使传感器测尖轴线Ltip与测量线起点s所在平面的法矢ns平行[27-28]。此时,将测杆轴线Lstylus沿ns在待测平面上的投影Lp与测量线之间的夹角记为传感器方位角θ,如图2所示,因此传感器方位角表示在测量某个位置的粗糙度时,测杆轴线方向与测量线方向在投影平面上形成的夹角。以测量线L为起始边,传感器逆时针旋转时方位角θ为正,反之为负,理论上方位角θ的取值范围为θ∈(-π,π]。测量粗糙度时,测座驱动传感器使测尖点到达测量线起点正上方安全平面位置,测量机驱动传感器使测尖沿ns反向移动,直到滑台与被测表面接触。因为测尖在Ltip方向上超出滑台,所以会向测杆内部收缩,如图2局部视图PV1所示。传感器沿测量线方向移动时,测量机给传感器施加一定压力,使滑台始终与被测表面接触,测尖在被测表面上移动,其伸缩变化反映了被测表面的微观起伏情况,并由测根处的反射镜和位置探测器(Position Sensitive Detector,PSD)记录。PSD发出的光始终不变,但接收到的反射光随反射镜的偏转变化,因此PSD可通过反射光的变化记录表面的微观起伏变化,如图2局部视图PV2所示。将PSD记录的数据进行处理和分析,得到被测表面的粗糙度。粗糙度五轴测量流程图如图3所示。

2 传感器无干涉方位
2.1 无干涉方位角的定义
粗糙度五轴测量之所以能够检测复杂零件粗糙度,主要原因是五轴联动不仅使粗糙度传感器能够以各种方位避免测量中的干涉,还可以使测杆与测量线以方位角的形式测量粗糙度。
理论上测杆方位角θ的取值范围为θ∈(-π,π](如图4a),然而在实际测量过程中,尤其是复杂零件的粗糙度测量往往会出现干涉问题,为避免干涉,测杆方位角的范围会发生变化(如图4b),此时方位角的取值范围为θ∈(θnmin,θnmax)。当测杆与工件、夹具等无干涉时,称测杆的方位角为无干涉方位角θn,即给定一条粗糙度测量线和测杆方位,如果在粗糙度传感器从测量线起点沿测量方向移动到测量线终点的过程中,传感器始终与工件和夹具无干涉,则该方位角为无干涉方位角θn(θn∈θ)。
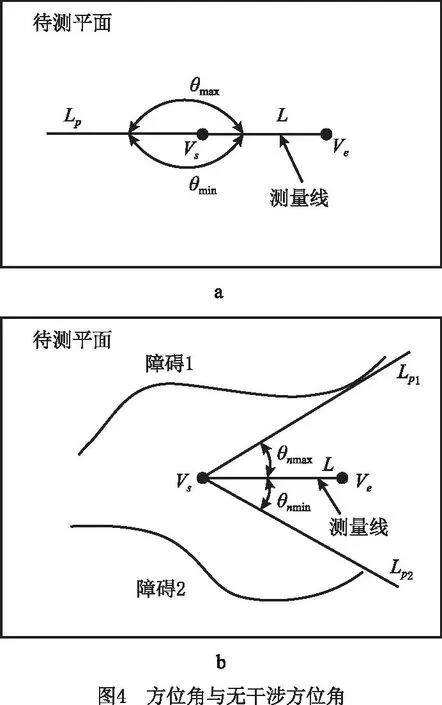
因此,将一条粗糙度测量线是否可测转化为对测杆无干涉方位角的求解。无干涉方位角由工件和传感器共同确定,因此对工件和传感器的位置关系进行分析。下面以曲面粗糙度测量为例建立传感器参数化模型,分析粗糙度测量过程中传感器与工件的位置关系。
2.2 粗糙度传感器与工件的位置关系
对粗糙度传感器进行三维建模,如图5a所示,粗糙度测针整体结构上主要分为粗糙度传感器和连接组件两部分。传感器部分包括粗糙度测量的关键零部件,其中传感器长度Lsensor=105 mm,测杆最大直径D1=3 mm,测根最大直径D2=11.3 mm;连接组件长度Lkit=153 mm,最小直径与测根直径相同。通常情况下,测根与连接组件同轴,传感器长度对一般叶片盘类零件的粗糙度测量已经足够,而且粗糙度测量过程主要发生在传感器部位,因此判断干涉时将传感器作为主要研究对象。
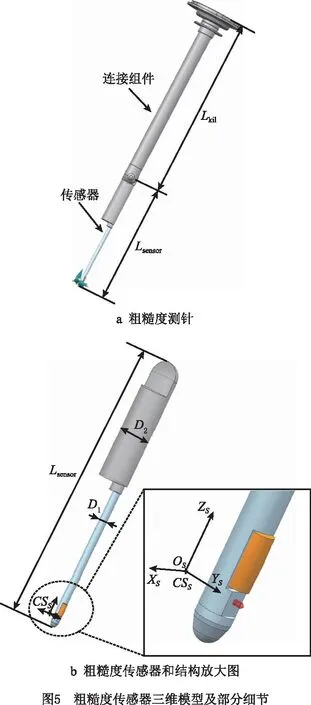
建立粗糙度传感器模型坐标系CSS时,为方便计算,将测尖的轴线方向定为模型坐标系CSS的YS轴,正方向指向测尖点;将测根轴线方向定为模型坐标系CSS的ZS轴,根据右手定则可以确定模型坐标系CSS的XS轴;测尖轴线与传感器轴线的交点记为模型坐标系CSS的原点OS。
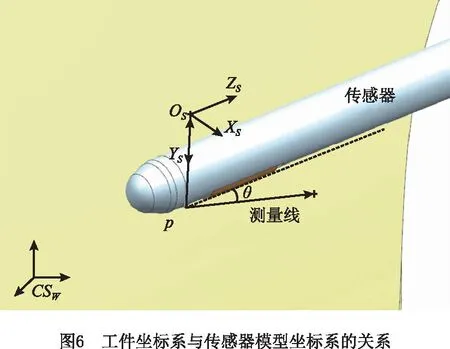
分别在模型坐标系CSS和工件坐标系CSW下确定传感器三维模型和被测工件,传感器与被测工件的位置关系通过粗糙度测量线联系起来。因此,只要确定传感器模型坐标系CSS与粗糙度测量线之间的位置关系,即可在工件坐标系下确定传感器与工件之间的空间位置关系。如图6所示,设在工件坐标系CSW中,粗糙度测量线上某点p的坐标为(xw,yw,zw),粗糙度测量线方向向量sline为(al,bl,cl),点p对应的表面法矢np为(up,vp,wp),传感器的方位角为θ,则工件坐标系CSW下,传感器模型坐标系CSS的原点坐标(xOs,yOs,zOs)为
(1)
式中lp为模型坐标系CSS的原点OS与点p之间的距离。
在工件坐标系CSW中,模型坐标系CSS的YS轴方向矢量(iYs,jYs,kYs)、ZS轴方向矢量(iZs,jZs,kZs)、XS轴方向矢量(iXs,jXs,kXs)分别为:
(2)
(3)
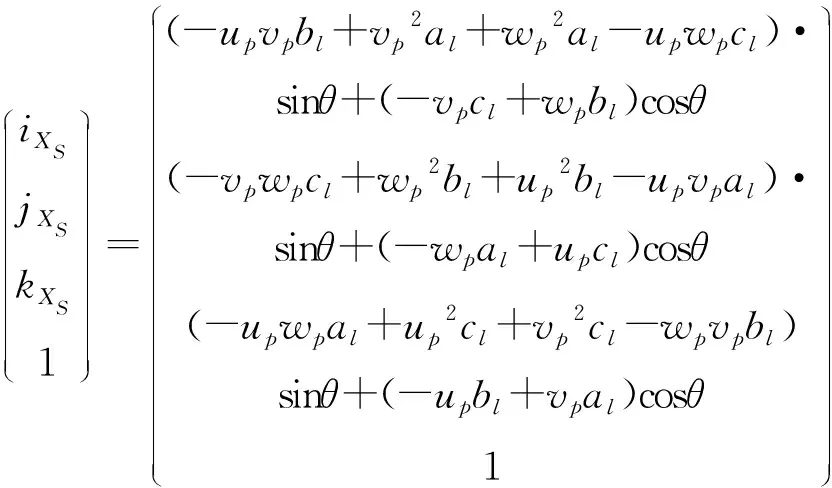
(4)
式中XS轴方向矢量(iXs,jXs,kXs)由YS轴方向矢量(iYs,jYs,kYs)和ZS轴方向矢量(iZs,jZs,kZs)叉乘得到。
因此,传感器模型坐标系CSS下任意一点坐标为(xs,ys,zs),在工件坐标系CSW下的坐标(xw,yw,zw)为
(5)
3 基于无干涉方位的可测区域预测
3.1 粗糙度传感器参数化表达
分析粗糙度传感器特征可知,粗糙度传感器由圆柱、圆锥、圆台、鼓形、球缺等基本几何体组成,这些基本几何体都属于回转体,回转体由母线绕回转轴旋转得到。如图7所示,记回转体底面圆心为Or,从Or出发沿回转体轴线指向回转体内部的单位矢量为轴线矢量Nr。垂直于轴线矢量Nr的平面与回转体相交形成的面为正截面,圆心Or与正截面的距离为h,正截面是一个以Oh为圆心、以rh为半径的圆。正截面半径rh与距离h的关系为

rh=r(h),h∈[0,hr]。
(6)
式中:r(h)是关于距离h的正截面半径函数;hr为回转体的最大高度。
空间中的基本几何体可以由空间方位和形状参数唯一确定,因此构成传感器的基本几何体可以参数化表示。
(1)圆柱体参数化表达 在传感器模型坐标系CSS下,圆柱体的空间方位由底面圆的圆心坐标O1(x1,y1,z1)和轴线矢量N1(i1,j1,k1)确定。圆柱体的形状由正截面半径r1确定,
r1=R1,h∈[0,h1]。
(7)
式中:R1为圆柱体底面圆半径;h为正截面高度;h1为圆柱体的高。
(2)圆锥体参数化表达 在传感器模型坐标系CSS下,圆锥体的空间方位由底面圆的圆心坐标O2(x2,y2,z2)和轴线矢量N2(i2,j2,k2)确定。圆锥体的形状由正截面半径r2确定,
(8)
式中:R2为圆锥体底面圆半径;h2为圆锥体的高。
(3)圆台参数化表达 在传感器模型坐标系CSS下,圆台的空间方位由圆台下底面圆的圆心坐标O3(x3,y3,z3)和轴线矢量N3(i3,j3,k3)确定。圆台的形状由正截面半径r3确定,
(9)
式中:R3,1为圆台下底面圆半径;R3,2为圆台上底面圆半径;h3为圆台的高。
(4)鼓形参数化表达 在传感器模型坐标系CSS下,鼓形的空间方位由鼓形中心坐标O4(x4,y4,z4)和轴线矢量N4(i4,j4,k4)确定。鼓形的形状由正截面半径r4确定,
(10)
式中:R4为鼓形基圆半径;R′4为鼓形圆弧母线半径;h4为鼓形的高。
(5)球缺的参数化表达 在传感器模型坐标系CSS下,球缺的空间方位由球缺中心坐标O5(x5,y5,z5)和轴线矢量N5(i5,j5,k5)确定。球缺的形状由正截面半径r5确定,
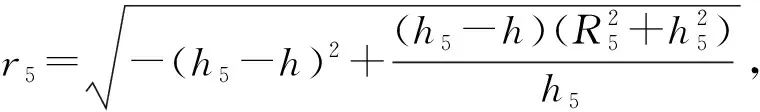
(11)
式中:R5为球缺底面圆半径;h5为球缺的高。
将上述基本几何体组合,得到整个传感器模型的参数化表示,为判断干涉奠定基础。
3.2 基本几何体的干涉判断方法
空间中的一点P和一个基本几何体G,两者之间的状态分为3种:①点P在几何体G内部;②点P在几何体G表面;③点P在几何体G外部。只有点P在几何体G外部时两者为无干涉,因此将无干涉问题转化为判断点与基本几何体之间的距离关系。
以圆柱体为例,如图8所示,在传感器模型坐标系CSS下,圆柱体的基本参数为圆心坐标O1(x1,y1,z1)、轴线矢量N1(i1,j1,k1)、正截面半径r1=R1,h∈[0,h1],点P的坐标为(xp,yp,zp)。

步骤1计算矢量O1P在轴线矢量N1上的投影长度d1,
d1=O1P·N1。
(12)
当d1<0或d1>h1时,点P在轴线矢量上的投影点P′不在几何体轴线段上,点P与几何体不干涉。当0≤d1≤h1时,执行步骤2。
步骤2计算点P到轴线段的距离l1:
PP′=O1P-N1·d1;
(13)
l1=|PP′|。
(14)
当l1>r1时,点P在几何体外,此时称点P与几何体无干涉。
空间中的一点P与其他基本几何体的干涉判断与上述方式相同,这里不再赘述。当点P与所有组成传感器的基本几何体均无干涉时,称点P与传感器无干涉;当工件上任意采样点Pi均与传感器无干涉时,称工件与传感器无干涉。
3.3 粗糙度可测区域的预测
在粗糙度测量过程中,传感器与工件之间须始终处于无干涉状态,否则不能完成测量。在工件坐标系CSW下,使用粗糙度传感器测量给定的粗糙度测量线L时,需要的测量参数有测量线起点坐标Vs(x0,y0,z0)、测量线方向sl(al,bl,cl)、测尖方向n0(u0,v0,w0)、传感器的空间方位角θ。将粗糙度测量线离散为若干个检查点Vi(i=0,1,2,…,n),其中V0和Vn分别为测量线的起点和终点。检查点Vi的坐标为
(15)
式中:i为遍历检测点的序号;n为检测点的个数。
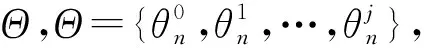


4 应用案例
作为航空发动机的典型零件之一,离心叶轮的粗糙度检测一直是检测中的难题,本章通过检测离心叶轮各部位的粗糙度验证上述模型和算法的可行性与正确性。
在叶轮表面上获得206 738个点作为叶轮模型采样点。基于无干涉方位理论预测大小叶片、叶根、流道的粗糙度可测区域,如图11所示,其中绿色区域为算法预测得到的粗糙度可测区域。图12所示为叶轮采样点和测量线的位置,可见离心叶轮大小叶片的叶身粗糙度均可测,但是在叶根处仅可评估进气口和出气口两端约25 mm位置的粗糙度,同样轮毂上也仅可评估进气口和出气口20 mm位置的粗糙度,这也符合直观的判断。


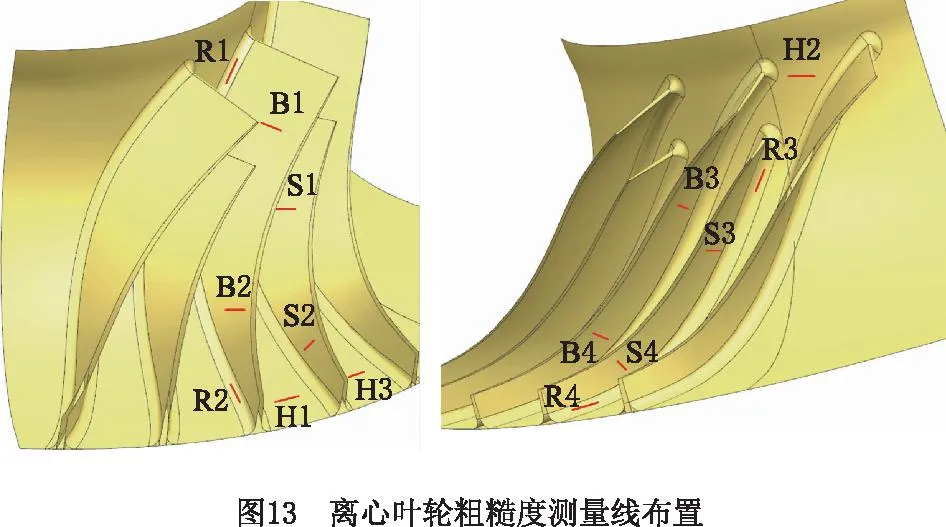
分析上述可测区域,结合粗糙度测量线布置原理,对各个区域沿垂直刀纹的方向自动布置测量线,如图13所示。在大叶片上布置4条测量线,编号为B1,B2,B3,B4;在小叶片上布置4条测量线,编号为S1,S2,S3,S4;在轮毂上布置3条测量线,编号为H1,H2,H3;在叶根过渡段上布置4条测量线,编号为R1,R2,R3,R4。
利用上述算法计算每条测量线的无干涉方位角,得到无干涉方位角集合,如表1所示。选取3个有代表性的位置B1,R1,H1,并在无干涉方位角集合中选取方位角。通过测量线信息和计算的方位角,得到传感器与叶轮的相对位置关系,利用该关系将传感器模型和叶轮模型在NX软件中进行装配,并利用软件自身的干涉检查功能查看干涉情况,如图14所示。
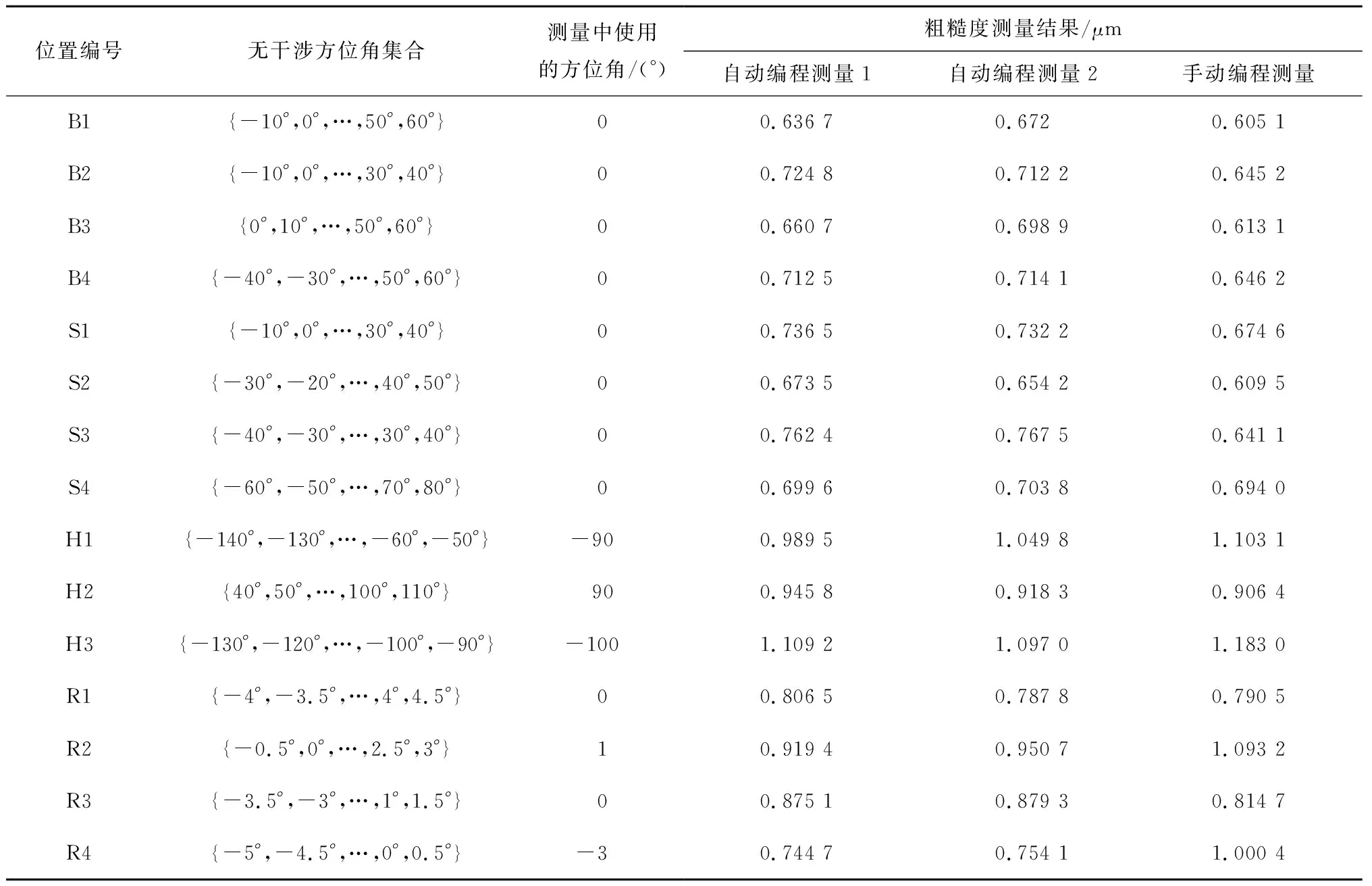
表1 粗糙度测量线无干涉方位角和测量结果

由NX软件中的装配情况可以看出,计算出的测杆方位在装配后与工件无干涉,证明算法理论上有效,而且该位置可以进行粗糙度评估。
为了进一步验证算法在实际测量过程中的可行性,通过现场实验对每个位置进行验证。粗糙度测量分为编程阶段和测量阶段两个阶段。
(1)编程阶段可采用的编程方式主要有手动编程和自动编程两种:①手动编程时,工件须安装到测量机上,通过手动调节传感器方位,采用人工试错的方式对每一条测量线编程,编程过程复杂、效率低,且易造成可测和不可测的误判。另外,编程时测量机处于非测量状态,降低了测量机的利用率,从而增加了单个工件测量的时间成本。②自动编程时,首先对零件三维模型进行预计算,预计算即利用上述算法得到可测区域和可测量方位角的过程。然后取计算结果中的一个无干涉方位角(一般选中间值)自动生成测量程序。该过程可完全脱离测量机进行离线编程。
(2)测量阶段是测量程序控制五轴测量机进行测量的过程,该过程为全自动,测量效率由测量程序决定。
实验采用的设备为搭载SFM-C2粗糙度传感器的Renishaw Agility五轴测量机,如图15所示。五轴测量机X,Y,Z行程分别为X=1.6 m,Y=2.5 m,Z=1.2 m;测针可绕A轴旋转的角度范围是[-110°,120°],绕B轴和C轴旋转的角度范围相同,均为[0°,360°]。五轴测量机的定位精度为1.9 μm+L/350 μm(18℃~22℃),重复定位精度为1.3 μm,粗糙度传感器的测量精度为粗糙度名义值的±5%+15 nm。

对某离心叶轮开展粗糙度测量实验,实验温度为20.6 ℃,湿度为42%。被测工件离心叶轮所处的工序为精铣后,理论上精铣后的粗糙度值为Ra1.6 μm,对其中两组大小叶片进行表面抛光处理,理论上抛光处理后的粗糙度值为Ra0.8 μm。现场测量的叶片为经过抛光处理的叶片,测量过程如图16所示。自动编程测量时每个位置重复测量两次,手动编程测量时每个位置测量一次,记录测量结果,如表1所示。

采用自动编程测量的方式测量上述各位置的粗糙度,测量过程中传感器与零件均未发生干涉,实现了对叶根过渡段这种微小特征粗糙度的评估,证明了五轴测量粗糙度的可行性,同时采用手动编程的方式评估了每个位置的粗糙度。图17所示为3次粗糙度测量结果对比,可见3次粗糙度测量结果存在一定偏差,对测量结果进行分析,定义自动编程测量结果之间的误差为绝对误差Ea,
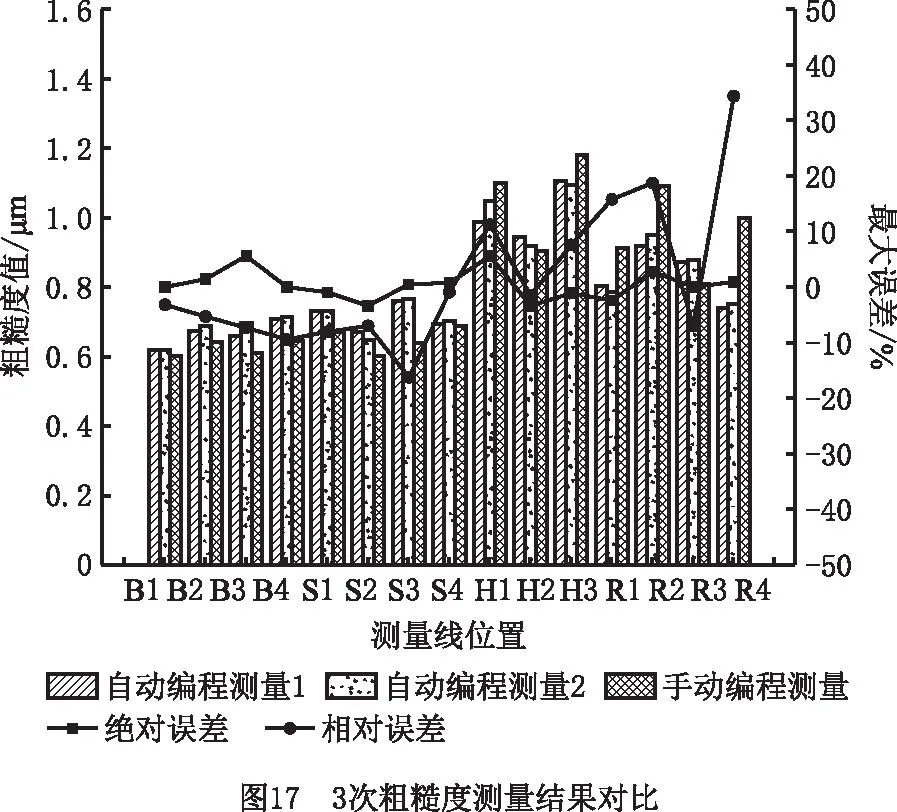

(16)
式中Ra1,Ra2分别为自动编程第1次和第2次粗糙度测量结果。
对3次测量结果进行分析,定义自动编程测量与手动编程测量结果之间的误差为相对误差Er,
(17)
式中Ra3为手动编程测量结果。
由绝对误差Ea的分布可以看出,两次自动编程测量结果之间的误差很小,最大误差在6%以内,说明两次测量结果的一致性较好。由相对误差Er的分布可以看出,手动编程测量结果与自动编程测量结果在大小叶片区域的测量误差较小,而在叶根区域的测量误差较大,最大误差出现在叶根R4位置,最大误差达到34.3%。针对该现象,观察测量得到的粗糙度波形图,如图18和图19所示。
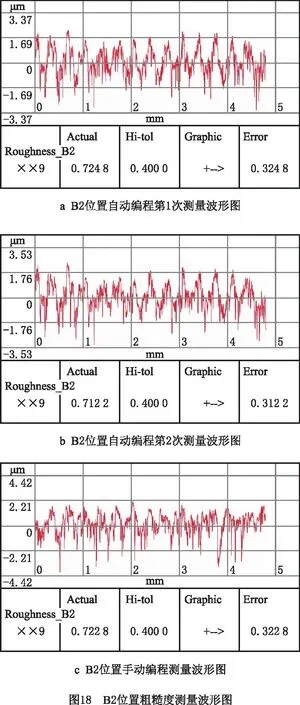
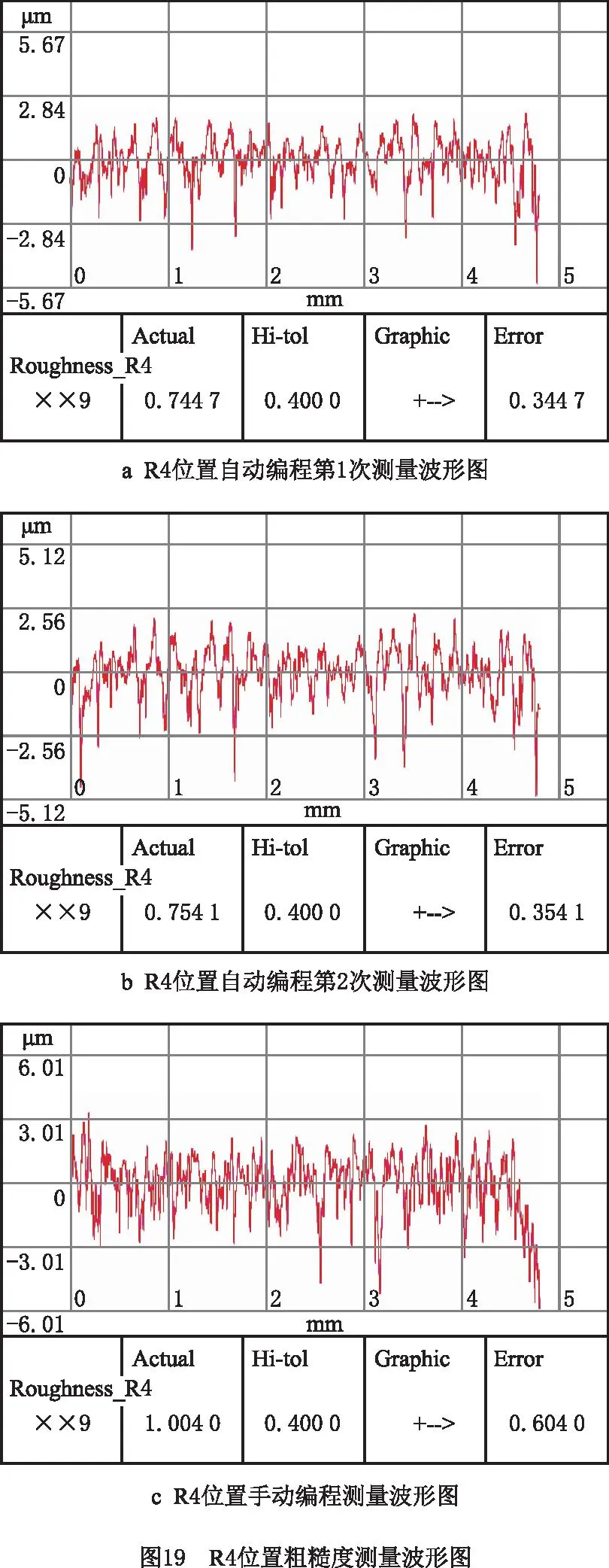
图18a~图18c分别为大叶片B2位置3次粗糙度测量得到的波形图,图18a和图18b的粗糙度波形图的起伏几乎完全相同;图18c与图18a的波形图起伏稍有不同,两次测得的粗糙度值也有偏差,但差异不大。这是因为大小叶片之间相对开阔,且在大小叶片上粗糙度测量线所在的附近区域曲率较小,无论自动编程还是手动编程,无干涉测杆方位比较容易获得,测量结果差异较小。测量结果存在差异的原因是,手动编程时无法精确控制测量线的位置和测杆方向,手动编程与自动编程测量的粗糙度测量线位置很近,但不完全相同,因此得到的粗糙度波形图和测量结果存在偏差。
然而,在比较狭小的区域中,如叶根处,获取无干涉测杆方位的难度比在开阔区域时大,如图19所示。自动编程可以准确计算出测杆无干涉方位,手动编程则很难做到,手动编程给出的测杆方位可能会影响测尖、滑台与工件正常接触,甚至在测量过程中发生干涉。对比图19a和图19c的波形可见,两副波形已经明显不同,说明手动编程与自动编程测量的位置已经发生明显偏移。由图19c还可以看出,在测量开始和结束位置,波形分别出现了突增和突减,此时测尖与滑台的位置已然偏离了正常状态。因此,在该方位角下,虽然可完成粗糙度测量,但是测量结果可信度不高。
自动编程测量与手动编程测量效率对比如表2所示。采用自动编程时,一条测量线的预计算耗时约5 s,15条测量线在编程阶段的预计算耗时约75 s。传感器测量粗糙度时的移动速度为1 mm/s,非测量时的移动速度为250 mm/s,测量阶段耗时约180 s,采用自动编程评估15条测量线总耗时约为255 s。采用手动编程时,需要对每条测量线手动试错,编程水平中等偏上的人员平均一条测量线编程需要尝试至少2次,完成一条测量线编程需要约220 s,15条测量线编程耗时约3 300 s。因为手动编程时为了保证测量不发生干涉,在非测量阶段,传感器的安全点位置设置得比较保守,导致传感器移动路径不为最优,所以测量阶段耗时较长,约240 s,采用手动编程评估15条测量线总耗时为3 540 s。相比手动编程测量,自动编程测量的效率提高了13.9倍,极大提高了粗糙度检测效率。

表2 自动编程测量与手动编程测量效率对比
5 结束语
本文针对复杂曲面粗糙度测量,借助五轴测量机灵活性高、可达域广的特点,搭载粗糙度传感器开展了复杂曲面五轴粗糙测量研究。通过分析粗糙度传感器与工件的相对位置,定义了传感器无干涉方位,研究了粗糙度传感器的无干涉定位方法,基于该方法进一步研究复杂曲面表面粗糙度的可测区域,并在某离心叶轮上进行实验验证,得到如下结论:
(1)分析粗糙度传感器在曲面上的测量过程,提出粗糙度五轴检测无干涉模型,基于无干涉方位计算模型实现了对曲面粗糙度可测量区域的预测。
(2)实验验证了复杂曲面粗糙度五轴测量方法的可行性,验证了粗糙度传感器无干涉定位方法测量曲面粗糙度的准确性。
(3)利用该模型可以预测复杂曲面表面粗糙度的可测性,并同样适用于微小特征粗糙度测量,例如叶根过渡段粗糙度的测量。
(4)相比手动编程测量粗糙度,五轴自动编程测量在精度上更可信,测量效率提高了13.9倍,为复杂零件粗糙度高精高效测量提供了新思路。
