兼顾模态的特种落下孔车轻量化研究*

王志远,李晓峰,韩新利

(大连交通大学 机车车辆工程学院,辽宁 大连 116028)

0 引 言

随着社会高速发展,人们对运输的需求逐步提升,铁路货车运输作为交通运输的重要一环,更需要提升其运输效率以提高运输效益。为了实现这一目标,降低货车车体质量成为一项重要措施。这不仅能够降低原材料的消耗和牵引能耗,节省能源,还能提升列车运行速度,增加载货量[1]。

在货运发展过程中,由于运输货物种类的多样化,因此并不是所有运输目标都可以使用集装箱平车或者敞车等进行运输。例如,大型机械转子等特殊形状货物的运输较为不便,无法使用常规车辆运输。此情况下,特种落下孔车应运而生,并成功解决了特殊货物运载难的问题。而当前轻量化已成为趋势,为了提高特种落下孔车的运输效率和运输效益,对其进行轻量化改进也十分必要。

国内外学者在优化领域展开了广泛研究,Suxi Tang等[2]采用基于BP神经网络(BPNN)的响应面法(RSM)研究了单桩支撑桥梁在可使用极限状态下的承载可靠性。作者采用单桩在泥线处的最大允许旋转角度作为结构破坏准则;采用考虑桩土相互作用的有限元模型确定了响应面各测点的函数值。首先详细介绍了FEM-BPNN-RSM耦合的分析过程;然后建立桩土相互作用的有限元模型,并通过与已有研究的对比验证了有限元模型的准确性。王剑等[3]基于结构应力法,对焊接结构的疲劳寿命进行了灵敏度分析,并将计算结果与全局差分法进行了比较,算例验证了灵敏度分析的正确性,为进一步对焊接结构疲劳寿命进行优化设计提供了理论基础和技术支持。李娅娜等[4]将安全问题和轻量化设计相结合,综合多个目标实现了对动车组应急蓄电池箱的多目标优化。作者结合第三代非支配排序遗传算法(NSGA-III)进行多目标优化,相较于单一的响应面法或遗传算法,其优化后的参数更加合理,轻量化和安全性均得到了保障。魏富栋等[5]以卧式连续混合机的质量为优化目标建立了二阶响应面模型,并优化了关键部件的结构参数。

目前,国内外学者在单目标轻量化领域已做出大量成果,部分学者应用多目标优化方法优化了质量和节点应力,但鲜有在考虑轻量化的同时,兼顾模态的提升,模态提升可以更好地防止车体与外部低频激励产生共振,从而能有效提升车辆运行的稳定性。由于板厚下降易导致车体刚度下降,从而进一步引起模态降低,因此在轻量化的同时兼顾模态,并达到合适的平衡点,对车辆运行平稳性十分重要。

笔者以某型号特种平车为研究对象,通过建立实体模型和有限元模型使其质量、形变、模态频率和板厚参数化;通过有限元分析软件得出其模态、强度和刚度参数;通过灵敏度分析,筛选出影响因子较大的尺寸参数;生成响应面模型,并采用多目标遗传算法对最优质量进行计算。所得结论对货运列车实际生产设计具有前瞻性价值,为货车优化提供了方法参考。

1 相关理论

1.1 Block Lanczos模态提取方法

(1)

(2)

式中:Bi,Ci∈Rr×r(i=1,…,m);Er为mr阶单位矩阵的后r列。同时有关系式:

(3)

(4)

1.2 刚度计算方法及评价依据

根据货车刚度标准TB 3550.2-2019要求,需使特种落下孔车在其使用期限内能具备承受正常载荷所需的足够刚度,要能满足维修和纠正脱轨的要求,使其在最大垂直载荷作用下车体静挠度不超过两转向架在支撑点之间距离的1/700,如式(5)所列:

(5)

式中:f为垂向位移;L2为车辆定距。

1.3 静强度计算方法及评价依据

有关特种落下孔车静强度评价标准,应参照第一强度理论,利用最大主应力作为评价标准,对于文中的Q450NQR1钢材料,利用有限元模型计算出Von-Mises应力作为结构研究点的等效应力,Von-Mises应力表达式为:

(6)

根据Q450NQR1钢材料属性要求,车体强度要求要满足焊缝处应力不得超过281 MPa。即:

σ<σS=281 MPa

(7)

2 有限元分析

文章以特种落下孔车为研究对象,采用板壳单元建立有限单元模型,共有节点360 711个、单元372 408个,如图1所示,整车质量为15.372 t。

图1 整车有限元模型

根据上节所述Block Lanczos模态提取方法对模态进行计算,提取除刚提模态外的前10阶模态,如表1所列。在实际线路中,一阶垂弯模态对车体振动性能影响最为明显,故选取一阶垂弯模态为后续优化目标,落下孔车关键模态一阶垂弯模态为第4阶模态,频率为9.54 Hz,模态振型如图2所示。

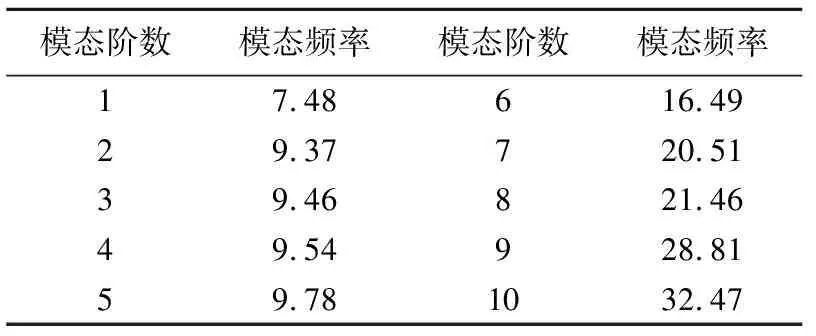
表1 前十阶模态频率表 /Hz

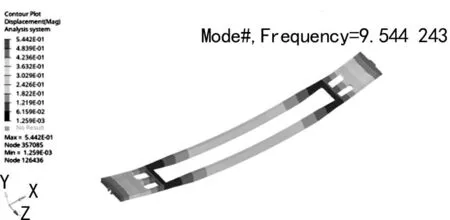
图2 一阶垂弯振型

根据前节所述强度与刚度计算及评价标准,按照TB 3550.2-2019施加载荷及边界条件,根据计算,落下孔车在17.76 t载重叠加1 780 kN拉伸工况下,工作条件最为恶劣,最大应力点如图3所示,其刚度最大位置为侧梁下盖板,位移结果如图4所示。

图3 应力最大点及位置

图4 刚度位移云图

3 特种落下孔车轻量化设计

3.1 灵敏度分析及设计变量选取

灵敏度分析即求导信息,它是一种评价设计变量或参数改变引起的结构响应变化率的方法[6]。在最优化方法中经常利用灵敏度分析来研究原始数据不准确或发生变化时最优解的稳定性。通过灵敏度分析还可以决定哪些参数对系统或模型有较大的影响。

从数学意义讲,灵敏度是函数F(x)对某些自变量xi的变化梯度,如果函数F(x)可导,那么其一阶灵敏度S在连续系统中可表示为:

S=∂F(x)/Xi

(8)

而在离散系统中则可表示为:

S=ΔF(x)/Δxi

(9)

式(8)、(9)分别为一阶微分灵敏度和一阶差分灵敏度。

文中灵敏度分析指的是分析车体板件整车质量变量M对厚度参数Ti变化的敏感度,即:

Sen(M∕Ti)=∂M∕∂Ti

(10)

对应的数值表示为厚度Ti对质量参数M的影响程度[7]。

选取落下孔车所有关键部位板的板厚为设计变量,以整车质量、模态、最大应力和下盖板最大变形为响应,分析不同板件厚度所对相应的灵敏度,以此得到灵敏度最大的板件。

为满足轻量化需求,板厚下限值设为原板厚减小20%;同时,为满足强度刚度设计需求,板厚上限值设为原板厚增加10%,设计变量的初始值与上下限如表2所列。设计离散步长0.1 mm,提取质量、最大结点位移以及最大应力为响应,进行50组样本实验。利用灵敏度计算方法对表2出现的所有板厚设计参数进行灵敏度计算,得到的各参数的灵敏度值如图5所示。

三是成立信用档案。工商部门与中国人民银行可以利用多样化的渠道，对消费者的投诉予以受理，并将投诉处理的结果进行公开，还商家和发卡机构的清白，维护好消费者的权益。同时以违法违规情况和投诉处理情况为依据，构建商家和发卡机构的信用档案，若其存在严重的违规违法行为，则将其纳入到失信企业黑名单，减少侵权纠纷，进一步完善社会信用体系。

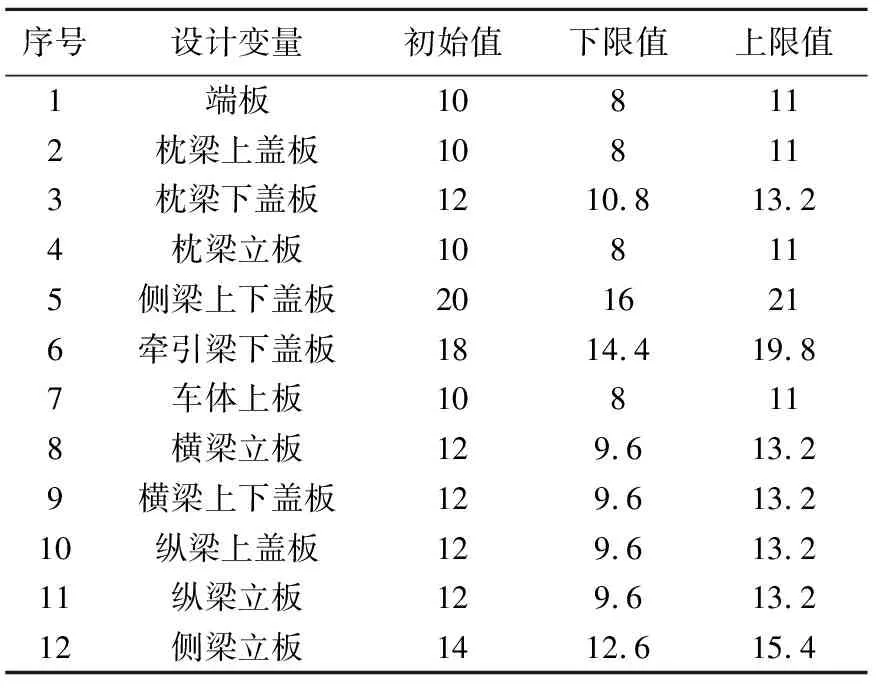
表2 设计变量及上下限 /mm

图5 灵敏度结果曲线图

灵敏度分析图表中,灵敏度绝对值越大,说明该设计变量的变化对目标变化的影响越强烈。

故根据图5可知,对于质量属性影响最明显的变量是编号为5、12的板件板厚,变化趋势皆为正相关,即随着板件厚度的增加,质量呈增加趋势;对于模态属性影响最为明显的是编号为7的板件板厚,变化趋势为负相关,即随着板厚的增加,一阶垂弯模态频率呈降低趋势;对于应力影响最为明显的是编号为6的板件厚度,呈负相关;对于结点位移影响最明显的为编号为5的板件厚度,呈正相关趋势。

综上所述,板件5与板件12的质量灵敏度高且应力灵敏度低,其变化可以在有效降低质量的同时保证应力不会出现较大变化;板件7的模态灵敏度高,应力灵敏度低,其变化可以在有效提高模态频率的同时保证应力不会出现较大变化,6号板件对应力影响较大,需要作为应力约束的参考,故选择序号为5、6、7、12的设计变量进行进一步优化设计。

3.2 响应面拟合

响应面法(Response Surface Methodology, RSM)是一种以实验设计为基础,将数学逼近法与工程优化问题结合,用简单的近似数学模型“代替”复杂的、具有大量自由度的仿真模型的方法。

常见近似模型包括最小二乘法(LSR)、移动最小二乘法(MLSM)、Kriging 法等。Kriging 法是一种可以拟合高度非线性响应数据的方法,适用于在数据函数的尖端也有点通过的情况,其具有局部估计的特点。与 LSR、MLSM 法相比,Kriging 法拟合精度更高,同时花费时间更多[8]。

响应面的数学模型选择二元多项展开式,多项式如下:

(11)

根据灵敏度分析结果,选取序号为5、6、7、12的板件作为输入参数,T5、T6、T7和T12分别为板件5、6、7和12的板件板厚,以关键节点垂向位移、整车模态、整车质量以及关键节点应力为输出参数,利用Design-Expert软件进行实验设计,并进行数据回归分析,拟合响应面。

此次实验采用Box-Behnken试验设计方法,对表 1 中的变量进行试验设计,共设计了25组样本,其中5组的样本设计如表3所列。

表3 Box-Behnken实验设计样本

(1) 质量回归方程求解

质量与设计变量板厚的关系趋于一阶线性,线性拟合如表4所列。

表4 质量线性拟合数据表

由上可得出线性回归方程如下:

Y=(0.199A+0.014B+0.093C+0.391D+4.736)

(12)

对响应面模型求解,得到板厚与质量mass的响应面图,如图6所示。

图6 质量响应面图

由响应面图分析可得T5、T6、T7和T12对质量的影响,其中T6和T7对质量变化的影响较小,T5与T12对质量变化的影响较大,并且在交互中皆与质量变化呈正相关,质量随着T5和T12的减小而减小。

(2)模态回归方程求解

建立的模态响应面模型拟合数据如表5所列。其中,若显著差异值P<0.05,说明建立的响应面模型可靠。

表5 模态线性拟合数据表

可得出线性回归方程如下:

Y=(14.12-0.175A-0.162B-0.339C-0.032D-0.000 986AB-0.006AC-0.016AD-0.001 7BC+0.001 185BD+0.007 4CD+0.012 9A2+0.004 26B2+0.013 8C2+0.0107 8D2)

(13)

通过对响应面模型求解,得到板厚与模态FQ的响应面图如图7所示。

图7 模态响应面图

由图7(a)响应面图分析可得,T5和T6均是增加到中间值18 mm、17.1 mm时模态值最低,在T5取最大值21 mm、T6取最小值14.4 mm时取得模态FQ最大值。

由图7(b)响应面图分析可知,在T5和T7交互影响下,T7对模态变化影响比T5更为明显,T7与模态频率值呈负相关,即随着T7的减小模态频率呈上升趋势。当T5取最大值21 mm、T7取最小值8 mm时,模态频率FQ取到最大值。

由图7(c)响应面图分析可知,T5和T12交互影响下,T12对模态的变化影响比T5更为明显。随着T5数值的增加,模态频率先下降后增加;随着T12数值的增加,模态频率呈单调递增,即T12与模态频率正相关。模态值在T5取最小值16 mm,T12取最大值19.8 mm时达到最大值。

4 多目标优化

文章采用多目标遗传算法对落下孔车进行优化,该方法是模拟自然界遗传机制和生物进化论而呈现的一种并行随即搜索最优化方法。该算法使用了快速非支配排序法、用拥挤度的方法替代了需指定共享半径的适应度共享策略等先进策略,是一种得到广泛认可的多目标优化算法[9]。

应用多目标遗传算法设计优化数学模型。

设计变量的变化范围:16

约束条件为:此次优化特种落下孔车材料为Q450NQR1,模型最大应力σ(T5,T6,T7,T12)应小于材料许用应力281 MPa,模型最大垂向变形UY(T5,T6,T7,T12)的绝对值需要小于25 mm,所以约束条件的表达式为:

C1(x)=σ(T5,T6,T7,T12)<281 MPa

(14)

C2(x)=UY(T5,T6,T7,T12)>-25 mm

(15)

目标函数为:质量Mass最小化,模态频率FQ最大化,可以确定特种落下孔车优化数学模型为:

OBJ:min Mass max FQ

(16)

式中:Mass为质量;FQ为模态频率;σ为von-mises应力;UY为结点位移(沿垂直负方向);T5、T6、T7和T12为各设计变量板的板厚。

优化计算后结果如表6所列。由表6可知,整车质量降低了1.3 t,降低百分率为8.63%;模态提升了0.0797 Hz,提升幅度为0.83%;由于增大了T12板厚,最大应力点应力减少了2.977 MPa;由于减小了T5、T6、T7板厚,车辆下侧梁形变增加了1.999 mm,变为22.204 mm,但仍处于标准要求范围内,优化结果可行。

表6 优化计算结果

5 结 论

文章利用响应面法和多目标遗传算法对特种落下孔车进行优化设计,以车体关键板件板厚为变量进行灵敏度分析,通过Box-Behnken设计方法设计实验建立响应面模型,最后以尺寸为设计变量进行优化。

(1) 根据模态提取方法提取落下孔车关键模态一阶垂弯频率为9.54 Hz,根据强度与刚度计算,得到最大应力为牵引梁附近,应力为224.447 MPa,得到挠度最大位置为侧梁下盖板中心,位移为20.205 mm。

(2) 通过灵敏度分析,选取出了对特种落下孔车车体质量和模态影响较大的板件,明确了后续优化使用的设计变量。结合Box-Behnken设计实验及二次多项式响应面模型和多目标遗传算法,在兼顾模态的情况下对特种落下孔车的质量进行了优化设计,结果表明:车体质量减小了8.63%,模态提升了0.83%,刚度和强度虽有变化但依旧符合标准,优化方案可行。