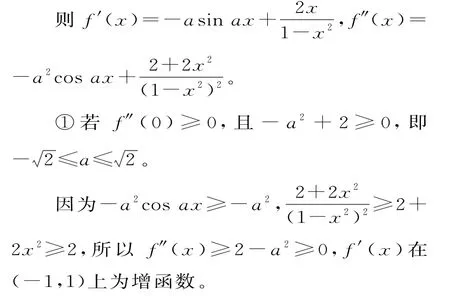乱花渐欲迷人眼，透过现象看本质——从全国卷三道三角函数与导数综合问题谈起

■南京市溧水区第二高级中学 蒋桃俊

函数与导数是高中数学的核心知识,是历年高考考查力度最大的主线之一,也是数学思想方法与能力、学科核心素养的载体。三角函数与导数的综合问题,在高考卷中往往以压轴题的形式呈现,由于此类问题立意新颖、灵活多变,创新性与综合性并存,与常规导数问题有所区别,对同学们有很大的挑战。它体现高考的选拔功能,实现命题“能力立意”向“素养导向”转变,因此备受命题者青睐。因为三角函数与其他函数综合,其导函数一般情况下不是多项式类型(多次求导也不行),所以一般无法求出零点(原函数极值点),只能以隐零点的形式存在,形成思维障碍,而同学们对其并没有形成好的处理方法和策略,很多时候会束手无策。事实上,虽然函数模型发生了变化,但是其数学本质并没有变,加上三角函数的特殊性(单调性、奇偶性、有界性、周期性等),倘若我们能够充分挖掘,掌握一些常用的方法策略,还是能够找到解决此类问题的突破口的。下面以全国卷中三角函数与导数综合的三道试题为例,总结出在解题过程中常用的一些处理方法,以期抛砖引玉,启发同学们对此类问题解决策略的进一步思考。

例1(2023年全国新课标Ⅱ卷第22题)

(1)证明:当0

(2)已知函数f(x)=cosax-ln(1-x2),若x=0是f(x)的极大值点,求a的取值范围。

解析:(1)记g(x)=sinx+x2-x,则g′(x)=cosx+2x-1,g″(x)=-sinx+2>0。

所以g′(x)在(0,1)上为增函数,即g′(x)>g′(0)=0,从而g(x)在(0,1)上为增函数,g(x)>g(0)=0,也即sinx+x2-x>0。

因此,x-x2

记h(x)=sinx-x,则h′(x)=cosx-1<0。

所以h(x)在(0,1)上为减函数,即h(x)

综上,当0

(2)易知f(x)=cosax-ln(1-x2),其定义域为x∈(-1,1)。

又f′(0)=0,故 当-10。

故f(x)在(-1,0)上单调递减,在(0,1)上单调递增。

所以x=0是f(x)的极小值点,不符合题意。

因为f′(0)=0,所以f′(x)<0,f(x)在(0,ξ)上单调递减。

因为f(x)为偶函数,所以f(x)在(-ξ,0)上单调递增。

所以x=0是f(x)的极大值点,符合题意。当a<- 2,取,同理可证。

综上,若x=0是f(x)的极大值点,则a的取值范围为(-∞,- 2)∪(2,+∞)。

说明:第一问中,先后利用了正弦函数和余弦函数的有界性(|sinx|≤1和|cosx|≤1),得到g″(x)和h′(x)的符号,这是处理三角函数与导数问题的常用方法。该小问的背景是正弦函数在x=0 处的泰勒展开式。第二问中,进行了两次求导,注意到f′(x)是奇函数,要使得x=0是极大值点,则要求f′(x)在0的附近先正后负(原函数先增后减);由于f″(x)为偶函数,则f″(x)在0附近小于0即可(此时f′(x)为减函数),所以只要分类讨论f″(0)的符号即可。情形①中,通过观察,利用三角函数的有界性,适当进行放缩,可以确定f″(x)的符号;情形②中,继续求导,利用三角函数的符号确定f‴(x)的正负,从而确定f″(x)在上的单调性,通过正负的讨论,分别直接得到或利用零点存在性定理得到f″(x)在0 右侧附近的符号,从而使得问题得到解决。

注:第二问的本质是“函数f(x)的极大值点为x0”的充分条件:f′(x0)=0,f″(x0)<0。而情形①和②的本质是高等数学中连续函数的性质——f(x)在x=x0处连续,若f(x0)>0,则存在δ>0,当x∈(x0-δ,x0+δ)时,f(x)>0;若f(x0)<0,则存在δ>0,当x∈(x0-δ,x0+δ)时,f(x)<0。其中区间(x0-δ,x0+δ)称为x0的邻域,上述性质很容易理解并被同学们接受。因此,考试时也可以采用这种有争议和超纲嫌疑(同极限一样)但非常简捷的方法加以说明,如②中,方法如下:

因为f″(0)<0,所以存在0<δ<1,当-δ

又f′(0)=0,所以当-δ0;当0

故f(x)在(-δ,0)上为增函数,在(0,δ)上为减函数,x=0是f(x)的极大值点,符合题意。

例2(2023年全国甲卷理科第21题)

(1)若a=8,讨论f(x)的单调性;

(2)若f(x)

解析:(1)若a=8,则

(2)记g(x)=f(x)-sin 2x=ax-

当00,g(x)在(0,ξ)上单调递增,g(ξ)>g(0)=0,不符合题意。

综上,若f(x)

说明:相对于其他三角函数与导函数的综合问题,该题中的导函数中只有三角函数(类似于2020 年全国Ⅱ卷理科第21 题),考查了同角关系、三角恒等变换、余弦函数的单调性等,有较强的综合性。第二问的不等式恒成立问题是一个典型的“端点效应”问题。其中的情形②也可以仿照例1,用连续函数及邻域加以说明。因为g′(0)>0,所以存在,当00,即g(x)为增函数,……,因为该问中易知g′(x)为减函数,所以采用了严格的演绎推理,同学们可以去体会。

例3(2019 年全国Ⅰ卷理科第20题)已知函数f(x)=sinx-ln(1+x),f′(x)为f(x)的导数。证明:

(1)f′(x)在区间内存在唯一的极大值点;

(2)f(x)有且仅有2个零点。

解析:(1)由题意知f(x)=sinxln(1+x),其定义域为(-1,+∞)。

易得f(0)=0。

当x∈(-1,0)时,f(x)>f(0)=0;

当x∈(0,x1)时,f(x)>f(0)=0。

又因为f(π)=-ln(1+π)<0,所以存在唯一的实数x2∈(x1,π),使得f(x2)=0。

当x≥π时,sinx≤1,ln(1+x)>1,所以f(x)<0。

综上,函数f(x)有且仅有2个零点。

说明:本题是三角函数与导数的完美融合,真正体现了导数在研究函数中的工具性,将三角函数与对数函数结合,创新性和综合性较高,是一道区分度非常高的试题。解题的过程中,正弦函数与余弦函数的单调性、有界性及在区间上的正负等得到了充分运用,利用它们来确定导函数的正负或函数值的正负,其中分区间讨论是处理此类问题的一种常用方法(如当时,f′(x)<0;当x≥π时,f(x)<0等,直接利用三角函数的符号和有界性得到),需要同学们有一定的观察能力和解题意识。

以上是2019 年至今全国卷中三角函数与导数综合的部分试题,虽然呈现方式各异(不等式恒成立、零点和极值问题、求单调区间等),考查的知识点不尽相同,但基本的思想方法还是有规律可循的,如分区间讨论、三角函数的符号及有界性等的应用。事实上,虽然此类问题涉及的函数往往较为复杂,但是我们要透过现象看清本质。由于三角函数的特殊性,它的融入有时反而会为问题的解决带来简便,当然这对同学们思维的灵活性、多样性、创新性等都有一定的要求。