基于鲸鱼优化算法的风力发电机组变桨模糊控制策略
2024-03-05赵南南马毓敏
赵南南, 杨 旭, 邹 琳, 马毓敏
(西安建筑科技大学 机电工程学院,陕西 西安 710055)
0 引言
风能是一种可再生清洁能源,对于可持续发展和应对气候变化具有重要意义。变桨控制是风力发电系统中至关重要的技术,变桨控制可以使风力发电机在不同风速条件下最大程度地捕获风能,提高发电效率,同时确保风力发电系统的安全运行。尽管传统的比例积分微分(Proportional Integral Derivative,PID)控制器在有精确模型的线性控制系统中表现优异,但在应对复杂的非线性风电系统时,其效果往往无法满足人们的期望[1]。因此,国内外学者对变桨控制进行了深入研究,将一些模糊控制器[2]、鲁棒控制器[3]、自抗扰控制器[3-4]以及滑模控制器[5]应用到风电变桨控制中,并取得较好的控制效果。
模糊控制是一种非线性控制方法,其不需要被控对象精确的数学模型,通过对输入和输出之间的关系进行模糊化处理,实现对系统的控制,具有较强的抗干扰性,响应速度快。鉴于模糊控制具有较好的控制效果,其已经被应用到风电机组变桨距控制中。但模糊控制器参数多,人工调节周期长且控制效果不理想。因此,相关学者提出将粒子群算法[6]、灰狼算法[4]等智能优化算法应用到模糊控制中,实现对参数的自寻优整定。鲸鱼优化算法是一种基于座头鲸行为的启发式优化算法,其模拟了座头鲸在寻找食物时的集群行为和迁移策略,具有全局收敛性和较快的收敛速度,适用于解决多目标优化工程问题,被广泛应用于函数优化、机器学习、故障诊断和工程设计等领域[7-10]。
模糊PID控制器的性能除了与模糊规则库有关以外,还与两类因子存在着紧密的联系,参数整定问题已成为目前模糊控制研究的焦点之一。为实现模糊控制器参数的自寻优整定,本文采用鲸鱼优化算法对量化因子、比例因子和模糊PID的三个初值进行最优整定,以消除人工基于经验调节的主观性以及不确定性。仿真结果表明:该方法具有较好的参数自寻优能力,同时改善了机组输出功率的波动性、提高了系统的动态响应和并网的安全性。
1 风电机组建模
风力发电系统是一个融合空气动力学特性、机械特性和电气特性的综合非线性系统。该模型主要由风力机模型、传动系统模型、永磁同步发电机模型以及变桨执行机构模型这四部分组成。
1.1 风力机模型
桨叶旋转时,其捕获的功率Pw为
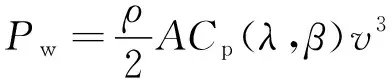
(1)
风力机转矩Tm为
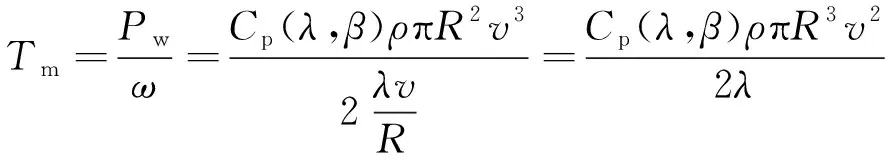
(2)
风能利用系数CP可表示为
0.001 84(λ-3)β
(3)
式中:ρ为空气的密度;v为风速;A为风轮面积;λ为叶尖速比;β为桨叶的桨距角;R为风力机转子半径;ω为风轮旋转角速度。
1.2 传动系统模型
直驱式风力发电机组中,它不使用传统的齿轮箱,风轮直接与发电机的转子相连,通过转子的旋转来产生电能。传动系统数学模型可以描述为
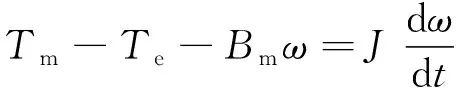
(4)
为了简化分析,忽略阻尼项,令其值为0,故:
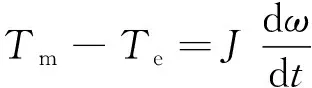
(5)
式中:Tm为风轮转矩;Te为电磁转矩;J为风电机组的转动惯量;Bm为阻尼系数。
1.3 永磁同步发电机模型
在d-q旋转坐标系下的数学模型为
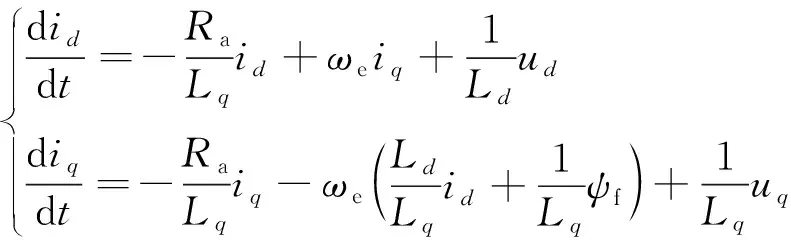
(6)
式中:id、iq分别为d、q轴的电流;Ld、Lq分别为d、q轴的电感;ud、uq分别为d、q轴的电压;Ra为定子电阻;ψf为磁链;ωe为转子电角频率。
则发电机的电磁转矩为
Te=1.5Np[(Ld-Lq)idiq+iqψf]
(7)
若Ld=Lq,则:
Te=1.5Npiqψf
(8)
式中:Np为发电机极对数。
1.4 变桨执行机构模型
考虑到风电机组的电气和机械极限,实际运行中,执行机构的变桨幅度在-2°~30°之间,变桨速率则不会超过±10 °/s。将其简化为一阶惯性环节:
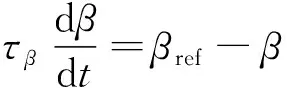
(9)
式中:τβ为时间常数;β为目前桨距角值;βref为给定桨距角值。
对上式进行拉氏变换:

(10)
2 模糊PID控制原理
模糊PID控制是一种结合模糊逻辑和PID控制的方法,具有两种控制策略的优点[11-15]。模糊PID控制器克服了传统PID控制在处理非线性、时变和复杂系统时的局限性。此外,模糊PID控制具有更高的灵活性,可以应对不同的系统和控制要求[16]。模糊控制器将风电机组的额定功率Peref与输出功率Pe的误差值e和误差变化率ec作为输入变量,经过模糊化、模糊推理、去模糊化三个部分,最后输出Δkp、Δki、Δkd三个参数变量,从而实现PID参数的实时调节[17],模糊PID控制原理框图如图1所示。

图1 模糊PID控制原理框图Fig.1 Fuzzy PID control block diagram
调整后的控制器参数为

(11)
式中:kp、ki、kd为调整后的参数;kp0、ki0、kd0为PID的三个初值;Δkp、Δki、Δkd为模糊控制器的输出参数变量。
3 模糊PID控制器设计
3.1 定义输入、输出变量及隶属函数
规定风电机组的功率偏差应小于额定功率的10%,即±200 kW。针对本文研究的2 MW风机,可以设定输入功率偏差e的论域为[-200 kW,200 kW]。输入与输出均采用七个语言值变量,其中NB(负大,e≤-200 kW);NM(负中,-200 kW≤e≤-100 kW);NS(负小,-100 kW≤e≤-20 kW);Z(零,-20 kW≤e≤20 kW);PS(正小,20 kW≤e≤100 kW);PM(正中,100 kW≤e≤200 kW);PB(正大,e≥ 200 kW)。同理,设定输入功率偏差ec的论域为[-400 kW/s,400 kW/s]。最后,将其映射到模糊论域[-6, 6]中。
将模糊控制器输出变量Δkp、Δki、Δkd分别作为PID控制器参数的修正值,结合传统PID参数调整原则,设置其模糊论域分别为[-0.3, 0.3]、[-0.06, 0.06]、[-3, 3]。为保证输出功率的平稳性,输入的隶属函数均采用平滑的高斯型,而当输出的模糊集为零(Z)时采用高斯型,其余隶属函数均采用简单的三角形。
3.2 模糊规则库的建立
模糊规则库是由一系列模糊规则组成的知识库,由专家和工作人员长期积累经验所建立[18],用于将输入模糊集映射到输出模糊集,以“Ifeandecthen Δkp、Δki、Δkd”的样式进行建立。模糊PID控制规则如表1所示。
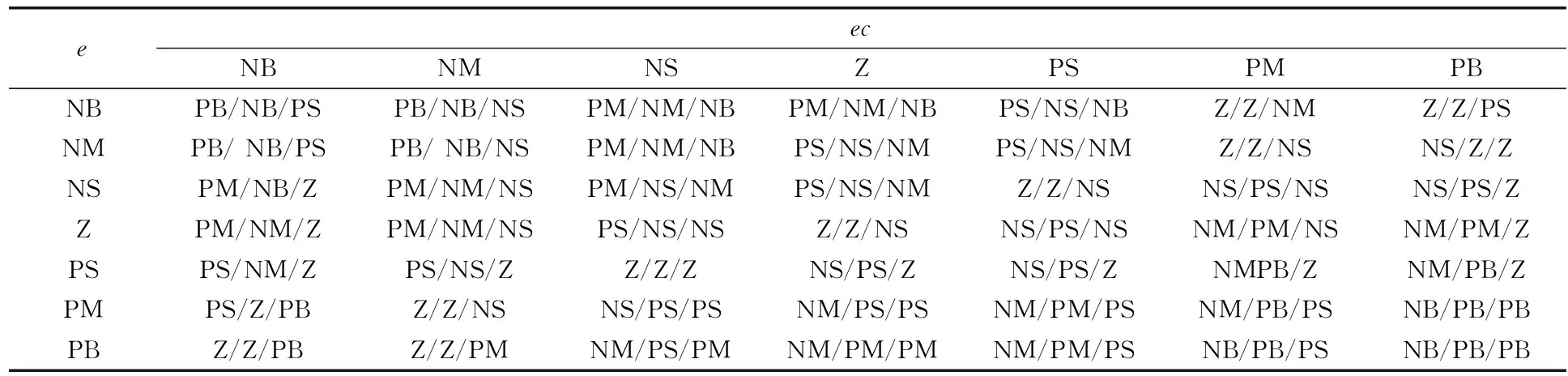
表1 模糊PID控制规则表Tab.1 Fuzzy PID control rule sheet
3.3 量化因子和比例因子的选择
量化因子和比例因子是用于调整模糊控制器输出的重要参数,起到调节输出离散级别、精度和增益的作用,以实现对系统的精确控制、确保系统的稳定性。起初,两类因子是通过近似计算和经验积累得出,不仅耗时而且十分困难。
3.4 模糊推理与去模糊化
模糊推理是模糊控制系统中的一个关键步骤,用于将模糊输入转换为模糊输出。在模糊推理过程中,首先根据系统的输入和定义的模糊规则,将输入值映射到模糊集合中合适的隶属度值。然后,通过应用模糊规则的逻辑关系,计算出相应的模糊输出值。
去模糊化是将模糊输出映射到实际输出空间的过程,以便进行实际的控制或决策。常用的去模糊化的方法主要有:最大隶属度法、中位数法以及重心法。在选择方法时,需要考虑系统的性能要求、实时性、复杂度和计算效率等因素。重心法计算直观简单,具有可解析性且物理含义清晰。因此,本文采用重心法进行去模糊化处理[19]。重心法由下式描述:
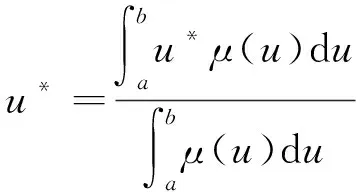
(12)
式中:u*为清晰量;u为输出的控制量;μ为隶属度函数;b为清晰化值的上限;a为清晰化值的下限。
4 鲸鱼算法寻优
4.1 鲸鱼算法
与灰狼算法、水循环算法以及粒子群算法等智能优化算法类似,鲸鱼算法也是一种自然启发式优化算法,最初是由Seyedali Mirjalili于2016年提出。其基本思想是模拟鲸鱼群体的行为,寻优过程主要包括3个环节:围捕猎物、局部搜索和随机搜索[20]。其本质思想是基于统计优化,与其他算法相比具有参数设置少、操作简单、易于实现以及寻优能力强等优点。
4.2 寻优过程
4.2.1 围捕猎物
类比于真实的鲸鱼行为,鲸鱼在觅食时会围绕着猎物,采取相应的捕食策略。假设某一鲸鱼个体所处的位置是目标函数的最优解,那么其他鲸鱼便会更新自己的位置,以增加找到更优解的机会,位置更新计算式为
D=|C·X*(t)-X(t)|
(13)
X(t+1)=X*(t)-A·D
(14)
式中:A、C为系数向量;t为迭代次数;X*(t)为当前最优适应度鲸鱼的位置向量;X(t)为当前鲸鱼所处的位置向量。
其中A、C的计算式如下:
A=2a·r-a
(15)
C=2r
(16)
式中:a在整个迭代过程中由2线性递减到0;r为[0,1]中的随机向量。
4.2.2 局部搜索
鲸鱼的捕食行为主要包含两种方式:
a) 气泡网捕食
采用气泡网捕食时,座头鲸会在猎物周围产生气泡网,以限制猎物的逃逸路径,从而更容易捕获猎物,位置更新计算式为
X(t+1)=D′·ebl·cos(2πl)+X*(t)
(17)
D′=|X*(t)-X(t)|
(18)
式中:D′为个体和最优鲸鱼的距离;b为一个常数,表示螺旋形状,取为1;l为区间[-1,1]均匀分布的随机数。
b) 包围捕食
捕猎时鲸鱼的群体位置需采用式(14)进行更新。
鲸鱼在围捕猎物时会采用上述两种捕食方式,通常设置鲸鱼采用两种捕食方式的可能性各为0.5,表达式为
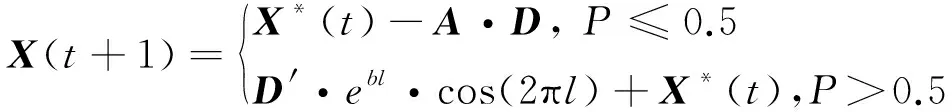
(19)
式中:P为值域为[0,1]的随机数。
4.2.3 随机搜索
随机搜索通常被用作初始阶段的探索机制,以便尽快地在搜索空间中找到一些潜在的解。此外,鲸鱼在捕食过程还会进行大范围的随机搜索猎物。在该算法中,是通过|A|的大小判断鲸鱼是否进入随机搜索这一过程。当|A|<1时,鲸鱼会游向最优鲸鱼所处的位置;当|A|≥1时,鲸鱼则会选择随机个体为目标进行位置更新,迫使鲸鱼偏离猎物,借此找到一个更合适的猎物,表达式为
X(t+1)=Xrand(t)-A·|C·Xrand(t)-X(t)|
(20)
式中:Xrand(t)为随机鲸鱼的位置向量。
鲸鱼算法优化流程可用图2来表示。

图2 鲸鱼算法优化流程图Fig.2 Whale algorithm optimisation flowchart
4.3 鲸鱼算法优化模糊控制器参数
模糊控制所涉及的参数繁多且相互影响,因此需要对参数进行协调组合以得到系统最优性能。本文采用鲸鱼算法,通过调用搭建的风力发电机组变桨控制模型,对模糊PID控制的参数进行最优整定,使控制效果达到最佳。鲸鱼的位置对应待优化的参数(Whale Optimisation Algorithm-Fuzzy Proportional Integral Derivative,WOA-FPID)控制结构图如图3所示。

图3 WOA-FPID控制结构图Fig.3 WOA-FPID control structure diagram
具体步骤如下:
(1) 设置初始种群数量和最大迭代次数;
(2) 设置参数的上下界;
(3) 确定适应度函数,本文采用衡量控制系统的性能评估指标ITAE作为适应度函数[21],指标越小,表示控制系统的性能越好,表达式如下:
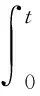
(21)
(4) 运行鲸鱼优化算法,输出优化后5个参数(分别为kp0、ki0、kd0、ke、kec)的数值;
(5) 通过sim函数调用风力发电机组系统仿真模型,通过适应度函数对优化后的参数进行评价;
(6) 若达到最大的迭代次数,则输出全局最优解,并将优化后的参数带入模型中,进行仿真。
5 仿真结果及分析
在鲸鱼优化算法中,种群规模过小易陷入局部最优,太大则会导致计算量增加和收敛性变坏;迭代次数过少会导致搜索不充分,过多则会导致计算时间增加,收敛速度变慢。因此,设定种群规模为10,最大迭代次数为20,种群维数为5。参数的寻优范围分别设置为Ke∈[0.02, 0.04]、Kec∈[0.01, 0.02]、Kp∈[0.5e-6, 4e-6]、Ki∈[1e-5, 8e-5]、Kd∈[3e-7, 1e-5],在Matlab/Simulink中进行仿真,得到WOA的迭代曲线,如图4所示。图中适应度值越小,表示当前鲸鱼的位置最优。从迭曲线可知,WOA在迭代6次后,适应度值收敛并且达到最优。

图4 WOA迭代曲线Fig.4 Iterative curve of WOA
为验证本文所设计的控制策略在风电机组中的效果,选取图5所示的高于额定风速的自然风速作为输入,将PID、FPID及WOA-FPID分别应用到模型中进行对比分析。机组参数如表2所示,风力发电机组整体仿真模型如图6所示,变桨控制器仿真如图7所示,不同控制策略的输出功率性能指标对比见表3,仿真结果如图8、9所示。
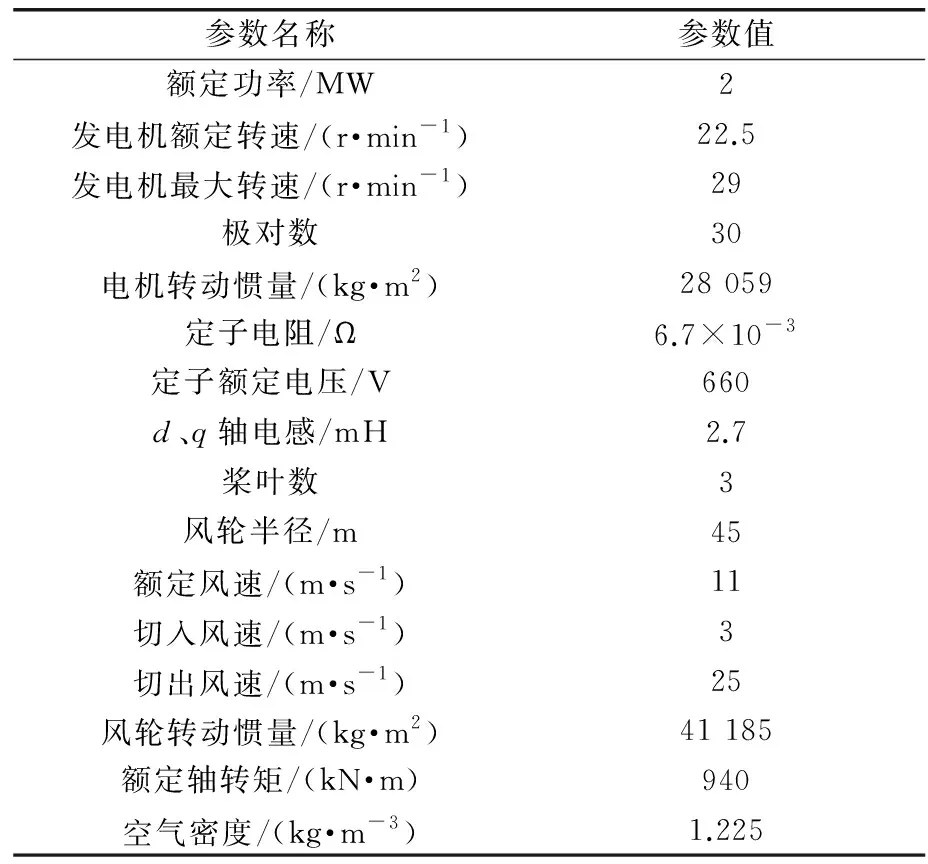
表2 永磁直驱风电机组(Permanent Magnet Synchronous Generator,PMSG)参数Tab.2 System parameters of PMSG
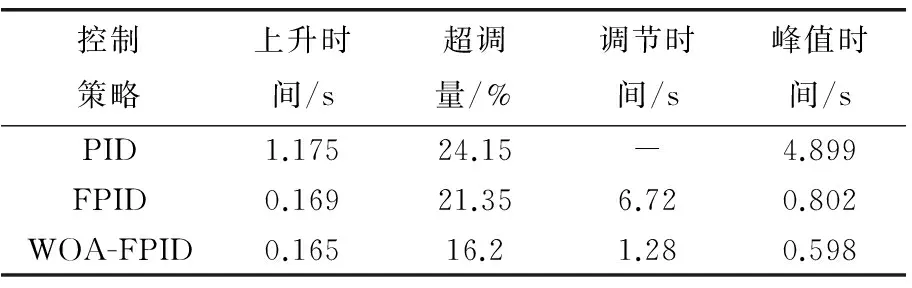
表3 不同控制策略下的输出功率性能指标对比Tab.3 Comparison of performance indexes of different control strategies
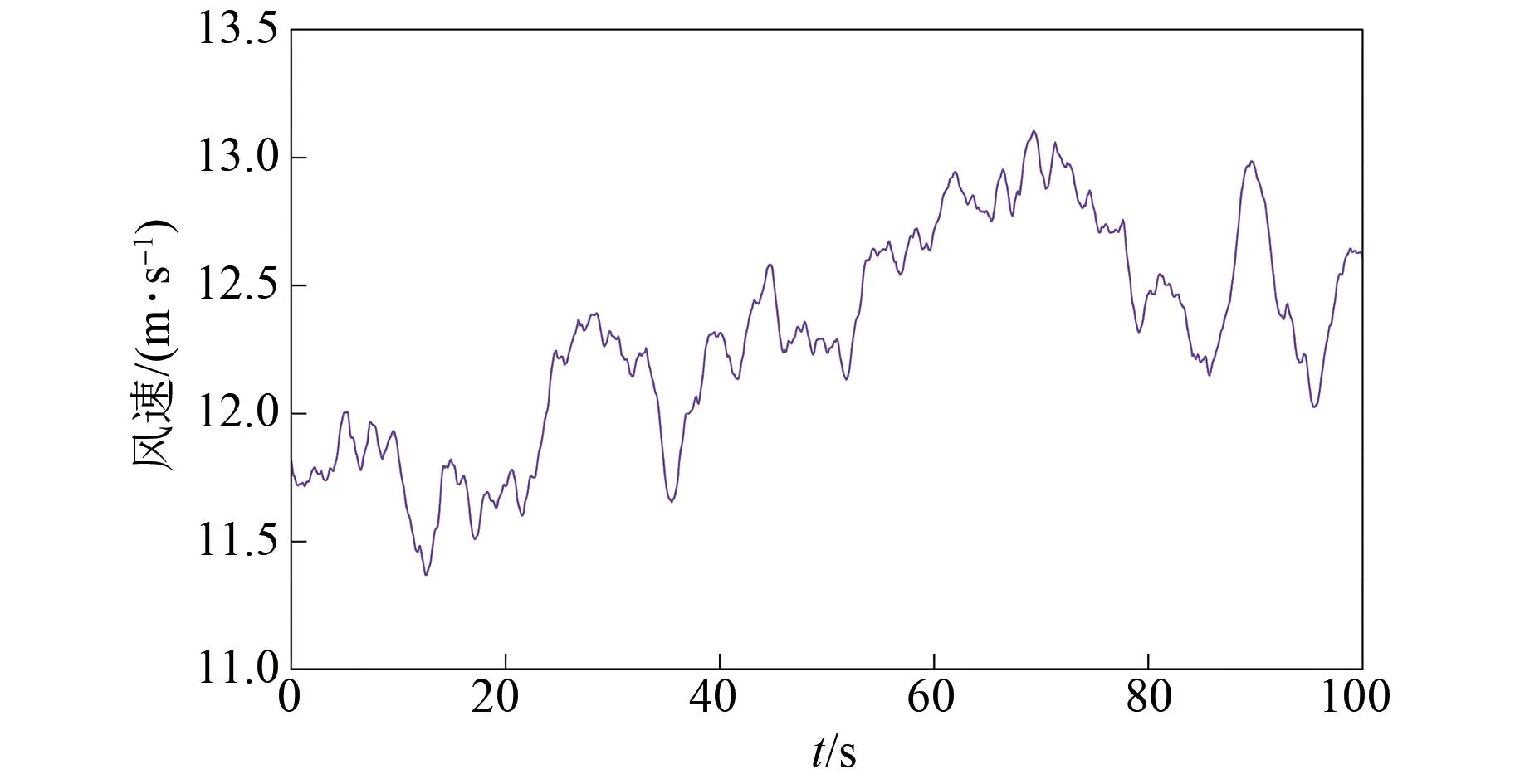
图5 高于额定风速的风速曲线Fig.5 Wind speed profile above rated wind speed

图6 永磁直驱风电机组仿真模型Fig.6 Simulation of PMSG
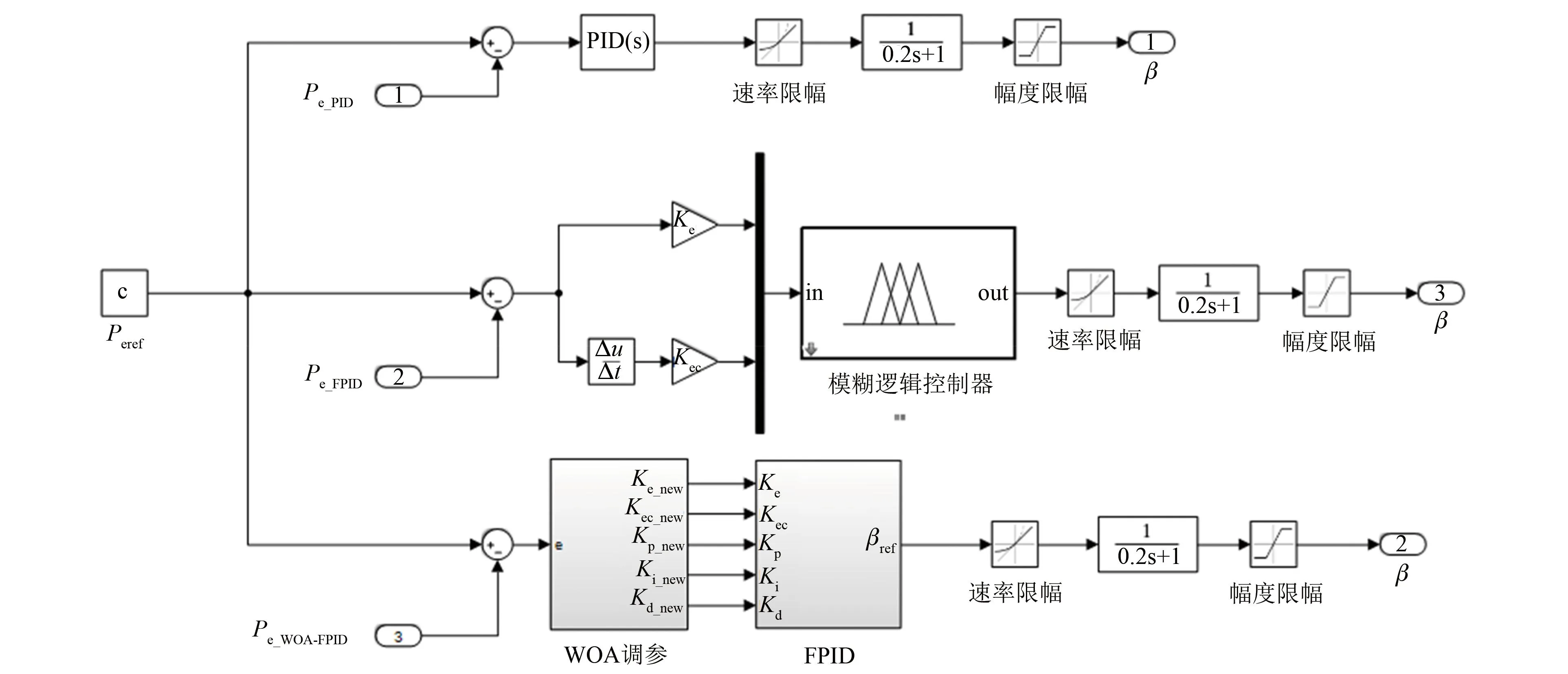
图7 不同变桨控制器仿真模型Fig.7 Simulation model of different pitch controllers

图8 桨距角曲线对比Fig.8 Pitch angle curve comparison
图8所示为桨距角变化曲线对比,3种控制下的曲线基本一致。第44.9 s时,风速突然下降,PID在第44.916 s、FPID在44.912 s、WOA-FPID在第44.901 s作出减小桨距角的响应。在第35.7 s时,风速突然上升, PID在第35.73 s、FPID在第35.711 s、WOA-FPID在第35.709 s做出增大桨距角的响应。因此,WOA-FPID控制的灵敏度优于其余两种控制方式。当第10 s、风速为11.84 m/s时,PID的桨距角为4.14°,未经鲸鱼算法优化的FPID的桨距角为4.38°,而经过鲸鱼算法优化的FPID的桨距角为4.48°。当风速大于额定风速时,桨距角的细微变动对功率有明显影响,因此,WOA-FPID控制的桨距角准确性最好,从而可以减少风机部件间的磨损,延长其使用寿命。
图9所示为风电机组的输出功率对比,传统PID的效果并不理想,FPID与WOA-FPID都可以将输出功率稳定在额定值附近,但后者波动范围更小且稳定速度快。在第12.8、35.8、95.6 s等风速突变时刻,PID的功率跌落幅值分别为144 kW、156 kW、155 kW;FPID的功率跌落幅值分别为98 kW、120 kW、99 kW;WOA-FPID的功率跌落幅值分别为6 kW、5 kW、8 kW。当风机并网后,功率的波动容易对电网造成冲击,导致机组端电压以及并网电压的波动,也会影响到电网的暂态稳定性。由以上分析可知,WOA-FPID具有更小的功率波动,有更好的输出性能,提高了系统的稳定性、安全性与抗干扰性。

图9 风电机组的输出功率Fig.9 Output power diagram for wind turbines
6 结语
本文首先介绍了风电机组各部分的数学模型以及模糊控制的基本原理,其次阐述了鲸鱼算法的原理与优化流程,很好地解决了风电机组变桨模糊控制的参数难以整定到最优的问题。通过Matlab/Simulink仿真软件搭建了风电机组仿真模型,将3种不同变桨控制策略应用其中并进行对比分析,结果显示,WOA-FPID性能明显优于其他两种控制器,减少了超调量,大幅度缩短了调节时间,并提高了抗扰动性能。同时,WOA-FPID可以更好地将输出功率快速稳定到额定值附近,使得功率跌落幅值更小,并对桨距角进行精确调整,提高了系统的稳定性与安全性。
