混合直流系统中基于平波电抗器与限流电抗器参数优化的限流策略

李 涛, 胡 迪, 杨 为, 祝雨晨, 刘宏达, 陈 忠, 官玮平, 祝 琳

(1.国网安徽省电力公司电力科学研究院,安徽 合肥 230022;2.天津大学 电气自动化与信息工程学院,天津 300072;3.国网浙江省宁波电力公司,浙江 宁波 315000)

0 引言

直流输电的发展大致可分为三个阶段:(1)基于线换相换流器(Line Commuted Converter, LCC)的常规高压直流输电技术:LCC的关键技术已经十分成熟,具有传输容量大、电压等级高、经济性好的优势,但LCC所使用的晶闸管为半控器件,无法避免换相失败的问题,因而其发展受到限制[1-2];(2)基于电压源换流器(Voltage Source Converter, VSC)的柔性直流输电技术:与LCC相比,VSC采用全控器件(Insulated Gate Bipolar Transistor,IGBT),消除了LCC的固有缺陷,同时还具有动态无功支撑的优势。但是IGBT耐流能力低,同时VSC无法仅通过触发控制来切断直流电流,需要配合直流断路器隔离故障,因而其经济性较差[3-4];(3)LCC和VSC组合的混合直流输电技术:综合了LCC和VSC的优点,可靠性较高、经济性较好,但是混联直流系统各设备之间的配合方式还需要进一步研究[5-6]。

与传统且成熟的交流输电系统相比,混合直流输电还面临诸多需要解决的问题,其中故障限流技术是其发展的关键之一。因为新能源开发和远距离输电的需要,混合直流电网工程中目前多采用架空线进行电能传输[7-8],与电缆线路相比,架空线更易受到雷击或挂线等干扰,线路故障率较高;混合直流电网结构复杂,导致其故障特性难以精确分析,交直流电网各部分之间协调控制困难;多电压等级的混合直流电网网架结构、运行方式以及故障类型多样,且直流电流不存在自然过零点。传统交流断路器很难切断直流故障电流,低成本大容量的直流断路器还未研制成功[9];多种电力电子设备之间存在强耦合关系,其故障发展迅速,影响范围更大;基于模块化多电平换流器(Modular Multilevel Converter, MMC)的柔性直流输电技术在故障时会由于子模块电容放电而导致短路电流迅速增大。因此深入研究能够应对直流线路故障的限流控制策略具有重要的现实意义和必要性[10-11]。

目前,混合直流系统中线路故障限流控制策略主要有两种[12]:一种是被动式限流控制策略,即通过限流电抗器抑制短路电流上升速率、利用断路器有选择性地切除故障线路;另一种是主动式限流控制策略,即通过对电网设备的主动控制来减小直流线路和换流站内故障电流的上升的过程。

其中,主动式限流控制策略的最大不足是无法从根本上切除直流故障,被动式限流策略主要依靠断路器和限流电抗器来实现。在断路器研发上,ABB公司在2012年研制出了世界上首台80 kV/2 kA混合式直流断路器[13-14],能够分断最大9 kA短路电流。随后,阿尔斯通公司也研制了120 kV混合式直流断路器,最大开断电流为5.2 kA[15]。国内直流线路故障保护起步较晚,被动限流方法中涉及的关键技术与国外仍有一定差距,部分断路器依赖进口。

限流电抗器虽能够限制故障电流上升速率和峰值,但也带来了成本增加、动态性能变差等问题,因此需要合理配置限流电抗器的容量。文献[16]推导了并联金属氧化物避雷器(Metal Oxide Varistors,MOA)的故障限流器投入前、投入过程和完全投入后的等效模型,为后续研究奠定了基础。文献[17]提出了一种考虑断路器切断电流和MOA能量耗散的电抗器优化配置方法,采用变动权系数法对多端电网的电抗器容量进行优化,其应用的前提条件为平波电抗器与限流电抗器容量之和为定值、适用性较差且没有给出这一定值的计算方法。文献[18]提出了一种考虑换流站闭锁的电抗器容量优化配置方案,能够实现换流站闭锁前后电抗器容量的最优配置。文献[19]提出了考虑电抗器容量和短路电流大小的优化配置策略,该方法使用粒子群算法对多目标优化问题进行求解。与文献[17]相比,该方法可以得到Pareto最优解,具有一定的实际意义。

综上所述,直流线路上的电抗器容量对于短路电流的抑制至关重要,同时考虑投资成本的合理性,需要适当配置电抗器容量。本文以直流线路上电抗容量占比较高的平波电抗器和限流电抗器为目标变量进行优化,旨在提高混合直流系统的经济性和可靠性。

1 交直流混联系统故障电流特性分析

本文使用的混合直流系统结构如图1所示,整流站采用换相换流器,使用定电流控制方式;逆变站采用模块化多电平换流器,使用定电圧控制方式。线路两侧分别装有平波电抗器(Ldc1、Ldc2)和限流电抗器(L1、L2),其中Ldc1和Ldc2串联在直流线路中,可以降低直流电流的谐波;L1和L2仅在故障时投入,正常工作时被旁路,可以抑制故障电流的幅值。直流断路器可以开断直流故障电流。

图1 交直流混联系统拓扑图Fig.1 Topology diagram of AC/DC hybrid power system

1.1 LCC整流侧故障电流特性分析

本文采用的换相换流器(LCC)由12脉动换流器构成,如图2(a)所示。三相全桥电路在正常运行时,任意时刻上、下桥臂均各有一相导通,因此当直流线路发生双极性短路故障时,短路电流主要由交流侧馈入。在换流站不闭锁的情况下,可以得到其等效电路,如图2(b)所示。图中:VT为晶闸管;Udc为整流输出电压平均值;Req1和Leq1分别为等效电阻和电感,具体参数计算如下:

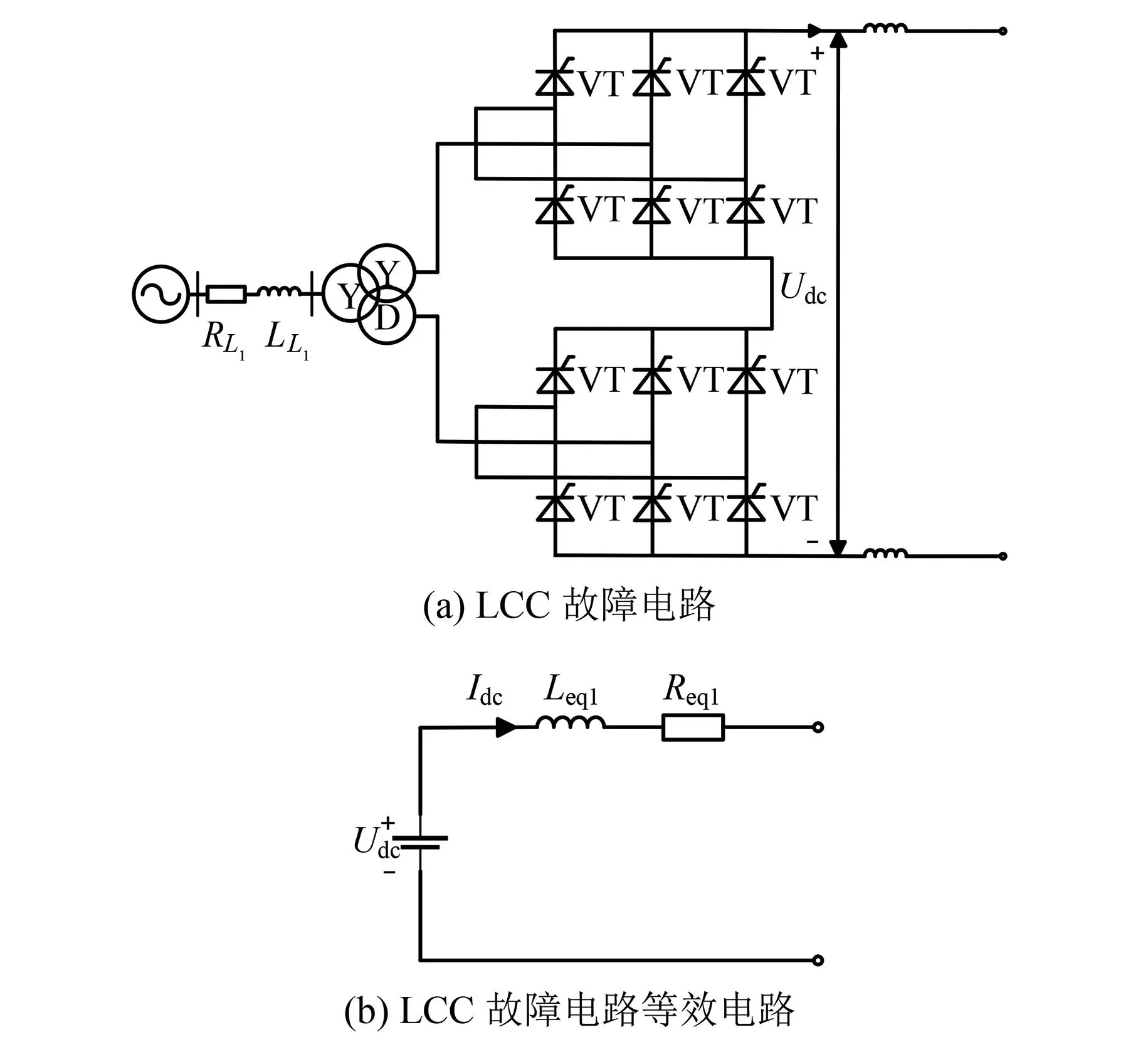
图2 LCC侧直流线路双极短路故障放电回路Fig.2 Discharge circuit in the event of a fault in the double pole short circuit of the LCC side DC line

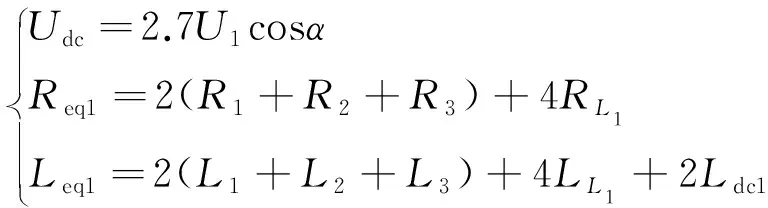
(1)

式中:U1为交流侧线电压有效值;α为触发延迟角;R1、R2、R3、L1、L2、L3分别为三绕组变压器高中低压侧的电阻和电感值;RL1、LL1分别为交流系统与整流站之间线路的电阻和电感值;Ldc1为整流侧平波电抗器电感值。

图2(a)中直流侧发生双极性短路时,故障放电回路等效为一个带有直流电源的R-L串联回路,在故障发生之前,系统处于稳态,故障发生瞬间电感电流等于稳态电流Idc,系统电压为直流电压Udc。假设故障发生在换流站出口侧,若考虑最严重的情况,忽略故障初期控制器的响应,即认为故障发生后的瞬间触发延迟角α不变,根据图2(b),由三要素法[20]可求得整流侧故障电流if1为

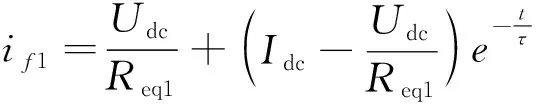
(2)

式中:τ为LCC侧短路电流时间因子。其中,τ可由下式求得:

(3)

1.2 MMC逆变侧故障电流特性分析

直流线路发生双极性短路之后的几毫秒内,交流系统馈入直流侧的短路电流远小于MMC子模块电容的放电电流[16],因此可以忽略交流侧对直流侧短路电流产生的影响。在换流站不闭锁的情况下可得到图3所示的等效电路。图中:SM为半桥子模块;R0为桥臂电阻;L0为桥臂电感;C0为子模块电容值;Req2、Leq2、Ceq2分别为等效电阻、电感和电容,具体参数计算如下:

图3 MMC侧直流线路双极短路故障的放电回路Fig.3 Discharge circuit of MMC side DC line with bipolar short circuit fault

(4)

式中:Ldc2为逆变侧平波电抗器电感值;N为一相桥臂子模块数。

故障放电回路可以等效为一个RLC串联回路,故障发生之前,系统处于稳态;故障发生的瞬间电感电流的初始值等于Idc,电容两侧放电电压的初始值与直流电压Udc的初始值相等。假设故障发生在换流站出口侧,根据图3(b),可以求得逆变侧故障电流if2和等效电容两侧的电压uc分别为

if2=

(5)

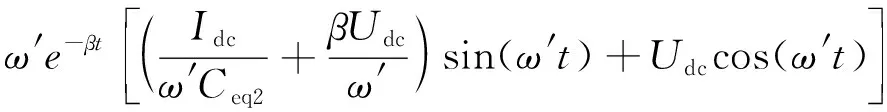
(6)

式中:β为MCC侧短路电流因子;ω′为旋转角速度。β、ω′可由下式求得:

(7)

1.3 考虑短路点位置的故障电流特性

上述章节分别推导短路点在整流侧出口和逆变侧出口时的短路电流表达式。当双极性短路故障发生在直流线路上时,设故障点与整流换流站出口的距离占线路全长的x%,线路单位长度的电阻、电感分别为RL、LL,线路长度为l。由于直流线路对地电容很小,因此可以忽略电容,则式(1)、(4)可修改为

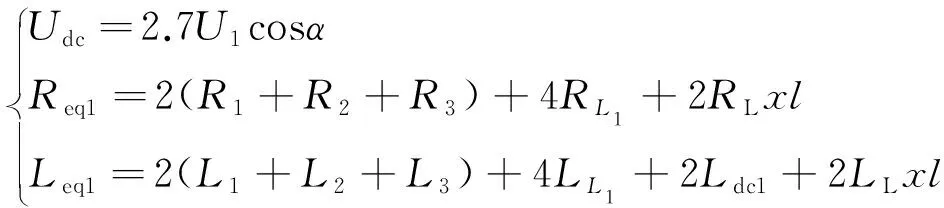
(8)

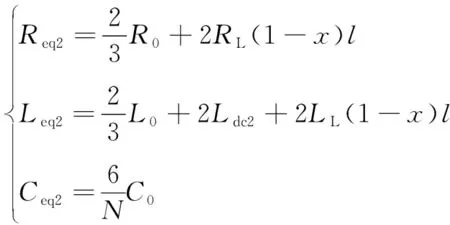
(9)

将式(8)、(9)分别代入式(2)、(5)中,并利用MATLAB软件绘制短路电流if1和if2的波形,如图4所示。由图可知,在断路器切断故障电流前,整流侧短路电流幅值随着时间的延长单调增加,而逆变侧短路电流幅值先减小至0、后反向增加。同时,整流侧短路电流幅值随着远离故障点而逐渐减小,逆变侧短路电流的幅值随着靠近故障点而逐渐增加。因此,两侧短路电流均在故障发生在该侧出口处时取得最大值。考虑系统需要承受最大短路电流冲击,故以换流站出口处故障的短路电流表达式来优化平波电抗器与限流电抗器容量。

图4 短路电流与短路点位置、时间关系图Fig.4 Relationship between short circuit current and short circuit location and time

1.4 限流电抗器完全投入之后两侧短路电流表达式

1.1与1.2章节主要推导了限流电抗器投入前阶段的短路电流表达式,本节将分析限流电抗器完全投入阶段的短路电流变化情况。

当限流电抗器完全投入后,此时式(1)、(4)分别转换为

(10)

(11)

令直流线路在t0时刻发生故障,系统检测故障并投入限流电抗器的时间为t1,在t2时刻直流断路器动作,切断故障电流。整流侧限流电抗器电感值为L1,逆变侧限流电抗器电感值为L2,由上述章节可知系统发生最严重的短路故障为换流站出口侧发生双极性短路。在忽略限流电抗器投入时间的前提下,限流电抗器投入前后,系统磁链保持守恒,电容电压保持不变:

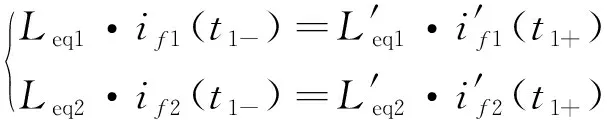
(12)

uc(t1-)=uc(t1+)

(13)

由式(2)、(5)、(6)、(10)、(11)、(12)和(13)可求出限流电抗器投入之后的短路电流表达式:

(14)

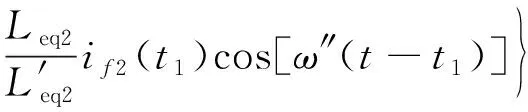
(15)

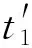
(16)

(17)

2 平波电抗器和限流电抗器参数优化配置数学模型

根据上述推导含有限流电抗器和平波电抗器的短路电流表达式可知,限流电抗器和平波电抗器的容量对故障电流产生一定的影响,且配置一定容量的限流电抗器和平波电抗器可以限制短路电流幅值。基于此,本节主要利用上一章节得到的故障电流表达式优化限流电抗器和平波电抗器的容量。

2.1 目标函数

为了保证限流能力的同时降低投资,建立了一个多目标优化模型,以平波电抗器与限流电抗器电感值之和最小minf1以及限流电抗器投入时的故障电流与断路器切断的故障电流之和最小minf2为目标函数,如式(18)所示:

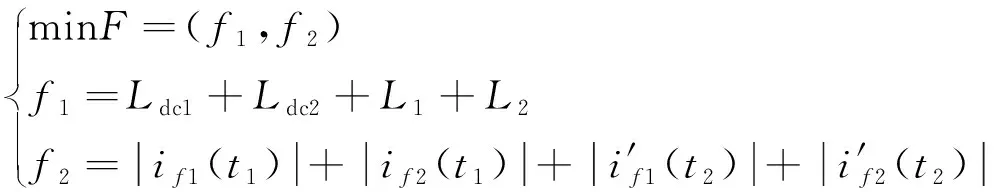
(18)

式中:F为优化目标函数;f1为系统中两侧平波电抗器与限流电抗器电感值之和,对f1进行优化可以实现系统中总电感值最小;f2为限流电抗器投入时的故障电流与断路器切断的故障电流之和,对f2进行优化可以实现故障限流效果的最大化以及断路器切断容量的最小化。为了在直流线路发生任意故障的系统都能够保证短路电流在允许的范围内,应以系统中发生最严重故障时的短路电流之和作为f2的优化目标函数。

2.2 约束条件

为了保证系统能够在合理范围内平稳运行,在优化目标函数的同时还要对电感值和短路电流进行约束。

(1) 电抗器大小约束

系统中两端的平波电抗器和限流电抗器每个电抗器的电感值必须保持在一个合理的范围内:

Limin≤Li≤Limax

(19)

式中:Li表示两侧的平波电抗器和限流电抗器电感值;Limin和Limax分别为满足系统动态特性要求以及占地面积要求的电感值下限和上限。

(2) 最大短路电流约束

当直流线路发生短路故障后,故障电流远高于额定电流,为了避免过流引起的过热以及电磁力引起的线路形变,应限制短路电流在直流线路允许的范围内:

|ifi(t1)|≤kIdc

(20)

式中:k为允许的过流系数;Idc为直流线路正常工作时电流。

(3) 直流断路器开断容量约束

直流线路发生故障后,需要依靠直流断路器切除故障线路,为了保证断路器能够可靠切断故障电流,需要将故障电流限制在直流断路器最大切断电流之内,并留有一定裕量,可以表示为

(21)

式中:α为裕度系数,本文取0.8;IDCCBmax为直流断路器的最大切断电流。

根据第1章节所介绍的内容,可得到电抗器优化的数学模型,式中k1和k2为权重系数。若k1系数较大,表明侧重于平波电抗器与限流电抗器电感值之和最小;若k2系数较大,表明侧重于限流电抗器投入时的故障电流与断路器切断的故障电流之和最小。

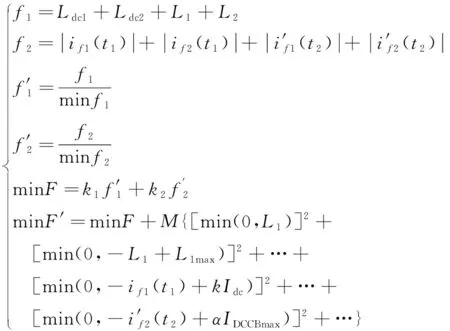
(22)

3 算例分析

本文以LCC-MMC两端交直流混联系统为例,研究平波电抗器与限流电抗器的参数优化配置,所采用的模型如图5所示,具体参数见表1。同时,为了验证上述电抗器优化配置方法的正确性,本节分别对两端交直流混联系统中平波电抗器和限流电抗器电感值进行优化配置。仿真中在F1、F2故障点分别设置双极短路故障,设故障发生时间t0=2.5 s,投入限流电抗器时间t1=2.503 s,断路器动作时间t2=2.506 s。

3.1 算例1

设平波电抗器取值下限为Ldcmin=10 mH,上限为Ldcmax=60 mH。限流电抗器取值下限为Limin=0,上限为Limax=200 mH。过流系数k=6,直流断路器最大开断容量为IDCCBmax=10 kA。

当k1=1、k2=0和k1=0、k2=1时,即分别以各个电抗器电感容量之和最小f1min和各个限流电抗器投入时的最大故障电流与断路器切断的最大故障电流之和最小f2min为单目标求解,分别求得单目标f1min=181.4 mH,f2min=13.945 kA。各个电抗器电感容量大小如图6所示。

图6 单目标优化下的电抗器参数Fig.6 Reactor parameters under single objective optimization

由图6可知,以电感容量之和最小为目标与以故障电流之和最小为目标相比,优化求解得到的各平波电抗器和限流电抗器电感容量均偏小。

根据2.1章节介绍的多目标优化方法,以0.1为步长,分别取权系数k1=0.1～0.9,得到9种不同权系数下的各平波电抗器和限流电抗器的优化结果,如图7所示。

图7 多目标优化下的电抗器参数Fig.7 Reactor parameters under multi-objective optimization

在图7中,不同的权系数ki表示对不同目标函数的侧重不同。在实际应用中,可根据需要来选择合适的权重系数,从而实现在特殊场合下的电抗器电感容量优化配置。对比图7中各权系数下电抗器电感容量,当权系数k1数值较小或较大时,改变k1对电抗器电感容量没有影响。当权系数k1数值在0.2～0.6时,增大k1能够降低电抗器电感容量。

为了验证上述平波电抗器和限流电抗器配置结果对短路电流的影响,应用图5所示系统进行仿真验证,得到整流侧、逆变侧短路电流随k1变化的关系曲线,如图8所示。

图8 短路电流随k1变化的关系曲线Fig.8 Relationship curve of short-circuit current with k1 variation

由图8可知,随着k1的增大,目标函数f1的权重在不断增大,目标函数f2的权重在不断减小,整流侧和逆变侧短路电流的绝对值逐渐增大,证明了优化结果的正确性。

3.2 算例2

设平波电抗器取值下限为Ldcmin=10 mH,上限为Ldcmax=60 mH。限流电抗器取值下限为Limin=0,上限为Limax=200 mH。过流系数k=6,直流断路器最大开断容量为IDCCBmax=12 kA。

当k1=1、k2=0和k1=0、k2=1时,即分别以各个电抗器电感容量之和最小f1min和各个限流电抗器投入时的最大故障电流与断路器切断的最大故障电流之和最小f2min为单目标求解,分别求得单目标f1min=100.7 mH,f2min=13.945 kA。电抗器电感容量分布结果如图9所示。

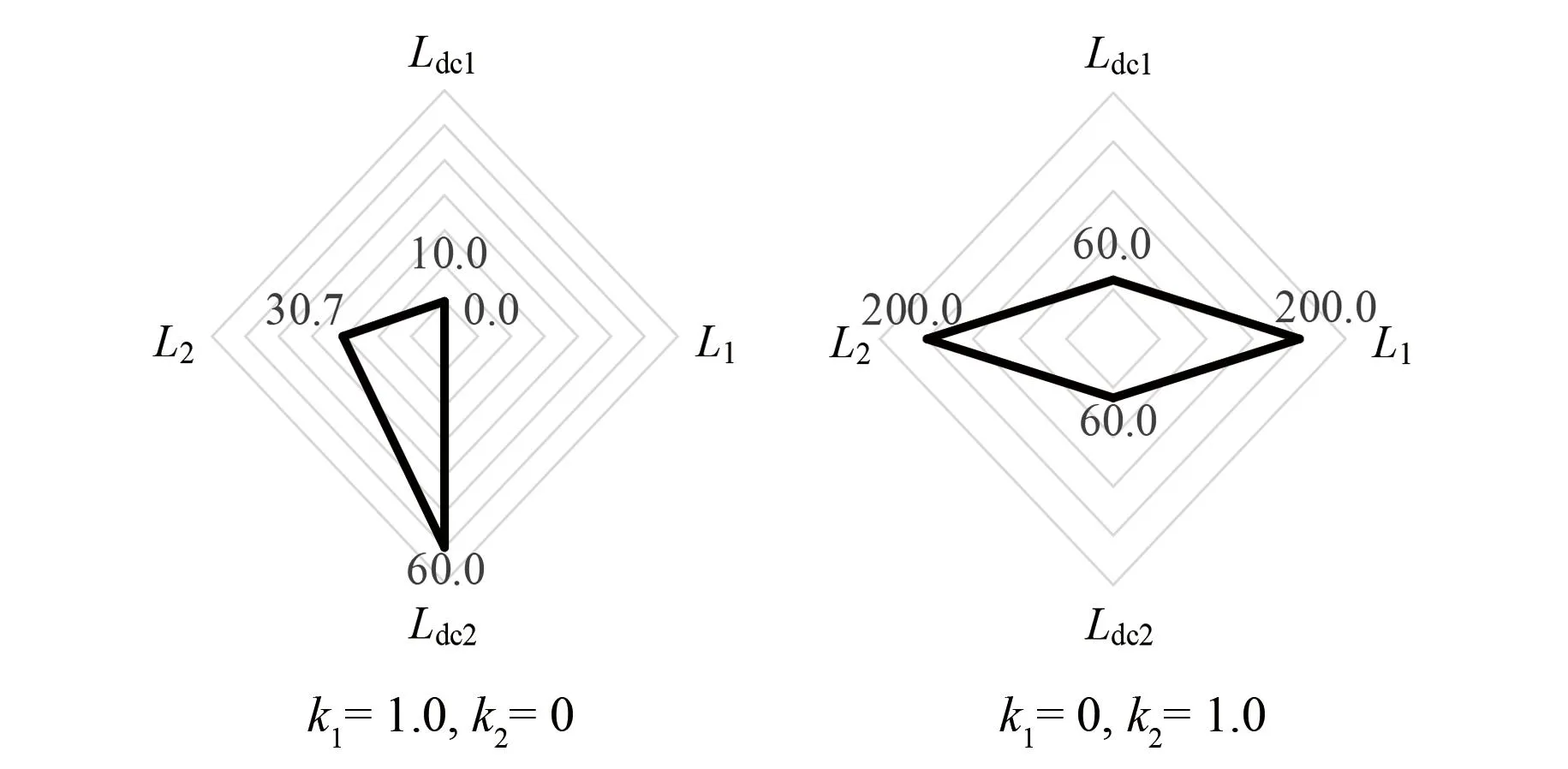
图9 单目标优化下的电抗器参数Fig.9 Reactor parameters under single objective optimization

对比图6可知,增加直流断路器切断容量后,以f1min为优化目标求得的电抗器电感容量有所降低,以f2min为目标所得电抗器电感容量没有发生变化。根据上述多目标优化方法,以0.1为步长,分别取k1=0.1～0.9,得到9种不同权系数下的各平波电抗器和限流电抗器的优化结果,如图10所示。

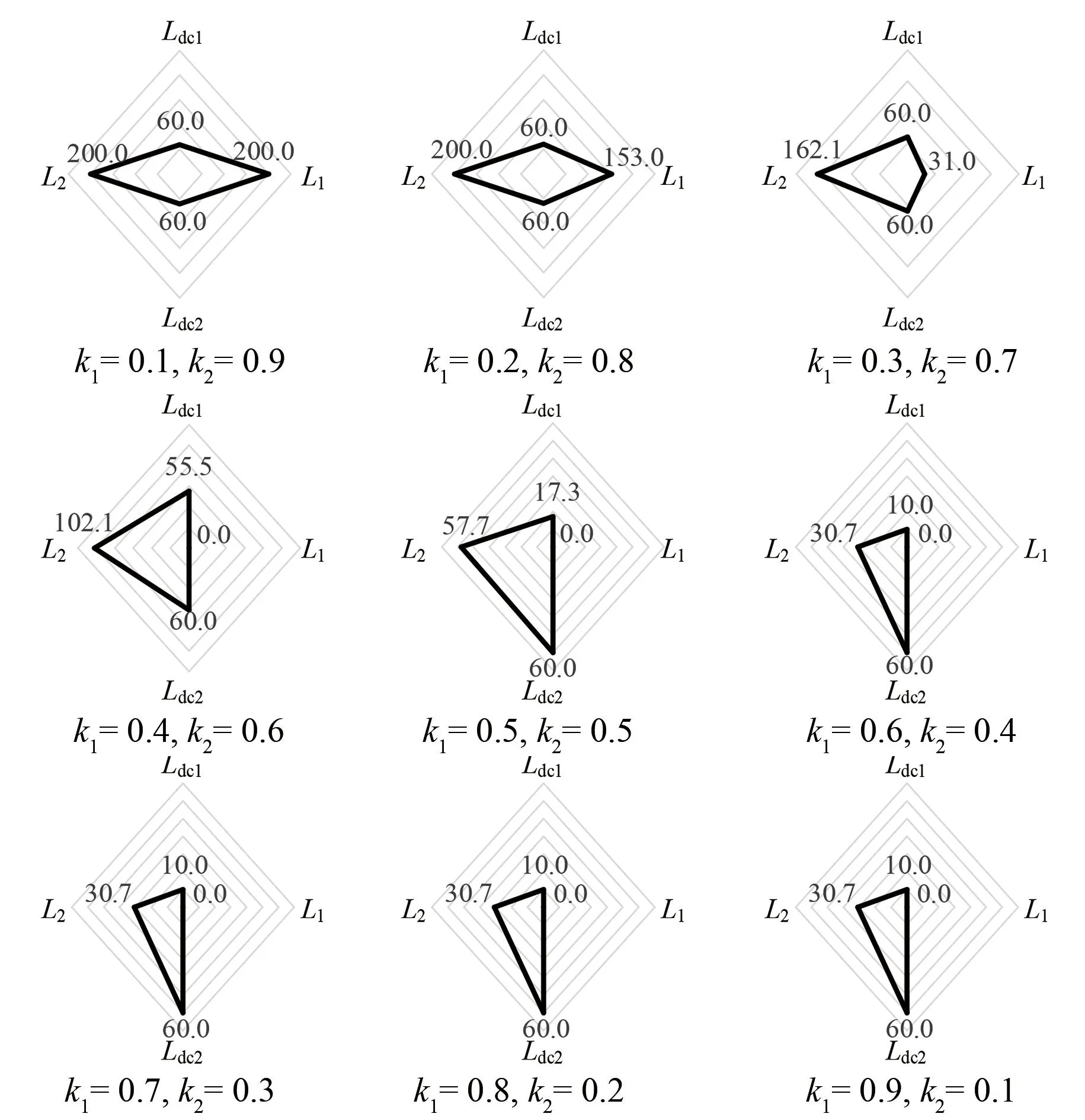
图10 多目标优化下的电抗器参数Fig.10 Reactor parameters under multi-objective optimization

对比图7和图10可知,增大直流断路器切断容量且k1取值为0.3～0.9时,MMC侧限流电抗器电感容量降低,且容量取值从3种增加到了5种,平波电抗器电感容量不变。然而,LCC侧平波电抗器和限流电抗器电感容量均不发生变化。综上,将新的优化结果代入图5所示的系统进行仿真验证,得到整流侧、逆变侧短路电流随k1变化的关系曲线,如图11所示。

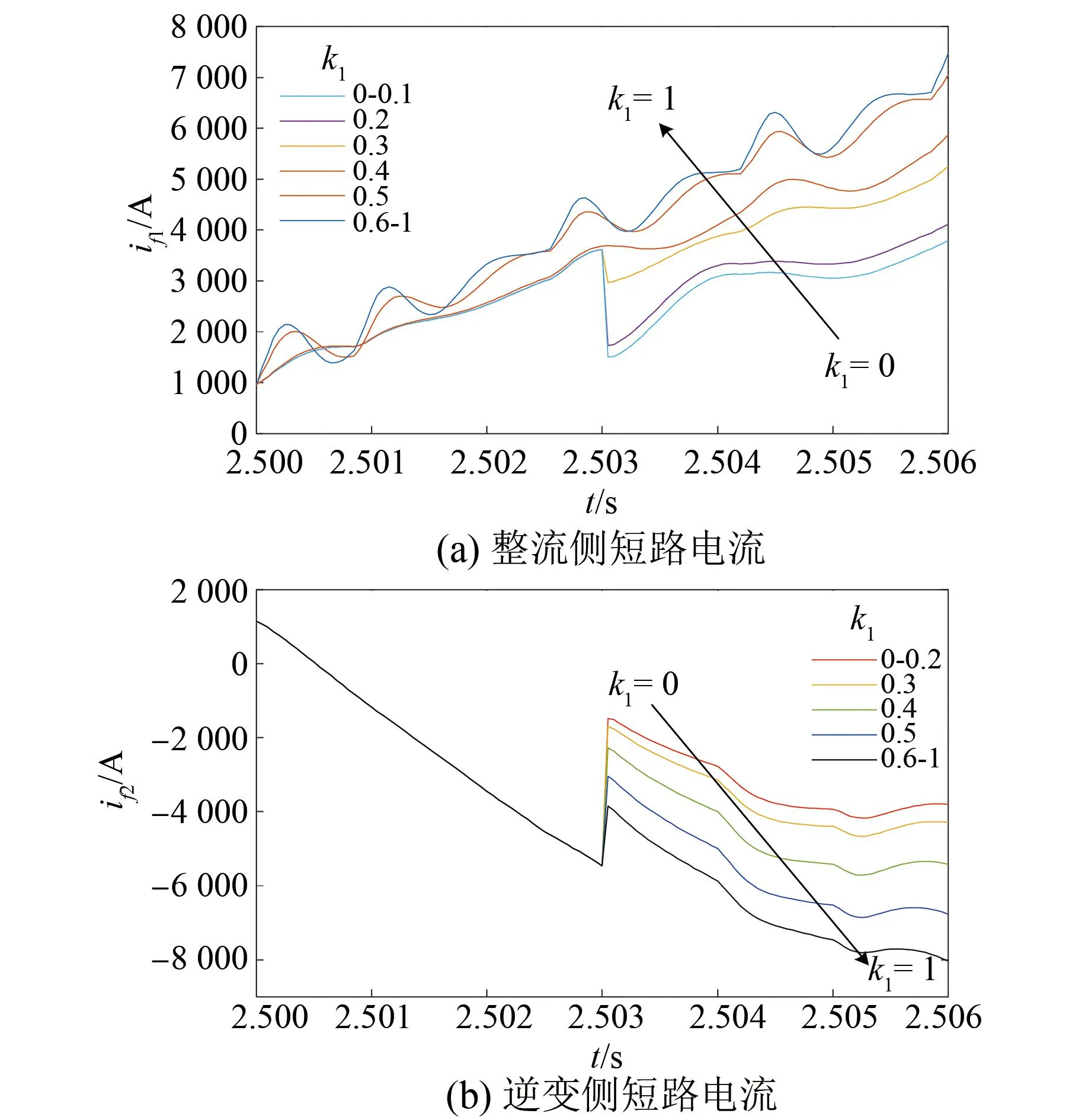
图11 短路电流随k1变化的关系曲线Fig.11 Relationship curve of short-circuit current with k1 variation

对比图8可知,改变断路器开断容量IDCCBmax后,整流侧短路电流没有发生变化,这是由于整流侧短路电流均小于算例1中的断路器开断电流,改变IDCCBmax对整流侧变量的约束条件几乎没有影响。逆变侧短路电流绝对值的最小值不变,最大值增大。同时,逆变侧短路电流曲线由3条增加至5条,增加了实际工程中电抗器电感容量配置的选择性。

3.3 算例3

设平波电抗器取值下限为Ldcmin=10 mH,上限为Ldcmax=60 mH。限流电抗器取值下限为Limin=0,上限为Limax=200 mH。过流系数k=6,直流断路器最大开断容量为IDCCBmax=15 kA。

当k1=1、k2=0和k1=0、k2=1时,即分别以各个电抗器电感容量之和最小f1min和各个限流电抗器投入时的最大故障电流与断路器切断的最大故障电流之和最小f2min为单目标求解,分别求得单目标f1min=68.6 mH,f2min=13.945 kA。各个电抗器电感容量分布结果如图12所示。

图12 单目标优化下的电抗器参数Fig.12 Reactor parameters under single objective optimization

对比图6、图9和图12,直流断路器切断容量越大,以f1min为优化目标求得的电感容量越小,以f2min为目标所得电感容量不变。以上仿真结果表明增大切断容量可以降低平波电抗器和限流电抗器电感容量,但是对短路电流的抑制没有影响。使用上述多目标优化方法,以0.1为步长,得到平波电抗器和限流电抗器的优化结果,如图13所示。

图13 多目标优化下的电抗器参数Fig.13 Reactor parameters under multi-objective optimization

对比图7、图10和图13可知,增大断路器切断电流,使得部分k1取值下MMC侧平波电抗器和限流电抗器电感容量降低,甚至降为0,极大的降低系统投资,增加系统响应速度。同时,MMC侧电感容量可选择方案相应增多。然而,LCC侧平波电抗器、限流电抗器电感容量均不发生变化。将新的优化结果代入图5所示的系统进行仿真验证,得到整流侧、逆变侧短路电流随k1变化的关系曲线,如图14所示。

图14 短路电流随k1变化的关系曲线Fig.14 Relationship curve of short-circuit current with k1 variation

对比图8、图11和图14可知,增大IDCCBmax后,整流侧短路电流没有发生变化,逆变侧短路电流绝对值的最小值不变、最大值增大。同时,逆变侧短路电流曲线数量逐渐增加,能够实现精细化短路电流限制,故可根据实际情况选择合适的权系数k1。

4 结语

本文采用平波电抗器和限流电抗器进行被动式限流,并对其容量进行了优化配置。首先,推导了整流侧和逆变侧的短路电流数学表达式,分析了故障时短路电流的特性。其次,以电抗器电感容量最小和短路电流最小为优化目标,利用罚函数法对交直流混联系统中直流线路两侧的电抗器容量进行优化配置,并对优化后不同权系数k1下的短路电流进行对比。最后,通过仿真试验验证了所提被动式限流策略的有效性。