宽转子无轴承开关磁阻电机的计及磁饱和径向力模型
2024-03-05周云红谭正一李汉杰
周云红, 谭正一, 王 东, 李汉杰
(南京工程学院 电力工程学院,江苏 南京 211167)
0 引言
二十一世纪前后,无轴承开关磁阻电机(Bearingless Switched Reluctance Motor, BSRM)因继承了普通开关磁阻电机结构简单、容错性好、效率高、更易于维护以及更利于高转速运行等优点,而备受国内外研究者的重视。
由于BSRM没有传统机械轴承,在进一步提高效率与高转速区间运行优势的同时,也对控制提出了更高的要求,绕组电流不仅仅要提供拖动转子旋转的转矩,还要提供转子悬浮所需的径向力。文献[1]提出了一种双绕组无轴承开关磁阻电机(Double-Winding Bearingless Switched Reluctance Motor, DWBSRM),两套绕组间存在复杂的耦合影响,需要特别的控制方法来进行解耦控制。针对DWBSRM,文献[2]选择了一种能计及相互垂直方向悬浮力耦合的积分路径,揭示了相互垂直方向上径向悬浮力的耦合关系,建立了径向力数学模型。文献[3]基于等效磁路法对DWBSRM建立了两相导通的数学模型。
为改进DWBSRM结构复杂的缺点,文献[4]提出一种了单绕组无轴承开关磁阻电机(Single-Winding Bearingless Switched Reluctance Motor, SWBSRM),其结构与普通SRM类似,具有结构上的通用性,但转矩脉动依然较大。针对SWBSRM转矩脉动大的缺点,文献[5]同时为12/8极开关磁阻电机的转子和定子分别开圆形槽和矩形槽,对现有SRM结构的改动小,但对SRM振动抑制有较好的效果。文献[6-7]改变了传统的定子结构,引入了不等宽的定子极,其中宽定子极上的绕组电流控制悬浮力,窄定子极上的绕组电流控制转矩,大大减小了转矩与悬浮力之间的耦合。在此基础上,文献[8-9]采用了内外双定子的方案实现了转矩与悬浮自解耦。其中文献[8]同时对内外定子极、转子极开窗,进一步减小了转矩脉动。文献[10]提出了一种12/14极的不等宽定子极结构,优化了电磁路径,在实现转矩与悬浮力解耦的同时,还进一步提高了转矩密度,降低了铁心损耗。文献[11]研究了锥形电机,其定、转子极并非传统的矩形而是存在倾斜角,转子受到的电磁力可以分解为转动力矩与径向力。其中文献[12]研究了一种宽转子单绕组无轴承开关磁阻电机(Single-Winding Bearingless Switched Reluctance Motor with Wide Rotor, BSRMWR),其绕组电感存在平顶区,通过双相导通可实现悬浮力与电磁转矩的解耦控制。
径向力是无轴承开关磁阻电机的重要性能指标,求解径向力常见的有麦克斯韦应力法、虚位移法以及等效磁路法等。针对传统SWBSRM,文献[13]基于有限元分析和麦克斯韦应力法,揭示了12/14极SWBSRM悬浮力的非线性时变规律,并建立了考虑磁饱和的数学模型。文献[14]提出了基于思维进化算法优化的反向传播神经网络算法的SRM非线性模型,更好地反映电机运行时的磁链特性和转矩特性;文献[15]运用了磁导法,建立了分段函数形式的全周期径向力模型。文献[16]研究了一种共悬浮绕组式单绕组开关磁阻电机(Sharing-Suspension-Windings Bearingless Switched Reluctance Motor, SSWBSRM),并基于等效磁路法推导了考虑磁链饱和的转矩模型。文献[17]则是从麦克斯韦应力法的角度建立了BSRMWR的径向力和转矩模型。文献[18]在不考虑磁饱和的情况下运用麦克斯韦应力法建立了BSRMWR的全周期径向力模型。文献[19]综合等效磁路法和麦克斯韦应力法,精确计算了SRM气隙磁通密度,得出了单相激励下定子径向电磁力的表达式,从而减少了误差。
考虑到无轴承开关磁阻电机经常在磁饱和状态工作,本文在文献[18]的基础上,以宽转子单绕组无轴承开关磁阻电机为研究对象,对铁心的磁化曲线进行拟合,结合麦克斯韦应力法推导了考虑磁饱和的径向力模型,并使用三维有限元仿真计算与所建立的径向力数学模型进行对比,验证了模型的有效性。该模型的建立可以提高对磁饱和工况的适用性。
1 BSRMWR基本结构与运行原理
以三相12/8极BSRMWR为例,基本结构如图1所示(略去了B、C相绕组),定子极弧为15°,转子极弧为30°,转子极弧宽于定子极弧。径向x、y轴方向上的四个定子极A1~A4上的绕组共同构成A相绕组,电流分别记作iA1~iA4,对应的气隙分别为a1~a4。区别于普通SRM,同相内的四极绕组互不连接,电流都单独控制,以便通过双相导通实现径向力与旋转力矩的解耦控制,其中一相作为转矩相,另一相作为悬浮相[18]。图中还标示出了A、B、C相绕组分别产生的两自由度径向力FAx、FAy、FBx、FBy、FCx、FCy与x轴和y轴的位置关系,其中相邻的两个力之间的夹角都为30°。
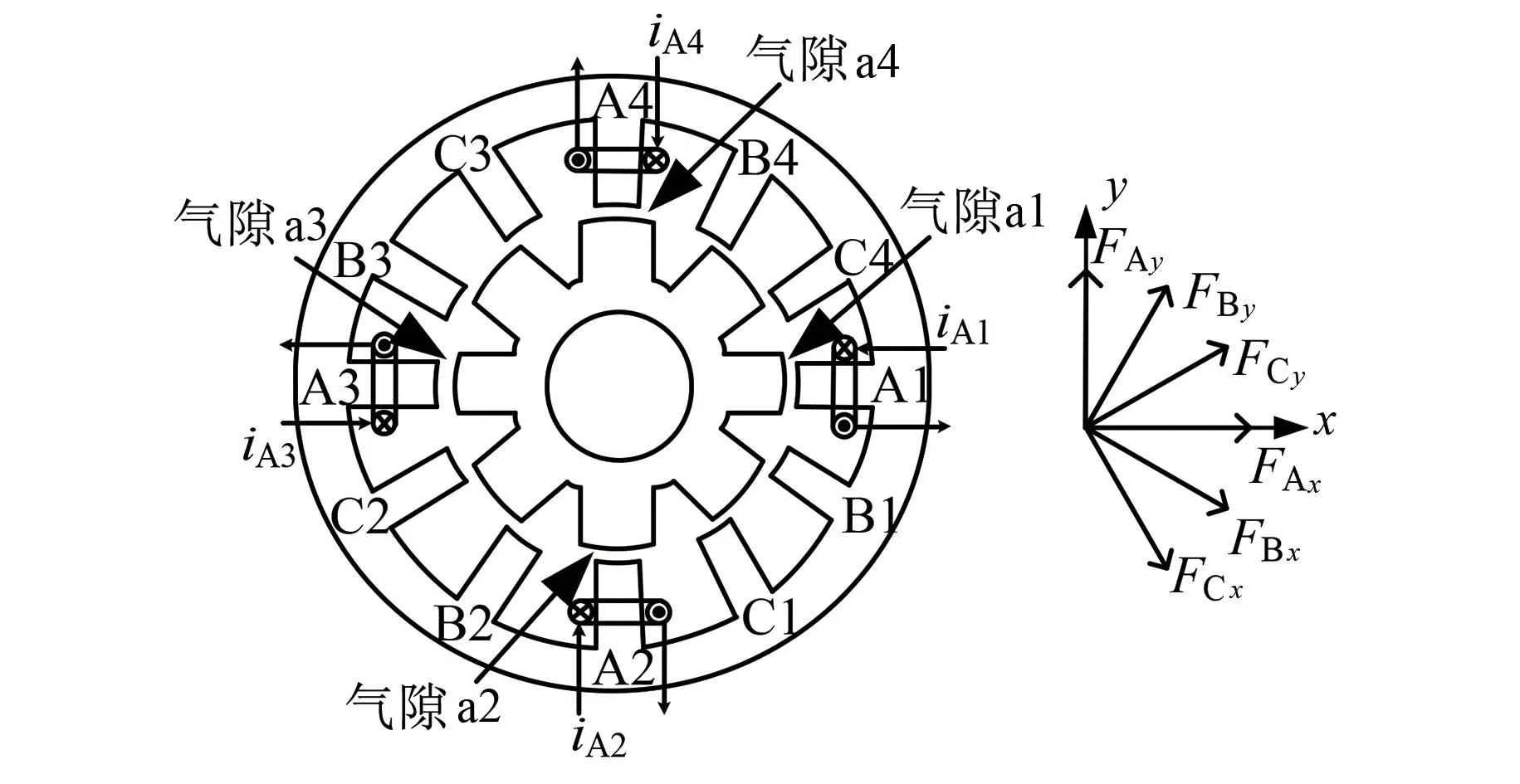
图1 BSRMWR基本结构示意图Fig.1 Basic structure diagram of BSRMWR
2 电感及径向力特性分析
2.1 电感特性
定义逆时针方向为转子旋转正方向。普通的SWBSRM中,转子极弧小于或者等于定子极弧,随着转子旋转,相电感变化规律如图2(a)所示。由于相电感正比于定、转子极的对齐面积,而在区域Ⅱ内转子极与该相定子极的重叠面积逐渐增大,因此相电感也相应线性增加,直至转子极与该相定子极完全重合时相电感获得最大值;在区域Ⅲ内,转子极与该相定子极的重叠面积逐渐减小,因此相电感也线性减小;在区域I和IV内,转子极与该相定子极完全错开,重叠面积为零,因此相电感维持最小值。
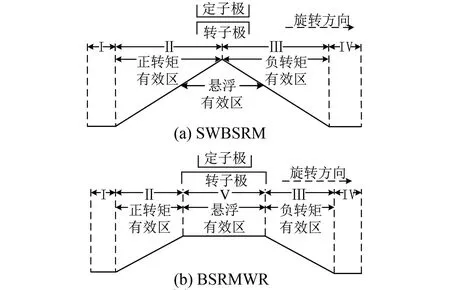
图2 电感曲线示意图Fig.2 Inductance curve schematic
当要求产生正转矩时,宜选择区域Ⅱ进行励磁;当要求产生负转矩时,则宜选择区域Ⅲ进行励磁。区域Ⅱ和区域Ⅲ中电感较大的区段是悬浮有效区,通过不对称励磁可取得较大的悬浮力。在实际控制过程中,通常是采用单相导通模式,因此在选择绕组的励磁区域时需要在转矩有效区和悬浮有效区之间进行折中,以便兼顾转矩和径向力要求。二者互相制约,且瞬时转矩与径向力之间还会存在严重的耦合影响。
在BSRMWR中,转子极弧大于定子极弧,随着转子旋转,相电感变化规律如图2(b)所示。区别于图2(a),可以看出相电感曲线中出现了一个平顶区域V,期间相电感维持最大值,这是由于在此区间内,转子极与该相定子极的对齐面积始终保持与定子极弧相等。在区域V内,通过不对称励磁可取得较大的悬浮力,因此可用作悬浮有效区。悬浮有效区与转矩有效区相互独立,不再互相制约。
不同于传统SWBSRM的单相导通模式,BSRMWR通过双相导通实现其瞬时转矩与径向力的解耦控制。具体来说,根据转子位置角,选择处于转矩有效区的一相绕组进行对称励磁以产生所需转矩,相应的相称为“转矩相”;而选择处于悬浮有效区的另一相绕组进行不对称励磁以产生所需径向力,相应的相称为“悬浮相”。由于平顶区内的绕组相电感关于转子位置角的变化率为零,因此励磁后不会产生电磁转矩,对转矩相无耦合影响。
2.2 径向力特性
以A相为例,在未磁饱和时,因铁心材料的磁导率远远大于气隙的磁导率,因此可忽略铁心磁阻。
等效磁路如图3(a)所示,其中N为绕组匝数;Pa1、Pa2、Pa3、Pa4分别为气隙a1、a2、a3、a4的磁导。图3(b)为不忽略铁心磁阻时的等效磁路图,其中Ps为各极磁路中所包含的铁心磁导。

图3 A相等效磁路图Fig.3 Equivalent magnetic circuit diagram for phase A
定义转子极轴线对准A相定子极轴线时的转子位置角为0°。由文献[14]的方法推导出的全周期径向力数学模型与由Maxwell计算出的径向力结果进行对比,结果如图4所示,可以看出随着电流的增加,该方法推导的径向力数学模型精度会逐渐降低。这是因为随着电流增加,铁心的磁导率会因磁饱和而逐渐减小,从而不再远大于气隙磁导率,因此忽略铁心磁阻会引起较大误差。若要计及磁饱和的影响,则应使用图3(b)所示不忽略铁心磁阻的等效磁路。

图4 不考虑磁饱和的径向力数学模型与有限元计算结果对比Fig.4 Comparison between the radial force mathematical model without considering magnetic saturation and finite element calculation results
3 气隙磁密及径向力计算
除了磁路中难以避免的电磁饱和以及漏磁现象外,BSRMWR在运行过程中容易因径向偏心而使得气隙不均匀。这些都使得建立完全符合实际运行情况的数学模型更加困难。为简化分析,做如下假设:
(1) 不考虑磁路中的漏磁及涡流损耗;
(2) 与气隙长度相比,转子的径向偏心很小;
(3) 忽略径向两自由度(即x、y方向)的耦合。
3.1 气隙磁密计算
利用Maxwell建立BSRMWR二维有限元模型,以分析电磁特性,主要参数如表1所示。
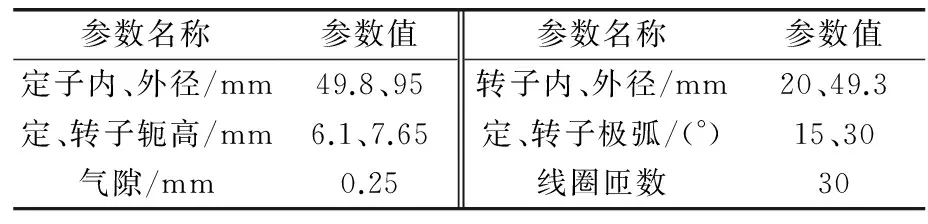
表1 BSRMW的二维模型参数Tab.1 Two-dimensional model parameters of the BSRMW
气隙磁密Bg、铁心磁密Bs与气隙磁场强度Hg、铁心磁场强度Hs分别满足关系:
Bg=μ0Hg
(1)
Bs=μ0μrHs
(2)
式中:μ0为真空磁导率,数值为4π×10-7;μr为铁心材料的相对磁导率。
根据磁通连续定律:Bg=Bs。结合式(1)、式(2),可知Hg与Hs满足关系:
Hg=μrHs
(3)
电机铁心采用硅钢材料DW310-35,其1/μr与Hs存在近似正比的关系。采用一次线性关系进行拟合,即:
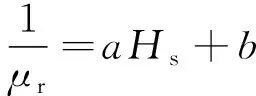
(4)
拟合结果如图5所示,其中拟合系数a=0.483 735 146 1μ0,b=196.699 233 4μ0。

图5 铁心材料的1/μr-Hs拟合结果Fig.5 Fitting results of 1/μr-Hs for iron core material
将式(4)代入式(2)中,得铁心磁密表达式:
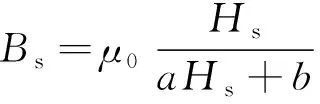
(5)
按式(5)对铁心的磁化曲线Bs-Hs进行拟合,结果如图6所示。根据Bs随Hs变化的程度,将磁化曲线分成三段:当0 T

图6 铁心材料的磁化曲线拟合结果Fig.6 The fitting results of the magnetization curve of the iron core material
在未磁饱和区,铁心材料磁阻远小于气隙磁阻,因此可以忽略掉Bs在安培环路定律中的影响。在部分磁饱和区和完全磁饱和区,随着Bs增大,磁饱和程度愈发严重,气隙磁阻不再远大于铁心磁阻,故需要考虑Bs在安培环路定律中的影响。
为了具体研究铁心中的磁饱和情况,分别为A1极绕组通入电流iA1=3 A,9 A,15 A,有限元静态分析所得磁密云图如图7所示。可以看出,在iA1=3 A时,定、转子铁心的所有部分都未磁饱和;在iA1=9 A时,通电A1极部分磁饱和;在iA1=15 A时,A1极部分区域完全磁饱和,而与之相邻的转子极以及部分定子轭则部分磁饱和。
仍以A1极为例,考虑铁心的影响,根据磁路欧姆定律,按图3(b)所示的等效磁路列写磁路方程:
Hglg+Hsls=NiA1
(6)
式中:lg为等效气隙磁路长度;ls为等效铁心磁路长度。
将式(1)和式(2)代入式(6),可得:
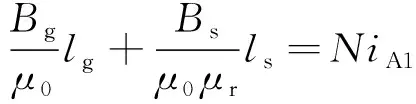
(7)
ls的大小与磁力线通过铁心的等效路径长度有关。在未磁饱和时,ls近似为0;在部分磁饱和时,ls近似等于定子极长度;在完全磁饱和时,ls以定子极长度为主,但还包含部分的磁路长度,本文在应用时,将ls近似取值为定子极长度。
根据转子极与定子极的相对位置,将一个电感周期分为非完全交叠区和完全交叠区:当转子位置角处于区间[-7.5°, 7.5°]时,为完全交叠区;当转子位置角处于[-22.5°, -7.5°]和[7.5°, 22.5°]这两个区间时,为非完全交叠区[14]。
(1) 完全交叠区的气隙磁密
如图8所示,以处于完全交叠区的气隙a1为例,由于其边缘气隙磁密很小,因此计算气隙磁密Bg时只考虑主气隙磁密Bm。

图8 完全交叠区气的隙磁密Fig.8 Air gap flux density in fully overlap region
对于主气隙磁密Bm,其磁路等效长度lm可以看作平均气隙长度l0,即:
lm=l0
(8)
将式(5)和(8)代入式(7),得到主气隙磁密Bm:
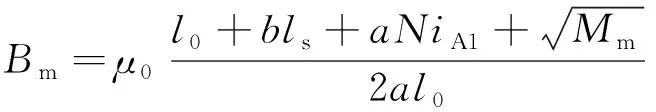
(9)
式中:Mm=(bls+l0)2+(aNiA1)2+2aNiA1(bls-l0)。
(2) 非完全交叠区的气隙磁密
如图9所示,以处于非完全交叠区的气隙a1为例,气隙磁密Bg中除了主气隙磁密Bm外,还有两个边缘磁密分量,分别记作Bf0、Bf1。
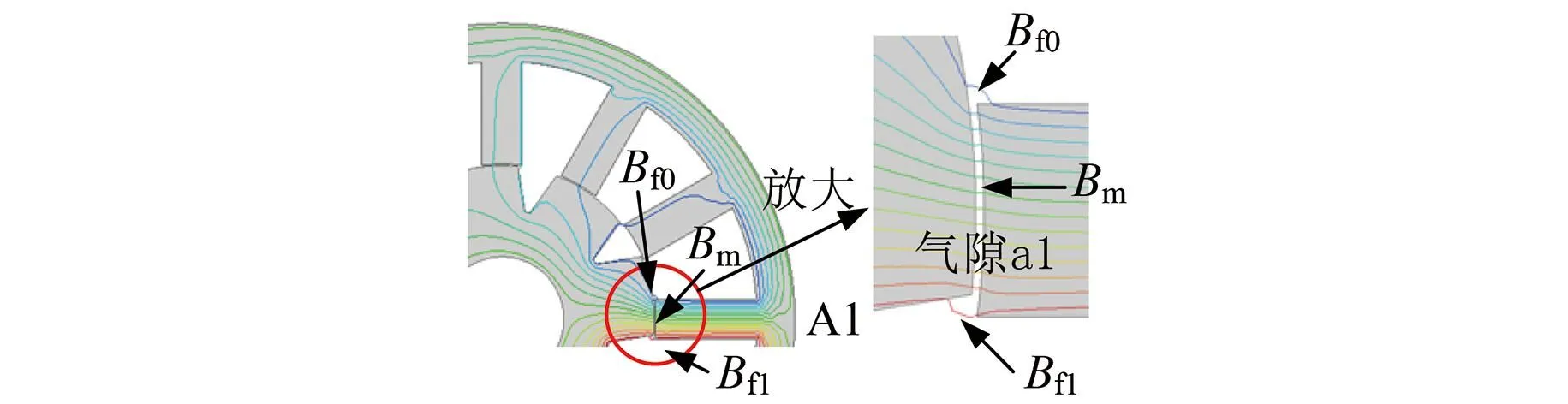
图9 非完全交叠区的气隙磁密Fig.9 Air gap flux density in non-overlap region
根据电磁场有限元分析结果,将边缘气隙磁密的路径近似看为四分之一圆弧与直线的组合,以此建立如图10所示的假定气隙磁路,用来计算气隙磁路长度。
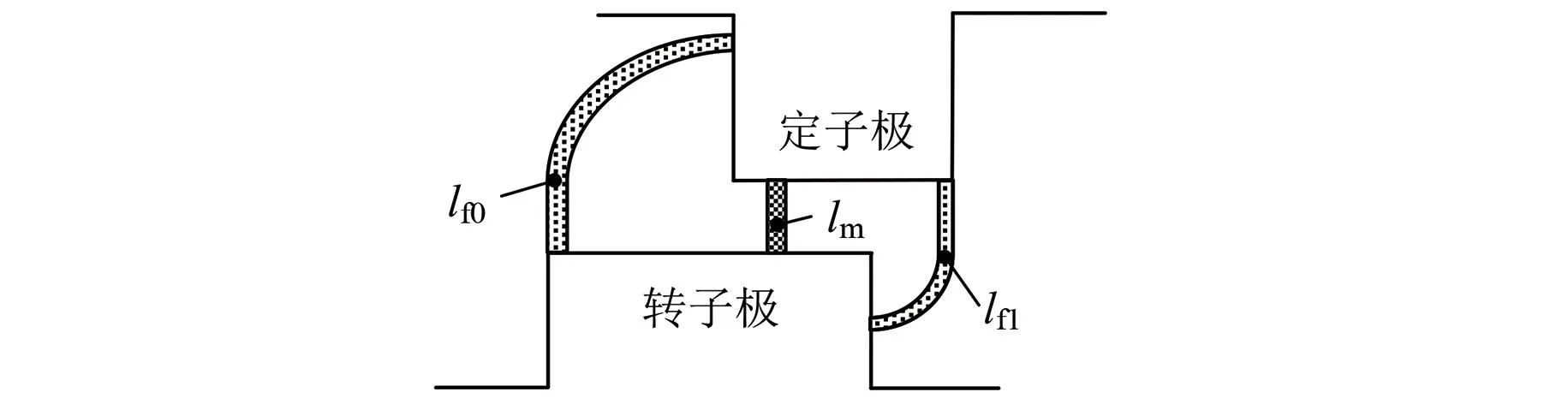
图10 非完全交叠区的假定气隙磁路Fig.10 Assumed air gap magnetic path in non-completely overlap region
由于此时主气隙磁密的等效磁路长度也满足lm=l0,因此Bm的表达式与式(9)相同。
边缘气隙磁密的等效长度lf0与lf1都与转子位置角有关,分别为
lf0=lg+πR[βr-(-θ+βs/2+βr/2)]/2
(10)
lf1=lg+πR[βs-(-θ+βs/2+βr/2)]/2
(11)
式中:βs为定子极弧;βr为转子极弧;θ为转子位置角;R为转子半径。
将式(5)和式(10)代入式(7),得出Bf0表达式:

(12)
式中:Mf0=(bls+lf0)2+(aNiA1)2+2aNiA1(bls-lf0)。
将式(4)和式(11)代入式(7),得出Bf1表达式:

(13)
式中:Mf1=(bls+lf1)2+(aNiA1)2+2aNiA1(bls-lf1)。
Mm、Mf0、Mf1是为简化气隙磁密表达式(9)、(12)、(13)而定义的中间变量。
3.2 径向力计算
麦克斯韦应力法认为磁场的张力张量T等效于有质动力F,即给定体积V的磁质内的合力及力矩等效于包围V表面的S面上各张力的合力,可表示为[20]
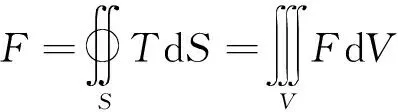
(14)
当仅有与积分路径垂直的磁场分量时,作用于曲面S上的磁应力的法向分量Fn关于磁通密度法向分量Bn的计算式为[21]
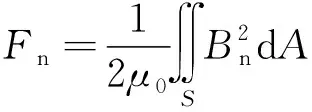
(15)
设转子铁心的轴向长度为h,则整个转子受到的径向力Fr可以表示为
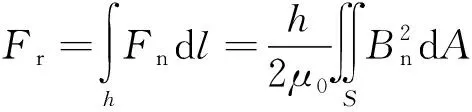
(16)
(1) 定转子非完全交叠区的径向力
在转子位置角处于区间[-22.5°, -7.5°]时,选取如图11所示的积分路径1→2→3。

图11 非完全交叠区的积分路径Fig.11 Integration path in non-overlap region
iA1在转子极上引起的径向力FA1与主气隙磁密Bm及边缘气隙磁密Bf0的关系满足:

(17)
式中:l12、l23分别为积分路径1→2和2→3的长度。
l12、l23可由转子位置角θ、定子极弧βs、转子极弧βr以及转子半径R计算:
l12=[βr-(θ+βs/2+βr/2)]R
(18)
l23=(θ+βs/2+βr/2)R
(19)
将磁密表达式(9)、(12)与积分路径长度表达式(18)、(19)代入式(17),即可得到iA1产生的径向力FA1:
FA1=m1(θ)k2(iA1)+m2(θ)k1(iA1)
(20)
式中的k1(iA1)和k2(iA1)与电流iA1有关,m1(θ)和m2(θ)与转子位置角θ有关,具体表达式分别为

(21)
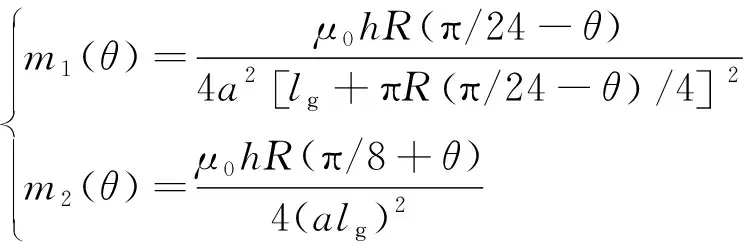
(22)
同理,转子位置角处于区间[7.5°, 22.5°]时,iA1产生的径向力FA1的表达式为
FA1=m1(-θ)k2(iA1)+m2(-θ)k1(iA1)
(23)
式中的k1(iA1)和k2(iA1)都与式(21)一致。
(2) 定转子完全交叠区的径向力
当转子位置角处于区间[-7.5°, 7.5°]时,选取如图12所示的积分路径4→5。
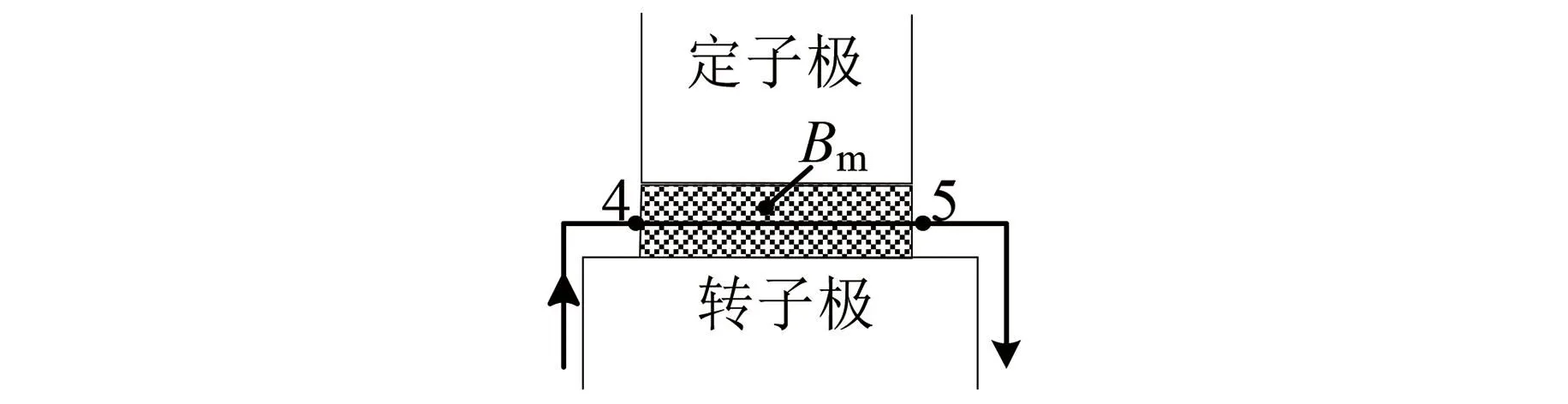
图12 完全交叠区的积分路径Fig.12 Integration path in fully overlap region
iA1在转子极上引起的径向力FA1与主气隙磁密Bm的关系满足:

(24)
式中:l45为积分路径4→5的长度,与定子极弧相等。

(25)
将磁密表达式(9)和积分路径长度表达式(25)代入式(24),即可得到径向力FA1的表达式:

(26)
式中的k1(iA1)与式(21)一致。
为便于表述,将[-22.5°, -7.5°]、[-7.5°, 5°]、[7.5°, 22.5°]区间分别记作Q1、Q2、Q3,则FA1的计算式为
FA1=
由式(27)可以看出,在定转子非完全交叠区,径向力FA1的计算式较为复杂,这是由于考虑了边缘气隙磁密。
3.3 径向力的简化
为了比较主气隙磁密和边缘气隙磁密,需要计算出气隙磁密在不同位置的大小。因此,如图13所示,在气隙a1内画一条与转子极弧等长的弧线Arc1,其中点位于定子极A1的中线上。点a、点b为该弧线的两个顶点,点c、点d分别为该弧线上与临近定子极端点和转子极端点相对齐的点。将弧线Arc1上各点与电机转轴中心点连线与x轴正方向的夹角θ1称为“气隙磁密位置角”,则点a、c、d、b的气隙磁密位置角分别为-15°、-6°、7.5°、15°。
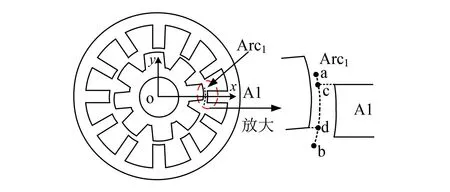
图13 非完全交叠区的Arc1示意图Fig.13 Schematic diagram of Arc1 in non-overlap area
在图13所示位置,转子位置角θ=9°,定转子极非完全重叠。设置激励电流iA1=9 A,利用有限元分析计算出弧线Arc1上的气隙磁密结果如图14所示。横轴代表气隙磁密位置角θ1,其中区间[-6°, 7.5°]对应主气隙磁密,(-15°,-6°)和(7.5°,15°)区间对应边缘气隙磁密。

图14 主气隙磁密与边缘气隙比较(θ=9°)Fig.14 Comparison of main air gap flux density and edge air gap flux density (θ=9°)

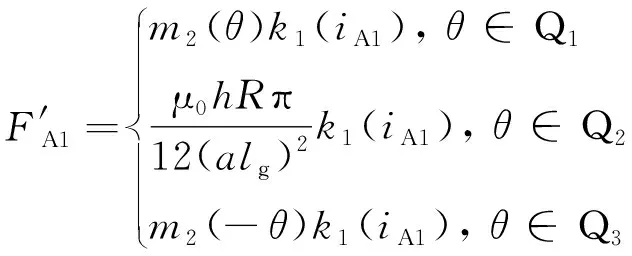
(28)
3.4 两自由度悬浮力计算
与计算FA1同理,不同定子极上绕组引起的径向力也可以分别由对应气隙内的磁密求出。将式(27)拓展为
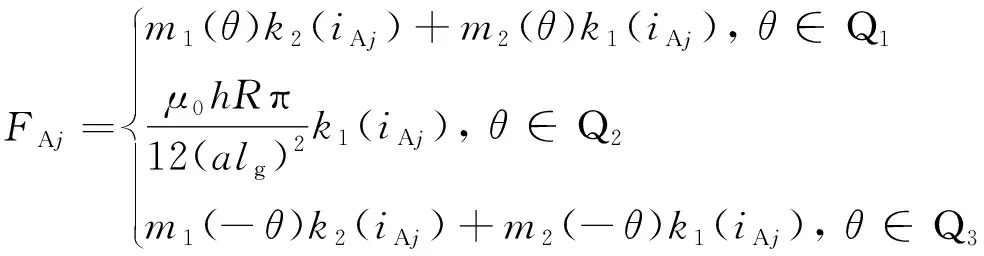
(29)
式中:j=1, 2, 3, 4;k1(iAj)和k2(iAj)与电流iAj的关系同式(21)。
径向相对的两个径向力相减,便可得到径向力FAx、FAy,同时也是沿x、y轴正方向的径向力Fx、Fy。
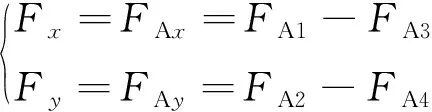
(30)
忽略边缘气隙磁密对径向力的影响后,径向力FAx、FAy简化为
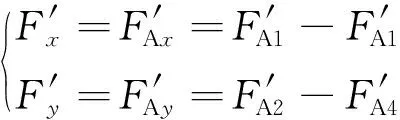
(31)
至此,单绕组BSRMWR在一个完整电感周期内,由A相绕组激励产生的径向力数学模型已经得到。
当B相、C相绕组分别通电时,可同理求出径向力FBj、FCj,并简化为
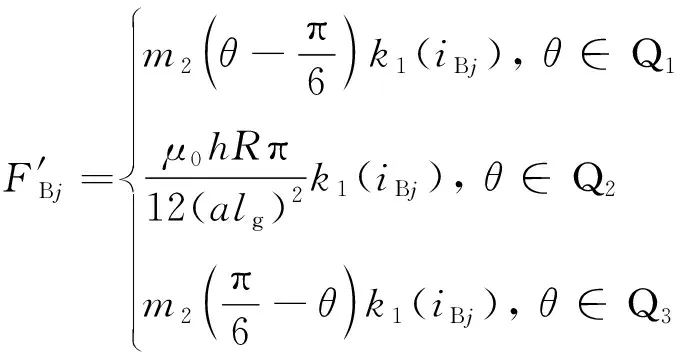
(32)
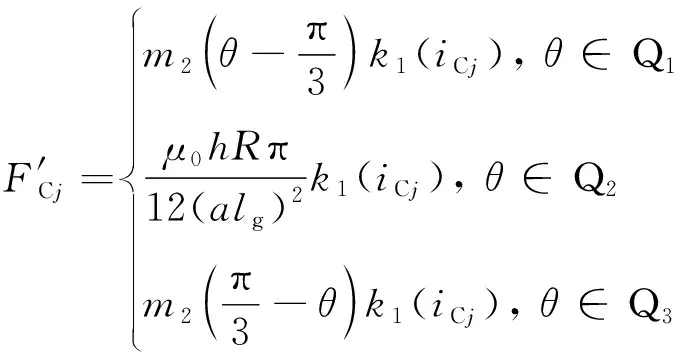
(33)
(34)

(35)
4 气隙磁密与径向力的验证
将前文基于Maxwell建立的二维有限元模型的铁心长度轴向拉伸为55 mm,建立的三维有限元模型如图15所示,用来验证本文所建数学模型的准确性。

图15 三维有限元模型Fig.15 Three-dimensional finite element model
4.1 气隙磁密的对比与验证
分别为A1极绕组通入3 A、9 A、15 A的电流,以验证所建磁密模型在未磁饱和、部分磁饱区以及完全磁饱和状态下的准确性。由于在计算径向力时采用的是主气隙磁密的平均值,即平均主气隙磁密,因此将式(9)计算结果与三维有限元计算结果及平均值进行比较。而对于边缘气隙磁密,则将式(12)计算结果直接与三维有限元计算结果进行比较。
设置转子位置角θ为0°,使电机处于完全交叠区,此时仅Bm对径向力结果造成影响,对比计算结果如图16所示。分析可知:iA1=3 A时,Bm有限元计算结果的平均值为381.89 mT,与式(9)计算结果的误差为15.58%;iA1=9 A时,Bm有限元计算结果的平均值为1.12 T,与式(9)计算结果的误差为10.86%;iA1=15 A,Bm有限元计算结果的平均值为1.41 T,与式(9)计算结果的误差为23.94%。
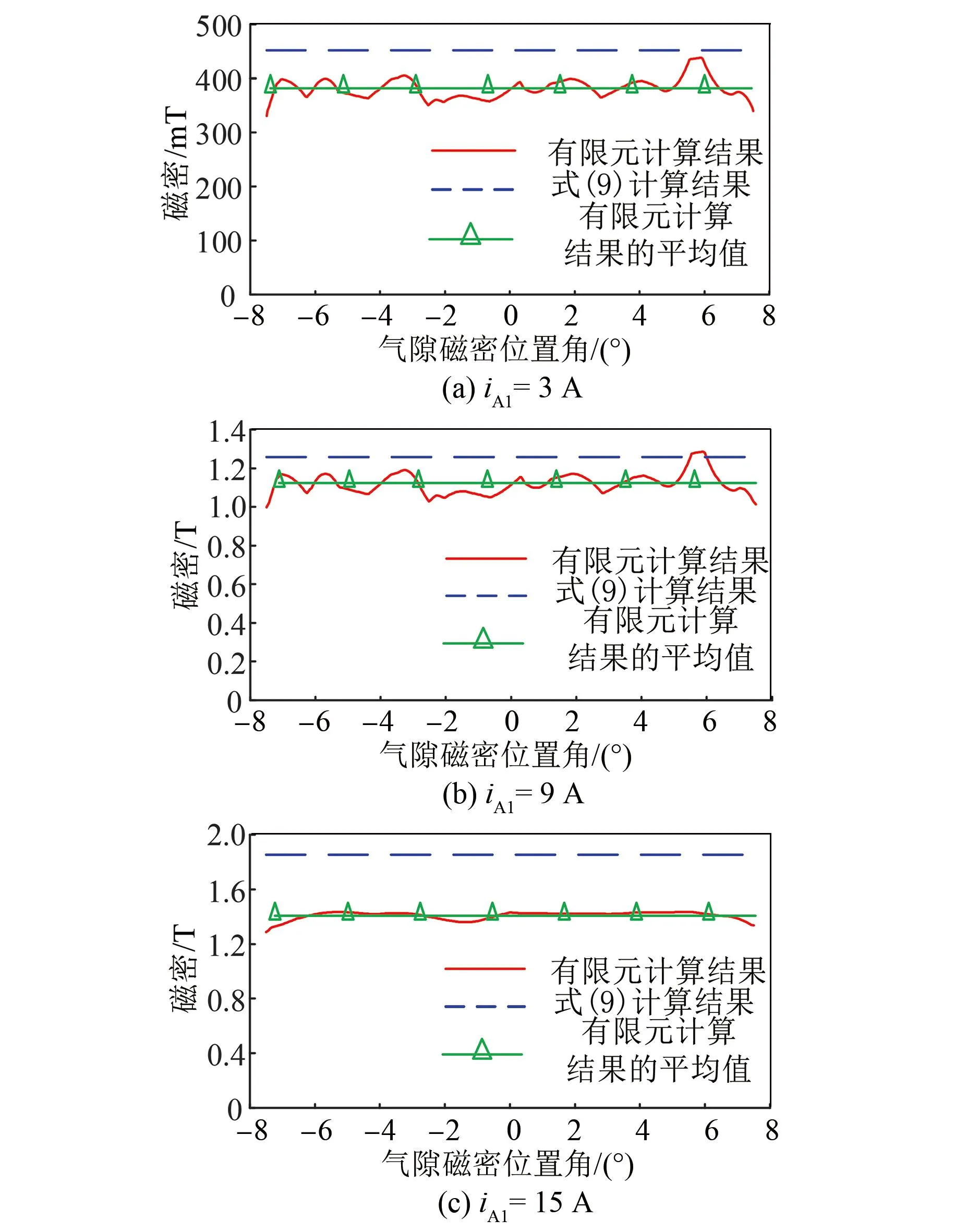
图16 主气隙磁密对比图(θ=0°)Fig.16 Comparison diagram of main air gap flux density (θ=0°)
设置转子位置角θ为9°,使电机处于非完全交叠区,此时Bm和Bf0都对径向力结果有影响。主气隙磁密对比如图17所示,分析可知:iA1=3 A时,Bm有限元计算结果的平均值为379.34 mT,与式(9)计算结果的误差为16.14%;iA1=9 A时,Bm有限元计算结果的平均值为1.13 T,与式(9)计算结果的误差为13.75%;iA1=15 A时,Bm有限元计算结果的平均值为1.46 T,与式(9)计算结果的误差为21.25%。
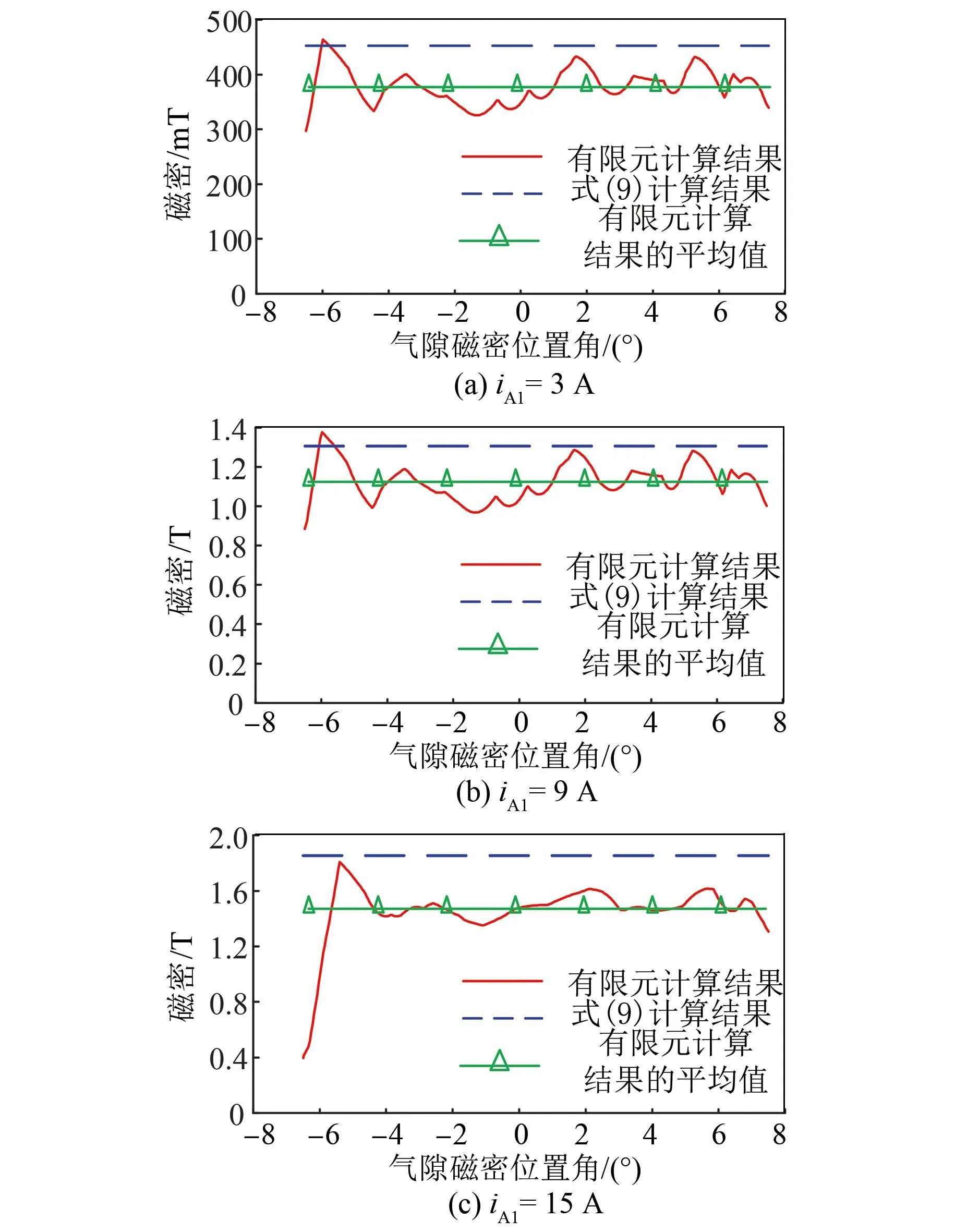
图17 主气隙磁密对比图(θ=9°)Fig.17 Comparison diagram of main air gap flux density (θ=9°)
边缘气隙磁密Bf0的对比图如图18所示,可以看出,气隙磁密模型的计算结果与有限元计算结果整体比较相符,只是在定子极端点的附近会有较大误差。推测主要原因是在定子极边缘的假想边缘磁通路径与实际情况偏差较大。值得注意的是,基于麦克斯韦应力法计算径向力时,在沿积分路径积分的过程中,主气隙磁密和边缘气隙磁密的误差会有一个累加的效果。因此,只要最终的径向力计算精度满足要求,则可以认为所建立的气隙磁密模型有效。
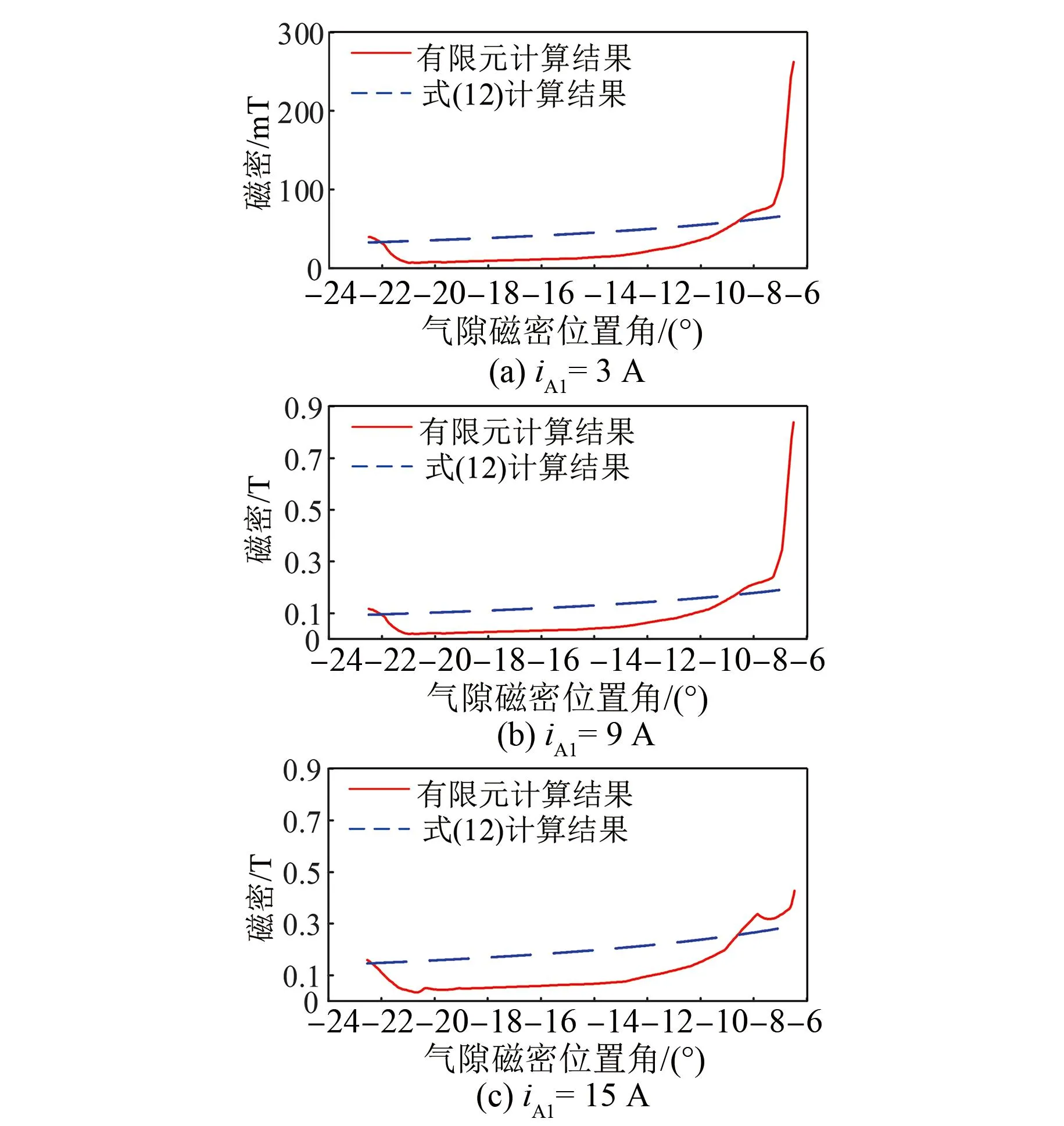
图18 边缘气隙磁密Bf0对比图(θ=9°)Fig.18 Comparison diagram of edge air gap Bf0 flux density (θ=9°)
4.2 径向力的对比与验证
分别为A1极绕组通入电流iA1=3 A,9 A,15 A以模拟未磁饱和、部分磁饱和以及完全磁饱和的情形,进行瞬态有限元分析。在一个完整周期内,以三维有限元计算结果为参考,将文献[14]中的径向力模型、本文式(27)所示径向力模型以及式(28)所示简化后的径向力模型计算结果作比较,如图19所示。

图19 x轴正方向径向力全周期模型对比图Fig.19 Comparison diagram of the full cycle model of radial force in the positive direction of the x-axis
可以看出,式(27)、(28)具有更好的精度,但是在θ=±22.5°处(即一个周期的始末),径向力模型的计算结果与有限元计算结果有非常大的误差。不能仅因为某处的大偏差就否认径向力模型的价值,因此尝试对径向力模型与有限元计算结果的绝对误差求均值,以更合理地量化误差,从而从整体的角度去评价径向力模型的适用性。
分析图19(a)可知,iA1=3 A时,三种径向力模型的计算结果均与有限元计算结果比较相符,精度良好。
分析图19(b)可知,iA1=9 A时,文献[14]径向力模型、本文式(27)、式(28)与有限元计算结果的绝对误差平均值分别是19.19%、11.19%、18.77%,本文式(27)、式(28)两种模型的精度更高。其中式(27)的精度最高,但在θ=±7.5°处有一个马鞍形的降落。
分析图19(c)可知,iA1=15 A时,文献[14]径向力模型、本文式(27)、式(28)与有限元计算结果的绝对误差平均值分别是43.33%、14.05%、25.84%。三种数学模型在完全交叠区的计算结果差异最大,因此在此区间内进一步进行比较,可得:文献[14]径向力模型与有限元计算结果的最大误差为75.41%,式(27)和式(28)与有限元计算结果的最大误差均为10.78%。但式(28)在θ=±7.5°处没有一个马鞍形的降落,因此比式(27)能更好地描述有限元计算结果的整体趋势。
综上,在铁心未磁饱和以及部分磁饱和时,所建考虑磁饱和的径向力模型能较准确得描述出径向力的整体变化规律,简化前的模型精度更高,而简化后的模型对径向力随转子位置角变化趋势的描述更好。在完全磁饱和时,所建考虑磁饱和的径向力模型在简化前后都能比不考虑磁饱和的径向力模型精度更好,但简化前的模型对径向力随转子位置角整体变化趋势的描述却不如简化后,这可能是由于此时的边缘气隙磁密与假定情况有较大差异。
需要说明的是,三维有限元分析对计算资源的占用以及所需的时长都远大于二维有限元分析,但对磁密和径向力的反映会更精确,能反映的影响因素也更多(例如漏磁和绕组端部效应)。
5 结语
径向力是无轴承开关磁阻电机的重要性能指标,有效的径向力数学模型可以为电机本体和控制系统设计提供理论参考。考虑到无轴承开关磁阻电机经常在磁饱和状态工作,而经典的忽略磁饱和影响的径向力解析模型具有不适用于磁饱和工况的局限性。因此本文以BSRMWR为研究对象,对铁心的磁化曲线进行拟合,结合麦克斯韦应力法推导了考虑磁饱和影响的全周期径向力模型,并在对比分析了边缘气隙磁密和主气隙磁密对径向力的影响后,对所建径向力模型进行简化,减小了计算量。最后利用三维有限元分析验证了所建径向力模型对未磁饱和、部分磁饱和以及完全磁饱和工况均适用。该模型的建立可以为电机运行特性分析、本体优化以及控制器设计提供更准确的理论参考。在忽略边缘气隙磁密后,还可使模型大幅简化,降低复杂度,从而有更高的应用价值。
