真空泵用屏蔽式永磁同步电机电磁场-温度场互相迭代计算方法

2024-03-05穆海琦周舒昊于添昊伦淑娴

电机与控制应用 2024年2期

穆海琦, 周舒昊, 于添昊, 伦淑娴

(渤海大学控制科学与工程学院,辽宁锦州 121210)

0 引言

真空泵凭借其安全、高效以及完全无泄漏等优点被广泛应用于化工、集成电路制造及核工业等领域[1]。为了提高真空泵驱动系统效率,当前真空泵通常采用屏蔽式永磁同步电机驱动,与常规永磁同步电机相比,屏蔽式永磁同步电机在电机定子内圆包含一个屏蔽套来防止真空泄漏。该屏蔽套固定于定子铁心内圆,在旋转磁场作用下,产生额外的涡流损耗,从而引起电机温度升高。此外真空泵用屏蔽式永磁同步电机的转子处于真空环境,散热条件差,因此相较于常规的永磁同步电机,屏蔽式永磁同步电机定转子发热严重[2]。因此准确计算真空泵用屏蔽式永磁同步电机温度场对于电机电磁性能的预测以及提高电机安全可靠性具有重要意义[3]。

科研人员针对屏蔽式永磁同步电机温度场计算开展了大量研究。在文献[4]中,郭纯冶对屏蔽电机进行温度场建模,利用有限元软件,得到屏蔽电机温度分布图以及各部件温度随时间变化的曲线。在文献[5]中,庄海军提出了带有补偿单元的热网络模型,可以快速的计算出电机各部件的温升,还利用有限元法对提出的模型进行了验证。在文献[6]中,王晓远等人建立了等效热网络温度场分析模型和三维有限元模型,利用轮毂电机温升实验,验证了等效热网络法和有限元法的有效性。然而上述研究采用的都是电磁-热单向耦合,影响温度计算精度。这样会导致电机温升计算与实际结果相比仍有误差。

为了进一步提高电机温度计算准确性,文献[7]提出了电磁场与温度场双向耦合计算方法,该方法能够充分考虑电机发热对电机电磁场的作用。研究结果表明双向耦合法相比于单向耦合法,温度计算精度提高了8.4%。文献[8]通过提出一种可以同时考虑温度场和电磁场的交流永磁电机多物理场计算方法,得出了温度变化对电机参数设计影响规律,分析了电机在大温差环境下的输出能力。文献[9]提出了一种双向磁热耦合计算方法,该方法考虑了电机温升对电磁场的影响,温升预测比单向耦合法更准确,但与实际结果相比,依然存在较大误差。

然而电机运行是一个多物理场耦合过程。因为电机材料的导热系数与电机散热能力都与电机自身温度相关,且温度越高,影响越大[10]。然而,目前关于电机温度计算时考虑温度对电机传热影响的研究较少。

因此,针对发热较为严重的真空泵用屏蔽式永磁同步电机,本文在基于现有电磁场-温度场双向耦合方法的基础上,提出一种能够考虑温度对电机传热影响的互相迭代计算方法。该方法能够充分反应电机传热的实际过程,能够有效提高电机温度预测精度,对于保证电机安全可靠运行具有重要意义。同时本文的研究可以为屏蔽式永磁同步电机受环境温度影响的温升计算提供重要的方法指导。

1 电磁热互相迭代计算方法

电磁热互相迭代计算方法是一种既可以考虑温度对电机电磁性能的影响,又能考虑温度对电机散热能力影响的计算方法。

1.1 流程图

本文提出的互相迭代法计算流程如图1所示。

图1 电磁热互相迭代计算方法流程Fig.1 Electromagnetic heat mutual iterative calculation method flow chart

根据图1,电磁热互相迭代计算方法的步骤为:(1)首先设定环境初始温度;(2)根据初始温度确定电机材料的物性参数和热特性参数;(3)求解电磁场获得电机各部件损耗;(4)在上述条件基础上对电机温度场进行求解,获得电机各部件温度;(5)电机各部件温度与上一次计算的温度差值若小于阈值则计算结束,否则更新温度数据进行迭代计算,直至满足计算精度要求;(6)重复步骤(3)、(4)、(5),迭代循环,直到符合误差要求。

在迭代计算过程中考虑电机部件温度对材料电磁物性参数和热特性参数的影响,电磁性能影响的参数包括损耗(铜耗、永磁体涡流损耗、屏蔽套损耗)、永磁体的剩磁密度和矫顽力以及屏蔽套电阻率等。对热特性影响的参数包括材料导热系数和散热系数。以下分别介绍温度对电磁物性参数和热特性参数的影响。

1.2 温度对电磁物性参数的影响

(1) 对铜耗的影响

铜耗计算式如下[11]:

PCu=mI2R(t)

(1)

式中:m为绕组相数;I为电流有效值;R为每相绕组的电阻值。

由于永磁同步电机功率密度高,其在工作过程中温升较快,这会引起绕组阻值的增加,电阻随绕组温度变化的关系为[12]

R(t)=R0[1+α0(t-t0)]

(2)

式中:R0为参考电阻值;α0为导体温度系数。

(2) 对永磁体涡流损耗的影响

永磁体涡流损耗计算式如下[13]:

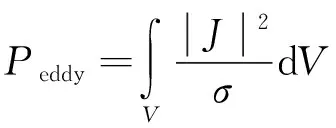
(3)

式中:J为涡流密度;σ为永磁体电导率;V为永磁体体积。

永磁体剩磁参数与温度之间的计算式为[14]

(4)

永磁体矫顽力参数与温度之间的计算式为[15]

(5)

式中:Br为永磁体的剩磁;αBr为永磁体剩磁密度的可逆温度系数;t0为设定的环境初始温度;t1为上一次迭代计算后永磁体的温度;Brt0为t0温度下的永磁体剩磁;Brt1为t1温度下的永磁体剩磁;Hrt0为t0温度下的永磁体矫顽力参数;Hrt1为t1温度下的永磁体矫顽力参数。

(3) 对屏蔽套损耗的影响

定子屏蔽套损耗简化计算式为[16]

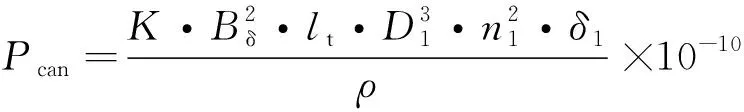
(6)

式中:Bδ为气隙磁通密度最大值;n1为电机转速;lt为铁心长度;D1为定子内径;δ1为定子屏蔽套厚度;ρ为屏蔽套材料的电阻率;K=0.25～0.43。

综上介绍了温度对电机电磁物性参数产生的影响,还需注意温度对电机热特性参数产生的重要影响。

1.3 温度对热特性参数的影响

热特性参数主要包括导热系数和散热系数,因此,本文的重点将放在对导热系数和散热系数的分析上。

(1) 温度对导热系数的影响

导热系数是当温度梯度为1时,单位时间内通过单位面积的导热量。同一材料的导热系数随温度变化,对于绝大多数物质而言,当材料温度尚未达到熔化或汽化以前,导热系数可以近似地认为是线性规律变化,即[17]:

λ=λ0(1+b·t)

(7)

空气的导热系数可用式(8)计算[18]:

λt=λ0e0.002 72t

(8)

式中:λ0为环境温度时的导热系数;b为试验确定的常数,b值可以为正值,也可能为负值。对于绝缘材料而言,b≈0.001 6～0.02,t为迭代计算后得出的温度。

(2) 温度对散热系数的影响

当固体的温度与流体温度不等时,二者之间就有热交换,热量从高温物体传向低温物体。对流散热时,表面散热能力与冷却介质的物理性能、固体表面几何形状、尺寸等因素有关。

如果用空气作为冷却介质,其物理性能比较稳定。忽略散热表面几何尺寸等因素的影响,则可以近似地认为散热系数仅与空气的流速有关。当空气流速在5～25 m/s时,α与流速v的关系如下[19]:

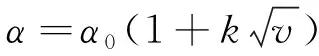
(9)

式中:α0为发热表面在平静空气中的散热系数;v为空气吹拂表面的速度;k为考虑气流吹拂效率的系数。

综上所述,本节从电磁物性和热特性两个方面讨论了温度对电机的影响,列举了电机电磁场和温度场之间相互迭代所需的公式,为进一步分析环境温度对电机电磁场和温度场的影响提供了基础。

2 屏蔽式永磁同步电机温度计算与分析

2.1 电机参数及多物理场计算模型

本文以一台1.5 kW屏蔽式永磁同步电机为例,基于互相迭代计算方法对电机进行研究,电机的基本参数如表1所示。

表1 电机主要参数Tab.1 Main parameters of motor

根据表1参数分别建立了如图2、图3所示的电机电磁场计算模型和电机温度场有限元计算模型。

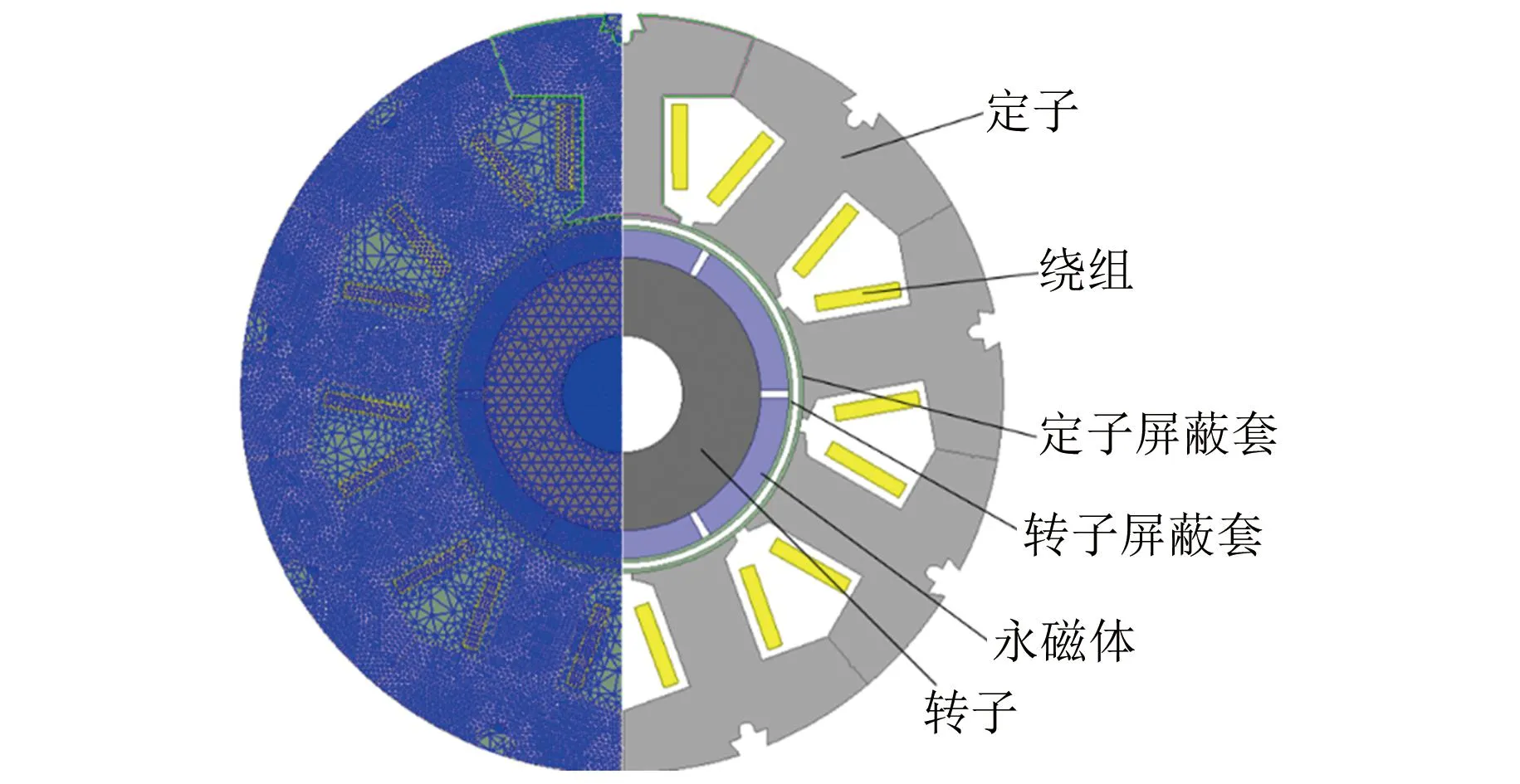
图2 电机电磁场有限元计算模型Fig.2 Finite element calculation model of motor electromagnetic field

图3 电机温度场有限元计算模型Fig.3 Finite element calculation model diagram of motor temperature field

然后在两种计算模型下分别对电机的气隙磁密、感应电动势、损耗、效率和功率因数等参数进行对比分析。

2.2 电机气隙磁密和感应电动势对比分析

在电机中,气隙磁密的分布和强度对电机的性能和效率产生了重要影响。感应电动势则是电机将电能转换为机械能的关键因素。因此,对气隙磁密和感应电动势进行分析对于理解电机的性能特征、控制和优化具有重要意义。

利用有限元模型,电机的空载气隙磁密变化如图4所示。从图4中可以观察到,两种方法对气隙磁密的影响趋势基本相似。然而,通过局部放大图像可以明显看出,使用互相迭代法获得的气隙磁密要大于使用双向耦合方法得到的结果。是因为当温度相同时,互相迭代法在考虑电机电磁参数的前提下,还考虑了导热系数和散热系数对电机温升的影响,从而使电机具备更出色的导热性能,促使电机温度降低,明显增加了永磁材料的剩磁,提高了气隙磁密。对比局部放大图像可知,双向耦合法得到的气隙磁密为0.646 T,而互相迭代法得到的气隙磁密为0.649 T,两者相差仅0.005 T,约为0.5%。

图4 电机气隙磁密对比Fig.4 Comparative analysis of air gap flux density of motor

图5为空载反电动势对比波形图。图5中两种方法的空载反电动势基本一致,但从局部放大图像中可以看出,双向耦合法的空载反电动势为104.27 V,互相迭代法的空载反电动势为104.80 V,相差0.53 V,约0.5%。对比图4空载气隙磁密可以看出,两种方法得到的气隙磁密和空载反电动势相差均约为0.5%,所以迭代方法对电机反电动势的影响与对气隙磁密的影响基本一致。

图5 电机空载反电动势对比Fig.5 Comparative analysis diagram of no-load back electromotive force of motor

2.3 电机损耗对比分析

电机运行时,温度升高会导致损耗变化,因此对电机损耗进行准确的分析至关重要。本文所分析的屏蔽式永磁同步电机在运行时产生的损耗主要包括:绕组铜耗、定子铁耗、屏蔽套损耗以及转子涡流损耗。这些损耗转化成热能在电机内部各部分之间传递,进而影响电机内部温度场的分布。

本文将根据负载率的变化对电机的绕组铜耗、定子铁耗、屏蔽套损耗以及转子涡流损耗进行分析,为下文的效率和功率因数提供依据。电机的铜耗随负载率变化如图6所示。

图6 电机铜耗对比Fig.6 Comparative analysis of copper consumption of motor

从图6中可以看出,采用两种方法获得的铜耗都随着负载率的增加而增大,但计算结果存在差别。当负载率从20%增加至100%时,采用双向耦合法铜耗增加了88.71 W,采用互相迭代法铜耗增加了86.17 W。当负载率为100%时,采用双向耦合法获得的铜耗为112.21 W,采用互相迭代法获得的铜耗为108.77 W,此时两者相差最大,相差了3.15%。在温度相同的情况下,本文采用的互相迭代法产生的铜耗比磁热双向耦合法产生的铜耗小,这是因为采用的互相迭代法在迭代后考虑了导体的导热系数和散热系数的影响,温升较之前未考虑的情况下要低,从而使绕组的电阻值降低。铜耗与绕组的电阻值成正比,所以导致铜耗减小。

电机的铁耗随负载率变化如图7所示。从图7中可以看出,随着负载率增大,铁耗在不断增大。当负载率从0增加至100%时,采用双向耦合法得到的铁耗增加了5.35 W,采用互相迭代法得到的铁耗增加了5.28 W。当负载率为60%时,采用双向耦合法获得的铁耗为26.3 W,采用互相迭代法获得的铁耗为26.5 W,两者相差最大,相差了0.9%。本文采用的互相迭代法所产生的铁耗更大,这是由于其考虑了温度场中电机材料导热系数和散热系数的影响,得到的铁耗更大。

图7 电机铁耗对比Fig.7 Comparative analysis diagram of iron loss of motor

电机的屏蔽套损耗随负载率变化如图8所示。从图8中可以看出,在负载率为100%时,采用互相迭代法获得的屏蔽套损耗为241.94 W,采用双向耦合法获得的屏蔽套损耗为244.58 W,两者相差最大,相差了1.09%。从图中可知采用互相迭代法所产生的屏蔽套损耗更小,而双向耦合法由于并未考虑温度场中导热系数和散热系数的变化,仿真计算得出的屏蔽套损耗较高,没有考虑实际情况的影响。

图8 电机屏蔽套损耗对比Fig.8 Comparative analysis diagram of motor shield loss

电机的转子涡流损耗随负载率变化如图9所示。从图9中可以看出,随着负载率的增大,转子涡流损耗在不断增加。当负载率从0增加至100%时,采用双向耦合法转子涡流损耗增加了14.65 W,采用互相迭代法转子涡流损耗增加了14.33 W。当负载率为100%时,采用双向耦合法获得的转子涡流损耗为17.56 W,采用互相迭代法获得的转子涡流损耗为17.15 W,两者相差最大,相差了2.4%。

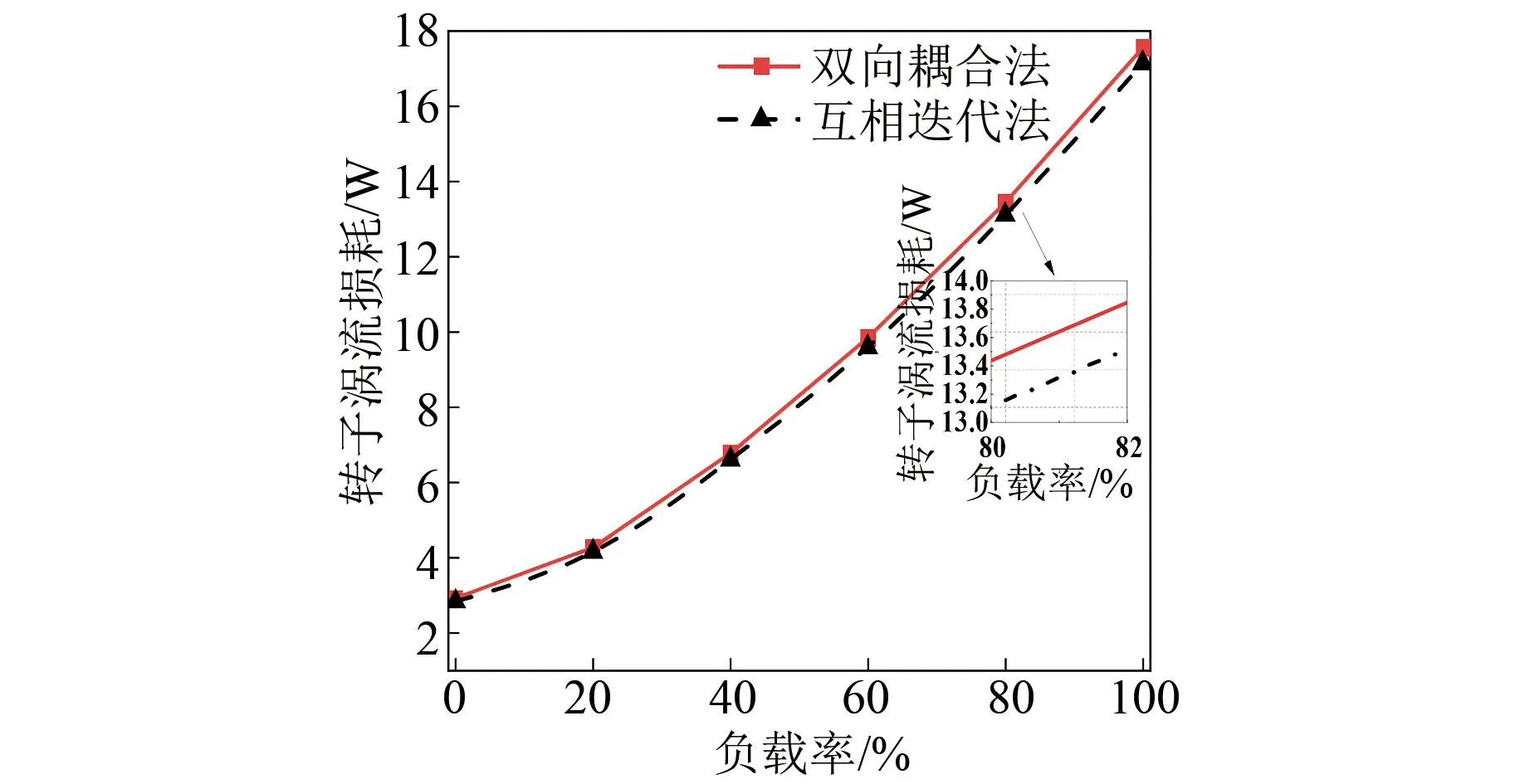
图9 电机转子涡流损耗对比Fig.9 Comparative analysis of eddy current loss of motor rotor

图6～图9中分别介绍了各部分损耗与负载率、分析方法之间的关系,这些分析结果将为下文对电机的效率和功率因数进行准确分析提供依据,使结果更贴近实际情况,并为后续电机温度场的分析提供准确性支持。

2.4 电机效率和功率因数对比分析

本节基于互相迭代法和双向耦合法对电机效率和功率因数进行对比分析。图10所示为屏蔽式永磁同步电机效率与负载率的关系,表2所示为两种方法的效率对比列表。

表2 电机效率对比Tab.2 Comparative analysis diagram of motor efficiency %

图10 电机效率对比Fig.10 Comparative analysis diagram of motor efficiency

从图10中可以看出,电机效率是随负载率的变化而变化的。从表2中可以看出,当负载率为20%时,采用互相迭代法得到的效率为27.539%,采用双向耦合法得到的效率为27.751%,两者相差最大,相差了0.77%。

屏蔽式永磁同步电机功率因数与负载率的关系如图11所示。从图11中可以看出,当负载率为25%时,采用双向耦合法下电机的功率因数为0.724,采用互相迭代法下电机的功率因数为0.727,两者相差最大,相差了0.5%。在负载率低于20%时,其功率因数升高明显。在负载率为60%～100%时,功率因数趋于稳定。

图11 电机功率因数对比Fig.11 Comparative analysis diagram of motor power factor

功率因数表示为有功功率与视在功率之比,反映了电力系统的供电能力和线路损耗。等效视在功率的计算式为[20]

Se=3UeIe

(10)

功率因数的计算式为[21]

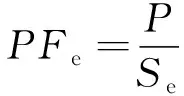
(11)

式中:Ie和Ue分别为电流和电压,且为等效定义值;P为有功功率。

本节主要对电机损耗与负载率之间的关系进行了分析,为接下来的负载率与效率、功率因数之间的关系分析提供了基础。同时,损耗的数值也将用于下文计算温度场中的生热率,从而实现更准确且实际可行的电机温升计算。

3 环境温度对屏蔽式永磁同步电机温度场影响

3.1 电机温度对比分析

电机的温度变化结果如图12所示。从图12中可以看出,采用两种方法电机的温度都随负载率的增加而增大,当负载率从0增加至100%时,采用双向耦合法,电机整体温度升高了16.881 ℃;采用互相迭代法,电机整体温度升高了15.419 ℃。当负载率为100%时,采用双向耦合法电机的温度为99.1 ℃,采用互相迭代法电机的温度为93.2 ℃,两者相差最大,相差了5.5%。造成这种现象的原因是在环境温度相同的情况下,本文提出的互相迭代法考虑了温度场中导热系数、散热系数的影响,导致温度相对于双向耦合方法更低,更贴近于实际情况,为以后电机电磁特性和热特性提供更为准确的分析。

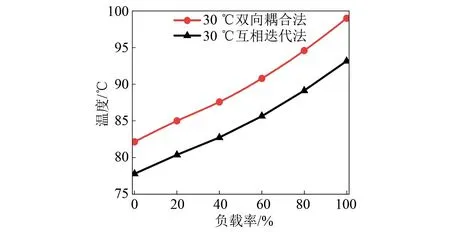
图12 电机温度对比Fig.12 Comparative analysis diagram of motor temperature

3.2 电机温度分布

电机各部件不同方法下的温度如图13所示。从图13中可以看出,采用磁热耦合法下电机的整体最高温度为99.02 ℃,永磁体最高温度为95.55 ℃,绕组绝缘和定子屏蔽套的最高温度为99.02 ℃;采用互相迭代法下电机的整体最高温度为93.17 ℃,永磁体最高温度为90.18 ℃,绕组绝缘和定子屏蔽套的最高温度为93.17 ℃。造成这种现象的原因是,在环境温度为30 ℃的情况下,磁热耦合法并未考虑电机导热系数和散热系数对电机温升的影响,这才导致了温度升高。