内置式永磁同步电机不同转子拓扑结构对电机性能的影响分析

李吉程, 王爱元, 王成敏, 殷世雄

(上海电机学院 电气学院,上海 201306)

0 引言

内置式永磁同步电机(IPMSM)是将永磁体放置于转子内部的一种永磁同步电机,与表贴式永磁同步电机相比,内置式永磁同步电机永磁体不易脱落、结构更加稳定,在转速较高的情况下也可以克服离心力。与其他类型的电机相比,IPMSM具有噪声小、质量轻以及效率高等优点。随着用户对电机性能要求的提高,进一步对电机的输出性能、振动以及噪声等的要求更加严格。

文献[1]以电机的噪声、转矩脉动作为优化目标,使用响应面法确定最优的设计参数,并对优化前后的电磁振动噪声进行了仿真对比,结果显示该方法优化后电机噪声和转矩脉动减少较为明显。文献[2]对单、双层永磁体转子结构的IPMSM进行了对比分析,分析结果显示双层永磁体转子结构的IPMSM电磁性能和噪声性能均更好。文献[3]提出了一种混合正交序列的田口优化方法来减小电机径向电磁力,试验表明,该方法可以有效降低电机的径向电磁力。文献[4]中提出了一种新型顺极永磁电机,与传统的混合极永磁电机相比,该类型电机拥有相同的转矩、效率以及更好的弱磁能力。文献[5]使用了一种模糊推理田口法将多个优化目标转化为单一目标,从而获得电机的最优设计参数组合。有限元仿真表明,该方法与传统田口法相比,各性能指标均得到更大的提升。文献[6]提出了一种spoke-type转子结构,结果表明,在保证电机输出特性不变的情况下,该转子结构能够有效减少永磁体的使用量。文献[7]研究了V型内置式永磁同步电机的气隙形状对电机性能的影响,通过有限元软件分析了平均转矩、转矩脉动和铁心损耗。结果表明:改变内置式永磁同步电机V形槽的气隙形状可以有效地降低转矩脉动和定子铁心损耗。文献[8]对无轴承永磁同步电机进行了多目标优化,使用了一种结合响应面法和粒子群算法的优化方法对其进行优化。结果表明,平均转矩、平均悬浮力均有所增加,转矩脉动、悬浮力脉动都有一定的减少。文献[9]使用了一种改进的Taguchi法对潜艇用电机的永磁体进行了改善,提升了电机的效率和稳定性,降低了齿槽转矩。文献[10]基于有限元分析法对永磁同步电机的永磁体形状、气隙宽度等进行了改善,通过有限元验证,优化后的转矩脉动、涡流损耗等均有所减少。文献[11]使用了一种改进迭代田口法对永磁同步电机的气隙长度、磁极厚度等进行了优化,以转矩脉动和转矩效率作为优化目标,最后通过有限元仿真表明改进田口迭代法比未改进的田口迭代法优化效果更明显。文献[12]使用了一种拟牛顿法和贯序田口法相结合的方法对电机进行了优化,通过有限元仿真验证了优化后的电机转矩脉动降低,并且电机的效率、功率因数也有一定的提升。文献[13]揭示了气隙磁场的谐波对齿槽转矩的影响,提出了一种部分反余弦削极技术来来削弱气隙磁场的谐波,达到削弱齿槽转矩的目的,进而达到削弱转矩脉动的目的,通过试验和仿真表明该方法有效。文献[14]研究了磁极偏心对混合励磁电机振动噪声的影响。文献[15]研究了转子开辅助槽和转子分段斜极对电机噪声的影响。文献[16]提出了一种新的混合解析法对电机气隙磁场进行建模,此方法有效处理了气隙磁场建模过程中存在的共性问题,提升了电机局部优化的效率和准确性。文献[17]使用迭代法对单相感应电机的定子尺寸、转子尺寸进行优化,通过对优化前后的电机进行有限元分析,结果表明优化后电机的运行性能得到了有效改善。文献[18]采用参数分层设计与响应曲面法相结合的方法对非对称V型IPMSM进行优化,通过有限元软件分析,结果表明该方法可以有效降低电机的转矩脉动,并且提升电机的转矩密度。。

为了研究不同转子结构对IPMSM电磁性能及噪声性能的影响,本文以8极48槽IPMSM作为研究对象,在永磁体使用量完全相同的情况下,分别建立了单层无隔磁桥、单层有隔磁桥、双层无隔磁桥以及双层有隔磁桥四种转子结构的内置式永磁同步电机模型。首先对四种电机的凸极率、输出转矩以及转矩脉动等电磁性能进行比较分析;其次对电机进行了模态分析;最后比较了四种电机的振动响应和噪声特性。

1 电磁及噪声相关理论分析

根据电机学相关理论,IPMSM向量图如图1所示[19]。

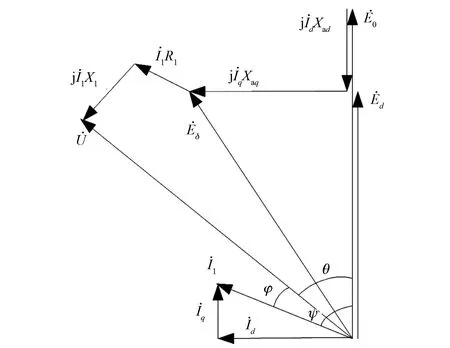
图1 IPMSM向量图Fig.1 IPMSM vector graph

根据图1可以推导出其基本电磁关系:

(1)

φ=θ-ψ

(2)

Usinθ=IqXaq+IdR1

(3)

Ucosθ=E0-IdXad+IqR1

(4)

式中:ψ为内功率因数角;θ为功率角;φ为负载功率因数角;E0为空载反电势;U为相电压;I1为定子相电流;R1为定子绕组相电阻。

联立式(3)、式(4)可以得到定子电流的直轴分量Id、交轴分量Iq,如式(5)、式(6)所示:

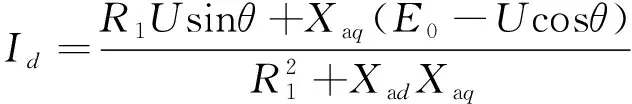
(5)

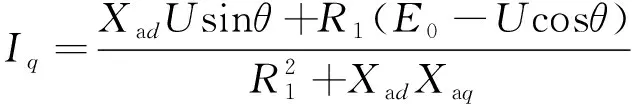
(6)

定子相电流为

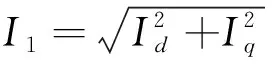
(7)

I1cosφ=I1cos(θ-ψ)=Idsinθ+Iqcosθ

(8)

P1=mUI1cosφ

(9)

将式(5)、(6)、(8)代入式(9)得:

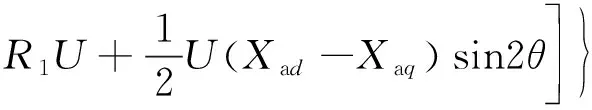
(10)

因为定子电阻R1远远小于直轴电抗Xad、交轴电抗Xaq,所以定子电阻可以忽略,式(10)可以简化为式(11),电磁转矩也可以表示为式(12)。

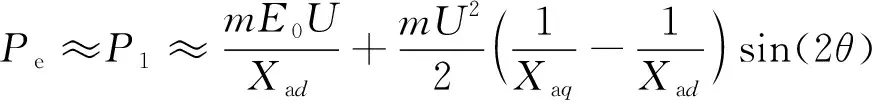
(11)

Tm+Tr

(12)

式中:Xad、Xaq分别为直、交轴同步电抗;Id、Iq分别为直、交轴电枢电流;p、Ω、m、ω分别为极对数、机械角速度、相数、电角速度。

IPMSM交、直轴定义图如图2所示。图中,d轴为直轴,q轴为交轴。

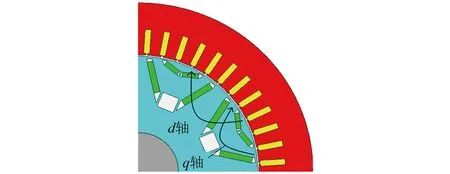
图2 IPMSM交、直轴定义图Fig.2 IPMSM definition diagram of d-axis and q-axis

IPMSM在d-q坐标系下,其直轴磁链ψd、交轴磁链ψq分别如式(13)、(14)所示,电磁转矩Te如式(15)所示:

ψd=Ldid+ψf

(13)

ψq=Lqiq

(14)

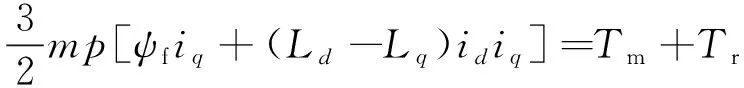
(15)

式中:ψd、id、Ld分别为定子磁链、定子电流、定子电感的d轴分量;ψq、iq、Lq分别为定子磁链、定子电流、定子电感的q轴分量;ψf为永磁体磁链;Tm、Tr、Te分别为电机的永磁转矩、磁阻转矩、电磁转矩。

由式(13)、(14)、(15)可以得到直轴电感、交轴电感,分别为式(16)、(17)。

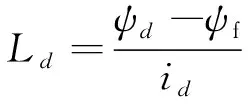
(16)

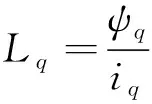
(17)

电磁振动是电机振动噪声的主要来源,气隙磁场中的径向电磁力作用在定子上会产生振动,进而产生噪声。因此径向电磁力和气隙磁密的分析是削弱电机噪声的重要部分。

与电机有关的振动加速度公式为

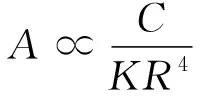
(18)

式中:A为振动加速度幅值;C为电机不平衡电磁力波;K为振动系数,是一个常量;R为不平衡电磁力波振动阶次。

根据电机相关理论,电机电磁力可以表示为

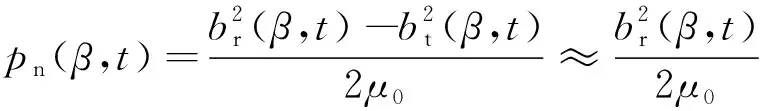
(19)

式中:pn为径向电磁力波:br为气隙磁密的径向分量;t为时间;bt为气隙磁密的切向分量,其数值较小,可以忽略;β为转子空间的机械角度;μ0为真空磁导率。

气隙磁密的径向分量为气隙磁势f(β,t)和磁导λ(β,t)的乘积,如式(20)所示:

br(β,t)=f(β,t)×λ(β,t)

(20)

当电机空载时,不考虑电枢反应,则气隙磁势由转子磁势产生,即:

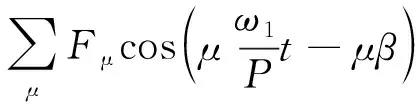
(21)

式中:μ为磁势的谐波次数;ω为角频率;p为极对数;Fμ为转子磁势,由励磁绕组和永磁体产生。

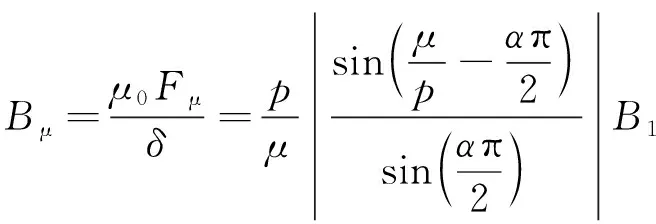
(22)

由式(18)可以看出,振动加速度的幅值与电磁力幅值成正比,与电机电磁力空间阶次的四次方负相关,这表明的阶次低、幅值大的力波应是重点分析对象。式(21)、(22)中证明,主极磁场谐波磁密幅值Bμ是决定径向电磁力大小的主要因素,径向电磁力谐波含量较高一般是因磁密谐波含量较高导致。

因此,要削弱电机的电磁振动噪声,削弱电机气隙磁密谐波含量尤为关键。

为维护欧盟内部金融稳定，确保在银行业危机时期，有效地清算处置金融机构，欧盟成立风险处置委员会，设立专项风险处置基金，用于问题银行的风险处置，各国层面的存款保险制度实际上只起到了付款箱的作用。其他国家也存在设立金融机构风险处置基金和存款保险基金的做法。如，德国2010年设立专项基金，专门用于问题银行的风险处置，包括提供过桥贷款、进行股权收购等。

2 模型建立与性能分析

2.1 设计指标

电机的基本参数如表1所示,本文设计了四台内置式永磁同步电机[20-21],其横截面如图3所示。四台IPMSM使用相同的定子结构、绕组;其转子使用相同的永磁体材料N48UH,且永磁体材料的使用量、轴向长度完全相同;硅钢片材料使用B27AVH1400。图3(a)为单层V形无隔磁桥IPMSM,图3(b)为单层V形有隔磁桥IPMSM,图3(c)为双层V形无隔磁桥IPMSM,图3(d)为双层V形有隔磁桥IPMSM。

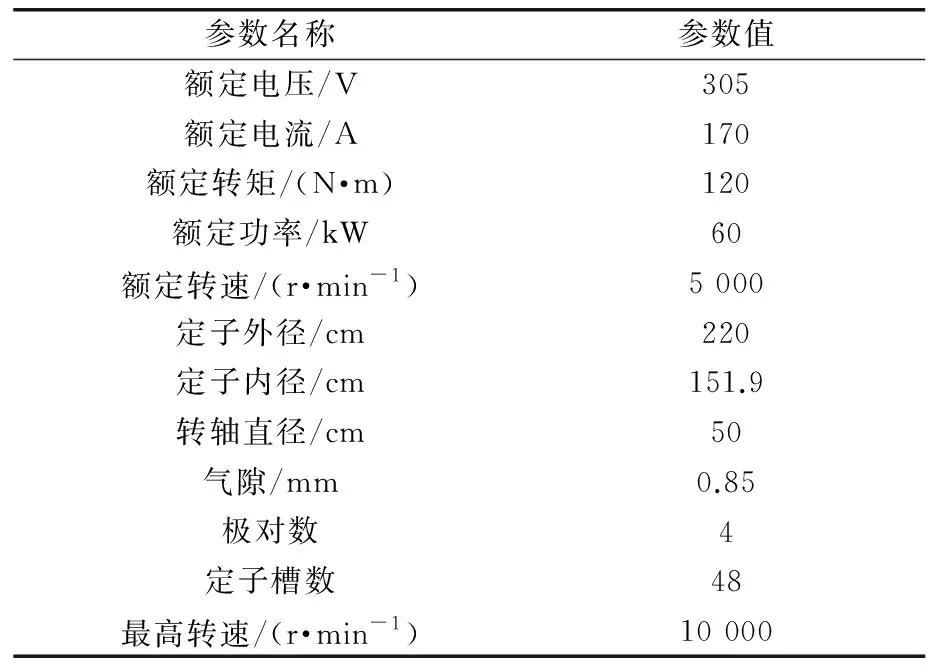
表1 IPMSM基本参数Tab.1 IPMSM basic parameters

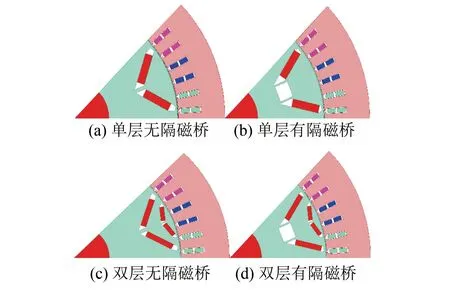
图3 电机横截面图Fig.3 Cross sectional view of motor

2.2 电机磁阻转矩分析

从式(12)、(15)中可以看出IPMSM的电磁转矩主要包含两部分:一是永磁转矩;二是磁阻转矩。在永磁体使用量受到限制的情况下, 永磁转矩不易提升,可以利用磁阻转矩来提升电机的电磁转矩。提升电机的磁阻转矩,有利于提升电机的过载能力和功率密度,有利于电机的弱磁扩速。电机的磁阻转矩和电机的凸极率往往成正比,电机的凸极率ε可以用d轴电感Ld和q轴电感Lq表示为

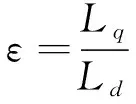
(23)

通过有限元仿真得到的图3所示的四种转子结构的电机在没有永磁体的情况下,d轴磁链ψd和q轴磁链ψq的输出如图4和图5所示。因为没有永磁体,所以永磁体磁链ψf=0,通过计算Ld、Lq和ε的均值得到结果如表2所示。从表2可以看出,电机在不同转子结构下其凸极率也是不同的,电机a、b、c、d的凸极率依次升高,磁阻转矩也随之依次增大。其中,电机d的凸极率最高,磁阻转矩最大。

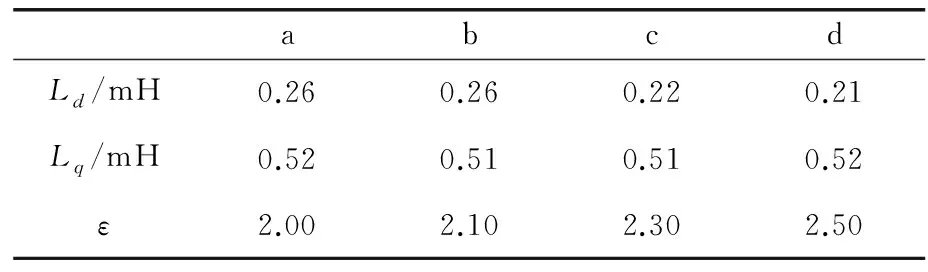
表2 电感及凸极率的均值Tab.2 Average value of inductance and salient pole

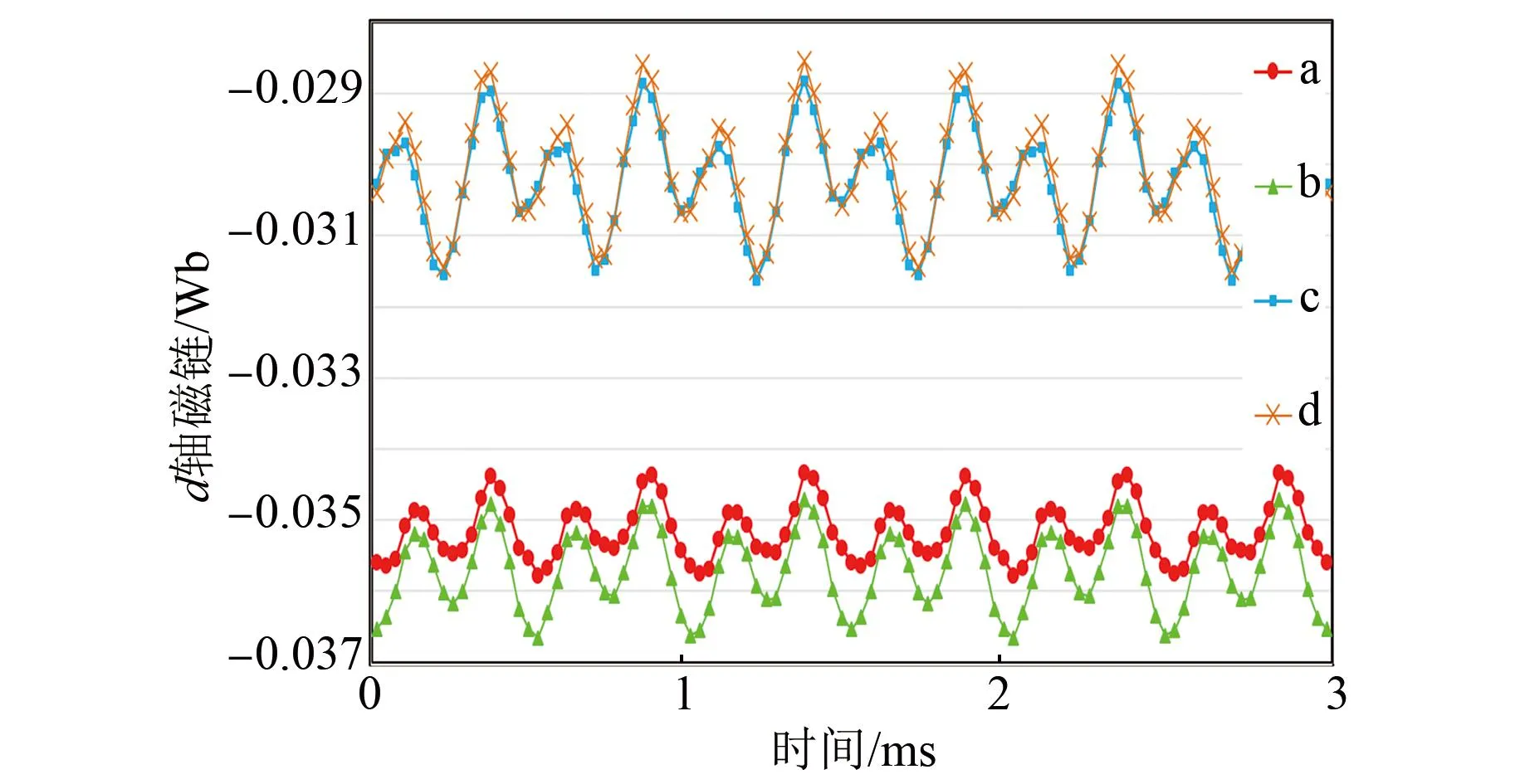
图4 d轴磁链Fig.4 Flux linkage of d-axis

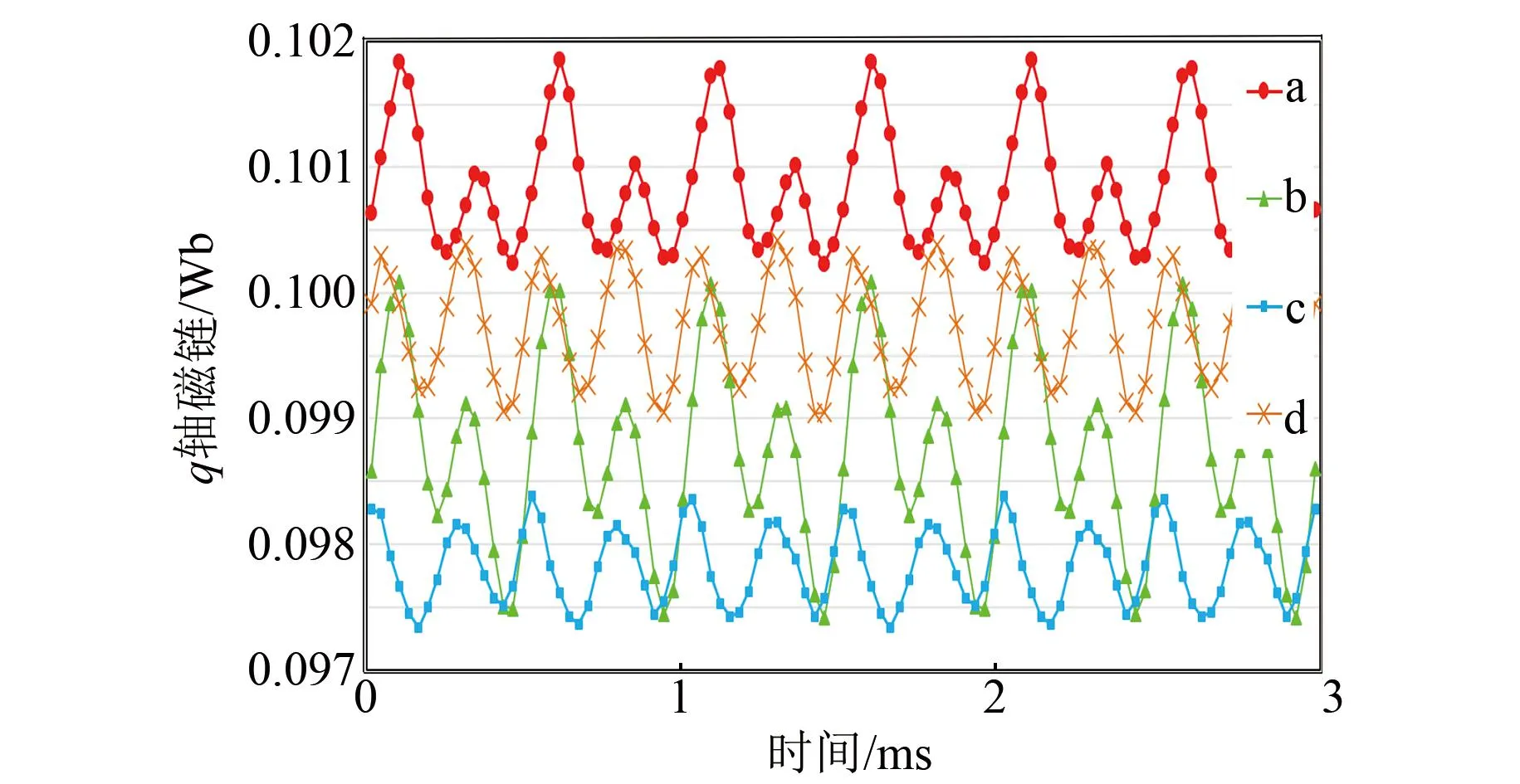
图5 q轴磁链Fig.5 Flux linkage of q-axis

2.3 输出性能分析

电机转矩脉动是产生振动和噪声的重要来源,若是电动汽车运行过程中电机转矩脉动过大,振动和噪声也会随之过大,会影响乘客的舒适度。所以在电机设计过程中总是希望电机拥有较小的转矩脉动。电机转矩脉动Kmb可以表示为式(24):

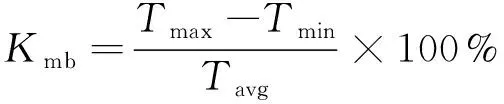
(24)

式中:Tmax、Tmin、Tavg分别为最大输出转矩、最小输出转矩、平均输出转矩。

图6为在转速为5 000 r/min时四种结构的电机的输出转矩,表3为四种结构的电机的平均输出转矩Tavg和转矩脉动Kmb。从表3可以看出,电机d的输出转矩最高且转矩脉动最小;电机a、c的输出转矩较高,但是转矩脉动较大;电机b的输出转矩小,且转矩脉动大。

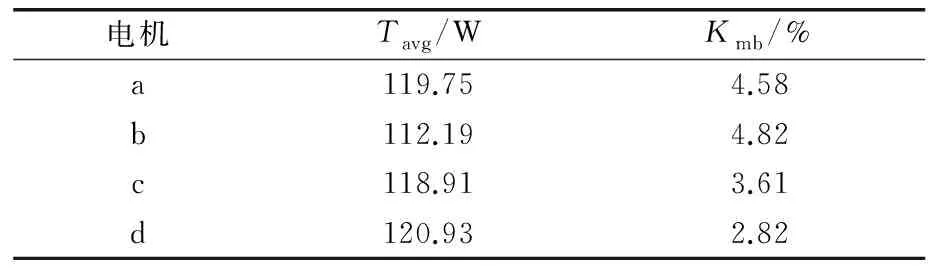
表3 各电机的输出转矩和转矩脉动Tab.3 Output torque and torque ripple of each motor

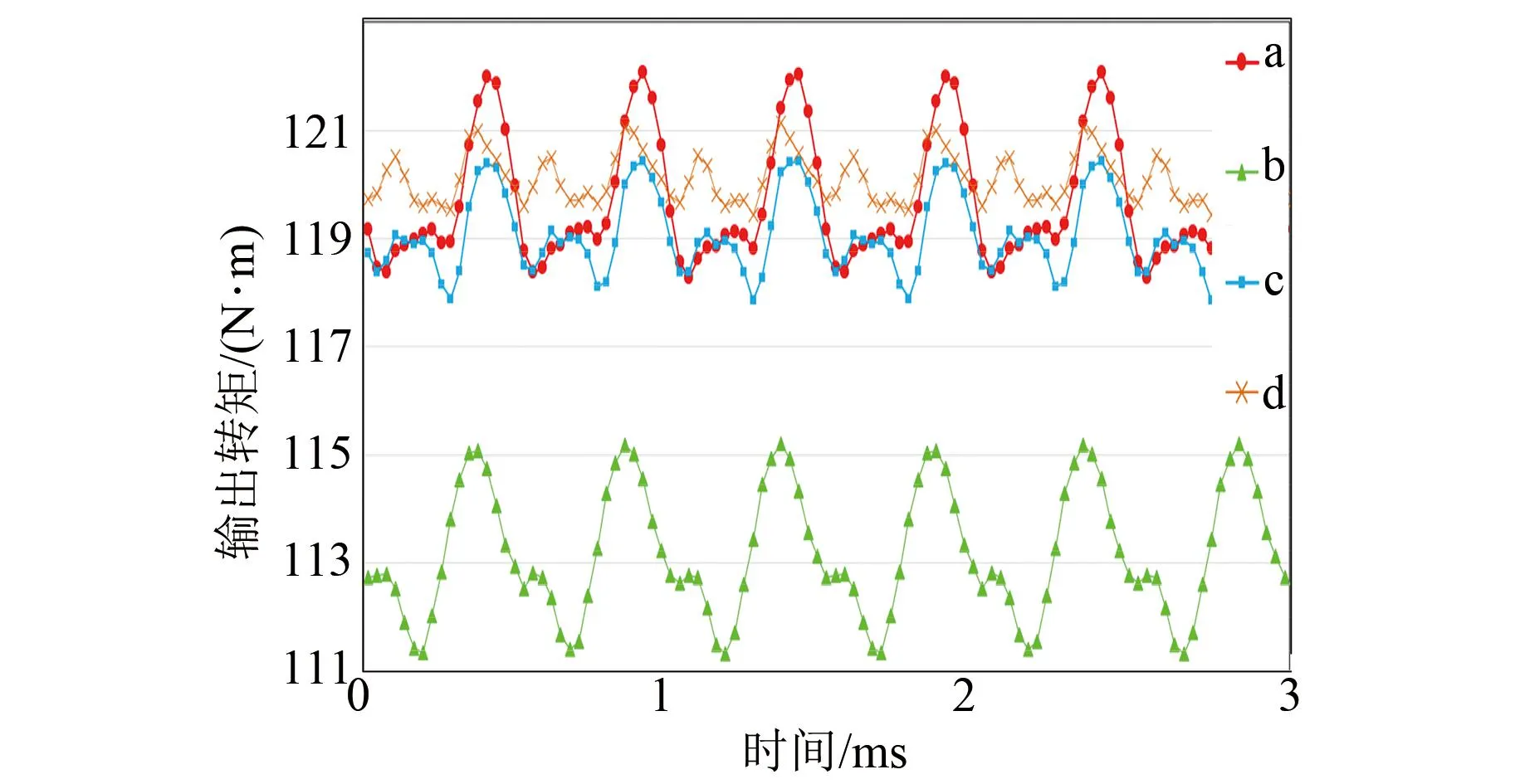
图6 电机a、b、c、d的输出转矩Fig.6 Output torque of a, b, c, d

如图7所示,在转速0～10 000 r/min下,电机d的输出转矩最高,按照输出转矩的大小从高到低依次为电机d、c、a、b,与从图6和表3中得出的结论一致。

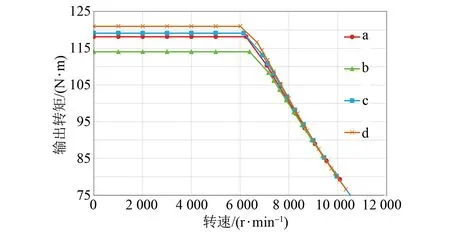
图7 四种电机在不同转速下输出转矩Fig.7 Output torque of four types of motors at different speeds

图8为四种电机的空载反电势的快速傅里叶变换结果。谐波畸变率是电气相关行业中表示波形畸变程度的一个性能参数。谐波畸变率越高,电机的噪声和不稳定性增加得越快;谐波畸变率越低,则电机的运行更加稳定。谐波畸变率可以表示为式(25),即:

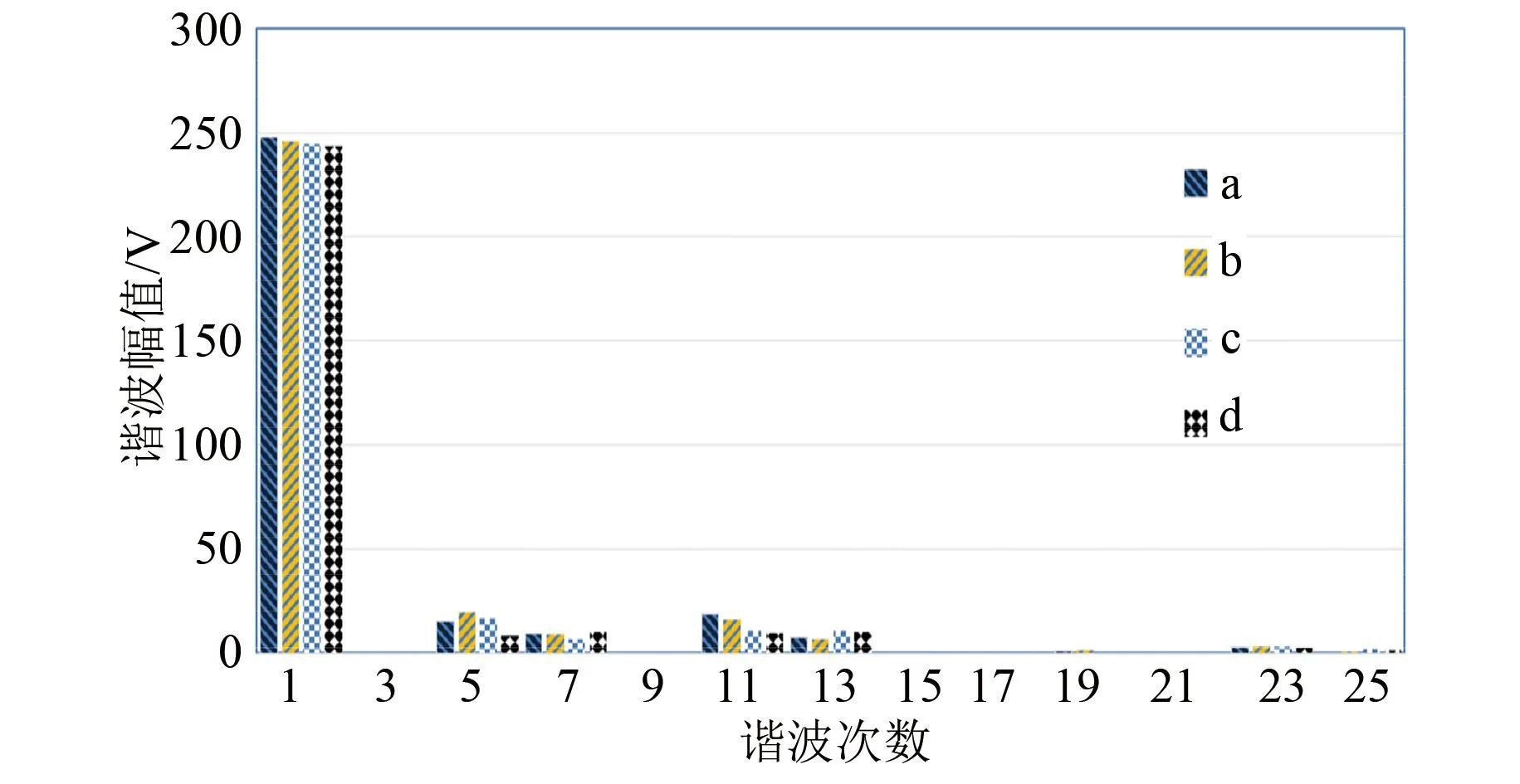
图8 空载反电势的谐波含量Fig.8 Harmonic distortion of no-load back electromotive force

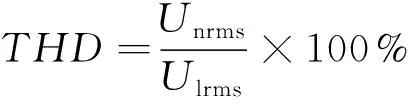
(25)

式中:THD为谐波畸变率;Unrms为谐波的均方根值;Ulrms为基波的有效值。通过式(25)计算,得到结果如表4所示。从表4中可以看出,电机a、c、b、d的谐波畸变率依次降低,其稳定性依次升高。

表4 空载反电势的谐波畸变率Tab.4 Harmonic distortion rate of no-load back electromotive force

2.4 径向电磁力分析和模态分析

对电机a进行有限元仿真得到其气隙磁密波形如图9所示,用同样的方法得到电机b、c、d的气隙磁密波形。对电机a、b、c、d的气隙磁密波形进行傅里叶变换得到图10,根据式(25)计算其谐波畸变率THD,得到结果如表5所示。从表5中可以看出,电机d的谐波畸变率最低、稳定性最好,电机b、a、c、d谐波畸变率依次降低。

表5 径向气隙磁密谐波畸变率Tab.5 Harmonic distortion rate of radial air gap magnetic density

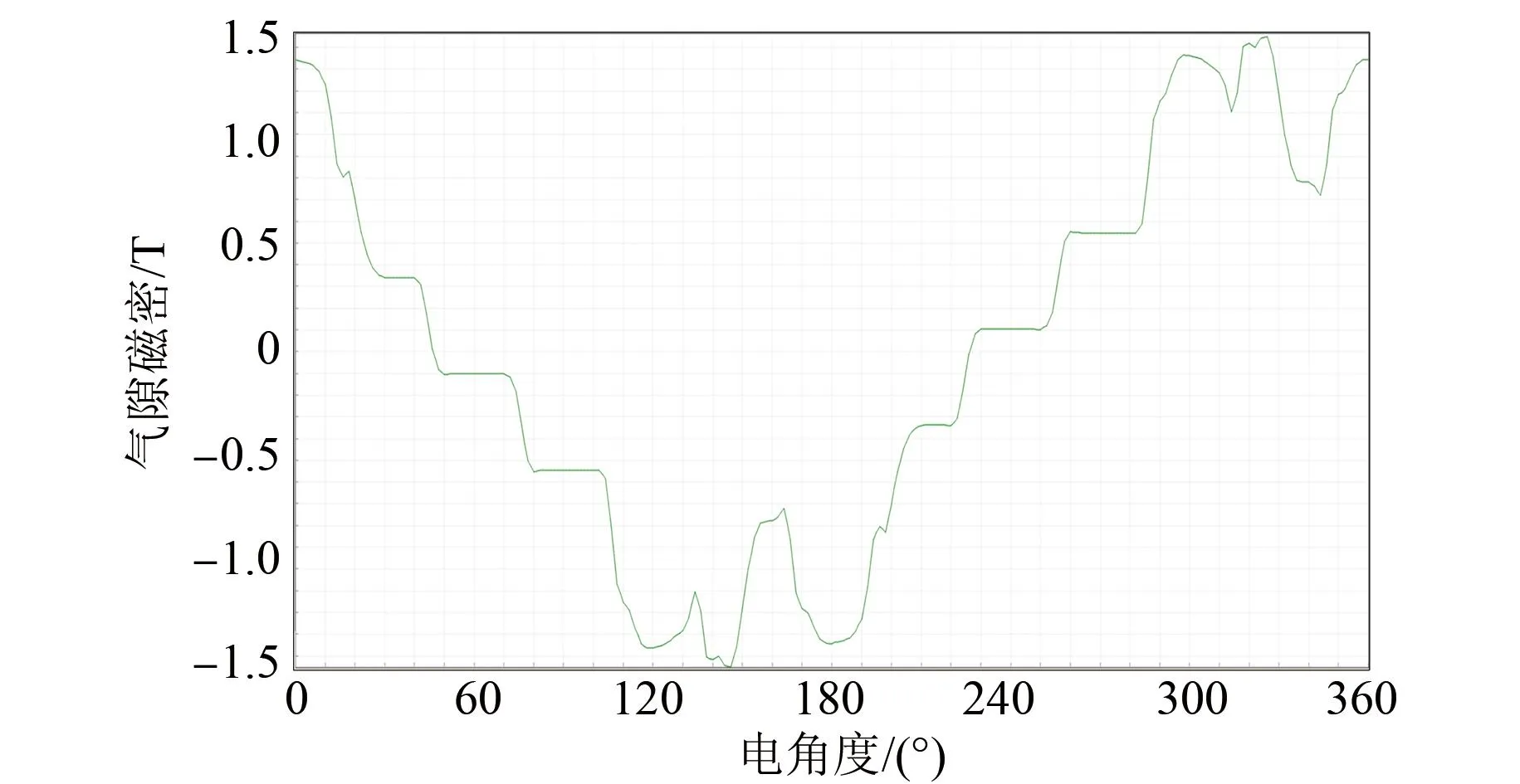
图9 电机a气隙磁密Fig.9 Air gap magnetic density of motor a

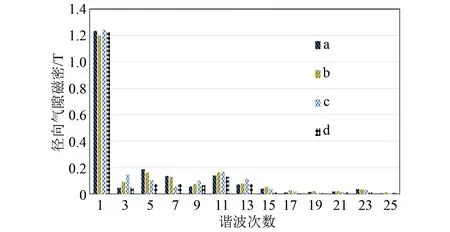
图10 气隙磁密谐波含量对比Fig.10 Comparison of harmonic content of air gap magnetic density

模态分析是研究电机径向电磁力和噪声的重要步骤,因为当电机径向电磁力阶次与定子模态阶数相同且电机定子的固有频率和径向电磁力密度谐波的频率相同或相近时会使电机产生共振。通过有限元仿真得到定子模态的固有频率如图11所示。径向电磁力的基波频率为333.33 Hz,径向电磁力的第2、4、6、8、10次谐波幅值较大,定子模态的第2、3次模态的固有频率分别和径向电磁力第2、6次谐波的频率相差不大,因此有可能会产生共振。

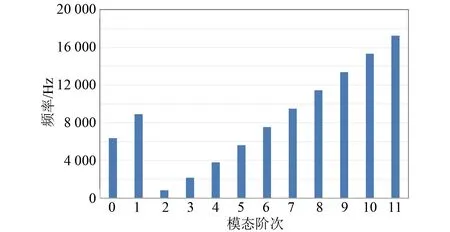
图11 定子模态的固有频率Fig.11 Natural frequency of stator mode

通过有限元分析得到电机a的径向电磁力的三维分布图如图12所示,用同样的方法得到电机b、c、d的径向电磁力三维分布图。通过对电机a、b、c、d的径向电磁力三维分布图进行快速傅里叶变换,得到图13。从图13中可以看出第14、16、18次谐波幅值较小且相差不大。电机a、b、c、d的第2、6、8、10、12次谐波幅值依次减小,电机b、a、c、d的4次谐波幅值依次减小。总体来看,电机a、b、c、d的噪声削弱效果依次升高,电机d的噪声削弱效果最好。

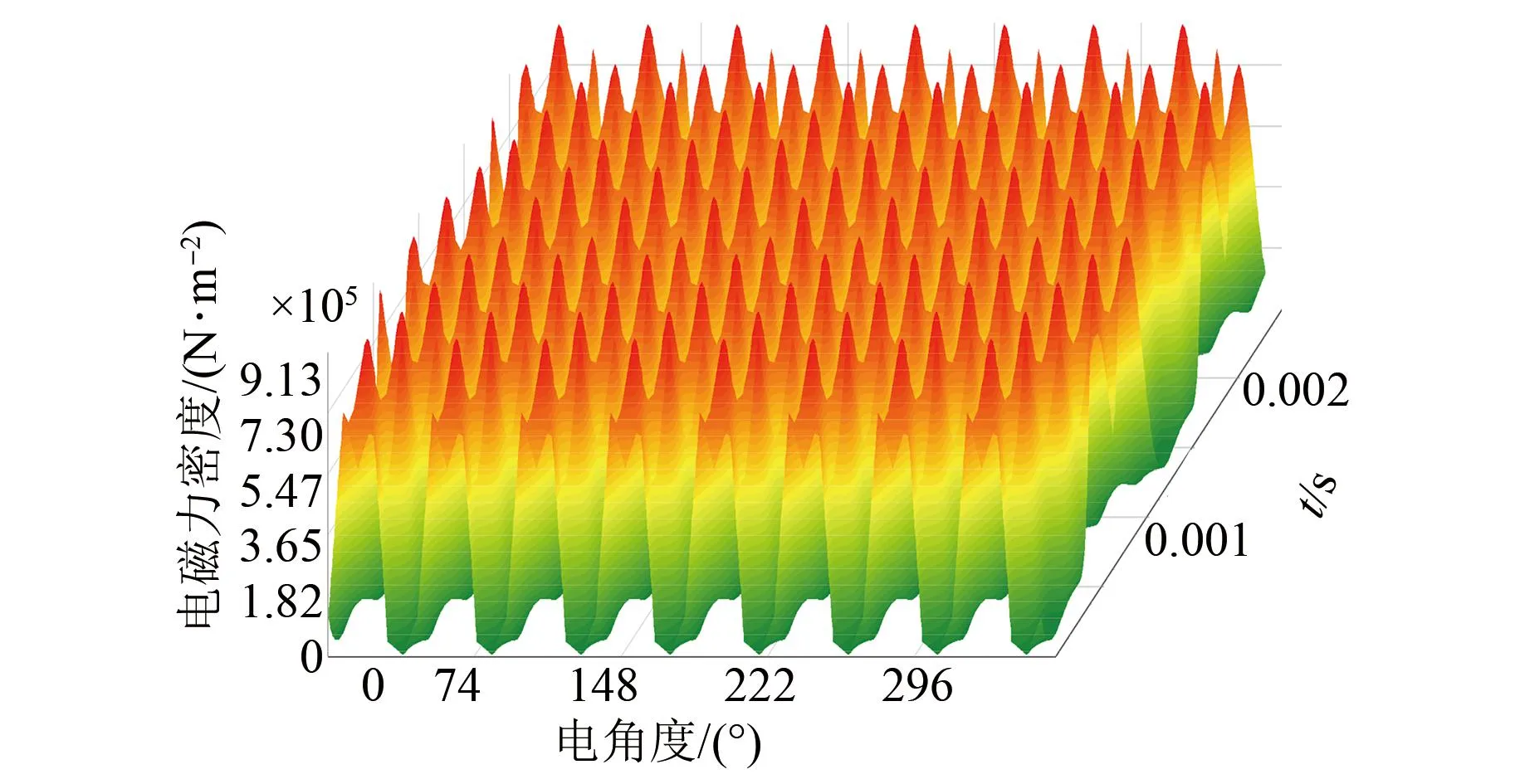
图12 电机a径向电磁力密度Fig.12 Radial electromagnetic force density of motor a

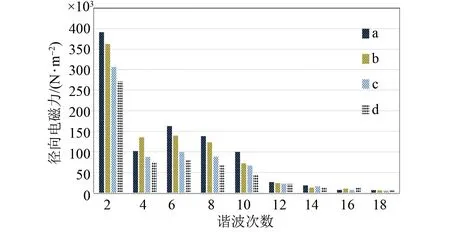
图13 径向电磁力谐波对比Fig.13 Comparison of radial electromagnetic force harmonics

2.5 噪声分析

从上述中分析得出,电机定子极有可能会产生共振,导致比较严重的振动响应。电机a振动噪声计算的有限元模型如图14所示,电机b、c、d的噪声计算的有限元模型类似,在此不一一列举。通过有限元仿真得到电机a、b、c、d的振动加速度和噪声如图15和图16所示,图中f为基频。2倍频和6倍频分别接近定子模态的2阶固有频率和3阶固有频率;10倍频、12倍频对应电机的一阶齿谐波频率,所以电机的2倍频、6倍频、10倍频、12倍频产生较大的振动加速度和声辐射功率。在2倍频、6倍频、8倍频、10倍频、12倍频、18倍频下,电机a、b、c、d的振动加速度的和声辐射功率依次递减。在4倍频、8倍频、16倍频、18倍频下,电机a、b、c、d的振动加速度的和声辐射功率幅值较小且相差不大。总体来看,与前文分析的径向电磁力结果相对应,电机d的噪声削弱效果最好。

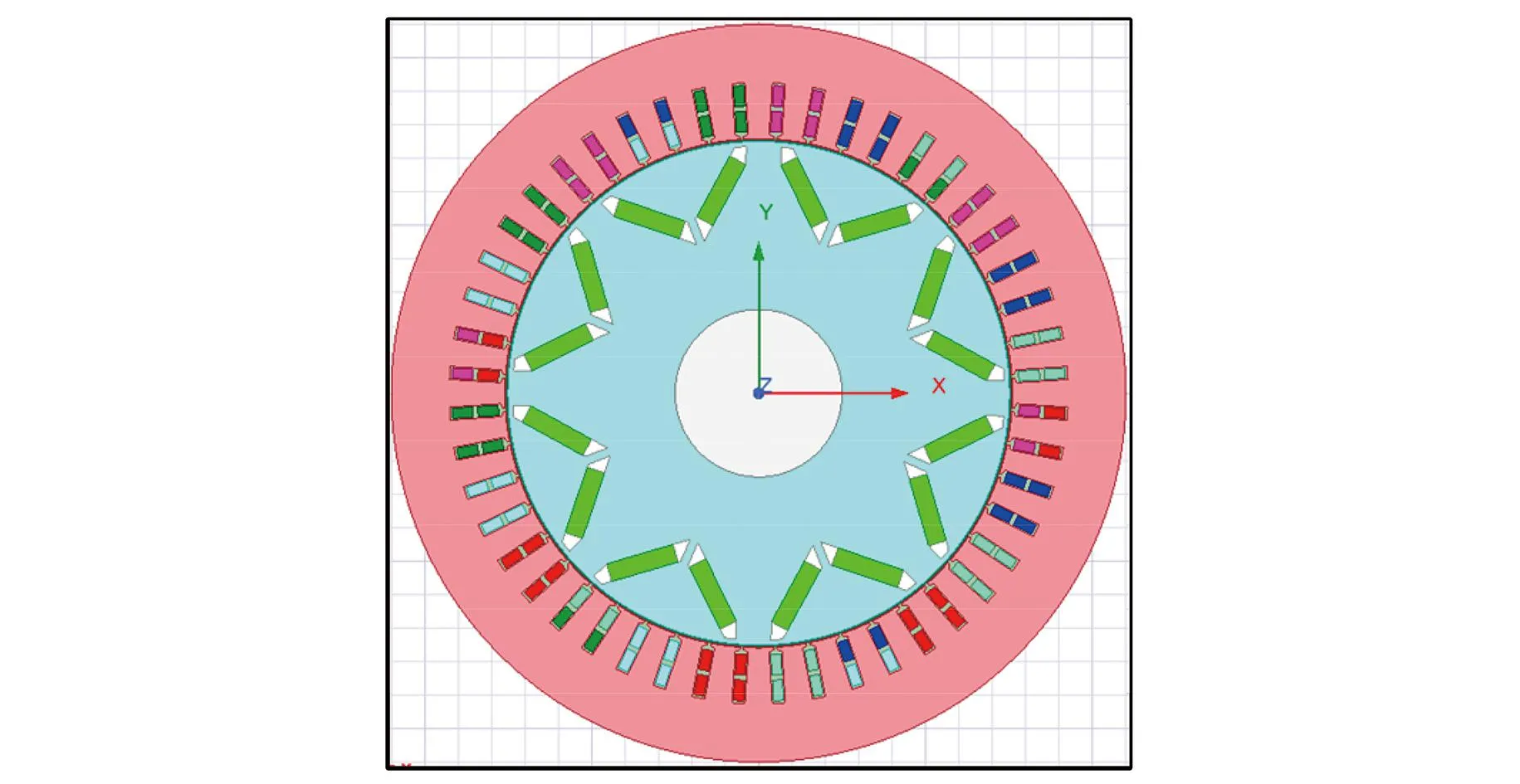
图14 电机a振动噪声计算的有限元模型Fig.14 Finite element model for vibration and noise calculation of motor a

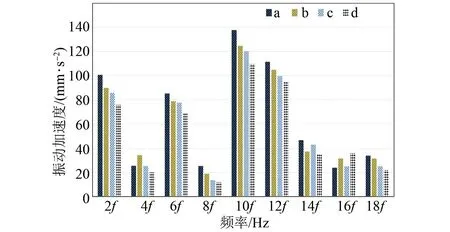
图15 振动加速度对比Fig.15 Comparison of vibration acceleration

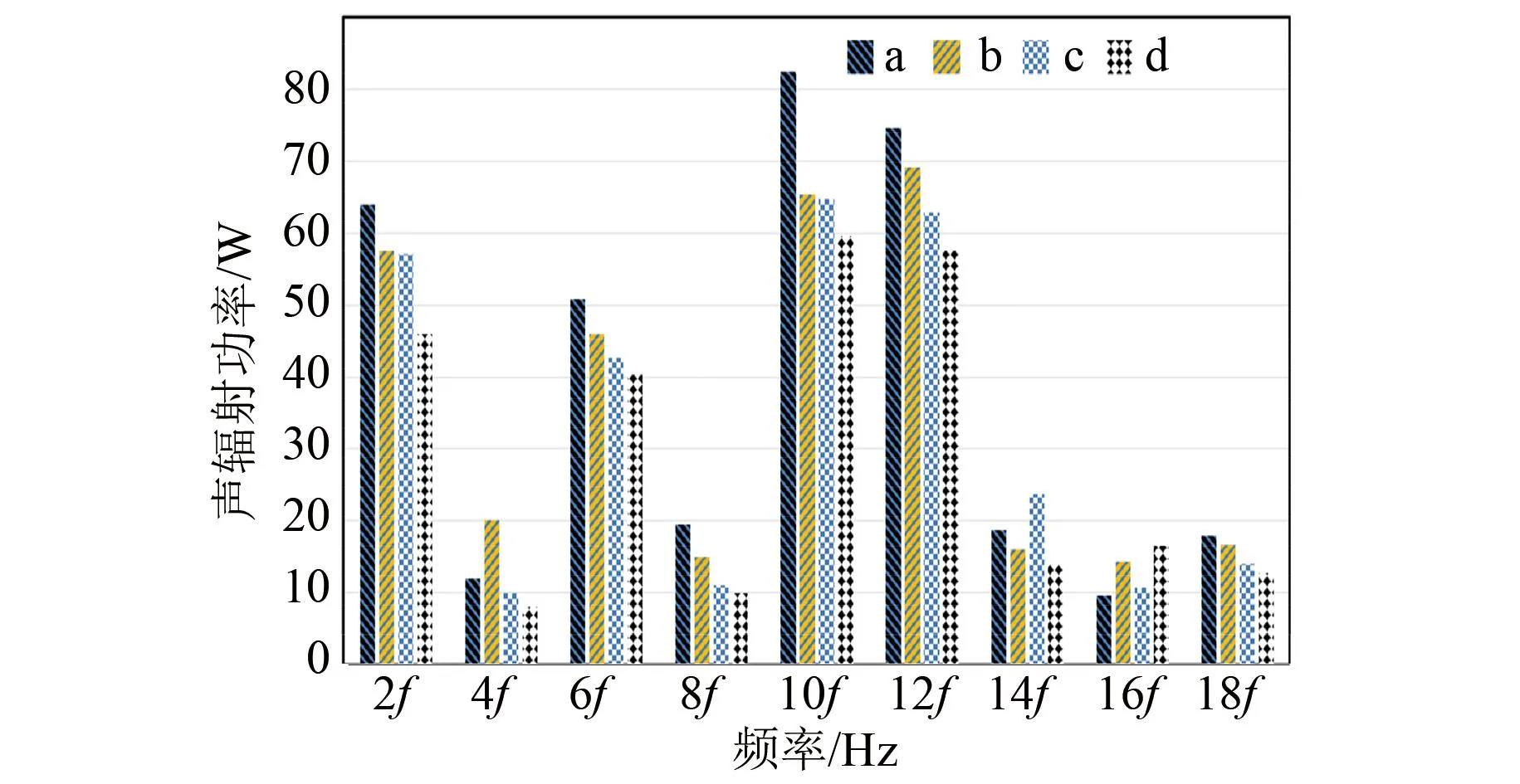
图16 声辐射功率对比图Fig.16 Comparison of sound radiation power

3 结语

本文在永磁体使用量完全相同的情况下分别设计了图3中四种转子结构的电机,并利用有限元仿真软件对电机的电磁性能和噪声性能等进行了对比分析,得出了以下结论:

(1) 单层无隔磁桥、单层有隔磁桥、双层无隔磁桥以及双层有隔磁桥转子拓扑结构的IPMSM的凸极率依次增大,磁阻转矩依次增加。双层有隔磁桥的IPMSM输出转矩最高且转矩脉动最小;无隔磁桥的IPMSM输出转矩较高,但是转矩脉动较大。单层有隔磁桥转子拓扑结构电机的输出转矩小,且转矩脉动大。单层无隔磁桥、单层有隔磁桥、双层无隔磁桥以及双层有隔磁桥转子结构电机的空载反电势的谐波畸变率依次增大,稳定性依次升高。

(2) 单层有隔磁桥转子结构电机的气隙磁场的谐波畸变率最高、稳定性最差。其余三种转子拓扑结构电机气隙磁场的谐波畸变率相差不大,因此更为稳定。

(3) 幅值较大的径向电磁力波频率与电机模态的固有频率相差较大,所以四种电机都不会发生共振。通过对四种电机的径向电磁力、振动加速度以及声辐射功率分析,发现四种电机的径向电磁力、振动加速度以及声辐射功率基本相对应,双层有隔磁桥转子结构的电机的噪声性能最好。