基于改进模糊评价法的无人艇碰撞风险计算

2024-03-05赵贵祥王晨旭李云淼

系统工程与电子技术 2024年3期

赵贵祥, 王晨旭,*, 周健, 李云淼

(1. 天津大学海洋科学与技术学院, 天津 300110;2. 中国船舶集团有限公司第七一六研究所, 江苏连云港 222061)

0 引言

水面无人艇(unmanned surface vehicle, USV)相比于人工控制操作的船舶,具有高速化、智能化和模块化等优势。在军事上,USV可应用于侦察、搜救和巡逻等场景;在民用领域中,USV的应用范围更加广泛,包括海面灾害预警、环境监测和海洋垃圾清理等工作中[1]。由于USV适用于复杂的工况,因此需要具备更强的自主性。障碍物检测与规避(obstacle detection and avoidance, ODA)是USV自主系统的重要组成部分,而碰撞风险评估是ODA的前提[2]。评估USV与目标船之间危险度的方法通常是计算本船与目标之间的碰撞危险度(collision risk index, CRI)[3]。

1977年,Kearon[4]首次采用最近会遇距离(distance at closest point of approach, DCPA)和最短会遇时间(time at closest point of approach, TCPA)加权的方法来计算CRI,为此后的数学计算模型奠定了基础。为提高计算精度,学者们将方位、距离、速度等因素引入计算CRI的模型中[2,5-6]。王雅丽[7]通过灰色关联法计算CRI,计算量小、速度快,得到了相对CRI。Lin等人[8]通过改进的反向传播(back propagetion, BP)神经网络计算CRI,该方法计算误差较小但依赖于样本数据。Wen等人[9]通过两船距离、相对速度和相交轨迹来构建CRI的计算模型。模糊评价法能够解决各因素的量纲不同的问题且计算量小,因此常被作为计算CRI的重要方法[10-11]。周江华等人[12]通过模糊评价模型计算CRI,并在隶属函数中考虑了船舶领域、动界和最晚施舵距离的概念。Hu等人[13]通过模糊评价法计算目标船的CRI,并在此基础上提出一种基于碰撞危险评估的USV的局部规划算法。Luo等人[14]则通过DCPA隶属度函数和TCPA隶属度函数建立了空间碰撞风险、时间碰撞风险和碰撞风险等级的模型。刘冬冬等人[15]通过四元船舶领域模型对传统模糊评价方法中DCPA的隶属度函数进行改进,改进后的安全距离可以根据会遇参数灵活确定。尽管上述学者对模糊评价法进行了改进,但传统模糊评价模型中的安全距离和碰撞威胁距离的取值较为固定,不能根据船舶的尺度、速度和操纵性进行调整,导致该模型无法适用于近距离USV的碰撞风险计算。此外,传统模型没有考虑船舶会遇局面以及各种局面下《国际海上避碰规则》要求的避让方法,导致船舶中心线对称的左右舷两船的碰撞风险相同,与航海实际避让情况不符。

为此,针对上述两个问题对传统的模糊评价模型进行了改进。本文综合考虑DCPA、TCPA、距离、方位和船速比5个因素,通过四元船舶领域和行动域对模糊评价模型中的DCPA隶属度函数、TCPA隶属度函数、距离隶属度函数进行了改进。同时,针对不同会遇情况将本船分为让路船、具有同等避让责任的船舶、紧迫危险局面中的直航船、非紧迫危险局面中的直航船,并制定了不同会遇情况的CRI计算方法,考虑到《国际海上避碰规则》的要求,增加了模型的适用性。

1 传统的模糊评价

传统的模糊评价模型考虑了以下因素:DCPA、TCPA、距离、方位和船速比。在隶属函数中考虑了船舶领域和动界以及最晚施舵距离的概念。当目标船闯入USV监视范围内,应计算两船的碰撞危险度CRI。当CRI接近于0时,表明碰撞风险较低;CRI接近1时,则表明极有可能发生碰撞。因素集和影响集如下:

K={DCPA,TCPA,D,θr,K}

(1)

CRI=αdcpaKdcpa+αtcpaKtcpa+αDKD+αθrKθr+αKKK

(2)

式中:Kdcpa,Ktcpa,KD,Kθr,KK分别为DCPA、TCPA、距离、方位和船速比的隶属函数;αdcpa,αtcpa,αd,αθ,αk分别为各自的权重值,DCPA和TCPA的计算公式可以参见文献[16]。

DCPA的隶属函数如下:

(3)

式中:d1表示安全通过距离,即船舶领域的边界值;d2表示绝对安全距离,d2=2d1。d1和d2的单位均为海里,d1的求取[17]如下所示:

(4)

式中:θt为目标船相对本船的方位。

TCPA的隶属函数如下:

(5)

式中:

式中:D1为在最晚施舵点时的两船距离,一般为12倍船长;D2为动界,即让路船开始避让的距离,求取[18]如下:

(6)

式中:Bt为目标船相对本船的真方位。

两船距离隶属函数如下:

(7)

式中:Dr为两船的距离。

方位隶属函数和速度隶属函数[18]如下:

(8)

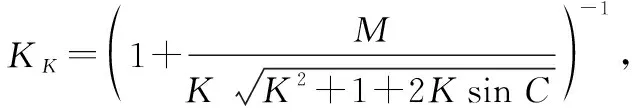
(9)

式中:φo和φt分别为本船和目标船的航向;K为目标船与本船的船速比;C为两船碰角;M为常数。

2 改进的模糊评价模型

2.1 船舶领域模型的筛选

传统的模糊评价模型中的安全距离d1是由Goodwin[19]提出的船舶领域边界值确定的。该领域包括左、右、艉3个方向上的圆形扇区,其半径分别为0.7海里、0.85海里和0.45海里。传统模型中,船舶领域d1是一个相对固定大小的值,在计算CRI时通常忽略了船舶尺度的影响。然而,对于不同的船所要求的安全通过距离应该是不同的,因此d1应根据会遇参数和船舶尺度做出实时的改变。Wang[20]提出的四元船舶领域模型考虑了船舶尺度、速度和操纵性,能够根据船舶的具体情况调整领域的大小,模型的计算公式如下:

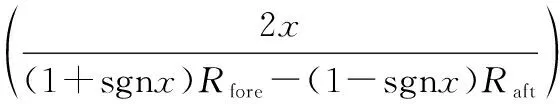
(10)

(11)

(12)

式中:Rfore,Raft,Rport,Rstarb分别为船首船尾、左舷和右舷的椭圆半径;kAD为船舶进距的增益;kDT为旋回初径的增益;L为USV船长。本文船舶领域d1的取值为

(13)

式中:φ为椭圆上一点与椭圆长轴的夹角。

2.2 动界模型的筛选

传统的模糊评价模型中,碰撞威胁距离D2采用的是Davis等人[21]提出的半径为2.7海里的偏心圆的动界作为让路船应进行避碰的临界区域值。然而,搭载激光雷达的USV最大探测量程通常在300 m左右,如果直接采用该动界进行小尺度USV的危险评估,虽然偏于安全,但距离过大。此外,该动界的范围不能随着两船速度的改变而发生变化,在实际应用中具有一定的局限性。Dinh等人[22]在研究船舶碰撞风险评估时提出“行动域”的概念。“行动域”也是动界模型的一种,能够描述让路船应进行避碰的临界区域值。然而,“行动域”考虑了船舶的尺度、速度和操纵性,更利于计算船舶之间的碰撞风险。本文将“行动域”的边界值替代传统让路船采取避碰行动的临界距离。改进后D2的取值如下所示:

D2=Df+k·vr

(14)

(15)

(16)

式中:vo和vt为本船和目标船的速度;Advo为本船的进距,可通过旋回实验得到;k为时间参数,本文设为0.167;Advt为目标船的进距可通过如下经验公式得到[22]:

Advt=2.531lobject+4.062bobject+23.83

(17)

式中:lobject为目标船的长度;bobject为目标船的宽度,可通过船舶自动识别系统获得。

2.3 紧迫危险局面中碰撞风险的计算

传统的模糊评价模型在计算CRI时仅考虑了船舶位置、方位、船舶速度等信息,而没有考虑《国际海上避碰规则》。为此,本文将船舶会遇划分为对遇、右交叉、左交叉和追越4种局面,并分析了不同会遇局面中CRI的计算方法,如图1所示。

图1 会遇态势的划分Fig.1 Division of encounter situation

具体而言,对于不同的会遇局面,本文分别给出了相应的CRI计算公式,以更准确地评估船舶碰撞风险。会遇局面的计算如下:

(18)

在对遇的局面中,本船与目标船具有同等避让责任,应正常计算CRI;当两船形成右交叉的局面时,本船为让路船,目标船为直航船,本船应及时做出避让的行动,因此也应该正常计算CRI;当形成左交叉和追越的局面时,本船为直航船,目标船为让路船,在两船形成碰撞危险的初始阶段本船不需要做出避让行动,因此可认为此时目标船相对本船的CRI为0;随着两船危险的进一步逼近,当构成碰撞危险的两船已经接近到单凭一船已难以避免碰撞的局面称为紧迫危险局面。本文认为当Kdcpa∈(0,1]且Ktcpa∈(0,1]形成紧迫危险局面[23],此时本船必须执行必要的避让行动,因此应正常计算CRI的值。

3 模拟实验与结果分析

为了验证本文改进的模糊评价算法的有效性,以本课题组“Dolphin-I”号USV为例,如图2所示。“Dolphin-I”的相关参数由实船实验得到。在模拟的计算中,为了简化计算,本船和目标的船舶尺度及操纵性能等参数都参考“Dolphin-I”的相关参数,如表1所示。

图2 Dolphin-I号USVFig.2 Dolphin-I USV

表1 Dolphin-I参数Table 1 Dolphin-I parameters

本文不考虑天气、水流等因素对实验的影响,假设实验中本船与目标船的定位准确,目标船在会遇时能够与本船构成对遇、右交叉、左交叉和追越的会遇态势。为了方便计算,在模拟器中随机生成并选取5条目标船,目标船的航速、航向、位置等信息随机生成。以本船中心点为原点建立北东坐标系,本船位置为(0,0),初始航向为000°,航速为5 m/s。目标船运动参数如表2所示。αdcpa,αtcpa,αd,αθ,αk的取值通常由层次分析法获得,本文参考了文献[24]的研究成果,分别取0.400、0.367、0.133、0.067、0.033。

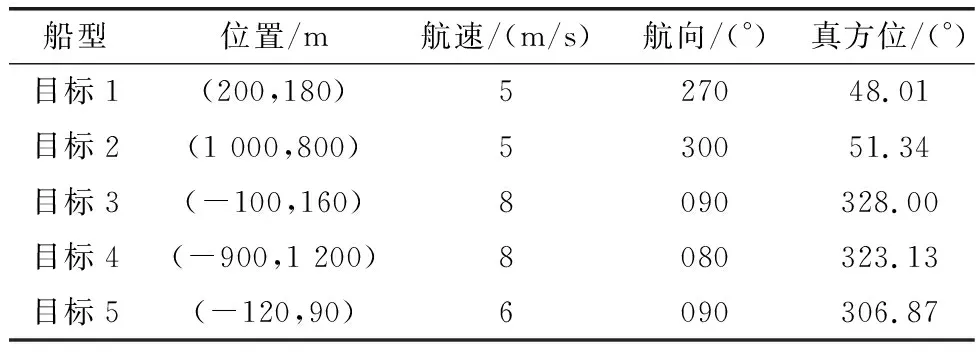
表2 目标船的相关信息Table 2 Information about the target ship

根据计算结果,可得出本船与目标船的DCPA、TCPA和距离等结果,如表3所示。目标船与本船的位置关系如图3(a)所示,其中目标2、目标4与本船距离均大于400倍,可视为远距离会遇;而目标1、目标3、目标5与本船的距离均不超过100倍,相较于目标2、目标4,可视为近距离会遇,本船的船舶领域如图3(b)所示。此外,目标1、目标2相对本船为直航船,目标3、目标4、目标5相对本船为让路船,其中目标5满足Kdcpa∈(0,1)∩Ktcpa∈(0,1)的条件属于紧迫危险局面,图4为3种模型中边界值的比较,图5为3种模型危险度的对比。

表3 两船的避碰参数Table 3 Collision avoidance parameters of two ships

图3 船舶会遇局面图Fig.3 Map of ship encounters

在传统模型中,安全距离d1通常是由Goodwin[19]提出的船舶领域模型确定的,碰撞威胁距离D2是由Davis等人[21]提出的半径为2.7海里的偏心圆确定的。其中,d1大于1海里,D2大于3海里,如图4(a)所示。传统模型计算的4条船舶与本船的CRI均在0.88之上,都属于高度危险的状态。然而,目标2和目标4距离本船的距离分别是USV船长的400倍和469倍,显然USV在此距离与目标船的碰撞危险应几乎为零。传统模型忽略了船舶的速度和尺度的影响,不适用于近距离和尺度较小的船舶之间的风险评估。

图4 3种模型中边界值的比较Fig.4 Comparison of boundary values in the three models

在刘冬冬等人[15]改进的模型中,船舶的安全距离d1是通过四元船舶领域确定的,碰撞威胁距离D2仍是由Davis等人[21]提出的动界确定的。四元船舶领域模型的优点是考虑了船舶的运动参数和操纵信息,能够适用于近距离的碰撞风险评估。然而,D2的设定较大且不能根据船舶的尺度、速度和操纵性进行改变,如图4(b)所示。在刘冬冬等人[15]的实验结果中目标1～目标5的DCPA的隶属度值有所降低,但TCPA的隶属度值和距离隶属度值仍不合理。例如,近距离的目标1和远距离目标2的TCPA的隶属度值和距离隶属度值均一致,如图5所示。

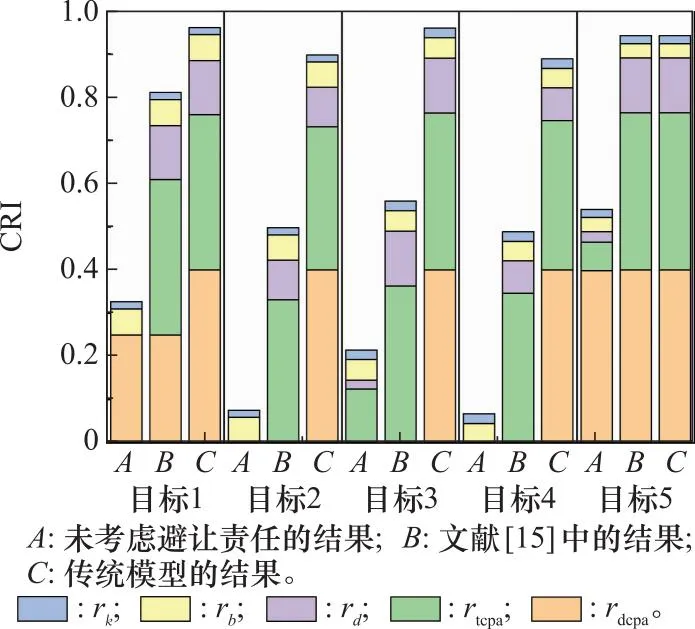
图5 3种模型CRI的对比Fig.5 Comparison of CRI of the three models

改进的模型在刘冬冬等人[15]的基础上对D2的值进行改进,通过行动域模型替换了Davis等人[21]的动界模型对模型中的碰撞威胁距离进行改进,改进后的碰撞威胁距离能够考虑船舶尺度、速度和操纵性,d1和D2的值都能考虑船舶尺度、速度和操纵性等因素。改进后5条目标船D2的值分别为235.20、171.14、303.28、284.54、258.06如图4(c)所示。

在考虑船舶避让责任之前,改进的模型能够区分远距离和近距离目标船的碰撞危险程度,提高了计算精度和辨识度。其中,与距离USV较远的目标2和目标4的CRI得到了降低。目标1～目标5的CRI分别为0.326 4、0.074 9、0.214 8、0.066 8、0.540 6,如图5所示。在考虑避让责任后,本船与目标1和目标2构成右交叉会遇局面,应执行避让行动,因此正常计算CRI;而本船与目标3～目标5之间构成左交叉会遇态势,且目标3和目标4与本船没有形成紧迫危险局面。对于目标3和目标4,本船对目标船构成威胁,但目标船并未对本船构成威胁,本船不需要执行避让行动,因此可认为本船与目标船之间的CRI为0;对于目标5,两船形成了紧迫危险局面,本船具有避让义务,需要采取避让行动,因此正常计算CRI是合理的。考虑避让责任后,目标1～目标5的危险度分别为0.326 4、0.074 9、0、0、0.540 6,如图6所示。

图6 考虑避让责任前后结果对比Fig.6 Results before and after considering avoidance duty

改进后的模型显著降低了近距离目标船的碰撞风险指数,提高了风险评估的计算精确度和辨识度。该模型考虑了《国际海上避碰规则》中船舶间的避让责任,分析了本船作为直航船时的危险程度。同时,该模型将两船是否形成紧迫危险局面的情况引入CRI的评价中,当本船属于未构成紧迫危险局面下的直航船时,碰撞危险度为零,结果更符合航海避碰实际情况。然而,该模型在考虑水域环境和通航密度等因素方面存在局限性。此外,当前各隶属函数的权重受到专家主观性的影响,下一步可以对各隶属度的权重进行深入研究。