两船距离与转向避让难度关系量化研究

刘 佳，柳成林，王艳杰

(交通运输部水运科学研究院，北京100088)



两船距离与转向避让难度关系量化研究

刘 佳，柳成林，王艳杰

(交通运输部水运科学研究院，北京100088)

转向避让是航海上最为常用也最有效的解除碰撞危险方法，但转向避让行动的幅度和难度会受到避让行动采取时机的极大影响。从船舶运动的数学模型出发，提出了转向难度、最小转向角度等概念并建立了相应的数学模型，并进一步推理出本船施舵时两船距离与最小转向角和转向难度的关系，定量解释了随着两船间距离的不断减小，转向难度急剧增大、最小转向角急剧增大的原因，并通过著名学者S.Lenart的实例进行计算验证。

交通运输工程；两船距离；转向避让难度；最小转向角

航海上避免船舶碰撞通常采用转向避让、变速避让及二者相结合的方法，考虑到船舶主机性能及换车响应时间对船舶避碰的影响，在开阔水域，单凭转向往往是避免碰撞最为常用也最为有效的方式[1]。两船的会遇是一个从远到近、从没有碰撞危险到危险逐渐增加的过程，当判定两船存在碰撞危险且本船为《1972年国际海上避碰规则》中指明的让路船时，本船负有采取避碰行动以“使它船安全通过”的责任，且明确指出该避碰行动应是“及早的”，但并未对“及早”的原因给出一个定量的解释[2]。在参考著名学者S.Lenart最近会遇距离一定情况下，船舶航向和速度相互关系算法的基础上引入转向难度和最小转向角的概念，并推理出最终的计算结果，该计算结果对提高对碰撞危险的理解和转向避让措施的采取有一定的指导作用。

1 建模假设和定义

研究和推理过程中，本船和目标船均被假设为一个理想化的质点，本船仅采取转向避让且无时间延时，该转向避让行动对船舶速度无任何影响。

最小转向角Δφ：当目标船与本船形成碰撞危险后，本船通过转向能使与目标船在安全的距离上驶过的最小转向角度[3]。

不可转向角度θ：采取转向避让行动时，本船航向所不能转到的航向值的累积。不可转向角度越大，船舶可航行的航向越少；相反，则越大。

转向难度f(d)：反映了本船可以采取转向避碰行为的难易程度，与采取行动时两船的距离有关，其值为不可转向角度与圆周360°的比值。其值越大，说明阻挡角度越大，转向越困难；相反，转向越容易。

2 建模与方程推理

2.1 安全避让措施计算

以本船中心为坐标原点，以正北方向为y轴，以正东方向为x轴建立平面直角坐标系[4-6]。本船速度为Vo，航向为φ，目标船速度为Vt，目标船相对速度为Vr，它们之间存在式(1)、式(2)所示关系：

Vo+Vr=Vt

(1)

(2)

式中：Vox，Voy分别为本船速度矢量在x轴和y轴方向上的分量；Vtx，Vty分别为目标船的速度矢量在x轴和y轴方向的分量；Vrx，Vry分别为相对速度矢量在x轴和y轴的速度分量。

假设(X,Y)为目标船在坐标系上的位置坐标，(X0，Y0)为目标船的初始位置，有式(3)所示关系：

(3)

假设D(t)为本船和目标船之间的距离，则有

(4)

对D(t)求导，运算可得

(5)

Dmin即为本船与目标船的最近会遇距离(DCPA或CPA)，为了保证本船和目标船能够在安全的距离Ds上驶过，需使得Dmin≥Ds。

对式(4)进行平方

Dmin2(Vrx+Vry)2=(XVry-YVrx)2

(6)

整理得

Vrx=AVry

(7)

其中

(8)

由式(1)、式(2)、式(7)可得，

整理得：

Voy=AVox-B

(9)

B=AVtx-Vty

(10)

将速度关系转化为距离关系，式(10)两边同乘以一个时间单位Δt：

y=Ax-BΔt

(11)

影响碰撞危险的两个重要因素是最小会遇距离DCPA和会遇时间TCPA。TCPA<0时，本船和目标船渐行渐远，没有碰撞危险；只有DCPA0的情况才会存在碰撞危险。

如图1，式(11)所对应的直线为两船DCPA=Ds时，本船航向与航速之间的关系，两直线交点的左侧为TCPA<0时的情况，对本船航行安全无影响，是可以接受的安全范围；交点右侧为TCPA>0的情况，阴影部分区域为本船不能保证目标船以安全距离驶过的区域，只要本船的速度矢量的终端不落在该阴影区域，则可以保证两船以大于Ds的最小会遇距离相互驶过。

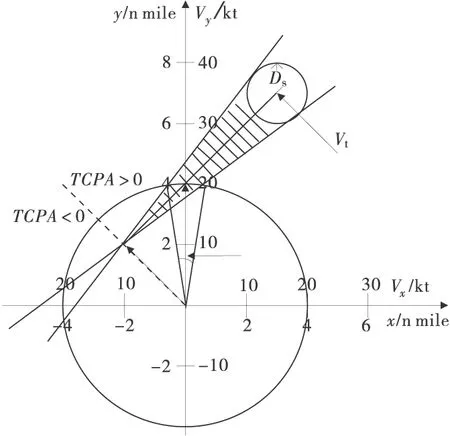
图1 θ与Δφ示意

2.2 转向难度计算

本船采取转向避让行动，可驶的速度矢量的末端为以本船中心为原点，以VoΔt为半径的一个圆，该圆与上述直线所围成的阴影部分相交，相交弧长部分为本船速度矢量所不能驶向的航向，即前面所定义的不可转向角度θ。对图1进行分析，圆的方程为：

x2+y2=(VoΔt)2

(12)

联立方程(11)、方程(12)，解得：

(13)

式(8)中A存在两个值，故B也存在对应的两个值，式(13)会有4个解，为(xi,yi) (i=1,2,3,4)，分别为式(11)所对应的两条直线与方程(12)所对应的圆的4个交点，其中两个交点在TCPA<0所在的区间内，对航行安全无影响，另外两个交点在TCPA>0的区间范围内，其两点间的圆弧正是文中所述的不可转向角度所对应的范围，依据弧长的计算公式(14)：

(14)

对应圆弧角度为：

(15)

θ即为本船的不可转向角度，本船航向可转向的角度范围为360～θ；根据定义，本船的转向难度由式(16)得出：

(16)

f(d)越大，表示本船的可转向范围越小，转向难度越大；f(d)越小，表示本船的可转向范围越大，转向难度越小。

2.3 最小转向角度计算

依据式(13)，求取在TCPA>0一侧的两个坐标值(x1,y1)和(x3,y3),依据避碰规则，两船互见中，不论是对遇局面还是交叉相遇局面，本船作为让路船都应该按照规则要求向右转向，则本船速度矢量终点右侧的那个坐标即为本船向右转向所应转到的位置点，其角度为新航向值，故最小转向角度Δφ可由式(17)求出[7-8]：

(17)

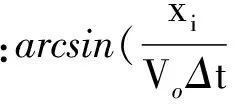
3 实例计算结果

以S.Lenart的一个实例进行计算。目标船相对本船的初始位置为(5nmile,5nmile)，本船和目标船的速度情况如表1。

表1 本船和目标船速度矢量

随着两船距离的不断接近，不可转向角度、最小转向角度和转向难度的计算结果如表2。

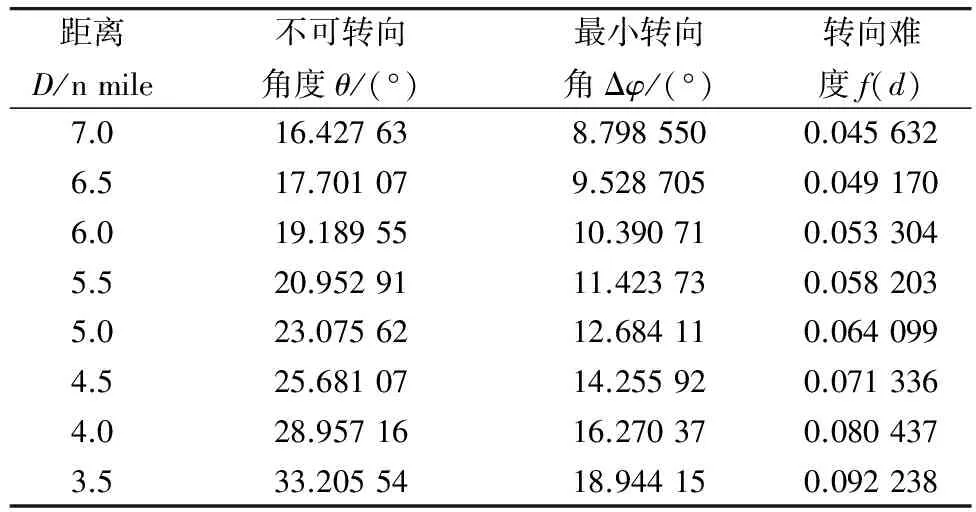
表2 θ，Δφ和f(d)的值

(续表2)

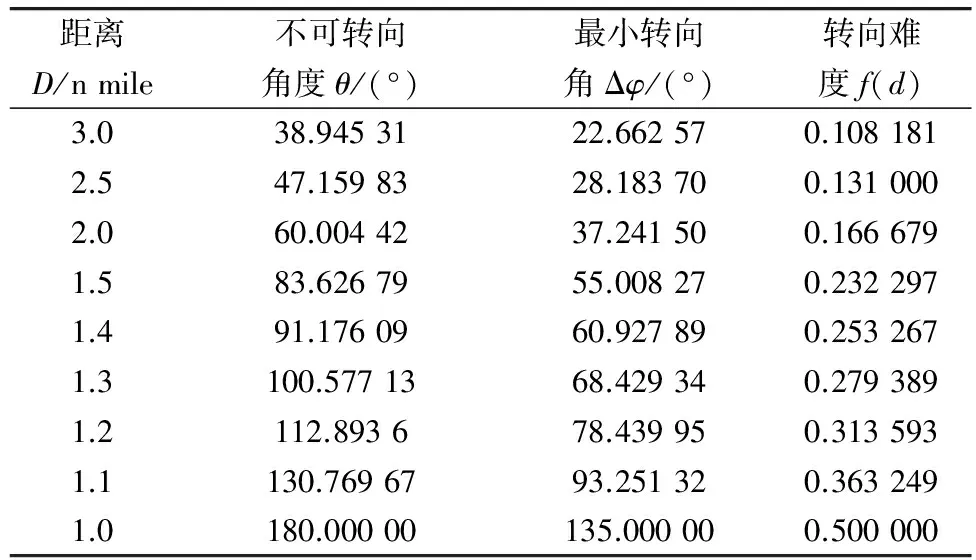
距离D/nmile不可转向角度θ/(°)最小转向角Δφ/(°)转向难度f(d)3．038．9453122．662570．1081812．547．1598328．183700．1310002．060．0044237．241500．1666791．583．6267955．008270．2322971．491．1760960．927890．2532671．3100．5771368．429340．2793891．2112．893678．439950．3135931．1130．7696793．251320．3632491．0180．00000135．000000．500000

4 结 语

从计算结果可以看出，在两船相距较远时，转向难度和最小转向角增长缓慢，基本呈线性增长状态；当两船距离接近到安全会遇距离的2倍以内时，转向难度和最小转向角呈指数级增长。航海中错过了较早的转向时机或发现目标太晚都会导致急迫局面的发生，且实际的航海过程中，由于舵的响应时间以及转向所带来的速降等原因，让路船应该更加“及早的”避让来船，确保两船在安全的距离上驶过。

[1] Lenart A S.Collision threat parameters for a new radar display and plot technique [J].Journal of Navigation,1983(36):404-410.

[2] 吴兆麟.船舶避碰与值班[M].大连:大连海事大学出版社,2008. Wu Zhaolin.Ships Collision Avoidance and Watch Keeping [M].Dalian:Dalian Maritime University,2008.

[3] Inoue K.Evaluation method of ship-handling difficulty for navigation in restricted and congested waterways [J].The Royal Institute of Navigation,2000,53(1):167-180.

[4] 毕修颖.船舶转向避让时机与行动确定及误差影响[J].广东海洋大学学报,2010,30(4):39-43. Bi Xiuying.Decision-making on alert course opportunity and action of ship’s collision avoidance and error effects on these results [J].Journal of Guangzhou Ocean University,2010,30(4):39-43.

[5] 赵劲松,王逢辰.船舶避碰学原理[M].大连:大连海事大学出版社,1999:342-351. Zhao Jinsong,Wang Fengchen.Principle of Ship Collision Avoidance [M].Dalian:Dalian Maritime University Press,1999:342-351.

[6] 毕修颖.船舶碰撞危险度及避碰决策模型的研究 [D].大连:大连海事大学,2000. Bi Xiuying.Study on Ship’s Collision Risk Index and Collision Avoidance Model [D].Dalian:Dalian Maritime University,2000.

[7] 洪碧光.船舶操纵[M].大连:大连海事大学出版社,2008:20-27. Hong Biguang.Ships Handling [M].Dalian:Dalian Maritime University Press,2008:20-27

[8] Pedersen E,Inoue K,Tsugane M.Simulator studies on a collision avoidance display that facilitates efficient and precise assessment of evasive manoeuvres in congested waterways [J].The Royal Institute of Navigation,2003,56(3):411-427.

Quantitative Relationship of the Distance between Ships and Difficulty to Avoid Collision by Altering Course

Liu Jia, Liu Chenglin, Wang Yanjie

(China Waterborne Transport Research Institute, Beijing 100088, China)

Altering course is the most common and effective method of collision avoidance, but the extent and effectiveness of altering course is significantly influenced by the time choice of avoidance. Starting from the ships’ maneuvering mathematics model, the difficulty to avoid collision by altering course and minimum alter angle were proposed and the corresponding mathematics model was established. Furthermore, the relationship between the distance between ships and the difficulty to avoid collision by altering course was deduced. The quantitative explanation why the difficulty of altering course and the minimum alter angle increased sharply with the decrease of the distance between ships was given. And the proposed point view is verified with the case study of famous scholar S.Lenart.

traffic and transportation engineering; distance between ships; difficulty to avoid collision by altering course; minimum alter angle

10.3969/j.issn.1674-0696.2015.04.27

2013-06-01；

2014-08-11

刘 佳(1983—)，女，黑龙江哈尔滨人，工程师，硕士，主要从事水运科学规划方面的研究。E-mail: liujia@wti.ac.cn。

U675.96

A

1674-0696(2015)04-140-03