多模式低副瓣阵列方向图综合方法

曾桂兰, 蒋彦雯, 范红旗, 冯一伦

(国防科技大学电子科学学院, 湖南 长沙 410073)

0 引 言

阵列天线是指按一定规律排布组成的许多天线单元[1]。与单个天线相比,阵列天线的方向性系数可以获得大幅提升;与抛物面天线等传统口径天线相比,阵列天线不需要通过机械转动就可以实现波束在空间内的扫描,在电子对抗系统与精确制导系统等领域得到广泛应用。复杂电磁空间博弈中,雷达导引头通常面临各种欺骗干扰[2]与环境因素的影响,特别是在对抗过程中,由于阵列天线通常具有较高的副瓣电平(sidelobe level, SLL),使得载体无法有效滤除敌方假信号干扰,且在尾追态势下目标信号被副瓣淹没导致无法发现目标,另外也增加了被截获和被反辐射导弹[3]袭击的可能性。低副瓣的阵列天线能够有效提高雷达天线抗干扰能力并降低其截获概率。因此,现代高科技战争中,阵列低副瓣方向图综合对精确制导武器系统的性能发挥有着至关重要的作用。

目前,阵列低副瓣方向图综合存在诸多研究问题,其基本优化方法大致可以分为以下两种,一是传统解析方法,如用切比雪夫多项式在特定主副瓣约束条件下求解阵列多项式系数的Dolph-Chebyshev综合法[4]和通过改造理想空间因子实现泰勒方向图的Taylor综合法[5]等。传统解析方法虽然速度较快,但只能处理一定范围内的简单问题,不适用于复杂问题。二是优化算法方法,如将低副瓣综合问题归纳成线性规划[6]、二次规划[7]、半定规划[8]等问题并利用凸优化函数进行求解的规划类方法以及用遗传算法(genetic algorithm, GA)[9-11]、差分进化算法[12]、粒子群优化(particle swarm optimization, PSO)算法[13]等求解低副瓣问题的智能优化算法。凸优化函数收敛速度快,但在解决复杂方向图赋形问题时由于约束条件过多可能会出现无解的情况,而智能优化方法利用进化算法几乎可以处理低副瓣方向图综合的所有问题,但时间复杂度高,容易陷入局部极值解。在低副瓣方向图综合的快速求解方面,文献[14-15]提出将傅里叶变换(Fourier transform, FT)用于阵列低副瓣方向图综合,使得通过快速FT(fast FT, FFT)计算求解合适的阵列加权矢量并实现低副瓣成为趋势。文献[16]用FFT反复计算加权矢量实现低副瓣;文献[17]基于FFT构造仅包含阵列副瓣均匀激励的方式实现低副瓣;文献[18]限制激励条件通过迭代FT实现低副瓣。以上算法和使用经典窗的线性加权算法抑制副瓣时均只在空间维进行,且基本都是在窄主瓣和低副瓣间做折中取舍而无法兼顾,其实现的低SLL有限,无法满足实际应用中对低副瓣的高要求。因此,在雷达阵列天线中,如何快速有效地求解加权矢量来实现高标准的低副瓣方向图,并同时保证最小化其方向性的弱化程度是天线阵列综合中的一个重要问题。

空时编码技术[19-20]最早在通信领域用来解决不同通道间互相干扰的问题,随后引进雷达领域,包括空间信道编码[21]和阵元脉冲编码[22-25]等,而阵元脉冲编码技术是对积累周期内多输入多输出(multi-input multi-output, MIMO)雷达不同发射天线辐射的不同脉冲初始相位分别进行编码[26],其不同发射阵元基带编码信号需满足彼此正交。本文针对均匀间距阵列天线的低副瓣综合问题,基于接收天线不同脉冲不同阵元的空时二维联合编码的加权矢量设计思路,提出了基于解析类方法思路的序贯FFT方法、约束方程计算方法和基于优化算法类的优化函数求解方法,分别从脉间副瓣相位调制、副瓣零点位置约束和目标函数约束SLL这3种不同的思路设计加权系数实现低副瓣。以上3种不同加权系数设计方法分别对应于不同脉冲间阵列加权矢量时变、不变和奇偶交替变的3种工作模式,并利用雷达系统进行多脉冲同向积累以实现低副瓣。文中首先分别对3种方法的低副瓣原理和方法步骤进行了简要概述;其次,通过仿真实验,利用方向图基本性能指标分析不同方法的优缺点及低副瓣性能,并研究随机幅相误差对各方法的低副瓣性能影响;最后,从抗干扰的应用需求出发,通过干扰抑制性能验证本文所提低副瓣方法在实际场景应用中的有效性。

1 基于加权矢量设计的低副瓣方向图综合方法

通过阵列加权矢量进行FFT能简单快速地实现方向图计算,对其加以特定的条件限制进行优化后能保证快速有效地综合低副瓣。因此,本文在对阵列加权矢量进行空时联合编码的优化设计框架下,首先利用方向图反相叠加可降低副瓣的原理,提出了加权矢量时变模式下的序贯FFT方法;其次,当脉冲数较少时,提出了基于加权矢量不变模式下的约束方程计算方法和基于加权矢量奇偶交替变模式下的优化函数求解方法,并对以上3种不同方法的低副瓣实现原理进行了理论分析。

1.1 序贯FFT方法

同幅同相的两个脉冲方向图进行相干叠加后其性能保持不变,而若对权矢量施加调制,使得前后两个脉冲的方向图主瓣同幅同相,副瓣同幅反相时,同向叠加后能得到抑制SLL的低副瓣方向图。在上述原理的基础上,提出了基于脉间相位调制的序贯FFT方法,通过多个脉冲间的副瓣反相叠加,从而获得低副瓣方向图。

设均匀线阵阵元数为N,阵元间距为d,波长为λ,假设其天线单元均为全向天线,则其远场方向图[27]可表示为

(1)

式中:u=sinθ,k为波数且k=2π/λ;a(n)为第n个阵列单元的加权系数,θ为远场方向和阵列法线之间的夹角。从式(1)中可以看出,等距线阵的阵列方向图F与阵列各单元加权系数组成的阵列加权矢量a=[a(0),a(1),…,a(N-1)]之间符合傅里叶变换对的形式,可利用FFT来实现加权矢量的快速方向图计算[28]。

方向图综合时,第i个脉冲信号的阵列加权矢量为ai,设过采样系数为M,加权矢量进行FFT运算后得到Fi:

(2)

令Fi中主瓣幅度和相位不变,其副瓣相位取反、幅度不变得到Fi+1:

(3)

式中:θ∈θML和θ∉θML分别表示位于方向图主瓣内的点和主瓣外的点。

取F=Fi+Fi+1,则

F(θ)θ∉θML=Fi(θ)+Fi+1(θ)= |Fi(θ)|ejargFi(θ)-|Fi(θ)|ejargFi(θ)=0

(4)

F(θ)θ∈θML=Fi(θ)+Fi+1(θ)= |Fi(θ)|ejargFi(θ)+|Fi(θ)|ejargFi(θ)=2Fi(θ)

(5)

同时,对Fi+1进行快速傅里叶逆变换(inverse FFT,IFFT)运算并截断后得到ai+1:

(6)

如式(5)所示,F同时实现了主瓣增益的扩大和SLL的抑制。因此,序贯FFT方法利用多脉冲间的连续副瓣反相,可最终获得超低副瓣的阵列方向图,算法流程如图1所示。

图1 序贯FFT方法流程图Fig.1 Flow chart of sequential FFT method

其具体计算步骤描述如下。

步骤 1初始化输入为长度N的阵列加权矢量ai(i=1);

步骤 2令过采样系数为M,阵列方向图Fi等于ai补零后再作M×N点FFT;

步骤 3令Fi的副瓣相位取反,主瓣不变,其相位变化矢量为

(7)

Fi+1=|Fi|ej(arg Fi+phase)

(8)

用式(8)得到Fi+1(M×N)后再进行IFFT,并对IFFT结果进行截断处理取前N点值组成ai+1;

步骤 4得到低副瓣方向图F=Fi+Fi+1,判断F的副瓣情况是否满足要求,若不满足,则令i=i+1,Fi=F,转至步骤3;

步骤 5若方向图F的峰值SLL(peak SLL, PSL)满足实际系统需求,则直接输出不同脉冲时刻得到的加权矢量组成的加权矩阵A=[a1,a2,…,ai+1]和低副瓣阵列方向图F,令p=i+1,则a为I×N维矩阵。

(9)

式中:n,l∈[0,N×M-1],且当n∈[N,N×M-1]时,ai(n)=0。

1.2 约束方程计算方法

当对方向图副瓣进行零点约束时,可有效降低选定零点及相邻区域的SLL。本节以副瓣零点建立约束方程,求解得到的阵列加权矢量可实现超低副瓣阵列方向图。

将式(1)写成近似于幂级数形式可得到:

(10)

式中:ω=exp(j2πdsinθ/λ)。

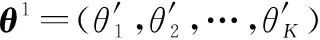
(11)

如式(11)所示,R和B中的第N行数据可以随意挑选位置,此行数据值能够保证约束a(0)=1,且当R奇异时,a=R-1B中使用伪逆。

约束方程计算方法流程图如图2所示,其具体流程如下所示。

步骤 3通过式(11)求出阵列加权矢量a,进而得到低副瓣阵列方向图F。

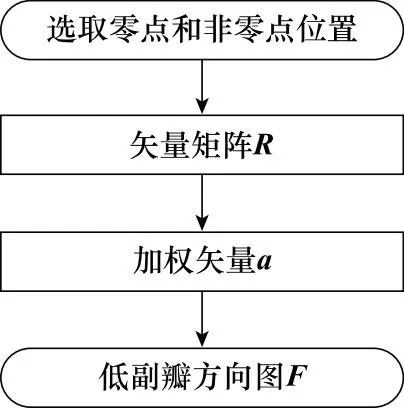
图2 约束方程计算方式流程图Fig.2 Flow chart of constraint equation calculation method

1.3 优化函数求解方法

优化函数求解方法实现低副瓣的关键在于设计恰当的目标函数和选用合适的优化算法,其中目标函数主要通过构造简单有效的约束公式来达到阵列方向图主瓣增强、副瓣抑制的目的。

常见的优化算法众多,运用范围最为广泛的主要是GA和PSO,PSO和GA都属于全局优化算法,且均属于随机搜索算法,通过随机优化算法更新种群和搜索最优点。已有研究表明,PSO相对于GA不需要进行编码,没有交叉和变异操作,且粒子只是通过内部速度进行更新,其原理更简单、参数更少、实现更容易。因此,本文选择PSO对目标函数进行求解。

文献[29]在研究副瓣消隐时采用GA实现了低副瓣方向图,本文进一步利用PSO在其基础上对目标函数进行优化,提出了基于加权矢量奇偶交替变模式下的优化函数求解方法,通过构造合适的阵列加权系数矢量ab(b∈{1,2}),从而计算得到所需低副瓣阵列方向图F。

本文提出的优化目标函数构建如下:

f=20×(10lgfG)+10lgfSLL

(12)

(13)

(14)

式中:Nθ是位于副瓣位置的总点数和。

目标函数f主要由利用加权系数矢量ab得到的阵列方向图Fb(θ)组成,并通过最大化目标函数f的值以得到ab的最优解。

式(13)求得F=[F1(θ)+F2(θ)]/2中位于主瓣内所有点的平方和,式(14)得到F位于副瓣所有点的2C次方和,通过最大化式(12)中目标函f能够保证式(13)尽量大和式(14)尽量小,从而得到压低副瓣,增强主瓣的低副瓣阵列方向图F。从式(14)中可以看出,参数C的选取对优化函数的求解及方向图性能优化结果至关重要。

2 低副瓣方向图仿真实验

本节中,假设阵列为一维均匀线阵,其阵元个数N=32,阵元间距d=λ/2,在统一的阵列模型下,分别从低副瓣性能和可变参数的取值影响对比分析3种方法的算法性能。

2.1 序贯FFT方法仿真结果与分析

在序贯FFT方法中,将阵列方向图过采样系数设置为M=10。在当i=1时,综合分析各窗函数性能特点,选取主瓣宽度较窄且SLL较低的汉明窗系数设置为a1:

(15)

式中:Q=0.54。

分别设置回波脉冲数为p=5和p=100,同向叠加后得到的阵列方向图如图3所示。

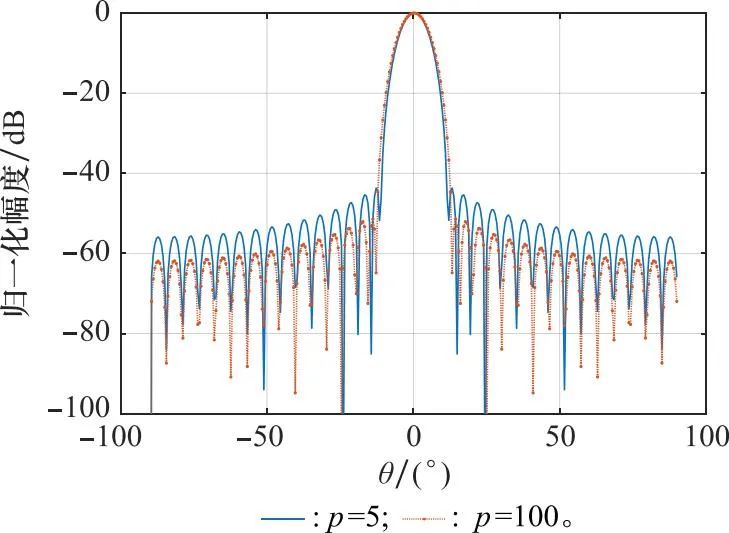
图3 不同积累脉冲数方向图综合结果Fig.3 Pattern synthesis results of different accumulated pulse numbers

图3表明,p=5和p=100均能实现低副瓣方向图,而p=100时其PSL低于-50 dB得到了超低副瓣,且相较于p=5时其副瓣平均电平明显下降,而主瓣宽度依然保持不变。

本文进一步分析了方向图性能受脉冲数变化的影响,利用PSL、副瓣平均电平、积分旁瓣比(integration sidelobe rate, ISLR)这几个典型指标对不同脉冲数下的方向图性能进行对比分析。令脉冲数p取1～100,在序贯FFT方法下得到各个脉冲数积累下的方向图性能指标和运行时长如图4所示。

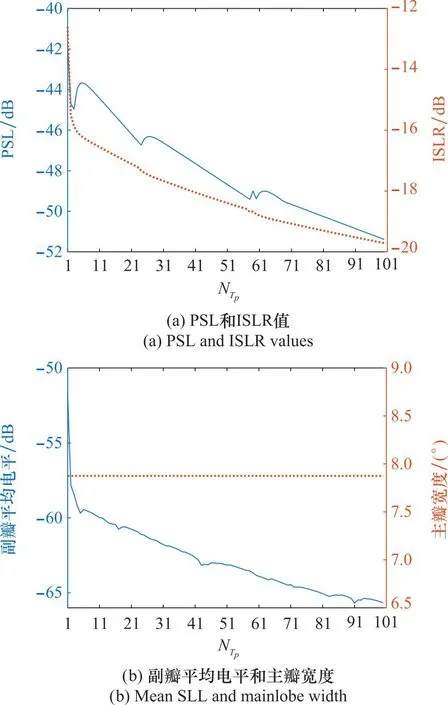
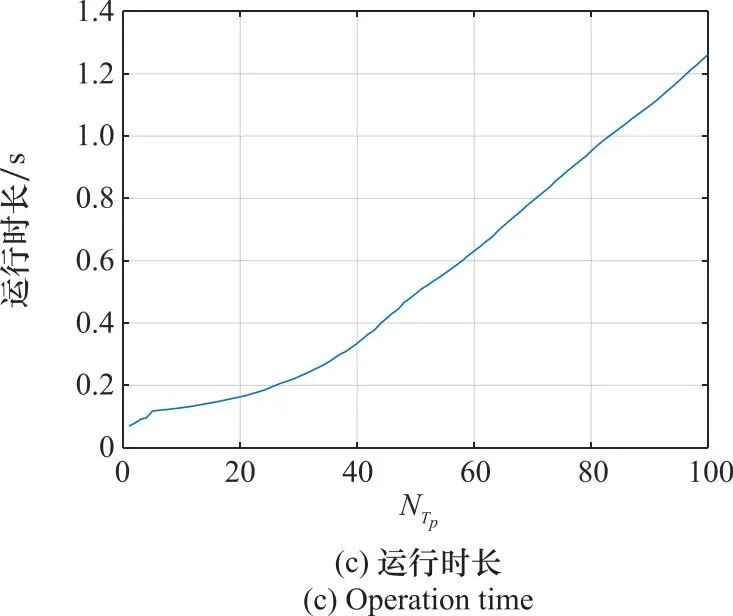
图4 各脉冲时刻方向图指标值和运行时长Fig.4 Index value and operation time of each pulse time pattern

从图4中可以看出,随着积累脉冲数不断增加,PSL和副瓣平均电平偶尔会出现随机抖动的现象,但从整体趋势来看,PSL、ISLR及副瓣平均电平均处于下降趋势,且副瓣平均电平始终保持在-50 dB以下,而主瓣宽度基本保持不变,说明序贯FFT方法既能有效降低副瓣,又能保证良好的主瓣性能,且积累脉冲数更多,获得的方向图副瓣更低。

从图4(c)中可以看出,随着脉冲数的增加,序贯FFT方法运行时长也稳步增加。而在实际应用中,针对固定阵列形式和确定的脉冲积累个数值p,可先离线计算好每一个脉冲时刻对应的阵列加权矢量组成矩阵A,当雷达系统在接收端进行数据采集时,在慢时间维上,可以利用加权矩阵逐行对各个脉冲接收信号进行调制,即接收处理同时进行,也可以先将p个脉冲信号全部接收存储后再统一调制,即先接收后处理。调制信号同向叠加后即可得到低副瓣方向图。因此,序贯FFT方法中在实际系统中也是可以高效运用的。

2.2 约束方程计算方法仿真结果与分析

从第1.2节中方法描述可知,约束方程计算方法得到的方向图性能与式(11)求解时零点的选取紧密相关。本文通过大量仿真实验,也发现在保证波形不发生畸变前提下,利用约束方程计算方法尽可能压低PSL以获得超低副瓣的关键在于零点位置的选取。以下面几种零点状态为例对所提方法进行性能分析:

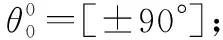
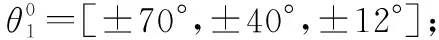
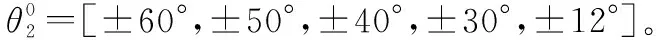
图5 不同零点约束下的阵列方向图Fig.5 Array patterns under different zero constraints

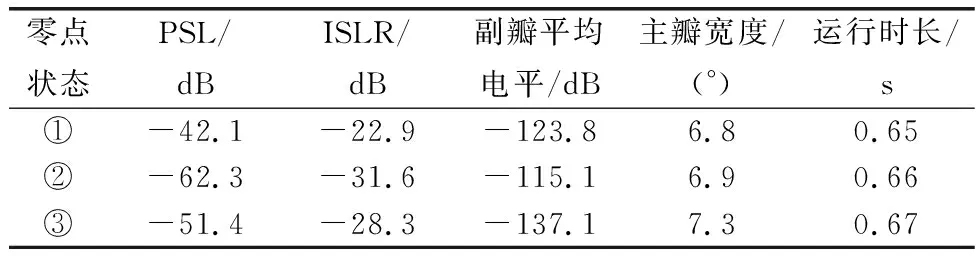
表1 不同零点约束下的阵列方向图性能对比Table 1 Comparison of array pattern performance under different zero constraints

从图5中还可以发现,第③种零点状态的PSL介于另外两种零点状态之间,但其SLL降低趋势最为明显,与表1相符,第③种零点状态具有最小的副瓣平均电平值。以上3种不同零点情况均获得了较好的低副瓣性能,方向图的PSL最高值为-42.1 dB,最低值为-62.3 dB,且两种情况下的主瓣宽度几乎不展宽,则其在降低副瓣的同时保持了良好的主瓣性能。

因此,在约束方程计算方法下得到的方向图,其低副瓣性能与零点位置的选取状态相关而与数量无直接关系。实际应用中,尝试多次零点取值状态以得到满足要求的低副瓣阵列方向图是此方法应用的前提。

2.3 优化函数求解方法仿真结果与分析

从式(14)中可以看出,C的取值会直接影响优化函数求解方法的性能,令C取1～20,分析不同C取值时各阵列方向图的典型性能指标和运行时长,结果如图6所示。

图6(a)和图6(b)表明,在同一阵列构型和参数下,当C的值达到9时,其方向图低副瓣性能基本达到了最优化,而随着C取值的进一步增大,方向图各指标参数变化趋势平稳,几乎不再发生显著变化。即当C大于9时,改变C的取值几乎不影响方向图的低副瓣性能,且其性能稳健后主瓣宽度一直保持为5°左右,数值较小,方向性性能较好。因此,在优化函数求解方法中,处于N=32的均匀一维线阵的阵列构型情况下,其目标函数中C的取值只需大于9即可。从图6(c)可以发现,C>5时方法的运行时长相较C值较小时显著增大,且当C>9后方法运行时长在175 s左右波动,数值较大。

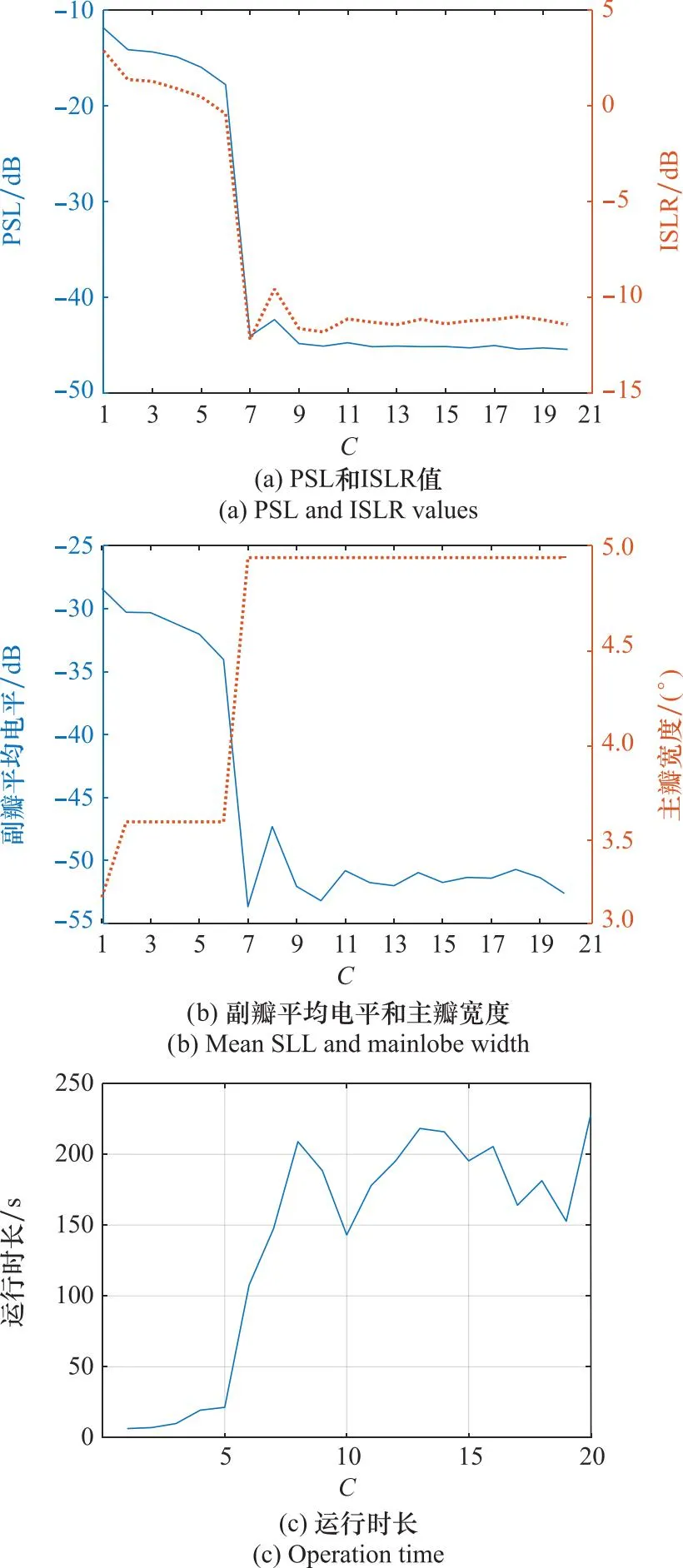
图6 不同C取值的各方向图指标值和运行时长Fig.6 Index value and operation time of each pattern obtained from different C values

为更直观地比较不同C值优化得到的方向图,C=2和C=9时的方向图优化结果如图7所示。图7表明,C=9时得到的方向图其PSL和副瓣平均电平远低于C=2的情况,结论与图6相对应。文献[29]中图3内与SLL相关的低副瓣方向图PSL大约为-18 dB左右,而文献[30]利用PSO达到的低副瓣方向图其最低,PSL大约只有-38 dB左右。本文提出的优化函数求解方法在C>9时,其性能稳定后显然具有更好的低副瓣性能。

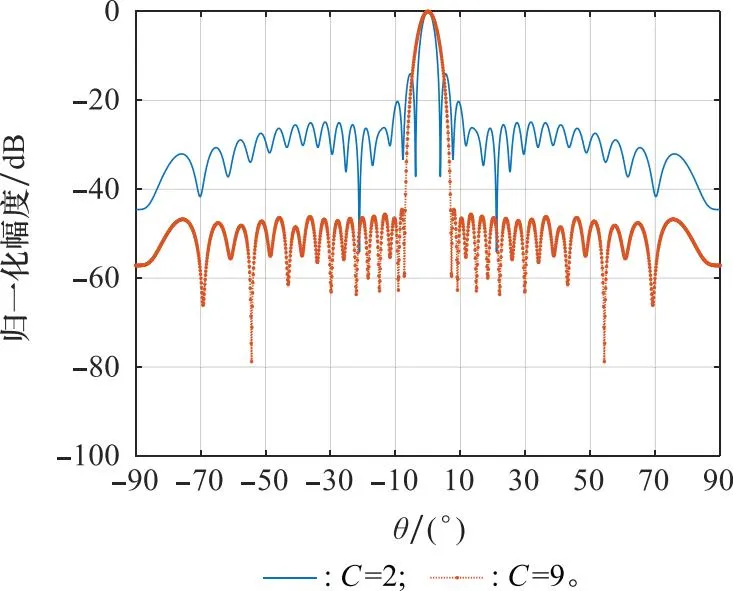
图7 不同C值时得到的低副瓣方向图Fig.7 Low sidelobe pattern obtained with different values of C

2.4 方法性能对比

为进一步综合对比分析本文所提不同方法的低副瓣性能,不同方法计算得到的方向图性能指标如表2所示。作为对比,本文同时计算了无调制和经典窗函数副瓣抑制方法下的方向图性能,其中无调制是指对阵列加权矢量不采取任何操作,窗函数副瓣抑制时采用汉明窗系数。表2表明,本文提出的3种方法降低副瓣的性能均优于直接加窗法,且在实现低副瓣的同时其主瓣展宽程度均小于直接加窗法,特别是约束零点法的主瓣展宽程度是上述方法中最小的,能够更好地保持良好的方向性。

本文3种不同方法各自的特点为:序贯FFT方法步骤较为繁琐,若需很低的副瓣时应进行多脉冲积累,而叠加的脉冲数越多,所需时间越长(当积累脉冲数p=54时所需时长约为0.68 s左右);约束方程计算方法步骤简单,但如何选取零点位置以得到满足要求的PSL需要进行多次实验仿真,其不同零点位置得到的方向图低副瓣性能具有不确定性和随机性;优化函数求解方法中可变参数和目标函数简单易懂,对方向性影响最小,而要得到最好的低副瓣结果需不断对目标函数中的未知参数C进行调整。

表2 不同方法得到的方向图性能比较Table 2 Comparison of pattern performance obtained by different methods

综上所述,以下是按照不同标准对各类方法进行性能评估的具体情况:

(1) 算法复杂度:序贯FFT方法(p≤p0)<约束方程计算方法<序贯FFT方法(p>p0)≪优化函数求解方法;(序贯FFT方法不同脉冲数下的运算时长不同,在本文中即当N=32时p0=54)

(2) 低副瓣性能:优化函数求解方法<序贯FFT方法<约束方程计算方法;

(3) 算法稳定性:约束方程计算方法<优化函数求解方法≪序贯FFT方法;

(4) 主瓣性能:序贯FFT方法<约束方程计算方法<优化函数求解方法。

因此,对于多脉冲低副瓣方向图综合,在脉冲数较多情况下,应优先选用序贯FFT方法,而在脉冲数较少的状态中应优先选择约束方程计算方法,若对方向性有较高要求的,可以优先考虑优化函数求解方法。

3 幅相误差影响分析与抗干扰应用

在低副瓣方向图综合中,常见的阵列位置误差、互耦误差等各种误差都可以归结为幅相误差。本节重点研究和探讨幅相误差对不同方法低副瓣性能的影响,并设计具体实验场景对本文所提方法的抗干扰性能进行验证,为实际阵列天线设计及本文方法适用性提供理论指导。本节仿真计算时,选用第2节中各方法实现性能最好的参数,即序贯FFT方法取p=100,约束方程计算方法零点状态取②,优化函数求解方法取C=9,从而避免不同方法参数选择的影响。

3.1 随机误差影响分析

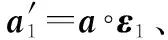
(16)

(17)

式中:∘为哈达玛积。

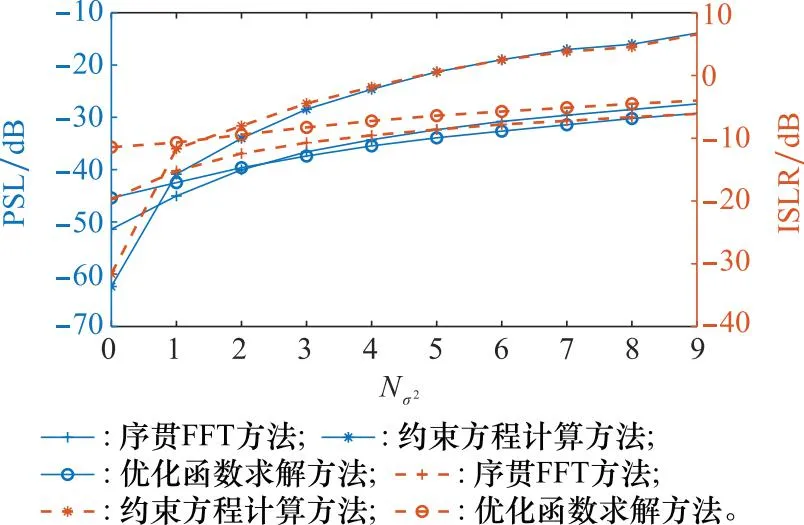
图8 幅相误差下不同方法的方向图PSL和ISLR值Fig.8 PSL and ISLR values of pattern for different methods under amplitude phase error

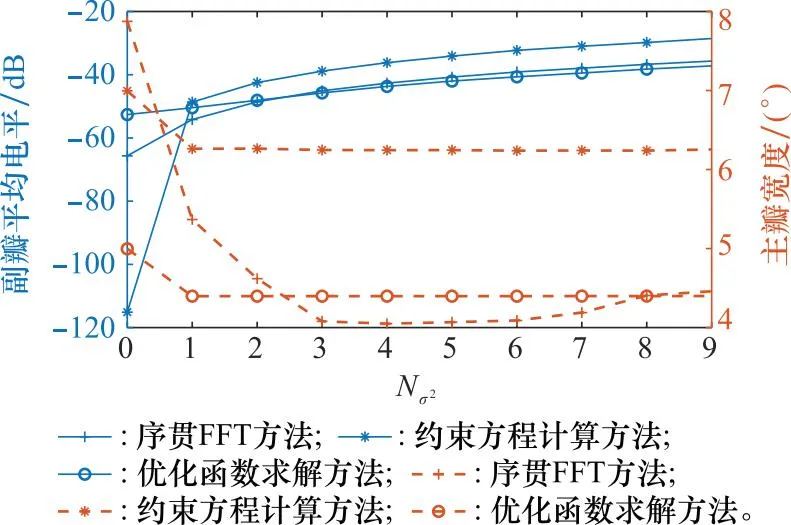
图9 幅相误差下不同方法的方向图副瓣平均电平和主瓣宽度值Fig.9 Mean SLL and width of mainlobe of pattern for different methods under amplitude phase error

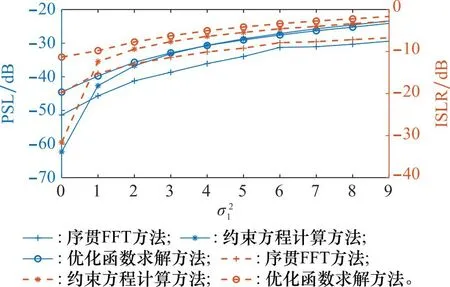
图10 相位误差下不同方法的方向图PSL和ISLR值Fig.10 PSL and ISLR values of pattern for different methods under phase error

图11 相位误差下不同方法的方向图副瓣平均电平和主瓣宽度值Fig.11 Mean SLL and width of mainlobe of pattern for different methods under phase error

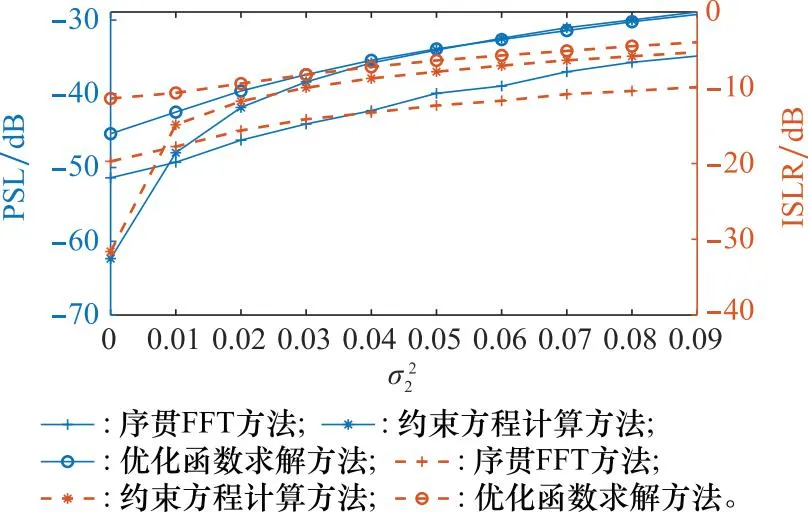
图12 幅度误差下不同方法的方向图PSL和ISLR值Fig.12 PSL and ISLR values of pattern for different methods under amplitude error

图13 幅度误差下不同方法的方向图副瓣平均电平和主瓣宽度值Fig.13 Mean SLL and width of mainlobe of pattern for different methods under amplitude error

无误差状态下,在低副瓣性能表现上,优化函数求解方法<序贯FFT方法<约束方程计算方法。从图8和图9中还可以发现,随机幅相误差存在后,低副瓣性能表现为约束方程计算方法<序贯FFT方法<优化函数求解方法。因此,随机幅相误差对不同方法的低副瓣性能影响为优化函数求解方法<序贯FFT方法≪约束方程计算方法。图8与图10以及图12中的PSL曲线变化大小进行对比分析可得,在本文幅相误差的取值大小中,对方法低副瓣性能影响较大的是幅度误差。

图10和图11表明,随着随机相位误差的变大,各方法的PSL、ISLR和副瓣平均电平值均逐渐增大,当相位误差较小时,方向图的低副瓣性能得以保留,当相位误差超过一定值后,各方法得到的方向图性能恶化导致低副瓣结果不理想。在图10中可以看到,随机相位误差对各方法的主瓣宽度影响微乎其微。

从图10和图11中可以看到,即使相位误差非常小,约束方程计算方法得到的方向图各指标相较于无相位误差时其数值上升比较大,而优化函数求解方法与序贯FFT方法的性能变化相较平缓。当相位误差存在时,各方法的低副瓣性能表现为约束方程计算方法≈优化函数求解方法<序贯FFT方法。因此,综合而言,随机相位误差对3种不同方法的低副瓣性能影响大小为优化函数求解方法≈序贯FFT方法≪约束方程计算方法。因此,在相位误差普遍存在的实际应用中可以优先考虑选用优化函数求解方法和序贯FFT方法。

从图12和图13中可以发现,各方法中与低副瓣性能相关的指标值随幅度误差的变换趋势与相位误差近似,且在本文相位误差和幅度误差的取值大小下进行比较,幅度误差对方法低副瓣性能的影响略大于相位误差。随机幅度误差对3种不同方法的低副瓣性能影响大小为优化函数求解方法≈序贯FFT方法≪约束方程计算方法。综上,在幅相误差普遍存在的实际应用中可以优先考虑选用优化函数求解方法。

3.2 抗干扰应用仿真实验

在强干扰状态下,假设雷达工作在毫米波频段,对接收端采集的基带信号进行仿真实验,设置各目标信号和干扰信号参数如表3所示,其中编号1和编号2是目标,编号3和编号4是干扰。

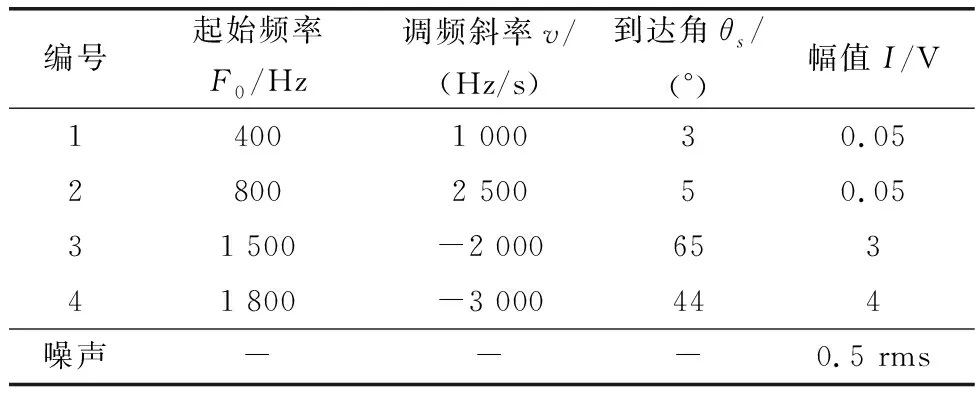
表3 目标和干扰信号参数Table 3 Target and jamming signal parameters

仿真时将采样频率设为fs=1 MHz,采样时间T=0.25 s,分别将本文所提3种阵列低副瓣综合方法得到加权矢量作用于雷达接收端,并对采集的基带回波信号进行时频分析,结果如图14所示。

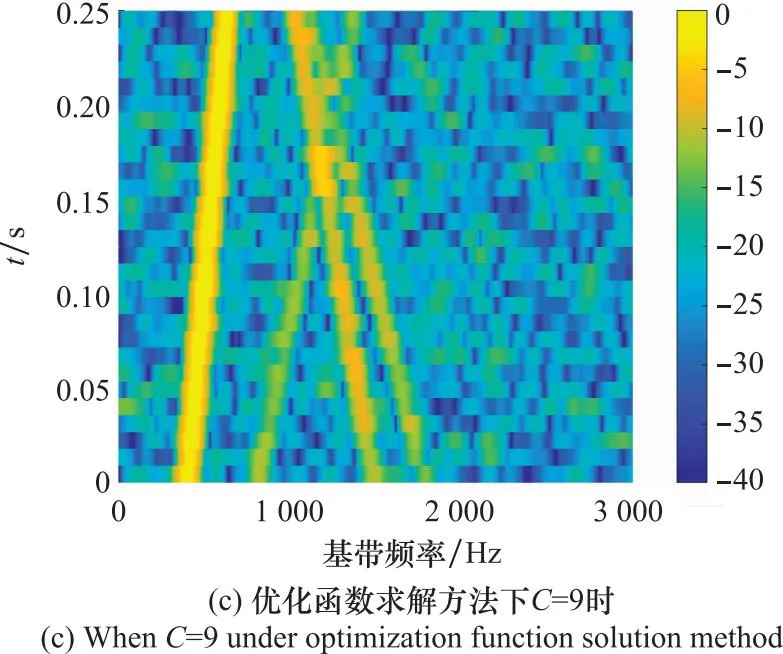
图14 不同方法下得到的回波信号时频图Fig.14 Time-frequency diagram of echo signal obtained by different methods

对比图14中不同方法得到的回波信号时频图,即使干扰信号幅值大于目标信号幅值,图14(a)和图14(b)中目标1、目标2的时频线清晰可见,而干扰目标3和目标4不可见,说明序贯FFT方法和约束方程计算方法均能完全抑制掉副瓣的干扰信号。

从图14(c)中来看,在副瓣强干扰条件下,目标2的时频曲线与干扰时频曲线发生交叉,使得无法直接从时频图上准确辨别出目标2的时频曲线。而目标1与干扰信号完全分开,时频图上则能清晰的分辨出其时频曲线,得到性能良好的目标1信号,也就是说虽然回波信号中副瓣干扰依然存在,但优化函数求解方法还是对副瓣干扰有一定的抑制作用。因此,即使在强干扰条件下,序贯FFT方法和约束方程计算方法下的模式仍能凭借方向图的低副瓣性能,实现有效获取目标信号抑制干扰的目的。

4 结 论

本文基于多脉冲低副瓣方向图综合提出了加权矢量时变模式下的序贯FFT方法、加权矢量不变模式下的约束方程计算方法以及加权矢量奇偶交替变模式下的优化函数求解方法。首先,对不同方法的低副瓣方向图性能指标进行了定量分析和评估,得出了不同方法的优缺点,其中序贯FFT方法各方面的性能表现较为突出。其次,从幅相误差对方法性能影响和抗干扰两个方面对所提方法进行了定性分析。结果表明,在本文误差大小取值下幅度误差对方法的低副瓣性能影响略大于相位误差。以上实验验证了3种不同方法均能实现低副瓣,且序贯FFT方法和约束方程计算方法下得到的方向图PSL均低于-50 dB,能够实现超低副瓣方向图综合。本文仿真分析为实际场景应用中不同方法的选取提供了理论参考,在提高雷达抗干扰能力和降低尾追目标影响等方面具有深刻意义。