基于随机风作用的直立锁边金属屋面系统损伤评估方法*

雷崇 周兵 刘文豪 陆怡雯 周臻

1.中铁第四勘察设计院集团有限公司 武汉 430063

2.东南大学混凝土及预应力混凝土结构教育部重点实验室 南京 210096

引言

金属屋面由于具有装饰效果好、质量轻、施工周期短等优点受到了建筑师的青睐，在火车站、机场、体育馆等获得了广泛的应用［1，2］。然而，直立锁边屋面系统因其高风敏感性，在强风作用下可能发生损伤甚至风揭破坏。因此，开展随机风作用下直立锁边金属屋面系统损伤评估具有重大意义。

目前，有大量关于直立锁边金属屋面系统抗风性能的研究成果。研究发现直立锁边屋面系统的破坏形式多为支座与屋面板在锁缝处的脱扣破坏［3，4］。此外，陈辉［5］和葛连福［6］揭示了直立锁边金属屋面系统的破坏机理，主要表现为屋面系统破坏始于屋面板跨中变形，随着跨中变形的增加，跨中板发生局部屈曲，然后沿着板宽度方向扩展，使得锁缝处的位移也由此产生突变，进而发生脱扣破坏。在金属屋面系统的易损性研究方面，目前主要包括三类损伤指标，包括锁缝变形［7，8］、屋面板应力和屋面板损伤参数［9，10］。在实际工程中，锁缝变形和屋面板应力两个指标要求必须提前确定屋面系统的破坏模式，以获得用于确定金属屋面系统损伤状态的具体结构响应。此外，实际工程中锁缝位移以及屋面板应力在风荷载作用下的响应难以获取，测量锁缝位移以及屋面板应力的方法操作性和实用性不强。屋面板损伤参数虽然计算公式简单，但不直观，不利于工程应用。

结合金属屋面系统的破坏机理，本文提出了基于跨中竖向变形的直立锁边金属屋面系统损伤评估方法。首先基于国内外大量的模型试验及数值模拟结果，给出直立锁边金属屋面系统的性能水准划分以及不同性能水准对应的破坏参数。其次，采用ABAQUS程序建立直立锁边金属屋面系统有限元模型，通过与已有试验数据进行比较，验证了有限元模型的准确性以及破坏参数的可靠性。然后，采用MATLAB软件模拟了随机风荷载并对其有效性进行了验证。根据某工程所在地的基本风压及典型区域的节点坐标，随机生成了11组风速时程曲线，并对每一块典型区域进行了非线性动力时程分析。最后，对典型区域的每一块金属屋面板的损伤程度进行了评估。

1 性能水准及指标量化

对直立锁边金属屋面系统进行风揭损伤评估，首先需要划分金属屋面系统的损伤等级。基于目前已有的研究成果［8］，本文将直立锁边金属屋面系统性能水准主要划分为4级，见表1。

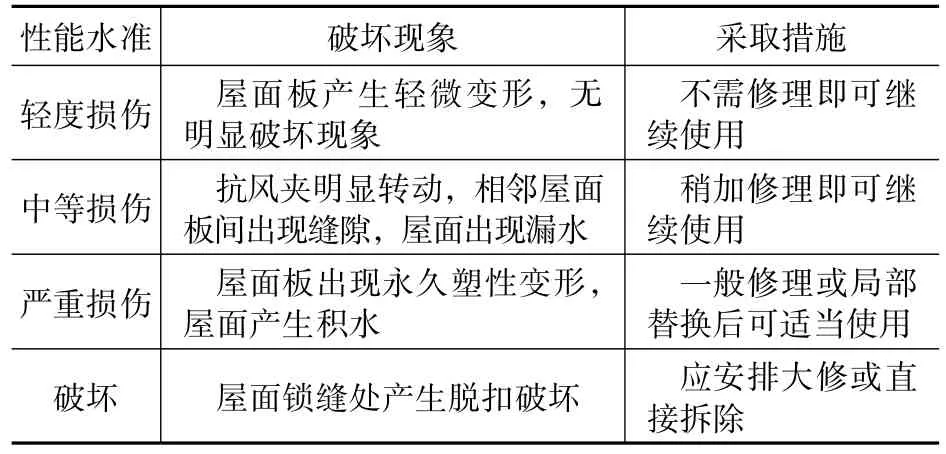
表1 直立锁边金属屋面系统性能水准划分Tab.1 Performance levels of standing seam roof systems

由于目前鲜见有关金属屋面系统风揭损伤评估的研究成果，本文结合已有的试验和数值模拟结果［9，10］，通过屋面板损伤参数β 的计算公式［9，10］反算得到了屋面板跨中竖向位移计算公式（1），然后经过统计分析与计算，综合考虑各研究成果，获得不同水准状态下对应的跨中竖向位移指标，见表2。

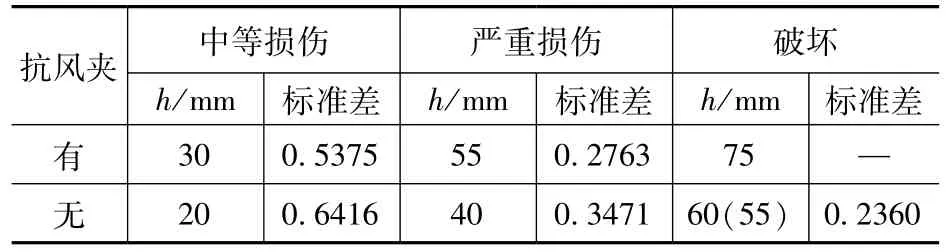
表2 不同性能水准对应的破坏参数Tab.2 Damage parameters corresponding to different performance levels

式中：S为支座间距；S0为模拟工况中最小的支座间距800mm；W为板宽（mm）；h为跨中竖向位移（mm）；α 为常数，考虑抗风夹的影响以及归一化因素，在有抗风夹时取5.38，无抗风夹时取6.79。

从表2 中可以看出，相比于屋面板损伤参数β，跨中竖向位移更加直观且易于获取，无需进行公式换算，观测结果可直接用于判断结构的损伤状态。因此，该指标工程适用性强且与现有规范结合紧密，合理且易于实施。

2 有限元模型

本研究采用ABAQUS有限元分析软件建立直立锁边金属屋面系统有限元模型，对其进行非线性分析。选取文献［11］中的一组典型试件进行模拟验证，试件的屋面板宽度为400mm，厚度为1.0mm，T形支座之间的间距为1500mm，T形支座的长度为60mm。通过与文献［11］中的试验数据进行比较，验证有限元模型的准确性以及破坏参数的可靠性。

2.1 有限元建模

建模时，金属屋面板采用壳单元，T 形支座采用实体单元。有限元模型的尺寸与试验试件的尺寸完全一致，如图1 所示。金属屋面板卷边网格尺寸为20mm，其他部位网格尺寸为50mm。T形支座顶端网格尺寸为5mm，其他部位网格尺寸为10mm。此外，金属屋面板的本构为双折线模型，其中材料屈服强度取195MPa，极限强度取240MPa，塑性应变取0.1。弹性模量取为70GPa，泊松比取为0.3，材料密度取为2.7 ×10-3g／mm3。T形支座采用线弹性模型，弹性模量为206GPa。模型部件之间采用面-面接触，法向为硬接触，接触后允许分离；切向可滑动，滑动摩擦系数取0.3［11，12］。为了尽可能与试验边界条件一致，T形码支座底部为固接。限制金属屋面板横向端部节点的三向自由度；在屋面板的纵向，一端为减小运算量设定沿xy面对称的边界条件，另一端限制y向位移。在荷载施加方面，对金属屋面板施加平行于板法向的压强。最后采用隐式动力求解器进行求解分析。

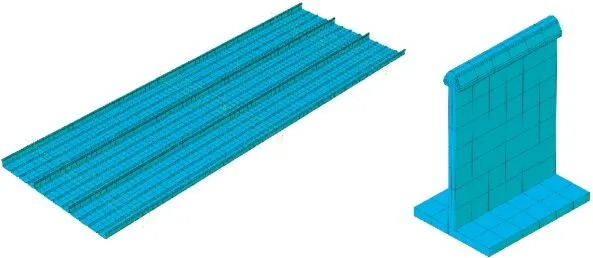
图1 有限元模型Fig.1 Finite element model

2.2 有限元模型验证

图2 给出试验和有限元模拟获得的金属屋面板的风压荷载-跨中竖向位移曲线。通过对比试验曲线和有限元曲线，发现两者之间的趋势保持一致。当风压荷载小于1.8kPa 时，由于有限元分析过程未考虑金属屋面板的初始缺陷以及采用的理想边界条件，导致有限元结果与试验结果存在一定的误差。由于试验过程中试件破坏现象较为严重，为了保障试验设备的安全，在变形达到一定程度后即拆除位移计，因此，位移计未记录完整的位移曲线。根据文献［11］，试验中试件破坏时的极限风压荷载为2.82kPa，而有限元模拟得到的极限风压荷载为2.85kPa，两者之间的误差小于5%。破坏模式与试验现象基本保持一致（见图3）。以上分析表明本文建立的有限元模型是准确的。此外，当跨中竖向位移大于20mm时，风压荷载超过1.0kPa，可认为试件已经发生中等损伤；当跨中竖向位移大于40mm 时，试件已经发生严重损伤；当试件破坏时，模拟得到的跨中竖向位移为59.36mm，小于破坏阶段允许的最大竖向位移，这表明试件破坏时的损伤取值偏不安全。为了使损伤评估结果偏保守，本文破坏阶段对应的跨中竖向位移取55mm。

图2 荷载-位移曲线比较Fig.2 Comparison of load-displacement curves

图3 破坏模式验证Fig.3 Failure mode validation

3 脉动风荷载的模拟

脉动风周期较短，并且会随时间和位置进行变化，因此可认为其是一种零均值平稳高斯随机作用［13］。为了考虑风荷载不确定性因素的影响，采用MATLAB软件编写谐波叠加法程序模拟脉动风，选择Davenport 谱作为风速谱，采用此方法模拟出的各点脉动风速表达式如式（2）所示：

式中：N为频率采样点数；j为模拟点标号；Δω ＝（ωu-ω1）／N为频率增量；ωu和ω1为截止频率的上限和下限；φkl为0 ～2π范围内满足均匀分布的随机变数，相互独立且与时间无关；Hjk（ωk）可通过S（ω）＝H（ω）H·T（ω）求得，S（ω）为目标功率谱函数矩阵；θjk（ωk）＝arctan［ImHjk（ωk）／ReHjk（ωk）］为2 个不同作用点之间的相位角。

以V10＝29.66m／s 为例，地面粗糙度系数k＝0.008，频率区间取为0 ～3Hz，频率采样点数取为1024，时间间隔取0.1172s，模拟时间为120s。结构在高度3.6m 处模拟的脉动风速时程曲线如图4 所示。

图4 脉动风速时程曲线Fig.4 Fluctuating wind speed time history curve

为了验证风速模拟的有效性，比较了风速时程的模拟谱和目标谱，如图5 所示。由图可知，目标谱与模拟谱之间吻合良好，这说明本文模拟出的脉动风是有效的，即脉动风的模拟程序是可靠的。

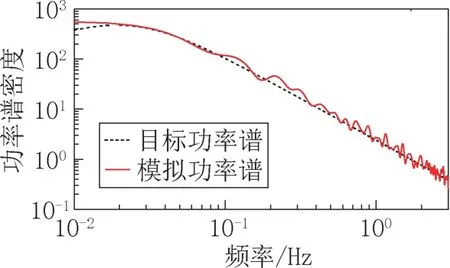
图5 模拟谱与目标谱比较Fig.5 Comparison of simulated and target spectra

针对金属屋面系统，将每一个坐标节点输入到脉动风场程序中，获得对应的风速时程曲线。每块金属屋面板有4 个角点，网格划分后会生成大量的节点，其中也包括4 个角点，如果将每块板的每一个节点对应的风速转化为风压然后施加在金属屋面系统上，必然会导致计算效率低下，不利于工程应用。为了简化有限元分析过程并提高分析效率，本研究选取金属屋面板模型4 个角点对应的风速时程曲线，并进一步得到屋面板的平均风速时程曲线，最后通过公式（3）求出相应节点的风压时程曲线。

式中：vl为i节点处的平均风速；vl（t）为i节点处的脉动风速。

4 金属屋面系统损伤评估

4.1 工程概况

本文选取东莞市城市轨道交通1 号线一期工程道滘站中某一横截面的直立锁边金属屋面系统进行损伤评估。如图6 所示，该工程的金属屋面板采用的是铝镁锰板，面板厚度为1.0mm。车站总跨度为19.80m，车站屋面标高为22.635m。

图6 结构立面Fig.6 Structural elevation

本工程所处区域抗震设防烈度为7 度，地面粗糙度为B 类，基本风压为0.55kPa。阵风系数为1.619，风压高度变化系数为1.278，构件突出区域的体型系数为-2。由于屋面板两侧是对称结构，为了简化建模及提高分析效率，将直立锁边金属屋面系统划分为3 块典型区域，针对每一块典型区域随机生成11 条风速时程曲线并将其转化为风压荷载，分别对这3 块区域进行建模分析与评估。最后，对每一块金属屋面板的损伤程度进行了评估。

4.2 评估流程

参考建筑抗震韧性评价标准［14］，本文给出了基于随机风作用下的直立锁边金属屋面系统损伤评估流程，如图7 所示。

4.3 非线性动力时程分析

图8 给出了3 组典型区域跨中板的竖向位移时程曲线。从图中可以看出，不同区域跨中板的动力响应有明显差异。在最大基本风压荷载作用下，金属屋面板跨中竖向位移均超过了20mm，即发生了中度损伤破坏。此外，不同区域最大损伤量以及对应的时间均有明显区别。为了便于后续开展金属屋面板损伤评估，提取所有工况下金属屋面板的跨中最大竖向位移。

图8 典型区域跨中动力响应Fig.8 Dynamic response for mid-span of typical areas

4.4 损伤评估

图9给出了典型区域在随机风作用下直立锁边金属屋面系统的损伤评估结果。从图中可以看出同一区域的不同位置处金属屋面板损伤评估结果具有明显的差异。在最大基本风压荷载作用下，各个区域均会发生不同程度的损伤，其中有50%以上的概率发生中等损伤，30%以上的概率发生轻度损伤，而发生严重损伤或破坏的概率均不超过10%。基于典型区域损伤评估结果，可以大概判定整个车站金属屋面系统在最大基本风压作用下发生中等损伤破坏的概率在50%左右，发生轻度破坏的概率在30%左右，而发生严重损伤或破坏的概率较小，这表明该工程屋面系统的设计是安全合理的。此外，根据计算结果绘制了直立锁边金属屋面系统的易损性曲线。从图10 中可以看出随着金属屋面板跨中竖向位移的增加，屋面板发生破坏的超越概率急剧增大。当破坏位移超过不同性能水准中位值时，超越概率约为100%。这表明本文提出的直立锁边金属屋面系统性能水准及量化指标是可靠的，同时也验证了本文提出的损伤评估方法的合理性。

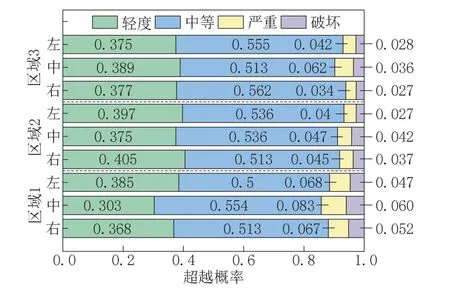
图9 典型区域损伤评估结果Fig.9 Typical regional damage evaluation results

图10 易损性曲线Fig.10 Fragility curves

5 结语

本文确定了直立锁边屋面系统性能水准及量化指标，提出了基于随机风作用下直立锁边金属屋面系统损伤评估方法，选取某实际工程案例典型区域进行了非线性动力时程分析，确定了金属屋面系统在最大基本风压作用下的损伤等级。对比评估结果可知本文提出的损伤评估方法具有较好的合理性和可靠性，为今后类似工程提供了参考。