多剑杆织机锁边机构设计及送纱叉优化
2022-05-09杨建成王慧勇何浩浩刘家辰
杨建成,王慧勇,何浩浩,刘家辰
(1.天津工业大学机械工程学院,天津 300387;2.天津工业大学 天津市现代机电装备技术重点实验室,天津 300387;3.天津工业大学天津市机械基础及纺织装备设计虚拟仿真实验教学中心,天津 300387)
由三维机织物形成的复合材料因其增强体结构中存在贯穿厚度方向的纱线,具有优异的整体性,克服了传统二维机织复合材料层间强度低、易分层等缺点[1-2],被广泛应用于航空航天、交通运输、矿山机械等重要领域[3-4]。
带芯剑杆织机是专门织造用于制作输送带骨架的多层立体织物的新型设备。国外的先进设备大多采用绞边原理来锁边,Promatex公司的天马织机,使用直线电机驱动电子绞边装置,所形成的布边抗拉强度小,且有一定的毛边[5]。天津工业大学成功研制了能够织造30层的立体织机[6]],但是其复合材料对于布边没有要求,故对锁边机构没有研究;刘健等[7]根据钩针锁边的原理,设计了多剑杆织机的针织边纱套圈锁边机构,但没有对锁边机构进行可靠性分析;董红坤等[8]利用携纱器上下移动穿过纬纱三角区来对多层织物进行锁边,其锁边线的长度受到一定的限制。
本文主要针对五剑杆织机的锁边机构进行研究,针对五剑杆同时引纬,设计了五钩针纬纱圈嵌套互锁工艺,以形成光整坚固且具有一定抗拉强度的布边。创新设计了新型锁边机构,并利用ANSYS Workbench对其关键部件送纱叉的刚度及强度进行有限元分析[9-11],基于响应面法[12-18]对送纱叉的结构参数进行优化设计,并对各参数进行敏感性分析,基于六西格玛分析法对送纱叉进行可靠性分析[19-20],使送纱叉达到增强刚度的优化目的,使锁边机构具有一定的可靠性,以解决现有带芯织机的缺陷,为五剑杆织机等多剑杆织机锁边机构的创新设计及可靠性分析提供借鉴与参考。
1 新型锁边工艺设计
针对五剑杆织机所织造的五层织物,设计了新型五钩针纬纱圈嵌套互锁工艺,如图1所示。

图1 五钩针纬纱圈嵌套互锁工艺示意图Fig.1 Schematic diagram of nested interlocking process of five crochet weft loops
五钩针纬纱圈嵌套互锁工艺是在织造过程中,由5根剑杆1次引5根纬纱,在每次引纬后利用5根锁边钩针,分别将同一层的纬纱圈嵌套形成互锁,每引纬一次完成一个循环。该工艺每一层的纬纱圈都进行互锁,在长度方向上有较大的抗拉强度;层与层之间通过经纱交织来进行连接,可以保证织物的强度。此锁边工艺所形成的布边坚固光整,与织物的厚度一致,且提高了织造效率。
对于五剑杆织机来说,其引纬时5根剑杆同时引纬,在布边的一侧就有5个纬纱圈需要锁紧,且需要保证纬纱圈在织物织口锁紧时与形成的织物厚度一致,纬纱圈在引纬时与在织口锁紧时的高度差就成为锁边的一大难点,以及将纬纱圈传送到织口处也是一个难点。具体布边截面示意图如图2所示。其中:m为剑杆与织口之间的距离;n为五剑杆的最大高度差;s为织物厚度。

图2 布边截面示意图Fig.2 Schematic diagram of selvage section
针对五钩针纬纱圈嵌套互锁工艺,制定锁边方案的原理,如图3所示。

图3 锁边方案的原理示意图Fig.3 Schematic diagram of locking scheme
整个锁边过程由5个送纱叉将纬纱传递至织口,并将5根纬纱圈的高度差降低,由5钩针将纬纱圈进行嵌套互锁,完成锁边。
2 锁边机构设计
根据上述锁边原理对锁边机构进行创新设计,图4为锁边机构简图。该锁边机构一共由3部分组成:传递机构、钩针机构、脱纱机构。这3部分分别实现不同的功能,相互配合共同完成锁边。

图4 锁边机构简图Fig.4 Schematic diagram of locking mechanism
传递机构主要解决五剑杆引纬过后5个纬纱圈之间的高度差从大变小,并且将纬纱圈向织口方向传递的问题。该机构也是整个锁边机构中最大的创新之处,本研究利用传递气缸以及直线滑轨来实现纬纱传送;利用伺服电机、具有双旋向的丝杠及一个移动方套来完成纬纱合拢。
钩针机构将5个纬纱圈分别在同一层织口处进行圈套圈互锁。该机构主要利用四连杆的原理,利用气缸使钩针进行往复运动,从而使纬纱圈进行圈套圈的锁紧。
脱纱机构将纬纱圈从送纱叉脱落到钩针上,继而完成锁边,该机构主要由一个“L”形杆和气缸组成。
整个锁边机构先利用传递机构将纬纱圈从送纬剑杆上脱下,并缩小纬纱之间的高度差,同时向织口方向传送,到达一定位置后,由脱纱杆将纬纱圈从送纱叉上脱到钩针内,最后由钩针往复运动完成锁边。整个系统由PLC控制,配合精准。
3 锁边机构的优化及可靠性分析
3.1 基于响应面法的送纱叉优化设计
本锁边机构通过3个机构相互配合来完成锁边,关键机构是传递机构与钩针机构。传递机构中,送纱叉是其可靠完成锁边的关键部件,在高速运行过程中,相邻2个钩针之间的距离为3 mm,为了能够交接准确,须使得送纱叉的最大变形不超过0.5 mm。
基于响应面分析法对关键部件送纱叉进行参数优化,以送纱叉杆长度L1、固定部分长度L2及固定部分直径D1为变量,以质量及最大变形为优化目标,优化变量的取值如表1所示,送纱叉的结构如图5所示。

表1 优化变量取值范围Tab.1 Optimize range of variable values
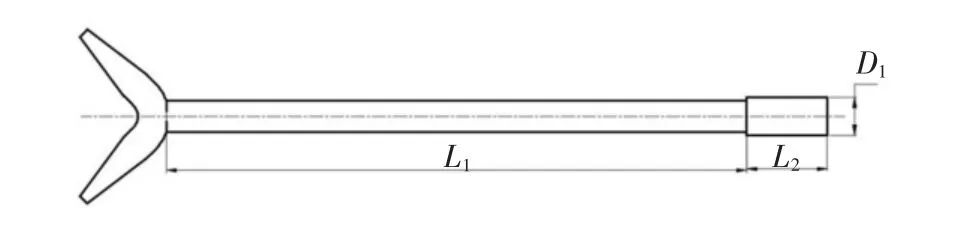
图5 送纱叉结构示意图Fig.5 Structure diagram of yarn feeding fork
先对送纱叉进行静应力分析,在实际工作中,送纱叉头部受到纬纱施加的压力约为2 N。故在ANSYS Workbench中,在进行静力学分析时,对送纱叉尾部固定约束,在头部施加纬纱对叉头的压力,方向在水平方向且与送纱叉杆成45°。送纱叉材料为轴承钢,材料属性如表2所示。

表2 送纱叉材料属性Tab.2 Material properties of yarn feeding fork
通过ANSYS分析得到送纱叉应力与变形的分布云图,如图6所示。由图6可以看出,送纱叉的最大应力为34.423 MPa,位于送纱叉的固定部分与杆连接处。此送纱叉采用轴承钢制造,轴承钢的许用应力为700 MPa,远远大于送纱叉所受应力的最大值。最大变形为0.510 2 mm,位于送纱叉头部,故需优化此最大变形量。

图6 送纱叉的应力与位移分布Fig.6 Distribution of stress and displacement of yarn feeding fork
在ANSYS Workbench软件中基于响应面法进行分析,得出的全局敏感性分析结果如图7所示。由图7可以得出,各个参数对于目标的影响各不相同。送纱叉最大变形对于各个参数的敏感性程度从大到小可以排列为P3(L1)>P2(D1)>P1(L2);最大应力对于各个参数的敏感性程度从大到小可以排列为P2(D1)>P3(L1)>P1(L2);送纱叉质量对于各个参数的敏感性程度,从大到小可以排列为P3(L1)>P2(D1)>P1(L2)。为判断拟合出的响应面结果的可信度,进行拟合度分析,图8为拟合度符合性分布图。

图7 全局敏感性分析Fig.7 Global sensitivity analysis

图8 拟合度符合性分布Fig.8 Distribution of conformity of fit
表3为拟合度评价值。由图8及表3可以看出,拟合出的响应面结果是可信的。

表3 拟合度评价结果Tab.3 Evaluation results of fitting degree
结合敏感性分析结果看,重点关注L1和D1对送纱叉最大变形、最大应力及质量的响应曲面,如图9—图11所示。

图9 最大变形量的响应曲面Fig.9 Response surface of maximum deformation

图11 质量的响应曲面Fig.11 Response surface of mass
由图9可以看出,L1、D1和送纱叉的最大变形为线性正相关,随着L1和D1的增大,送纱叉的最大变形量也相应增大。由图10可以看出,随着L1的增大,送纱叉所受最大应力增大;随着D1的增大,送纱叉所受最大应力值减小。由图11可以看出,L1、D1和送纱叉的质量为线性负相关。

图10 最大应力的响应曲面Fig.10 Response surface of maximum stress
送纱叉优化前后的变量对比如表4所示。

表4 送纱叉优化前后的变量对比Tab.4 Comparison of variables before and after optimization of yarn feeding fork
由表4可以看出,设计变量以及目标函数值都有了相应的变化。优化后送纱叉的最大变形为0.453 1 mm,减小了11.2%;最大应力为31.722 MPa,减小了7.8%;质量为0.001 633 9 kg,减小了0.08%。
3.2 基于六西格玛法的送纱叉可靠性分析
分析送纱叉最大变形在小于0.5 mm情况下的可靠性,根据分析结果,该送纱叉最大变形的累积分布函数如图12所示,其中的曲线为送纱叉最大变形的累积分布函数曲线。

图12 送纱叉最大变形的累积分布函数Fig.12 Cumulative distribution function of maximum deformation of yarn feeding fork
由图12可以看出,进行1 000次抽样后,输出变量的分布柱状图没有出现较大的间隙和跳跃,符合累积函数抽样条件。在上述分析中,送纱叉的最大变形在0.5 mm以内,在参数概率表中插入0.5 mm,分析结果如表5所示。由表5可以看出,抽样分析得出的送纱叉最大变形小于0.5 mm的样本数为96.1%,即送纱叉的最大变形小于0.5 mm的可靠度为96.1%,安全可靠。
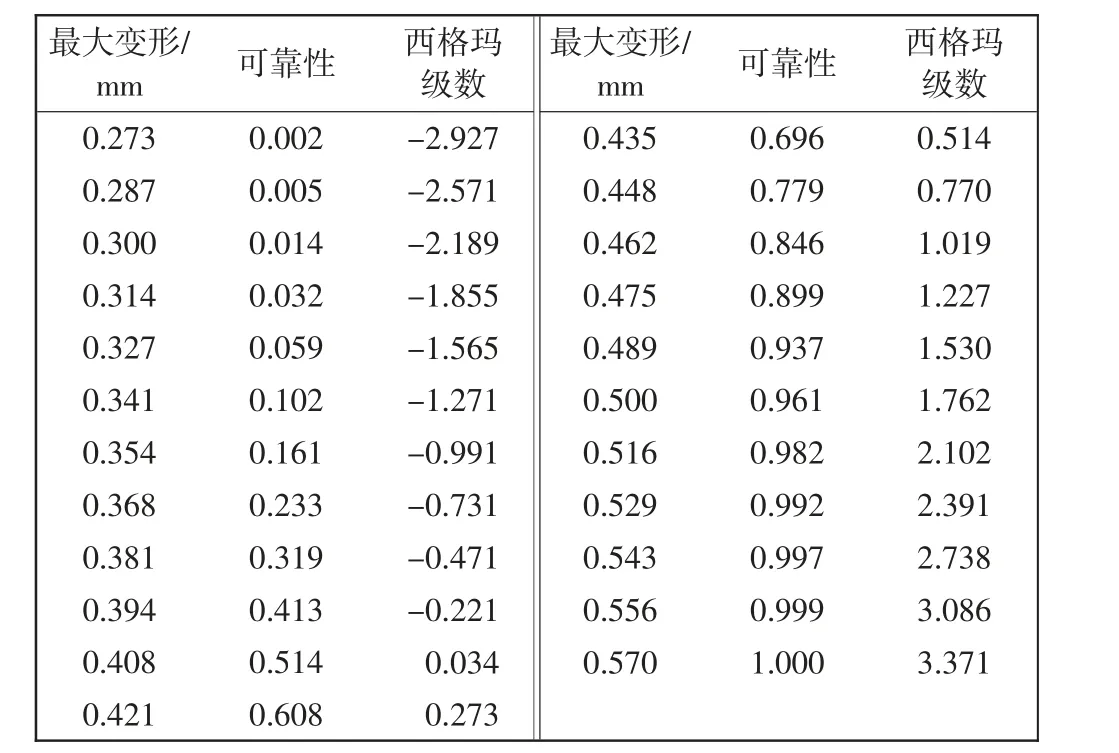
表5 参数概率列表Tab.5 List of parameter probability
4 结论
(1)本文设计了新型五钩针纬纱圈嵌套互锁的新型锁边工艺,织物每层上的纬纱圈都进行了互锁,使得布边光整且具有较大的抗拉强度;同时,针对此锁边工艺设计了新型锁边机构,攻克了5个纬纱圈从五剑杆所在位置的高度距离缩小至织物厚度的距离,并传送至织口进行锁边的难点。
(2)通过响应面法及敏感性分析发现,送纱叉杆长L1对送纱叉最大变形的敏感度最高,且与送纱叉最大变形成线性正相关;送纱叉杆长L1和固定部分直径D1对送纱叉的最大应力的敏感度最高,随着L1的增大,所受最大应力增大,随着D1的增大,所受最大应力值减小。
(3)与原方案相比较,优化方案的最大变形减小了11.2%,最大应力减小了7.8%,质量也减轻了0.08%,达到了增强送纱叉刚度、强度及减轻质量的目的。
(4)基于六西格玛法的可靠性分析得出,送纱叉最大变形小于0.5 mm的可靠度达到96.1%,可以保证剑杆与送纱叉的交接配合及送纱叉在后续动作中的可靠性,完成对多层立体织物的锁边。
