预制地下管廊内连续管道的纵向抗震分析

王长祥 李东桥 梁建文 黄宇昊 柳晓科

1.中国市政工程华北设计研究总院有限公司 天津300074

2.天津大学建筑工程学院 300350

引言

地下综合管廊是城市地下管道综合走廊，将电力、通信、燃气、供热、给排水等各种工程管线集于一体，实施统一规划、统一设计、统一建设和管理，是保障城市运行的重要基础设施和“生命线”。有关学者对地下预制管廊及其廊内管道的横向地震作用进行了分析，认为管廊-管道整体系统与管道自身、管廊廊体自身的自振频率和模态具有明显差别［1］，在地震作用下综合管廊和管廊内管道的动力影响存在明显差异［2，3］，为此，一些学者考虑了管道支墩对管廊及廊内管道的抗震影响［4，5］。

上述研究针对整体现浇式管廊及其廊内管道的横向抗震研究居多，且大多采用二维模型，而预制管廊由于其分节处管道连续，其纵向抗震分析为三维问题，因此既有研究结果难以直接用于预制管廊的抗震研究。另外，由于地下综合管廊还处在初步发展阶段，管廊内管道的抗震设计还没有相应的抗震设计规范，且针对预制管廊内连续性管道的抗震分析较为少见。因此在地震作用下，管廊与其内部管道之间的相互影响、管廊内管道的抗震设计等问题亟待解决。

本文基于ABAQUS通用有限元平台，建立三维土-管廊-管道系统相互作用模型，进行管廊内管道纵向抗震分析，求解不同地震波入射角度下管廊-焊接钢管体系的地震响应，为管廊内管道的纵向抗震设计提供参考依据。

1 管廊内管道纵向抗震分析三维模型

1.1 抗震分析方法

对于地下结构的纵向抗震设计，《地下结构抗震设计标准》（GB／T 51336—2018）［6］建议采用弹性地基梁模型模拟地下结构，沿地下结构纵向的地层变形假定为正弦形式分布，并将相应位置的地层变形输入到地基弹簧的非结构端，进行拟静力分析，如图1 所示。

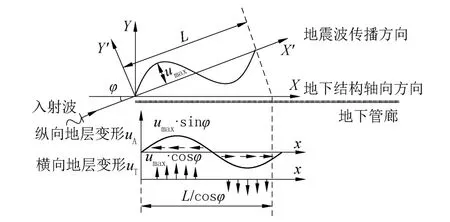
图1 地下结构纵向抗震分析模型Fig.1 Longitudinal seismic analysis model of underground structure

地层变形按式（1）、式（2）计算：

式中：uA（x）和uT（x）分别为纵向地层变形和横向地层变形；φ 为入射波与地下结构纵轴的夹角；umax为地震作用下场地变形峰值；L为地层变形波长；x为地下结构轴向位置。

本文将传统梁-弹簧模型拓展为三维实体-弹簧模型，考虑了综合管廊工程内部支墩和管道的实际工程构造，可比较全面地反映地震作用下综合管廊系统的变形及内力响应。

1.2 土-管廊-管道系统有限元模型

1.模型概况

采用ABAQUS有限元软件建立计算模型，研究对象为预制单舱管廊及其内部焊接钢管体系。廊体横断面为矩形截面，横向总宽度4050mm，高4050mm，顶板和侧板厚400mm，底板厚450mm。管廊埋深3m，预制管廊节段长2m，标准段间由承插口连接。廊内敷设管径为DN800 的焊接钢管给水管道，管道钢材等级为Q345。管道下部采用120°滑动支墩，支墩上抱箍钢材等级为Q235。管道底部距离底板500mm，轴线距离侧板1000mm。钢管支墩均匀布设，间距为6.0m，管廊及支墩的计算尺寸如图2 所示。

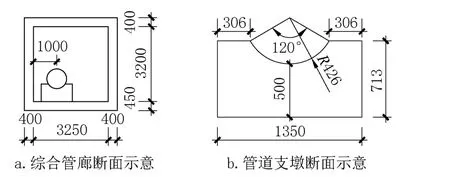
图2 管廊及内部支墩Fig.2 Utility tunnel and internal buttress

2.建模方法及模型参数

为反映该管廊工程中管廊廊体和焊接钢管的实际构造，以及管廊内部支墩的偏心布设方式，本文采用实体单元C3D8R 模拟管廊混凝土结构及管道下部支墩，单元大小取0.4m × 0.4m ×0.5m；采用S4R 壳单元模拟焊接钢管，单元大小约为0.2m ×0.2m。焊接钢管的横向运动由支墩及抱箍进行约束，纵向运动则通过管道与橡胶垫板之间的摩擦进行约束。采用ABAQUS中罚函数模拟管道与支墩橡胶垫的接触行为，切向摩擦系数取为0.5。为考虑管道中流体对计算结果的影响，将管道中流体的质量进行折算后以附加质量形式施加于到管道质量上，预制管廊及其内部焊接钢管布置如图3 所示。

图3 管廊及其内部焊接钢管布置Fig.3 The utility tunnel and internal pipe

对于计算模型尺度，参照《地下结构抗震设计标准》［6］，本文中管廊及其内部焊接钢管体系计算模型取3 个地层变形波长（3L≈1599m）。

模型中材料参数如表1 所示。

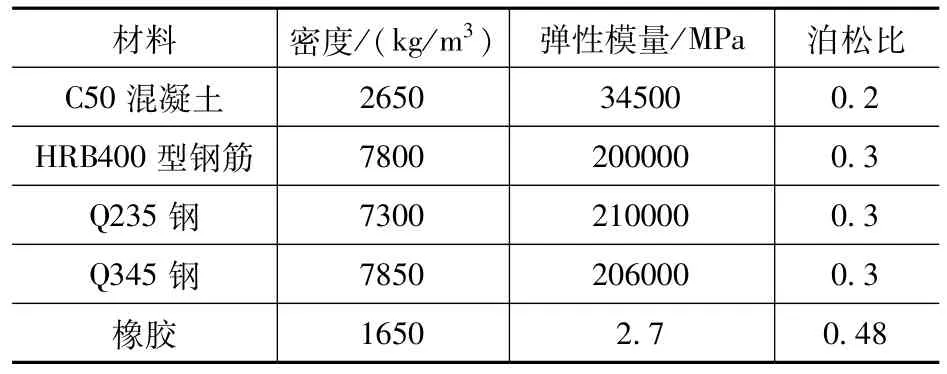
表1 模型本构参数Tab.1 Model intrinsic parameters

考虑混凝土的塑性损伤，采用混凝土塑性损伤模型（又称CDP 模型），CDP 模型参数取自文献［7］，如表2 所示。

表2 CDP模型参数Tab.2 Model parameters of CDP

1.3 场地参数与设计地震动

《地下结构抗震设计标准》［6］建议由一维地震反应分析确定土层位移。本文中综合管廊系统处于水平层状场地，故选用一维地震反应分析程序EERA［8］计算土层地震响应。土层参数、土体动模量和阻尼比与剪应变之间关系参见文献［9］，设计地震加速度时程如图4 所示，峰值加速度0.38g。

图4 设计地震加速度时程Fig.4 History curve of earthquake acceleration

1.4 管廊企口接头弹簧刚度

管廊节段间相互作用包括止水橡胶和混凝土的受压和受剪作用，以及钢绞线在腋角处施加的抗拉作用。管廊接头受压弹簧的力-位移曲线如图5 所示，为双线性模型［9］。

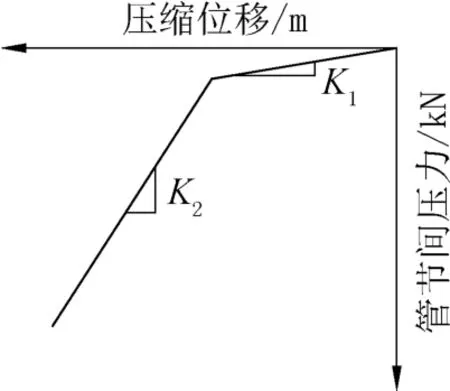
图5 管节间刚度Fig.5 Pipe joint stiffness

根据模型网格划分，管节间橡胶板面积为0.4m×0.4m，厚0.01m。橡胶垫压缩模量E1为2.71MPa，混凝土压缩模量E2为34.5GPa，可计算得到K1＝4.336×104kN／m和K2＝5.52×108kN／m。

管廊接头抗拉刚度由预应力钢绞线承担，钢绞线有效截面积为140mm2，可计算得到腋角处受拉弹簧刚度K3＝2.474 × 104kN／m 和K4＝4.438 ×102kN／m。

对于预应力的施加，采用修改连接节点间弹簧刚度系数方法达到模拟预应力的效果，即通过调整受压弹簧和受拉弹簧的力-位移关系曲线来进行模拟［9］。

1.5 地基弹簧刚度

通过EERA计算得到土体动剪切模量G，进而换算得到土体动弹性模量。根据每组弹簧所处位置取相应的土体动弹性模量，得到地基弹簧法向及切向刚度［1］。

2 管廊-焊接钢管体系抗震计算分析

2.1 廊内钢管应力分析

计算不同地震波入射角度下管廊-焊接钢管体系的地震响应，其内部焊接钢管的Mises 应力峰值与入射角度的关系如图6 所示。可以看到，随着地震波入射角度的增大，管廊内部焊接钢管的Mises应力峰值先减小后增大，在入射角0°时达到峰值。

图6 不同入射角度下廊内管道的Mises 应力峰值Fig.6 Peak Mises stress of pipe in utility tunnel at different incident angles

2.2 廊内钢管内力分析

图7 给出了不同地震波入射角度下，综合管廊内焊接钢管的轴力、剪力和弯矩沿管道轴向的分布。

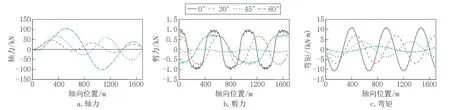
图7 不同入射角度下管道内力分布Fig.7 Distribution stress of pipe at different incidence angles

可以看到，不同地震波入射角度下，管廊内部焊接钢管的各类内力沿轴向均呈现出标准的正弦形式分布，其中，轴力和弯矩的分布形式较为圆滑，而剪力曲线在峰值处出现一定波动，这是由于地震作用下，预制管廊标准节段间的相互错动导致。随着地震波入射角度的增大，焊接钢管的轴力逐渐增大，在入射角60°时达到峰值104.433kN；而剪力峰值呈现出先减小后增大的趋势，入射角45°时最小，入射角0°时达到峰值1.014kN；随入射角度增大，管道的弯矩峰值逐渐减小，入射角0°时弯矩达到峰值10.891kN·m。

2.3 廊内钢管的抗震验算

《室外给水排水和燃气热力工程抗震设计规范》（GB 50032—2003）［10］中规定，设防地震作用下埋地焊接钢管的允许拉应变标准值［εat，k］为0.01，允许压应变标准值［εac，k］可按式（3）计算：

式中：tp为管壁厚度；D1为钢管的外径。

为了验算本文中管廊内焊接钢管的变形是否满足抗震要求，表3 验算了安评波大震作用下，不同入射角度下管廊-焊接钢管体系中焊接钢管的地震应变值。

表3 不同入射角度下管廊-焊接钢管体系抗震验算Tab.3 Seismic testing of utility tunnel-pipe at different incidence angles

可以看到，不同地震波入射角度下，焊接钢管的最大拉应变为6.296 ×10-5，最大压应变为8.661 ×10-5，远小于《室外给水排水和燃气热力工程抗震设计规范》［10］规定的允许拉应变标准值0.01 与允许压应变标准值4.99 ×10-3（忽略地震作用分项系数1.20 和抗震调整系数0.90）。因此，安评波大震作用下，管廊-焊接钢管体系中钢管的应变满足抗震设计规范要求并具有较大的裕度。

3 结论

1.随着地震波入射角度的增大，管廊内焊接钢管的轴力逐渐增大，在入射角60°时达到峰值。而钢管剪力峰值随入射角增大呈现出先减小后增大的趋势，入射角45°时最小，入射角0°时达到峰值。管道的弯矩峰值随地震波入射角增大逐渐减小，入射角0°时弯矩达到峰值。

2.管廊内焊接钢管为连续管道，其结构刚度沿纵向一致，在纵向地震作用下地层变形时，支墩抱箍将与钢管间出现一定的摩擦滑移。