双柱悬索拉线塔风致倒塌易损性分析

李正良，张智航，王涛

(1.重庆大学 土木工程学院，重庆，400045；2.重庆大学 风工程及风资源利用重庆市重点实验室，重庆，400045；3.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨，150040；4.哈尔滨工业大学 重庆研究院，重庆，401151)

随着我国经济社会的发展，电力在国民经济建设中占据了越来越重要的地位。我国西北沙漠地区能源丰富，是我国重要的能源基地[1]，随着西电东送项目的逐步实施，经过新疆等大片戈壁荒漠区域的特高压输电线路逐渐增多。双柱悬索拉线塔具有结构简单、节约材料、造价低廉等优点，因而常被应用于戈壁、沙漠等空旷开阔的平地，目前其已在我国西北地区得到了广泛应用。

与传统自立式输电塔相比[2-3]，目前国内外对双柱悬索拉线塔的研究相对较少。在确定性分析方面，KEMPNER等[4]研究了拉线式悬索塔的动力特性，发现在高频区域拉线塔趋向于出现“子导线震荡”现象；BEHNCKE等[5]对双柱悬索拉线塔的设计、施工和运行过程进行了阐述，总结了双柱悬索拉线塔相较于自立式输电塔的优缺点；李正良等[6-7]开展了双柱悬索拉线塔体系气动弹性模型风洞试验，发现0°、45°、60°风向角为双柱悬索拉线塔结构工程设计的最不利工况，改变拉线初张力对塔线体系的受力性能影响显著；肖正直等[8]基于广义变分和应变能相等原理将双柱悬索拉线塔简化为等截面压杆，根据压杆稳定理论得到了立柱计算长度系数μ与初始预拉力和风速之间的关系。而在概率分析方面，XIAO等[9]将其所建立的风速风向联合分布模型与矩方法相结合，求解得到了双柱悬索拉线塔的可靠指标，对极限破坏状态下双柱悬索拉线塔的失效概率进行了评估。值得注意的是，获取不同风速下双柱悬索拉线塔发生倒塌破坏的条件概率一方面可用于强风区的风致灾害预测，为设计人员有针对性地提高结构的抗风能力提供参考；另一方面，可用于风致灾害评估，为后续风灾损失统计提供依据。而通过易损性分析可以建立风荷载和双柱悬索拉线塔倒塌破坏概率之间的关系，得到结构在不同风速下的失效概率，因此，开展双柱悬索拉线塔的风致倒塌易损性评估亦具有重要的工程价值。

目前国内外学者对传统输电塔的风灾易损性已进行了一定研究。CAI等[10]基于拉丁超立方抽样和塔架非线性静力分析结果建立了输电塔的承载力曲面，采用Kriging替代模型结合蒙特卡罗模拟得到了输电塔的易损性曲线。TIAN等[11]考虑了风荷载的不确定性，基于ABAQUS建立了某输电塔的有限元模型并对其进行了增量动力分析，随后对结构进行了易损性分析。李宏男等[12]提出了一种基于深度学习模型的风致易损性评估框架，以某输电塔为例进行了分析，结果表明该框架能更高效地进行输电网系统的风致易损性评估。然而，上述研究者均是对传统自立式输电塔的风灾易损性进行分析，而本文所研究的双柱悬索拉线塔是一种高柔性的混合悬索结构，结构的整体刚度与拉线密切相关，并且在风荷载作用下结构表现出了不同于传统输电塔的风力特性[13]。目前研究者对双柱悬索拉线塔在强风作用下的易损性分析较少。

鉴于此，本文以±800 kV哈密—郑州直流输电线路中某双柱悬索拉线塔为研究对象建立有限元模型，研究结构材料参数等不确定性因素对双柱悬索拉线塔抗风承载力的影响，在此基础上，采用对数正态分布函数对结构的倒塌临界风速和顶点位移进行拟合，得到双柱悬索拉线塔的倒塌易损性曲线，进而研究风向角和拉线初张力等因素对结构倒塌易损性曲线的影响，以期为强风作用下双柱悬索拉线塔的倒塌及损失评估提供参考。

1 双柱悬索拉线塔有限元模型

双柱悬索拉线塔由格构式立柱、拉线、钢索、悬索、绝缘子及导、地线组成，如图1所示。格构式立柱为结构主体，其主材和缀材分别采用Q345和Q235等边角钢制成，各构件的几何物理属性如表1所示。

图1 双柱悬索拉线塔示意图Fig.1 Schematic diagram of double column suspended guyed tower

本文基于ANSYS有限元软件建立上述双柱悬索拉线塔有限元模型。由于角钢构件整体受力状况较为复杂，故采用七节点自由度的梁单元BEAM188模拟格构式立柱杆件。结构中拉线、悬索、钢索和绝缘子等构件则均可视为索类结构，基于索单元特性，分别选用杆单元LINK8和LINK10对拉线和剩余构件建模。立柱和4根拉线底部均采用固定约束，同时将拉线等构件与立柱柱顶对应位置进行耦合，拉线的初张力取为其设计承载力的16%。对于导、地线，由于在对结构进行非线性静力推覆分析时无需考虑输电塔和导地线之间的动力耦合效应，因此，可将导、地线荷载简化为作用在对应挂点处的外力荷载。此外，为准确模拟钢材在强风作用下可能出现的大变形，本文采用双线性随动强化模型来模拟钢材的本构关系。

最终建立的双柱悬索拉线塔有限元模型共计598个节点和1 116个单元。其中梁单元930个，杆单元186个。对所建立的双柱悬索拉线塔有限元模型采用分块兰索斯法进行模态分析，获得绝缘子振动、拉线绝缘子耦合振动及左侧立柱扭转等双柱悬索拉线塔的典型模态振型，如图2所示。

图2 双柱悬索拉线塔典型模态振型Fig.2 Typical vibration patterns of double column suspended guyed tower

2 考虑结构不确定性的双柱悬索拉线塔风致倒塌易损性分析方法

2.1 双柱悬索拉线塔结构不确定性参数选取

本文选取双柱悬索拉线塔中立柱和拉线的屈服强度、弹性模量、泊松比等作为结构的随机变量。分别根据JCSS规范[14]和参考文献[15-16]得到立柱中钢材屈服强度fy_Q235和fy_Q345、弹性模量E和泊松比ν以及拉线屈服强度fs和弹性模量Es的概率统计参数，如表2所示。

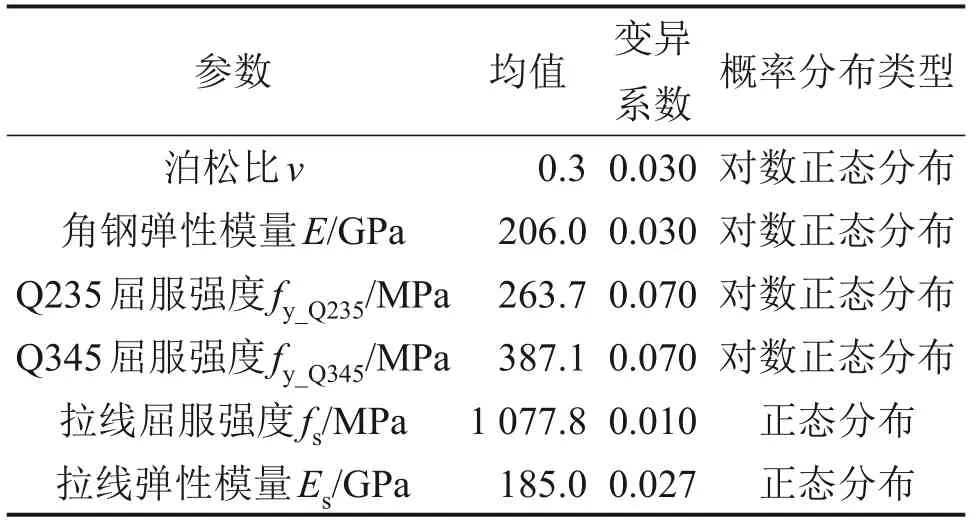
表2 材料参数的概率分布Table 2 Probability distribution of the random material parameters

2.2 双柱悬索拉线塔风荷载计算

在一定高度范围内，大气边界层平均风速剖面可近似用指数率V(z)表示：

式中：vr表示10 m标准高度处的平均风速；z和zr分别为高度和标准高度；a为不同地貌下的地面粗糙度指数，本文按B类地貌计算取为0.15。

塔身和导地线的风荷载根据DL/T 5154—2012《架空输电线路杆塔结构设计技术规定》[17]分别按照式(2)和式(3)计算。

式中：Ws为风向与双柱悬索拉线塔立柱垂直时杆塔风荷载标准值；W0为基准风压标准值；μz为风压高度变化系数；μs为构件体型系数；B2为杆塔构件覆冰风荷载增大系数；As为迎风面构件投影面积；βz为杆塔风荷载调整系数；Wx为垂直于导、地线方向的水平风荷载标准值；a1为风压不均匀系数；μsc为导、地线的体型系数；βc为导、地线的风荷载调整系数；d为导、地线的外径；Lp为杆塔的水平档距；B1为导、地线的覆冰风荷载增大系数；θ为风向与导、地线之间的夹角，参数的具体取值详见上述规范。

2.3 双柱悬索拉线塔风致倒塌易损性分析框架

2.3.1 双柱悬索拉线塔风致倒塌易损性分析理论

双柱悬索拉线塔风致倒塌易损性是指结构在给定风荷载作用下发生倒塌破坏的条件概率，可采用式(4)表示。

式中：C表示结构整体处于倒塌破坏状态；Pf为当风荷载强度参数SIM取值为sim时双柱悬索拉线塔发生倒塌的条件概率。

由式(4)可知，对双柱悬索拉线塔进行风致倒塌易损性分析需要对结构的风致响应和倒塌准则进行分析。由于索类结构的存在，相较于计算复杂耗时的增量动力分析(IDA)而言，采用非线性静力推覆分析(Pushover)求解双柱悬索拉线塔的结构响应更为高效。

利用LHS抽样将双柱悬索拉线塔有限元模型与表2中不确定性参数相结合生成n个结构样本；不断调整风速，结合式(1)～(3)对每个结构样本进行非线性静力推覆分析即可得到各样本的Pushover曲线。以确定性有限元模型为例，可得到双柱悬索拉线塔的Pushover曲线，如图3所示。

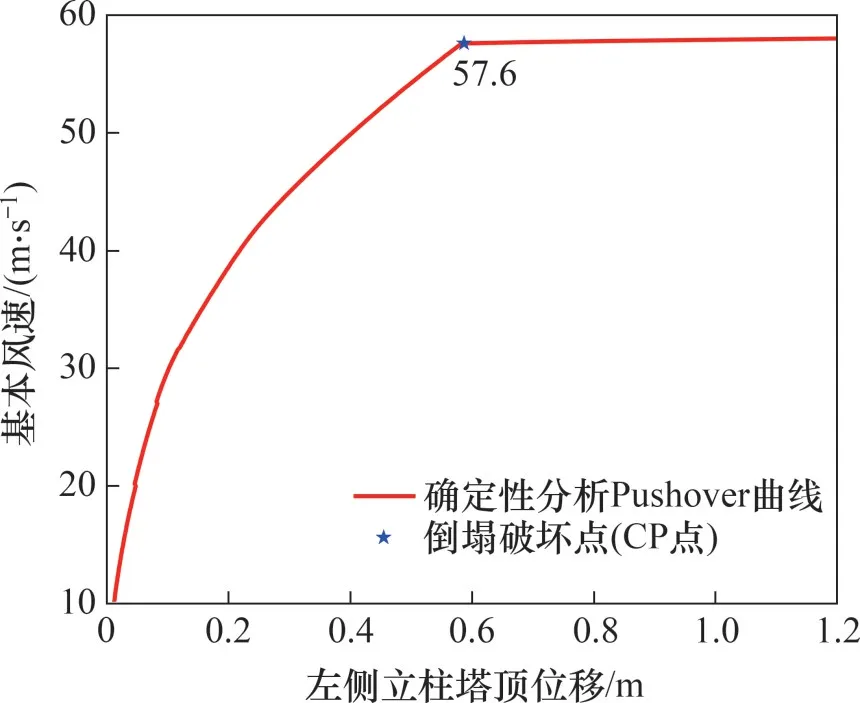
图3 双柱悬索拉线塔倒塌破坏点的确定Fig.3 Determination of collapse failure point of double column suspended guyed tower

由图3可知，双柱悬索拉线塔的风致倒塌破坏本质上属于极值点失稳问题，即在微小风速增量下双柱悬索拉线塔的塔顶位移响应急剧增大，此时即可认为结构处于失稳的临界状态。参考B-R准则[18]，本文将双柱悬索拉线塔的倒塌破坏点定义如下：当基本风速发生微小变化时，结构响应发生显著变化的临界点(在Pushover曲线上表现为曲线的转折点，见图3)即为倒塌破坏点(CP点)。

对双柱悬索拉线塔的每个结构样本进行非线性静力推覆分析即可获得对应的倒塌破坏点及相应的倒塌临界风速vi和顶点位移di(i=1，2，…，n，n为双柱悬索拉线塔样本总数)。采用统计方法对双柱悬索拉线塔风致倒塌易损性进行分析，则结构的倒塌概率可用下式表示：

式中：基本风速v即为本文选取的风荷载强度参数；vim为基本风速的具体取值；vi为第i个样本倒塌破坏时所对应的临界风速；为当基本风速v=vim时双柱悬索拉线塔发生倒塌破坏的样本数。ai取0或1分别表示对于第i个样本，当基本风速v=vim时，双柱悬索拉线塔未发生或发生倒塌破坏。

进一步利用对数正态分布函数对由式(5)得到的离散数据点进行拟合，可得到双柱悬索拉线塔风致倒塌易损性函数，如式(7)所示。

式中：μ和σ分别为双柱悬索拉线塔倒塌临界风速的对数均值和对数标准差。

式(7)中的2个关键参数μ和σ可分别根据式(8)和(9)求得。

需要注意的是，若以双柱悬索拉线塔塔顶位移作为倒塌易损性曲线的拟合对象，则分析过程与上述过程类似。

2.3.2 双柱悬索拉线塔风致倒塌易损性分析实现流程

双柱悬索拉线塔风致倒塌易损性分析的具体流程如图4所示，其分析框架主要包括输电塔不确定模型的建立、非线性静力推覆分析以及结果统计分析3个部分[19]，具体分析步骤如下。

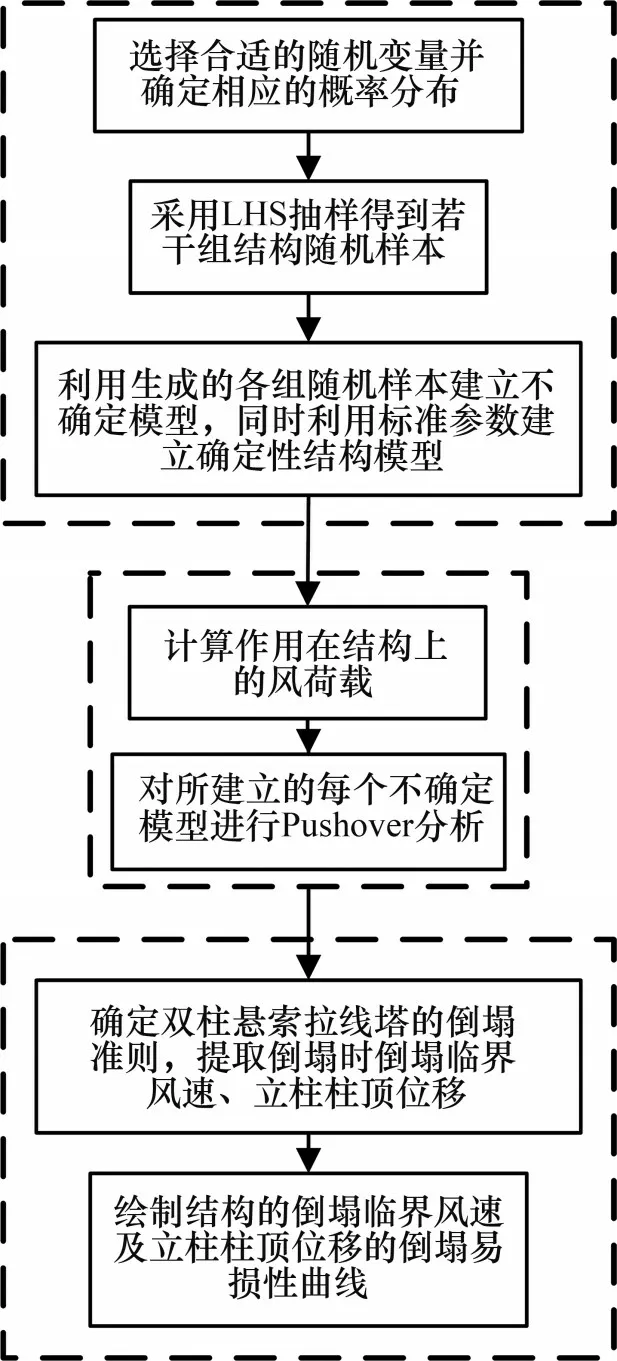
图4 双柱悬索拉线塔风致倒塌易损性分析流程Fig.4 Flow chart of wind-induced collapse fragility analysis of double column suspended guyed tower

1) 根据双柱悬索拉线塔的结构特性选取合适的随机变量并确定其概率分布及统计参数，如表2所示。

2) 利用拉丁超立方抽样(LHS)对表2中所选取的随机变量进行Monte Carlo模拟，生成若干组结构随机样本。

3) 利用生成的各组结构样本结合确定性有限元模型建立若干个考虑结构不确定性的双柱悬索拉线塔有限元模型。

4) 根据式(1)～(3)计算出作用在结构上的风荷载，将其转换为各单元所受风荷载并施加到对应的主材节点上。

5) 不断增大基本风速，对每个模型进行非线性静力推覆分析，得到结构的Pushover曲线。

6) 参考B-R准则[18]并结合前述分析理论确定结构的倒塌破坏点，提取结构倒塌时的倒塌临界风速vi、左右侧立柱顶点位移di。

7) 利用对数正态分布函数并结合式(5)～(9)拟合倒塌临界风速及对应的左右侧立柱顶点位移，绘制双柱悬索拉线塔的倒塌易损性曲线，并结合拉线对结构倒塌易损性进行分析。

2.4 样本数量的确定

参考现有风灾易损性分析思路，本文选取双柱悬索拉线塔倒塌时左右侧立柱顶点位移作为结构响应，计算不同样本数量下结构响应标准差并以其稳定时所对应的样本数量作为后续分析的总样本[20]。LHS技术可在较低样本容量下实现Monte Carlo大样本抽样的效果，因此，本文利用LHS抽样获取表2中材料参数的样本，结合有限元模型和图4计算结构响应，得到样本容量和响应标准差的关系，如图5所示。由图5可知，当样本容量达到40个后，各工况下结构响应标准差均趋于稳定。兼顾计算成本和精度，本文选取样本容量为50个，对其进行双柱悬索拉线塔风致倒塌易损性分析。

图5 响应标准差与样本容量的关系Fig.5 Relationship between response standard deviation and the sample size

3 结果分析

基于上述双柱悬索拉线塔风致倒塌易损性分析方法并结合有限元模型对双柱悬索拉线塔进行分析。根据步骤1)～5)建立50个双柱悬索拉线塔不确定性有限元模型并对其进行非线性静力推覆分析，利用所得Pushover曲线研究各项参数对双柱悬索拉线塔抗风承载力的影响；随后，根据步骤6)和7)确定各样本的CP点，并由式(5)～(9)拟合得到结构倒塌临界风速和位移的易损性曲线，对双柱悬索拉线塔进行风致倒塌易损性分析，进而研究风向角和拉线初张力对结构倒塌易损性曲线的影响。

3.1 双柱悬索拉线塔抗风承载力分析

假定风速方向垂直于导、地线走向(对应90°风向角)，最终模拟得到的双柱悬索拉线塔左、右侧立柱Pushover推覆曲线分别如图6和图7所示。

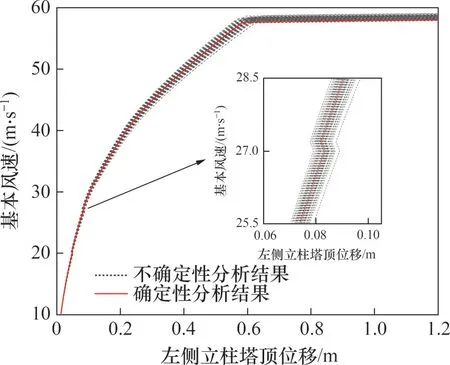
图6 左侧立柱Pushover曲线Fig.6 Pushover curve for the left column

图7 右侧立柱Pushover曲线Fig.7 Pushover curve for the right column

3.1.1 不确定性结构参数对抗风承载力的影响

由图6和图7可知，确定性模型左右侧立柱的推覆曲线位于50条不确定性推覆曲线中间，其倒塌临界风速小于绝大多数不确定性模型的结果；同时，不确定模型的倒塌临界风速主要集中在基本风速58 m/s附近，分布的离散性较小。这是因为确定性模型中仅材料屈服强度取为其概率分布的0.05分位值，其余大部分材料参数值均采用的是其概率分布的0.5分位值[21]。因此，双柱悬索拉线塔确定性模型的抗风承载力要小于绝大多数不确定性模型的分析结果，而结构刚度则位于各不确定性模型所得刚度中间。同时，由于钢绞线屈服强度的变异系数较小，因此，结构最终倒塌破坏时屈服点的分布呈现出较为集中的特征。

3.1.2 荷载参数对抗风承载力的影响

双柱悬索拉线塔左右侧立柱的Pushover曲线在风速为20.0、27.0(见图6中的局部放大图)和31.5 m/s时出现了3次较小幅度的跳跃现象。这是由于在根据式(3)计算导、地线风荷载时，风压不均匀系数a1和导、地线风荷载调整系数βc存在不连续跳跃。随着基本风速增大，一方面，导、地线的风压不均匀系数减小，另一方面，导、地线的风荷载调整系数会增大，因此，在两者综合影响下，Pushover曲线仅出现较小幅度跳跃。

3.1.3 左右侧立柱承载力曲线对比

对比图6和图7可知：当双柱悬索拉线塔发生倒塌破坏时，右侧立柱的顶点位移均大于左侧立柱的顶点位移，且当基本风速达到40 m/s左右时图7中右侧立柱推覆曲线的斜率出现了较为明显的下降。本文从抗侧刚度出发对上述现象进行分析。

以标准模型为例，当风速达到40 m/s左右时，右侧拉线的拉应力仅为初始拉应力的19.56%，其对右侧立柱的约束相较于初始状态显著降低，为立柱提供的抗侧刚度也相应减小，故Pushover曲线的斜率降低。在90°风向角下，随着基本风速增加，左侧拉线拉应力逐渐增大，表现为拉线张紧；右侧拉线拉应力则逐渐减小，拉线相对松弛。右侧拉线为结构体系所提供的抗侧刚度要远小于左侧拉线所提供的抗侧刚度，因此，左侧立柱的顶点位移均比右侧立柱的小。由此可见双柱悬索拉线塔的拉线应力对双柱悬索拉线塔的抗侧刚度起着十分重要的作用。

3.2 双柱悬索拉线塔风致倒塌易损性分析

根据步骤6)定义图6和图7中各Pushover曲线转折点为各不确定性模型的倒塌破坏点并提取相应的vi和di，利用式(5)～(9)拟合得到双柱悬索拉线塔倒塌临界风速和顶点位移的易损性曲线，分别如图8和图9所示。

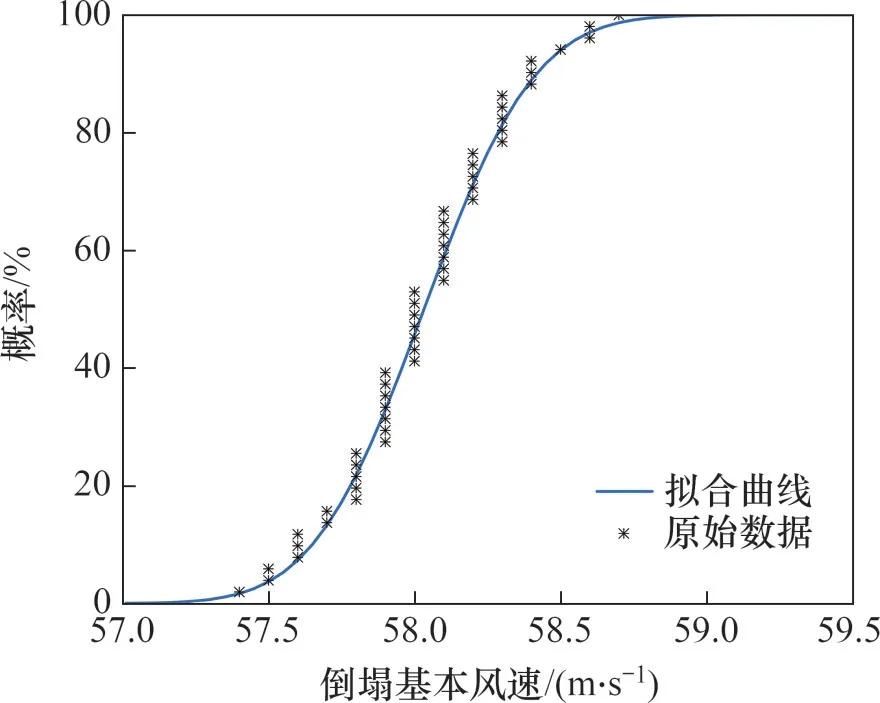
图8 基于风速的双柱悬索拉线塔风致倒塌易损性曲线Fig.8 Wind-induced collapse fragility curves for double column suspended guyed tower based on wind speed

图9 基于顶点位移的双柱悬索拉线塔风致倒塌易损性曲线Fig.9 Wind-induced collapse fragility curves for double column suspended guyed tower based on vertex displacement

从图8和图9可以看出，大多数倒塌临界风速和立柱顶点位移的原始值与对数正态分布函数较吻合。其中，倒塌临界风速原始值呈“葫芦串”形状，这是因为在进行Pushover分析时，为节约计算成本，基本风速是由10 m/s开始以0.1 m/s的增量逐渐增加的，因此，结构最终发生倒塌破坏时的倒塌风速也是按照0.1 m/s的增量增加的。

3.2.1 倒塌参数对比

由图8和图9中的双柱悬索拉线塔倒塌易损性曲线可得到与倒塌概率为10%时对应的倒塌临界参数值，FEMA-P695规定，一旦超过该限值，即认为结构发生倒塌破坏[22]。经分析可得双柱悬索拉线塔确定性模型得到的倒塌临界风速和左、右侧立柱顶点位移分别为57.6 m/s、0.587 2 m和0.766 3 m，对应的倒塌破坏概率分别为7.35%、30.31%和29.47%；同时由图8和9可知易损性曲线中对应10%破坏概率的倒塌临界风速和左、右侧立柱顶点位移分别为57.65 m/s、0.572 5 m和0.747 0 m。与确定性倒塌分析相比，不确定性倒塌分析得到的倒塌临界风速略大于确定性分析下的结果；而左、右侧立柱的顶点位移均小于确定性倒塌分析的结果，相对误差分别为2.568%和2.584%，这说明确定性倒塌分析略微高估了双柱悬索拉线塔的抗风承载力。

3.2.2 最大位移增长百分比

定义双柱悬索拉线塔的最大位移增长百分比Q为

式中：Ddeter与Duncert分别为双柱悬索拉线塔确定性倒塌分析和不确定性倒塌分析下柱顶最大水平位移。

在90°风向角下，计算得到双柱悬索拉线塔左右侧立柱的最大位移增长百分比分别为12.91%和12.27%，这说明对双柱悬索拉线塔而言，仅采用由确定性分析得到的左右侧立柱顶点位移作为判断输电塔倒塌破坏的指标是不合理的，有必要对输电塔进行不确定性倒塌分析。

3.3 风向角的影响

风向角会对双柱悬索拉线塔的抗风承载力产生较大影响，进而影响到结构的倒塌易损性，因此，有必要研究风向角对双柱悬索拉线塔风致倒塌易损性曲线的影响。

风向角示意图见图10。由图10可知双柱悬索拉线塔为双轴对称结构，因此，取风向角的变化范围为0°～90°。由DL/T 5154—2012[17]可知：输电线路可能存在的最不利风向角为0°、45°、60°和90°；同时，该规定[17]还给出了上述4个风向角下输电塔塔身和导地线的风荷载分配表，如表3所示。

表3 不同风向角下荷载分配表[17]Table 3 Load distribution at different wind angles[17]

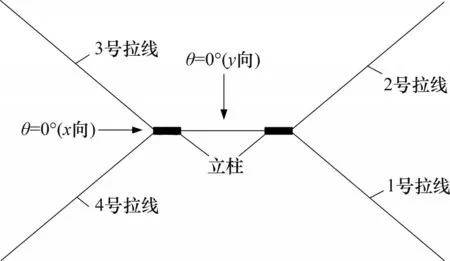
图10 风向角示意图Fig.10 Diagram of wind angle

根据表3和图10，结合双柱悬索拉线塔风致倒塌易损性分析方法，在不同风向角下重复步骤4)～7)，最终得到不同风向角下双柱悬索拉线塔的倒塌易损性曲线，如图11所示。

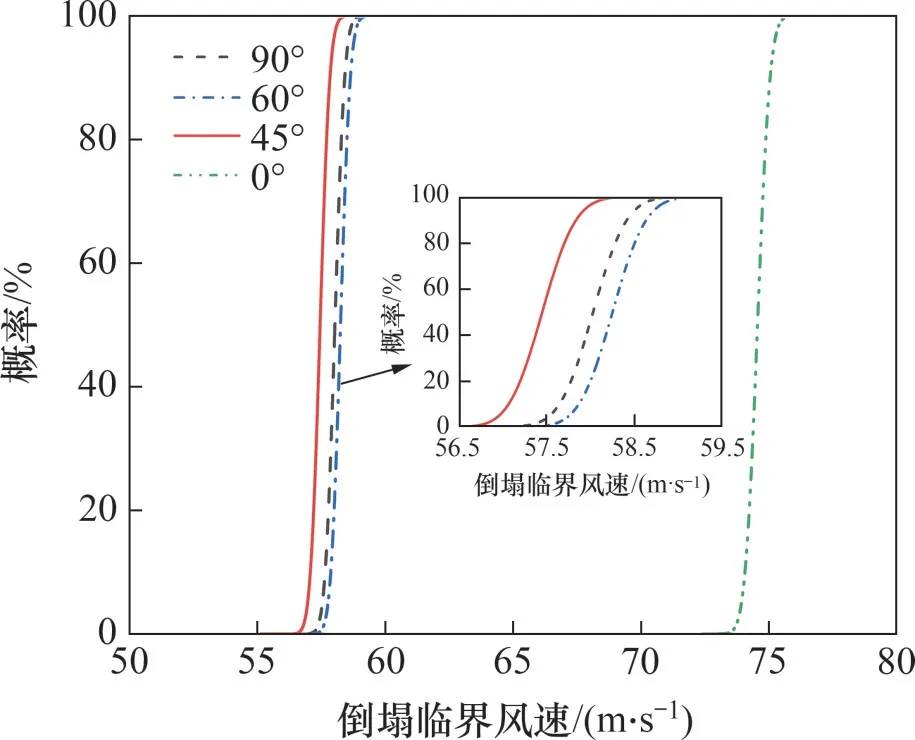
图11 不同风向角下的倒塌临界风速易损性曲线Fig11 Collapse critical wind speed fragility curves at different wind angles

由图11可知：当风向角由0°逐渐增大时，曲线整体呈现向左移动的趋势；当基本风速小于56.5 m/s时，结构在任一风向角下发生倒塌破坏的概率都很小。由表3和图11可知：在0°风向角下，风向沿着双柱悬索拉线塔导、地线顺线路方向，此时，导、地线上的风荷载远小于其余风向角下的风荷载，因此，对应的倒塌破坏风速最大，结构在该角度下较安全；在45°风向角下双柱悬索拉线塔的倒塌破坏风速最小，在同一基本风速下最容易发生倒塌破坏，结构的最不利风向角为45°。这也说明对双柱悬索拉线塔而言，其最不利风向角方向并不一定为垂直于输电线路的方向。

3.3.1 不同风向角下倒塌参数对比

表4所示为不同风向角下由式(10)计算得到的左、右侧立柱最大位移增长百分比。由表4可知，各风向角下不确定模型的最大位移相较于确定性模型均增长了10%以上，这表明在进行双柱悬索拉线塔风致倒塌易损性分析时需要考虑结构不确定性。

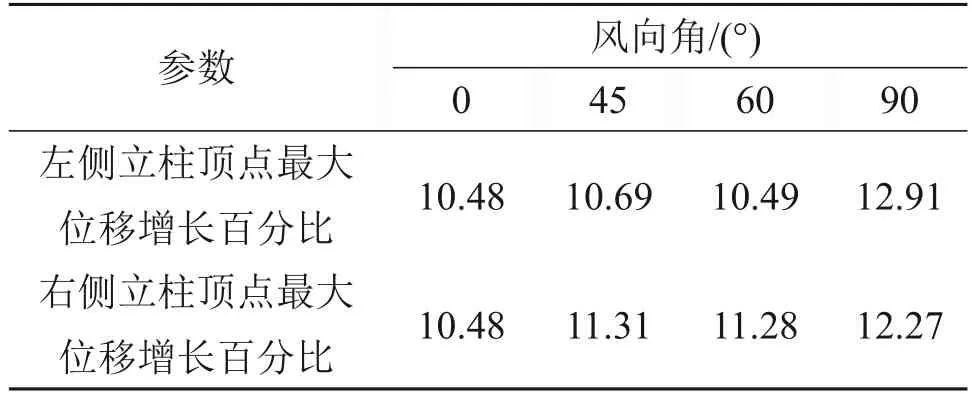
表4 不同风向角下最大位移增长百分比Table 4 The maximum displacement growth percentage under different wind angles%

表5所示为确定性倒塌破坏分析与倒塌破坏概率为10%时不确定性倒塌分析所对应的参数对比。由表5可知：在不同风向角下，双柱悬索拉线塔确定性分析的倒塌临界风速与不确定性分析下的对应值相差很小；同时确定性分析下左、右侧立柱的顶点位移均要大于不确定性分析下的相应值，这说明采用确定性分析在各风向角下均会高估双柱悬索拉线塔的倒塌位移。

3.3.2 拉线屈服分析

与传统自立式输电塔不同，双柱悬索拉线塔结构的倒塌破坏与4根拉线的状态密切相关。结合图10分析可知：当风向角为90°时，3、4号拉线的拉应力随着基本风速增加而逐渐增大，为结构整体提供的抗侧刚度也逐渐增加；与此同时，背风侧1、2号拉线则随着风速增加而逐渐松弛，在图9中反映为右侧立柱柱顶水平位移比左侧的大；当风向角为60°和45°时，由图10可知3号拉线与风速方向近乎平行，随着风速增加，3号拉线的拉应力增速比4号拉线的大，结构最终发生倒塌破坏的原因是3号拉线屈服而无法为立柱提供有效约束；当风向角为0°时，2号和3号拉线与风速方向相反，此时两者受力较1号和4号拉线更大，结构最终发生倒塌破坏是由2号和3号拉线屈服所致。

3.4 拉线初张力的影响

由于双柱悬索拉线塔拉线初张力与结构体系的整体刚度及稳定性密切相关，故有必要分析拉线初张力对结构风致倒塌易损性曲线的影响。

在45°风向角下，分别取拉线初张力为设计承载力的16%、20%、25%和30%共4种工况(分别对应初张力1、初张力2、初张力3和初张力4)进行对比，其余参数与前文所取参数一致，对不同拉线初张力下各有限元模型进行非线性静力推覆分析，最终得到双柱悬索拉线塔在不同初张力下的风致倒塌易损性曲线，如图12～14所示。

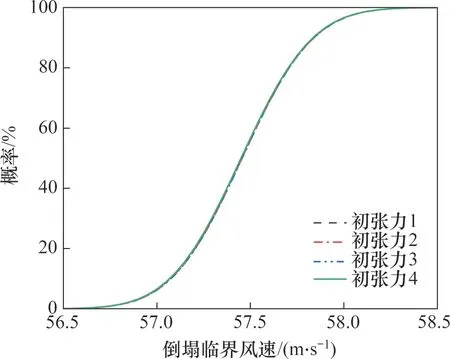
图12 不同初张力下倒塌临界风速易损性曲线Fig.12 Collapse critical wind speed fragility curves under different initial tension

由图12～14可以发现，增大拉线初张力对双柱悬索拉线塔体系的倒塌临界风速几乎没有影响，而对结构倒塌时左右侧立柱的顶点位移则具有较大影响。随着拉线初张力增大，左、右侧立柱的顶点位移易损性曲线均向左移动；在同一倒塌概率下，拉线的初张力越大，发生倒塌破坏时左右侧立柱的顶点位移越小。提高拉线初张力为双柱悬索拉线塔左右侧立柱提供了更强的侧向支撑刚度，使得结构在同一风速下的位移响应降低。对比图13和14可知，与左侧立柱相比，增大拉线初张力对右侧立柱顶点位移的易损性曲线影响更大。

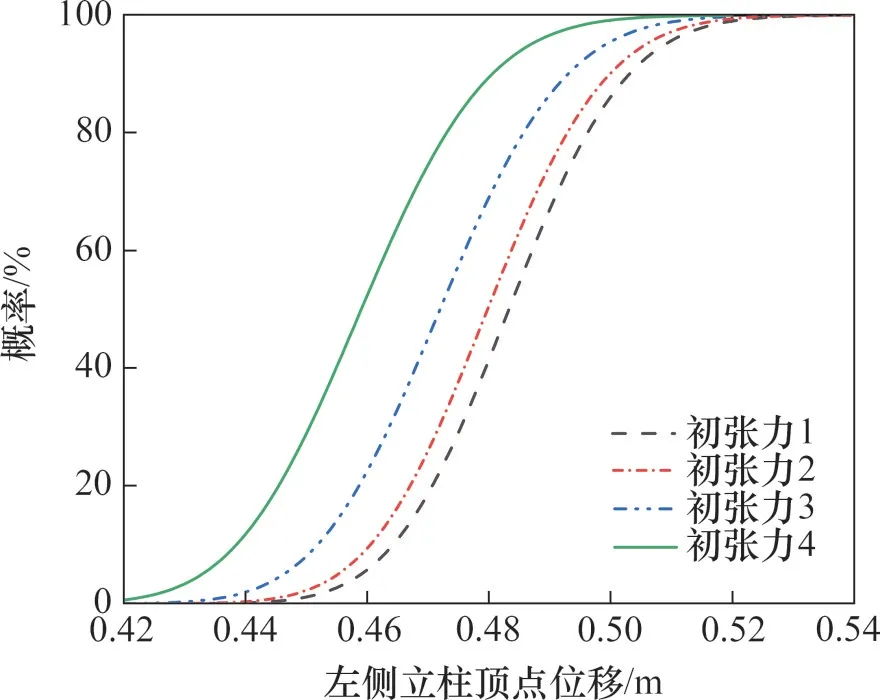
图13 不同初张力下左侧立柱顶点位移易损性曲线Fig.13 Displacement fragility curves of left column vertex under different initial tensions

为解释上述现象，本文从拉线的应力变化出发来进行分析。以标准模型为例，提取不同工况下4根拉线(即1～4号拉线)的应力，绘制不同初张力下标准模型拉线应力图，见图15。

由图15可知：当基本风速小于40 m/s时，拉线应力在不同初张力下呈现出明显的差异性；拉线的初张力越大，拉线的应力也越大；随着风速不断增加，当基本风速大于40 m/s后，不同工况下的拉线应力曲线逐渐趋于一致。以3号拉线为例，当拉线最终屈服时，不同初张力下的倒塌破坏风速均为同一量值，因此，增大拉线的初张力对结构倒塌时的临界风速基本无影响。同时，由图15还可知，拉线初张力在较低风速下对拉线应力影响较为显著。初张力越大，拉线的应力也就越大，为立柱所提供的侧向支撑刚度也越强，表现为易损性曲线左移(见图13和图14)。在45°风向角下，1、2号拉线仍可近似视为背风侧拉线，由图15易知其应力相较于3号和4号拉线更小，改变拉线初张力对于1、2号拉线的影响相对更大，因此，增大拉线初张力对右侧立柱的顶点位移易损性曲线影响更大。

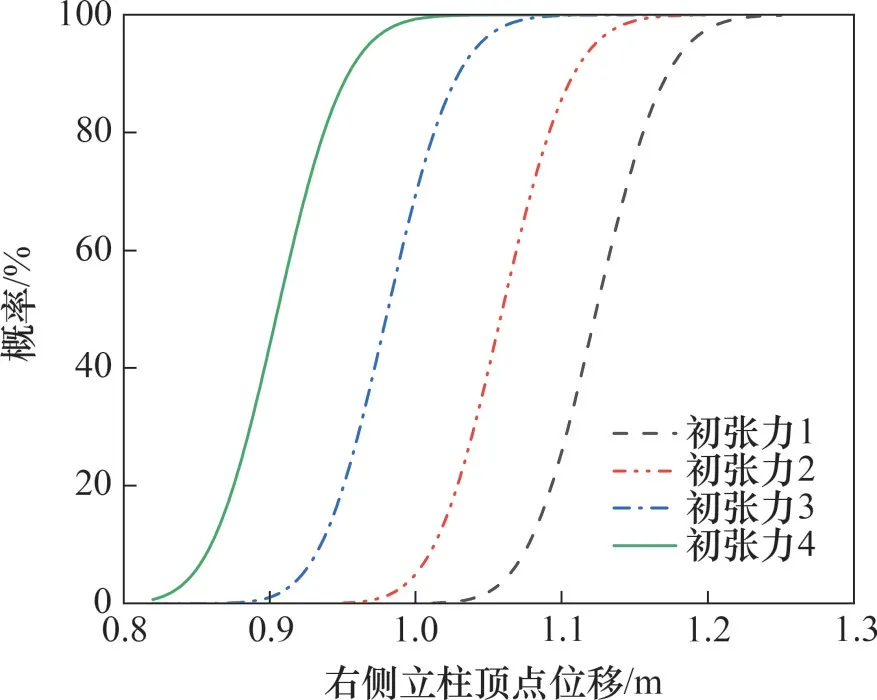
图14 不同初张力下右侧立柱顶点位移易损性曲线Fig.14 Displacement fragility curves of right column vertex under different initial tensions

图15 不同初张力下标准模型拉线应力图Fig.15 Stress diagram of standard model pulling cable under different initial tensions

综上所述，拉线初张力的增加降低了双柱悬索拉线塔左右侧立柱的顶点位移响应，在同一顶点位移限值下，初张力越大，结构发生倒塌破坏的概率越高；同时，其还会使得双柱悬索拉线塔各构件的初始应力增加，对结构的抗风承载力产生一定不利的影响。因此，本文建议在选取拉线初张力时应取较小值，即选取拉线初张力为设计承载力的16%为宜。

4 结论

1) 与不确定性倒塌分析相比，确定性倒塌分析高估了双柱悬索拉线塔的抗风承载能力，采用不确定分析方法可以更合理地评估双柱悬索拉线塔的抗风承载力。

2) 由易损性分析可知，0°风向角下双柱悬索拉线塔的抗风承载力最强；45°风向角为结构的最不利风向角，此时，结构的抗风承载力最低，倒塌破坏的概率最高；当风速小于56.5 m/s时，结构在任一风向角下发生倒塌破坏的概率都很小；当风向角在0°～90°之间变化时，3号拉线最易发生屈服破坏，在设计使用时，应注意结合当地风速与风向来考虑拉线的断线问题。

3) 增大拉线初张力对双柱悬索拉线塔的倒塌临界风速基本无影响，但对倒塌时的塔顶位移影响较大。随着拉线初张力的增大，左右侧立柱顶点位移易损性曲线均向左移动，并且改变拉线初张力对右侧立柱的顶点位移影响更大。拉线初张力的提高为立柱提供了更强的侧向支撑刚度，但在一定程度上降低了结构的抗风承载力，在双柱悬索拉线塔的设计和使用中宜选择较低的拉线初张力。