特高压单柱拉线塔的静力稳定性分析

杨文刚, 王宏飞， 李鹏

(华北电力大学机械工程系， 保定 071003)

中国虽疆域辽阔，但是能源分布不均衡，随着经济发展，西部电力资源丰富与东部电量消耗大的矛盾日益突出[1-2]。为了能够改善资源分布与消耗不均衡的状况，国家开展了“西电东送”的工程，±800 kV哈郑线、±800 kV酒湖线以及±1 100 kV吉泉线等多条特高压直流输电线路已经建成。与此同时一些输电线路往往要经过一望无际的戈壁，地广人稀的草原等特殊地区。这些地区的地势平坦，人口和建筑物的密度低，很适合利用占地面积大的拉线塔进行输电。拉线塔不仅在中国的西部地区得到了应用，而且在巴西的±600 kV伊泰普高压直流线路中，大部分输电塔都是使用拉线塔进行输电[3]。拉线塔的经济优势在这些地区得到展现。

然而对于特高压输电线路来说，拉线塔变高的同时受到的载荷也变大。特高压拉线塔在强风作用下，容易出现失稳的情况。因此，为了避免出现这种事故，对于特高压单柱拉线输电塔的静力稳定性研究是必要的。近些年来很多学者都对输电塔的稳定性进行了研究。输电塔的稳定性研究大致分为：针对塔的基础稳定研究[4]、塔的构件稳定研究[5-6]，以及塔的整体稳定研究[7]。曹新款[8]通过计算地表残余变形、建筑物的载荷影响深度等参数，对采空区输电铁塔的地基进行了稳定性分析。Zhou等[9]研究输电塔在极端工况和极端载荷下的塔基础的稳定性，并验证了500 kV输电塔基础位移满足现有的规范要求。吴海洋等[10]针对钢管输电铁塔的构件，对原有的稳定理论模型进行了修正，推导出新的针对钢管构件的稳定性计算公式，同时还进行了实验验证，为钢管塔的设计提供了参考。肖正直等[11]基于哈密顿原理，对双柱悬索拉线塔进行动力稳定分析，求解出拉线塔的动力不稳定域。上述研究对输电塔的基础、构件以及整体进行了研究，解决了输电塔的一些稳定性问题。但是对于特高压单柱拉线塔这种特定的输电塔，没有针对其静力稳定性进行分析。为此，可以考虑利用结构力学的稳定性原理分析特高压单柱拉线塔，建立起拉线塔简化模型，计算出简化模型中的重要参数。

拉线塔不同于其他自立式输电塔，拉线塔具有拉线结构，拉线会影响单柱拉线塔的稳定性。针对拉线塔的拉线，陈湘阳[12]将拉线塔简化为索-梁结构，推导出了拉线的非线性振动方程。文献[13]基于拉线的非线性静力特性，将拉线分段线性化，建立拉线的简化模型。吴玲等[14]对水平载荷下拉线塔拉线的刚度做出分析并探讨拉线对地夹角，拉线自重等因素对拉线塔的影响。上述研究建立了拉线塔的有限元分析和耦合振动研究模型。将这种拉线的简化模型推广应用到特高压单柱拉线塔的静力稳定性分析中，值得探索。

现针对特高压单柱拉线塔的静力稳定性问题，首先建立拉线的分析模型，推导出拉线的等效弹性模量以及拉线临界初应力的公式，然后将拉线塔的主柱简化为顶端为弹簧铰支座、底端为固定铰支座的等截面压杆，推导出弹性刚度K与主柱的计算长度系数μ的公式。最后研究不同风荷载以及不同拉线初始预应力的情况下计算长度系数μ的变化规律。通过分析变化规律，探究出提高拉线塔稳定性的方法。

1 拉线等效弹性模量公式的推导

1.1 拉线模型假设

拉线受到的载荷和拉线的变形之间具有非线性关系[15]，同时拉线的弦向应力会对主柱起一个支撑的作用，因此引入等效切线弹性模量(简称“等效弹性模量”)来研究拉线应力与变形之间的关系。

建立拉线的模型如图1所示，其中，拉线挂在A点，锚固在地面上的O点，OA为拉线的弦向距离，其长度为l[16]。以O点为原点，x轴方向为拉线的弦线方向，建立xOy直角坐标系。把水平方向定为x′轴方向，建立x′Oy′直角坐标系。x轴方向与x′轴方向的夹角为θ。

为了简化计算，在进行公式的推导之前，提出以下假设。

(1)拉线只受拉，不考虑拉线受压，并且把拉线看作是斜拉索，即弯曲刚度为0。

(2)拉线在载荷作用后，夹角θ不发生改变。

(3)拉线所受载荷沿拉线弦线分布。

图1 拉线的分析模型Fig.1 Analysis model of stay wire

1.2 等效弹性模量公式推导

在假设条件下，拉线的轴向应力在弦线方向的分量记为σx，按照前述假设(2)可知，在整个拉线中σx为常数。设拉线单位长度的质量为ρ，重力加速度为g，则拉线的曲线方程可写为

(1)

假设拉线的原始弦长在初始和当前状态下保持不变，可建立出拉线的状态方程为

(2)

式(2)中：初始状态和当前状态下的弧线长度分别用L0和L表示，两种状态下的轴向应力分别由σ0和σ来表示；Ew为拉线的弹性模量；ds表示拉线弧微分。

拉线的弧线长度可通过对拉线的曲线形状方程积分求得，即

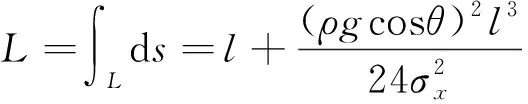
(3)

同理可得

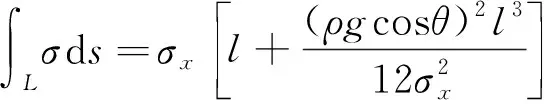
(4)

将其代入拉线的状态方程式(2)中，并整理得

(5)

定义等效切线弹性模量为

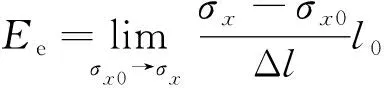
(6)

式(6)中：σx0、σx为变形前后拉线的弦向应力； Δl为拉线变形后弦向长度的增加量。

由于σx≪Ew、σx0≪Ew，因此整理得拉线静力等效弹性模量为

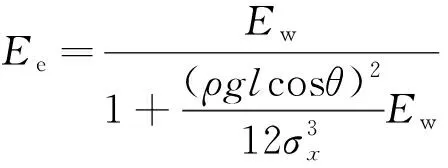
(7)

2 拉线临界初应力的定义及公式推导

当拉线绷得很紧即初始预应力较大时，可以把拉线看作是一根杆，该杆只受到拉力，其弹性模量可由式(7)计算得到。在风载荷作用下迎风侧和背风侧的拉线都会受到拉力作用，假设迎风拉线的应力与预应力的差等于迎风拉线的应力与预应力的差，即

σa-σ0≈σ0-σb

(8)

式(8)中：σa为迎风拉线的应力；σ0为拉线的预应力；σb为背风拉线的应力。

当拉线的初始预应力较小的时候，背风侧的拉线松弛，此时其工作应力近似为

σb≈0

(9)

在大风载荷的作用下，迎风的拉线受拉，此时对主柱底的铰接点取矩，列出平衡方程为

Faha-∑Fwihwi=0

(10)

式(10)中：Fa为迎风拉线的张力；ha为Fa对主柱铰接点的力臂；Fwi为主柱上各点风载荷；hwi为Fwi对主柱铰接点的力臂。设迎风侧拉线的横截面积为Aa此时迎风侧拉线工作应力为

(11)

定义：在大风载荷的作用下，背风侧的拉线处于松弛和受拉之间的一个状态，此时的拉线的初始预应力称为临界初应力，记为σc。当σ0=σc时，拉线应同时满足式(8)、式(9)、式(11)，从而得到临界初应力的表达式为

(12)

可以看出拉线临界初应力约为迎风侧拉线的工作应力的一半。当σ0=σc时，背风侧拉线应力为0，此时的主柱可以看作是两端铰支，其计算长度系数μ应为1。

3 主柱简化模型的刚度系数

3.1 单柱拉线塔主柱简化模型

根据单柱拉线塔主柱的受力特点，将其简化为顶端为弹簧铰支座支撑、底端为固定铰支座的压杆，简化后模型如图2所示。

3.2 弹簧刚度系数的推导

在迎风面的拉线会被风吹紧，于是可忽略迎风拉线的几何非线性，而背风面的拉线会松弛，这就使得迎风的拉线可以为主柱提供很大的抗弯刚度，而背风的拉线几乎不能为主柱提供抗弯刚度，因此把顶端的约束简化为弹性支座，拉线塔受力简化模型如图3所示。

设AC=BC=L′，拉线的等效弹性模量为Ee，假设拉线AC的内力为FAC、拉线BC的内力为FBC、拉线AC、BC在垂直OC方向上的合力为FC，C点在FC的作用下沿着垂直主柱OC方向产生位移δ，则根据拉压变形与力系平衡的原理得

FC=2FACcosα+2FBCcosα

(13)

(14)

(15)

图3 拉线塔受力简化模型Fig.3 Simplified model of tension of cable tower

根据胡克定律有FC=Kδ,可求出K表达式为

(16)

4 主柱计算长度系数的推导

在图2所示简化模型的基础上，进行拉线塔主柱的受力分析。假设主柱轴向受到的压力为P，弹性支座给主柱的力为F，方向垂直于主柱，底端的铰接支座会传递给主柱一个水平力FOx和一个竖直方向上的力FOy，则有FOx=F，FOy=P，拉线塔主柱的受力分析如图4所示。

假设主柱的位移为y(x)，主柱的弹性模量为E，惯性矩为I，在x处对y(x)求二阶导为

(17)

任取主柱的一个截面列出的力矩平衡方程为

Fx-EIy″(x)-Py(x)=0

(18)

图4 主柱受力分析图Fig.4 Stress analysis diagram of main column

对式(18)求二阶导数得

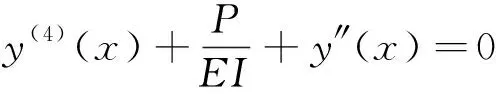
(19)

解式(19)得

(20)

设主柱失稳的临界荷载为Pc，Pc应该尽量小，所以应取n=1。

当P1≤P2时，临界荷载Pc=P1，此时有

(21)

当P1>P2时，临界荷载Pc=P2，此时有

Pc=P2=KL

(22)

根据压杆的稳定理论[17]有

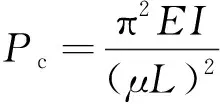
(23)

式(23)中：μ为压杆的计算长度系数，其计算公式为

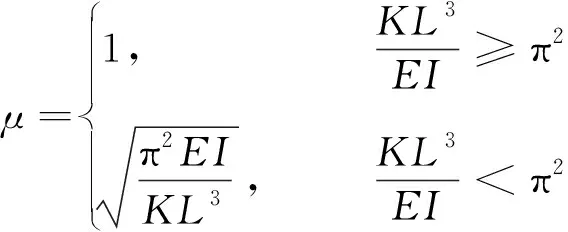
(24)

由式(24)可知，当KL3/EI≥π2时，计算长度系数 恒等于1，根据细长杆件欧拉理论，压杆两端都是铰接时计算长度系数μ=1，所以当KL3/EI≥π2时主柱上端可以近似看作铰接状态。当KL3/EI<π2时，主柱的计算长度系数μ随着KL3/EI的减小而持续增大。

5 算例分析

5.1 单柱拉线塔的参数

以某±800 kV特高压直流单柱拉线塔为例进行算例分析算例中的单柱拉线塔的工程条件如表1所示。算例中的单柱拉线塔的参数如表2所示。算例中的拉线塔的结构如图5所示。

表1 单柱拉线塔的工程条件Table 1 Engineering conditions of single column cable tower

表2 单柱拉线塔的参数Table 2 Parameters of single column cable tower

图5 拉线塔的结构Fig.5 Cable tower structure

改变风速与拉线初始预应力，根据式(24)计算得到不同风速与拉线初始预应力下的计算长度系数。在按照式(24)计算μ之前先计算出主柱的弯曲刚度，根据文献[18]的等效刚度方法对主柱弯曲刚度进行简化计算得EI=3.12×109N·m2。

5.2 风速对主柱计算长度系数的影响

在风载荷的作用下，拉线弦向应力σx发生改变，导致等效弹性模量Ee和弹簧刚度系数K改变,从而影响主柱的计算长度系数。在研究风速对拉线塔主柱计算长度系数的影响之前，需要先对拉线塔所受的风荷载进行计算。由于拉线的挡风面积小，所以受到的风载荷很小，因此忽略拉线所受到的风荷载。所以只计算导地线，绝缘子串以及塔身所收到的风载荷。依据国家标准[19]分别计算出风速分别取30、33、35、42、45 m/s时的导地线风载荷、塔身风载荷以及绝缘子串风载荷。

为了简化计算，把计算出的导地线、塔身以及绝缘子串所受到的风载荷都简化为作用在弹簧铰支座上的集中力。将计算出的导地线风载荷、塔身风载荷以及绝缘子串风载荷转化为不同风速下的作用在弹簧铰支座上的等效风荷载的大小如表3所示。

取拉线的初始预应力150 MPa，风向角为90°，通过计算得到的风速和计算长度系数的关系如图6所示。可以看出：在保证拉线预应力不变的前提下，风速与计算长度系数成正相关即风荷载越大，拉线塔主柱沿垂直线路方向上的计算长度系数μ越大。

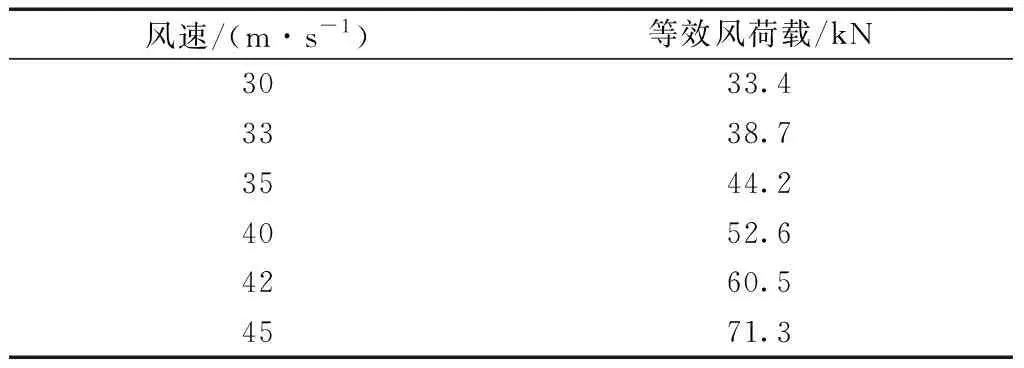
表3 作用在弹簧铰支座上的等效风荷载Table 3 Equivalent wind load on spring hinge support

图6 不同风速下的计算长度系数Fig.6 The calculated length coefficients under different wind speeds

5.3 拉线初始预应力对主柱计算长度系数的影响

风速恒定设为35 m/s，风向角为90°，取拉线初始预应力分别为不同的数值进行研究，分别计算出不同初始预应力下的计算长度系数，得到结果如图7所示。

在保证恒风速即风载荷不变的前提下，拉线的初始预应力与计算长度系数成负相关即随着拉线初始预应力增加，拉线塔主柱的沿垂直线路方向上的计算长度系数减小，但当拉线初始预应力逐渐增加达到250 MPa以后，拉线塔计算长度系数不再减小且恒为1。

图7 不同初始预应力下的计算长度系数Fig.7 The calculated length coefficients under different initial prestress

根据式(12)以及拉线塔的参数，可以计算出拉线临界初应力σc≈232 MPa，再根据图7，在误差范围内可以认为当拉线初始预应力超过拉线临界初应力时拉线塔计算长度系数不再减小且恒为1。因此将拉线初始预应力置为大于等于拉线临界初应力可以使计算长度系数降为1，从而提高拉线塔的稳定性。

6 结论

利用压杆稳定理论对特高压拉线塔进行静力稳定性分析，结合±800 kV特高压直流单柱拉线塔的算例分析，可以得到以下结论。

(1) 在保证拉线预应力不变的前提下，风速越高即风荷载越大，拉线塔主柱沿垂直线路方向上的计算长度系数越大，拉线塔就越容易失稳，在设计过程中要充分考虑风载荷对拉线塔的影响。

(2) 在保证恒风速即风载荷不变的前提下，随着拉线初始预应力增加，拉线塔主柱的沿垂直线路方向上的计算长度系数减小，但预应力超过临界初应力时，背风侧的拉线工作应力为0，拉线塔主柱可以近似看作是两端铰支，计算长度系数不再减小且恒为1，此后即便继续增加拉线初始预应力，拉线塔的稳定性也不会出现明显的提高。

(3) 在设计和实际施工当中，拉线临界初应力具有重要的参考价值，可以提前计算出拉线临界初应力，通过将拉线的初始预应力设置为大于等于计算出的临界初应力来提高拉线塔的稳定性。