声速测量实验原理讨论

宿德志,张纪磊,孙晓伟,段金鹏,马帅奇

(海军航空大学 航空基础学院,山东 烟台 264001)

声波特性测量在声波定位、探伤、测距等应用中具有重要的实用意义[1],空气中的声速测量是大学物理基础实验之一,该实验通常采用驻波法和相位比较法两种方式测量声速[2]. 而这两种方法从概念上是存在矛盾的,驻波法认为发射端和接收端之间形成了驻波,而相位比较法又认为这是一个行波. 此外,实验中发现声压振幅并不以正弦或余弦规律变化,实验中S1为发射端,S2既是接收端也是反射端(如图2所示),当S2移动时所形成的波并不是一列波[3]. 正是由于以上种种问题,该实验一直存有争议,从20世纪90年代开始,很多人都针对该实验进行了研究,很多物理实验教材认为在S1和S2间产生了由入射波和反射波叠加而形成的驻波,因此,可根据驻波的波节间距为半波长进行测量[4-6]. 而文献[7]和[8]指出由于声波传输过程中存在衰减,因此,S1和S2间形成的并非理想驻波,但其仅考虑了入射波和反射波的叠加,仿真精度有限. 文献[9]也指出S1和S2间并非理想驻波,并指出应采用声压方程进行计算.

在此基础上,部分研究人员认为是声波无限次反射叠加的结果,如文献[10]指出S2接收的声压信号为正方向传播的波在S2处无限次叠加的结果,并进行了仿真分析. 文献[11]认为实验测量结果应为无穷多列波的叠加,并将这些波列按照正方向和反方向两个进行分别相加,进行了理论公式的推导. 但是其仅计算了S1和S2距离为半波长整数倍这些特殊点的结果,所得到的结论不具有普适性. 文献[12]利用一维黏性介质波动方程的稳态解和边界条件对S1和S2间的声压分布进行了求解,并针对声吸收系数远远小于1的情况进行了讨论. 文献[13]在这种假设下,进行了理论推导,获得了和实验现象较为吻合的结果,但是在推导中声波振幅和声压振幅概念有些混淆,且没有对相位比较法进行分析,缺少实验数据的支撑. 随后文献[14]指出接收器的声压信号应该包括正方向和反方向传播的波的无限次叠加,并利用一维时谐平面声压方程进行了理论推导,通过函数拟合得到的理论结果与实验测量结果吻合较好,但是,理论推导中采用的近似条件为声吸收系数远远小于1,而其实验拟合的均值却为2.357,此外也没有对相位比较法给出解释.

从以上分析可知,该实验中接收端移动时声压变化的推导还不够完善,尤其是对相位比较法的原理研究还不清楚. 因此,本文从振幅与声压的关系出发,利用平面简谐波函数、声压反射系数公式和波的叠加原理深入研究S1和S2间的声压振幅和相位变化情况,为正确理解该实验的物理本质提供理论指导.

1 基本原理

由于实验中采用声压换能器作为发射端和接收端,因此测量的物理量是声压而非位移,声压p通常定义为某点压强相对于静态声压的增量. 所以首先由声波位移平面简谐波函数推导出声压的波函数. 当传播介质为均匀弹性介质时,考虑沿正向传播的平面简谐声波,取介质中的一个微元进行受力分析,如图1所示.

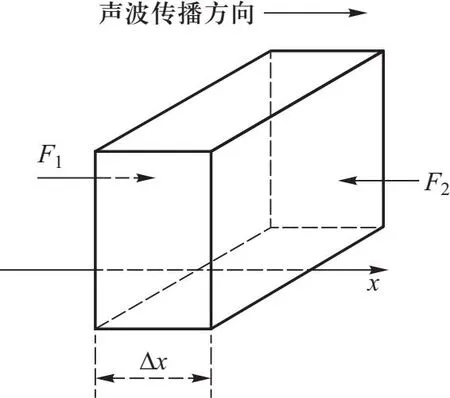
图1 介质微元受力分析图

设图1中微元的厚度为Δx,截面积为S,且与声波传播方向垂直,则该介质微元质量为

Δm=ΔxSρ

(1)

其中ρ为介质的密度. 则该微元所受的合外力可由左右两侧压强差Δp=p2-p1(其中p1和p2分别为该微元左侧和右侧相对于静态声压的增量)进行求解为

F1-F2=-SΔp

(2)

又由牛顿第二定律有

F1-F2=Δma

(3)

其中a为微元振动的加速度. 联立以上3式可得

(4)

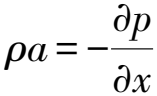
(5)

令ξ表示微元偏离平衡位置的位移,则根据加速度的定义可将上式转换为

(6)

上式即一维声场中的介质微元运动方程. 考虑实验中超声波为一维简谐波的情况,其平面简谐波函数为

ξ=ξ0cos(ωt-kx+φ)

(7)

(8)

令上式对x进行积分可得

(9)

(10)

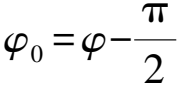
(11)

这就是理想的均匀弹性介质平面简谐波的声压波函数. 当介质存在损耗时,波数k=k0-iη为复数,其中η表示振幅随传播距离的衰减速度,也被称为声吸收系数. 不妨设φ0=0,则式(11)可以化简为

p=p0e-ηxei(ωt-k0x),

(12)

上式即为存在介质损耗时的声波传播函数. 此外,声波在由介质1入射到交界面的反射和透射可分别用声压反射系数R和声压透射系数T进行描述[15]

(13)

(14)

其中,Z1=ρ1u1和Z2=ρ2u2分别为介质1和2的声阻抗率,pi0、pr0和pt0分别为入射波、反射波和透射波的声压振幅.

2 多次反射叠加的声场

实验采用装置如图2所示,其中S1为发射端,S2为接收端. 根据前述分析,声波会在S1和S2间往复传播,多次叠加.

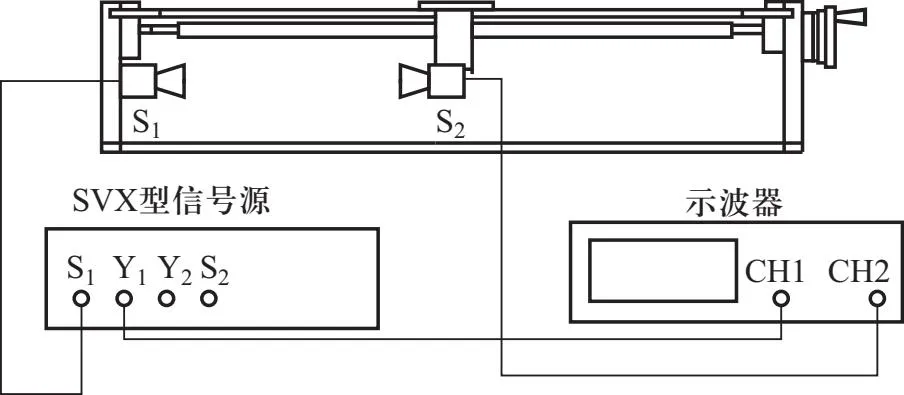
图2 实验装置图

设置S1和S2间的距离为L,则根据式(12)可得第1列至第n列正向声波在S2处的声压振动方程分别为:

(15)

其中,R为声压反射系数,同理可得n列反向声波在S2处的声压振动方程为

(16)

将式(15)和式(16)对应项相加可得

(17)

则当n→∞时,利用等比数列公式可求得式(17)各项的和为

(18)

将上式化简后可得

(e-ηLei(ωt-k0L)+R2e-3ηLei(ωt+k0L+π))

(19)

则式(19)的可理解为两个同方向同频率的简谐振动的合成,可知合成后仍为简谐振动,则S2处的声压方程的可表示为

pL=ALcos(ωt+φL)

(20)

其中,振幅AL和初相位φL为

(21)

(22)

3 仿真分析与实验验证

3.1 驻波法测量讨论

为研究S2处声压振幅AL随距离L的变化规律,取η=0.1,R=0.95,λ=0.01,进行了仿真计算,结果如图3所示.

图3 AL随距离L的变化规律

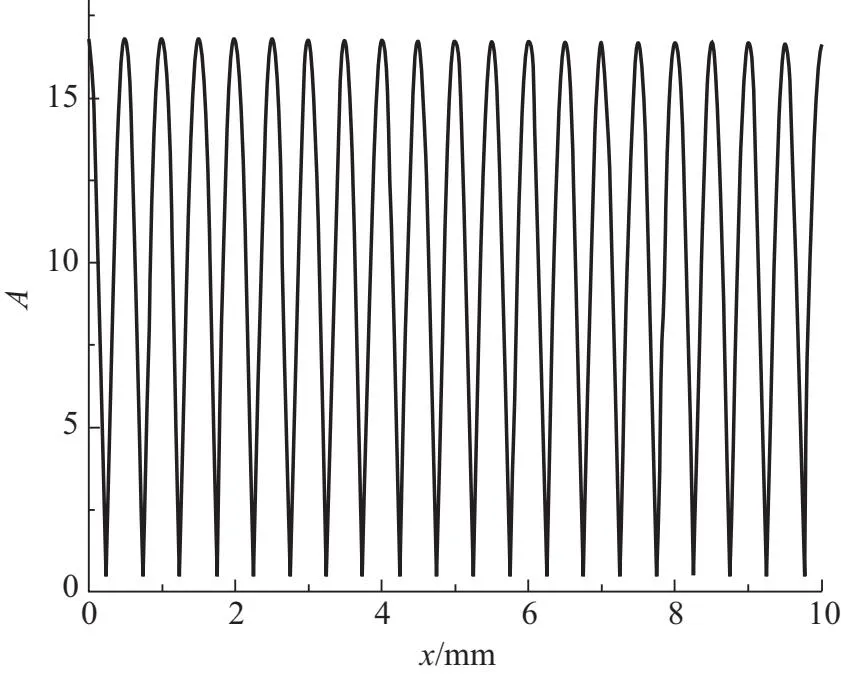
图4 固定L时的声压分布

图5 波列数对测量结果的影响

从图5中可以看到随着波列数的增大,各极大值的位置基本不变,但是极大值的幅值随这波列数增大而增大. 为进一步考虑声吸收系数对结果的影响,计算了η=1时的AL随距离L的变化情况,如图6所示.

图6 AL随距离L的变化规律

(23)

化简后有

(24)

当S1和S2的距离满足式(24)时,会出现声压极大值,即等式两侧函数的交点即为极值位置. 令R=0.9,绘制了声吸收系数η分别为0.04、0.4和4时的曲线,如图7所示.

图7 极值位置分布情况

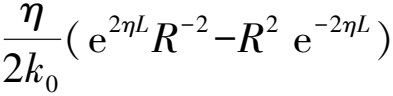
3.2 相位比较法测量讨论

从式(22)可以看到,φL并不是严格的周期函数,将其化简后可得

tan(φL)=f(L)tan(k0L)

(25)

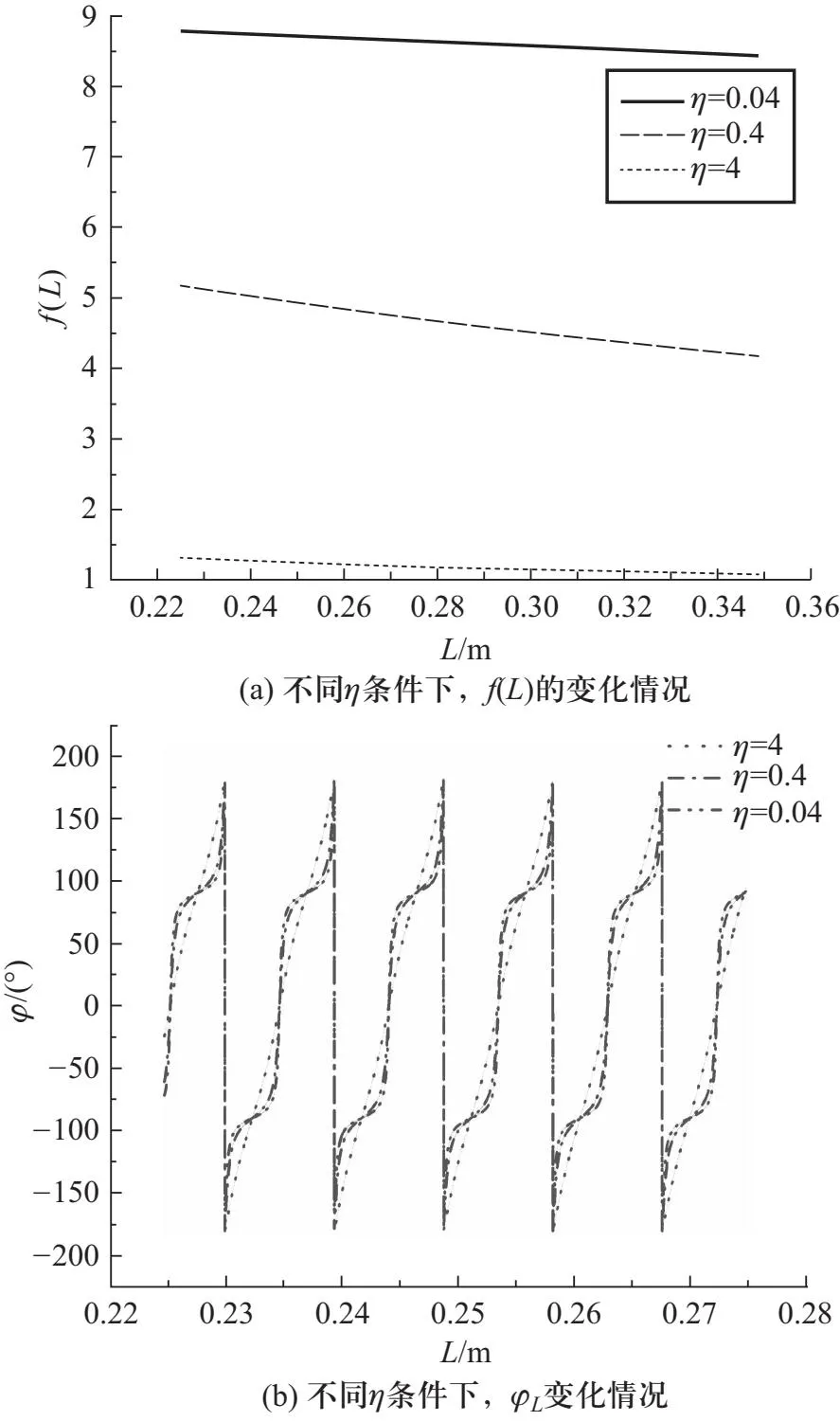
图8 相位比较法测量精度的影响因素分析

3.3 实验验证

为了验证本文建立的声压多次反射模型的正确性,利用SV-DH-8型声速测定仪、SVX-6型声速测定信号源和DS1102c型数字示波器,分别采用驻波法和相位比较法进行了实验测量,采用的超声波频率为37 kHz,实验室温度为20.6 ℃,空气相对湿度为41%,文献[15]给出当前实验条件下声吸收系数的测量值η=0.027 38,而声压反射系数R通常难以测量,因此部分文献采用式(13)对其进行估算,而实际上式(13)仅对无限大的理想交界面成立,导致这种估算具有较大的误差. 因此,本文利用式(21)对声压的实测值进行函数拟合,从而估算声压反射系数R,拟合结果如图9所示.

图9 驻波法声压拟合结果

声压反射系数的拟合值为R=0.305,拟合的相关系数为0.971 2,从图9中可以看到,实验结果与仿真结果吻合较好,很好的验证了本文模型的正确性. 从图9中可以发现,声压信号在极大值附近拟合较好,而在极小值附近吻合程度要差一些,其主要原因是极小值附近的声压信号受噪声等因素影响较大,因此,很难进行准确测量. 进一步将拟合得到的声压反射系数R=0.305代入式(22)可计算得到相位比较法的理论值,将其与实验测量值进行对比,结果如图10所示.

图10 相位比较法测量结果对比

从图10中可以发现,相位随距离的变化近似为线性关系,但由于相位求解采用反正切函数,相位测量值对距离较为敏感,因此,相位测量值存在一定的随机误差,使得其较为分散. 此外,实验中利用数字示波器测量相位,信号传输线中的噪声干扰也会对实验结果产生一定影响.

4 结论

本文从物理本质上分析了声速测量的原理,针对当前声速测量实验存在的疑问进行了详细的建模和理论推导,并利用得到的结果正确解释了实验现象. 相比于理想的驻波法模型,本文模型与实验结果吻合更好. 传统的驻波模型仅仅是与实际声压分布具有相同的极大值间距才得到了正确的测量结果,但并不能反应该实验的物理本质. 因此,声压的多次反射模型是更完善的理论模型,本文的研究对正确理解该实验的物理本质具有指导意义.