基于新型时空混沌系统的隐私图像加密算法
2024-02-29杜鹏崔琦王思翔董有恒李晖
杜鹏,崔琦,2,王思翔,董有恒,李晖
(1.西安电子科技大学网络与信息安全学院,陕西 西安 710126;2.国家市场监督管理总局信息中心,北京 100820;3.中国农业发展银行信息科技部,北京 100045;4.北京电子科技学院密码科学与技术系,北京 100070)
0 引言
随着通信技术的发展,图像由于其直观性和信息的丰富性越来越成为信息传输中的重要载体,特别是在社交网络和互联网中,图像不仅加快了信息传播的速度,也易于使人理解和识别。然而,随着传输图片的增多,很多存有隐私信息的图像也渐渐出现在互联网中,如个人的肖像照、证件照以及一些存有重要信息的报告图片等。不法分子很容易从中获取个人信息,甚至用于破解人脸识别系统等[1],因此在存储或传输时对于隐私图像进行加密处理显得尤为必要。现有的传统加密算法,如AES 等分组密码算法,主要是针对文件进行加密,由于图像中信息存在大量冗余,加解密时还需分组然后重构图像,影响加密效率,这大大限制了这类算法在图像加密的应用[2],传统序列密码算法RC4 已经被证明不太安全[3],因此也不适用于进行隐私图像加密,故亟需设计一类新型图像加密算法,该类算法应该高效且安全。
混沌系统是一类具有初值敏感性、遍历性以及长期不可预测性的确定非线性系统[4]。这类系统和加密算法中扩散性和随机性的要求十分吻合,因此大量基于混沌的图像加密算法被提出。文献[5]基于细胞神经网络超混沌系统和Logistic 映射提出一种高效率的视频图像加密算法,文献[6]利用新型三维离散混沌映射实现了对图像的扩散和混淆,文献[7]结合混沌映射和基因编码技术实现了对医疗图像的加密。然而,上述加密算法用到的混沌映射均是基于单一混沌系统,该类系统每次迭代仅能输出一个元素,输出密钥流的效率较慢,同时混沌系统在数字系统中运行时存在动力学特性退化的问题,因此并不能很好地适用于隐私图像加密。
耦合映像格(CML)的出现,大幅改善了上述问题[8]。基于CML 的时空混沌系统,利用格子之间的耦合关系相互扰动,有效地削弱了动力学退化的问题,同时CML 中的各个格子同步迭代并行运行,可以在短时间内产生大量的混沌序列,因此相比于单一混沌系统,基于CML 的时空混沌系统拥有更强的混沌特性,同时提高了生成序列的效率,也更适合进行隐私图像加密[9]。基于时空混沌系统的图像加密算法逐渐成为混沌图像加密的研究热点,其中包括基于交叉耦合映像格的时空混沌系统设计出的图像加密算法[10]、基于非线性耦合映像格[11]以及基于分数阶混沌系统的耦合映像格[12]等。然而,根据相关的对比分析[4,13],上述所设计的时空混沌系统往往存在弱混沌的现象,比如系统分岔图存在周期窗口或遍历性不好的问题,同时输出分布不均,易受到相空间重构或者回归映射分析攻击等针对混沌加密算法的攻击。同时,某些密钥固定的基于时空混沌的加密算法极易被选择明/密文破解,文献[14]提出一种针对置换-替换网络的混沌图像加密破解方法,解决了该类的12 种加密算法。
本文设计一种新型时空混沌系统,该混沌系统可解决单一混沌映射输出数据有限的问题,削弱动力学退化的影响,在控制参数可取范围内系统的输出不存在周期窗口,拥有较好的遍历性和随机性,输出序列可覆盖整个值域。基于该新型时空混沌系统提出隐私图像加密算法,以解决混沌图像加密图像密钥固定而无法抵抗选择明/密文攻击的问题,同时添加动态替换盒和两次异或来提高算法的安全性。
基于上述研究以及存在的问题,本文的主要贡献和创新点如下:
1)基于Henon 映射和CML 设计了一种新型时空混沌系统,即基于Henon 映射的置乱耦合映像格系统(PRSCML-Henon)。该混沌系统相比于单一的Henon 映射以及传统的CML 系统拥有更强的混沌特性。此外,PRSCML-Henon 在本文提到的近两年的新型时空混沌系统中,混沌特性较强,可生成随机性更好的混沌序列,适合应用于隐私图像加密算法。
2)基于PRSCML-Henon 系统设计了一种有效且可靠的隐私图像加密算法。该加密算法有如下特点:种子密钥与明文相关,在每次加密不同的明文图像时,生成的种子密钥和密钥流不同,因此可有效抵抗选择明/密文攻击;添加了非线性的替换操作,利用密钥流来生成替换盒,该替换盒会随着种子密钥的变化而发生变化,因此在每次加密不同明文时生成的替换盒也是不同的,可提高算法的安全性。
3)进行了两次与明文图像等长的异或操作,有效隐藏明文图像和密钥流本身的统计特性。
1 预备知识与设计原理
1.1 Henon 映射
Henon 映射是由法国数学家HENON 于1976 年提出,作为洛伦茨模型的庞加莱截面的简化模型[15-16]。该映射为离散的二维映射,其数学表达式如下:
其中:t代表时间维度,即迭代次数;x和y代表Henon映射的输出;a和b代表映射的控制参数,当a=1.4、b=0.3 时,映射处于混沌状态,输出的序列具有较好的随机性和长期不可预测性。
1.2 基于耦合映像格的时空混沌系统
传统的耦合映像格是由一个个格子构成的,每个格子中包含一个映射进行迭代,通常称之为底层映射,相邻格子之间通过耦合联系在一起。当底层映射为混沌映射时,便构成了时间和空间上都可处于混沌状态的时空混沌系统[17]。基于耦合映像格的时空混沌系统数学表达式如下:
其中:i(i=1,2,…,L)代表格子索引;t代表迭代次数;L为系统总的格子数;代表第i个格子在t次迭代时的当前值,需要注意的是,耦合映像格的边界一般默认为是周期的,即最左侧格子和最右侧格子看作是相邻的;ε(ε∈(0,1))为耦合强度;函 数f代表底层映射。传统的基于CML 的时空混沌系统,底层映射一般为简单的Logistic 映射,表达式如下:
其中:μ(μ∈(3,4))为控制参数,当μ>3.67 时该映射处于混沌状态,但当控制参数在3.84 附近时存在部分周期窗口,即弱混沌现象。
1.3 初等元胞自动机
元胞自动机(CA)最初是由文献[18]提出的,用来模拟自然界中的自我复制现象,是一个在空间和时间上都离散的动力学系统。一个典型的CA 由元胞、元胞空间、元胞邻居、迭代规则等构成。初等元胞自动机(ECA)是其中最为简单的一类元胞自动机[19]。ECA 的元胞空间是一维的,元胞邻居仅包括与该元胞相邻的两个元胞,同时每个元胞的状态仅有两种,可以表示为“0”或“1”。某一元胞下一时刻的状态由其本身和其元胞邻居当前的状态以及迭代规则所共同决定,ECA 与CML 类似,其边界亦是周期的,ECA 的迭代过程可表示为布尔函数:
其中:i和t分别代表空间维度和时间维度;代表第i个元胞在第t次迭代时的状态值;r为迭代规则;布尔函数fr的迭代结果是由迭代规则r所决定的。例如,当r=90 时,该布尔函数的迭代结果可表示为真值表,如表1 所示。
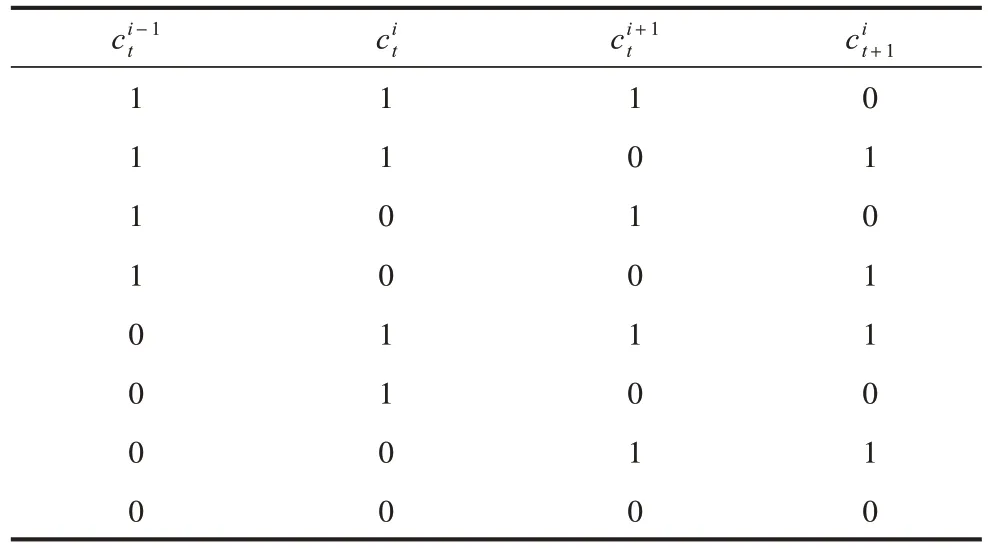
表1 布尔函数f90的迭代结果 Table 1 Iterative results of Boolean function f90
显然,由表1 可知,f90的迭代结果即表格中的最后一列就是数字“90”的二进制表达方式。故对于ECA 来说,其共有256 种迭代规则,根据每种迭代规则所表现的不同动力学行为,可分为5 类:无效规则,固定点规则,周期规则,局部混沌规则和全局混沌规则。其中,全局混沌规则控制下的ECA,其迭代结果呈现出长周期和混沌特性,根据文献[20],共有34 种全局混沌规则,如图1 所示。

图1 全局混沌规则 Fig.1 Global chaotic rules
由于ECA 是一类在时间和空间上均离散的动力学系统,并不存在动力学退化的问题,因此全局混沌规则控制下的ECA 其输出的序列可以作为混沌系统的伪随机扰动来削弱动力学退化的问题,以提高系统的混沌特性。
2 新型时空混沌系统及其特性
2.1 系统描述
本文所提出的新型时空混沌系统是基于Henon映射及CML 设计的。Henon 映射作为底层映射,其中一维作为输出,另一维作为置乱耦合的控制信号,此外ECA 的输出作为扰动以提高系统的混沌特性。该新型时空混沌系统,本文称为基于Henon 映射的伪随机置乱耦合映像格系统(PRSCML-Henon),该系统的数学表达式如式(5)~式(7)所示:
其中:i和t分别代表空间维度和时间维度;函数f代表Henon 映射,该映射的控制参数为常数a=1.4、b=0.3,使该映射处于混沌状态;x*和y*为各个格子经过Henon 映射迭代一次的中间值。
其中:函数sort(y*)是对向量y*进行升序排列;Iy是升序排列后,原始元素的索引在升序排列后的乱序结果;x*则通过向量Iy实现了伪随机置乱。
其中:ε为耦合强度,则将置乱后的中间值x**和y**进行耦合运算;mod 1 运算的目的是保留运算结果的小数部分;扰动p(i,Ct)由ECA 第t次迭代结果得到。
p(i,Ct)计算过程如下:
其中:Ct代表ECA 第t次迭代的结果,即各个元胞的状态值构成的向量;i与式(7)中相等,此处代表元胞索引;函数bin 2dec 的目的是将二进制数转化为十进制数;m为格子的中间位置索引;L为格子总数。因此,式(8)就是将ECA 迭代结果的中间32 bit 转化为十进制数,并量化到(0,1)区间上得到扰动的绝对值;乘Ct(i)-0.5 的目的是使得每个格子虽然每次迭代时添加的扰动绝对值相同,但正负符号不同,且该扰动的符号是随ECA 迭代伪随机变化的。
PRSCML-Henon 系统利用Henon 映射的其中一维控制格子实现置乱,以加快能量传递速度,提高系统的混沌特性。同时,引入ECA 的输出作为伪随机扰动,进一步削弱了动力学退化的影响。需要注意的是,该新型时空混沌系统的输出有两维,其中,输出x作为最终的输出,而y作为中间参数不输出。
2.2 混沌特性分析
为了凸显本文提出的新型时空混沌系统设计的有效性,本节引入传统的基于邻近耦合的时空混沌系统CML 和单一Henon 映射进行对比分析。
2.2.1 分岔图
分岔图可以直观地判断混沌系统的非周期性、遍历性等混沌特性。单一Henon 映射、传统CML 系统以及PRSCML-Henon 系统的分岔图如图2 所示。

图2 分岔图Fig.2 Bifurcation diagram
图2(a)~图2(d)为单一Henon 映射不同控制参数下不同输出对应的分岔图。其中,图2(a)和图2(b)是控制参数b固定的条件下输出随a变化的分岔图,显然无论是输出x还是y,当控制参数a<1.2 时,Henon 映射存在明显的固定点和周期点,只有接近1.4 时,映射的非周期性和遍历性才较好。与之对应,在图2(c)和图2(d)中,当控制参数a固定时,输出随b的变化也呈现同样的趋势,在b接近0.3 时,输出所占据的值域范围才较大,拥有较好的遍历性。同时,由图2(e)可知传统的CML 由于底层映射为简单的Logistic 映射,因此分岔图在控制参数小于3.67 时存在明显的周期窗口,只有在其接近于4 时才具备良好的遍历性,即输出可以充满整个区间。
与上述情况不同,本文提出的新型时空混沌系统PRSCML-Henon,对于输出x,无论控制参数a和b如何变化,在整个区间上都不存在固定点或者周期点,且输出可以覆盖整个值域[0,1],如图2(f)和图2(h)所示,而输出y由于进行了排序运算,因此在控制参数较小时存在部分值无法取到,但y并不作为系统的输出,而作为中间值使用,对后续生成序列的随机性影响不大,因此出现这种情况是可接受的。
2.2.2 K 熵分析
Kolmogorov-Sinai 熵(简称K 熵)是用来衡量时空混沌特性强弱的重要参数[21],K 熵与系统中各个格子混沌映射的李雅普诺夫指数密切相关。K 熵分为K 熵密度和K 熵阔度,两者的计算过程如下:
其中:λ+(i)代表由第i个格子生成序列所求得的正的李雅普诺夫指数,本文采用Wolf 法[22]求取,若λ+(i)为负值,则令其为0;L为系统的格子总数;h代表K 熵密度,能够反映系统整体的混沌特性强度,h越大代表混沌特性越强;hhu代表K 熵阔度,即处于混沌状态的格子数占比,其理想值为“1”。
为凸显PRSCML-Henon 系统的优越性,引入除传统CML 系统外新近(均为2022 年)提出的时空混沌系统作为对比,它们分别为:基于动态耦合强度和交叉耦合的改进型Tent-动态交叉耦合映像格系统(TDCCML)[23],基于双参数分形排列向量和耦合映像格的时空混沌系统(DPFSV-CML)[24]。
上述4 类系统的K 熵密度和K 熵阔度分别如图3 和图4 所示。

图3 K 熵密度Fig.3 K entropy density
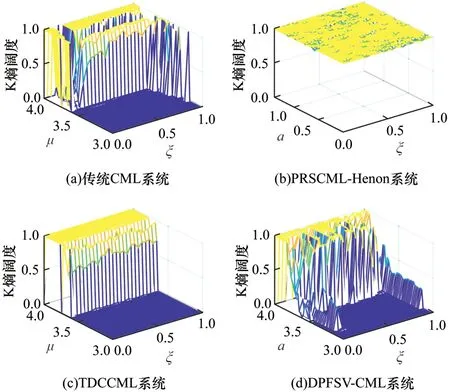
图4 K 熵阔度Fig.4 K entropy breadth
由图3(a)可知,传统CML 系统仅在控制参数大于3.67 时才存在正的K 熵密度,而与之对应的图3(b)中,本文所设计的PRSCML-Henon 系统在整个控制参数区间上,其K 熵密度均大于0,而在图3(c)和图3(d)中,K 熵也只有在控制参数大于3.67 时才存在正值,这说明要使得系统TDCCML 和DPFSV-CML 处于混沌状态,控制参数的可取范围是有限的,同时由 图3(d)可知,DPFSV-CML 系统的K 熵密度对耦合强度也十分敏感,耦合强度在0.5 附近时,K 熵较大,而在接近0 或1 时K 熵密度较小,对于TDCCML 和PRSCML-Henon 系统则不存在这种问题,两种系统对耦合强度不敏感,在整个耦合强度区间上其K 熵密度的变化基本是一致的。进一步地,由 图4(a)~图4(d)可 知,传 统CML 系 统、TDCCML 系统及DPFSV-CML 系统仅在控制参数大于3.67 时才存在理想值“1”,而PRSCML-Henon 系统的K 熵阔度在整个控制参数区间上均接近于“1”,也就是说大部分格子在任意控制参数下均处于混沌状态。综上所述,所提新型时空混沌系统PRSCMLHenon 的混沌特性不仅强于传统CML 系统,而且还强于新提出的TDCCML 和DPFSV-CML 系统,可见置乱耦合和扰动的存在大幅增强了新型时空混沌系统的混沌特性,这为后续该系统作为密钥流产生器提供了良好性能基础。
3 隐私图像加密算法
鉴于PRSCML-Henon 系统所具备的良好混沌特性,如非周期性和遍历性以及混沌系统本身的初值敏感性,本文进一步基于该系统设计了一种隐私图像加密算法。
该加密算法由4 个部分构成:种子密钥生成,混沌系统初始化,密钥流生成与量化以及图像加解密。
1)种子密钥生成
首先利用SHA-256 计算明文的哈希值,然后将该哈希值与用户设置的256 bit 秘密密钥相异或,得到了256 bit 的种子密钥:
其中:HASH 函数代表SHA-256 算法,该算法保证了计算的单向性,使得敌手无法通过HASH 值得到明文的有效信息,同时该过程使得种子密钥与明文相关,使得选择明/密文攻击无效,提高了算法的安全性。此外,SHA-256 算法可以有效地将明文的微小变化反映出来,有效提高了算法的扩散性,K作为种子密钥在加解密端通过秘密信道进行传输。
2)混沌系统初始化
PRSCML-Henon 系统需要初始化的值包括ECA的初值和迭代规则、置乱耦合映像格的初值、系统的初始迭代次数等。为了保证系统具备良好的混沌特性,令控制参数为固定值a=1.4、b=0.3,同时系统中格子总数和元胞总数均为256,与种子密钥长度一致。
ECA 中各元胞的初值即为256 bit 的种子密钥K,其迭代规则由K的Hamming 重量决定,计算过程如下:
其中:r代表全局混沌规则在图1 中的索引,由于共有34 个不同的规则,此处进行模34 的运算,并加“1”,使r为1~34 的整数。
接着将K分为8 个32 bit 二进制数,并进行如下的量化:
其中:xi和yi代表各个格子的初值构成的向量;K(1:32)代表种子密钥的第1~32位,以此类推,函数bin 2dec将二进制数转化为十进制数。初始化上述4 个格子(第1、65、129、193 个格子)后,再由Henon 映射迭代初始化完成余下的格子,初始化过程如图5所示。

图5 各格子初始化过程Fig.5 Initialization process of each lattice
耦合强度ε由K的中间32 bit 决定,计算过程如下:
其中:函数bin 2dec 与式(15)中的作用相同。此外,算法还设置了初始迭代次数n0,它的值由K的中间10 bit 决定,计算过程如下:
显然n0为区间[10,1 033]中的整数。系统在生成密钥流前,会预先迭代n0次,并不输出,以此来隐藏初始值,提高系统的安全性。
3)密钥流生成与量化
系统初始化完成后,便迭代生成密钥流,生成密钥流的长度由明文图像的大小所决定,一般图像的存储单元为无符号的8 bit 二进制数,假设明文图像的存储单元共有N个,则需要由PRSCML-Henon 系统迭代生成长度为3×N+256 的密钥流。密钥流共分为4 个部分,如图6 所示。

图6 密钥流的构成Fig.6 Constitute of key stream
在图6 中,初始异或和最终异或部分的密钥流需要量化为无符号的8 bit 二进制数,量化过程如下:
其中:函数floor 的目的是向下取整;X为时空混沌直接输出的在区间(0,1)上的序列;Y为量化后的用于异或的密钥流。
4)隐私图像加解密
与生成密钥流的4 个部分相对应,对于隐私图像的加密共分为4 个步骤:初始异或,替换,置换与最终异或,该流程如图7 所示。

图7 加解密流程Fig.7 Procedure of encryption and decryption
在图7 中,初始异或和最终异或就是利用与明文图像等长,且经过量化后得到的密钥流进行简单的按位异或运算。初始异或是利用密钥流与明文图像进行异或,而最终异或是将置乱后得到的中间值与密钥流进行异或。
替换则是由密钥流的替换部分生成替换盒,也叫S 盒,然后由该S 盒进行非线性的替换过程。S 盒的生成过程如下:
其中:KSSbox为密钥流中的替换盒部分;sort 函数是对KSSbox进行升序排列,并得到其中元素升序排列后的乱序索引Ik,利用该索引向量减1 便能够生成只含有0~255 整数的替换盒SSbox。该替换盒的输入为初始异或后得到的无符号的8 bit 二进制数,该数加1 作为索引,输出该索引对应下的替换盒中的元素,完成替换操作。
置换过程与置乱耦合过程与式(6)类似,利用密钥流的置乱盒部分对其进行升序排列,得到乱序后的索引,利用该乱序索引实现对图像存储单元的乱序。
由于种子密钥相同,加解密过程生成的密钥流是完全相同的,因此解密过程与加密过程相对称,此处不再赘述,需要注意的是,解密过程中使用的替换盒为式(19)生成的S 盒的逆。
4 加密结果与分析
为验证该算法在隐私图像加密中的有效性,使用示例体检单和示例身份证图像作为传输对象进行加解密,加解密的结果如图8 和图9 所示(彩色效果见《计算机工程》官网HTML 版,下同)。

图8 体检单加解密结果(灰度图)Fig.8 The encryption and decryption of medical examination report(gray map)

图9 身份证加解密结果(彩图)Fig.9 Encryption and decryption results of identity card(color map)
由图8 和图9 可知,无论加密对象是体检单类型的灰度图,还是证件照类型的彩图,利用本文算法均可以有效隐藏原始隐私图像的信息,且加解密过程是无失真的。
为进一步验证该加密算法的安全性和可靠性,本文将引入统计分析、安全性分析以及鲁棒性分析。
4.1 统计分析
4.1.1 直方图
直方图可以直观地判断加密结果的有效性,密文的像素直方图分布越均匀平滑,则说明加密质量越好。上述体检单和身份证加密结果的直方图如图10 所示,其中,图10(a)左图为明文(体检单),右图为密文(体检单),图10(b)上为明文(身份证),下为密文(身份证)。

图10 直方图加密结果分析Fig.10 Analysis of histogram encryption results
图10 中各个直方图的横坐标代表像素值,纵坐标代表当前像素值下的总像素数。其中对于彩图,分别对红绿蓝三色通道进行了统计。由图10 可知,无论加密的隐私图像是灰度图还是彩图,密文的直方图分布总是均匀的,说明了该加密算法生成的密文图像接近于真随机图像。
4.1.2 相关性分析
由于图像的信息冗余较大,明文图像中相邻像素的相关性较强,为了更好地隐藏原始图像的信息,密文图像中相邻像素之间的相关性应较弱,甚至无关。图11 和图12 所示为明文和密文图像相邻像素的相关性对比,其中,在图11(a)、图11(b)中,从左到右分别为水平、垂直、对角线方向,在图12(a)、图12(b)中,第1~3 行分别为水平、垂直、对角线方向。

图11 体检单明文与密文的相关性分析(灰度图)Fig.11 Correlation analysis of plaintext and ciphertext of medical examination report(gray map)
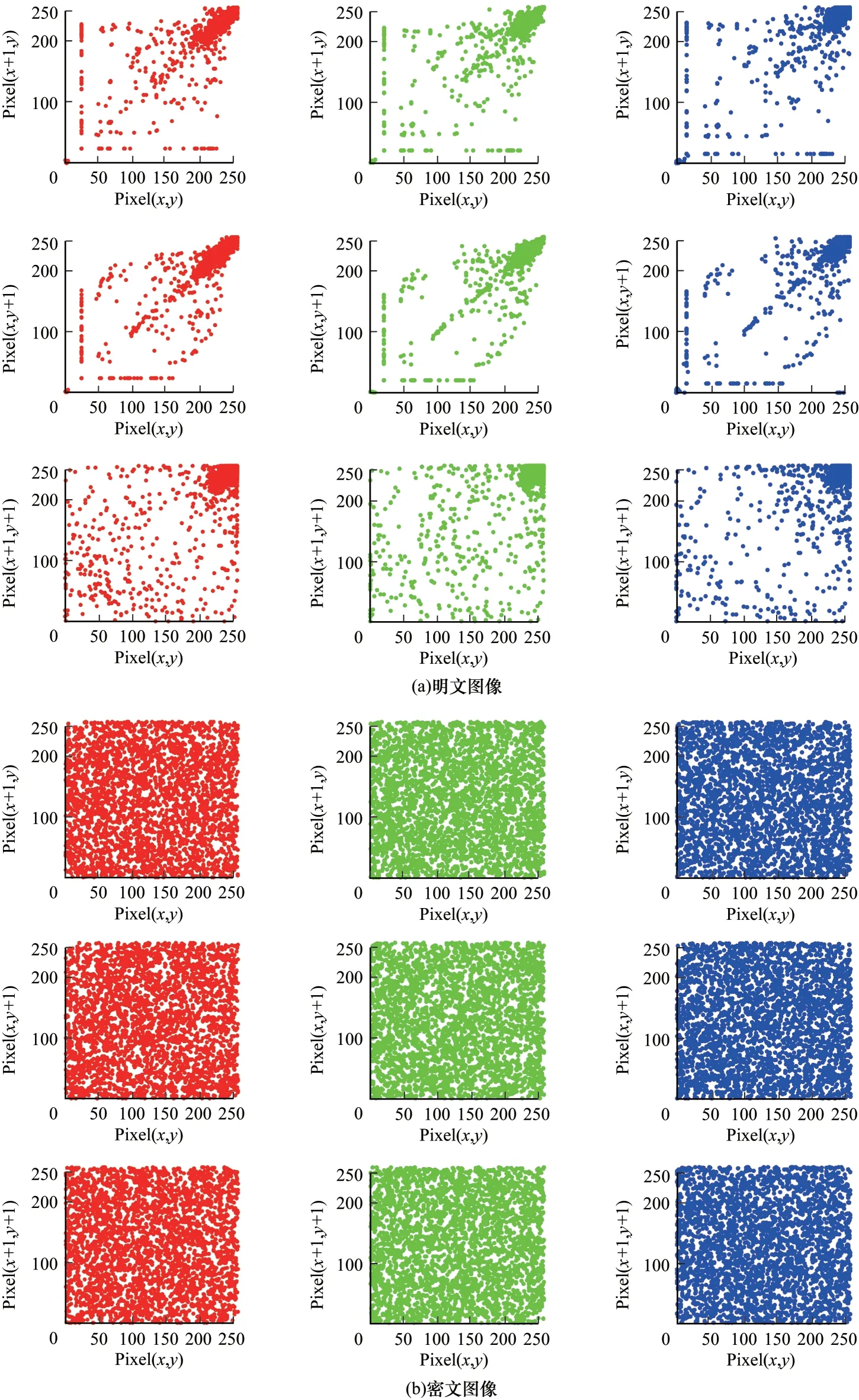
图12 身份证明文与密文的相关性分析(彩图)Fig.12 The correlation analysis of plaintext and ciphertext of identity card(color map)
由图11(a)和12(a)可知,明文图像中任意方向相邻的像素,像素值都是相近的,因此其分布基本在图中的对角线上。由图11(b)和图12(b)可知,在密文图像中,相邻像素之间几乎是无关的,其分布接近于噪点。进一步地,计算上述图像中相邻像素的相关性,如表2 和表3 所示,其中,R 代表红色,G 代表绿色,B 代表蓝色。
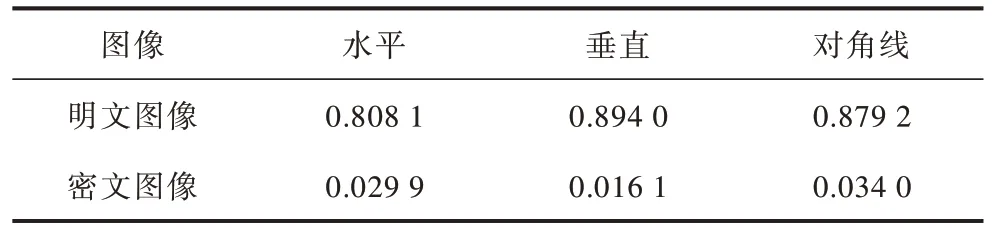
表2 体检单(灰度图)相关性分析 Table 2 The correlation analysis of medical examination report(gray map)

表3 身份证(彩图)相关性分析 Table 3 The correlation analysis of identity card(color map)
由表2 和表3 可知,在明文图像中,相邻像素的相关性均大于0.5,甚至接近于0.9,具有强相关性,但经过本文加密算法加密后,密文图像中相邻像素的相关性始终小于0.1,具有极弱的相关性。
进一步地,对Lena 图像进行加密,并与其他方案进行对比分析,对比结果如表4 所示。
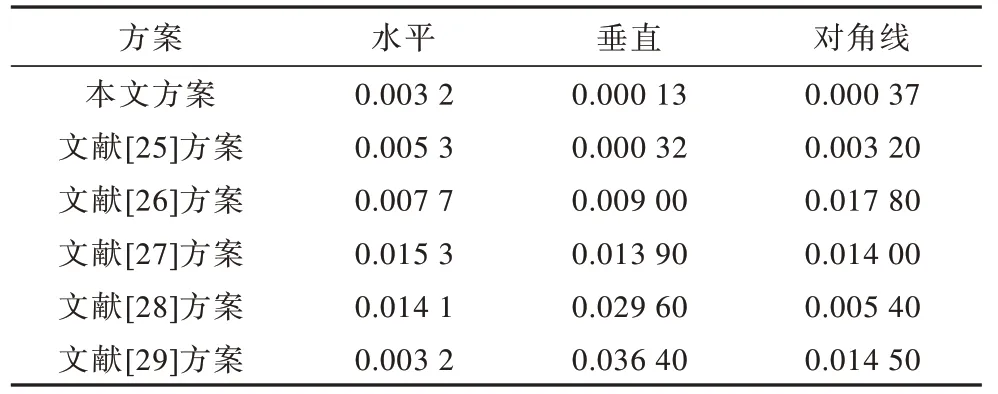
表4 Lena 图像(灰度图)的相关性分析 Table 4 Correlation analysis of Lena image(gray map)
由表4 可知,经本文方案加密后,密文图像相邻像素之间的相关性显著降低,并且低于其他方案。综上所述,相比其他方案,本文所提出的加密方案能够更好地降低相邻像素之间的相关性,有效隐藏明文信息。
4.1.3 信息熵分析
对于存储单位为无符号8 bit 二进制数的图像,其信息熵越接近8,则说明随机性越好,所含的有用信息越少。为了使本文加密算法的有效性更加可靠,不仅对上文两张隐私图片进行信息熵分析,另外还对以南加州大学信号与图像处理研究所标准图像数据库中的一些图片(见图像编号)也进行了分析,结果如表5 所示。

表5 信息熵分析结果 Table 5 Analysis results of information entropy
由表5 可知,原始明文的信息熵都远离8,这是由于其中含有有用信息较多,而经过加密后,密文图像的信息熵都大于7.999,且十分接近于8,因此密文图像具有较好的和真随机图像类似的随机性,有效地隐藏了原始图像的有用信息。进一步地,加密Lena 图像,与其他图像加密方案的对比结果如表6所示。

表6 Lena 图像(灰度图)的信息熵对比分析 Table 6 Comparative analysis of information entropy in Lena image(gray map)
从表6 可以看出,本文方案与文献[25]的加密结果信息熵最接近8。因此,相比其他方案,本文方案加密后获取的Lena 密文图像更接近于真随机图像。
4.2 安全性分析
4.2.1 密钥空间
本文所提算法的秘密密钥和传输的种子密钥均是256 bit 的二进制数,其密钥空间远大于2128,敌手想要通过暴力破解的方法去猜测密钥,所需要的时间在实际中是不可接受的,因此可以抵抗穷举攻击。
4.2.2 密钥流随机性测试
本文引入随机性测试套件NIST SP800-22 对PRSCML-Henon 系统生成的密钥流进行随机性测试,该测试套件包含15 项子测试,每项测试的p值用于判断其是否通过该项测试,p值越大越好,当p值大于0.01 时,则认为通过该项测试,且置信度为0.01[30]。令PRSCML-Henon 系统中格子数为256,迭代生成256 组序列,采用式(18)对序列进行量化,每组序列的长度为106bit,根据NIST 官方文件,对于256 组序列只有通过率达到或超过248/256,测试序列则被判定为具备良好的随机性且无法与真随机数区分。PRSCML-Henon 系统输出序列的测试结果如表7 所示,其中,标记有*的子测试表示该子测试下含多个小测试,因此通过率那一列以“—”表示,数字为通过该项测试的最少样本数/测试样本总数,此时p值给出的是这些小测试中的均值,“通过”代表序列在这些小测试下的通过率均能够达到要求,即序列的随机性能够通过这些小测试。

表7 NIST 测试结果 Table 7 Test results of NIST
由表7 可知,本文所设计系统PRSCML-Henon生成的序列经过量化后得到的密钥流能够通过NIST 的随机性测试,包括全部的15 项子测试。NIST 随机性测试是极为严格且权威的,通过此测试说明密钥流的随机性是满足安全性要求的。
4.2.3 密钥敏感性
一个安全可靠的密码算法对密钥应具备良好的敏感性,即发生微小改变的密钥无法正确解出或部分解出密文。本文改变密钥中的某一位(包括第1 位、中间位以及末位),或改变整个密钥,使其取反。利用改变后的密钥解出的结果如图13 和14 所示。在图13 和14 中,KEY1、KEYmid、KEYend、KEY~分别代表种子密钥改变第1 位、中间位、末尾以及全部取反的值,图片为密文解密后的结果。可以看出,无论是灰度图还是彩图,在密钥发生微小改变后密文均不能正确解出或部分解出,说明该算法具备良好的密钥敏感性。

图13 体检单(灰度图)密钥敏感性测试Fig.13 Key sensitivity test of medical examination report(gray map)

图14 身份证(彩图)敏感性测试Fig.14 Key sensitivity test of identity card(color map)
4.2.4 扩散性
理想的图像加密算法是当明文发生微小变化时,密文也应地相应发生巨大的变化,这就要求加密算法具有良好的扩散性,即雪崩效应。这里引入归一化像素变化率(NPCR)和统一平均变化强度(UACI)来衡量明文图像发生一位变化时,密文图像发生的变化。NPCR 和UACI 的计算过程如下:
其中:C1和C2分别代表不同明文生成的密文图像;C1(i,j)代表图像中第i行、第j列的像素值;M×N代表图像的尺寸;F为图像中支持的最大像素值,即255。
任意改变明文图像中的某一像素值,得到的密文图像和原图像之间的NPCR 和UACI 如表8 和表9所示。同样地,为了使结果更具普适性,此处引入数据库中的标准图片进行测试,测试结果如表8 所示。根据文献[13,31],不同尺寸下的图像其NPCR 和UACI 是有临界值的,如表9 所示。
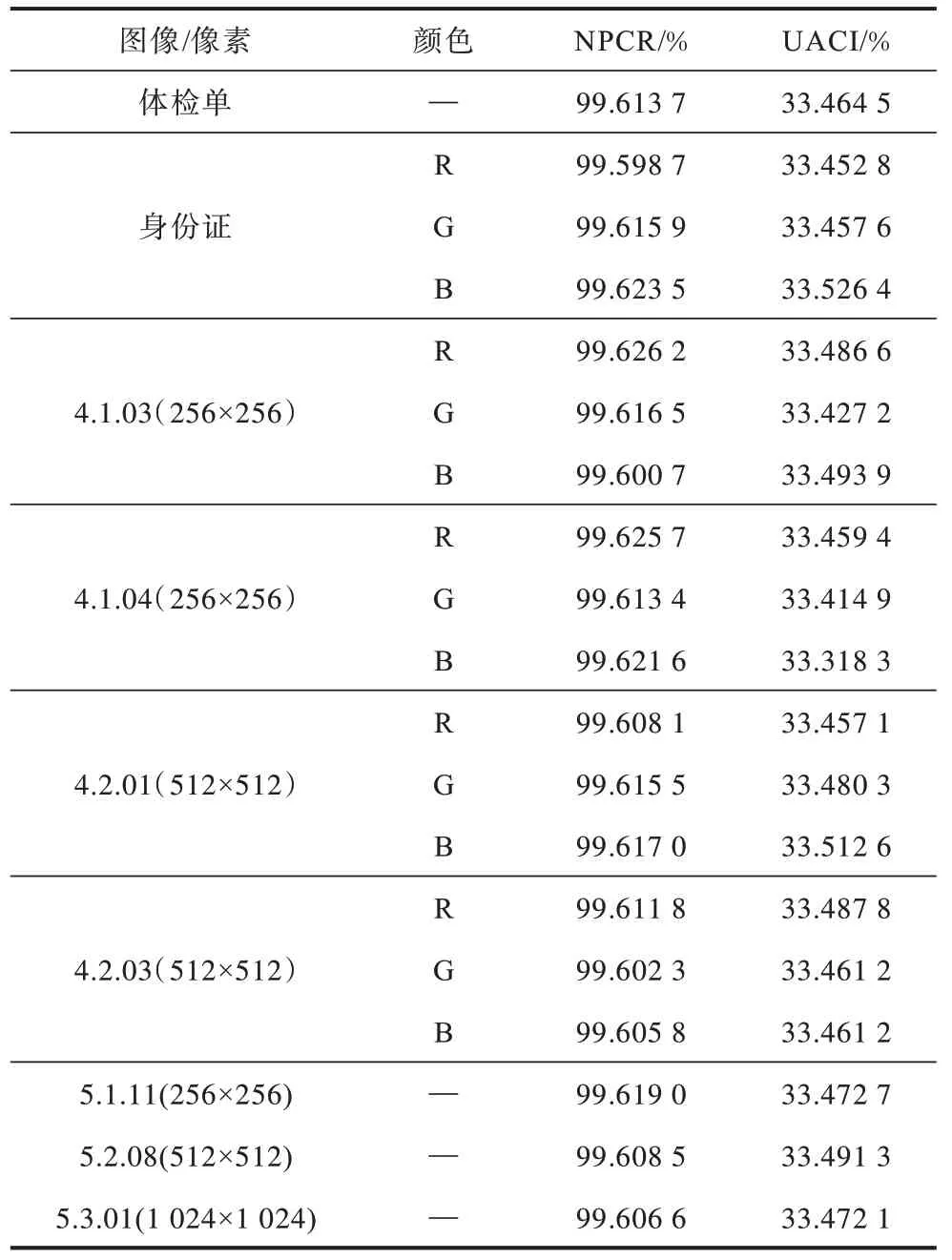
表8 扩散性分析 Table 8 Diffusion analysis
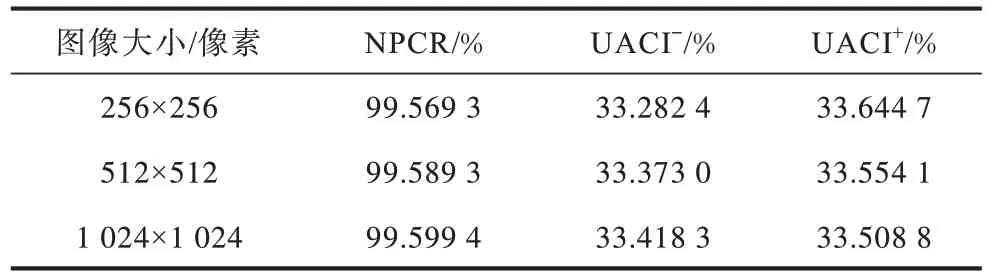
表9 NPCR 和UACI 的临界值 Table 9 Critical values of NPCR and UACI
只有当NPCR 的值大于临界值、小于100%、UACI 的值处于区间[UACI-,UACI+]时,表明两张图像C1和C2近似于随机生成,且相互无关。显然表8中标准数据库中的图像,其原始图像得到的密文和改变任意像素值后得到的密文之间的NPCR 和UACI 均处于临界值内,说明本文所提出加密算法具有良好的扩散性。
4.2.5 抗选择明/密文攻击
只有当密钥为固定值时,利用不同的明/密文对才能够实现选择明/密文攻击,破解出密钥。然而本文所提算法种子密钥与明文HASH 值相关,当明文发生变化时,种子密钥必然发生变化,所生成的密钥流由于算法良好的扩散性,也会发生巨大的变化。这就导致当敌手试图进行选择明/密文攻击及所选明密文对发生变化时,种子密钥也会随之发生变化,不再固定,因此选择明/密文失效。综上所述,该隐私图像加密算法能够抵抗选择明/密文攻击。
4.3 鲁棒性分析
密文在公共信道传输时,难免会受到噪声的影响,或者敌手的阻塞攻击。因此,加密算法应具备较好的鲁棒性,即使密文发生了一些篡改或阻塞,依旧能够正确解出明文。为验证本文所提算法的鲁棒性,向密文图像中添加不同强度的椒盐噪声,并阻塞不同大小的部分密文,使用正确种子密钥解出的结果如图15~图17 所示。

图15 噪声鲁棒性分析Fig.15 Robust analysis about noise

图16 体检单阻塞攻击后的解密结果Fig.16 Decryption results after medical examination report blocking attack

图17 身份证阻塞攻击后的解密结果Fig.17 Decryption results after identity card blocking attack
由图15~图17 可知,当传输的密文添加的椒盐噪声强度为0.1 时,依旧可以较为清晰地解出明文。而当遭受阻塞攻击时,即当丢失信息低于图片大小的1/2 时,解密结果中依旧能够依稀看到明文图像中的信息。综上所述,本文提出的隐私图像加密算法能够有效抵抗信道中的噪声和阻塞攻击,具有较好的鲁棒性。
4.4 效率分析
RSCML-Henon 系统中各个格子是并行运行的,因此密钥流生成与量化的过程相比其他混沌加密算法要更快,效率更高。同时,本文提出方案的加密过程又相对简单,因此整个加密方案的运行速度很快。不同方案在处理器固定主频下加密512×512 像素灰度图的平均时间消耗如表10所示。显然,在加密相同大小的图像条件下,尽管处理器主频只有2.20 GHz,但本文方案为所有方案中最快的,仅耗时0.127 s,效率较高。

表10 效率分析 Table 10 Efficiency analysis
5 结束语
基于Henon 二维混沌映射和耦合映像格,本文提出一种新型的时空混沌系统,即伪随机置乱耦合映像格系统PRSCML-Henon。相比于单一Henon 映射、传统CML 系统以及其他新型时空混沌系统,该系统均具有更好的非周期性、遍历性和强混沌特性,输出的密钥流随机性也更好,更适合于进行隐私图像加密。在PRSCML-Henon 系统的基础上,本文提出一种隐私图像加密算法,安全性分析结果表明,该算法相比其他混沌图像加密算法具有更好的随机性、扩散性及可靠的安全性,同时拥有较好的鲁棒性和较快的加密速度。
