基于AVX512 的格密码高速并行实现

雷斗威，何德彪，罗敏，彭聪

（武汉大学国家网络安全学院，湖北 武汉 430072）

0 引言

随着量子计算的迅速发展，现有的公钥密码体系受到了严重威胁。Shor 量子算法［1］利用量子计算机，可在多项式时间内破解大整数分解问题和椭圆曲线上的离散对数问题，从而攻破现有的公钥密码算法（RSA）和椭圆加密算法（ECC）。为了应对量子计算带来的威胁，能够抵抗量子攻击的密码即后量子密码（PQC）成为国内外的研究热点。

美国国家标准技术研究院（NIST）于2016 年开启了后量子密码标准的征集活动，旨在提出PQC 标准，以应对随时可能到来的量子计算的威胁。格密码因性能与安全性的优秀表现，在后量子密码标准征集活动中占据了重要地位。经过多年的筛选和评估，NIST 于2022 年5 月确定 了4 个PQC 标准算 法，涵盖公钥加密（PKE）、密钥封装（KEM）和数字签名，其中3 个算法是基于格的，可以看出格密码在PQC中的重要地位。

Kyber 是NIST 确定的4 个PQC 标准算法之一，安全性基于模误差学习（MLWE）问题。简单而言，判定性MLWE 问题是指：给定上的随机矩阵A以及上服从特定分布的s和e，区分(A，t=As+e)和随机选取的(A，t)是困难的。搜索性MLWE 问题是指：给定随机矩阵A以及t=As+e，其中s和e服从上的某些分布，求得s是困难的。现有的量子算法并不能有效地解决MLWE 问题，从而保证了Kyber的抗量子安全性。

随着PQC 标准的确定，为了后续的推广和落地工作，对标准算法的高速实现的需求也日益增加。Kyber 包括一组PKE 算法以及利用Fujisaki-Okamoto转换得到的KEM 算法。由于Fujisaki-Okamoto 转换主要是哈希（Hash）操作，并非实现的重点，因此主要聚焦于对其PKE 算法的优化实现。本文基于512位高级向量扩展（AVX512），针对不同安全级别下的Kyber进行高速实现。根据Kyber 中q为12 bit 的特点，使用16 bit对其进行存储与运算，将512 bit寄存器分为32组16 bit 进行并行处理，实现32 路并行多项式运算。同时，利用惰性模约减的思想大大减少模操作的次数，充分发挥了16 bit存储空间的性能。在抽样过程中，利用AVX512 每次同时产生8 组伪随机比特串并对其进行合理分配，从而高效完成了对多项式的抽样。

1 相关工作

为了更好地构建格密码，REGEV［2］提出容错学习（LWE）问题，使得格密码方案的构造更加便捷。为了得到更优的计算效率，LANGLOIS 等［3］将LWE问题进行了扩展，得到了其模格形式MLWE，极大提高了格 密码的 计算效 率。BOS 等［4］基 于MLWE 问题，构建了选择明文不可区分（IND-CPA）安全的公钥加密方案，并使 用Fujisaki-Okamoto 转换［5］，得到了选择密文不可区分（IND-CCA）下安全的密钥封装方案。SEILER［6］利用高级向量扩展2（AVX2）指令集，加速实现了快速数论变换（NTT），并将其运用到格密码方案NewHope 上，获得了较好的性能提升。LONGA 等［7］针对特殊的素数q，提出一种新的模约减技巧，提高了模约减效率，并利用该技巧加速NTT的实现。GUERON 等［8］利用冗余抽样技术，提高了拒绝抽样的成功率，降低了对伪随机比特串的需求，同时结合AVX2 指令集，实现了高效的并行抽样。ROY［9］利用AVX2，并行实现了不同安全级别下的格密码算 法Saber。CABRAL 等［10］利 用AVX512 指 令集，以2 种不同的方式并行实现了安全哈希算法3（SHA-3）系列函数：第1 种方式是通过将函数内部并行化，提升了单个函数的执行效率；第2 种方式是同时执行8 组不同输入的SHA-3 函数，从而可以同时输 出8 组不同 的Hash 运算结果。ALKIM 等［11］在ARM Cortex-M4 处理器上实现了Kyber 和NewHope两种格密钥方案，填补了该方面实现的空白。ALKIM 等［12］对RISC-V 指令集进行扩展，并基于该扩展设计一种非常紧凑的PQC 软硬件协同实现方式，获得了较大的性能提升。WONG 等［13］设计一种平衡速度和资源的架构，并用该架构在现场可编程门阵列（FPGA）上实现了SHA-3 系列函数，实验结果显示：最终吞吐量达到较为理想的16.51 Gb/s。顾丽红等［14］通过分析AES 加解密算法，结合龙芯平台体系结构特征，提出基于多媒体指令扩展（SIMD）优化AES 性能的方法，获得了较好的性能提升。KARMAKAR 等［15］研究了Saber 在资源受限的ARM Cortex-M 系列微控制器中的实现方式，并针对速度和内存资源的平衡进行优化，为未来物联网设备中使用格密码方案做好了前期准备工作。FRITZMANN 等［16］针对格密码方案NewHope、Kyber和Saber 提出一系列硬件加速器，并将其整合进RISA-V 的流水线，同时增加了29 条新的RISA-V 指令集，并在FPGA 上进行了模拟，最终提升了格密码方案的实现性能。ZHOU 等［17］针对Dilithium 方案提出一种基于FPGA 的软硬件协同处理方式，提高了实现效率。郭渝洛等［18］提出一种基于SIMD 的并行傅里叶空间图像相似度算法，经该算法优化后的程序可获得平均5.132 倍的加速，并且具有较强的鲁棒性。

2 相关知识

2.1 基本符号和定义

2.2 快速数论变换

对于环Rq=Zq[X]/(Xn+1)上的多项式乘法，如果直接进行相乘，则计算复杂度是O(n2)。在格密码方案频繁使用多项式相乘的情况下，效率低下。通过快速数论变化可以将多项式乘法的计算复杂度从O(n2)降到O(nlbn)，从而有效提高计算效率。

NTT 是有限域上的离散傅里叶变换，详细内容可参见文献［19］，下面对其核心思路进行概括描述。在Kyber 所选参数中，n取256，满足n|q-1 且n=2d（d=8）的条件，因此有限域Zq上存在n原根，记作ζn，满足条 件且那么环Rq=Zq[X]/(Xn+1) 可以写作另一种形式Rq=通过利用环上的中国剩余定理［20］可以得 到，其中×表示直积。利用同构性质，可以将环上的多项式计算投射到环上。继续对环使用环上的中国剩余定理并重复迭代该过程，最终可以得到同构

2.3 Kyber 和AVX512 指令集

Kyber 详细算法可参见文献［21］，不再进行重复说明。

2008 年，英特尔发布了高级矢量扩展（AVX）指令集，引入256 bit 位宽矢量指令。2013 年，英特尔将其位宽扩展至512 bit 并命名为AVX512 指令集。利用AVX512 指令集，计算机既可直接对512 bit 数据进行处理，如进行比特异或非等操作，又可将512 bit数据进行划分，并行处理多组数据，如32 组16 bit 数据、16 组32 bit 数据、8 组64 bit 数据等。AVX512 指令集的诞生扩展了计算机处理位宽，提高了计算机并行效率。

为了能够使编程人员不用进行汇编编程就可以直接编写汇编语句，英特尔设计了内联指令并将SIMD 指令集（包括AVX512 指令集）与内联指令进行一一对应。采用内联指令避免了繁琐的汇编编程，增强了程序的易读性和可移植性。在后续使用AVX512 时，本文将使用内联指令描述算法，使表达过程更加通俗易懂。内联指令_mm512_loadu_epi16可通过给定地址将512 bit 数据从内存装入寄存器中，_mm512_storeu_epi16 可将寄存器内512 bit 的数据存到给定地址的内存中，在使用AVX512 指令集进行实现的过程中，会频繁使用这两条指令进行数据的装载和存储。在后续部分，将忽略重复性的数据装载和存储操作，并专注于算法本身，从而使对算法的描述更加简洁。对于一些算法计算过程中所要用到的参数，利用_mm512_set 和_mm512_set1 系 列指令，通过立即数装载进寄存器，这在后续部分将多次重复使用且不再赘述。

3 多项式计算优化

Kyber 上的计算包括多项式向量相加减、多项式向量相乘、多项式矩阵乘以多项式向量以及多项式向量内积。由于后两者的计算可由前两者得到，因此本文的重点在于前两者的优化，即多项式向量相加减和多项式向量相乘的优化。

3.1 Zq上的计算优化

多项式Rq=Zq[X]/(Xn+1)上的计算在具体实现过程中最终取决于Zq上的模运算。为了提高多项式的计算效率，需要对Zq上的模运算进行优化。

3.1.1 惰性模约减

惰性模约减技术即不再每一次计算过程中进行模约减，而是等到数据快要溢出存储空间时再进行统一处理。在Kyber 中，q取3 329，占12 个比特长，但本文采用16 bit 存储Zq上的数据。因此，在计算过程中，如果数据未超过16 bit 而是仅超出绝对最小剩余系Sq，便可正常存储与计算，将不再对其进行模约减操作。利用该方法，通过合理利用计算机存储资源，减少了大量的模约减操作，提高了Zq上的计算效率。对于模加减而言，当结果未超出16 bit 时，直接进行加减忽略模约减操作，将这种直接加减法记作DAdd 和DSub。

3.1.2 优化的蒙哥马利模约减

当Zq上的数据达到16 bit 长度时需要对其进行模约减操作。在进行Zq上的模乘运算时会得到一个无穷范数较大的相乘结果，因其比特长度已经超过16 bit，需要对其进行模约减操作。一般而言，对无穷范数较大的数据进行模约减操作需要除法运算，对于计算机而言，这将耗费大量的计算资源。1985 年，MONTGOMERY［22］提出一种快速的模约减方法，即蒙哥马利模约减。蒙哥马利模约减仅利用少量的加法和乘法操作，便可完成对较大数据的模约减操作，解决了一般模约减过程中除法效率过低的问题。传统的蒙哥马利模约减会在最后一步进行一次判断操作，并依据判断结果对数据进行修正，从而将数据彻底约减到Sq。仿照惰性模约减的思路，取消最后一次判断以及修正操作，在数据不溢出16 bit 存储空间的情况下，不会影响最终的计算结果，具体见算法1 所示，在后文中，将算法1 简记作MontRed。需要注意到的是：对于最终得到的结果r1≡a·b·β-1(modq)中额外引入的β-1，将在后续统一处理。

3.1.3 模乘运算

由于相乘后的数据一般超过16 bit 的存储范围，因此需要对结果进行模约减，直接采用MontRed 进行模约减。在Kyber 的具体实现过程中，所用到的模乘可分为2 种：1）一般情况下的模乘，两乘数均未知，这常用于多项式相乘中，本文将其记作MMul；2）一乘数提前确定的模乘，这常用于NTT 和INTT转换的过程中，将其记作FMMul。对于MMul，对相乘后的结果直接使用MontRed 进行模约减，如算法2所示；对于FMMul，对提前确定的乘数进行预处理再进行后续操作，如算法3 所示。在后续部分，将采用合适的方法消除MontRed 引入的β-1。

3.2 Rq 上的计算优化

3.2.1 NTT 优化方案

在Kyber 中进行NTT 转换的多项式系数范围为(-q，q)。在算法4的第6行中，DAdd 和DSub不会进行模操作，因此每一轮迭代均会使数据的范围发生改变。在经过7 轮迭代后，多项式系数的范围从(-q，q)增加到(-8q，8q)。由于(-8q，8q)内的数据仍能被16 bit 正常存储，因此不对其进行额外处理。

3.2.2 多项式乘法优化方案

通过NTT将n-1 阶多项式上的乘法转换为个一阶多项式的乘法。不妨设(a1x+a0)，(b1x+b0)∈Zq[X]/(X2-σi)，相乘的过程可以写作(a1x+a0)·(b1x+b0)=(a1·b1)x2+(a0·b1+a1·b0)x+a0·b0=(a0·b1+a1·b0)x+(a1·b1·σi+a0·b0)。对于a0·b1、a1·b0、a1·b1、a0·b0，使用MMul进行乘操作；对于(a1·b1) ·σi，由于σi是提前确定的乘数，预计算σi·βmod±q及σi·β·q-1mod±β，并使用FMMul 进行乘操作。对于加法，使用DAdd。由于省略了部分模约减操作，最终得到的结果范围为(-2q，2q)。由于使用MontRed，最终计算的结果乘上了额外的β-1。这些将在INTT中统一处理。

3.2.3 INTT 优化方案

在INTT 的过程中，需要处理由MontRed 引入的β-1，同时需要防止计算过程中数据溢出16 bit 长度。在INTT 的每一轮迭代过程中系数的无穷范数均会翻倍，而16 bit 最多可以存储的数据范围为(-9q，9q)。因此，在数据即将产生溢出前，使用MontRed 对其进行模约减。设输入数据的系数范围为(-4q，4q)，整个INTT 迭代过程的数据变化如下：

第2 轮迭代：(-q，q)→(-2q，2q)；

第3 轮迭代：(-2q，2q)→(-4q，4q)；

第5 轮迭代：(-q，q)→(-2q，2q)；

第6 轮迭代：(-2q，2q)→(-4q，4q)；

在第1 和4 轮迭代中使用MontRed 进行模约减，同时不会将预乘上β。这样在每一次模约减后，数据范围将变成(-q，q)且会引入β-1，如算法5 的第11 和12 行所示。在INTT 的最后一轮迭代过程中，通过乘上2-(m-1)来消除每一轮迭代过程中引入的倍数2，通过乘上β-2来消除第1 和4 轮迭代中进行模约减引入的β-2，通过乘上β来消除最后一轮迭代过程中使用FMMul 进行模乘引入的β-1，如算法5 的第21 和22 行所示。利用改进的INTT 算法，消除了之前运算引入的β-1并得到了无穷范数较小的结果。

4 基于AVX512 的并行实现

本节详细描述如何利用AVX512 进行具体实现。采用16 bit 存储Zq上的元素，每512 bit 可存储32 组16 bit 数 据。

4.1 Rq 上计算的并行实现

4.1.1 32 路并行加减

对于加减法而言，使用惰性模约减技术，利用_mm512_add_epi16 和_mm512_sub_epi16 实 现32 路并行加减法。

4.1.2 32 路并行模约减

4.1.3 32 路并行模乘

MMul 的实现思路是将两输入乘数相乘后进行MontRed 处理。本文同样利用_mm512_mulhi_epi16和_mm512_mullo_epi16，32 路并行获得两相乘结果的高16 bit 和低16 bit 并将得到的结果输入32 路并行MontRed 进行处理，如算法7 所示。FFMul 的32 路并行计算方法和上述类似，但需要注意的是由于提前确定了1/2 的乘数并存入了寄存器y中，可以预计算得到yqinv=y·q-1mod±β，因此，与MMul 相比，FFMul 少了一 次_mm512_mullo_epi16 运 算，提高了计算效率，如算法8 所示。

4.1.4 32 路并行NTT 和INTT

将第4.1.1～4.1.3 节中的32 路并行计算方法运用到NTT 和INTT 过程中，即可得到32 路并行NTT 和INTT，但有2 点需要注意：1）将预计算的参数进行冗余存储使其达到512 bit，通过该方法，当向512 bit 寄存器装载数据时可以直接读入512 bit 冗余存储的数据，而不再需要通过复杂的广播指令进行数据的扩展；2）在NTT 和INTT 的第1 次迭代过程中，将多项式的系数装载进寄存器，256 个系数共需要8 个寄存器，这对于AVX512 来说是可实现的。在所有迭代完成后，再将8 个寄存器中的数据存入内存，通过该方法，省去了大量装载数据与存储数据的操作，从而提升了计算效率。

4.1.5 32 路并行多项式乘法

利用NTT 将n-1 阶多项式上的乘法转换为个一阶多项式的乘法。因为输入的多项式是不确定 的，所以采 用MMul 进行相 乘。将32 组a1、a0、b1、b0分别装载 到4 个不同的512 bit 寄 存器，再使用相应的32 路并行MMul 和32 路并行加法完成32 组一阶多项式的相乘，从而实现32 路并行多项式乘法。

4.2 8 路并行SHAKE 函数

SHA-3 是NIST 于2015 年8 月5 日 发布的安全 哈希算法系列标准。SHAKE128、SHAKE256 是SHA-3中的两个函数［23-24］，最大的特点是可以输出任何比特长度。Kyber 通过SHAKE128 和SHAKE256 扩展随机种子，获得所需长度的伪随机比特串，用于执行后续的抽样操作。使用AVX512 可以同时执行8 路SHAKE128（SHAKE256）操作［10］，从而同时抛出8 组伪随机比特串，具体如图1 所示。

图1 8 路并行SHAKE 函数Fig.1 8-way parallel SHAKE functions

4.3 并行抽样

在Kyber 中利用拒绝抽样技术［25］和SHAKE128，通过给定的种子生成上的随机矩阵，具体如算法9 所示。由于是上的随机矩阵，因此可以将其作为已经经过NTT 运算的矩阵使用，从而节省NTT 运算所耗费时间。

4.3.1 并行拒绝抽样

对于随机的12 bit，当数值在[0，q)时将其取出，否则将不使用该12 bit，继续使用下一串随机的12 bit 进行上述处理。根据条件概率，当成功抽取一个数值时，满足[0，q)的均匀分布。这种抽样方式被称为拒绝抽样［25］。设是第i行、第j列的元素的每一 个系数 范围均 为[0，q)。为了使满足上的均匀分布，需要使的每一个系数满足[0，q)上的均匀分布。在具体抽样过程中，将重复进行拒绝抽样，直至抽出整个。

一个512 bit 寄存器可以装载64 Byte 数据，每3 Byte 可以组成2 组12 bit 数据。利用_mm512_permutexvar_epi8，将3 Byte的中间部分重复一次，接着使用_mm512_mask_srli_epi16、_mm512_and_si512以及预先计算好的mask 消除多余部分，如图2 所示。利用上述方法可以将寄存器中前48 Byte 数据同时转换为32 组12 bit 数据存放在一个512 bit 寄存器中，其余数据在下一次抽样中使用。使用_mm512_cmplt_epi8_mask 判断哪些数据在[0，q)内并生成标志位。利用标志位，将满足要求的数据作为的系数存入内存。

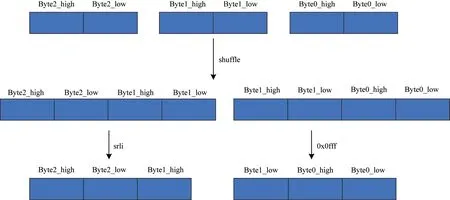
图2 数据排列与处理Fig.2 Arrangement and processing of data

4.3.2 伪随机比特串分配

由于直接生成随机比特串较为复杂，Kyber 中利用SHAKE128 扩展输入的种子得到伪随机比特串，并利用该伪随机比特串替换随机比特串完成对A的抽样，从而提高效率且不会降低安全性。如4.2 节所述，通过AVX512 能够进行8 路SHAK128 操作，同时生成8 组伪随机比特串，充分利用该8 组伪随机比特串对抽样性能的提升非常重要。本文的核心方法是通过对多项式进行拆分抽样，使其能够完全利用8 组伪随机比特串。

当k取2 时中共有4 个多项式。对于中第i行、第j列的元素αi，j，利 用SHAKE128(seed‖ ‖i‖j0)生成其低128 bit 系数，SHAKE128(seed‖i‖j‖1)生成其高128 bit 系数。通过该方法，生成4 个多项式需要用到8 组伪随机比特串，从而充分利用了8 路并行SHAKE128 函数且降低了SHAK128 的循环次数。

当k取3 时，中共有9 个多项式。对于中第3 行、3 列的元素，将其拆分成8 个部分，每个部分有32 项系数。利 用SHAKE128(seed‖ 3 ‖3 ‖index)为每一部分生成伪随机比特串。对于的其他元素，直接利用SHAKE128(seed‖i‖j)生成对应的伪随机比特串，不再进行拆分。通过该方法，充分利用了8 路并行SHAKE128 函 数。

当k取4 时，中共含16 个多项 式，正好是8 的倍 数。因 此，对 于中 第i行、第j列的元 素，直 接利用SHAKE128(seed‖i‖j)生成对应的伪随机比特串，不再进行拆分，从而充分利用了8 路并行SHAKE128 函数。

4.4 并行抽样Sη

在Kyber 中，利用中心二项分布（CBD）抽样抽取Sη，如算法10 所示。CBD 抽样利用固定长度的伪随机比特串抽取Sη上的元素，未使用较为繁琐的拒绝抽样技术，运行效率更高。

由于直接生成随机比特串较为复杂，Kyber 中利用SHAKE256 扩展输入的种子得到伪随机比特串，利用伪随机比特串替换随机比特串完成对Sη的抽样，η取值为2 或者3。当η为2 时，每个长度为4 的伪随机比特串可通过CBD 抽样得到Sη的一个系数，整个Sη的CBD 抽样需要消耗长度为1 024 bit 的伪随机比特串，而SHAKE256 一次循环能产生长度为1 088 的伪随机比特串，因此只需一次Squeeze 操作，便可完成一次Sη的CBD 抽 样。当η为3 时，每个长度为6 的伪随机比特串可通过CBD 抽样得到Sη的一个系数，整个Sη的CBD 抽样需要消耗长度为1 536 bit 的伪随机比特串，需要SHAKE256 循环2 次。当进行实现时，较难处理3 bit 的并行操作，因此利用冗余比特技术，对每4 bit 进行并行处理，并忽略最高比特。通过上述方法，整个Sη的CBD 抽样需要消耗长度为2 048 bit 的伪随机比特串，SHAKE256依然只需循环2 次，未造成额外的开销，如图3所示。

图3 CBD 抽样的比特处理Fig.3 Bit processing of CBD sampling

5 性能分析

利用AVX512 实现了不同安全参数下的Kyber算法，即Kyber512、Kyber768 和Kyber1 024，并与其C 语言版本的实现进行了性能对比与分析［21］。使用的处理器是11th Gen Intel®CoreTMi5-1135G7@2.40 GHz 2.42 GHz，内存大小为16 GB。操作系统选用Windows 10，编译器选用GCC，优化等级为-O3。将各算法运行20 000 次，并计算其平均时钟周期作为性能指标。

通过表1～表3 可以看出：在多项式计算方面，由于对算法进行优化且利用AVX512 实现了32 路并行，从而获得了55～95 倍的加速；在多项式抽样方面，利用8 路SHAKE 函数以及优化的抽样方法获得了4～7 倍的加速；从整体来看，对于包含抽样操作的密钥生成算法和加密算法获得了10～16 倍的加速，对于主要由多项式计算构成的解密算法获得了约56 倍的加速。

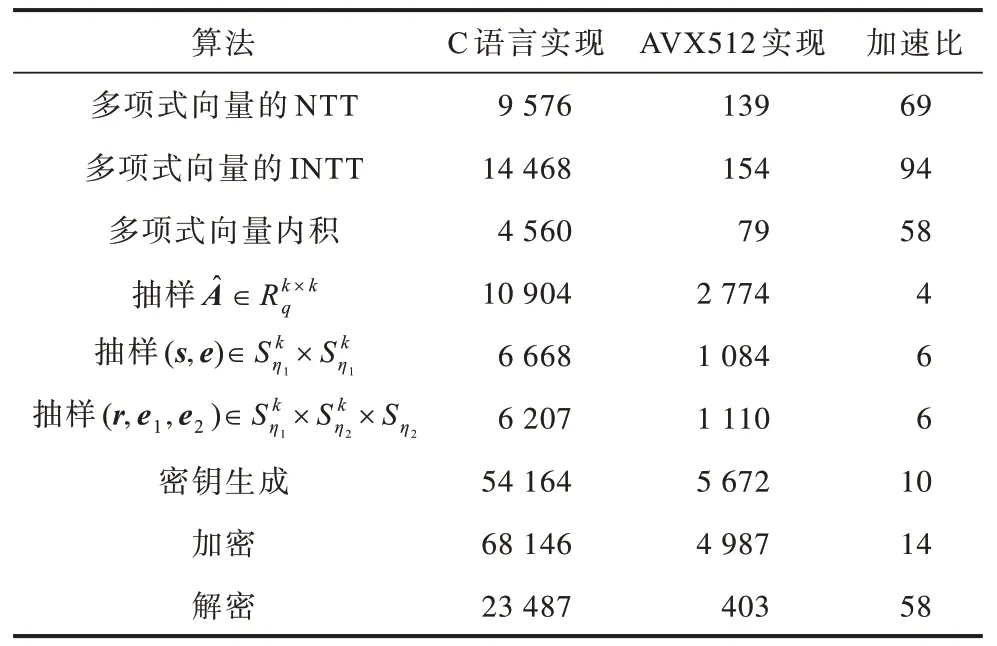
表1 Kyber512 的性能测试与对比 Table 1 Performance testing and comparison of Kyber512

表2 Kyber768 的性能测试与对比 Table 2 Performance testing and comparison of Kyber768

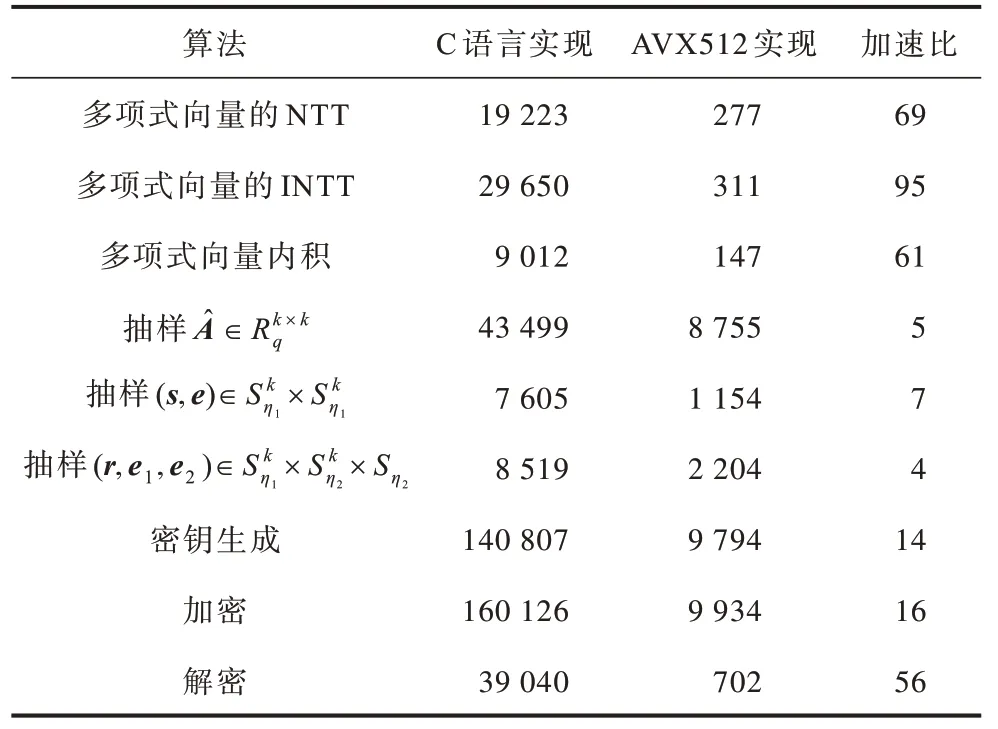
表3 Kyber1 024 的性能测试与对比 Table 3 Performance testing and comparison of Kyber1 024

6 结束语

本文针对Kyber 算法的公钥加密部分进行高速并行实现。在多项式计算方面，利用惰性模约减、优化的蒙哥马利模约减、一般模乘和固定乘数模乘等技术，提高了模运算的效率，采用NTT 和INTT 变换提高了多项式计算的效率，将优化后的模运算融入NTT 和INTT 过程，同时利用AVX512 进行高速并行实现，获得了55～95 倍的加速。在多项式抽样方面，通过拆分抽样、冗余抽样等技术优化抽样过程，同时利用AVX512 进行高速并行实现，获得了4～7 倍的加速。在整体上，获得了10～56 倍的性能提升。在后续工作中将继续研究不同后量子密码标准在不同硬件平台上的高速实现。