圆弧足被动行走机器人动力学参数影响研究

张婉婉，高建设，高家昌，王高峰

（郑州大学机械与动力工程学院，河南 郑州 450001）

1 引言

由于双足机器人对复杂地形具有较强的适应性，受到了研究人员广泛关注［1-2］。目前，为了实现其稳定行走，许多机构已经开发了各种具有复杂控制系统的主动双足机器人［3-5］。然而，复杂控制系统的设计往往会导致机器人不可避免地存在能量损耗大、控制难度高、步态僵硬等问题。这些问题极大地制约了双足机器人的发展和应用。

20世纪90年代，文献［6］提出了被动动力学理论并实现了二维无膝关节和有膝关节双足被动行走机器人在斜坡上的自发步行。文献［7］表明被动行走机器人研究不仅有助于理解人类步行的内在机理，而且可以指导设计更高效灵巧的双足机器人。然而，被动行走机器人的稳定行走在很大程度上依赖于初始条件和动力学参数［8］。为避免被动行走机器人出现不稳定甚至摔倒的情况，动力学参数影响研究成为被动行走领域至关重要的课题。

继文献［6］开创性工作之后，许多学者对双足被动行走机器人进行了大量相关性研究。文献［9］提出了一种最简模型，研究发现，当斜坡倾角增大时该模型步态呈现出倍周期分岔现象。文献［10］提出了一种罗盘模型，除斜坡倾角外，他们还研究了质量和腿长对模型步态的影响。文献［11］进一步证明，随着斜坡倾角增大，最简模型具有周期3 到周期7 步态。文献［12］研究表明增大斜坡倾角导致被动双足机器人稳定性下降。文献［13］详细分析了罗盘模型的极限环步态和能量转化关系并证明了被动行走过程中机械能守恒。文献［14］通过计算雅克比矩阵的特征值讨论了罗盘模型中机械参数和斜坡角对稳定性的影响。文献［15］研究了具有点足、圆弧足和平板足的最简模型，对比分析得出圆弧足可以扩大稳定步行范围而平板足的情况则取决于足形参数。文献［16］证明了引入摆臂结构能够提高被动行走机器人稳定性。文献［17］发现当转动惯量增大、质心位置降低或足半径减小，都会导致圆弧足罗盘模型步态发生分岔。文献［18］证明了具有合理髋关节质量的圆弧足罗盘模型有更强的行走稳定性与鲁棒性。

尽管上述几位学者针对圆弧足罗盘模型已有了显著的研究成果，但缺少系统地讨论动力学参数对圆弧足罗盘模型运动特性的影响，特别是双参数变化对机器人稳定步态的影响。另一方面，由于被动行走机器人为非光滑系统，方程中不连续处雅克比矩阵不可导，采用传统方法求解李雅普诺夫指数比较困难。在此首先以圆弧足被动行走机器人为研究对象，对其运动过程进行了分析与建模，着重研究了圆弧足半径、质心位置、转动惯量和斜坡倾角变化时机器人步态演变规律，特别是当足半径和质心位置同时变化对机器人稳定参数区间的影响。另外，采用正交扰动向量法求解被动行走机器人的李雅普诺夫指数，这种方法可以避免直接计算雅可比矩阵。

2 圆弧足被动行走机器人动力学建模

2.1 模型介绍

首先给出圆弧足被动行走机器人模型，如图1所示。该模型是由两个具有完全相同质量和长度的刚性杆件在髋关节处通过铰链连接而成。由于髋关节和圆弧足质量可以等效简化为两腿质量，为简化模型研究，不考虑髋关节和足部质量。设腿质量为m，长度为l，腿质心与髋关节的距离为c，腿相对质心的转动惯量为Jc，圆弧足半径为r且圆心在腿上，斜面倾角为φ，重力加速度为g。

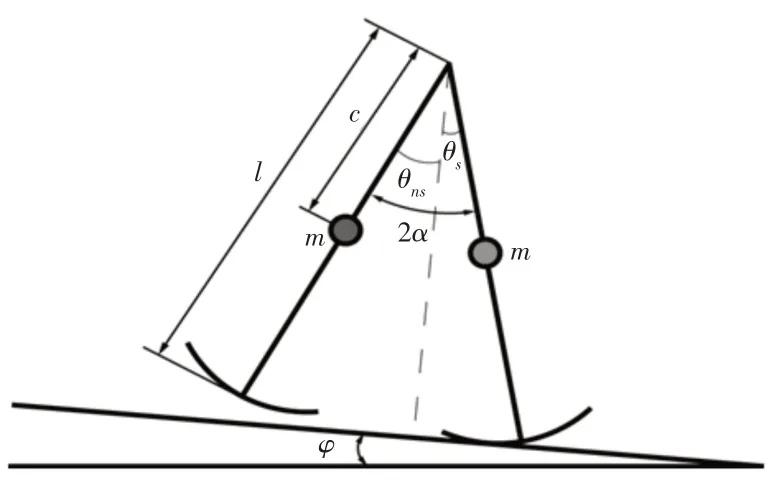
图1 圆弧足被动行走机器人模型Fig.1 The Model of a Passive Walking Robot with Arc Feet

机器人单步运动过程，如图2所示。主要是支撑腿和摆动腿之间的转换。机器人运动过程分为两个阶段，第一个阶段是摆动阶段，第二个阶段是碰撞阶段。在摆动阶段，支撑腿绕其圆弧足做倒立摆运动，摆动腿绕髋关节做单摆运动，如图2（a）、图2（b）所示。在碰撞阶段，摆动腿与斜面发生碰撞，为清楚了解两腿角色变换，又将碰撞时刻分为碰撞前和碰撞后，如图2（c）、图2（d）所示。碰撞发生后摆动腿和支撑腿角色互换。

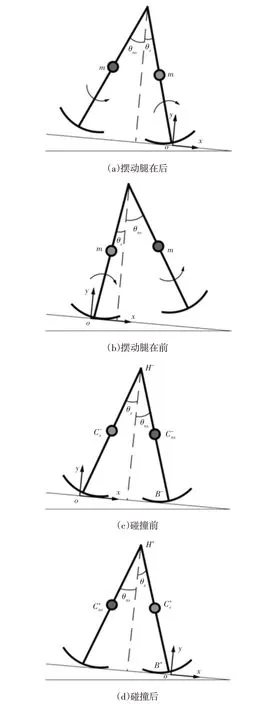
图2 单步运动过程Fig.2 The Process of Motion in One Step

为了便于进行动力学建模，参考前人研究［9-10］，对模型做如下假设：

（1）整个模型为刚体，没有弹性变形；

（2）髋关节与腿之间无阻尼无摩擦；

（3）支撑腿与地面之间为纯滚动约束，不产生滑动与变形，且忽略摩擦；

（4）摆动腿与地面碰撞为完全非弹性碰撞且是瞬时发生。

2.2 摆动阶段动力学方程

该圆弧足被动行走机器人模型为二自由度保守系统，可利用拉格朗日方法进行建模。将系统坐标系建立在斜面上，x轴沿斜面向下，y轴垂直斜面向上，选取支撑腿与斜面垂直时的垂足O为坐标系原点。设支撑腿与轴的夹角为θs，摆动腿与轴的夹角为θns，取逆时针为正方向，图2（a）中的θs为正，θns为负。选θs和θns为广义坐标，则系统微分形式的动力学方程为：

其中，

2.3 碰撞阶段动力学方程

在碰撞阶段，摆动腿足端与斜面发生碰撞。设原摆动腿足端与斜面的碰撞点为B，在碰撞前后，摆动腿与斜坡之间的作用力只有冲击力。故碰撞前后，摆动腿和支撑腿的角度不变，角速度发生改变。根据角动量守恒定律，模型整体关于碰撞点B的角动量守恒，且原支撑腿（即新摆动腿）对于髋关节质心位置处点的角动量守恒。

设CH为髋关节质心位置，Cns为摆动腿质心位置，Cs为支撑腿质心位置，髋关节质心速度为v→H，负号和正号的上标分别代表为碰撞前和碰撞后的状态符号。碰撞前的坐标系选取为摆动阶段建立的坐标系，即以原支撑腿与斜面垂直时的垂足为原点建立坐标系，x轴沿斜面向下，y轴垂直斜面向上。碰撞后，以B点附近新支撑腿与斜面垂直时的垂足为原点建立坐标系，x轴沿斜面向下，y轴垂直斜面向上。

（1）参考点为H时

碰撞前，原支撑腿对参考点H的角动量为：

碰撞后，原支撑腿变为新的摆动腿，对参考点H的角动量为：

（2）参考点为B时

碰撞前，系统整体对碰撞点B的角动量为：

碰撞后，系统整体对碰撞点B的角动量为：

碰撞前后，摆动腿和支撑腿的角度不变，角速度发生改变。根据角动量守恒定律，得L1=L2，L3=L4。由此可得系统碰撞方程为：

2.4 方程无量纲化

为了基于一个贡献标尺计算不同参数对机器人动力学特性的影响，需要对方程进行无量纲化。在此引入无量纲参数：

其中，

经化简得碰撞方程的无量纲形式为：

其中，

式中：x1—摆动阶段支撑腿角位移；x2—摆动阶段支撑腿角速度；x3—摆动阶段摆动腿角位移；x4—摆动阶段摆动腿角速度；y1—碰撞后支撑腿角位移；y2—碰撞后支撑腿角速度；y3—碰撞后摆动腿角位移；y4—碰撞后摆动腿角速度。

取定参数：

由上面所取定参值可得无量纲常量

β1=0.24，β2=0.5，β3=0.04

3 单参数变化对机器人步态的影响

根据第二节所述动力学方程，选择β1、β2、β3和φ作为目标参数，它们分别与圆弧足半径、质心位置、转动惯量和斜坡倾角有关。接下来借助分岔图进行参数变化影响研究。

3.1 圆弧足半径变化的影响

设置参数β2=0.5，β3=0.04，φ=0.01，β1从0到0.9变化。机器人支撑腿角位移随足半径参数β1变化的分岔图，如图3所示。可以看出，随着足半径参数β1增大，机器人支撑腿角位移未发生分岔现象，当在区间（0，0.805）变化时，机器人始终具有稳定周期一步态。但当足半径参数β1在0.805之后增加时，角位移急剧增大并最终发散，此参数下的机器人在行走过程中将会极易跌倒。

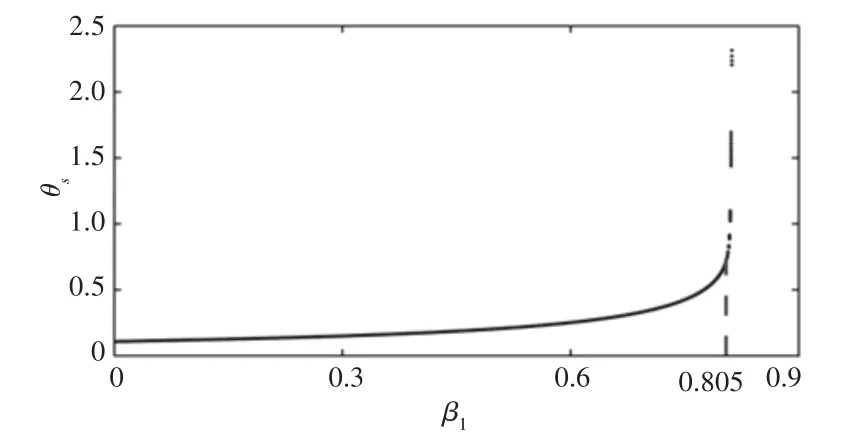
图3 β1变化时的分岔图Fig.3 Bifurcation Diagram When β1 Changes

3.2 质心位置变化的影响

设置参数β1=0.24，β3=0.04，φ=0.01，β2从（0.5～0.72）变化。机器人支撑腿角位移随质心位置参数β2变化的分岔图，如图4所示。从图中可以看出，随着β2增大，机器人步态出现了倍周期分岔现象。其中，稳定的周期一步态占据了较大参数区间，后在区间（0.6629，0.7094）内表现为周期二步态且两个分支存在汇交于一点的现象。当β2继续增加时，经过短暂的周期四步态后，机器人将失去失稳性。

图4 β2变化时的分岔图Fig.4 Bifurcation Diagram When β2 Changes

3.3 转动惯量变化的影响

设置参数β1=0.24，β2=0.5，φ=0.01，β3从0.04 到0.19 变化。机器人支撑腿角位移随转动惯量参数β3变化的分岔图，如图5所示。从图中可以看出，随着β3增大，机器人步态同样出现了倍周期分岔现象。这与质心位置增加对机器人步态的影响相同，只是分岔发生位置不一致。由图知，机器人周期步态分别在0.109和0.184处发生分岔。以上现象说明转动惯量的增大也会导致机器人周期步态发生分岔现象并最终失稳。

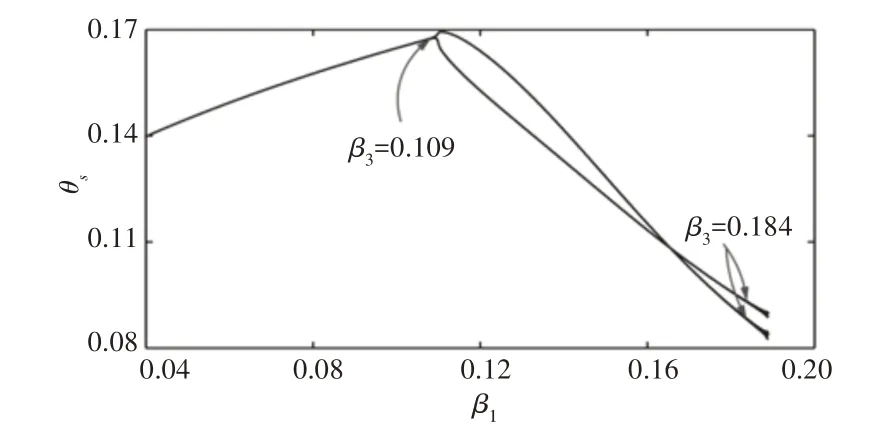
图5 β3变化时的分岔图Fig.5 Bifurcation Diagram When β3 Changes

3.4 斜坡倾角变化的影响

设置参数β1=0.24，β2=0.5，β3=0.04，φ从0.01到0.16变化。机器人支撑腿角位移随斜坡倾角φ变化的分岔图，如图6所示。

图6 φ变化时的分岔图Fig.6 Bifurcation Diagram When φ Changes

从图中可以看出，随着斜坡倾角φ增大，机器人步态同样地出现了倍周期分岔现象。与上述倍周期分岔不同的是，此时机器人步态由倍周期分岔通向混沌。从图中观察到，机器人在区间（0.01，0.138）内表现为周期一步态，区间（0.138，0.151）内为周期二步态。随着斜坡倾角φ继续增加，机器人经过短暂的周期四步态后进入混沌状态。

4 李雅普诺夫指数计算

上述分岔图定性地表现出机器人步态随参数变化的演变规律，而李雅普诺夫指数能够定量地确定系统在特定参数下的步态特性。由于碰撞发生，导致被动行走机器人运动方程不连续。因此，机器人运动轨迹相对于初始条件的导数即雅克比矩阵变得病态或根本无法计算，用传统方法求解李雅普诺夫指数比较困难。利用初始正交向量的小扰动估计雅可比矩阵的思想求解被动行走机器人李雅普诺夫指数，这种方法极大地简化了非光滑系统的李亚普诺夫指数求解问题，因为这种估计方法可以避免直接计算雅可比矩阵［19］。估计方法过程如下。根据第二节被动行走机器人运动方程为：

式中：x=[x1，x2，x3，x4]T；f=[f1，f2，f3，f4]T；Γ—碰撞面。

非线性系统庞加莱截面的一般形式是：

被动行走系统通常选取碰撞面为庞加莱截面。针对圆弧足被动行走机器人，这里选取庞加莱截面为：

对于等式（6）中的离散映射，直接计算雅可比矩阵是不可能的，因为等式（6）的右边是未知的。此时引入一个扰动向量Δn=[δ1，δ2，δ3，δ4]T，其中，δi(i=1，2，3)是小量值，可以得到：

其中，

Dui(xn)=雅可比矩阵的列向量；

DU(xn)=[Du1(xn)，Du2(xn)，Du3(xn)，Du4(xn)]T—雅可比矩阵。由等式（7）可知，雅可比矩阵中列的近似值可由下列等式求得：

具体求解步骤如下：

（1）设初始条件x00=[x10，x20，x30，x40]，将x00代入机器人动力学方程进行求解得到x10；（2）设扰动初始条件为x01=[x10+δ，x20，x30，x40]，x02=[x10，x20+δ，x30，x40]，x03=[x10，x20，x30+δ，x40]，x04=[x10，x20，x30，x40+δ]，将x01，x02，x03，x04分别代入动力学方程进行求解得到x11，x12，x13，x14；（3）求解此时雅克比矩阵的估计值为：[(x11-x10)/δ，(x12-x10)/δ，(x13-x10)/δ，(x14-x10)/δ]T；（4）将x10作为初始条件返回第一步，不断进行迭代即可求解机器人运动轨迹的雅克比矩阵估计值。根据构造的雅克比矩阵利用传统方法［19］即可求解李雅普诺夫指数。与图6相对应的李雅普诺夫指数图，如图7所示。从图中可以清楚地观察到两个分岔点和混沌分布位置。在区间（0.01，0.138）与（0.138，0.151）内，最大李雅普诺夫指数为负，说明机器人此时处于稳定运动状态，与分岔图中周期一和周期二参数区间相对应；在0.138 和0.151位置处，最大李雅普诺夫指数为零，此时系统处于不稳定状态，与分岔图中的分岔点一致。通过对最大李雅普诺夫指数进行分析，为机器人分岔动力学提供了强有力的验证。

图7 最大李亚普诺夫指数图Fig.7 The Largest Lyapunov Exponent Diagram

5 双参数变化对机器人步态的影响

上几节讨论了单参数变化对机器人步态的影响，但不同参数联合作用下的影响仍需探究。圆弧足半径参数β1和质心位置参数β2组合变化下对机器人步态的影响，如图8所示。与图8相对应的机器人稳定行走参数区间，如表1所示。由图8和表1可得，当β1取0时，减小质心位置参数β2可增大机器人周期步态参数区间；当β1取0.2时，随着质心位置参数β2的增大，机器人周期步态参数区间先增大后减小；当β1取0.4时，增大质心位置参数β2，机器人周期步态参数区间增大；而当β1取0.6时，减小质心位置参数β2可以增大机器人周期步态参数区间，且β2取0.6时机器人步态出现了逆倍周期分岔现象。

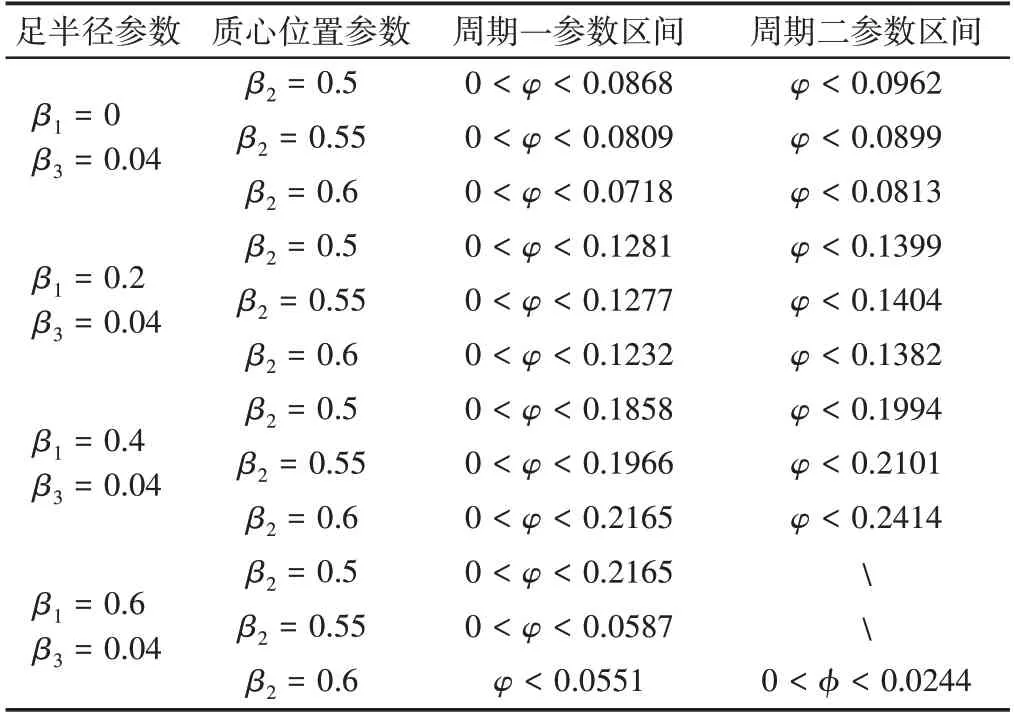
表1 机器人稳定行走参数区间Tab.1 Parameter Ranges of Stable Robot Walking

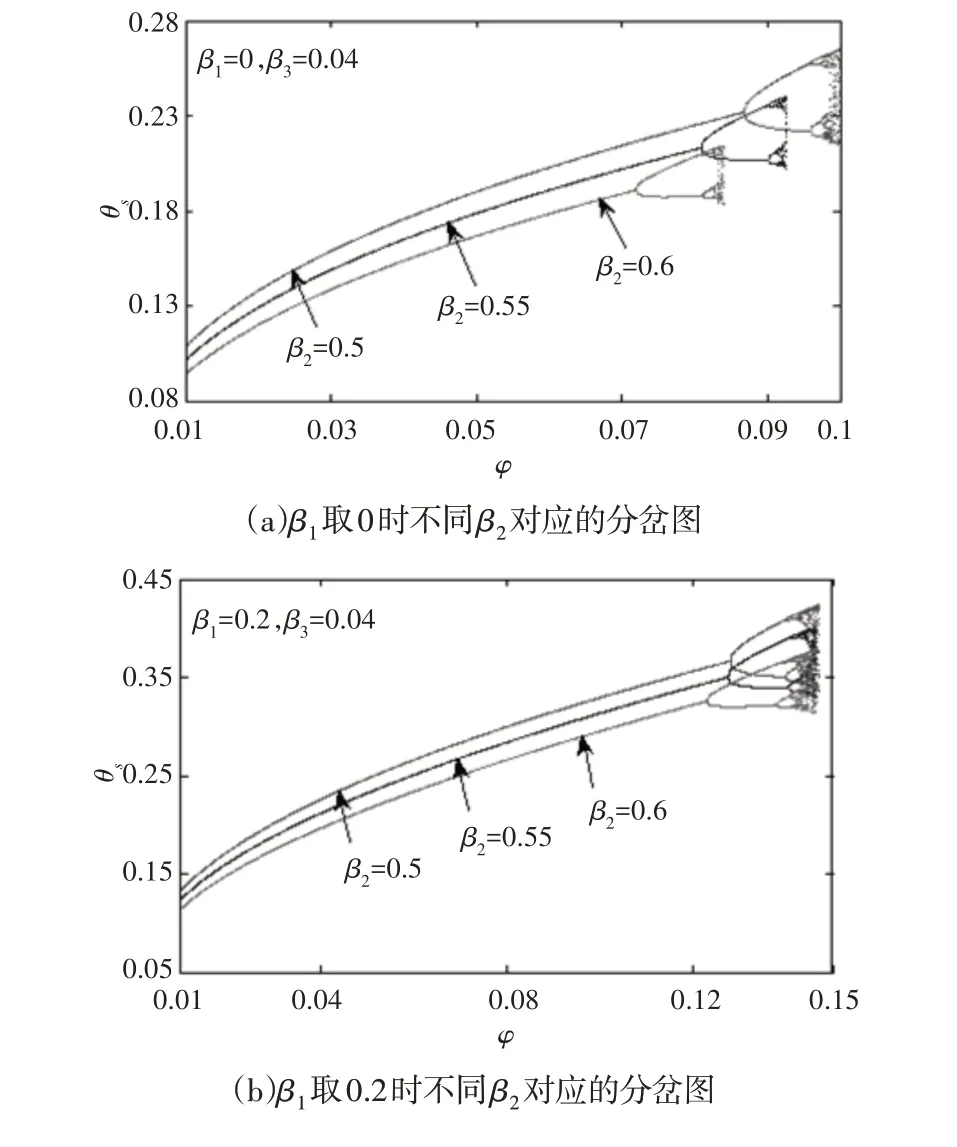
图8 β1和β2取值不同时的分岔图Fig.8 Bifurcation Diagrams of Different Values of β1and β2

另一方面，当质心位置参数β2分别取0.5，0.55，0.6，且圆弧足半径参数β1在（0，0.4）内增大时有利于增加机器人周期步态参数区间，β1取0.6会导致周期参数区间减小。以上对圆弧足半径参数β1和质心位置参数β2组合变化下机器人稳定参数区间分析为机器人结构设计和稳定行走提供参考。

6 结论

（1）详细介绍了圆弧足被动行走机器人运动过程和动力学方程的建立。借助分岔图深入讨论了单参数变化影响，研究结果表明，当圆弧足半径参数β1在（0，0.805）内增大时机器人仍保持周期一步态，但当足半径参数β1大于0.805时会导致机器人无法稳定行走，而随着质心位置参数β2、转动惯量参数β3和斜坡倾角φ增大，机器人步态均出现了倍周期分岔现象。

（2）双参数变化影响研究表明，当β1取0和0.6时，减小质心位置参数β2可增大机器人周期步态参数区间，且β2取0.6时机器人步态出现了逆倍周期分岔现象。当β1取0.4时，增大质心位置参数β2，机器人周期步态参数区间增大；当β1取0.2时，随着质心位置参数β2增大，机器人周期步态参数区间先增大后减小；当质心位置参数β2分别取0.5，0.55，0.6，且圆弧足半径参数β1在（0，0.4）内增大时有利于增加机器人周期步态参数区间，β1取0.6会导致周期参数区间减小。上述研究结果为圆弧足被动行走机器人结构参数设计和稳定步态分析与控制提供了重要参考意义。此外，利用正交扰动向量法求解被动行走机器人的李雅普诺夫指数，为未来研究其他非连续机械系统提供了思路。