变流器虚拟惯量和阻尼协同自适应控制策略

王珺, 凌志斌, 李旭光

(上海交通大学 电力传输与功率变换控制教育部重点实验室,上海 200240)

0 引 言

近年来,随着大量新能源设备并网,以同步发电机为主导的传统电力系统暂态稳定性和抗干扰性变差[1]。对此,学者提出了虚拟同步发电机(virtual synchronous generator, VSG)控制策略[2]。该策略模拟了同步发电机的机械和电磁部分,使变流器具备了惯量阻尼特性。

在并网模式下,当系统给定有功功率发生改变时,VSG输出的频率和有功功率会发生暂态振荡,需要动态调节虚拟惯量和阻尼来改善系统暂态性能。文献[3-4]分析了虚拟惯量对系统暂态振荡的影响,提出了一种虚拟惯量自适应控制策略,但并没有对阻尼对暂态性能的影响进行分析。文献[5-6]提出了一种虚拟惯量和阻尼协同自适应控制策略,提升了系统的暂态性能,但并未考虑所提的自适应函数引入的微分环节存在放大噪声和对控制器运算要求高等问题,且虚拟惯量和阻尼系数在自适应变化中存在突刺现象。文献[7]提出了一种虚拟惯量和阻尼协同自适应控制策略,有效地减小了暂态过程中的频率超调,但并没有分析所提自适应控制策略中不同临界阈值的选取对自适应调节性能的影响。

为了解决上述问题,本文在建立VSG变流器控制系统数学模型的基础上,分析VSG有功和角频率暂态特性曲线,给出虚拟惯量和阻尼的选取原则,提出一种虚拟惯量和阻尼协同自适应控制策略。借鉴同步发电机的小信号模型分析方法建立有功功率环路的传递函数,给出参数选取范围。最后在MATLAB/Simulink平台进行仿真分析,通过对比不同控制策略的仿真结果验证本文所提控制策略的有效性和优越性。

1 VSG变流器系统拓扑与控制策略

1.1 系统拓扑与控制流程

虚拟同步发电机模拟了同步发电机的机械和电磁部分,使得变流器具备了惯量阻尼特性。图1为VSG变流器系统拓扑与控制示意图。图1中:Lf、Rf分别为滤波电感及寄生电阻;Cf为滤波电容;Lg为交流电网线路电感;ea、eb、ec为变流器输出三相电压;isa、isb、isc为三相电感电流;ua、ub、uc为三相并网点(point of common connection, PCC)电压;udq为dq轴分量;ia、ib、ic为三相电网电流;idq为dq轴分量;Pe、Qe分别为VSG输出的有功功率和无功功率;Pref、Qref分别为有功和无功功率给定值;E、θ分别为VSG控制输出的电压和相位。

图1 VSG变流器系统拓扑与控制示意图

1.2 VSG控制

图2为VSG控制框图,包括有功-频率控制器和无功-电压控制器。在有功-频率控制器中,其模拟的转子运动方程为:

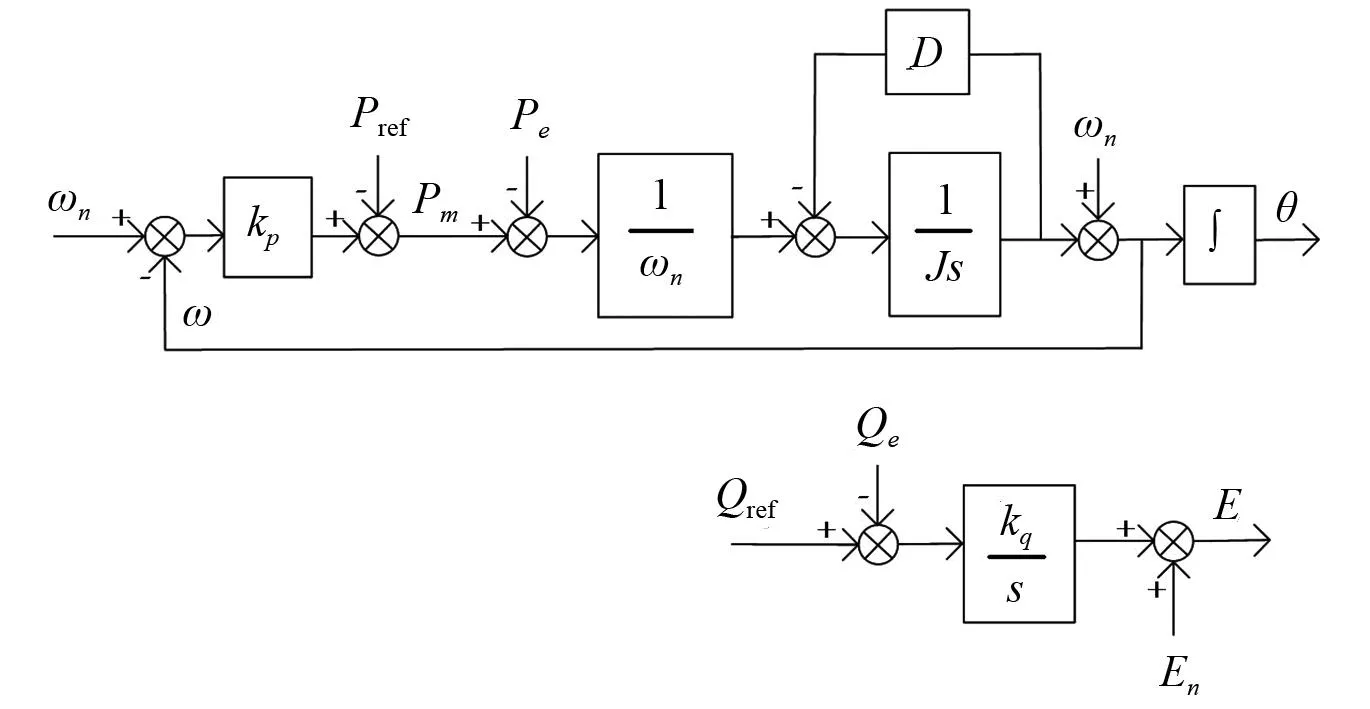
图2 VSG控制框图

(1)

式中:J、D分别为VSG的虚拟惯量和阻尼;Pm为模拟的原动机输出功率;ω、ωn分别为VSG角频率和额定角频率;θ为VSG相位。

原动机输出功率模拟了同步发电机一次调频功能,其计算公式为:

Pm=Pref-kp(ω-ωn)

(2)

式中:Pref为有功给定值;kp为有功调差系数。

无功-电压调节器模拟同步发电机无功功率下垂特性,并且采用积分环节进行调节,其计算公式为:

(3)

式中:En为相电压额定幅值;kq为无功调节系数;Qref为无功给定值。

2 虚拟惯量和阻尼协同自适应控制策略

2.1 自适应控制原理

图3给出了给定有功功率指令改变时,VSG的功角特性曲线和虚拟转子角频率振荡曲线。图3中:系统初始给定有功为P1,对应的功角为δ1,稳定运行在图3(a)中的A点;当给定有功变为P2时,功角最大会达到C点,然后在曲线AC间不断衰减,最终稳定在B点。

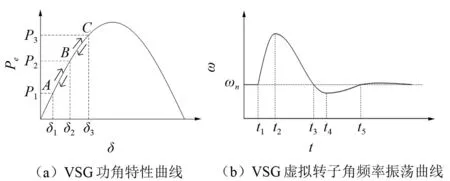
图3 VSG暂态响应曲线

本文仅对一个振荡周期t1～t5中阶段一(t1～t2)进行分析,其余阶段分析与之类似。

阶段一(t1～t2):当有功指令由P1跃升为P2时,对式(1)做等式变化,得式(4):

(4)

由式(4)可知,该阶段角频率变化率dω/dt>0。在该阶段内,角频率逐渐变大,但角频率变化率逐渐减小,致使角频率偏差Δω=ω-ωn>0,对应图3(b)中阶段一(t1～t2),功角δ是Δω对时间的积分,故也随之增大,VSG输出功率Pe增大,对应图3(a)中曲线AB阶段。在该阶段应取较大的J,从而减缓dω/dt,防止Δω过大。

阶段二(t2～t3)、阶段三(t3～t4)与阶段四(t4～t5)分析方法与阶段一(t1～t2)类似。综上可得J的选取规则如表1所示。

表1 虚拟惯量选取原则

在阶段一、三中,增大D可使|dω/dt|减小得更快;在阶段二、四中,增大D可以进一步加快角频率回归额定值。因而,在|ω|增大到一定程度时,应增大D。

根据表1,可得自适应控制策略为:

(5)

(6)

式中:J0、D0为稳态时虚拟惯量和阻尼系数值;ωJ、ωD为J、D自适应变化临界阈值,其作用是为了滤除Δω·dω/dt接近0时的微小波动,避免控制器因正负判断紊乱而失效。

2.2 参数整定

结合VSG控制框图,并借鉴传统同步发电机小信号模型分析方法[8],可得有功功率环路小信号模型如图4所示。

图4 有功功率环路小信号模型

由图4可得有功功率环路闭环传递函数为:

(7)

由式(7)可知,该响应为二阶系统,根据自控理论的相关知识可以得到无阻尼自然振荡角频率ωN和阻尼比ζ,如式(8)所示。

(8)

评估二阶系统欠阻尼暂态性能的指标有超调量σ%和调整时间ts,取误差带为±2%,可得σ%和ts的计算公式为:

(9)

对于同步发电机而言,可用惯性时间常数H来衡量不同尺寸和功率等级下的同步机惯性,H的定义式如式(10)所示。

(10)

式中:H为同步发电机在额定转矩下空载由静止加速至额定角速度的时间。通常,同步发电机的惯性时间常数为2～9 s。

对于D0的选取,可在确定了J0之后,根据有功功率控制环路所得的闭环传递函数阶跃响应的超调量来确定,即根据式(8)和式(9)中σ%和ζ计算式确定。综上,可得J0和D0的表达式如式(11)所示。

(11)

依据国家标准GB/T 15945—2008《电能质量电力系统频率允许偏差》的规定:电力系统正常运行情况下,频率偏差范围为0.2 Hz[9]。并且有ω=2πf,因而自适应调节的临界阈值ωJ、ωD的选取需满足:

(12)

式中:fallow为0.2 Hz。

为了不改变系统的稳态性能并且简化算法判断,可取ωJ=ωD。

3 仿真分析

基于MATLAB/Simulink平台搭建图1所示的拓扑与控制算法,考察不同临界阈值ωJ对自适应系统的影响,验证所提变流器虚拟惯量和阻尼协同自适应控制算法的有效性,主要仿真参数如表2所示。

表2 主要仿真参数

3.1 不同临界阈值对自适应性能影响分析

初始时刻0 s处,系统有功功率参考值Pref=10 kW,无功功率参考值Qref=2 kvar,分别取ωJ为0.1%ωn、0.05%ωn和 0.01%ωn。

图5为三种ωJ时JD协同自适应控制策略的VSG输出频率f的响应曲线和J自适应曲线。

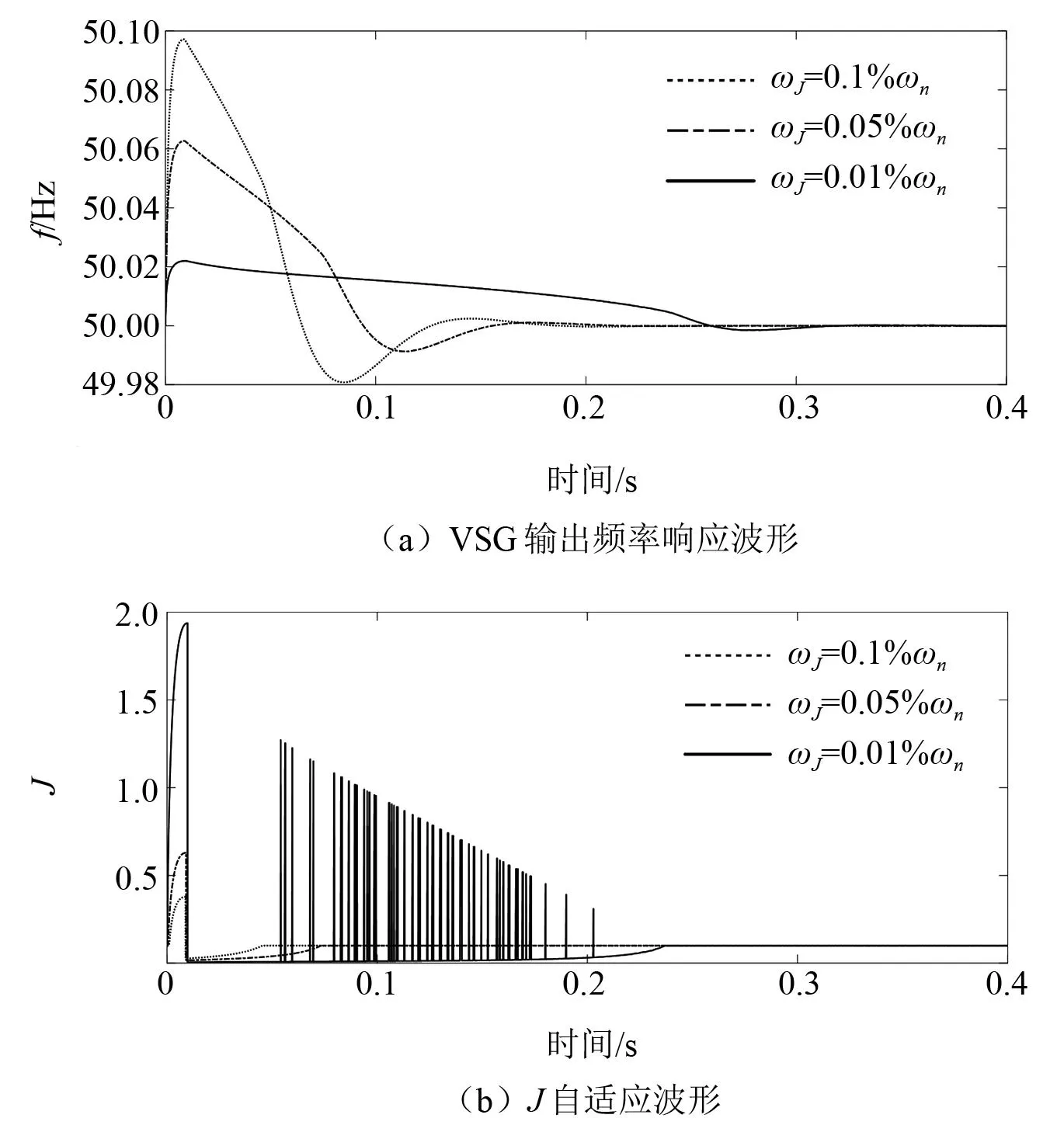
图5 不同ωJ时JD协同自适应控制策略暂态响应曲线

由图5可以看出,随着ωJ的减小,VSG输出频率的超调量随之减小,但是在ωJ=0.01%ωn时,在0.05～0.25 s之间,J的自适应出现了误动。这是由于临界阈值ωJ可以看作自适应的死区,根据自适应原理,死区越小,频率超调会越小。但是随着ωJ的逐渐减小,其对于Δω·dω/dt的微小抖动的滤除效果也会变差。因而对于ωJ的选取,应兼顾改善频率的暂态性能与滤除Δω·dω/dt的微小抖动。

3.2 虚拟惯量和阻尼协同自适应控制效果验证

取ωJ=0.1%ωn,对所提自适应控制策略进行验证。系统初始稳定运行在4 kW处,在0.5 s时,有功功率突增至12 kW,在1 s 时,有功功率突增降至6 kW。图6(a)～图6(d)分别为传统VSG控制、J自适应控制和JD协同自适应控制策略下的有功功率响应曲线、频率响应曲线以及J、D参数变化波形。

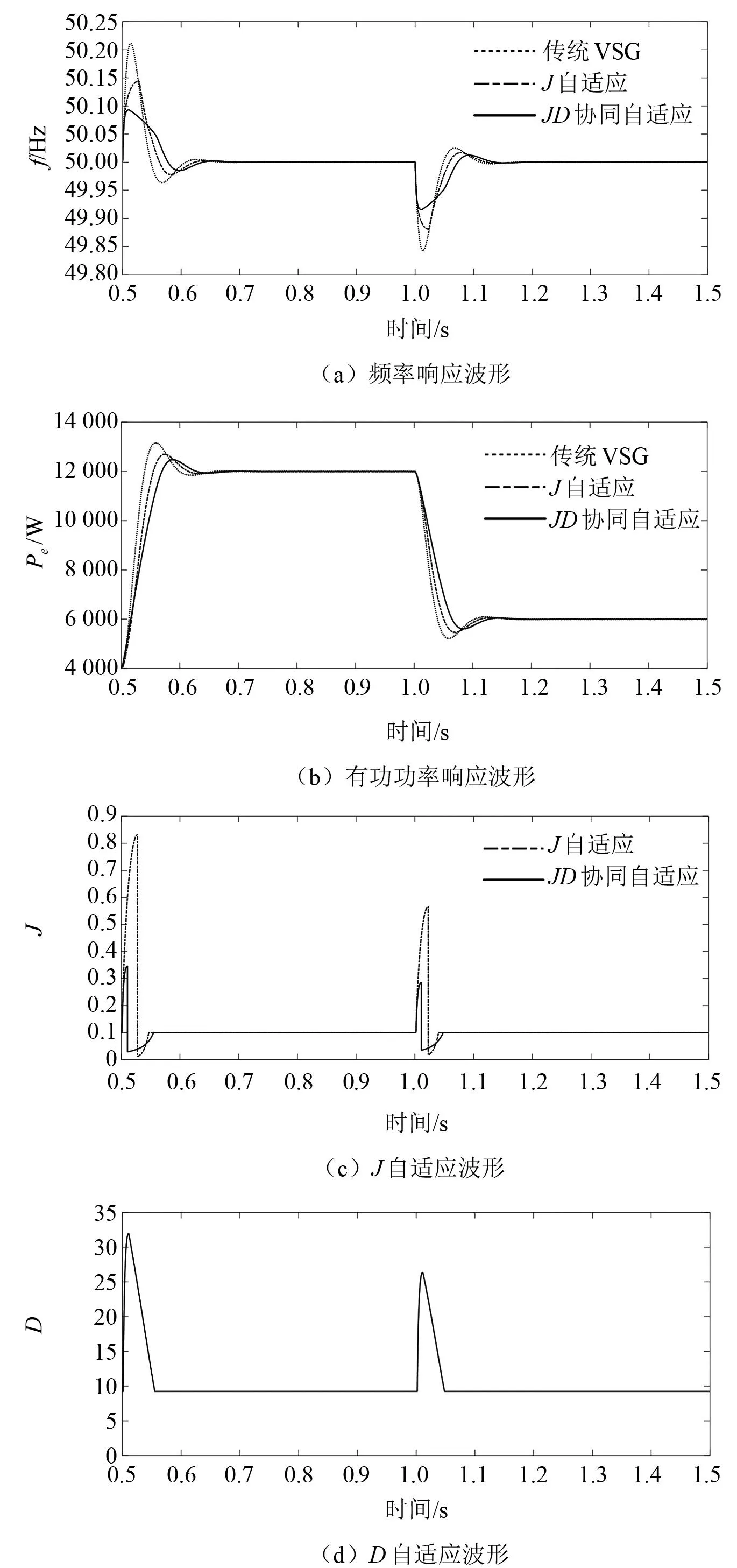
图6 不同控制策略动态响应曲线

从图6(a)可以看出,在相同的功率阶跃下,JD协同自适应控制策略的频率偏差量绝对值最小。经测量,在0.5 s有功从4 kW阶跃为12 kW时,传统VSG频率最大偏差为0.21 Hz,超过了GB/T 15945—2008所规定的频率偏差范围,而JD自适应变化和J自适应变化分别为0.14 Hz和0.09 Hz,均满足国标的频率偏差要求。因而从频率偏差角度,JD协同自适应控制策略效果好于J自适应与传统VSG控制。

对图6(b)有功功率超调量进行测量:在0.5 s的有功阶跃时,传统VSG、J自适应、JD协同自适应超调量分别为14.3%、8.8%、6.0%;在1 s的有功阶跃时,亦有JD协同自适应控制策略的有功功率超调量最小的结论。调整时间以2%误差带估算,经测量,JD协同控制与J自适应控制近似相等,均明显小于传统VSG。从减小有功功率的超调量和降低调整时间两者综合来看,JD协同自适应效果最优。

从图6(c)、图6(d)可看出,JD协同自适应控制策略的J和D均可随着频率波动自适应变化,且波形具有连续光滑特性。

4 结束语

本文在研究传统VSG控制的基础上,结合功角特性曲线,提出了一种变流器虚拟惯量和阻尼协同自适应控制策略,该算法避免了引入微分环节导致的放大噪声和对控制器运算要求高等问题。基于MATLAB/Simulink仿真,验证了本文所提控制策略可减小暂态过程中频率和功率的超调量,降低调整时间,且自适应参数变化平滑,不存在突刺的问题。