大扰动下缺额功率分配及频率分布特性研究

荀道玉, 郝思鹏

(南京工程学院 电力工程学院,江苏 南京 211167)

0 引 言

频率稳定是电力系统稳定运行的关键指标。目前,我国新能源发电装机规模居世界第一,发电比例稳步提高。截至2022年4月底,新能源发电装机容量大幅增长,同比增长20.5%。随着新能源渗透率提高,传统火电机组占比不断下降,电力系统惯量水平持续降低,频率稳定支持能力下降[1]。至2020年底,我国成功投运“十四交十六直”30个特高压工程,跨省跨区输电能力达1.4亿kWh时。特高压交直流输电提升了线路的传输容量,也提高了扰动的冲击性。两者相互叠加进一步放大了电力系统频率失稳的风险。

国内外对频率稳定方面取得了一定的成果。单从惯量角度分析:文献[2]以时间尺度为原则,从离线评估、在线估计以及趋势预测三个方向来评估电力系统的整体惯量的时空分布特性;文献[3]和文献[4]创新提出节点惯量特性的概念,前者基于惯性时空特性进行辨识电力系统节点计算惯量大小,后者则从电网结构和参数角度分析系统的惯量分布特性,得出节点计算惯量的解析表达式,并研究区域间惯量的相互影响。综合惯量与系统频率的关系看:文献[5]从不同系统出发,探究新能源机组惯量特性以及惯量分布对频率稳定性的影响;文献[6-12]针对多起停电事故这一现状进行分析,事故造成频率大幅跌落,诱发一系列连锁故障;文献[13]侧重于研究解决惯量水平下降引起系统频率调节能力降低问题的方法,欧洲电网从增加系统惯量和实时监控角度提出一系列应对措施;文献[14]提出频率空间存在分布性差异,基于惯量量度指标反应提出改善各点频率的最大偏移量和变化率两个特征值的有效措施;文献[15-19]为应对系统惯量降低,调频能力不足等问题,提出一次调频和二次调频综合控制策略方案以提高电网频率稳定性;文献[20]侧重于发生扰动时不同负荷类型对频率稳定性的影响。

目前个别学者虽已提出节点惯量和节点频率的观点,但缺乏针对系统不同节点惯量、频率分布特性的定量描述以及扰动点附近的附加连锁故障的研究。新能源(海上风电)并网增加了系统调频困难。本文从分布惯量调频的角度,分析了电网中扰动点缺额功率分配规律、节点频率分布特性以及在新能源(海上风电)机组附近产生的连锁反应,并在此基础上提出考虑网架结构不同的分区域方法,为大规模海上风电接入后系统调频措施提供支撑。

1 扰动功率大小分配

特高压交直流输电线路上大功率扰动事件增多,有功功率损失引起节点的频率响应特性发生很大的变化,系统中的发电机组无法迅速响应扰动功率的波动,系统就会发生频率失稳的现象。基于电网结构参数对缺额功率分配重点研究并猜想提出:缺额功率的分配与电气距离有关。

1.1 扰动功率分配原理

在两机系统中,扰动功率从扰动点向线路两侧分布输送到两侧发电机组。考虑线路各节点电压角度差变化不大时(额定电压附近),扰动功率ΔP可近似为ΔI,即电网某点K处发生功率扰动时,不平衡功率相当于给电路施加一个反向电流源,该反向电流由扰动点K向两侧电路分流,电流大小与电网结构参数线路阻抗成反比,分配功率大小与电流大小呈正相关。当发电机内部阻抗较线路阻抗可以忽略不计时,改变节点K到两区发电机的线路参数(即电气距离),分析扰动后产生的功率分配与电气距离的关系。

1.2 扰动功率分配模型

研究考虑发电机内电势功率分配模型,如图1所示。计及发电机内电势的不平衡电流分配公式如下:

(1)

图1 考虑发电机内电势的功率分配等效图

不平衡功率分配情况等同于上述电流分配情况,缺额功率分配与线路阻抗参数成反比。因此邻近机组拾取的分配功率比较大,较远机组拾取的分配功率较小。这为电网分析确定扰动的位置、掌握功率分布情况提供了理论指导。

2 扰动大小对各点频率的影响

电力系统稳态运行时,用系统任一节点量测到的频率来表征系统的频率。但电力系统时刻发生各种大扰动和小扰动,在电网不同节点位置发生有功功率扰动后引起节点的频率发生偏差[21],用节点频率变化率(节点处不平衡功率的大小与发电机惯量的比值)刻画偏差程度。在不同节点的位置点测量到的频率跌落大小不一样,电网中频率变化率呈现分布特性。

频率变化率具有分布特性。单个机组频率跌落的大小与扰动功率大小以及发电机组惯量有关,扰动产生的不平衡功率越大,机组的惯量越小,响应的频率变化率就越大。一旦频率跌落至低频减载保护装置整定值,减载动作将引发系统大面积停电。因此,研究频率变化率的分布特性至关重要。

教学内容是开展体育课堂教学的前提和基础，因此构建生活化的课堂教学，自然要引进生活化的教学内容。对于体育课堂教学，教师不能一成不变，要积极寻求新的亮点，寻找新颖和新奇，激发学生的学习兴趣，吸引学生的眼球，让学生积极踊跃参与体育运动。在小学的体育教学中，有很多基础知识对于小学阶段的学生来讲理解比较困难，因此教师就要引进生活化的教学内容，来进一步提高小学生的学习自信心。

定义电网中节点K的频率变化率为节点K处发生功率扰动后,扰动功率的大小与所加发电机的惯性时间常数的比值有关。

3 新能源并网下各扰动点产生的附加连锁反应

随着新能源的快速发展,传统火电机组比例显著下降,电网中可提供的惯量持续下降,再加上电网出现单线路故障,产生较大功率缺额,两者引起系统频率大幅下降。当线路故障附加新能源保护连锁反应,进一步加大扰动大小,将导致频率进一步下降,一旦下降超过新能源机组的频率变化保护动作阈值(0.125 Hz/s),导致机组再次脱网,加剧系统频率大幅跌落,产生连锁反应诱发一系列低频减载动作。

为了确保电网稳定运行,提高新能源机组的惯性响应特性,采取了一系列新能源参与频率控制技术[22]。但电网中新能源机组经过层层升压,阻抗放大数倍后,等同于远距离机组,当电网线路某点发生扰动后的暂态过程中,远端机组(扰动点与发电机组之间线路阻抗较大)由于端口电压波动较小,励磁调节不起作用,发电机内阻抗一般为稳态电抗,再加上线路阻抗较大。因此远端机组分配的功率较小,即使远端机组具有较大的惯量,频率变化率较小,对该点的频率支撑能力较小,因此电网的虚拟惯量支撑能力极其有限。

4 仿真分析

4.1 扰动功率分配

理论分析可知:缺额功率分配与线路阻抗成反比。为了验证所提结论的有效性,本文采用时域仿真软件BPA建立如图2所示的四机两区系统模型。图2中:两区之间线路K点(母线7)切负荷,模拟线路上发生功率扰动(规定:区域一为发电机1和2,区域二为发电机3和4)。

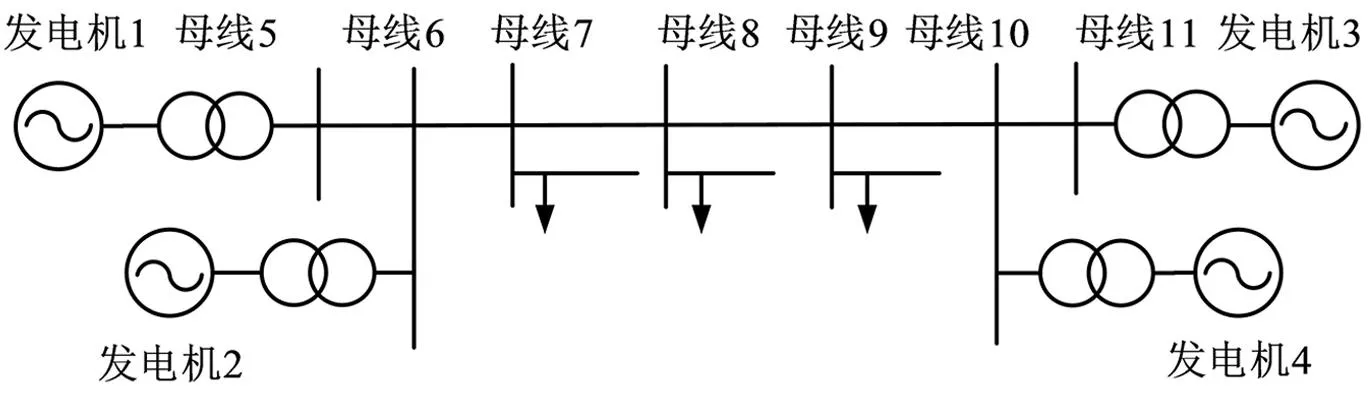
图2 IEEE四机两区系统图

由发电机内部阻抗与线路阻抗比值量级可得出:当线路长达400 km及以上时,不平衡功率分配以线路阻抗为主,仅研究线路长达400 km以上的模型即不平衡功率分配以线路阻抗为主。

表1为四机两区系统的参数值,设置系统基准容量均为900 MVA。

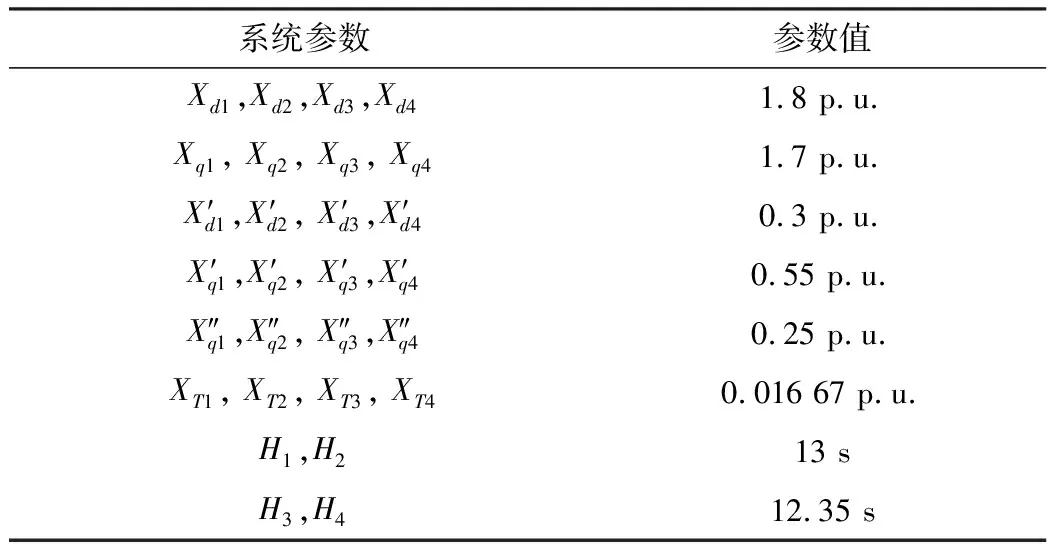
表1 四机两区系统参数

在仿真验证中,通过加大扰动点K与区域2的发电机组的电气距离(即不断增大节点K与区域2的阻抗)得出:点K分配到区域2的功率越来越小,功率大小和阻抗大小近似成反比。因此,该仿真结果与理论分析结果相一致。

4.2 频率变化率分布特性

发电机转子的转速和母线频率下降的快慢与发电机惯量大小和扰动的功率分配相关。扰动点分配的不平衡功率分配上文已具体研究,简单了解发电机惯量。

(2)

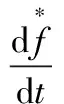
以上公式只适用于系统惯量或者区域惯量是一致的情况,在实际电力系统运行中,惯量具有分布特性,相应的节点频率变化也具有分布特性。理论推导中假设不考虑发电机励磁调节器的作用,发电机空载电动势Eq为常数,将系统的状态方程在平衡点线性化可得式(3)和式(4)。

(3)

(4)

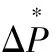
式(3)和式(4)即为系统某点发生功率扰动时,扰动功率大小、惯性时间常数和频率变化率之间的关系。

在时域仿真软件BPA中建立如图3所示的两机五节点系统仿真模型分析频率跌落具有分布特性。上述模型中,两台发电机位于母线1、2处,发电机为考虑阻尼绕组的次暂态模型,基准容量100 MW, 发电机1机端母线1可看作是无穷大母线,发电机2机端电压为13.8 kV位于母线K处接有恒阻抗负荷90 MW。系统参数设置具体如表2所示。

表2 两机五节点系统参数

图3 IEEE两机五节点系统图

算例中:在发电机1与发电机2中间一条线路母线K处切除负荷后,观察发电机2的功率变化以及频率跌落情况;在另一条线路上不同节点插入母线,观察各节点处母线偏差。由图4(频率偏差最大为母线6,最小为母线5)可以看出,仿真与理论分析结果相一致。节点K处受到功率扰动时,线路上各节点测量到的频率跌落大小不一样,电网中频率变化率呈现分布特性,低惯量机组附近的频率偏差较大。

图4 不同节点频率偏差曲线

接着调整两台发电机惯量一致,不断改变节点K在线路上的位置(距离发电机2由近到远)。

验证分析时,为了避免测量的偶然性,取扰动发生后初始0.2 s内的数据(仅考虑系统产生偏差功率后频率变化最为剧烈的初始时间段)。根据式(3)、式(4)(假设Eq恒定,U取故障处的母线电压)计算。仿真结果如表3所示。

表3 线路测量点的频率变化率

由图5可知:两台发电机等惯量时,由故障点到发电机2机端距离越小,频率偏差越小,故障节点K处初始频率偏差最大,故障点到发电机端线路上各节点频率偏差逐渐减小;即发电机2对电网频率响应支撑能力就越强。近端发电机对故障点的频率支撑能力比较强,远端发电机对故障点的频率支撑是比较薄弱的。

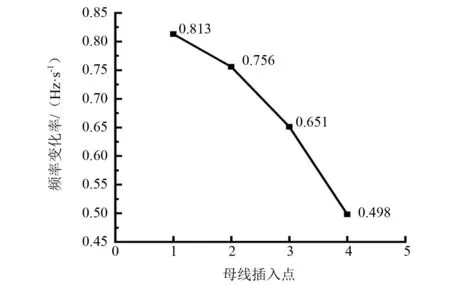
图5 不同测量点的频率变化率

4.3 分析讨论

上述算例属于联系紧密的小型电网,电网运行时同步性较强,推想:在一个大电网系统中,发生扰动后的暂态过程中,频率变化量最大通常发生在闭锁换流站附近的小机组和远处的大机组之间。根据电网频率变化率分布情况,提出区域惯量调频提高新型电力系统的惯量支撑能力。

5 结束语

针对电网惯量下降且分布不均、线路发生扰动的风险增加,频率分布差异显著,本文采用两机系统和四机两区系统进行推导验证,得出如下结论。

(1) 故障点处发生扰动后,扰动功率由该点向两侧线路分布,两侧拾取功率大小与阻抗(线路阻抗与发电机内部暂态电抗之和)成反比。

(2) 发生扰动后电网各节点的频率响应变化率具有分布特性。

(3) 虚拟惯量支撑能力有限,需配置更合理的频率变化保护阈值,避免附加连锁故障。

本文为后期新能源并网惯量调频措施的研究具有一定参考价值。一方面,在计及储能的新能源并网控制研究中,选取频率偏差较大的点作为储能并网点,增强并网点的电网强度和频率变化保护动作值,确保故障时针对各点设置相应的频率保护动作值以配合储能系统提升电能质量。各点在储能配置的协调控制下,系统恢复动态稳定运行。另一方面,从实际工程角度考虑,研究华东电网中江苏省周边远距离的机组可以为江苏电网惯量调频提供支撑。