含双馈风机接入的电力系统送端暂态稳定性研究

刘洪波, 于汉清

〔现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132012〕

0 引 言

随着“碳达峰”“碳中和”目标的提出,高比例新能源并网对电网功角稳定产生了深远影响[1]。

文献[2]总结了风电机组建模和含风场的系统暂稳特性等相关技术研究成果。文献[3]通过仿真计算得出系统临界清除时间随非同步机电源比例、同步机制、并网位置、故障类型和故障位置5个影响因素的变化趋势。文献[4]依据等面积定则性分析了双馈风机(doubly fed induction generator,DFIG)接入方式、接入比例对系统暂态功角稳定性的影响。文献[5]利用暂态能量函数法识别不稳定平衡点和动能函数以及势能边界面函数来分析不同风电渗透率、故障位置和系统运行条件对暂态稳定的影响。文献[6]基于扩展等面积理论分析了当送受端机组惯量不同情况下风电接入比例对系统功角暂态稳定性的影响机理。文献[7]在此基础上,研究了风电接入多机系统时系统暂态稳定性的变化。文献[8]指出同步机初始功角随风电比例的增加呈一定线性比例减小,DFIG的有功慢恢复特性和故障后的无功功率支撑提高了系统暂态稳定性。以上文献主要研究了风电不同接入方式、接入比例及接入位置对系统暂态稳定性的影响,未考虑风电接入点电压问题。

文献[9]提出了抑制系统暂态过电压的措施来保证风机正常并网运行。文献[10]提出了用无功补偿装置实现风机的高压穿越策略。文献[11]针对几种典型的稳态电压主动支撑技术,从机组性能、控制能力、运行差异及协调配合等方面进行综述。文献[12]分析了适用于光伏/风电场站暂态电压支撑的聚合建模方法和多无功源协调控制的思路。以上文献没有考虑风电接入方式、接入比例及接入位置对系统暂态稳定性的影响。

综上所述,本文基于稳压设备-静止无功补偿器作用的风机等值阻抗模型,采用并联静止无功补偿器的方法可维持风机接入点的电压在合理范围内,并将其简化为电容器模型视为风机等效外特性的一部分,以此研究风电接入单机系统后对同步机功率特性的影响。本文推导了单端送电系统同步机电磁功率公式,分析了风电接入后对同步机功角曲线的影响,根据等面积定则得出DFIG接入系统后对于加/减速面积的影响。由此分析不同风机接入方式、接入比例以及接入位置对系统暂态稳定性的影响,最后通过仿真对研究结果进行验证。

1 双馈风电机组的等效外特性

1.1 单端送电系统传输功率

图1为DFIG接入单机无穷大系统结构示意图。

图1 DFIG接入单机无穷大系统结构示意图

接入风机前同步机的传输电磁功率P为:

(1)

接入风机后单端送电系统输出电磁功率Pe为:

(2)

式中:Z11、Z12分别为送端同步机的自阻抗和互阻抗;α11、α12分别为自阻抗和互阻抗对应阻抗角的余角。

1.2 风机等效模型

目前,大多数研究都将风电机组看作一个不具惯性的功率源,其等效外特性为一个负电阻和负电抗。系统稳定时,双馈风机在恒功率因数控制下只输出有功功率而不输出无功功率,此时DFIG等效为一个负电阻。当系统发生故障后,系统母线电压下降,此时双馈风机会在其控制系统的调节下,向系统发出一定比例的无功,此时将其等效为一个负电阻和负电抗并联的模型,如式(3)所示。

(3)

式中:upcc为风机接入点电压;k为风电接入比例;Pf、Qf分别为风机输出有功和无功。

此时正常运行时等值电路如图2所示。

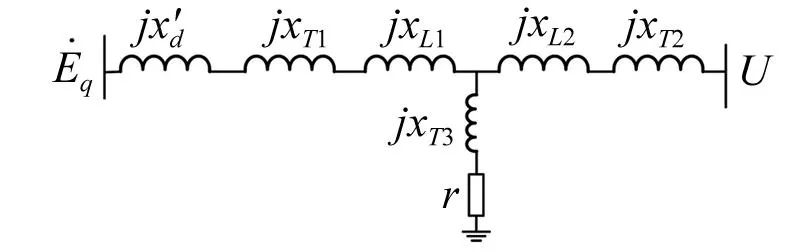
图2 传统阻抗模型正常运行时等值电路图

等值电路的自阻抗和互阻抗为:

(4)

式中:λ为风机距离负荷的位置;xL1为第一段线路电抗;xL2为第二段线路电抗。

为使在不同渗透率时风机接入点电压能保持在合理范围内,提出含静止无功补偿器的风机等效模型:

(5)

式中:QC为补偿无功容量。

在系统正常运行时将DFIG等效为一个可变的负电阻和静止无功补偿器并联的模型;在系统发生故障时,将DFIG等效为一个可变的负电阻、一个可变的负电抗和静止无功补偿器并联的模型。

采用新型等效模型的等值电路图如图3所示。

图3 并联静止无功补偿器后等值电路图

此时等值电路的自阻抗和互阻抗的其他参数不变,式(4)中x3变为:

(6)

并联无功补偿器后x3减小,因此|Z11|和|Z12|减小,由此得出风机接入点接入静止无功补偿器前后同步机的功角曲线如图4所示,含有静止无功补偿器的风机等效模型增加了系统在暂态过程中的减速面积,更有利于系统暂态稳定性。

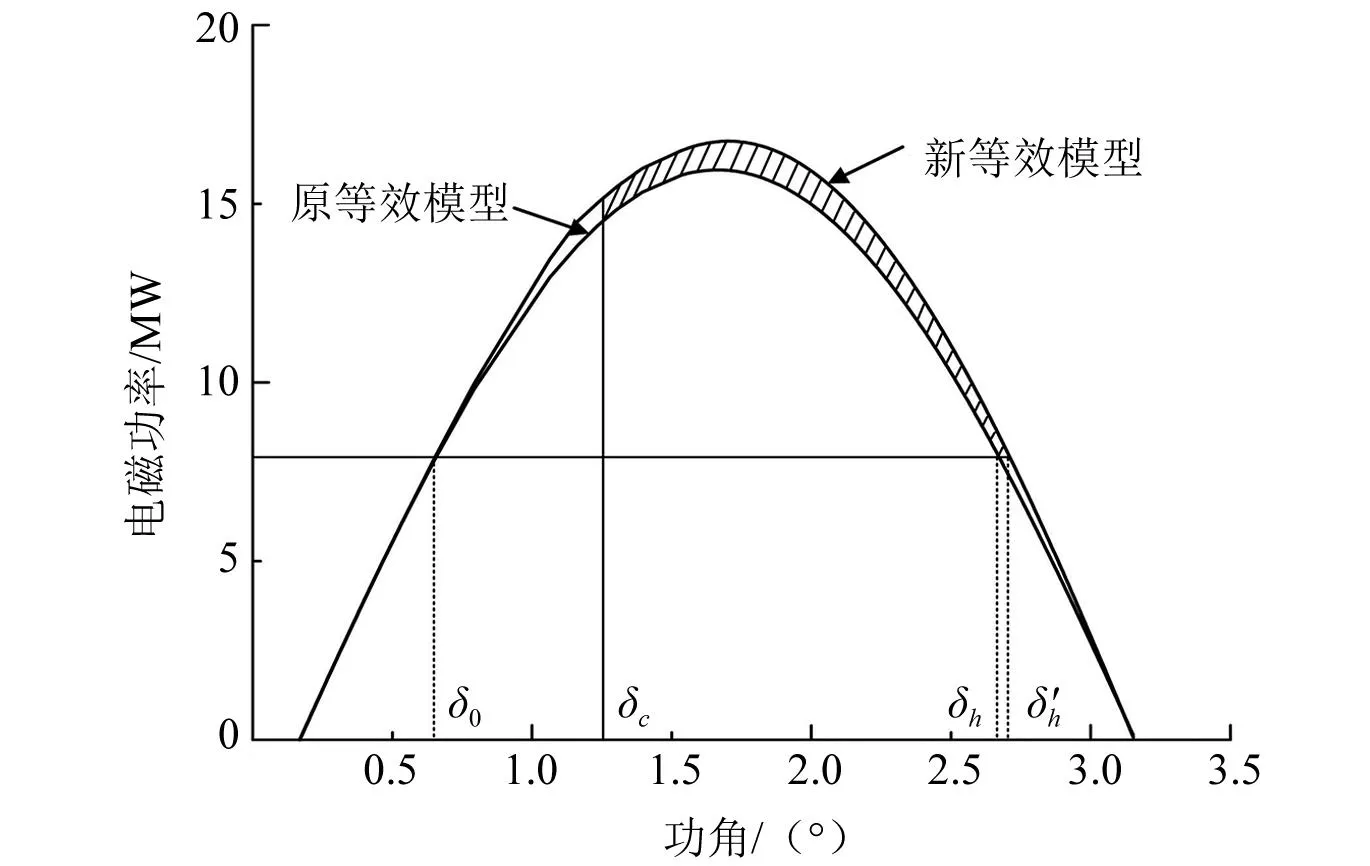
图4 接入静止无功补偿器前后同步机功角曲线变化

2 DFIG接入单机无穷大系统对系统暂态稳定性影响机理

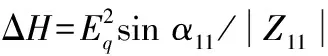
图5 风机接入后同步机功角曲线

设置在线路中间处发生三相短路故障,故障期间等值电路如图6所示,此时式(4)中x2与x3发生变化,如式(7)所示。

(7)

图6 系统故障后单端送电系统等值电路

此时自阻抗和互阻抗为Z21和Z22,阻抗角余角分别为α21和α22。Z21实部绝对值都与风电输出的有功功率正相关,虚部与风电输出的有功功率负相关,θ21>90°逐渐增大,因此角度α21=90°-θ21<0,且与风电有功输出负相关。|Z22|与风电有功功率正相关,且θ22<90°逐渐减小,因此阻抗角α22=90°-θ22>0,且与风电有功输出正相关。|Z21|的虚部与DFIG无功输出Q正相关,实部的绝对值与Q负相关,|Z22|与DFIG无功输出Q负相关,最终风机的无功输出会使故障期间同步机功角曲线上移,如图7所示。|Z21|和|Z22|随λ增大而减小,功角曲线向上偏移,如图8所示。

图7 故障期间功角曲线偏移

图8 不同接入位置对同步机功角曲线的影响

3 不同因素对加减速面积的影响

3.1 风机等容量替换同步机

风机等容量替换同步机即保持总负荷不变,逐渐增加风机出力。由图5可知,当风电机组接入单机无穷大系统后,同步机的功角曲线会向右下偏移,进而对系统故障后加速面积和减速面积产生影响。图9为不接入静止无功补偿器、风电接入比例30%和50%时,当系统发生故障后,对系统加速面积和减速面积的分析。由于这两种情况下故障期间同步机功角曲线较为接近,加速面积变化不大,故忽略不计。如图9所示,当接入比例为50%时,故障后加速面积为阴影Sbghc和阴影Sefgb,相较于接入比例30%加速面积减小了Sabcd,增加了阴影Sefgb,显然Sabcd>Sefgb;接入比例50%时故障后系统减速面积为Sjck,相较于接入比例30%减速面积增加了阴影Sdckl,减小了Sijl,显然Sdckl>Sijl,因此风电接入比例增大后,系统故障后的减速面积增大,加速面积减小,系统暂态稳定性提高。

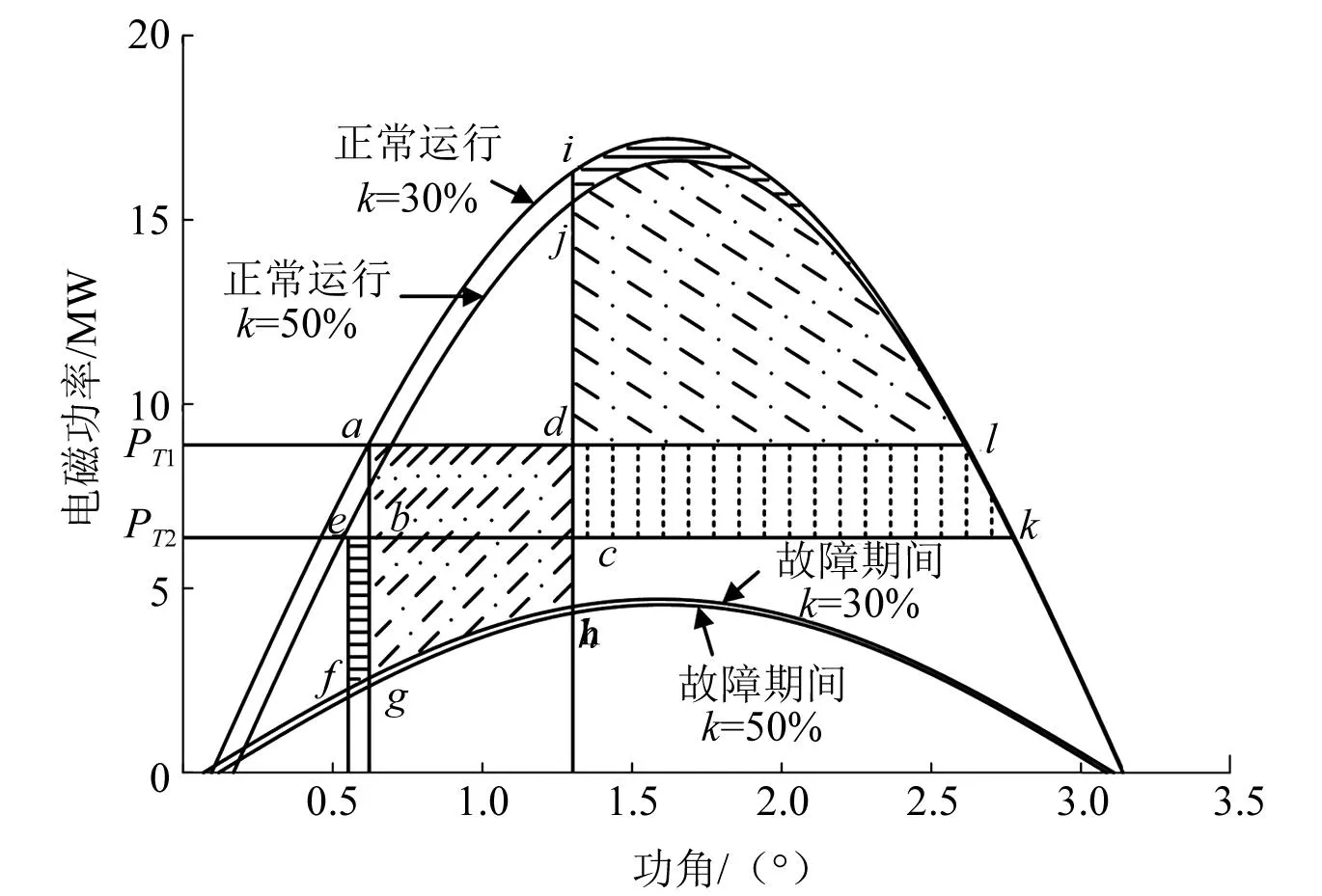
图9 等容量替换故障后加减速面积

并联静止无功补偿器后,增大了系统暂态过程的减速面积,使得风电接入比例增大后更有利于系统暂态稳定性,但随着风电接入比例的增大,增加的减速面积逐渐减少,如图10所示。

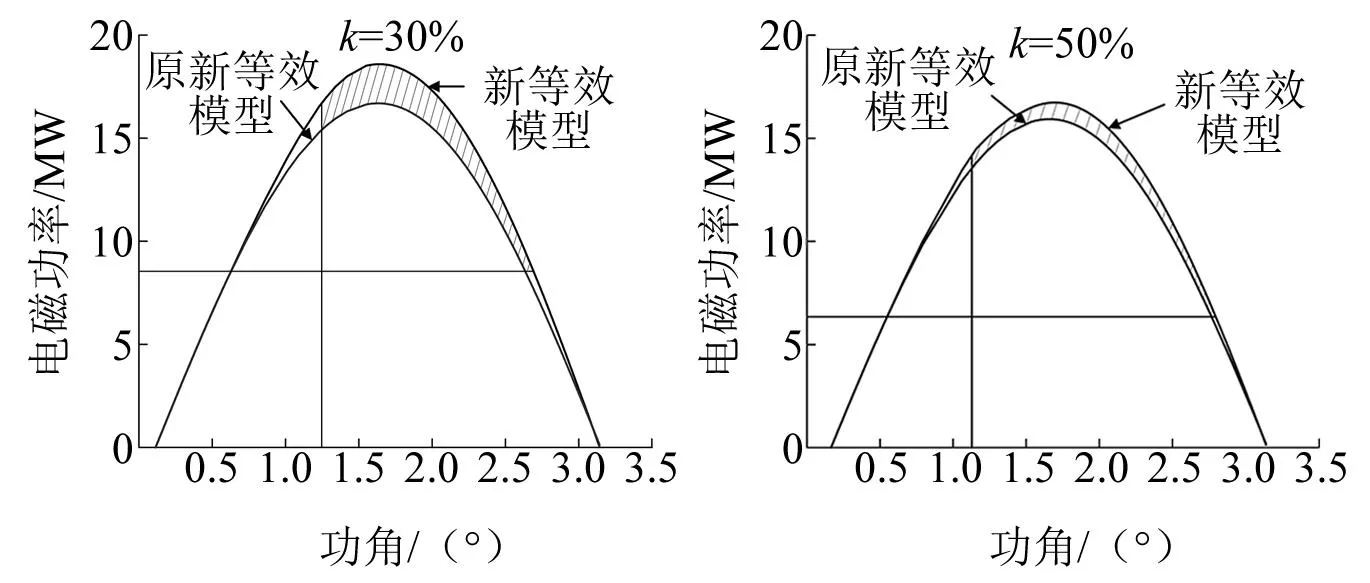
图10 有无静止无功补偿器调压时功角曲线比较

3.2 风电直接接入

风电直接接入系统即保持同步机出力不变,随负荷的增大逐渐增加风机的出力。图11为不接入静止无功补偿器、风电直接接入系统30%和50%时加减速面积的分析。接入比例为30%时,加速面积为Sabfe,当接入比例增大到50%时,加速面积减小了阴影Sabcd,增大了阴影Scghf。由计算可知,Sabcd和Scghf基本相等,因此接入比例增大前后加速面积保持不变;接入比例30%时减速面积为Siek,当接入比例增大到50%时,减速面积减小了阴影Sijk,因此当风电接入比例增大时,系统的加速面积保持不变,系统暂态稳定性降低。

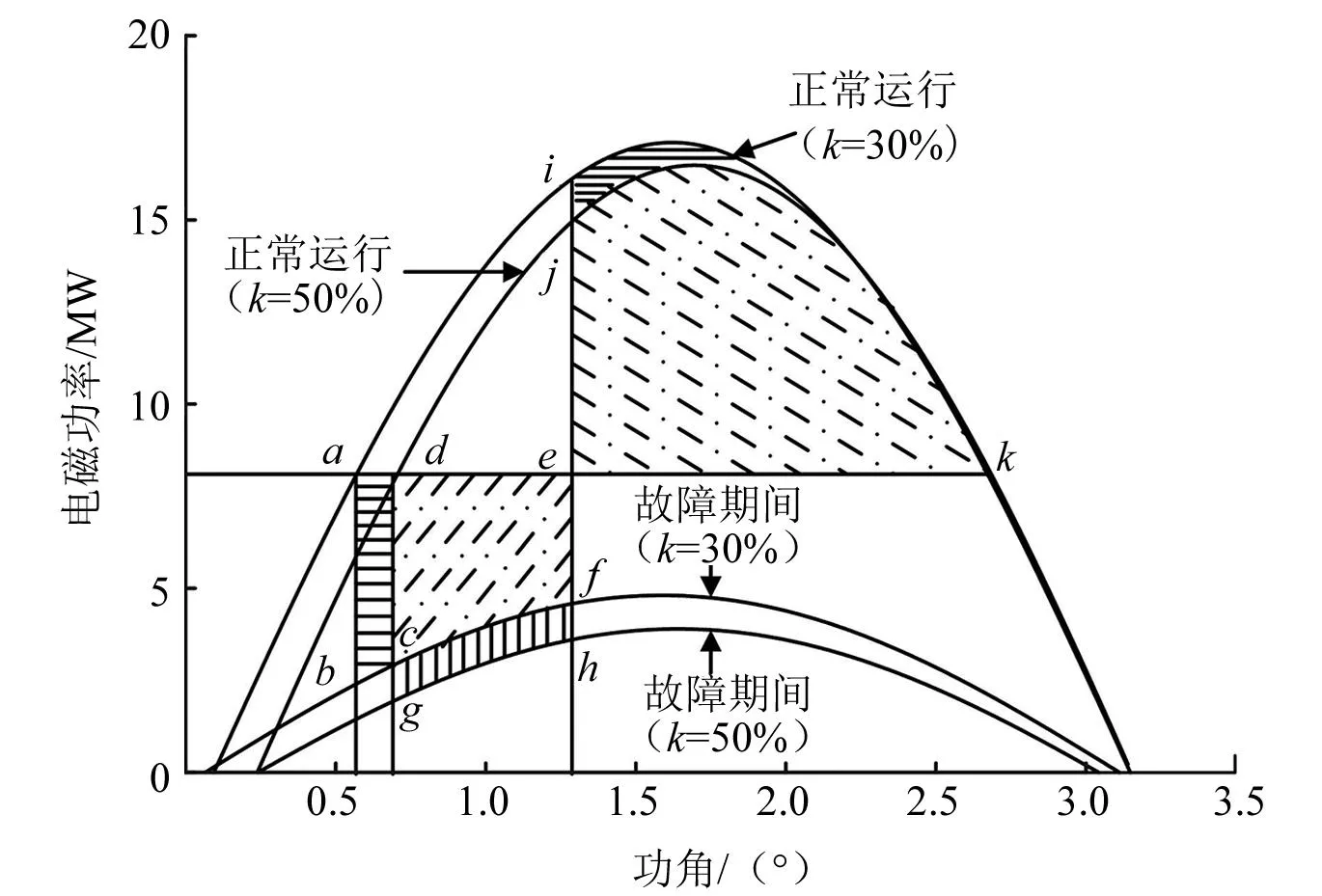
图11 风电直接接入故障后加减速面积

风电直接接入降低系统的暂态稳定性,因此并联静止无功补偿器后增大系统减速面积,改善了系统的暂态稳定性,增加的减速面积随风电接入比例的增大而减少,如图12所示。

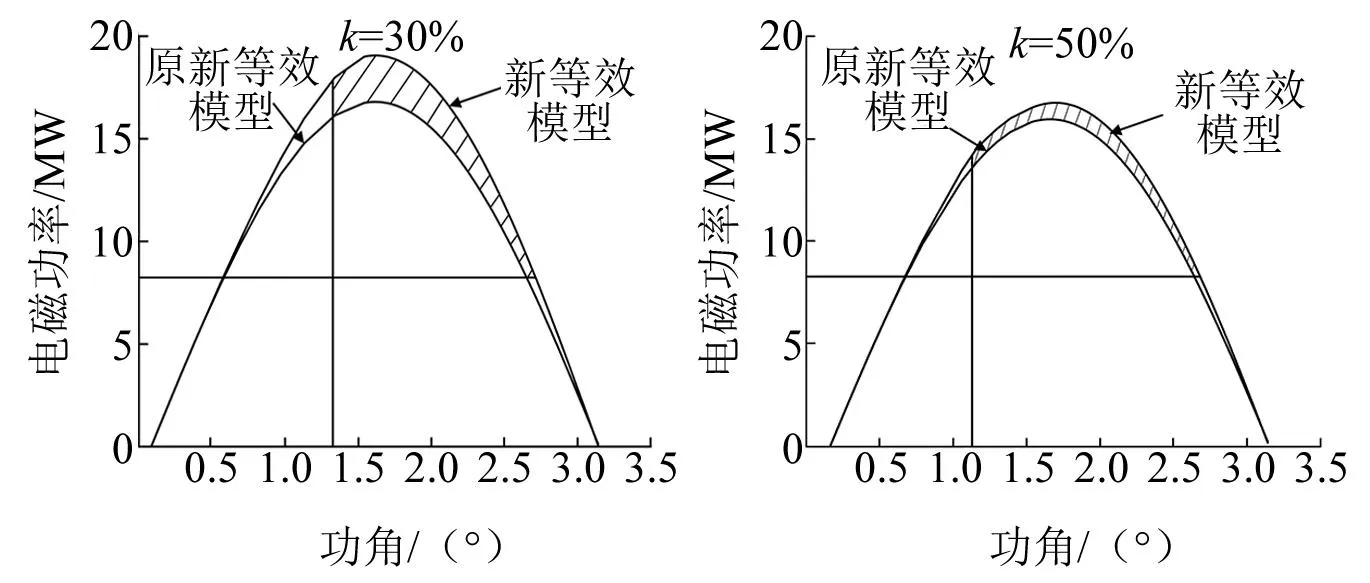
图12 有无静止无功补偿器调压时功角曲线比较

3.3 不同接入位置

风机不同接入位置会对系统暂态稳定性产生影响。图13为风机直接接入下接入位置不同时对功角曲线的影响,接入位置按照送端为0到受端为100%规划,当接入位置为0时加速面积为Sbghe,接入位置为50%时加速面积为Sadfe,相较之下,加速面积减小了阴影Scghf,增大了阴影Sadcb,通过计算可知,Scghf略大于Sadcb,因此加速面积略微减小;接入位置为0时减速面积为Sjek,当接入位置为50%时,减速面积增大了阴影Sijkl,因此,当接入位置靠近负荷时,系统暂态稳定性提高。

图13 接入位置不同时故障后加减速面积

4 算例分析

图14为单端送电系统拓扑结构。

图14 单端送电系统拓扑结构

为了验证本文的推导和分析过程的准确性,在ADPSS中搭建单端送电系统,G1为送端同步机,G2为受端同步机,G3为风机。如图15所示,保持风机出力不变,通过改变同步机出力得到对应同步机功角,描点得到同步机实际功角仿真曲线。对比结果表明采用新型等效模型提高了理论推导的精度。

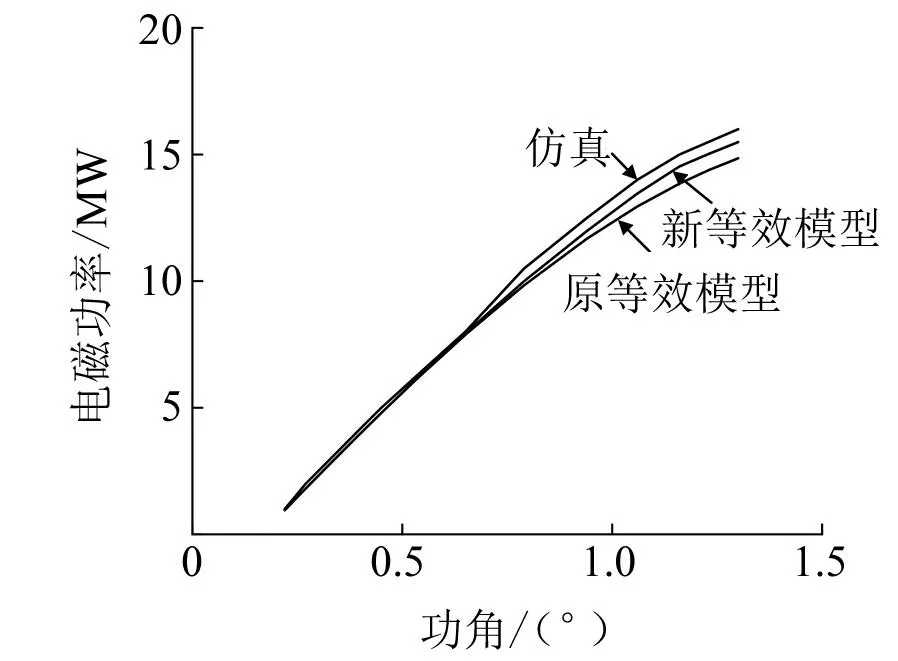
图15 等效外特性误差分析

发生三相短路后电压跌落,故障清除后电压恢复过程中风机输出的无功不足以支撑接入点电压,导致高压穿越失败,进而将风机切除,并联静止无功补偿器后,提升了风机在故障时电压支撑能力,如图16所示。

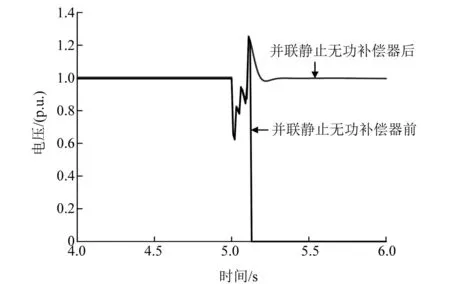
图16 并联静止无功补偿器前后DFIG端电压

设置在线路中间发生三相短路故障,0.15 s后切除故障。当风机等容量替换同步机时,设总负荷为12 MW,依照不同风电渗透率调整风机和同步机的出力;当风电直接接入系统时,选定同步机出力6 MW,随负荷增大,调整风机出力。本文以故障极限切除时间和功角首摆作为衡量系统暂态功角稳定性的指标。

风电等容量替换同步机情况下,随风电接入比例增大功角第一摆逐渐减小,如图17所示,即提高了系统暂态功角稳定性。

图17 0.15 s故障下等容量替换同步机功角

并联静止无功补偿器后,

由表1和表2可知,极限故障时间随风电接入比例的增大而增大,增强了系统的暂态稳定性。

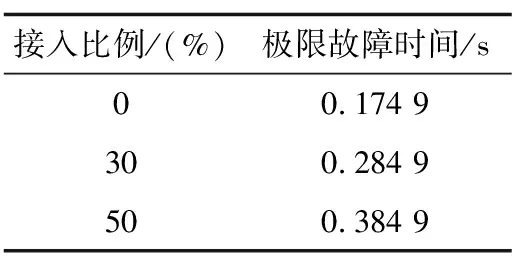
表1 原等效模型风机等容量替换数据

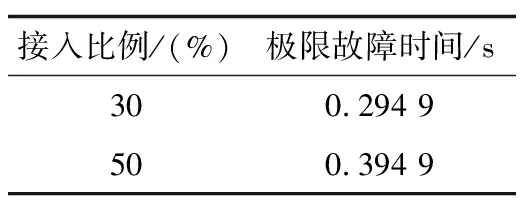
表2 新等效模型风机等容量替换数据

当风电渗透率过高时,风机接入点母线电压过低,系统无法正常运行,此时接入有无静止无功补偿器调压时功角曲线比较后能够提高系统的风电接入比例,如图18所示。

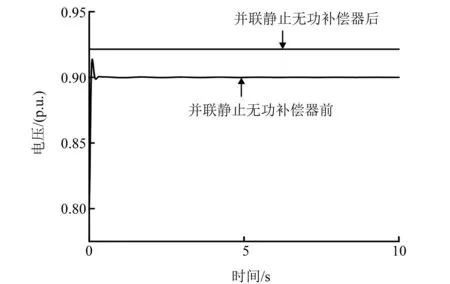
图18 静止无功补偿器接入前后风机接入点电压

风电直接接入情况下,随风电接入比例增大功角第一摆分别逐渐增大,如图19所示,即降低了系统暂态功角稳定性。

图19 0.15 s故障下风电直接接入同步机功角

由表3和表4可知,并联静止无功补偿器后极限故障时间随风电接入比例增大而增大,提高了系统的暂态稳定性。

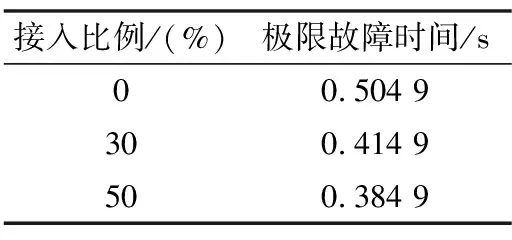
表3 原等效模型风电直接接入数据

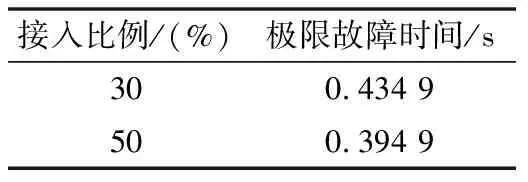
表4 新等效模型风电直接接入数据

设置同步机出力6 MW,风机出力6 MW,得出风机不同接入位置时,同步机功角随风电接入比例功角第一摆分别为63.56°和47.45°,即提高了系统暂态功角稳定性。图20为λ=0和λ=50%时同步机功角,表5为其极限故障时间。

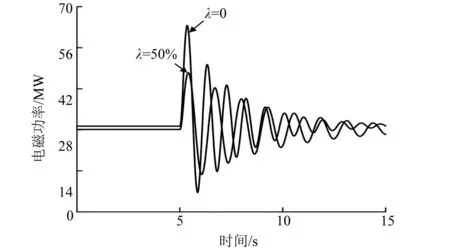
图20 不同风电接入位置同步机功角

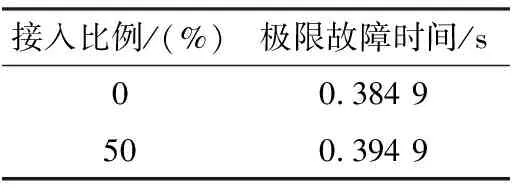
表5 不同接入位置数据

5 结束语

本文分析了双馈风机接入单端送电系统对系统暂态功角稳定性的影响,研究了考虑风机接入点并联静止无功补偿器的单端送电系统的功率特性,得出以下结论。

(1) 考虑风机接入点并联静止无功补偿器的稳压措施的双馈风机等效外特性计算时误差更小。在系统正常运行时,风机接入点电压在允许范围内,将DFIG等效为一个负电阻;在风机接入点电压过低时,将DFIG等效为负电阻和静止无功补偿器并联;在故障期间时,将DFIG等效为负电阻、负电抗和静止无功补偿器并联。表明新等效模型能够提升系统的风电接入比例,增大系统的极限切除时间,降低风电机组高电压脱网风险,有利于系统暂态稳定性。

(2) 风机等容量替换同步机时,随风电接入比例的增大,极限故障时间逐渐增大,功角第一摆逐渐降低,系统的暂态稳定性逐渐提高。风电直接接入系统时,随风电接入比例的增大,极限故障时间逐渐降低,功角第一摆逐渐增大,系统的暂态稳定性逐渐减弱。

(3) 当双馈风机并网位置越远离送端同步机时,极限故障时间增大,功角第一摆减小,系统暂态稳定性越好。