区域负荷惯性时间常数分析及辨识
2024-02-22李强王佳钰汪惟源汪成根郝思鹏
李强, 王佳钰, 汪惟源,汪成根,郝思鹏
(1.国网江苏省电力公司电力科学研究院,南京 江苏 211103;2. 南京工程学院,南京 江苏 211167)
0 引 言
“双碳”目标推动可再生清洁能源快速发展,2020年我国风光发电占比已达11.4%,预计到2050年将超过50%。大规模新能源接入电网,传统异步电机为主的负荷通过电力电子变流器并网比例也日益增长。新能源接入电网,“双高”系统惯量不足,影响电力系统频率稳定[1]。英国“8.9”、澳大利亚“9.28”大停电原因都与惯量不足有关[2-3]。
传统惯量主要关注同步发电机,采用同步转速动能和发电机额定容量比值-惯性时间常数表示。多机系统发电机惯性时间常数通常采用加权折算表示。负荷分布较为分散,其综合惯量效应缺乏研究,一般采用经验取值。随着电力系统惯量日益恶化,准确的负荷惯量评估是电力系统频率安全的基础[4-9]。
本文提出负荷的惯性时间常数量表达方程,基于受扰系统负荷并网点的功率和频率曲线辨识单个负荷点惯性时间常数,推广应用于负荷多点接入系统,计算出区域负荷综合惯性时间常数,为电力系统综合惯量评估提供技术支撑。
1 惯量、广义惯量与惯性时间常数
电力系统惯量表现为对频率波动的抵抗[10],响应频率变化,对系统频率稳定具有重要意义。
1.1 同步发电机惯量表示
惯量是描述物体惯性大小的量值[11]。同步发电机惯量表现为同步机转子对转速变化的抵抗力,发电机惯量为转动惯量,表达式为:
(1)
式中:r为转动半径;m为转子质量;J为转子转动惯量。
工程中更加关注发电机转速改变时能量的变化,对于同步发电机,其转子旋转动能为:
(2)
式中:ω为转速;Ek为转子旋转动能。由此可知,发电机动能取决于转动惯量和转速。工程中常用惯性时间常数TJ衡量机组惯性大小,物理意义为发电机转子施加额定转矩达到额定转速所需的时间,表达式为:
(3)
式中:TJ为惯性时间常数;SB为机组额定容量。
即发电机惯性时间常数和额定容量、惯量、额定转速相关,和负载率无关。
转子运动方式为:
(4)

由于标幺化角频率和频率相同,不平衡功率和频率变化率的关系表示为:
(5)
式中:df*/dt为频率变化率;ΔP*为标幺化不平衡功率。
即同步发电机惯性时间常数也可描述为不平衡功率和频率变化率的量化关系[12]。
多机系统的同步机惯性时间常数可以表示为:
(6)
式中:TJi为第i台机组惯性时间常数;SBi为第i台机组额定容量;TJi_total为总惯性时间常数。
1.2 广义惯量
系统惯量响应包括电源侧同步机惯量、负荷侧异步机惯量以及虚拟惯量等[13-14],称为电力系统广义惯量。和同步发电机不同,广义惯量构成复杂,虚构了和频率相关的转子动能,且由于缺乏发电机额定容量这一指标,难以用惯性时间常数表示。采用有名值的广义惯量虚拟转子动能表达式为:
(7)

其物理意义是频率改变时系统虚拟动能的改变量。如何构建以惯性时间常数描述的广义惯量还有待于进一步深入研究。
1.3 负荷的惯性时间常数
系统中负荷构成复杂且负荷分布分散,通常只能表示其综合惯量效应。由式(7)可知,负荷广义惯量有名值为功率变化和频率变化率关系[15-19]。
发电机惯量由转子决定,负荷缺乏明确的转子但通常工作于额定负载状态,其额定出力取决于额定电压和频率,正常运行的负荷出力就是其额定容量。
根据式(8),在负荷变化不大的情况下,TJ_total为常数。即:
(8)
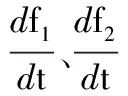
根据式(8)则有:P1/SLoad=TJ_totaldf1/dt,P2/SLoad=TJ_totaldf2/dt。可得:
(ΔP1-ΔP2)/SLoad=TJ_tatal(df1/dt-df2/dt)
(9)
即负荷惯性时间常数由式(10)获取:
(10)
2 负荷惯性时间常数辨识
当系统失去部分电源时,起始阶段受惯量影响频率近似线性下降,下降速度主要由发电机和负荷的综合惯量确定。发电机惯量一般由厂家给定,负荷惯性时间常数需另外测算,由式(10)可知,负荷的惯性时间常数由频率变化时出力变化确定,实际系统中频率跌落相关数据获取较为困难[20]。根据系统受扰后产生频率和功率的摇摆曲线进行参数辨识。
2.1 辨识数据选择及处理
取负荷并网点电压频率曲线和负荷功率曲线,如图1(a)所示,反映频率变化对功率变化的影响。考虑受扰过程中降低电压波动对辨识结果的影响,选择稳态电压点附近参数进行惯性时间常数辨识。如果电压数值变化不大,则取整个摇摆数据进行参数辨识。

图1 辨识数据选择和处理示意图
由于系统惯性表现为对扰动引起频率变化的抵抗作用,受扰后系统易发生功率和频率波动情况,两者改变具有一致性,见图1(b)(图中纵坐标为标幺值无量纲)。考虑到摇摆曲线参数变化幅度较小,根据单点频率和功率变化的辨识易受噪声干扰,需要计及群体效应。若负荷功率和频率相关,二者变化曲线相位相同,存在同步性。根据谐振特性二者有效值关系散点呈一条直线,辨识斜率可获得惯性时间常数。为防止频率变化过小,引起功率和频率变化比值偏差大,对数据预处理,舍去频率变化小于设定阈值的点。
2.2 参数辨识方法
参数辨识根据数据与既有模型通过算法来确定参数值,使预测值尽量拟合实际值[21-22]。本文采用最小二乘拟合法,数据来源于ETAP12.0对IEEE 3机9节点系统仿真得出受扰后负荷并网点母线频率与并网功率值。

(11)
2.3 区域负荷惯性时间常数折算
区域负荷通常多点接入,每个点负荷存在一定差异,其惯性时间常数也不同。对于多点接入的负荷,其惯性时间常数可以参照同步发电机采用式(12)加权折算。
(12)
式中:TJ_Load_total为区域负荷惯性时间常数;TJ_Loadi为第i并网点负荷惯性时间常数;SLoadi为第i并网点负荷功率。
计算流程如图2所示。
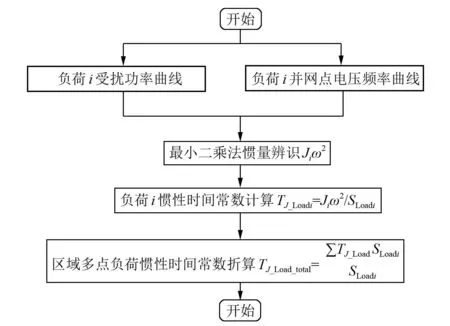
图2 区域负荷惯性时间常数计算流程
采用IEEE 3机9节点模型验证方法正确性,求解区域负荷惯性时间常数,分析含新能源机组的华东电网频率响应。
传统区域负荷参与调频,随着系统频率的升降,出现输出功率的升降。新能源环境下,频率变化不会影响电动机功率输出,区域负荷的等效调差系数会下降,利用PMU量测的负荷功率-频率等信息,通过参数辨识获得区域负荷惯性时间常数。
3 算例分析
各区域按照是否含有新能源机组来分析。
3.1 3机9节点模型
以IEEE 3机9节点为例,如图3所示。
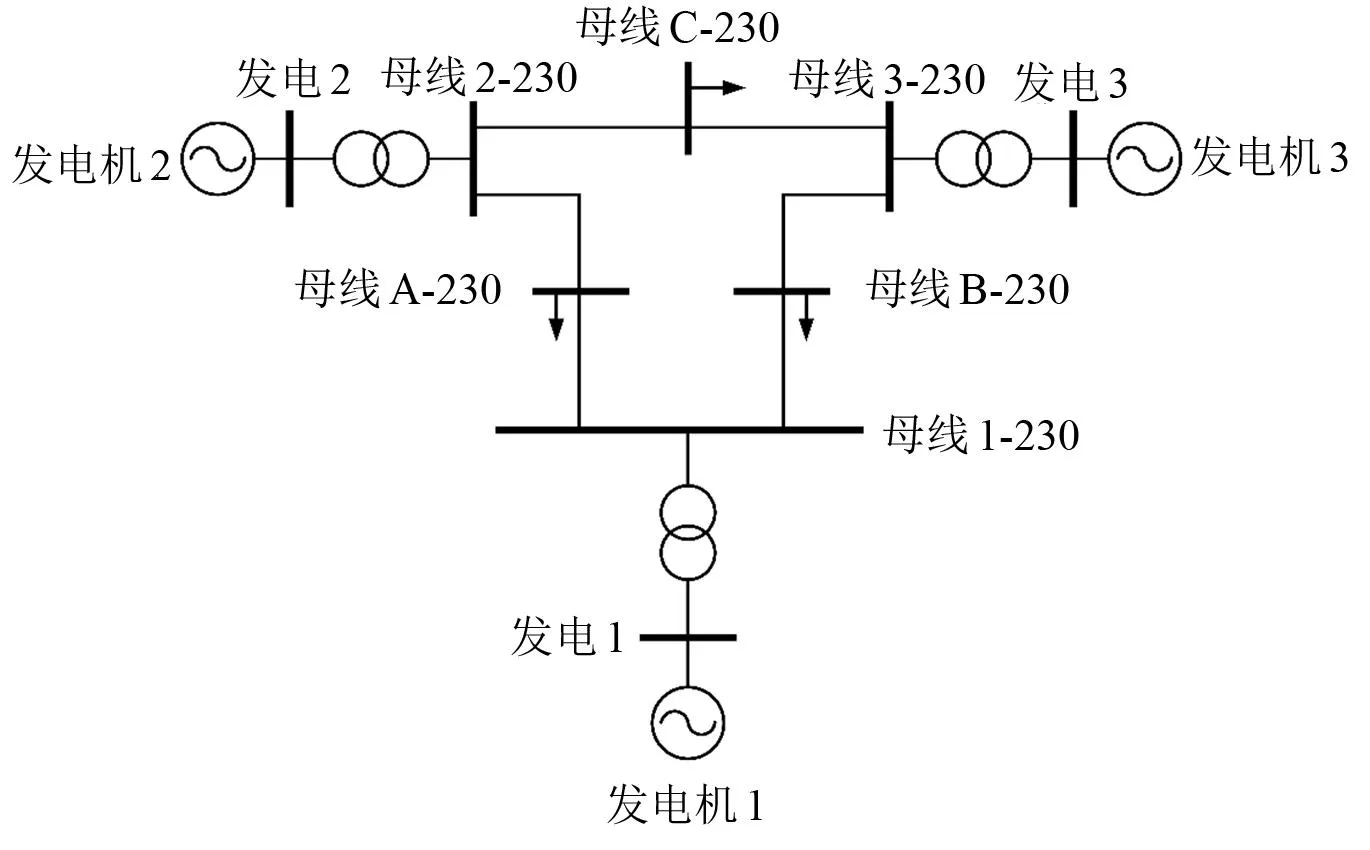
图3 IEEE 3机9节点系统图
考虑系统平稳将发电机1惯量设为最大,母线A负荷为100%恒功率负荷(计及动态)、母线B为50%恒功率(计及动态)和50%恒阻抗,母线C负荷为100%恒阻抗负荷。为简化分析恒功率电机动态负荷设置如图4所示。图4中:ΔP为电机电磁功率变化;ΔPm为电机机械功率变化;Δf为频率变化。
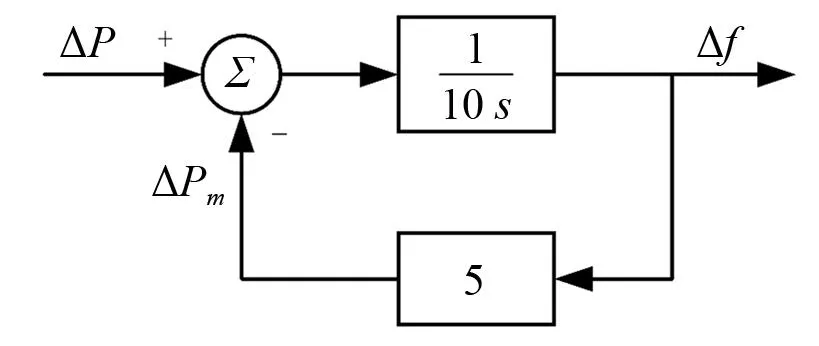
图4 恒功率电机负荷动态模型
发电机和负荷参数见表1、表2。

表1 发电机参数发电机额定容量/MVA惯性时间常数/s发电机1247.5∞发电机2192.06.7发电机3128.04.7表2 负荷参数负荷有功负荷/MW无功负荷/Mvar负荷A125.070.0负荷B90.040.0负荷C100.055.0
扰动设为发电机2母线发生三相短路,0.2 s故障清除。ETAP12.0仿真获各负荷并网点母线频率和功率波动曲线。
为检验辨识方法的有效性,对发电机2功率和频率曲线辨识,辨识图如图5所示,结果为y=6.758x,即TJ=6.758,和发电机2惯性时间常数6.667接近,说明辨识方法正确。
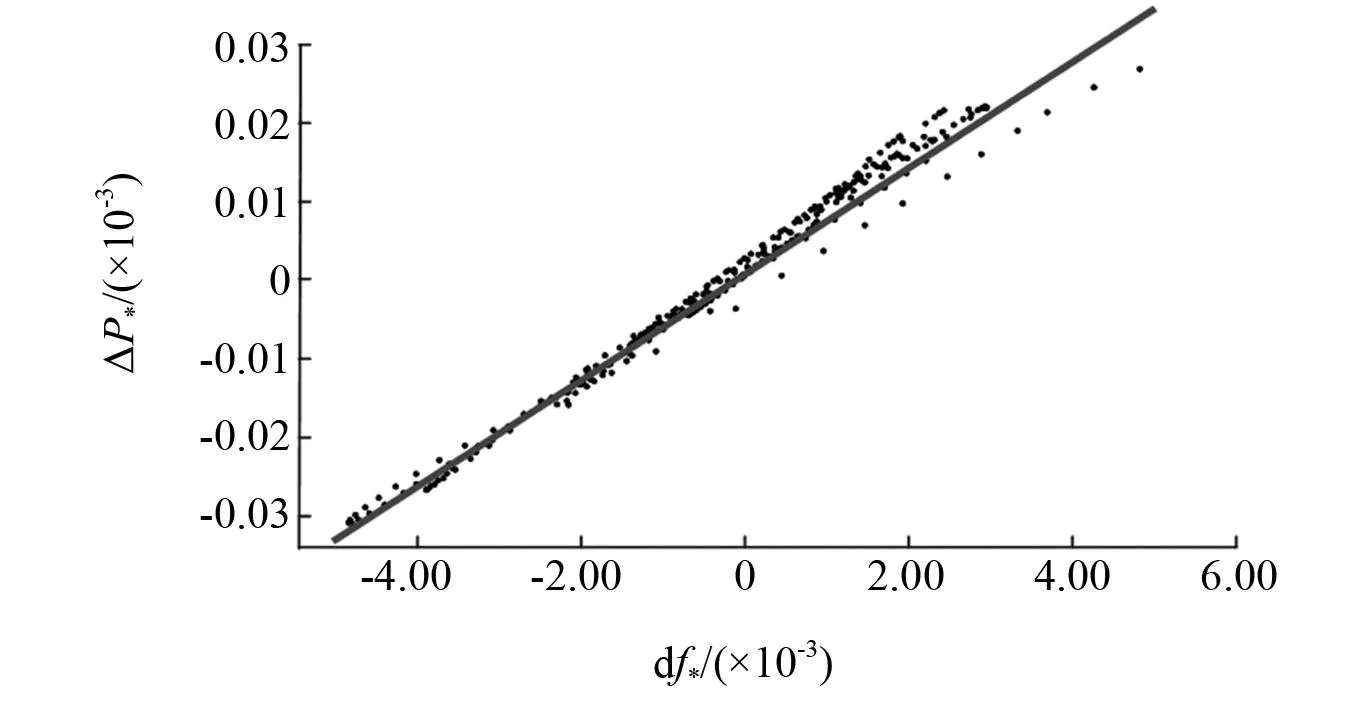
图5 发电机2惯性时间常数辨识
分别对负荷A、B、C摇摆曲线进行参数辨识。图6为负荷A出力波动曲线和并网点母线的频率波动曲线,TA=0.398。

图6 负荷A惯性时间常数辨识
图6中呈现椭圆环效应是因为功率和频率变化存在一定时滞。
由图7负荷B的惯性时间常数辨识得y=0.202x,即负荷B惯性时间常数为TB=0.202。
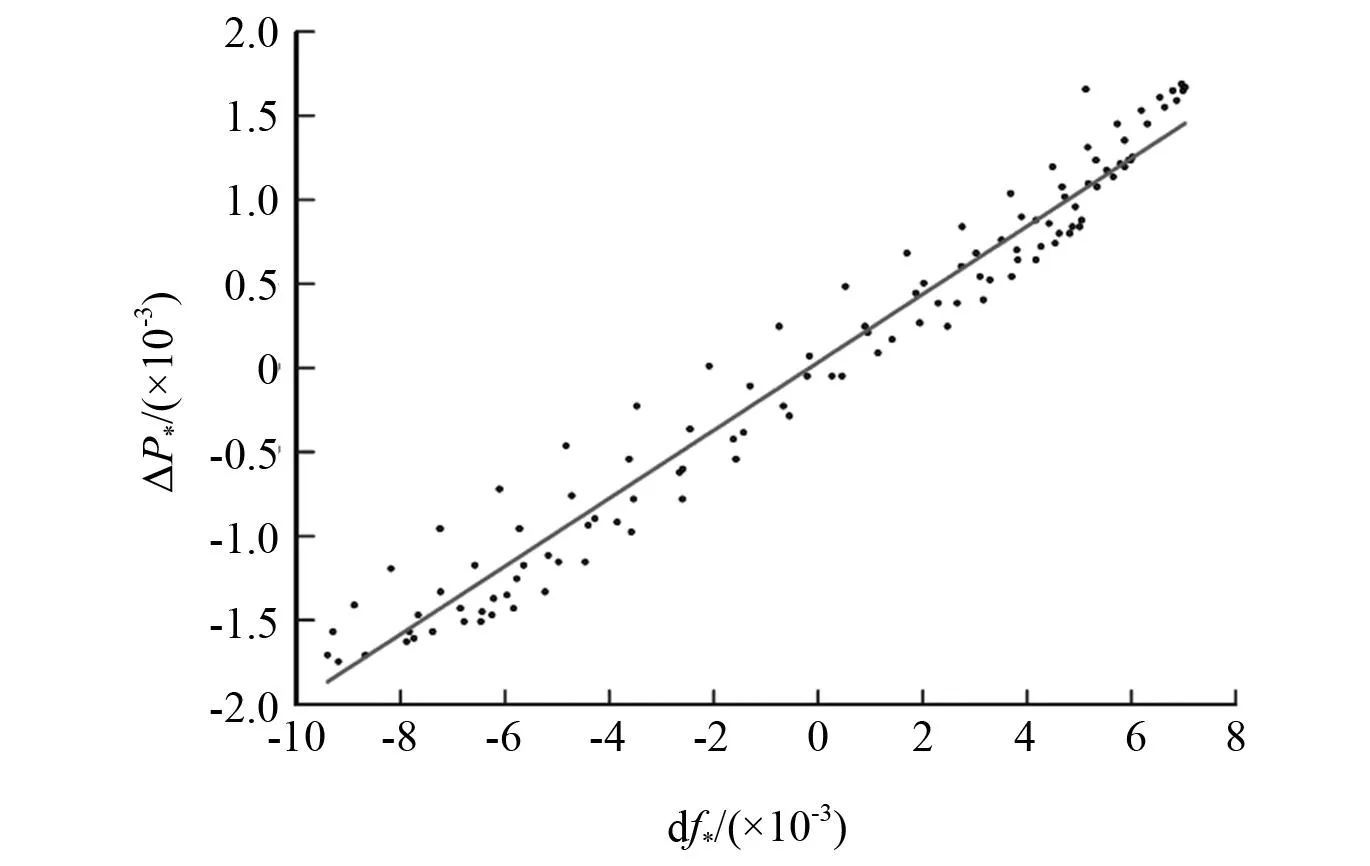
图7 负荷B惯性时间常数辨识
由图8负荷B的惯性时间常数辨识得y=0.008x,即负荷C惯性时间常数TC为零,恒阻抗负荷缺乏惯量。
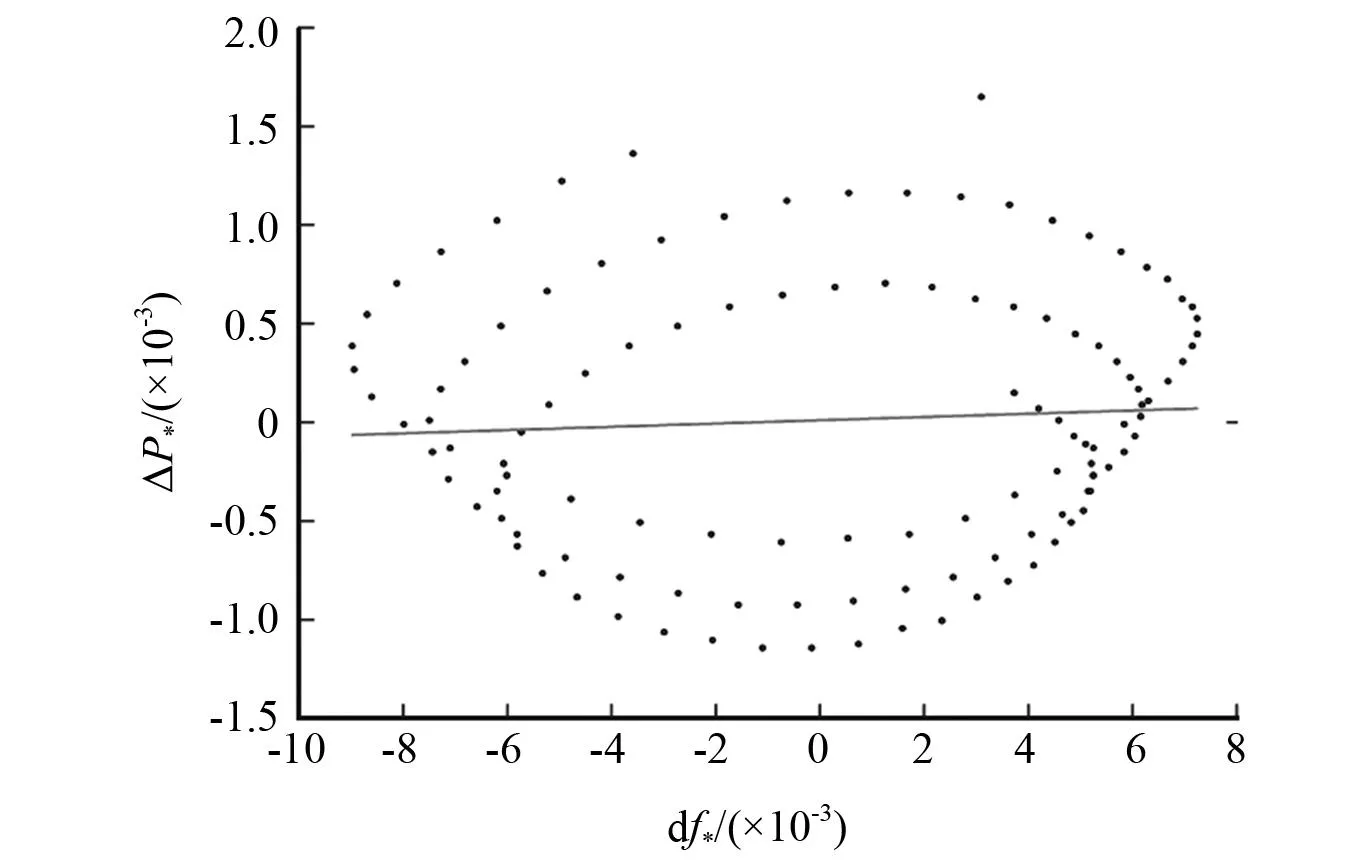
图8 负荷C惯性时间常数辨识
根据式(13),区域负荷总惯性时间常数为TJ_Load_total=0.212 s。
3.2 含新能源的华东电网模型
考虑 0.1 s 华东电网直流发生双极闭锁事故(多直流馈入电网在小负荷方式下开机规模较小,导致系统转动惯量和调节能力降低),频率调节措施参与前的4 s内,系统中节点的最低频率及部分特高压线路的频率跌落曲线如图9所示。
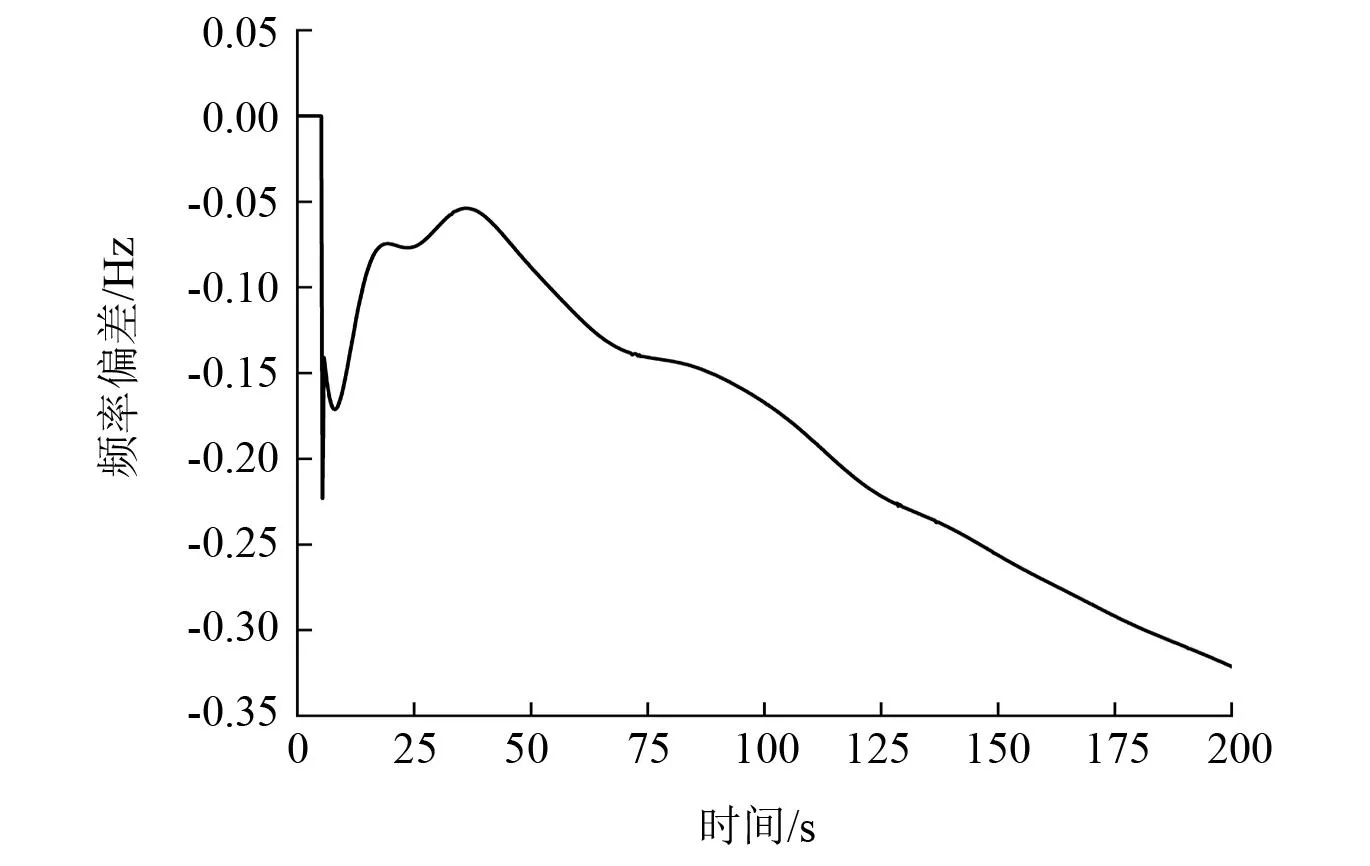
图9 华东电网(525 kV)母线频率偏差(最低频率)
由图9可知,特高压等级线路频率下降超过 0.3 Hz,系统频率稳定受到强烈冲击。事故发生后频率跌落初期阶段,计及传统机组与负荷等效惯量的调频能力,母线频率跌落有一定程度的缓解,而惯量支撑作用在0.7 s左右开始减弱,必须及时增加调频措施,防止失稳。
在含新能源的电力系统中,考虑负荷惯量的调频作用、对惯性时间常数准确辨识,有助于改善短期内频率跌落深度。
4 结束语
“双高”系统逐步发展,传统惯量恶化,影响系统频率稳定。频率跌落速度由发电机和负荷综合惯量决定,负荷惯量成为频率稳定的重要因素。基于广义惯量,构建负荷惯量定义式,并进一步给出单点负荷惯性时间常数计算方法。对于单点负荷,提出基于负荷受扰功率摇摆曲线和并网点母线频率曲线的参数辨识方法,并进行了算例验证其有效性;对于多点负荷,构建负荷综合惯性时间常数计算式,实现对不同区域负荷惯量的综合评价,为后续评价大电网负荷惯性时间常数奠定了基础。
目前研究主要基于自定义的负荷动态模型进行仿真[23],后续将通过系统中PMU量测数据进一步研究江苏电网乃至全国的负荷惯量效应,为准确的频率稳定提供详细的技术支撑。
