基于等效同步功率的孤岛并联构网变流器系统暂态稳定性分析

邹赵悦，吴 超，王 勇，田 杰，詹长江

（1.上海交通大学电子信息与电气工程学院，上海市 200240；2.南京南瑞继保电气有限公司，江苏省 南京市 211102）

0 引言

随着分布式风光新能源在微电网中的广泛应用，构网型（grid-forming，GFM）变流器在微电网中的重要性逐渐凸显［1-2］。相比于呈现电流源特性的跟网型（grid-following，GFL）变流器，GFM 变流器呈现电压源特性［3］，可以主动支撑电压和频率，也能实现离网运行，是构建以新能源为主体的新型电力系统的重要组成部分［4］。然而，GFM 变流器在运行中也存在暂态同步问题［1］，由于其功率特性类似同步发电机，在严重故障情况下可能出现功率振荡甚至失步现象［5-6］；除此之外，由于电力电子器件的过流能力不如同步机的绕组，电压骤降时产生的过流问题也威胁着GFM 变流器的稳定运行［7］。因此，对GFM 变流器系统进行暂态稳定性分析，寻找合适的参数设计方案或者控制改进策略，是使其能在新型电力系统中广泛应用的必经之路。

为了改善GFM 变流器在电力系统中的暂态功角稳定性，现有的提升策略主要包含3 个方面［8］：自适应参数调整［9-10］、控制结构改善［11-12］和控制指令的调整［13-14］。这些对GFM 变流器暂态稳定性的分析和优化控制大多基于单机无穷大系统，电网通常采用理想电压源串联阻抗表征，这与实际的电网有很大差异。实际情况中，电网并非理想电压源，而是由多种类型的机组构成的系统［15］，其控制和交互的情况多种多样［16-17］，不再只是单机与理想电压源之间的交互，更需要考虑机组间的交互。例如：文献［18］提到了当系统含有多个并联运行的GFM 变流器时，可能会由于GFM 变流器之间互阻尼的缺乏导致更容易出现功率振荡；文献［19］指出当GFM 变流器与同步机并联时，同步机调速器的时延可能会恶化并联GFM 变流器的暂态稳定性。

目前，对多机并联系统的稳定性研究仍有不足，一方面，高阶的建模大多是基于小信号模型的特征值分析，不适用于分析故障时的暂态响应；另一方面，聚焦于暂态稳定分析的建模研究，由于非线性方程分析的难度，通常采用简化假设等效成与单机无穷大系统形式相似的二阶方程，从而忽略了一些参数差异导致的动态。文献［17］借助特征值分析，详细揭示了三机并联系统参数对系统动态响应的影响，并提到特征值对与其他两机相邻、位于系统中间的GFM 变流器的参数尤为敏感。然而，由于是基于特征值分析的一种假设，具体机理和内在原因分析并未纳入讨论；文献［19］主要关注调速器参数差异的影响，但是由于假设功率环参数统一，得到的方程简化了一阶动态，从而未分析出力和功率环参数差异造成的暂态稳定性影响；文献［20］研究了两个GFM 变流器并联系统中功率控制环的差异对暂态稳定性的影响，由于双机系统中的其中一个被简化为下垂控制分析，得到的等效摆动方程也为二阶。

综上所述，在多GFM 变流器并联组成的微网系统中，各个控制参数对暂态稳定性的影响机理有所不同，基于单机无穷大系统获取的GFM 变流器暂态同步模型以及控制策略不再适用［21］。因此，本文拟研究由两台GFM 变流器并联组成的微电网系统中GFM 变流器的建模与暂态稳定性分析，探究影响并联GFM 变流器暂态同步稳定的关键因素，主要贡献如下：

1）建立了并联GFM 变流器系统考虑双机频率和功角耦合的三阶暂态稳定性模型，不仅考虑双机频率差和功角差的同步关系，还需要考虑双机频率和功角差的耦合关系，并利用相轨迹在两个平面上的投影，反映三阶动态模型的稳定性。

2）构建双机系统的等效同步功率分析模型，并揭示了机组出力和下垂系数差异会降低等效同步功率，进而恶化双机系统的暂态同步稳定性。

3）提出基于自适应下垂系数的暂态稳定性提升策略，根据出力差异自适应调整双GFM 变流器的下垂系数，提升暂态同步稳定性。

本文首先给出双机系统的暂态数学模型，并分析了系统的暂态稳定性及其影响因素；然后，对系统进行等效同步功率分析，并提出基于自适应下垂系数的双机系统暂态稳定性提升策略；最后，进行了实时仿真验证。

1 双机系统的暂态同步模型

1.1 GFM 变流器的暂态模型

GFM 变流器的典型控制框图如图1 所示，图中显示了并网GFM 变流器的硬件电路拓扑部分和软件控制部分。硬件电路部分为简化的两电平逆变器电路，直流侧电压为Vdc，输出侧通过滤波阻抗Zf后接入公共耦合点（point of common coupling，PCC），在该点的电压和电流分别为Vabc和Iabc，转换到dq坐标系下的电流为Idq，网侧电压和线路阻抗分别为Vg和Zg。软件控制部分又可以分为内环控制和外环控制部分。内环包含电流-电压控制和虚拟阻抗控制，用于调节逆变器的输出电压和电流，其中，内环输出电压参考为Vdq。由于响应速度较快，内环对暂态稳定性的影响在本文中暂时忽略；外环是功率控制回路，根据有功功率和无功功率的参考值P0和Q0输出电压参考值和控制角度的参考值θ。

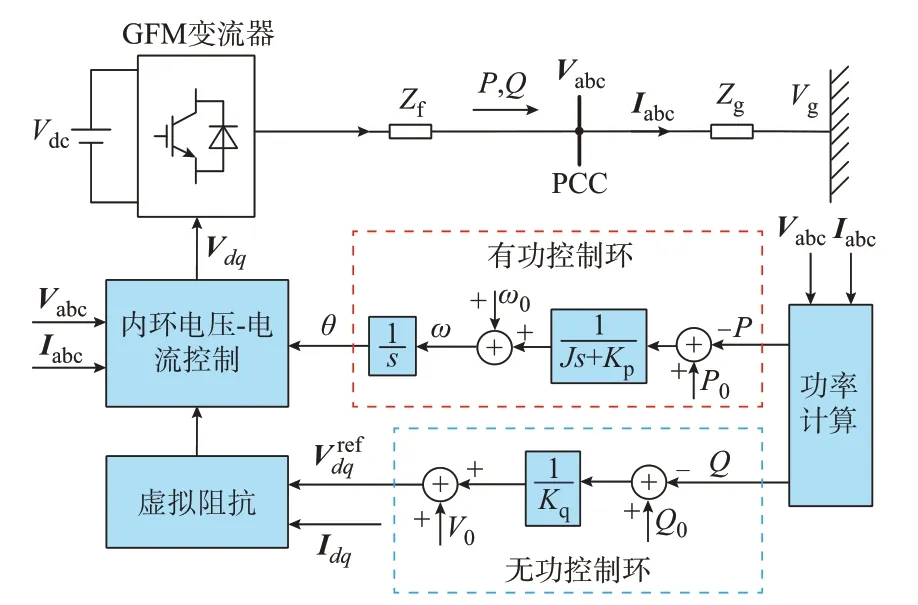
图1 GFM 变流器电路拓扑与控制结构Fig.1 Circuit topology and control structure of GFM converter

与GFL 变流器不同，GFM 变流器通过功率环与电网同步。根据控制框图，有功环和无功环的下垂控制表达式为：

式中：P和Q分别为GFM 变流器输出的有功和无功功率；V为GFM 变流器外环输出参考电压；J为惯量系数；s为微分算子；Kp和Kq分别为有功和无功功率下垂系数；V0为输出电压参考值；ω和ω0分别为GFM 变流器的输出频率和参考频率。

考虑到本文主要分析暂态稳定性，GFM 变流器的控制环节主要考虑有功功率环的动态式（1），而忽略了对暂态稳定性影响较小的无功环动态以及速度较快的电压-电流控制内环，可以得到描述GFM 变流器暂态同步特征的二阶动态方程为：

式中：δ为定义的GFM 变流器功角；ωg为电网频率。

在单机无穷大系统中，可以不用考虑网侧的频率和电压波动，GFM 变流器输出功率的表达式与输出功角和线路阻抗有关。利用式（3）的摆动方程和功角曲线即可分析系统的暂态过程，与同步发电机的暂态过程类似，不再赘述，下面着重分析孤岛微网中双机系统的暂态同步模型。

1.2 并联等效系统暂态模型

本文所研究的双机并联系统的结构如图2 所示。类似电力系统中多同步发电机的并联简化系统，多台GFM 变流器的并联系统也可以等效为双机并联系统［22］，且双机并联系统的稳定性研究是多台并联系统的基础，故本文以双GFM 变流器系统为例研究并联系统的暂态特性。

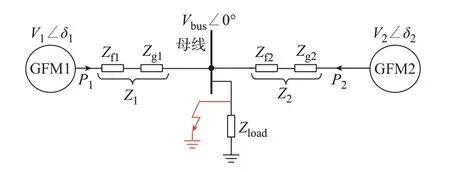
图2 双机并联系统的结构Fig.2 Structure of system with two parallel GFM converters

两台GFM 变流器通过PCC 并联，经过线路总阻抗Z1和Z2接到交流母线上，其中，Zf1、Zg1和Zf2、Zg2分别为变流器GFM1 和GFM2 输出滤波器和线路阻抗；两台GFM 变流器输出的功率为P1和P2，电压为V1和V2，功角为δ1和δ2，并联母线的电压幅值为Vbus，负载用阻抗Zload表示，当系统发生线路故障或者负载波动时，等效对地阻抗相应发生改变。

从并联GFM 变流器系统的等效电路中可以看出，GFM 变流器可以看作是与阻抗串联的电压源。当线路发生故障时，等效负载阻抗大小改变，并联系统输出的功率将随之改变。因此，线路故障时，如果控制调节不当，系统可能会出现功率振荡的现象。孤岛双机系统中GFM 变流器的动态方程分别为：

式中：i=1，2；P0i和Pi分别为第i台逆变器的额定功率和输出功率；Ji和Kpi分别为第i台逆变器的惯性系数和下垂系数；ωi为第i台逆变器的频率；ωbus为交流母线的频率。可以发现与单机无穷大系统不同，孤岛并联系统的ωbus不是理想的额定值，而是会随故障特征而改变，进而导致双机频率耦合，加剧暂态稳定分析的难度。除此之外，系统的同步情况不再由功角δ1和δ2分别表示，而是可以通过两机间的功角差δ12=δ1-δ2的稳定情况反映。

根据并联电路拓扑以及化简得到的节点电压、电流公式，可以计算两机间线路的自导纳Y11、Y22和互导纳Y12为：

式中：Y1=1/Z1；Y2=1/Z2；Y3=1/Zload。

根据线路参数，可以计算得到两机间功率传输的表达式为：

式中：G11和G22为两机处的自电导；G12和B12分别为两机之间线路的互电导和互电纳。φ12定义为两机间的线路阻抗角，即Y12=G12+jB12，φ12=arctan（B12/G12）。从式（6）可以看出，并联系统输出功率的变化与两机的功角差δ12的变化情况直接相关。

综合两台GFM 变流器的动态方程式（4）和线路的电压、功率表达式（6），可以发现双机系统的两个功角δ1和δ2的动态并不独立，这是由于功率输出是关于功角差变化的，可以利用系统的功率表达式（6）消去一阶动态。因此，双机并联系统可以用一个三阶的非线性微分方程来表征。由于系统的功率振荡与两机的功角差和频率差密切相关，在分析系统的稳定性时，可以定义该并联系统的状态变量为：

式中：x1为两机的功角之差，稳态时保持不变，x2为两机的频率之差，即ω12=ω1-ω2，稳态时由于两机以相同频率运行，故x2为0，这两个变量可以反映并联系统的同步情况；x3为GFM1 的角频率，稳态值为额定频率，该变量可以反映系统的频率稳定性。

由此，系统的三阶动态方程可以写为关于功角差和频率差的形式：

式中：Pm为等效机械功率；Pe，max为等效电磁功率的幅值。

可以发现，关于频率差ω12的微分方程也具有与二阶摆动方程类似的形式，可以由等效机械功率项、等效电磁功率项以及频率偏差项构成。各个参数分别计算为：

观察该三阶动态方程可以发现，与单机无穷大系统不同的是，双机系统中包含了两个摆动方程，一个是单个GFM 变流器自身的摇摆方程，还有一个是两个GFM 变流器保持同步的摇摆方程。要使双机系统在暂态下能保持稳定，需要保证两个摇摆方程的频率差ω12关于功角δ12的动态方程以及ω1关于δ12的动态方程均达到稳定。

2 双机系统的暂态稳定性分析

为了对双机系统进行暂态分析，本文采用非线性系统稳定性分析的典型三步法［11］：

1）求解三阶系统的平衡点；

2）根据雅可比矩阵判断平衡点的小信号稳定性，以确定系统在平衡点处能否稳定运行；

3）对于非线性的三阶微分方程，用相平面法分别作出相轨迹在两个相平面上的投影，求解暂态同步过程，判断是否可以达到稳定平衡点。

在上述稳定分析步骤中，小信号稳定是大信号稳定的前提，暂态稳定性首先要确保系统在新的稳态工作点是稳定的，然后是评估系统能否从原有工作点达到新的工作点。

2.1 稳态平衡点的求解

为了分析非线性系统的稳定性，需要分析该系统在暂态期间是否存在平衡点，令：

可以求得平衡点满足条件：

可以发现，双机并联系统的稳态平衡点与单机无穷大系统有一定的相似性，其双机间的功角差在稳态时能使得系统达到功率平衡。

根据式（8），假设两台GFM 变流器的控制参数（即下垂和惯量系数）相同，则KΔ为0，γ也为0，消除额外的频率差项，双机系统的输出功率动态特性也可以用一个摆动方程来衡量：

其中，等效机械功率Pm和等效电磁功率Pe分别为：

根据（13）和式（14），绘制双机系统的等效功角曲线如图3 所示。对于双机系统的摆动方程，系统达到平衡时有机械功率Pm等于电磁功率Pe，Pe是关于功角差的正弦函数。图3 中：蓝色直线代表等效机械功率Pm，当两机出力水平确定后，该项就是确定的常数，它们的交点即为系统的稳定平衡点。线路发生故障，导致系统负载变化，电压降低，并联系统的等效电磁功率曲线也降低。然而，与单机系统不同，根据表达式可知等效机械功率Pm与两机出力P0之差有关，即当P01＞P02时Pm为正，当P01＜P02时P'm为负。由此求得的平衡点也有两种可能，即当GFM1 出力大于GFM2 出力时，GFM1 功角总是超前于GFM2 功角，也就是δ12＞0，若是GFM1 的出力小于GFM2，则功角δ1滞后于GFM2 的功角δ2，也就是δ12＜0。图3 中蓝色实线即为GFM1 出力大于GFM2 时的等效机械功率，a1和a2即为求得的系统平衡点，蓝色虚线则为出力相反时系统的等效机械功率，此时平衡点b1和b2对应的功角差均为负值。

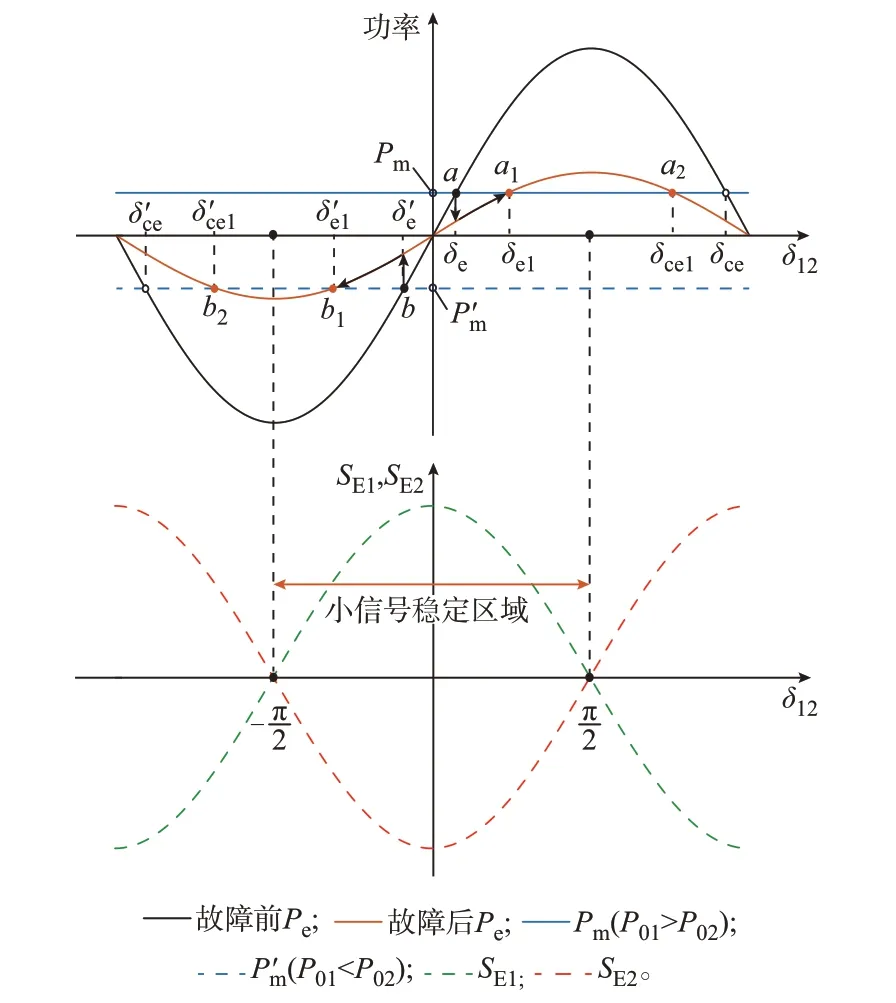
图3 双机并联系统等效功角曲线Fig.3 Equivalent power angle curve of system with two parallel GFM converters

2.2 线性化模型和平衡点的小信号稳定分析

为了对系统的平衡点进行小信号分析，以确定其稳定情况，可以将三阶系统在平衡点进行线性化，近似表示为ẋ=Ax的形式，其中，A为雅可比矩阵，A的各行元素为状态空间方程组中的每个函数fi对3 个状态变量xj分别在平衡点处求偏微分得到，即：

则平衡点xe=［δ12，0，ω0］处的雅可比矩阵为：

其中

为了得到该矩阵的特征值以确定线性化方程的稳定性，求解det（λΙ-A）=0，其中，I为单位矩阵，得到：

对于该三阶特征方程，由劳斯判据可以证明Kp1/J1+Kp2/J2＞0 且SE1Kp2-SE2Kp1＞0 是线性化系统能渐进稳定的充要条件。通常情况下控制参数均为正值，第1 个条件显然能满足；当两机的控制系数基本相等时，该稳定性条件简化为SE1＞SE2。在图3中作出SE1和SE2关于δ12的曲线，由于线路感性较大，φ12近似为π/2，可以发现，满足条件的稳定性区域为δ12∈（-π/2，π/2），即在图3 中，a1和b1为稳定平衡点，a2和b2为不稳定平衡点。

2.3 相平面分析非线性系统的暂态过程

在获得了系统的初始稳定点和暂态特性方程后，可以通过相平面展示系统的暂态过程，根据相轨迹最终是否收敛于稳定平衡点判断系统的稳定性。根据双机系统的三阶动态方程式（8）获取不同故障程度的影响，如图4 所示。图中：Zloadf表示暂态故障时的线路负载，Zloadf越小表示故障程度越深。当GFM1 出力大于GFM2 出力时，在暂态过程中，系统的功角差从初始平衡点a向新的平衡点移动，当系统的暂态故障较轻时（如图4（a）中蓝线所示），由于系统具有稳定平衡点，在经历频率波动后系统可以稳定在新的平衡点处；然而，当暂态故障较大时（如图4（a）中红线所示），由于暂态功角曲线不存在稳定平衡点或者暂态过程中系统的功角超调量超出了边界导致相轨迹发散，系统失去稳定。当GFM1出力小于GFM2 出力时，双机功角差的稳态值为负值，暂态故障时功角差也有相似的过程，但是功角差的移动方向为负向，如图4（b）所示，稳定性也是随着故障程度的加深而变差。

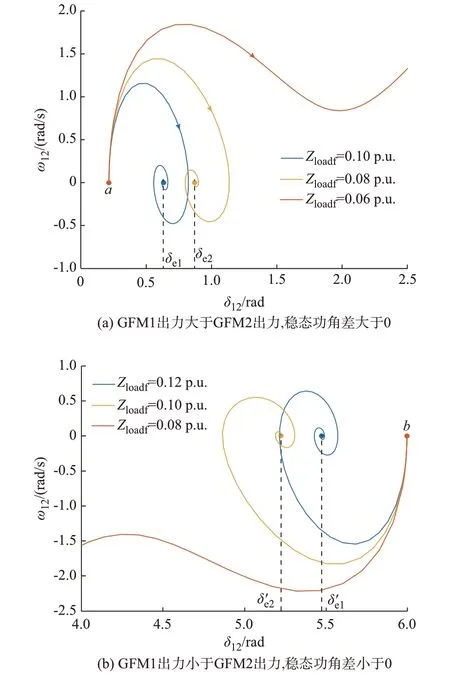
图4 不同程度故障对于双机并联系统暂态过程的影响Fig.4 Influence of different degrees of fault on transient process of system with two parallel GFM converters

综上，保证双机系统暂态同步稳定性的充要条件如下：

1）双机系统存在平衡点；

2）平衡点是小信号稳定的；

3）暂态过程中，双机系统的工作点可以从初始状态回到新的稳定平衡点。

第1 个条件表示在本文提到的等效功角曲线中，等效电磁功率的曲线与等效机械功率有交点；第2 个条件表示系统在平衡点的线性化雅可比矩阵无右半平面极点；第3 个条件需要系统的三阶非线性暂态同步模型能收敛到稳定平衡点。可以发现，这3 个稳定性条件与单机无穷大系统中功角暂态同步稳定条件类似，但由于双机系统为三阶非线性系统，其稳定性条件与单机系统不完全相同：重回平衡点的条件需要考虑从二阶方程扩展到三阶方程。在第3 个条件中，对双机系统的等效阻尼效果有两方面的要求：一方面，要使并联系统基础频率水平不会波动较大，偏离额定频率；另一方面，使得暂态过程中并联系统不会失去同步，即功角差不会超过稳定边界导致振荡失稳。这两方面即对应三阶方程式（8）中的两个摆动方程的稳定性，然而在双机系统暂态稳定性分析时，往往容易只关注功角差摆动方程的同步稳定性，而忽略另一个摆动方程揭示的基础功角和频率稳定。

注意到三阶系统与单机系统的不同之处在于还需要考虑式（8）中另一个摆动方程，即ω1的动态方程。由于只用一个相平面难以展现三阶的动态，为判断是否可以达到稳定平衡点，选取两种定制相平面（ω12-δ12和ω1-δ12平面）展示频率差和频率动态，只有保证两个相平面上的轨迹均收敛才能确保系统的稳定性。即在保证双机间有足够的互阻尼，从而不会失去同步的同时，还要保证单机的频率动态满足要求，否则可能会出现即使并联双机系统仍能保持同步，但是频率并不稳定的情况。如图5 中的相轨迹所示，两者出现了分歧，若只观察左图必然认为系统达到了稳定，然而右图的相轨迹发散反映了系统仍需注意频率的稳定性。

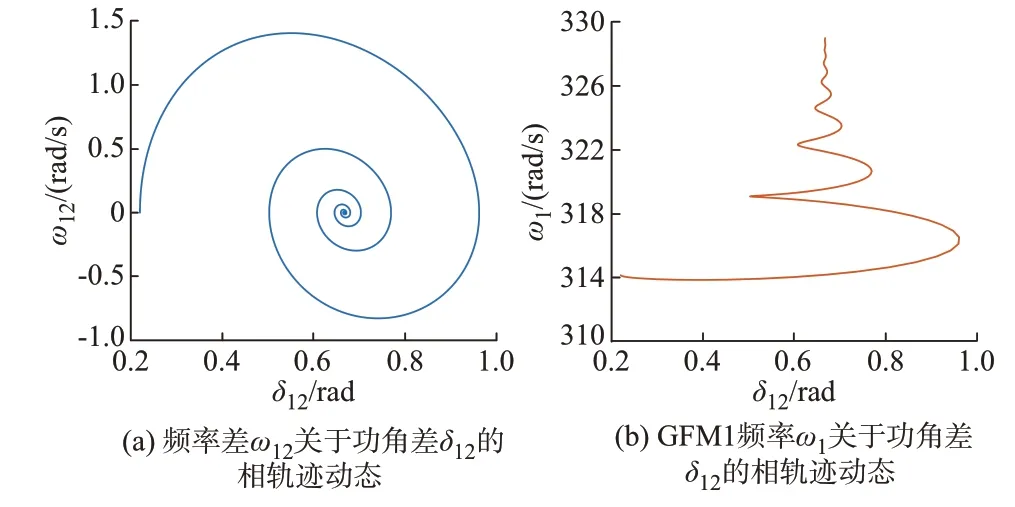
图5 双机并联系统功角差稳定但频率不稳定的暂态过程Fig.5 Transient process with stable power angle difference but unstable frequency in system with two parallel GFM converters

3 双机系统的等效同步功率分析

第2 章分析了三阶系统的暂态过程，并总结了稳定性条件，为了使并联系统保持暂态同步，首要就是系统具有足够的同步功率，即暂态时需要增加双机的等效电磁功率进而与等效机械功率有交点。因此，为研究双机系统的暂态同步稳定性，首先对双机系统的等效同步功率进行分析。对于式（8）所表示的三阶非线性系统，通过推导其解析解来评估暂态稳定性是非常困难的。但将其与同步机转子的摇摆方程进行比较，发现两者之间存在结构相似性，可以类比单机的二阶系统，将双机系统的动态方程分为等效机械功率、等效同步功率、等效阻尼功率几个部分进行分析，可以画出双机系统的暂态同步过程框图，如图6 所示。

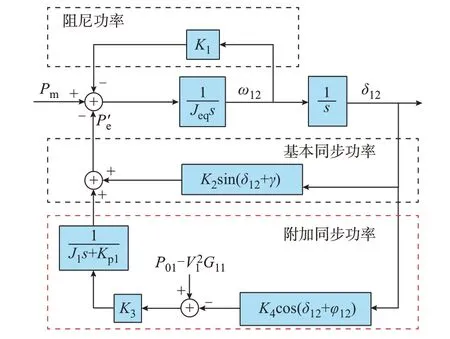
图6 双机并联系统有功功率控制框图Fig.6 Block diagram of active power control for system with two parallel GFM converters

根据系统的三阶动态方程，系统的数学表达式可以写为：

式中：K1为等效阻尼系数；Jeq为等效惯量系数；P'e为等效同步功率。

可以注意到，与同步机摇摆方程不同的是，在双机系统等效同步功率表达式中，第1 项为基本同步功率项，为功角差δ12的正弦函数，与单机无穷大系统一致，第2 项只在两机控制参数不完全相等，即K3不为0 时出现，为附加的同步功率项。根据传递框图可知，等效同步功率的表达式为：

其中，各个参数计算方法为：

3.1 下垂系数对附加同步功率的影响

通常情况下，可以假设惯量系数设计统一并且不随意调节，则对于双机系统，该附加同步转矩的大小主要受功率控制环下垂系数Kp1、Kp2的影响。以GFM1 出力大于GFM2 出力、功角差δ12＞0 的并联系统的分析为例进行分析，作出基本同步功率和附加同步功率关于功角差δ12变化的曲线如图7 所示。

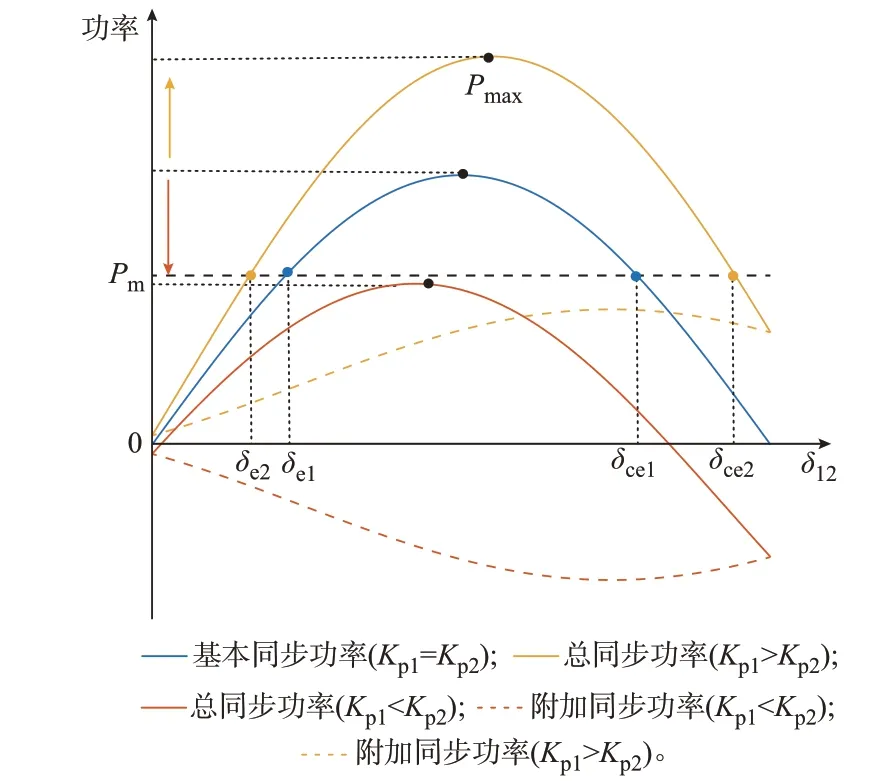
图7 不同下垂系数对等效同步功率的影响Fig.7 Influence of different droop coefficients on equivalent synchronous power

可以发现，在δ12＞0 时，附加同步功率的方向主要取决于K3，即Kp1＞Kp2时，双机系统具有正的附加同步功率，而Kp1＜Kp2时，系统具有负的附加同步功率。根据2.3 节中的分析可知，当线路故障较为严重时，导致系统暂态失稳的主要原因就是等效同步功率和机械功率不平衡。因此，正的附加同步功率使得系统更容易存在稳定平衡点，也意味着系统能更快地恢复稳定，有利于系统的暂态稳定性。除此之外，附加同步功率的值也与两下垂系数的差值有关，当GFM1 出力大于GFM2 出力时，增大Kp1或者减小Kp2可以使得附加同步功率曲线幅值更大，从而进一步提升系统的暂态稳定性。这说明了出力不同的机组的下垂系数，对暂态同步稳定性的影响不相同，增加大出力机组的下垂系数有利于暂态稳定，但是增加小出力机组的下垂系数反而会恶化暂态稳定。这是与单机无穷大系统不一样的特征，单机无穷大系统中增大下垂系数就是增大等效的阻尼，进而提升暂态稳定性，但是对于孤岛双机系统，盲目增大下垂系数可能恶化暂态稳定性。

为了揭示不同出力机组下垂系数对于暂态稳定性的影响，图8 给出了双机系统在同样故障下不同下垂系数组合的功角差和频率差关系图。通过相轨迹也可以观察到两机下垂系数的不同影响。首先，当两机下垂系数相等时绘制的两条相轨迹（红色和蓝色实线），由于没有额外的同步功率项，系统新的稳定平衡点不会发生改变，但红色实线相对于蓝色实线相当于增大了系统的等效阻尼系数，系统的功角差和频率差的超调量减小；其次，对于GFM1 出力较大、GFM2 出力较小的系统，可以观察当增大Kp1时，黄色虚线所示的相轨迹功角差超调量减小，稳定平衡点左移，系统暂态稳定性增强，而当增大Kp2时，绿色虚线所示的相轨迹发散，系统反而失去稳定。这与借助等效功角曲线分析的结果相同，都说明了机组的下垂系数设计应与有功出力水平进行匹配：出力较大机组的下垂系数Kp1越大，出力较小机组的下垂系数Kp2越小，越有利于系统的暂态稳定性。

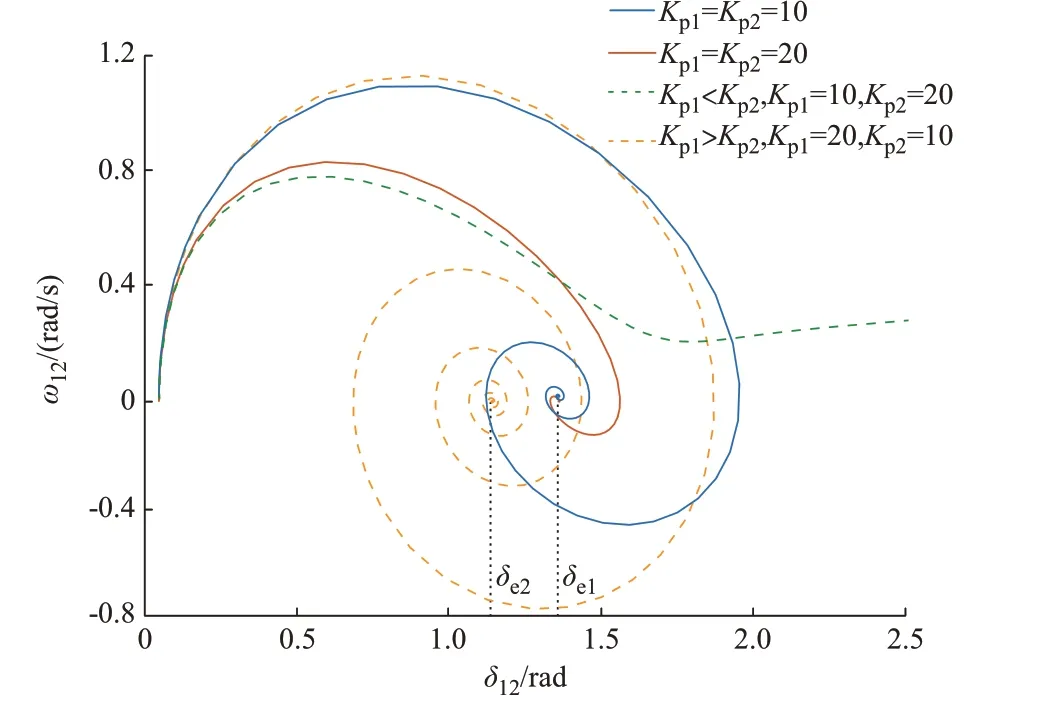
图8 不同下垂系数组合的暂态频率差和功角响应图Fig.8 Transient frequency difference and power angle response of different combinations of droop coefficients

3.2 基于自适应下垂系数的暂态稳定提升策略

基于3.1 节分析可知，双机系统中下垂系数的不同会影响暂态稳定性，而且对比单机无穷大系统，双机系统额外的同步功率项构成更为复杂，且会随着出力的调整而发生大小甚至方向的变化。因此，为了提升并联系统暂态稳定性，可以对GFM 变流器的下垂系数进行自适应调整，以匹配双机系统运行时的出力水平。

如图9 所示，红框中即为自适应下垂系数的控制原理。图中：Δω1和Δω2分别为GFM1 和GFM2频率与额定频率的差值。首先，利用机组间的通信获得本机相对于另一机组的功角差信息；然后，反馈此功角差信息用来对下垂系数进行调整，新的下垂系数计算原则由式（23）决定。

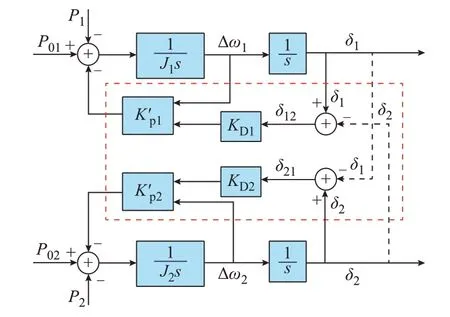
图9 双机并联系统自适应下垂系数控制原理Fig.9 Control principle of adaptive droop coefficient of system with two parallel GFM converters

式中：Kp10和Kp20分别为变流器GFM1 和GFM2 预先设定的基本下垂系数；δ12=δ1-δ2，δ21=δ2-δ1；KD1和KD2分别为变流器GFM1 和GFM2 的反馈调节系数，需要满足式（24）。

式中：Kp1，max、Kp1，min和Kp2，max、Kp2，min分别为变流器GFM1 和GFM2 基于自身单机频率稳定要求设置的下垂系数上、下限，可参考国家标准［23］中关于构网型变流器下垂系数上下限的设计；Δδ12，max、Δδ21，max为暂态时两机功角差的最大允许波动范围。这样的KD1和KD2设计在满足提升双机系统同步功率、快速阻尼暂态功角差发散要求的同时，也能保证两机自身的频率稳定性在合理的范围内。

根据第2 章分析可知，系统的出力水平大小可以通过功角差反映，出力较大的机组功角会超前于另一机组。式（23）保证了并联系统两机的下垂系数与出力相关，暂态时，对于出力较大的机组，由于反馈的功角差为正值，下垂系数将自适应增大，反之，出力较小的机组。由于反馈的功角差为负值，在暂态时下垂系数的值将自适应减小，这样可以保证较大的等效同步功率，进而提升并联GFM 变流器系统的暂态稳定性。

4 实时仿真验证

为了验证双GFM 变流器系统暂态模型的准确性和提升等效同步功率策略的有效性，本文基于NI-PXI 系统的CPU-FPGA 实时仿真平台开展实验验证。其中，控制部分在CPU （Intel i7-3610QE 处理器）模块进行仿真，采用100 μs 的仿真步长，拓扑部分仿真在FPGA（Xilinx XC7K410T）模块进行，其模型参数如表1 所示。表中：Zline、Zload和Zv分别为并联系统中的线路阻抗、负载阻抗和控制部分的虚拟阻抗；Vpcc为并联点母线的电压。

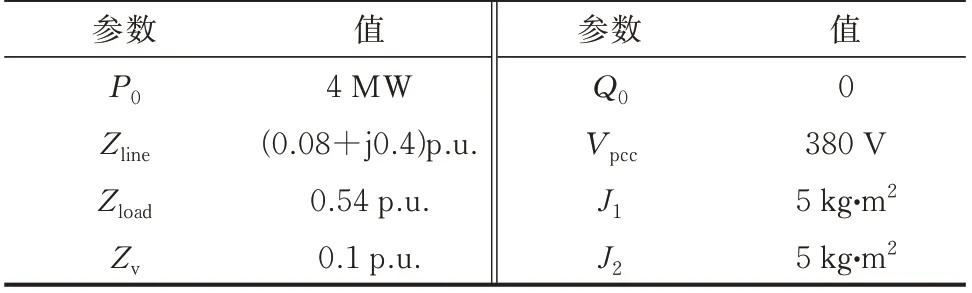
表1 模型参数Table 1 Model parameters

4.1 下垂系数对系统暂态稳定性的影响

为了验证双机下垂系数对系统暂态稳定性的影响，在不同控制环参数的条件下观察系统的暂态稳定性情况。图10 为并联GFM 变流器系统中GFM1和GFM2 的频率和有功功率，以及并联系统功角差的时域响应。在图10 中，两GFM 变流器的有功功率参考值分别为0.5 p.u.和0.25 p.u.，用来模拟并联的两个机组的出力情况。模拟系统发生三相接地故障，持续时间为0.8 s。与第3 章分析所得的暂态过程类似，故障发生后，由于系统的电压下降，GFM1和GFM2 的功率输出都发生了骤降，输出频率发生改变，功角差逐渐增加。若并联系统同步功率不够或者故障切除不及时，则会出现如图10（a）所示的情况，两机功角差持续增大，即使故障切除后，系统的功率和频率都有着持续振荡，属于暂态失稳。

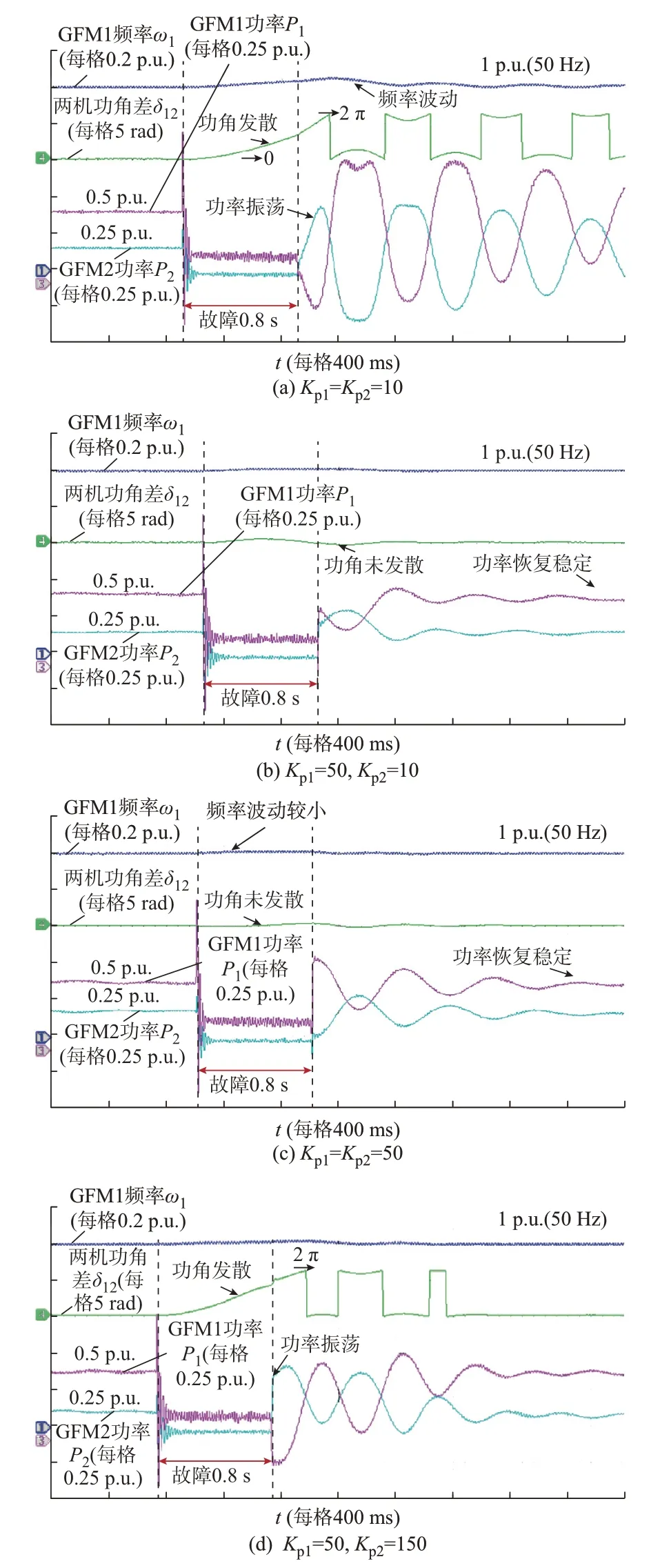
图10 不同下垂系数组合的系统暂态响应波形Fig.10 Transient response waveforms of system with different combinations of droop coefficients

在同样的暂态条件下，如果增大出力较大的GFM1 的下垂系数Kp1，在图10（b）中可以观察到功角差上升的速度减缓，系统的功率和频率在故障切除后都可以重新恢复稳定，证明较大的Kp1有利于系统的暂态稳定。图10（c）与（a）对比可以发现，针对双机下垂系数相等的情况，两机的下垂系数同时增大，系统从不稳定变为稳定，这是因为虽然下垂系数相等时没有附加的同步功率，但是增大下垂系数后增大了阻尼，也能提升暂态稳定性。然而，对比图10（c）和（d），在图10（c）稳定的基础上，增大出力较小的GFM2 的下垂系数Kp2，可以发现又出现功角发散和功率振荡的不稳定现象。这表明和单机无穷大系统不一样，更大的Kp2反而会使系统从稳定变得不稳定，说明双机系统中增大下垂系数并不是直接增大了阻尼，也可能是降低了系统的等效同步功率进而导致暂态稳定性恶化，故需要根据出力来调节下垂系数。

另外，为了验证不同下垂系数的不同稳定性影响是否与出力相关，不改变负载水平和控制参数值，修改并联系统中GFM1 和GFM2 的功率参考值分别为0.25 p.u.和0.5 p.u.，其暂态响应如附录A 图A1 所示。可以发现，如第3 章的分析，交换出力后，由于GFM1 的出力较小，GFM2 的功角超前于GFM1，稳态功角差δ12为负值。对比图A1（a）与（b），在相同的控制参数下，仅调整机组的出力，系统由暂态稳定变为暂态不稳定，证明出力的大小会影响下垂系数构成的附加同步功率的正负，将原本的正附加同步功率变为负值。

4.2 暂态稳定性提升策略的作用

为了验证自适应下垂系数调整策略对双机系统的暂态稳定性提升作用，在相同的线路和暂态条件下，观察采用了自适应下垂系数调整方法的效果。附录A 图A2 展示了对下垂系数进行自适应后的效果。图A2（b）与（a）相比，可以看出由于自适应的下垂系数保证了附加同步功率始终为正，双机系统的暂态频率差被缩小，从而减小了功角差的超调量，使系统更易恢复稳定。

值得注意的是，由于两机间功角差需要通信获取，通信造成的延时对本文所提自适应下垂系数调整策略的效果也具有一定的影响。在附录A 图A2（b）中，该策略的使用考虑了2 ms 的延时误差，提升效果明显，系统能迅速恢复稳定；考虑更高时间尺度如50 ms 的通信延时，系统的故障响应波形如图A2（c）所示，虽然对比图A2（a）仍能帮助系统较快地恢复稳定，但是延时带来的误差仍会出现两个周期的功角发散。因此，此方法对获取两机间功角差的通信时间具有一定的敏感性。

总体来看，实验的波形结果验证了自适应下垂系数能通过补偿系统的功率不平衡使系统重新恢复稳定，从而有利于暂态稳定性。

5 结语

为探究孤岛双GFM 变流器系统的暂态同步稳定性，本文考虑双机频率与功角耦合关系，建立完备表征双机系统的三阶暂态同步模型。基于该模型，采用等效功率法揭示双机出力和下垂系数对于暂态稳定性的影响，表明下垂系数的设计必须与机组出力进行匹配，即出力大的机组需要设计大的下垂系数，出力小的机组需要设计小的下垂系数，否则会导致双机系统暂态功率不平衡，进而恶化暂态稳定性。在此基础上，提出自适应下垂系数调整策略，提升孤岛并联GFM 变流器系统的暂态稳定性。

本文的建模与所得结论仍基于对并联系统的一些简化和假设，未来的研究将从以下几个方面进行：一是利用所提的稳定性分析方法探究不同机组并联的暂态稳定性，以及分析其他参数对双机系统暂态稳定性的影响；二是进一步研究并联GFM 变流器系统的稳定性提升策略，以减小对机组间通信时间的敏感性。

本文研究得到南京南瑞继保电气有限公司科技项目（CGSQ220300434)的资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。