考虑长距离输电缆特性的逆变器并网系统谐波不稳定分析及抑制
2024-02-20解润生张国荣
解润生,张国荣,解 宝
(1.合肥工业大学电气与自动化工程学院,安徽省 合肥市 230009;2.光伏系统教育部工程研究中心(合肥工业大学),安徽省 合肥市 230009)
0 引言
风能和太阳能等可再生能源广泛分布于海岛、戈壁和山区等偏远地区[1-2],以新能源并网逆变器为代表的接口装置通常需采用长距离输电缆(long transmission cable,LTC)并入交流电网,而沿LTC的分布寄生电容使得并网系统中发生谐波不稳定性现象[3-4],其振荡频率从数百到数千赫兹不等,这种谐波振荡可能会传播到大电网中,进一步恶化系统的电能质量。因此,有必要对考虑LTC 特性的逆变器并网系统谐波振荡特性及其抑制方法展开研究。
目前,关于谐波不稳定的研究方法主要有2 种:阻抗分析法[5-9]和状态空间法[10-14]。文献[6]建立了静止坐标系下变流器端口和电网端口的序阻抗模型,分析了控制器带宽和电网强度对系统谐波不稳定的影响,文献[7-8]考虑了电缆线路分布参数特性,基于欧拉公式和奈奎斯特判据判定系统谐波稳定性,但其忽略了dq轴耦合影响。文献[9]建立了计及dq轴耦合的并网系统阻抗模型,提出基于广义奈奎斯特判据的系统极点分布间接判定方法,但该判据计算繁杂,且较难定位引起系统失稳的相关因素。与阻抗法相比,基于状态空间模型的特征根、参与因子等可以确定谐波稳定性的主导模态及关键参与变量[10-13]。文献[14-15]建立逆变器并网系统的状态空间模型,分析时延、控制系统和电网强度等参数对谐波不稳定的影响,并通过参与因子分析评估了不同状态变量对振荡模式的贡献。目前,状态空间法在并网逆变器与电网间交互作用研究中仅将电缆线路表示为集总参数模型,缺乏考虑电缆线路分布参数特性的并网系统状态空间模型及相关特征值分析的研究工作。
电力电缆不仅具有分布参数特性,同时其在不同频率下呈现出不同的阻抗特性,然而目前计及线路参数频变特性的并网系统稳定性研究较少。文献[16-17]利用改进贝杰龙模型模拟线路高频段衰减特性,但仅利用时域仿真分析法来复现高频段不稳定现象,无法给出系统稳定性的判定方法及影响规律。文献[18]建立考虑电缆线路参数频率特性的并网系统开环传递函数,但其重点是分析电力电缆对谐波放大的影响,未判断系统的稳定性。
电缆分布参数模型中未计及线路参数频变特性时,会影响系统谐波稳定性评估的准确性[16,19]。然而在谐波稳定性评估中,电缆分布参数模型引入了复数双曲线函数使得阻抗分析法存在极点分布难以确定的问题[7-9,20]。此外,当计及线路参数频变特性时,基于广义奈奎斯特判据判定系统稳定性具有一定局限性。因此,需要对计及线路参数频变特性的电力电缆状态空间模型进行深入研究。
与频域阻抗模型相比,基于时域状态空间模型的参与因子、灵敏度等量化评价指标可以为振荡抑制措施提供指导,但现有文献中基于时域状态空间模型提出谐波不稳定抑制策略的研究较少。基于此,本文通过状态空间法研究了考虑LTC 特性的逆变器并网系统谐波振荡特性,计及电缆线路分布参数特性和频变特性,提出了基于矢量匹配法对含LTC 的交流系统进行等值,并考虑内外环控制、锁相环、控制延时等环节,建立dq坐标系下表征并网系统全部动态特征的高频状态空间模型,通过参与因子分析辨识引起谐波振荡的关键影响因素,采用根轨迹法分析线路参数频变特性及关键因素对谐波稳定性的影响。进一步,基于系统状态空间模型,提出一种结合灵敏度分析和矩阵相似变换的系统稳定性改善方法,并利用根轨迹对改进控制策略后系统进行了稳定性分析。最后,基于RT-LAB 构建硬件在环实验平台,验证了本文理论分析的正确性。
1 逆变器并网系统及其状态空间模型
图1 为典型的三相LCL 逆变器并网系统的接线图。图中:可再生发电单元经过电能变换后汇入直流母线,再经过并网逆变器、LCL 滤波器、变压器以及LTC 等结构并入交流电网。为简化分析,将系统各参数统一折算到变压器低压侧,图2 给出了逆变器并网系统的等效拓扑及控制框图。图中:逆变侧滤波电感L1、滤波电容Cf和网侧滤波电感L2构成LCL 滤波器;R1和R2分别为L1和L2的等效电阻;ic为桥臂侧电感电流;if为LCL 滤波电容电流;ig为并网电流;uc为滤波器电容支路电压;Cdc为直流母线电容;Id为理想电流源;udc为直流母线电压;Pin为直流侧输入有功功率;uinv为逆变侧输出电压;up为公共连接点(point of common coupling,PCC)电压;变压器漏感计入电网阻抗Lg;ug为电网三相电压;ω1为电网基波角频率;θ为锁相环输出相角;并网逆变器采用定直流电压和定无功功率的双闭环矢量控制策略;和Q*分别为直流母线电压和无功功率的参考值;Hdc为直流母线电压控制器;Idref、Iqref分别为并网电流d轴和q轴分量的参考值;Hc为电流内环控制器,考虑了有源阻尼系数kc及数字控制引入的延时环节Hd;md、mq分别为d轴和q轴上的调制信号;PWM 表示脉宽调制;PI 表示比例-积分控制器。
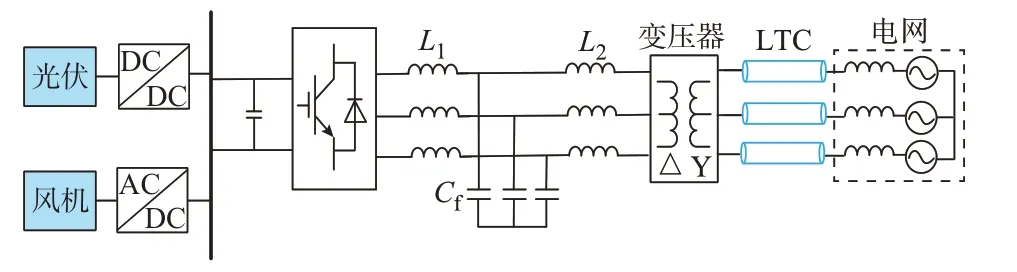
图1 三相LCL 型逆变器并网系统接线图Fig.1 Wiring diagram of three-phase LCL-type gridconnected inverter system
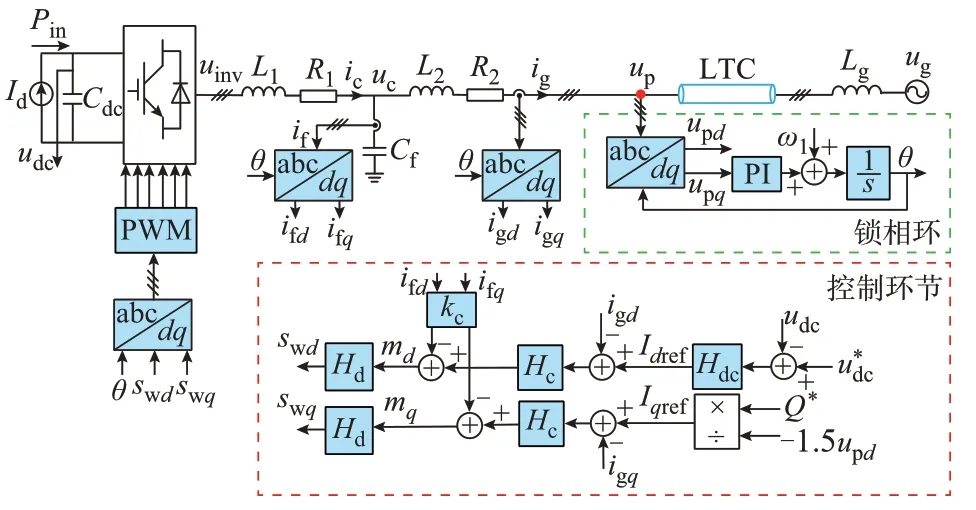
图2 逆变器并网系统等效拓扑及控制框图Fig.2 Equivalent topology and control block diagram of grid-connected inverter system
1.1 并网逆变器模型
本文基于dq坐标系对逆变器并网系统进行建模,由主电路、控制内外环、锁相环、控制延时等环节构成,本节将对各部分进行建模。
1.1.1 主电路模型
LCL 滤波器的动态方程为:
式中:下标d、q分别表示相应物理量在其各自坐标系下的d轴和q轴分量,下同;uinvd=swdudc/2,uinvq=swqudc/2,其中,sw表示控制系统输出的调制信号。
将式(1)线性化,选取状态变量为xe=[icdq,igdq,ucdq]T,其中,icdq=[icd,icq]T,igdq=[igd,igq]T,ucdq=[ugd,ugq]T,控制变量为updq=[upd,upq]T、swdq=[swd,swq]T和udc,忽略系统频率的变化,主电路LCL 滤波器的线性化状态空间模型为:
式中:Δ 表示小信号量,下同;Ae、Be1、Be2和Be3具体如式(3)所示。
式中:A11、A13、A22、A23、A31、A33、G11、G22和G33可通过式(1)线性化得到。
根据功率平衡原理[21],忽略Id扰动的影响,则逆变器直流侧的线性化状态空间模型如式(4)所示。
式中:UdcN为逆变器额定直流电压;Icd0、Icq0、Swd0、Swq0、Udc0分别为icd、icq、swd、swq、udc的稳态量。
1.1.2 锁相环模型
锁相环结构如图2 所示。当端口电压发生扰动时,控制系统中将出现两个旋转坐标系,一个为电气系统dq坐标系,相关物理量不进行标识;另一个为控制器dq坐标系,用上标c 表示。本文以电网电压ug电气系统dq坐标系为参考基准,控制系统坐标系定向于电压up方向,则锁相环的s域线性化模型为:
式中:θ0为PCC 电压相对电网电压的相位差;Hpll为前向通路增益;kppll、kipll分别为控制器的比例和积分系数;Up0为PCC 处相电压幅值。
由式(6)可得锁相环线性化状态空间模型,选取状态变量Δxpll=[Δxb,Δθ]T,其中,xb为PLL 控制器积分状态变量,θ为输出变量,则有
式中:Cpll=[0,1];Apll=[0,-kipllUp0;1,-kppllUp0];Bpll=[-kipllsinθ0,kipllcosθ0;-kppllsinθ0,kppllcosθ0]。
进一步,可以得到电气dq坐标系中电压和电流在控制系统中的表达式为:
式中:Tp1=[cosθ0,sinθ0;-sinθ0,cosθ0];Tp2=[Igq0,-Igd0]T,其中,Igq0和Igd0分别为igq和igd的稳态量;Tp3=[Icq0,-Icd0]T;Tp4=[Upq0,-Upd0]T,其中,Upq0和Upd0分别为upq和upd的稳态量。
1.1.3 控制内外环模型
外环采用定直流电压和定无功功率的控制策略,其中,定无功功率模式采用直接功率控制方式。假定=0 和ΔQ*=0,外环控制器输出的线性化状态空间模型为:
内环采用基于输出电流ig和LCL 滤波电容电流if的双反馈闭环控制,忽略交叉耦合项的电流内环可表示为:
式中:电流内环控制器Hc=kp+ki/s,其中,kp和ki分别为比例和积分系数,则线性化状态空间模型如式(11)所示。
式中:xcdq=[xcd,xcq]T,其中,xcd、xcq分别为d轴和q轴电流内环积分环节状态变量;Ac=[ki,0;0,ki];Bc=[kc-kp,0;0,kc-kp];Bc1=[-kc,0;0,-kc];Bc2=[kp,0;0,kp]。
1.1.4 控制延时模型
图2 中数字控制延时环节可表示为:
式中:n为Pade 近似中分子和分母的阶数;i=0 ,1, …,n;di= [(2n-i)!n!]/[(n-i)!i!];ei=(-1)i[(2n-i)!n!]/[(n-i)!i!]。
文献[11]分析指出,为了准确地分析高频段稳定性问题,应至少选择3 阶以上的Pade 近似代替延时环节。因此,本文采用4 阶Pade 近似,则根据Pade 近似可得控制延时环节的线性化状态空间模型为:
式中:xdelay=[xd1,xd2,…,xd8]T,xd1至xd8为Pade 近似转换过程中引入的8 个状态变量;Ad=[Ade,0;0,Ade],Bd=[Bde,0;0,Bde],Cd=[Cde,0;0,Cde],Dd=[Dde,0;0,Dde],其中,元素Ade、Bde、Cde和Dde可通过式(13)得到。
式中:Tp5=[-Swq0,Swd0]T。
1.2 交流系统模型
建立含LTC 的交流系统高频状态空间模型的基本思路是:计及电缆线路参数的分布特性和频变特性,根据电缆首末端口电气参数频域关系式,可推导得并网点电压与其电流、电网电压的关系,在此基础上,基于矢量匹配法对表达式中等效阻抗和电压系数的频域响应进行有理函数拟合,进而得到状态空间模型。
1.2.1 矢量匹配法
矢量匹配法是一种快速有效的有理函数拟合方法,假设用矢量匹配法拟合函数f(s),则可得有理函数部分分式和的形式为:
式中:N为拟合阶数;Ti和Pi分别为第i个留数和极点,两者可以是实数或者共轭复数对;D、E为实数,视情况选用。
将函数式(16)中f(s)转换为状态空间形式,假设y=f(s)u,其中,u为输入量,y为输出量,则
式中:x为引入的状态变量,A=diag[P1,P2,…,PN],C=[T1,T2,…,TN],B为元素均为1 的列向量;D和E值同式(16)。
1.2.2 状态空间模型建立
附录A 图A1 给出了交流系统的等效模型,当输电缆过长时一般采用考虑分布参数特性的分布参数模型,其主要思路是假设传输线由无穷小的包含电阻、电抗、电导和电纳的微元组成,图A1 中虚线框内代表一个微元。
一般线路的绝缘良好,可忽略并联电导,由此可建立输电线路的传输方程,根据传输线模型中相应的边界条件可对传输方程进行求解,得到电缆首末两端电气参数在频域中的关系式为:
式中:u2、i2分别为电缆末端电压和电流;L为输电线的长度;γ=为传播系数;Zc=为特征阻抗,其中,单位长度的阻抗Z(ω)=r0+jωl0和单位长度的导纳Y(ω)=jωc0,r0、l0和c0分别为单位长度的电阻、电感和电容;ω为角频率。
式(18)考虑了线路参数分布特性,但没有计及线路参数频变特性。文献[17]表明单位长度的电阻和电感参数均与频率有关,其中,电阻随着频率的增加而增加,电感随着频率的增加略微减少。因此,输电线路在不同频率下将呈现出不同的传输特性,有必要对电缆线路的Z(ω)进行修正,得:
式中:Z0(ω)为导体内阻抗;r0(ω)为频率相关的单位长度电阻;li(ω)为磁通作用于导体内部产生的频率相关的单位长度内电感。r0(ω)、li(ω)都随频率变化而变化。
根据文献[22],Z0(ω)的表达式为:
式中:rdc为频率f0时电缆线路的单位长度电阻。
根据附录A 图A1,对电缆线路末端的交流侧串联阻抗支路列写方程,得:
式中:Zg=sLg。
结合式(18)和式(21),得PCC 电压up与电流ig和电网电压ug间的关系式为:
式中:ZL、HL分别为含频变LTC 的交流系统的等效阻抗和电压系数频域传递函数。
假设up1=ZLig,up2=HLug,利用矢量匹配法对频域传递函数ZL、HL进行拟合,得有理函数g1(s)和g2(s),则
式中:g1(s)和g2(s)的具体形式可参照式(16)。
根据式(17),可认为up1为输出量,ig为输入量,同理,up2为输出量,ug为输入量,则将式(24)转换为状态空间方程:
式中:xL1=[xL11,xL12,…,xL1i,…,xL1N]T,xL11至xL1N为ZL拟合过程中引入的N个状态变量;xL2=[xL21,xL22,…,xL2i,…,xL2N]T,xL21至xL2N为HL拟合过程中引入的N个状态变量;AL1、BL1、CL1、DL1和AL2、BL2、CL2、DL2的具体形式可参照式(17)中A、B、C和D。
在以电网电压ug为定向的电气系统dq坐标系下,Δugd=Δugq=0,结合式(22)和式(25),可选取状态变量xL1dq=[xL1d,xL1q]T和xL2dq=[xL2d,xL2q]T,控制变量igdq=[igd,igq]T,输出变量updq=[upd,upq]T,忽略系统频率的变化,则可得电气系统dq坐标系下含LTC 的交流系统线性化模型为:
式中:AL1dq=[AL1,ω1IN;-ω1IN,AL1],其中,IN为N阶 单 位 矩 阵 ;BL1dq=[BL1,0;0,BL1];AL2dq=[AL2,ω1IN;-ω1IN,AL2];CL1dq=[CL1,0;0,CL1];CL2dq=[CL2,0;0,CL2];DL1dq=[DL1,0;0,DL1]。
为了分析是否存在高频段的稳定性问题,并且能够模拟交流系统在3 kHz 范围内幅值和相位特性,当Lg为0.2 mH 且电缆参数如表1 所示,选取ZL、HL拟合的阶数分别为20 阶和16 阶,附录A 图A2 为ZL、HL拟合的幅值和相位曲线。由图可知,矢量匹配法可以很好地拟合ZL、HL的幅值和相位特性。

表1 电缆参数Table 1 Parameters of cable
1.3 考虑LTC 的并网系统状态空间模型
整合式(2)、式(4)、式(7)、式(9)、式(11)、式(14)和式(26),消去中间变量后可得电气系统dq坐标系下整个闭环系统的状态空间模型为:
式中:xs=[icdq,igdq,ucdq,udc,xu,xcdq,xdelay,xpll,xL1dq,xL2dq]T;AT表达式详见附录B 式(B1)。
1.4 考虑LTC 的并网系统线性化模型验证
为验证所建立的并网系统线性化模型的正确性,在MATLAB/Simulink 仿真系统中搭建电磁暂态仿真模型,电缆参数和并网逆变器参数如表1 和表2 所示,系统工频为50 Hz,直流电压参考值为750 V。
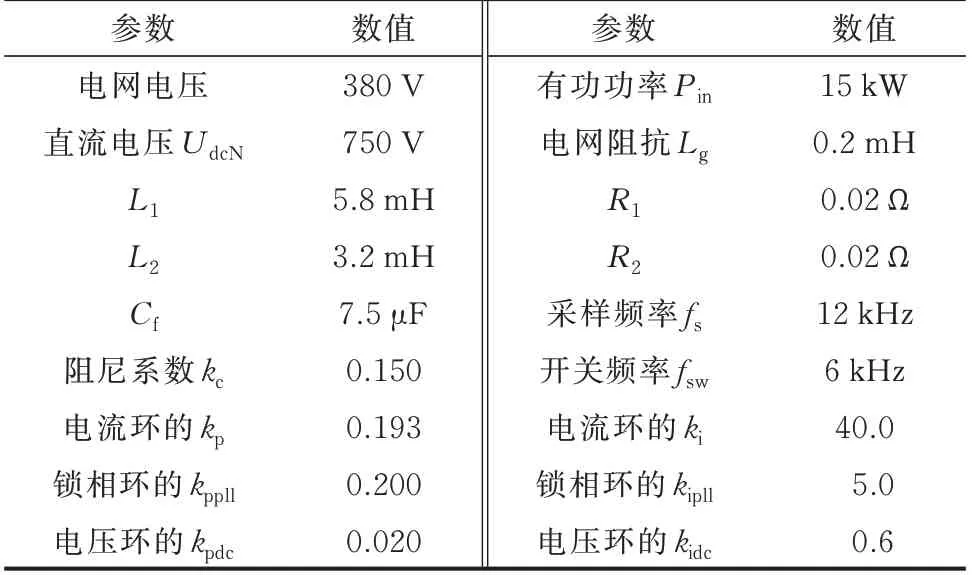
表2 并网逆变器参数Table 2 Parameters of grid-connected inverter
初始时系统运行在额定状态,有功功率为15 kW,无功功率为0 var,在0.3 s 时,有功功率参考值阶跃至18 kW,通过将线性化模型计算波形与电磁暂态模型仿真结果进行对比,系统的动态响应如附录A图A3 所示,从上至下分别为d轴电流、q轴电流和a相LCL 滤波电容电压。由图A3 可知,线性化模型计算曲线基本从中间穿过电磁暂态模型仿真曲线,由此验证了所建系统线性化模型的正确性。
2 逆变器并网系统的稳定性分析
并网逆变器和输电缆设计的参数往往能够保持自身稳定,即两者的参数对自身来说均设置合理,为分析影响稳定性的关键因素,需进行根轨迹和参与因子分析。考虑到外环带宽较低,外环控制对谐波不稳定的影响较小,本文将通过调整有功功率来定量识别各个影响环节对谐波不稳定的参与程度。
本文是基于正序dq坐标系建立的状态空间模型,如果建立的理论模型中存在虚部为fh1和fh2的不稳定特征根,且这2 对不稳定特征根的虚部相差在100 Hz 附近,则可认为abc 坐标系下的谐振频率为(fh1+fh2)/2。根据表1 和表2 所示参数,经计算,当系统的有功功率Pin为21.2 kW 时,出现2 对不稳定共轭复根λ27,28=70.6±j12 068.2 和λ31,32=36.3±j11 473.5,振荡频率约为1 873.5 Hz。
对上述的失稳模态进行参与因子分析(归一为最大值),可以得到如附录A 图A4 所示的状态变量的参与因子,所给数据均为参与因子的模。由图A4可知,交流系统中拟合的d轴和q轴变量xL1、延时环节的d轴和q轴拟合变量及电感L1的d轴和q轴电流对谐波振荡贡献较大,而锁相环及外环控制器对应的状态变量基本没有贡献,表明系统谐波振荡的主要影响环节为含频变LTC 的交流系统、延时环节和电流内环。因此,表明了失稳模态是由并网逆变器和交流系统两者共同相互作用导致。
2.1 线路参数频变特性对稳定性的影响
根据表1 和表2 所示参数,附录A 图A5 为电缆线路参数考虑频变特性和未考虑频变特性的系统特征根分布图。由图可知,当线路参数未考虑频变特性时,系统的主导特征根向虚轴移动,这表明与考虑频变特性相比,系统的稳定性范围将缩小,使得系统易引发高频谐波振荡。因此,未考虑线路参数频变特性会导致系统谐波不稳定评估中得到错误的结论。下文将详细分析考虑线路参数频变特性下各关键环节对稳定性的影响。
2.2 逆变器控制参数对稳定性的影响
为研究控制延时、电流环控制器和锁相环带宽对系统运行稳定性的影响,图3 给出了系统的根轨迹,其中,有功功率为15 kW,图3(a)为控制延时对稳定性的影响,延时Td逐渐从125 μs 增加至145 μs;图3(b)为电流环控制器参数对稳定性的影响,积分系数ki=40 保持不变,比例系数kp从0.19 以步长0.001 增加至0.215;图3(c)为锁相环带宽对稳定性的影响,其中,积分系数不变,通过调节比例系数来实现锁相环带宽的变化,根据文献[23]提供的方法计算锁相环带宽,锁相环带宽从10 Hz 以步长5 Hz增加至55 Hz。
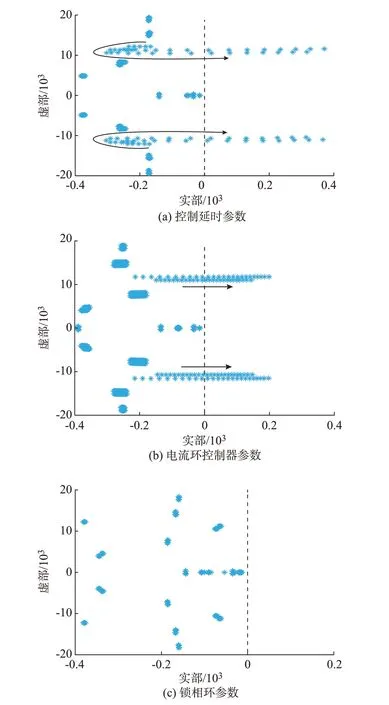
图3 控制器参数对稳定性的影响Fig.3 Influence of controller parameters on stability
图3(a)中,随着延时时间Td的增加,2 对主导特征根先向左移动再向右移动,并最终到达右半平面,当延时Td接近137 μs 时,系统临界不稳定。因此,控制延迟时间较高将导致系统不稳定。图3(b)中,电流环控制器的比例系数kp从0.19 增加到0.215,当控制器比例系数小于0.201,系统能够稳定运行,随着kp的增加,系统的2 对主导特征根从左向右移动,当kp=0.202,2 对主导特征根穿过虚轴进入右半平面,即系统临界不稳定。因此,增大控制器比例系数,系统的稳定性降低。图3(c)中,随着锁相环带宽的增大,系统特征值基本不改变,说明当系统振荡频率达到数千赫兹频段时,锁相环参数几乎不影响系统谐波不稳定,与参与因子分析中锁相环对稳定性的影响较小一致。
2.3 交流系统对稳定性的影响
并网系统的谐波不稳定是由逆变器和交流系统共同产生的,本节将从交流系统角度分析电缆长度和电网阻抗对系统稳定性的影响。
设置电缆长度L从25 km 增加至56 km,步长为0.5 km。将L分为两段进行分析:Ⅰ段,25~40 km,L从25 km 增加至40 km;Ⅱ段,40.5~56 km,L从40.5 km 增加至56 km。将L分为两段来分析是由于电缆长度在Ⅰ段区间和Ⅱ段区间对应的失稳特征根不同,Ⅰ段区间对应的失稳特征根为λ25,26、λ29,30,而Ⅱ段区间对应的失稳特征根为λ27,28、λ31,32。
附录A 图A6(a)为Ⅰ段区间L变化时的系统根轨迹,图A6(b)为Ⅱ段区间L变化时的系统根轨迹。由图A6 可知,在Ⅰ段和Ⅱ段的区间内随着L的逐步增大,系统的2 对主导特征根先从左向右移动,然后再从右向左移动,由此表明随着电缆长度增加,系统的稳定性并不是逐渐降低,而是存在一种不连续稳定区域,先是从稳定区域穿越到不稳定区域,之后再次从不稳定区域回到稳定区域。该工况下Ⅰ段和Ⅱ段的电缆长度不稳定区间分别为[28.5 36.5]和[44.5 52.5]。此外,在不稳定区间内电缆线路越长,潜在的振荡频率越低。
通过改变网侧等效电感Lg的大小来分析电网阻抗对系统稳定性的影响,设置Lg从0.2 mH 逐渐增加至20 mH,步长为0.4 mH,系统的根轨迹如附录A 图A7 所示。从图A7 可以发现,2 对主导特征根先从左向右进入右半平面,然后又从右向左进入左半平面。由此可知,系统的稳定性存在一种不连续区域,先从稳定状态变化到不稳定状态,再从不稳定状态回到稳定状态,同时,当电网阻抗越大时,潜在的振荡频率越低,该工况下网侧电感Lg的不稳定区间为[3,15.8]mH。
3 灵敏度分析及稳定性改善方法
本章在所建系统时域状态空间模型基础上,通过参与因子分析辨识出对不稳定模式贡献较大的状态变量,在该状态变量对应的行列位置添加参数以改变系统特征值分布。利用灵敏度分析,分析振荡模式对所添加参数的灵敏度,确定可提高系统稳定性的参数,并进一步基于矩阵相似变换将其转换到控制行,从而使得得控制环路中添加了额外的阻尼控制。
3.1 灵敏度分析
灵敏度分析是量化系统参数与振荡模式间相互关系的有效工具,可直观反映系统参数变化对稳定性的影响。定义矩阵J的第i个特征根λi对矩阵中某一参数b的一阶灵敏度为:
式中:mi和ni分别为第i个振荡模式的标准化左特征向量和右特征向量。假设∂λi/∂b=p+jp,其中,p、q分别为灵敏度实部和虚部,若p<0,有利于提高系统稳定性;若p>0,不利于改善系统稳定性。
选取系统状态空间模型矩阵中贡献较大的状态变量对应行列位置添加元素,根据第2 章的参与因子分析可知,状态变量icdq对系统谐波不稳定贡献较大,故选取矩阵AT中状态变量icdq对应的二阶方阵对角线位置分别添加扰动元素±b1/L1(b1>0)和±b2/L1(b2>0),即矩阵AT中A11+DdBc1Tp1的位置添加元素F=[±b1/L1,0;0,±b2/L1](b1>0,b2>0),得矩阵ATb如附录B 式(B2)所示。
矩阵ATb中关于参数b1、b2的偏导数分别如附录B 式(B3)和式(B4)所示,式(B3)和式(B4)中f1=[±1/L1,0;0,0],f2=[0,0;0,±1/L1]。由第2 章可知,λ27,28是系统谐波不稳定的主导特征根,故需重点关注其受参数b1和b2的影响。分别对矩阵ATb中所添加元素进行灵敏度分析,如表3 所示。

表3 b1和b2的参数灵敏度分析Table 3 Parameter sensitivity analysis of b1 and b2
为实现等效控制,仅考虑添加的元素同号情况,故添加元素F1=[b1/L1,0;0,b2/L1](b1>0,b2>0)的参数总灵敏度实部为:
添加元素F2=[-b1/L1,0;0,-b2/L1](b1>0,b2>0)的参数总灵敏度实部为:
综上可知,添加F1=[b1/L1,0;0,b2/L1](b1>0,b2>0)时,参数总灵敏度实部为正,使得特征根λ27,28向右半平面移动,不利于系统稳定性改善;而添加F2=[-b1/L1,0;0,-b2/L1](b1>0,b2>0)时,参数总灵敏度实部为负,使得特征根λ27,28向左半平面移动,有利于系统稳定性改善,提高了稳定裕度。
3.2 稳定性改善的控制策略推导
在矩阵AT中添加元素F2=[-b1/L1,0;0,-b2/L1](b1>0,b2>0)得矩阵ATb1,为推导稳定性改善控制策略,根据矩阵相似变换将添加元素F2变换到控制行,即状态变量xcdq所在行,选取初等行变换矩阵R和列变换矩阵R-1分别如附录B 式(B5)和式(B6)所示,式(B5)和式(B6)中I为与其行列对应阶数的单位矩阵,由于控制延时环节取四阶Pade 近似模拟,故Dd=[1,0;0,1],从而可得U1=[2b1/Udc0,0;0,2b2/Udc0],利用RATb1R-1得到相似变换后的矩阵ATb2,如附录B 式(B7)所示。
定义矩阵ATb2中电流内环积分系数对应状态变量为与附录B 式(B1)对比,得到以下关系式:
上文已说明锁相环对谐波振荡影响较小,故可忽略Δθ,将新变量x'cdq代入式(11),则可得为:
将式(33)反映到电流内环控制电路中,假设b1=b2=b,则故可知,通过添加元素F2后,得到的新变量相当于在原变量mdq基础上增加icdq的反馈环节,即在控制电路中添加了逆变侧电感电流ic的反馈信号,比例系数为2b/Udc0,如附录A 图A8 所示。
3.3 改善控制策略对谐波不稳定的影响
以电流环参数kp=0.208、ki=40 为例分析比例系数中b增大时系统的稳定性,图4 为相应的根轨迹,其中,b以步长1 从0 增加至30。从图4 可以看出,随着b的增大,系统的2 对主导特征根从右向左移动,当b=19 时,主导特征根穿过虚轴进入左半平面,系统处于稳定状态。由此可知,添加逆变侧电感电流反馈控制可抑制系统谐波不稳定。
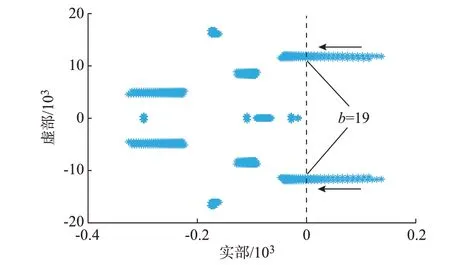
图4 b 变化时的系统根轨迹Fig.4 Root locus of system when b changes
通过对比电网阻抗和电流环控制参数的稳定区域来分析添加逆变侧电感电流反馈控制对系统稳定性的影响。当b=19,Lg从0.2 mH 以步长0.4 mH 逐渐增加。附录A 图A9 为添加逆变侧电感电流反馈后Lg变化时的系统根轨迹。由图A9 可知,随着Lg的增大,系统的2 对主导特征根从左向右移动,当Lg=11.8 mH 时,2 对主导特征根穿过虚轴进入右半平面,而当Lg=18.4 mH 时,2 对主导特征根返回到左半平面,对比未添加逆变侧电感电流反馈时Lg的不稳定区间,表明添加逆变侧电感电流反馈控制后缩小了Lg的失稳范围。
附录A 图A10 为添加逆变侧电感电流反馈前后kp和ki的稳定域。图中:绿色区域表示未添加逆变侧电感电流反馈的稳定域;红色区域表示添加逆变侧电感电流反馈后增加的稳定域。由图A10 可知,当添加了逆变侧电流反馈控制时,电流内环控制参数kp和ki的稳定范围增大,为电流环控制器参数的调整提供了更大自由度。
4 实验验证
为了验证上述理论分析的正确性,本文基于实时仿真机RT-LAB 构建了硬件在环实验平台,所述实验平台照片如附录A 图A11 所示,在RT-LAB 中搭建了图2 所示的含LTC 的三相并网逆变器系统主电路拓扑,其中,具有频变特性的输电缆模型由OPAL-RT 中 ARTEMIS-SSN 库提供。 采用MC56F84789 DSP 为核心的控制器硬件架构,实际控制器和RT-ALB 之间通过采样信号的交互和控制脉冲信号的发送完成闭环控制,实验机箱为OP4510,通过RT-LAB 的I/O 口测量实验波形,具体的实验参数与表1 和表2 相同。
设置模型1 和2 分别表示为分布参数模型和分布-频变参数模型。为了对比分析两个模型在不同电网阻抗条件下的稳定性,论文设置了2 种场景:
1)场景1:L=12 km 时,Lg分别取2.6、4.2、7.8 mH。
2)场景2:L=42 km 时,Lg分别取1.5、2.8、5.3 mH。
进一步,根据第2 章的理论分析其稳定性,如附录A 图A12 所示,场景1 和场景2 对应不同Lg的稳定性判定结果如表4 所示。由表4 可知,2 种场景下,唯一区别是仅当Lg=2.8 mH 或Lg=4.2 mH 时,模型1 和2 分别对应的系统是不稳定和稳定的,故实验结果只需与该理论分析结果一致,即可验证本文理论分析的准确性,同时也说明忽略线路参数频变特性,将导致系统稳定性的误判。
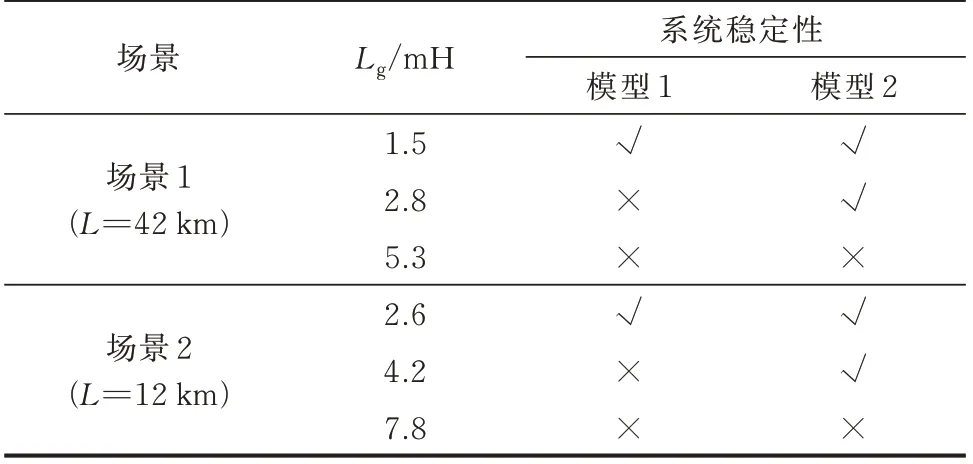
表4 2 个场景下不同Lg的稳定性Table 4 Stability of different Lg in two scenarios
图5 为2 个仿真场景下模型不同时并网逆变器的输出电流波形。由图5(a)可知:场景1 取Lg=2.8 mH,当线路采用模型2 时,并网电流波形稳定;但切换到模型1 后,并网电流波形发生振荡,系统失稳。类似地,由图5(b)可知:场景2 取Lg=4.2 mH,当线路采用模型2 时,并网电流波形稳定;但切换到模型1 后,并网电流波形发生振荡,系统失稳,实验结果与附录A 图A2 所得理论结果相一致。
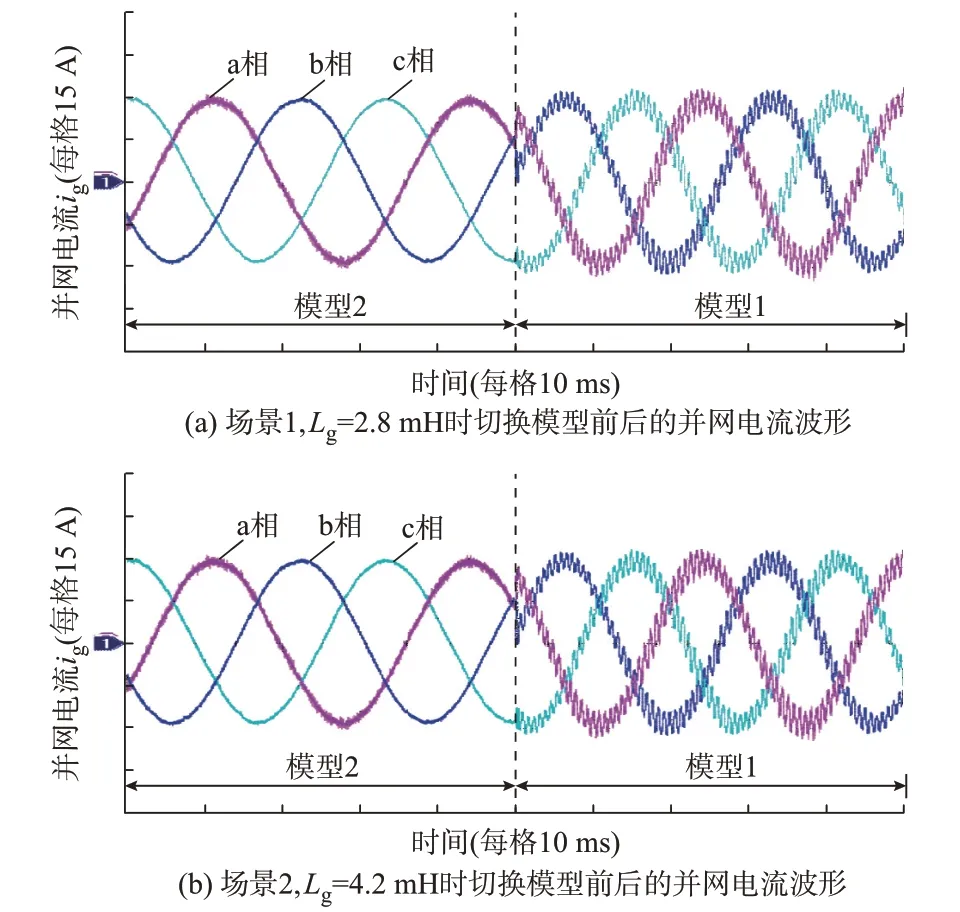
图5 2 个场景下的并网电流波形Fig.5 Waveforms of grid-connected current in two scenarios
图6 为不同有功功率下的并网电流波形及谐波分析,其中,图6(a)为并网逆变器的有功功率由15 kW 变化到21.5 kW 时的实验结果。从图6 中可以看出,当有功功率为15 kW 时,并网电流波形良好,系统稳定,但切换到21.5 kW 后,并网电流波形发生振荡,系统失稳。图6(b)为切换到有功功率21.5 kW 后,系统发生谐波不稳定时a 相电流频谱(快速傅里叶变换(FFT)基频为5 Hz,THD 表示总谐波畸变率),a 相电流FFT 分析表明振荡频率为1 870 Hz,与理论分析所得谐振频率基本一致,由此说明了理论模型构建的正确性。
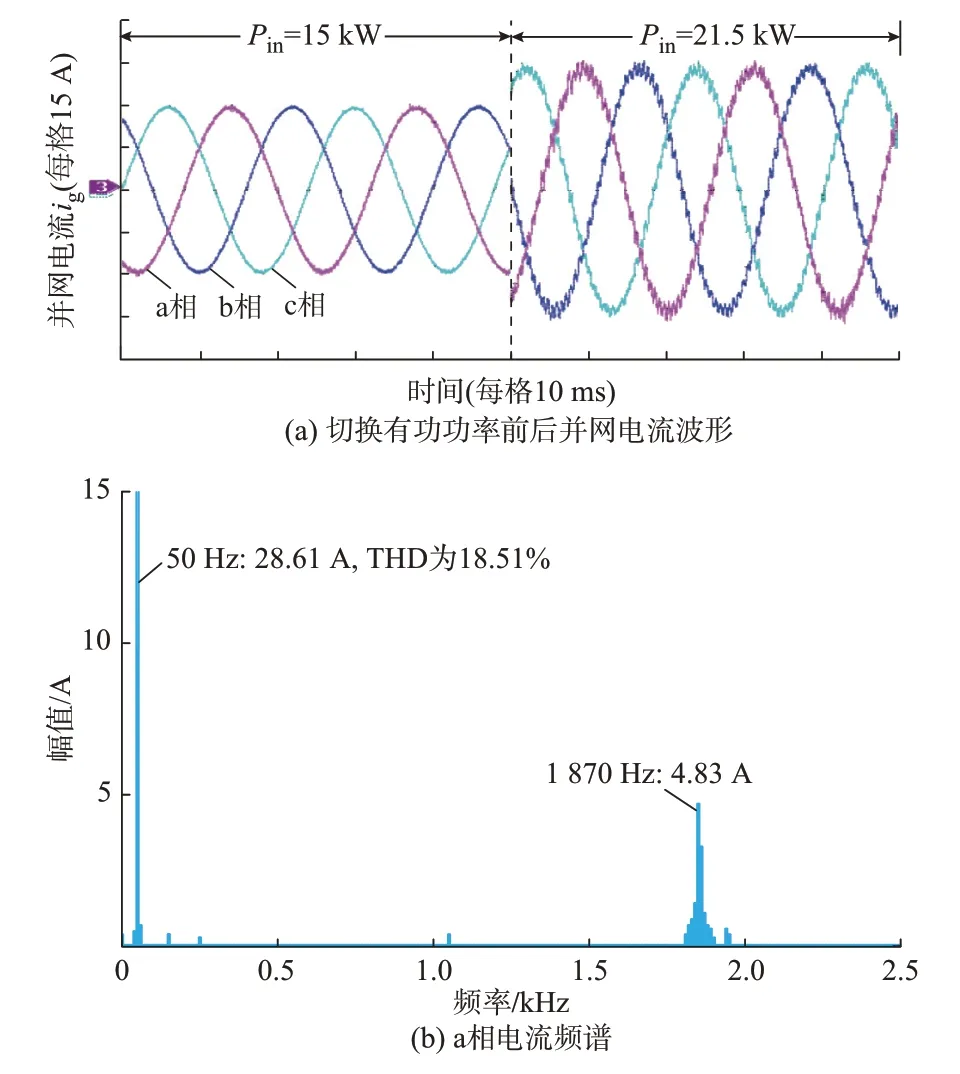
图6 不同有功功率下的并网电流波形及谐波分析Fig.6 Waveforms of grid-connected current and harmonic analysis with different active power
附录A 图A13 为延迟时间Td=139 μs 时系统不稳定的实验结果,其中,图A13(a)至(b)分别为并网电流和PCC 电压的稳态波形。可以看出,当Td=139 μs 时,并网电流和PCC 电压的波形严重恶化,系统处于不稳定状态,验证了图3(a)中Td大于137 μs会导致系统出现失稳现象的理论结果。
附录A 图A14 为ki=40 时kp变化的并网电流波形,结果表明随着kp从0.190 增加至0.214,并网电流波形质量逐渐恶化。当kp为0.19 时,并网电流波形良好,而当kp为0.198 时,如图A14(b)所示,并网电流波形开始稍有畸变,但系统处于稳定状态;当kp为0.206 和0.214 时,并网电流波形质量严重恶化,系统失稳。实验结果表明,随着kp的增大,系统逐渐进入不稳定状态,同时也验证了图3(b)中kp大于临界值0.202 时会导致系统失稳的理论分析结果。
附录A 图A15 为Ⅰ段区间不同电缆长度L的并网电流波形,当L=27 km 时,如图A15(a)所示,并网电流波形良好,系统稳定;当L=33 km 时,如图A15(b)所示,并网电流波形质量严重恶化,系统失稳,验证了L大于28.5 km 会导致系统不稳定的理论分析。如图A15(c)所示,当L=38 km,大于临界值36.5 km 时,并网电流波形良好,系统重新处于稳定状态。实验结果与图A6(a)所得理论分析结果相吻合,验证了随着电缆长度增加时,系统稳定性并不是逐渐降低,而是存在一种不连续稳定区域的结论。电缆长度在Ⅰ段和Ⅱ段区间对系统谐波不稳定影响规律类似,由于篇幅有限,本文不作分析。
附录A 图A16 为不同网侧等效电感Lg的并网电流稳态波形。如图A16(a)所示,当Lg=2 mH 时,并网电流波形良好,系统稳定;当Lg=5 mH 时,如图A16(b)所示,并网电流波形质量严重恶化,系统失稳,验证了Lg大于3 mH 时会导致系统不稳定的理论分析;从图A16(c)可以看出,当Lg=17 mH,大于临界值15.8 mH 时,并网电流波形良好,系统重新处于稳定状态,实验结果与图A9 所得理论分析结果相吻合。
附录A 图A17 为锁相环带宽变化时并网逆变器输出电流波形,其中,锁相环带宽从10 Hz 变为50 Hz,并网电流均保持稳定,与图3(c)所得理论分析结果相吻合。外环控制器带宽变化时并网电流波形如图A18 所示,其中,外环控制器带宽从30 Hz 变为80 Hz,并网电流均保持稳定,从而说明外环控制器对系统谐波振荡影响很小。
基于RT-LAB 平台搭建如附录A 图A8 所示的逆变器并网系统主电路拓扑,并在控制程序中实现逆变侧电感电流反馈控制。当电流内环控制参数kp=0.208 和ki=40 时,图7 为不同参数b下的并网电流波形。当参数b=17,如图7(a)所示,此时并网电流质量严重恶化,系统失稳,当参数b增大到22 时,如图7(b)所示,系统波形良好,处于稳定状态。实验结果与图4 所得理论分析结果相符。
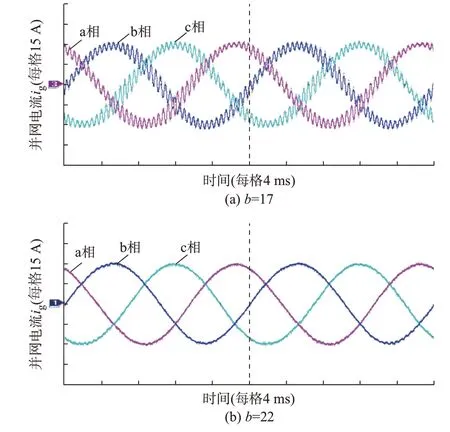
图7 不同参数b 下的并网电流波形Fig.7 Waveforms of grid-connected current with different values of parameter b
5 结语
本文建立了考虑LTC 特性的逆变器并网系统高频状态空间模型,通过参与因子和根轨迹法研究了系统谐波不稳定机理及关键影响因素,进一步基于系统状态空间模型提出了改善系统稳定性的方法,并通过与RT-LAB 实验结果进行对比,验证了本文稳定性分析及所提出稳定性改善方法的正确性。得到如下结论:
1)本文所提出的含频变LTC 的交流系统高频状态空间模型能够准确反映逆变器并网系统的高频谐波振荡特性。
2)电缆线路参数的频变特性对系统稳定性影响不容忽视。此外,电缆长度变化会影响系统谐波稳定性,当电缆长度增加时,系统的稳定性并不是逐渐降低,而是存在一种不连续稳定区域,且电缆长度在Ⅰ段和Ⅱ段区间对系统稳定性的影响规律基本相同。
3)基于根轨迹变化规律,增大控制延时及电流内环比例系数会引发系统谐波不稳定现象,而电网阻抗逐渐增加时,系统稳定性与电网阻抗之间并不具有线性关系,存在不连续稳定区间。
4)提出了基于灵敏度分析和矩阵相似变换的谐波不稳定抑制方法,可有效降低系统谐波不稳定的风险。
本文的研究仅针对电网电压平衡情况下分析LTC 特性对并网系统谐波不稳定的影响,后续工作将基于电网电压不平衡或输电缆线路参数不对称情况,开展相关的逆变器并网系统谐波不稳定性问题研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
