基于MGAT-TCN模型的可解释电网虚假数据注入攻击检测方法
2024-02-20苏向敬栗风永萧士渠
苏向敬,邓 超,栗风永,符 杨,萧士渠
(1.上海电力大学电气工程学院,上海市 200090;2.上海电力大学计算机科学与技术学院,上海市 200090)
0 引言
在新型电力系统背景下,虚拟电厂、负荷聚合商、综合能源系统等新型电力业务不断涌现。作为电网和海量终端资源的中间桥梁纽带,新型电力业务不仅可大幅降低终端接入对电力专网的通信和数据交互压力,而且可使分布式灵活资源呈现出更大的可控效能。然而,新型电力业务的通信和数据平台普遍基于公用互联网设计运行,其公网开放性强的特性使得电力系统在信息交互过程中极易受到恶意网络攻击,如拒绝服务攻击、负载重分布攻击、拓扑篡改攻击和虚假数据注入攻击(false data injection attack,FDIA)等[1-5]。其中,FDIA 作为隐蔽性网络攻击,通过破坏数据完整性严重威胁电网安全运行,故须建立快速有效的FDIA 检测机制[6]。
针对虚假数据注入攻击,近年来提出的检测方法主要分为以下2 类:1)模型驱动的方法[7-8];2)数据驱动的方法[9-15]。其中,基于模型驱动的方法不需要历史数据集训练,仅通过量测数据与系统状态之间的关系即可建立FDIA 检测模型。但是,模型检测的准确度受系统参数影响较大,且电网规模的不断扩大会导致模型的复杂度增加。而相比之下,基于数据驱动的FDIA 检测算法不涉及参数设定问题,只与数据量紧密相关,海量的电网数据恰好为其提供了强大的数据支撑[6],正受到越来越多的关注。例如,为捕捉FDIA 过程中的电网量测数据时序特征,文献[9]利用长短期记忆(long short-term memory,LSTM)网络在时间序列预测方面的强大记忆能力来识别潜在的受损测量值。文献[10]针对LSTM 网络无法同时处理量测数据前后参数信息和FDIA 关联的问题,提出了一种基于Transformer的FDIA 检测框架。同时,为捕获虚假与正常数据的空间差异,文献[11]通过多层卷积神经网络(convolutional neural network,CNN)提取量测数据空间特征,并与不良数据检测(bad data detection,BDD)结合实现FDIA 检测。文献[12]则通过变分模态分解提取量测数据的空间特征,并结合轻量型CNN 实现FDIA 检测。但是,上述传统神经网络没有考虑不同测量设备在电网部署时的空间关联,难以对电网拓扑结构进行建模,导致检测性能不佳[16]。对此,近年来发展迅速的图神经网络可很好地捕捉图网络的拓扑连接,为上述问题提供了良好的解决方案。文献[13]提出采用切比雪夫图卷积网络 (Chebyshev graph convolution network,ChebGCN)识别FDIA,通过电力系统固有图拓扑结构提取量测数据的空间特征。文献[14]通过门控图神经网络(gated graph neural network,GGNN)提取电网拓扑连接信息和运行数据的空间特征,实现FDIA 检测。
总之,上述基于深度学习的FDIA 检测研究主要仅针对电网量测数据的时序或空间特征进行建模,鲜有同时提取其时空特征。考虑到电力系统发生FDIA 时,其运行状态会发生显著变化,数据采集与监控(supervisory control and data acquisition,SCADA)量测数据呈现出时间和空间强关联的特点[17]。仅用单一空间或时序特征,FDIA 检测模型会存在攻击检测精度不足、抗噪声能力差等不足。对此,文献[15]通过卷积神经网络和长短期记忆网络(CNN-LSTM)捕获量测数据的时空特征,实现FDIA 检测。但该文献模型把量测数据作为欧氏数据处理,将电网所有节点特征通过长向量拼接,无法有效利用电网固有图拓扑结构与量测数据空间相关性,导致其时空特征信息挖掘不充分。
更重要的是,基于深度学习的FDIA 检测方法普遍为“黑盒”模型,其模型透明性低,从而降低了检测模型的可解释性和检测结果的可信度。如何实现神经网络模型的可解释性已成为当前研究的热点[18]。文献[19]提出了一种基于时空注意力机制的海上风机齿轮箱状态监测方法,实现了故障诊断的可解释;文献[20]在海上风电超短期出力预测中引入特征和时序双重注意力模块,在提升模型预测性能的同时,实现了模型特征和时间维度上的可解释性。
针对上述挑战并结合已有研究基础,本文提出了一种基于多头图注意力网络和时间卷积网络(multi-head graph attention network and time convolution network,MGAT-TCN)模型的可解释电网FDIA 检测方法。首先,通过多头图注意力网络(multi-head graph attention network,MGAT)模块考虑不同测量设备在电网部署中的拓扑结构关联,以全面提取量测数据的空间特征。同时,MGAT 空间拓扑感知注意力机制通过分配权重量化模型在学习过程中对量测数据的空间关注程度,实现模型的可解释性;接着,为避免时序信息丢失并提升模型训练效率,利用时间卷积网络(time convolution network,TCN)模块并行提取量测数据的时序特征;最后,在IEEE 14 节点系统和IEEE 39 节点系统对所提MGAT-TCN 模型进行仿真验证。
1 虚假数据注入攻击相关问题描述
1.1 状态估计和不良数据检测机制
状态估计是通过SCADA 量测数据估计电力系统运行状态的一种重要机制[21]。图1 展示了新型电力系统背景下电网虚假数据注入攻击的可能场景。海量分布式终端资源借助公用互联网平台聚合接入,逐渐成为新型电力系统的重要组成部分。网络攻击者可以较低成本攻击公用互联网平台终端设备,进而跨越公用互联网和电力专网边界危害电力专网,如入侵测量终端和数据传输通道等。基于设计好的虚假量测数据,攻击者可规避状态估计不良数据检测机制,而造成的错误状态估计结果又会导致调度中心对潮流计算、事故分析和调度控制等做出错误决策,危害电网运行安全[17]。
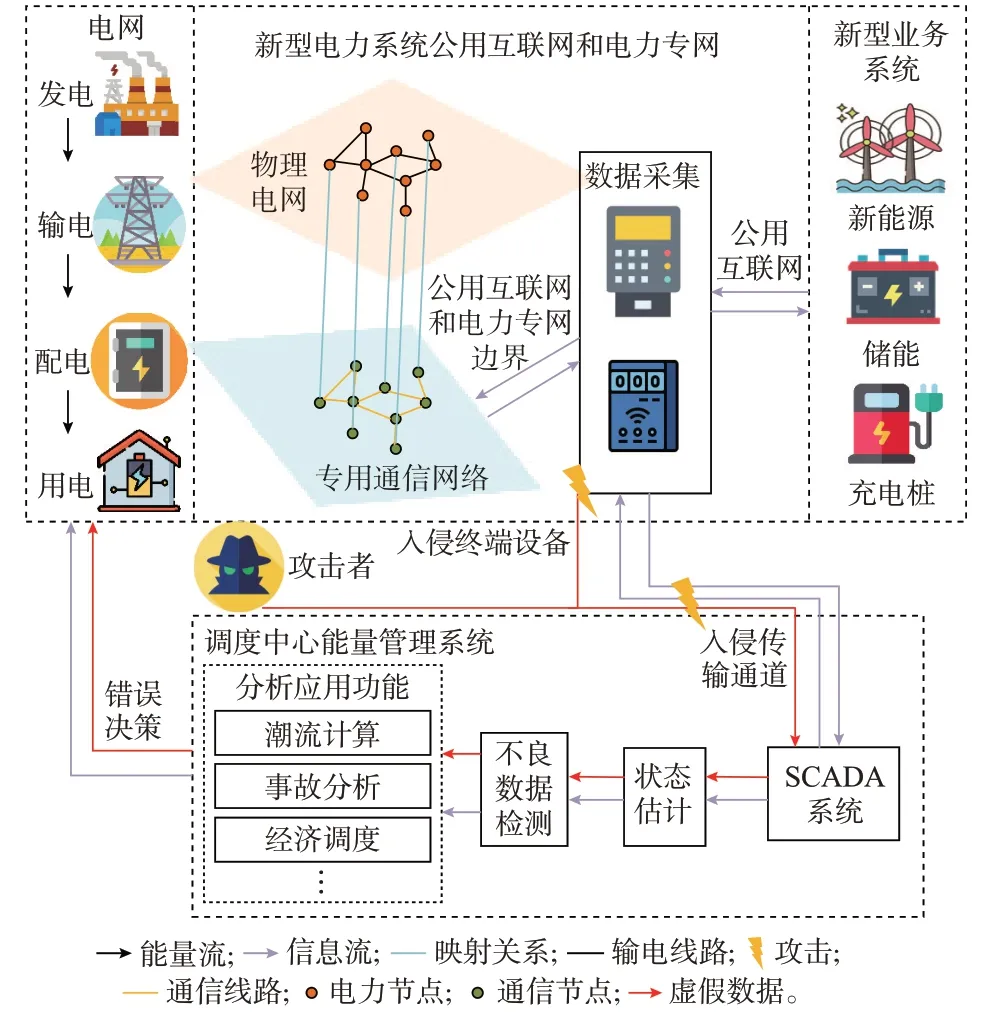
图1 电网FDIA 可能场景Fig.1 Possible scenarios of FDIA in power grid
电力系统状态估计通常假设电压幅值为1,忽略电阻和接地支路的影响,仅考虑相位角的状态变化[14]。具体计算公式如下:
式中:Z∈Rm×1为测量向量,包括传输线有功潮流和节点注入有功功率,其中,m为测量向量维数;x∈Rn×1为系统状态向量,包括节点电压相位角,其中,n为状态向量维数;H∈Rm×n为状态估计的非线性函数,是表示电网物理拓扑信息的矩阵[14];ϵ∈Rm×1为测量误差向量。
在此基础上,采用线性加权最小二乘法得到状态估计的目标函数F(x):
式中:R为测量值的误差协方差矩阵。
接着,利用加权最小二乘法求解式(2)的最小化目标函数,得到系统状态向量估计值x̂:
为确保状态估计结果的可靠性,基于残差检验原理的不良数据检测机制得到了广泛应用[22]。其中,残差r表示测量向量Z与其估计值Ẑ=Hx̂差值的欧氏范数,如式(4)所示。
将残差r与残差阈值τ进行比较:当r>τ时,检测机制认为SCADA 量测数据存在坏数据;当r<τ时,则认为数据正常。
1.2 FDIA 原理
如果攻击者入侵控制中心并获得电网物理拓扑信息矩阵H,则可以根据H生成特定的攻击向量。这种攻击向量可躲避不良数据检测机制,并影响电力系统状态估计结果。
假设攻击向量为a∈Rm×1,与测量向量Z同维数,则被攻击的测量向量为Za=Z+a。如果向量a中的第i个元素不为零,则意味着第i个测量值被攻击。经状态估计后得到系统状态值xc=x+c,其中,c∈Rn×1表示系统状态的攻击注入向量,xc为被攻击的状态向量。不良数据检测机制通过计算相应的测量残差来检测错误数据,在受到FDIA 后的残差rc为:
由式(5)可知,若a=Hc,则攻击向量可通过不良数据检测,且测量残差不会增加[22]。
2 检测模型构建
本文所构建MGAT-TCN 模型,主要包含MGAT 模块、TCN 模块和全连接层。
2.1 MGAT-TCN 模型的输入和输出
本文选择SCADA 量测数据的所有节点注入有功功率和无功功率作为输入特征,通过滑动时间窗将其转化为MGAT-TCN 模型所需的时序图数据V,即V=[v1,v2,…,vN]∈RN×W×2,其中,vi=分别为时间窗内节点i的时序图数据、时序注入有功功率和无功功率[12],i=1,2,…,N;W为滑动序列长度;N为测量设备数量。模型输入滑动时间窗口设置如附录A 图A1所示。
邻接矩阵是图结构数据的重要组成部分。考虑不同测量设备在电网部署的图拓扑关联,本文选取电网邻接矩阵A作为输入矩阵,如式(6)所示。
式中:lij为元素,若节点i和j相连,则lij=1,否则lij=0,i=1,2,…,N,j=1,2,…,N。
根据上面定义,该FDIA 检测模型的输出表示为:
2.2 提取空间特征的MGAT 模块
为充分考虑电网图拓扑结构和量测数据间的空间相关性,MGAT 需对图中节点间的关系进行建模。假设每个节点的输入vi由序列向量vi={∈[0,W]}表示,图注意力层数为3,则对应的MGAT 在附录A 图A2 中展示。给定N个节点的图,即{v1,v2,…,vN},计算节点的输出为:
式中:vi,out为节点i的输出,与输入vi维数相同;Ωi为与节点i相连接的邻域节点集合,由Ai决定,Ai为电网邻接矩阵的第i行向量;σ(·)为sigmoid 激活函数;αij为注意力得分,用于衡量节点j对节点i的贡献,可由式(9)和式(10)计算。
式中:⊕为表示2 个节点特征拼接的运算符;w∈RF×1为可学习参数的列向量,F为每个节点特征向量的维数;eij和eio分别为节点j和节点o对节点i的注意力系数,其中,节点j和节点o为Ai中与节点i连接的节点之一;LeakyReLU(·)为非线性激活函数。此处通过图神经网络实现空间特征提取,并采用多头注意力机制突出关键空间特征表达,进而实现对量测数据空间特征的有效提取。
由于深度学习的“黑盒”属性,模型对FDIA 的检测可信度不足。而注意力机制作为一种资源分配机制,可自适应地为输入变量分配注意力权值,使模型关注重要信息,并可借助热力图可视化注意力权重的形式来实现模型的可解释性[23]。附录A 图A3展示了空间拓扑感知注意力机制计算相邻节点特征向中心节点聚集的过程。
为解决FDIA 检测模型黑盒、可信度低问题,本文对数据预处理后包含正常样本和攻击样本的时序图数据V在电网邻接矩阵A上通过空间拓扑感知注意力机制赋予贡献权重,并以权重热力图实现可视化,提升FDIA 检测模型对攻击判别的可解释性和可靠性。具体而言,采用注意力机制动态计算电网中节点功率注入权重,通过变化的空间注意力系数与输入变量进行加权,得到的加权注意力权重可用来表达电网各节点量测数据对FDIA 的贡献度,从而实现模型在空间维度的可解释性和可信度,降低其“黑盒”属性。
2.3 提取时序特征的TCN 模块
在处理电网量测时序数据时,为避免时序信息丢失并提升模型训练效率,此处采用TCN 模块进行提取。具体在滑动时间窗口内,基于目标时刻W之前的时序图数据[v1,v2,…,vW-1],利用TCN 模块的扩张因果卷积对上一层的输出进行扩张采样,从而提取时序特征,实现W时刻的数据输出v̂W。其中,扩张因果卷积计算公式如下。
式中:G(s)为第s个神经元扩张卷积后的输出;g(h)为第h个过滤器;vs-dp为s-dh时刻的输入序列;k为卷积核大小;h为卷积核序号;d为扩张系数;s为扩展因果卷积神经元序号。
为使时序特征输出能够考虑更长的历史序列信息,本文TCN 模块通过2 层残差网络和多层卷积的不同扩张系数来实现。其中,残差网络结构见附录A 图A4(a),包含扩展因果卷积、权值归一化、ReLU激活函数和Dropout 随机丢弃层,4 部分的组合可防止模型过拟合,且通过卷积并行计算捕获时序特征,可加快模型训练速度。附录A 图A4(b)为扩张因果卷积计算图,卷积核大小k为3,扩张系数d分别为1、2、4。
2.4 全连接层和损失函数
基于MGAT 模块提取的空间特征ysp和TCN模块提取的时序特征ytem,全连接层通过softmax 函数完成输入特征的非线性映射,具体公式如下。
式中:ypred为模型的预测输出;λ为映射权重参数;b为偏置误差向量。
为降低模型训练损失和提高FDIAs 检测精度,本文采用交叉熵(cross-entropy,CE)函数作为损失计算函数,并通过adam 优化器自适应调节学习率更新模型参数。其中,损失ψloss如式(13)所示。
式中:M为批尺寸大小;ypred,i为第i个模型预测结果;ui为第i个实际电网运行状态标签。
3 基于MGAT-TCN 模型的可解释FDIA 检测流程及评估指标
3.1 基于MGAT-TCN 模型的可解释FDIA 检测流程
基于MGAT-TCN 模型的可解释FDIA 检测流程主要分为3 个部分:数据预处理及电网图拓扑构建、MGAT-TCN 模型训练和模型测试评估,如图2所示。
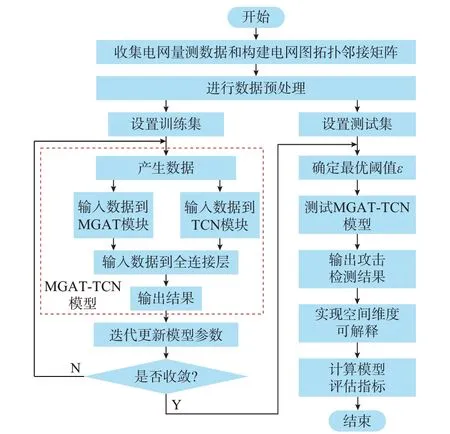
图2 基于MGAT-TCN 模型的可解释FDIA 完整检测流程Fig.2 Complete interpretable detection process for FDIA based on MGAT-TCN model
可解释FDIA 检测具体流程如下。
步骤1:对SCADA 量测数据进行预处理。首先,将包含正常量测数据和受攻击量测数据通过滑动时间窗处理为MGAT-TCN 模型输入所需的时序图数据V,维数为M×N×W×F;接着,在此基础上,完成相应系统的图拓扑并构建A,同时,对图数据V进行最大最小归一化处理;最后,将预处理后的图数据V划分为训练集和测试集,并结合A作为整个MGAT-TCN 模型的输入。
步骤2:模型训练。首先,将训练集图数据V和电网邻接矩阵A输入到MGAT 层,感知并提取电网拓扑结构和量测数据的空间特征ysp,并将数据V输入到TCN 层,提取量测数据的时序特征ytem;接着,将提取的时空特征输入到全连接层,并根据所设训练轮数(epoch)进行模型参数迭代更新,完成MGAT-TCN 模型训练;最后,利用训练集对训练好的MGAT-TCN 模型进行阈值ε网格搜索,以检测最大准确率为条件,在[0,1]区间选择最优阈值ε。
步骤3:模型测试。首先,将测试集的数据V和电网邻接矩阵A输入到MGAT-TCN 模型完成目标特征预测,利用预测值与阈值ε实现FDIA 检测;然后,通过预测攻击标签与真实标签进行对比,完成模型测试评估;同时,为实现模型空间维度可解释,将MGAT 层的空间拓扑感知注意力权值进行可视化,通过观察不同节点量测数据对FDIA 检测的贡献度,降低所提MGAT-TCN 模型的“黑盒”属性,提高模型检测可信度。
实际应用中,本文所提可解释FDIA 检测模型可与状态估计的不良数据检测配合开展。例如,SCADA 量测数据可借助所提MGAT-TCN 模型进行FDIA 检测,以剔除攻击数据;利用状态估计的不良数据检测机制,筛除不良量测数据;经过上述处理后的数据,可有效支撑能量管理系统对电网运行状态的可靠估计和控制决策。
3.2 评估指标
本文采用准确率(accuracy)、精确率(precision)、召回率(recall)和F1 分数等机器学习目标检测领域通用的评测指标,评价所提模型的检测性能[24]。评估指标所涉及统计变量定义如下:
1)真负类(true negative):表示将电网正常量测数据正确识别为正常数据的数量,记为βTN。
2)假正类(false positive):表示将电网正常量测数据错误识别为FDIA 的数量,记为βFP。
3)真正类(true positive):表示将电网FDIA 数据正确识别为FDIA 的数量,记为βTP。
4)假负类(false negative):表示将电网FDIA 数据错误识别为正常数据的数量,记为βFN。
相应地,给出4 个评估指标的计算表达式如下。1)准确率计算表达式为:
式中:IAcc为所有被正确判断的样本所占的比值。准确率越高,表明检测模型总体效果越好。
2)精确率计算表达式为:
式中:IPre为预测攻击样本中真实攻击样本所占的比值。精确率越高,表明检测模型误报率越低,检测效果越好。
3)召回率计算表达式为:
式中:IRec为在真实攻击样本中预测正确攻击样本所占的比值。召回率越高,表明检测模型漏报率越低,检测效果越好。
4)F1 分数计算表达式为:
式中:IF1为精确率和召回率的谐波平均值,在选择精确率或召回率可能导致模型分别给出高误报和漏报的情况下用做综合评价指标。F1 分数越高,表明检测模型总体性能越好。
4 仿真分析
4.1 实验数据说明
实验选择IEEE 14 节点系统和IEEE 39 节点系统作为测试案例,其中,网络拓扑、节点数据、支路参数等均从MATPOWER 获得。对于攻击样本,本文基于1.1 节和1.2 节的FDIA 原理与构建方法生成。对于IEEE 14 节点系统,攻击节点设为节点3、5、11;对于IEEE 39 节点系统,攻击节点设为节点3、5、11、17、26。附录A 图A5 展示了IEEE 14 节点系统和IEEE 39 节点系统受攻击前、后状态变化情况。同时,考虑到FDIA 的真实性,设置正常样本数量远大于攻击样本,并结合攻击强度和量测噪声来实现检测模型的性能评估。其中,攻击强度定义为攻击节点状态估计值与真值的比值,并默认取0.1;设定量测噪声满足高斯分布N(0,0.25);设置每次攻击注入虚假数据的持续时间为15 个步长,每个步长内采用MATPOWER 工具包进行1 次潮流计算,且攻击后测量残差小于残差阈值τ,以规避不良数据检测。表1 和表2 分别给出了IEEE 14 节点系统和IEEE 39 节点系统的训练和测试数据集。
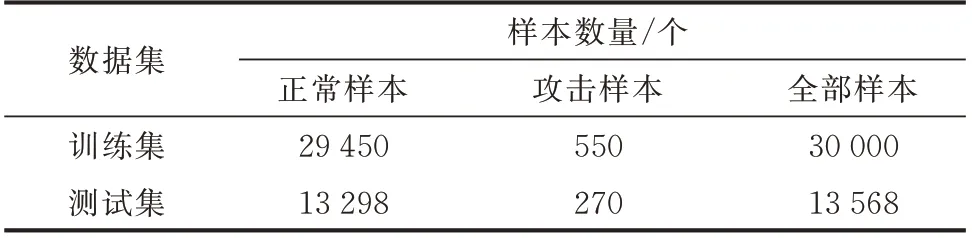
表1 IEEE 14 节点系统的训练数据集和测试数据集Table 1 Training data set and test data set of IEEE 14-bus system
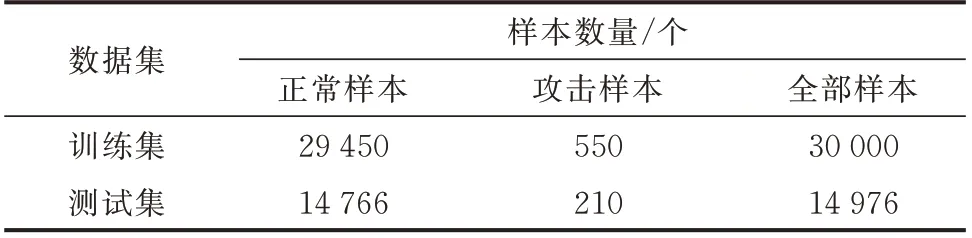
表2 IEEE 39 节点系统的训练数据集和测试数据集Table 2 Training data set and test data set of IEEE 39-bus system
4.2 不同检测模型性能对比
为验证所提MGAT-TCN 模型的优越性,在相同数据集下,本文采用CNN、MGAT、LSTM、TCN,以及同样提取时空特征的CNN-LSTM 模型作为对比模型,并设置epoch 为15。表3 给出了MGAT-TCN、MGAT、TCN、CNN-LSTM、CNN 和LSTM 模型在IEEE 14 节点系统和IEEE 39 节点系统中的FDIAs 检测性能。表4 给出了LSTM、TCN、CNN-LSTM 和MGAT-TCN 模型的训练时间。
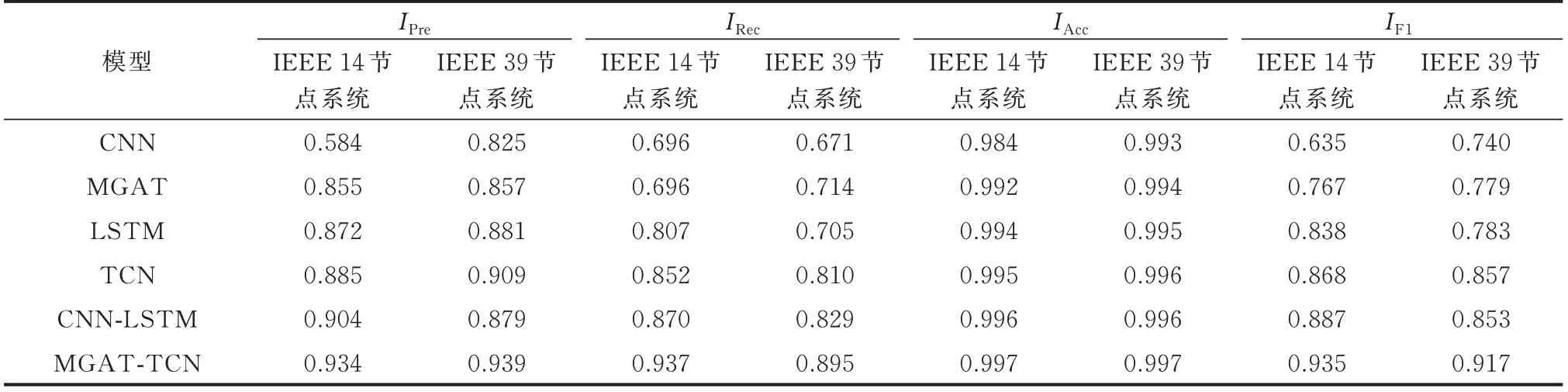
表3 不同模型检测性能对比Table 3 Detection performance comparison of different models

表4 不同模型训练时间对比Table 4 Comparison of training time with different models
由表3 可知,6 种模型对FDIA 检测的准确率均不低于95%,说明这些模型对FDIA 和正常数据均能做到有效分辨。但由于真实场景中FDIA 属于小样本事件,正常样本的数量会远超FDIA 样本数量,单凭检测准确率不足以验证模型的性能。因此,通过对比分析模型的精确率、召回率和F1 分数来进一步验证检测方法的性能。表3 给出了以上指标的测试结果。
从表3 可以看到,在IEEE 14 节点系统和IEEE 39 节点系统中,CNN 检测模型的精确率分别只有0.584 和0.825。由于精确率表征检测模型的误报率,故CNN 模型预测的攻击样本中,正常数据被预测为攻击样本的数量占比高,攻击样本被误判数量过大。相比之下,所提MGAT 模型在2 个测试系统中,检测精确率分别高达0.855 和0.857,表明正常样本被预测为攻击样本的数量占比较低,攻击样本被误判的数量相对减少。同样,F1 分数作为精确率和召回率的综合评价指标,在2 个测试系统中,CNN模型分别为0.635 和0.740,而MGAT 模型则分别为0.767 和0.779,这表明所提MGAT 模型在提取空间特征上更全面,检测效果也更加稳定。另外,从表4可以看出,无论是单个epoch 模型训练时间,还是总训练时间,TCN 模型的训练时间均优于LSTM 模型。这是因为TCN 模型通过扩张卷积并行计算可捕获多个序列的时序特征,加快了模型计算速度,并避免时序信息丢失,使得模型具有更优越的时序特征提取能力。
最后,结合表3 和表4 可知,所提模型与CNNLSTM 相比,其F1 分数在2 个测试系统中分别提升了0.048 和0.064,模型训练时间分别减少了66 s 和112 s。这表明所提MGAT-TCN 模型充分挖掘了电网量测数据的时空特征信息,使得检测性能进一步得到提升。
4.3 所提检测模型可解释性分析
为验证所提MGAT-TCN 模型可解释的合理性,对空间拓扑感知注意力的学习权重进行可视化,并结合FDIA 领域知识实现合理性验证。图3 分别展示了IEEE 14 节点系统和IEEE 39 节点系统在不同的样本条件下和模型训练过程中的空间注意力权重变化情况,其中,颜色越深表示权重越大。
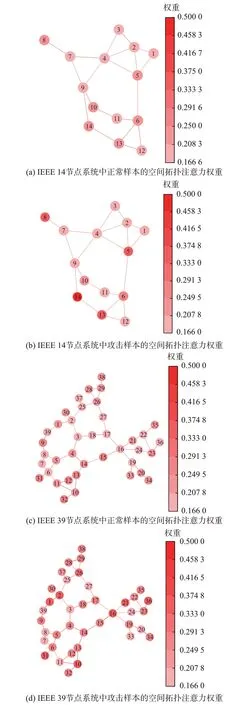
图3 正常样本和攻击样本的空间拓扑注意力权值可解释图Fig.3 Interpretable graph of spatial-topology attention weights for normal samples and attack samples
由4.1 节数据说明可知,对于IEEE 14 节点系统,设计攻击目标是系统节点3、5、11 的状态值。同时,依据本文FDIA 原理的领域知识,攻击向量a是假定攻击者掌握电网物理拓扑信息矩阵H,通过对H中对应节点5、6、8、13、14 进行虚假量测数据注入,从而改变节点3、5、11 的状态值来实现FDIA。由图3(b)可以看到,在IEEE 14 节点系统攻击样本下,节点5、6、8、13、14 颜色较深,其空间拓扑注意力权重值稳定在0.375 左右,该结果与上述FDIA 的领域知识基本保持一致。攻击者通过对H中的节点5、6、8、13、14 进行虚假量测数据注入,从而改变了节点3、5、11 的状态变量值,且成功躲过了不良数据检测,故这几个节点的权重在模型学习过程中也相应地被赋予较高的权重。相比之下,其他节点输入变量与FDIA 的相关性有限,空间拓扑注意力权重被赋予了较小的数值。由图3(a)可知,对于正常样本,由于没有受到攻击,电网物理拓扑信息矩阵H的相应节点没有虚假量测数据注入,故在模型训练迭代过程中,空间拓扑注意力权重对正常样本的分配会更趋于平均。
对IEEE 39 节点系统同样存在上述结论。由图3(d)可以看到,节点1、2、10、16、21、26、31、36颜色较深,其空间拓扑注意力权重值稳定在0.291~0.375 范围内,这表明攻击者通过对电网物理拓扑信息矩阵H中相应节点进行虚假量测数据注入,改变了节点3、5、11、17、26 的状态值,故所提模型的空间注意力权重在学习过程中对这几个被虚假数据注入的节点赋予了更高权值。结合图3(c)可知,对于IEEE 39 节点系统的正常样本,因没有受到攻击,空间拓扑注意力权重对所有节点的权值赋予也趋于平均。
由上述分析可知,本文所提空间拓扑感知注意力机制可以实现模型的可解释性,提高了检测结果的可信度,并且针对可解释图中经常被攻击的节点,电网可提前对空间注意力权重较高节点采取相应防御措施[25]。
4.4 所提检测模型的鲁棒性分析
基于IEEE 14 节点系统,进一步对不同环境噪声下所提模型的鲁棒性进行验证。将环境数据噪声的方差分别设为0.25、0.30、0.35、0.40、0.45、0.50,并对所提MGAT-TCN 模型和CNN-LSTM 模型在不同环境数据噪声下的性能进行了测试,测试结果如图4 所示。由图4 可以看出,随着噪声方差增加,本文所提模型的F1 分数缓慢下降,而CNN-LSTM 模型的F1 分数则快速降低。这是因为当噪声水平升高时,CNN-LSTM 模型很难区分正常测量值和受到干扰后的正常测量值。但是,所提MGAT-TCN模型的F1 分数始终显著优于CNN-LSTM 模型,特别是当噪声方差小于0.4 时,依然可达到0.8 以上。这说明当量测环境噪声引起的差异小于FDIA 引起的差异时,所提MGAT-TCN 模型的抗噪声能力更强,检测性能更具鲁棒性。
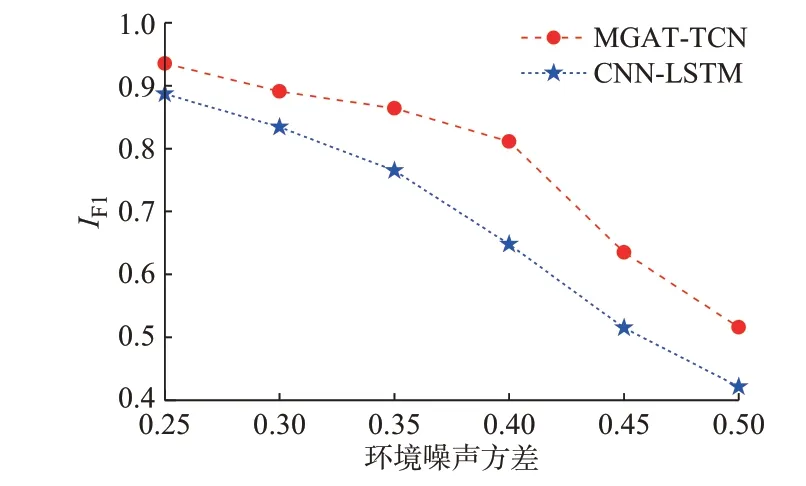
图4 不同环境噪声下的模型鲁棒性对比Fig.4 Comparison of model robustness with different environmental noises
4.5 所提检测模型的消融实验
为验证所提模型中不同模块对FDIA 检测的有效性,在IEEE 14 节点系统和IEEE 39 节点系统上进行消融实验。表5 给出了消融实验结果。由表5可见,在2 个测试系统中,当禁用TCN、仅用MGAT时,所得F1 分数相比MGAT-TCN 分别下降了0.168 和0.138。同样,当禁用MGAT、仅用TCN时,所得F1 分数相比MGAT-TCN 分别下降了0.067 和0.060。事实上,电网图拓扑结构和量测数据是高度时空相关的。面向空间特征的MGAT 模块通过空间拓扑感知注意力机制有助于准确捕捉空间相关性;而面向时序特征的TCN 模块对所提模型性能也至关重要,扩张因果卷积并行运算在加快模型训练速度的同时,也防止了早期信息丢失,可更好地挖掘时序依赖关系。
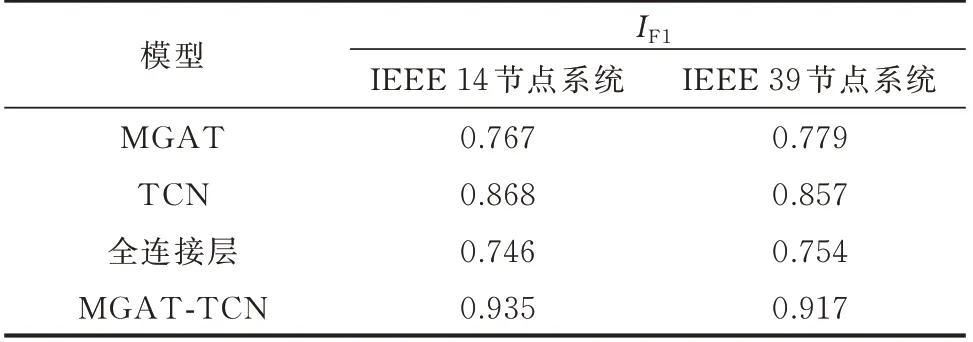
表5 MGAT-TCN 模型中每个模块的消融实验结果Table 5 Ablation experiment results of each module in MGAT-TCN model
5 结语
针对电网面临的FDIA,为充分提取SCADA 量测数据和电网拓扑信息的时空特征,本文提出了一种MGAT 和TCN 结合的可解释检测模型,即MGAT-TCN 模型。通过在IEEE 14 节点系统和IEEE 39 节点系统上进行仿真验证,得到以下结论:
1)MGAT 充分考虑不同测量设备在电网部署中的拓扑结构关联关系,从而提取更全面的量测数据空间特征;TCN 通过并行卷积提取电网量测数据的时序特征,缩短了模型训练时间。
2)在不同节点测试系统中,与现有主流模型进行检测性能对比的结果表明,MGAT-TCN 模型具有更高的检测准确率和模型训练效率,验证了所提方法的有效性和优势;在不同量测噪声环境下验证了所提MGAT-TCN 模型的鲁棒性。
3)本文方法展现出良好的可解释性,空间拓扑感知注意力机制可以引导模型自适应聚焦重点特征,通过权重量化模型在学习过程中计算不同样本的空间关注程度,实现空间维度上攻击检测可解释性。
本文验证了所提模型对FDIA 检测的有效性,未来研究可关注公用互联网与电力专网互动的新型电力业务系统更加复杂的攻击行为和场景,拓展可信人工智能在电力网络安全中的应用。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
