虚拟同步直驱风机低频振荡机理分析及阻尼补偿控制

王子骏，庄可好，辛焕海，，李少林，齐 琛，程雪坤

（1.浙江大学工程师学院，浙江省 杭州市 310027；2.浙江大学电气工程学院，浙江省 杭州市 310027；3.中国电力科学研究院有限公司，北京市 100192；4.国网冀北电力有限公司电力科学研究院，北京市 100045）

0 引言

为实现中国“碳达峰·碳中和”的战略目标，风光等新能源设备的装机容量不断提升，电力系统呈现低短路比、低惯量的特征，使得系统稳定运行面临着严峻挑战［1-3］。为保障高比例新能源电力系统稳定运行，新能源也逐渐由被动跟随向主动支撑转变。其中，在传统电流源机组中采用虚拟惯量控制可使新能源参与电网的频率调节［4-5］，但难以为电网提供电压支撑［6-7］，无法突破低短路比电网的约束。相比之下，新能源采用虚拟同步机（virtual synchronous generator，VSG）技术可模拟电压源特性，同时实现对电网的电压/惯量支撑［8］，并突破低短路比电网对新能源功率稳定送出的制约。目前，中国沙漠戈壁等地区的大规模新能源基地在不断建设，亟须研究可靠的虚拟同步控制技术。与小容量的微电网系统不同，若完全依赖储能型VSG 提升送端系统短路比，所需储能的建设成本将极为高昂。因此，依赖新能源自身能量环节的虚拟同步控制逐渐受到工程界及学术界的重视［9-12］。但新能源设备通过控制模拟转子动态也不可避免地继承了同步机的低频振荡问题，且因设备复杂的级联控制环节，其低频振荡特性与同步机特性也有所不同，引起了国内外学者的关注和研究［13-14］。

目前，传统VSG 并网系统（本文指利用储能实现虚拟同步的新能源设备）多假设直流电压恒定且功率参考值为给定常数，其低频振荡研究已经较为成熟［15-18］。文献［15-16］建立了考虑电压外环的VSG 小信号状态空间模型，发现增大虚拟阻抗及有源阻尼系数有利于提高系统低频稳定性。当VSG引入频率检测环节时，会产生负阻尼转矩并恶化系统低频特性，使得VSG 更容易引发系统低频振荡［17］。进一步，文献［18］建立了多VSG 系统的闭环模型，指出当各VSG 开环模式相近时会降低系统低频稳定性，并提出了多VSG 参数整定方法。但上述分析仅适用于传统VSG，对于依赖新能源自身能量环节的虚拟同步设备缺乏深入研究。

永磁直驱风机作为新能源主流机组之一，其依赖自身能量环节的虚拟同步研究受到广泛关注［9，19-20］。其中，典型的虚拟同步直驱风机控制结构中，其网侧虚拟同步控制的功率参考值由降载后的最大功率点跟踪（deloading maximum power point tracking，DL-MPPT）给定，机侧变流器则控制直流电压恒定。由于直驱风机的机侧动态与网侧虚拟同步动态耦合，其低频振荡特性比传统VSG 更加复杂。为此，国内外学者开始考虑直流动态和机侧动态展开研究，但尚处于起步阶段。文献［21］建立了直驱风机的阻抗模型，提出了直流动态对VSG 系统影响的量化方法，并分析了直流参数的影响，但未考虑功率跟踪下风机转子与网侧虚拟同步控制的耦合关系。此外，基于虚拟同步直驱风机的全阶状态空间模型可以发现，忽略机侧动态将导致稳定性分析的不准确［22-23］。但基于状态空间的方法难以量化风机各环节阻尼特性并揭示低频振荡机理，虚拟同步直驱风机的低频振荡特性还需进一步研究。

为此，本文首先建立了计及机侧、直流侧及网侧动态的虚拟同步直驱风机统一阻尼转矩模型；其次，基于阻尼转矩法量化了风机低频段的阻尼特性，并揭示了各环节动态对低频振荡的影响机理；进一步，提出了阻尼补偿控制（damping compensation control，DCC）以削弱机侧动态的负阻尼效应，并给出参数整定方法，可有效抑制风机的低频振荡；最后，简要分析了所提控制方法在多机系统的适用性，并基于MATLAB/Simulink 的时域仿真模型验证了理论分析的准确性及所提控制的有效性。

1 虚拟同步直驱风机的统一阻尼转矩模型

1.1 虚拟同步直驱风机的实现原理

构网型直驱风机通过电压矢量控制保障电压幅值恒定，并基于类摇摆方程动态的虚拟同步控制调节电压相位实现功率的控制，从而使风机呈现电压源特性［24］。本文主要考虑无附加能量源的虚拟同步直驱风机，需要机侧变流器控制直流电压恒定，网侧变流器模拟摇摆方程动态控制机侧功率，如图1所示［10］。图中：LF和CF分别为滤波电感和电容；Lg和Rg分别为线路电感和电阻；θ为网侧旋转坐标系相位；Igabc为网侧变流器输出电流；Vgabc为公共耦合点电压；Ioabc为线路电流；分别为网侧电流的d、q轴分量对应参考值；分别为网侧电压的d、q轴分量对应参考值；分别为机侧电流的d、q轴分量对应参考值；为直流电压参考值。由于风机无附加能量源，在外界扰动下需要风机转子提供能量支撑以维持电压源运行，故风机转子需要工作在降载运行状态，并预留能量提供惯量支撑，即虚拟同步控制的功率参考值为KDLPMPPT，其中KDL为降载系数，PMPPT为最大功率点跟踪（MPPT）环节计算的MPPT 值。

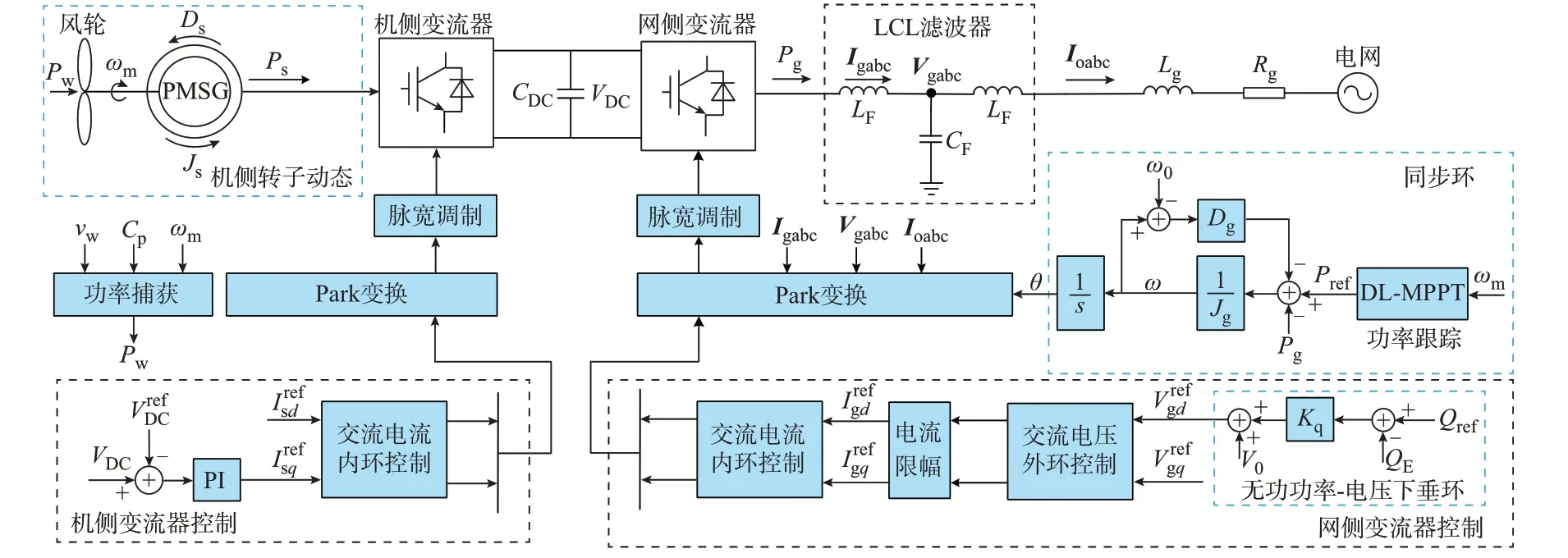
图1 风机并网系统控制框图Fig.1 Control block diagram of grid-connected system with wind turbine generators

1.2 风机各环节动态建模

如图1 所示，虚拟同步直驱风机通过机侧外环控制直流电压稳定，网侧采用VSG 控制，进而可使风机实现对电网的主动支撑。风机模型主要由机侧、直流侧、网侧3 个环节组成。

首先，建立风机系统的机侧模型，其主要包含直驱风力发电机及机侧变流器。直驱风力发电机主要由风轮和风力发电机组成，其中，风轮所捕获的机械功率Pw由风速vw、风能利用系数Cp及风机转子角速度ωm共同决定，进而风轮带动风力发电机转子发电，风力发电机的转子动态方程可表示为［25］：

式中：Js为风力发电机惯量系数；Ds为风力发电机阻尼系数；Tsw、TsE分别为发电机机械转矩、电磁转矩。

对于机侧变流器，其包含外环及内环控制。其中，电流内环控制采用传统的矢量解耦控制得到变流器调制电压；外环控制利用直流电压偏差得到q轴电流参考值，并置d轴电流参考值为0 以实现风机转子磁链定向。

其次，直流环节则通过直流电容实现机侧与网侧的功率传递，其动态方程可表示为：

式中：Ps、Pg分别为机侧和网侧有功功率输出；CDC为直流电容；VDC为直流电压。

此外，风机的网侧模型中网侧线路动态、电压-电流双环控制动态及无功功率-电压下垂环动态已有大量文献进行建模，本节对此不再展开。另外，网侧虚拟同步控制可表示为：

式中：ω为dq旋转坐标系的角频率；Pref为功率参考值；ω0为电网频率参考值，稳态下等于电网频率；Dg为阻尼系数；Jg为惯量系数。

虚拟同步控制的功率参考值Pref可表示为［26］：

式中：KM为MPPT 跟踪系数。风机模型具体推导见附录A。

1.3 风机统一阻尼转矩模型

进一步，线性化各环节动态可得到风机系统的统一阻尼转矩模型，如图2 所示。

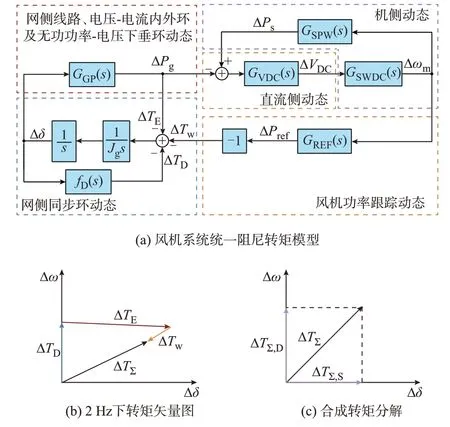
图2 风机并网系统统一阻尼转矩模型及转矩矢量Fig.2 Unified damping torque model and vector of grid-connected system with wind turbine generators

推导及变量详细说明见附录A，各环节等效转矩可表示为：

式中：Δω为网侧频率扰动量；Δδ为网侧旋转坐标系相对电网电压的夹角；ΔTw、ΔTE、ΔTD分别为机侧等效转矩、网侧电磁转矩、网侧阻尼转矩；fw(s)、fE(s)、fD(s)分别为对应的传递函数。

统一阻尼转矩模型：利用等效转矩回路刻画风机动态，并将其分解为机侧等效转矩回路（图2（a）黄色、紫色和橙色框图）、网侧电磁转矩回路（图2（a）红色框图）和网侧阻尼转矩回路（图2（a）蓝色框图）。基于该模型可分析各回路动态交互下阻尼转矩的变化，如分析机侧动态影响时，由图2（a）可知，机侧等效转矩回路中机侧动态通过直流侧动态及功率跟踪动态与网侧同步环动态耦合，进而改变了风机的低频特性。此外，该模型同样适用于分析不考虑直流侧和机侧转子动态的传统VSG 并网系统，令功率参考值扰动量ΔPref=0 可得到对应的阻尼转矩模型，即传统VSG 并网模型是本节统一阻尼转矩模型的特例。

2 风机并网系统的低频振荡分析

2.1 基于阻尼转矩法的风机低频振荡机理分析

在传统电力系统中，阻尼转矩法被广泛用于小干扰稳定性评估中，可以较好地揭示低频振荡的机理［27］。阻尼转矩法的优点在于阻尼转矩分量可量化虚拟同步直驱风机在低频段的阻尼能力，并清晰地解释为什么系统中会出现弱阻尼，进而指导控制设计以减轻低频振荡。为此，本节基于阻尼转矩法来进一步分析虚拟同步直驱风机的低频动态。

首先，基于图2 的统一阻尼转矩模型可知，风机包含3 个直接作用的等效转矩，其中，网侧电磁转矩ΔTE由网侧线路动态、无功功率-电压下垂环及内外环动态决定；网侧阻尼转矩ΔTD由网侧阻尼系数决定；机侧等效转矩ΔTw则由网侧线路动态、无功功率-电压下垂环动态、内外环动态、直流侧动态、机侧动态及功率跟踪动态共同决定。3 个等效转矩的合成转矩决定了网侧的虚拟转子动态，其中，合成转矩ΔTΣ=ΔTE+ΔTD+ΔTw。因此，基于阻尼转矩法分析合成转矩即可分析风机系统的同步阻尼特性。

其次，由于fw(s)、fE(s)、fD(s)的振幅和相位都随频率变化，相应的3 个等效转矩也随频率变化。图3（a）至（c）显示了低频范围（0.1～2.5 Hz）内3 个等效转矩传递函数的Bode 图。根据图3（a）至（c）可以得到这些传递函数在特定频率下的幅值和相位，进而可得到对应的转矩矢量图。而关注低频振荡频率处转矩矢量图即可分析风机的低频振荡特性，其中，低频振荡频率可基于相关比［28］方法得到，具体计算方法见附录B。例如，若根据附录B 计算得到的低频振荡频率fLFO为2 Hz，根据图3（a）至（c）可得到各转矩的矢量图如图2（b）所示。图中：Δω方向为阻尼转矩分量方向；Δδ方向为同步转矩分量方向。可以看出，ΔTD为阻尼转矩分量，ΔTE和ΔTw均包含阻尼转矩和同步转矩分量，但ΔTE的阻尼转矩分量很小，主要为同步转矩分量。

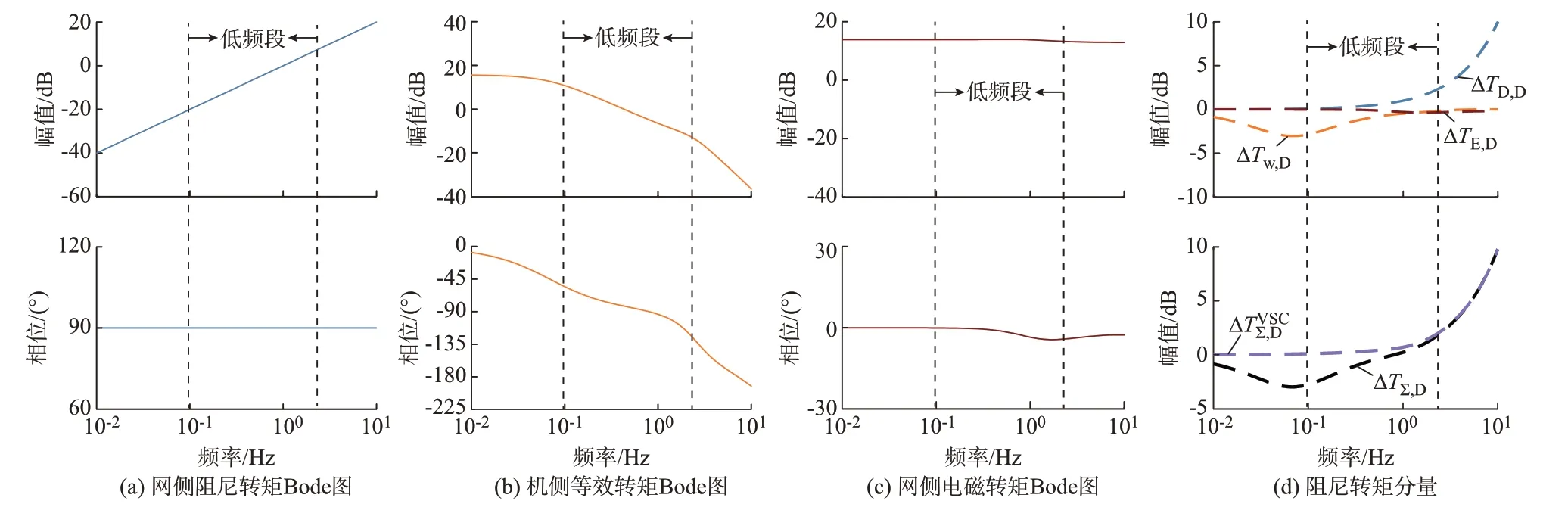
图3 风机等效转矩的Bode 图及阻尼转矩分量Fig.3 Bode diagrams and damping torque components of equivalent torque for wind turbine generators

根据经典电力系统理论，当且仅当合成转矩ΔTΣ在任意频率下可以分解为正阻尼转矩和正同步转矩时，系统是稳定的。一方面，若并网系统不能提供正的阻尼转矩，则会产生低频振荡；另一方面，若并网系统无法提供正的同步转矩，则并网系统将失去与电网的相位同步，发生功角失步。

图2（c）展示了合成转矩ΔTΣ如何分解成同步转矩ΔTΣ，S和阻尼转矩ΔTΣ，D。其中，阻尼转矩可由下式得到：

式中：ΔTE，D、ΔTD，D、ΔTw，D分别为ΔTE、ΔTD、ΔTw的阻尼转矩分量，|ΔTE|、|ΔTD|、|ΔTw|为对应转矩幅值，φE、φD、φw为对应转矩和Δδ的夹角。

根据图3（a）至（c）及式（6）可计算得到某个频率下的系统转矩分量，其中，低频段的阻尼转矩分量ΔTΣ，D主导风机系统低频振荡的阻尼能力。本文主要关注低频振荡问题，不再对同步转矩ΔTΣ，S展开分析。

根据图3（a）至（c）及式（6），可得到如图3（d）所示风机系统3 个等效转矩ΔTD、ΔTE、ΔTw及合成转矩ΔTΣ的阻尼转矩分量ΔTD，D、ΔTE，D、ΔTw，D、ΔTΣ，D。在低频段，ΔTD的φD=90°，故ΔTD，D始终大于0，为系统提供正的阻尼；ΔTE的φE为负数且接近0，故ΔTE，D在低频段很小，呈弱负阻尼特性，其影响相对较小。由图3（d）可以发现，ΔTw，D始终小于0 且幅值较大。因此，ΔTw会在低频段给系统提供主要的负阻尼转矩，恶化系统的低频动态。而对于ΔTΣ，通过观察在低频振荡频率fLFO处的ΔTΣ，D可量化系统低频振荡的阻尼能力。因此，可按如下步骤量化系统的低频阻尼能力，并判断风机系统是否会引发低频振荡：

1）按照第1 章建立风机统一阻尼转矩模型。

2）按照附录B 的相关比方法计算系统低频振荡模态的频率。

3）基于统一阻尼转矩模型和式（5）计算3 个等效转矩ΔTD、ΔTE、ΔTw。

4）根据式（6）计算ΔTΣ，D，若ΔTΣ，D在fLFO处大于0，则系统拥有足够正阻尼以抑制低频振荡发生；反之，系统在扰动下可能会引发低频振荡。

风机低频振荡机理如下：机侧转子动态通过功率跟踪与网侧虚拟同步控制动态耦合，其机侧等效转矩ΔTw在低频段提供较大的负阻尼转矩，是风机低频振荡的主要原因；网侧线路和内外环动态所构成的网侧电磁转矩ΔTE提供弱负阻尼转矩，其影响相对较小；阻尼系数则直接提供低频段的正阻尼转矩ΔTD，3 个等效转矩共同主导了风机的低频特性，当合成阻尼转矩ΔTΣ，D小于0 时，风机会发生低频振荡。

此外，上述分析同样适用于传统VSG 并网系统，其中ΔTw=0，图3（d）给出了对应的合成阻尼转矩分量。可以发现，传统VSG 并网模型由于忽略机侧和直流侧动态会产生较大误差，其相关分析应用于直驱风机时，可能会得到不正确的稳定结论。

2.2 风机参数对低频振荡的影响规律

根据2.1 节可知，3 个等效转矩的阻尼分量反映了风机不同环节对低频振荡的作用机理。因此，可进一步通过研究参数变化对3 个等效转矩的影响，进而分析参数对低频振荡的影响规律。

首先，为了研究线路参数的影响，附录A 图A1（a）给出了网侧电网电感Lg对阻尼转矩分量的影响。可以发现，随着Lg的增加，ΔTw，D及ΔTE，D的幅值均减小，即降低了ΔTw及ΔTE的负阻尼效应，系统低频振荡抑制能力得到提升。随着Dg的增加，如附录A 图A1（b）所示，系统合成转矩阻尼分量ΔTΣ，D也随Dg的增大而增大。因此，增大Dg可提高系统低频正阻尼转矩。而随着机侧发电机转子惯量Js的增加，如附录A 图A1（c）所示，低频段的ΔTw，D幅值随之减小，即降低了ΔTw的负阻尼效应，提高了风机低频振荡的抑制能力。

此外，附录A 图A1（d）至（e）给出了机侧和网侧外环积分系数Ksi及Kgi对风机阻尼转矩的影响。可以发现，Ksi的增大降低了机侧负阻尼转矩ΔTw，D，Kgi的增大降低了网侧电磁负阻尼转矩ΔTE，D，都有效提高了风机的低频稳定性。

进一步，附录A 表A1 总结了不同参数对直驱风机低频振荡的影响规律。结合附录A 图A1 可知，尽管不同参数会对各等效转矩的阻尼分量产生一定影响，但系统参数主要是通过改变机侧等效转矩ΔTw的负阻尼和网侧阻尼转矩ΔTD的正阻尼来影响系统阻尼特性，而对网侧电磁转矩ΔTE影响较小，且机侧负阻尼转矩是风机弱阻尼的主要原因。因此，需要采取稳定措施来降低机侧的负阻尼效应，进而防止低频振荡的发生。而由附录A 表A1 可知，增大线路电感、机侧转子惯量及外环积分系数均可降低风机低频段的负阻尼效应。但调节线路电感Lg及机侧转子惯量Js都需要改变原有系统的固有物理参数，使系统偏离初始设计预期；而调节外环控制参数可能会使外环跟踪性能偏离预期，引发新的稳定问题。因此，相关稳定控制也亟须进一步研究。

3 DCC

3.1 DCC 设计

基于第2 章的风机低频振荡机理分析可知，负阻尼转矩主要来源于机侧等效转矩ΔTw。为此，本节针对功率跟踪回路设计了DCC，通过相位校正减小机侧动态的负阻尼效应，提高风机的低频振荡抑制能力，其控制原理可表示为：

式中：fDCC(s)为阻尼补偿传递函数；Tlead、Tlag分别为超前和滞后时间常数。

根据式（7）可得到图4（a）所示DCC 框图，其通过在网侧同步环的功率跟踪回路中增加阻尼补偿环节fDCC(s)来改善机侧动态的低频阻尼特性，进而降低机侧动态的负阻尼效应。

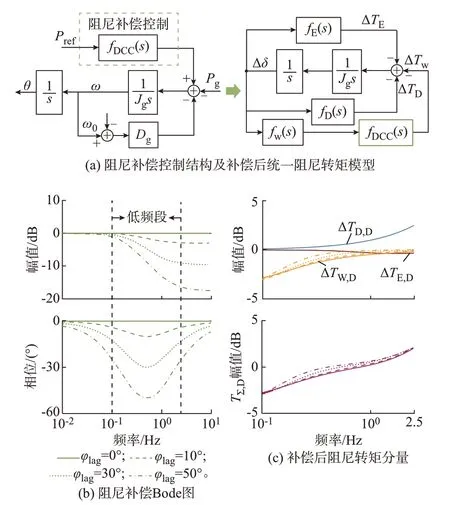
图4 DCC 框图、Bode 图及阻尼转矩分量Fig.4 Block diagram, Bode diagrams and damping torque components of DCC

3.2 DCC 参数整定

阻尼补偿环节fDCC(s)的本质为超前滞后矫正器，其最大相位滞后角φlag可由式（8）计算（原理参考附录C）。

最大相位滞后处的频率flag可表示为：

根据式（8）和式（9）可知，通过整定φlag和flag可实现对时间常数Tlead、Tlag的整定。其中，φlag可根据阻尼补偿需求进行整定，φlag越大则在flag的阻尼补偿越多，但同时也要避免φlag过大导致的超低频段响应变化。而flag可通过使其等于fLFO来获取较好的低频振荡抑制效果。图4（b）给出了不同φlag下（flag=fLFO=0.5 Hz）的fDCC(s) Bode 图，其在f＜0.01 Hz 的超低频段响应近似为单位增益。因此，对风机系统稳态影响可近似忽略。而随着φlag的增大，fDCC(s)在flag附近的滞后相位增大。图4（c）给出了风机系统的阻尼转矩分量，图中实线、虚线、点线、点划线分别表示φlag为0°、10°、30°、50°时的情况。可以发现，低频段的ΔTw，D随φlag的增大而减小，降低了机侧负阻尼效应，系统合成阻尼转矩ΔTΣ，D也随φlag的增大而增大，提高了风机低频振荡抑制能力。此外，flag的整定需要获取风机低频振荡频率fLFO，若按附录B 的方法进行获取，其模型复杂且需要详细参数，整定过程繁琐。为此，可基于三阶简化模型近似获取fLFO，实现参数的快速整定（具体可参考附录C）。

目前，尚缺乏考虑机侧动态的阻尼控制。例如，文献［29］基于序阻抗分析提出了阻抗重塑控制器，主要是抑制VSG 与串补电容耦合引起的次同步振荡。针对低频振荡问题的阻尼控制往往通过增加正阻尼转矩来抑制低频振荡，但这会受到自身能量和电压/电流应力的约束，如阻尼系数过大时需要更大的能量提供一次调频，但受限于风机最大功率限制会增加频率跌落下的暂态失稳风险［30-31］；通过外环虚拟励磁改变电压幅值提供阻尼会因有限的过电压能力而受到制约。另外，上述控制设计也均未考虑机侧动态的影响，其应用于虚拟同步直驱风机的控制效果也不理想。因此，在上述增强阻尼控制的基础上，有必要从源头减少机侧动态的额外负阻尼转矩，从而避免大电网下交互引发的低频振荡。但值得注意的是，本文的阻尼控制主要削弱机侧动态的负阻尼效应，而现有的阻尼增强控制则是提供正阻尼转矩，两者针对不同环节来优化系统阻尼特性。因此，两者也可一起使用来提升虚拟同步直驱风机的低频稳定性。不同阻尼控制的对比也将在算例中详细分析。

4 仿真算例验证

本章首先基于MATLAB/Simulink 搭建如图1所示风机并网系统仿真模型，在不同运行工况下验证了风机系统阻尼转矩分析的准确性，并验证了DCC 的有效性。其次，简要分析了所提控制在多机系统的适用性，并搭建多机仿真进行验证。

4.1 低频振荡分析验证

为了验证本文统一阻尼转矩线性化模型的正确性，设置系统运行工况如下：在5 s 时，公共连接点（PCC）接入0.1 p.u.负荷，并于5.1 s 恢复，附录D 图D1 给出了网侧频率及功率输出的仿真波形。根据图D1 可知，本文的线性化模型与电磁暂态模型曲线基本吻合，验证了线性化模型的正确性。

为了验证2.1 节风机系统阻尼转矩及低频振荡分析的有效性，本节搭建如图1 所示仿真模型，具体参数见附录D 表D1。假设t=2 s 时，PCC 接入0.1 p.u.的负荷，并于2.1 s 恢复，图5（a）给出了不同系统工况下的时域仿真波形。根据2.1 节的阻尼转矩计算步骤，可分别计算图5（a）中的情形1 至情形3的合成阻尼转矩分量ΔTΣ，D，其分别小于0、等于0、大于0。由图5（a）可知，情形1 波形由于缺少足够的阻尼转矩，发生2.082 Hz 的低频振荡，其振荡频率fLFO与附录B 方法计算得到的fLFO，clu=2.084 Hz 相近，这也验证了附录B 低频振荡频率计算的准确性。而情形2 波形由于处于临界阻尼而发生等幅振荡，情形3 由于具有足够阻尼转矩而可使系统维持稳定运行。基于情形1 至3 的分析及时域仿真，有效验证了2.1 节理论分析的准确性。

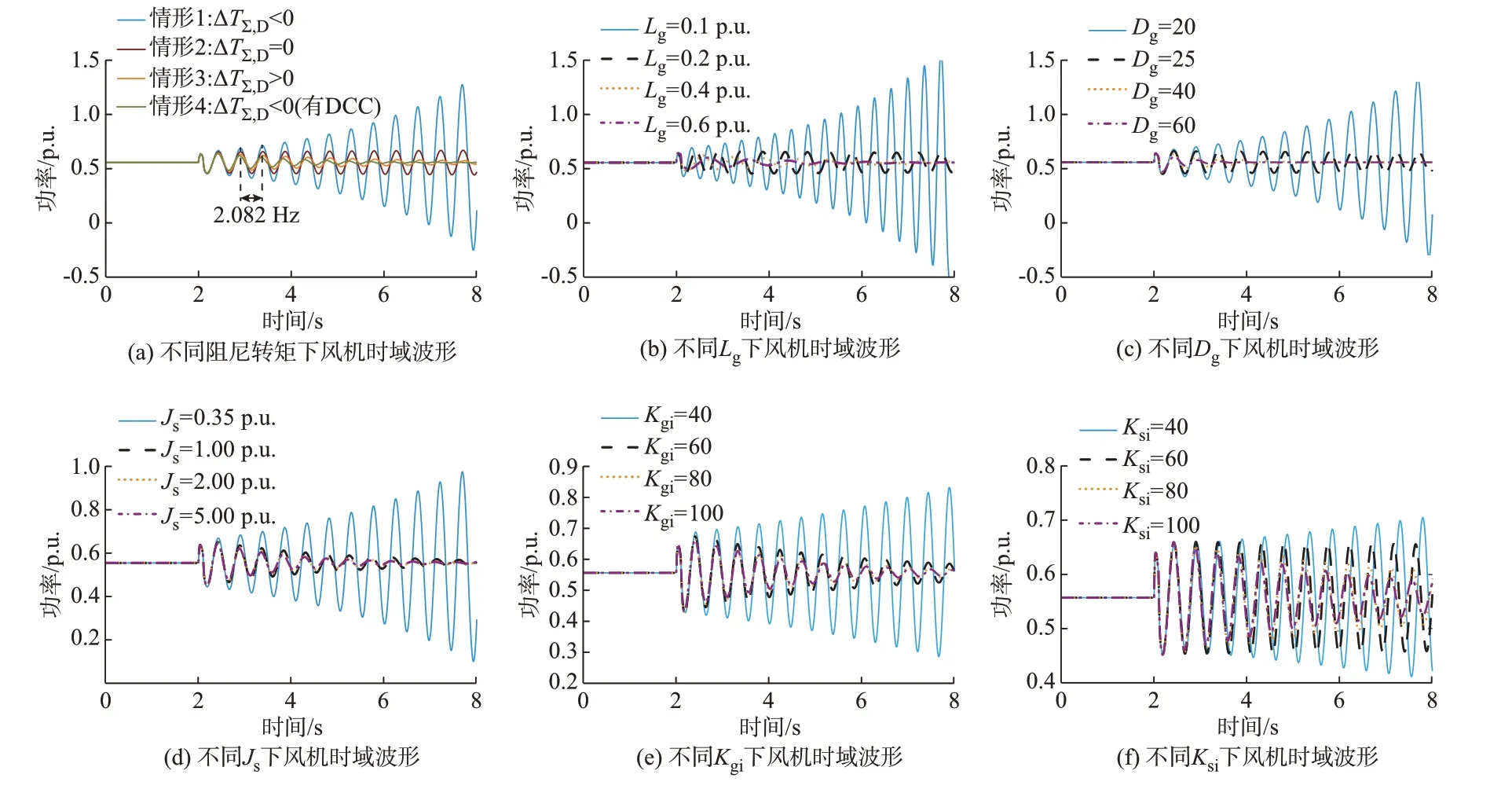
图5 风机系统时域仿真结果Fig.5 Time-domain simulation results of wind turbine system

为了验证2.2 节系统参数对低频振荡影响的正确性，图5（b）至（f）给出了不同参数下风机系统的时域仿真波形。由图5（b）可知，随着电网阻抗的增加，风机系统的低频振荡逐渐得到抑制，验证了附录A 图A1（a）所示阻尼转矩分析。由图5（c）可知，随着网侧阻尼系数的增加，系统由不稳定趋于稳定，稳定恢复速率也得到提升，验证了图A1（b）所示阻尼转矩分析。而由图5（d）可知，增大机侧发电机转子惯量Js也可有效增强风机对低频振荡的抑制能力，验证了图A1（c）所示阻尼转矩分析。而通过图5（e）和（f）可知，提高外环积分系数Kgi和Ksi也可有效提升风机低频稳定性，验证了图A1（d）至（e）的阻尼转矩分析。

4.2 DCC 验证

为了验证3.1 节所提DCC 的有效性，图5（a）给出了基于风机并网系统的时域仿真波形。其中，情形4 在情形1 的基础上增加了DCC，基于3.2 节整定DCC 参数，其中简化模型得到的振荡频率fLFO，DCC=2.212 Hz，与仿真振荡频率相近。由图5（a）可知，基于简化模型整定的DCC 可有效提高风机低频阻尼能力，并维持风机系统稳定运行。

为了验证3.2 节不同阻尼控制分析的正确性，分别搭建了传统VSG 系统及虚拟同步直驱风机系统的仿真模型，并在2 s 给予与前文一样的负荷扰动，系统时域波形如附录D 图D2 所示。其中，在传统VSG 系统中，如图D2（a）所示，无附加控制的情形1 可维持扰动下的稳定运行，而情形2 则采用了文献［32］的虚拟电力系统稳定器（virtual power system stabilizer，VPSS），且相较情形1 更快地进入稳态，有效改善了系统阻尼特性。而在直驱风机并网系统中，如图D2（b）所示，无附加控制的情形3 和具有VPSS 控制的情形4 均发生了低频振荡，验证了2.2 节传统VSG 系统的分析结论应用于直驱风机时可能得到错误的稳定结论。同时，也验证了3.2节未考虑机侧耦合的阻尼控制往往难以保障风机的低频稳定性。进一步，根据图D2（b）可知，情形5 采用本文的DCC 后可有效抑制低频振荡，而情形6 同时采用阻尼补偿和VPSS 控制后，系统阻尼特性相较情形5 进一步提升，有效验证了3.2 节阻尼控制分析的正确性。

4.3 多机系统的适用性验证

对于多机系统来说，系统存在多个振荡模式，但每个振荡模态一般是由一个机组（机群）相对其他机组的戴维南等效电压源或两个机组（机群）所主导的，即任一振荡模态可用等效的两机系统或单机无穷大系统进行近似分析。设备自身特性本文已展开了详细的分析，而为了进一步分析多机下设备间的交互特性，需要建立相应的多机分析模型。为简化多机下的分析难度，考虑n台同步机（二阶简化模型）及m台虚拟同步直驱风机的系统（附录C 三阶简化模型），并考虑网络动态可得到：

式中：A为状态矩阵；X为状态变量；Δδsg和Δωsg分别为同步机的相位及频率的扰动量；Δδvsg为风机的相位扰动量；Δωvsg和Δωs分别为风机网侧和机侧频率的扰动量；Knn、Knm、Kmn、Kmm、Ksmn、Ksmm为设备与网络交互动态的表达式，描述了设备与网络的交互动态；Dnn、Dmm、Dsmm为设备阻尼系数动态的表达式，描述了设备阻尼系数的动态；Rmm为风机机侧动态影响的表达式，描述了风机机侧动态对系统稳定特性的影响。

进而，可得到简化系统的状态矩阵A并计算系统特征根。然后，基于相关比方法判断系统低频模态，并通过参与因子分析各个机组的交互动态，找到主导模态（阻尼比最弱）影响因子最大的机组，将其他机组进行戴维南等值，等效为单机无穷大系统进行控制整定。整定后再次计算主导模态重复上述步骤，直到系统主导模态的阻尼比满足要求（整定流程可参考附录C 图C3）。而值得注意的是，当考虑更详细模型分析多机系统的低频动态时，只需对式（10）增补相应动态的状态变量，进而可考虑该动态分析系统的低频特性。

为了验证上述简化模型的准确性，如附录D 图D3 所示，分析IEEE 标准3 机9 节点系统（包含2 台虚拟同步直驱风机及1 台同步机）的机电振荡模式可以发现，系统包含2 个机电振荡模式，分别由同步机和VSG2 主导。对比可以发现，上述简化模型可近似逼近详细模型的振荡模式，其中，简化的同步机由于忽略了励磁控制等环节的正阻尼，其阻尼比相较详细模型更低；而简化的VSG 由于忽略了外环等环节动态的负阻尼效应，其阻尼比相较详细模型反而得以提高。因此，基于上文的简化模型可简单分析系统的机电振荡模式，而考虑更详细的模型也能更准确地刻画系统的低频动态。

进一步，为了说明所提控制在多机系统的有效性，如附录D 图D4 所示，搭建了新英格兰39 节点系统，额定频率为60 Hz，并包含新能源为主的10 台发电机：5 台跟网型直驱风机，3 台虚拟同步直驱风机，2 台汽轮机。负荷考虑为恒功率负荷；系统其余参数见文献［33］。

首先，为了分析机组间的交互影响，机组G3 和G7 采用完全一致的控制参数（单机并网时具有相同的振荡模式），并计算系统的机电振荡模式如附录D表D2 所示（跟网型机组视为功率输出恒定折算到网络）。可以发现，最弱振荡模式已发生失稳，该模式的参与因子分析如附录D 图D5（a）所示。由图可知，G3 与G7 呈强交互（两机摇摆主导）特性，两者均对该模式呈高参与性，且系统阻尼比较低；而调整G3 控制参数后，G7 的机电振荡模式如图D5（b）所示，G3 与G7 交互明显变弱，G7 自身主导了该振荡模式（等效单机无穷大摇摆主导），且阻尼比得到提高。

为进一步验证，在2 s 时，节点8 接入0.2 p.u.的负荷，并于2.1 s 恢复，仿真结果如图6（a）所示。可以发现，当G3 和G7 强交互时，虚拟同步直驱风机由于强烈的交互动态，引发了系统低频振荡；而跟网型直驱风机由于具有较快的响应速度，扰动后受其他机组影响发生功率振荡，但功率波动很小，即短时间内近似呈恒功率特性；而同步机也同样发生失稳。相比之下，调节G3 控制参数，使G3 和G7 呈弱交互特性，可有效降低系统的低频振荡风险。

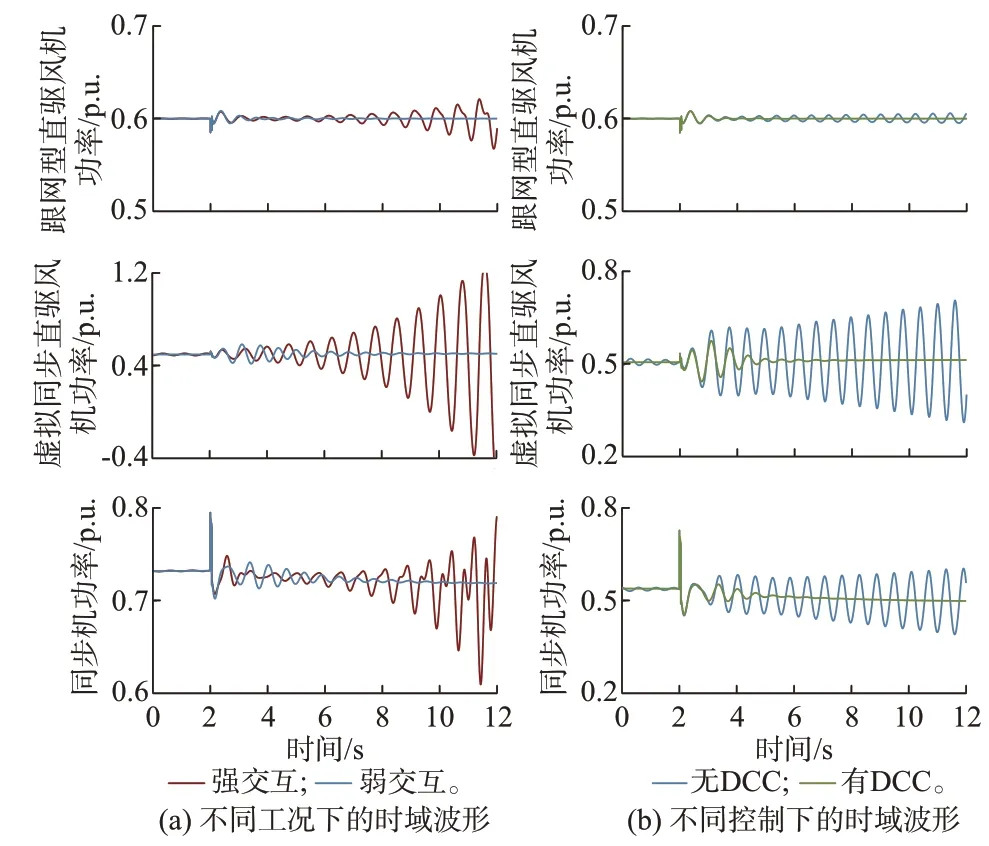
图6 多机系统时域仿真结果Fig.6 Time-domain simulation results of multi-machine system

进一步验证所提控制在多机系统中的适用性，在机组间交互较弱且系统阻尼不足时，图6（b）给出了同样负荷扰动下的仿真结果。可以发现，当系统阻尼转矩不足时会引发系统的低频振荡。相比之下，按附录C 图C3 所示的流程整定风机的DCC（或同步机的电力系统稳定控制），可有效抑制设备自身的负阻尼效应，提高系统稳定性。

5 结语

针对虚拟同步直驱风机低频振荡机理不清晰的问题，本文考虑直流侧及机侧动态，建立了风机的统一阻尼转矩模型，基于阻尼转矩法揭示了风机的低频振荡机理，并提出了降低机侧负阻尼效应的DCC，得到结论如下：

1）传统VSG 并网模型忽略了机侧和直流侧动态，相关研究应用于直驱风机时可能会得到不正确的稳定结论。而基于所提统一阻尼转矩模型可准确分析直驱风机或传统VSG 并网系统，并揭示各环节动态的影响与交互。

2）基于阻尼转矩法分析风机低频动态可以发现，机侧转子动态通过功率跟踪与网侧虚拟同步控制动态耦合，并在低频段提供负阻尼转矩，是风机低频振荡的主要原因；网侧线路和内外环动态提供弱负阻尼转矩；阻尼系数则直接提供低频段的正阻尼转矩，3 个等效转矩共同主导了风机的低频特性，当合成阻尼转矩小于0 时风机会发生低频振荡。

3）传统阻尼控制由于未考虑机侧影响往往效果不佳，本文所提DCC 可有效抑制机侧耦合带来的负阻尼影响，与传统阻尼控制配合使用可以更有效地抑制风机的低频振荡。

如何考虑多机设备强交互及控制耦合，分析风机等设备的低频振荡特性，是未来的工作之一。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。