基于二极管分散整流的风电机组中压直流汇集直接送出系统
2024-02-20杨明扬张建文
杨明扬,王 晗,蔡 旭,张建文
(上海交通大学电子信息与电气工程学院,上海市 200240)
0 引言
中国东南沿海地区(广东、福建等),在离岸距离100 km 以内仍有大量海域适合海上风电开发。上述海域风能资源充足,但海水较深,美国和欧洲也有大片类似海域[1]。对于海上风电接入,传统的高压交流输电或高压直流输电需建设海上升压或换流平台,而在深水区建设海上平台成本较高。风电机组中压直流汇集直接送出技术能省去海上升压及换流站[2]。该方案采用直流输出型风电机组将风能转换为中压直流电,再经过中压直流海缆直接接入岸上换流站。研究表明,对于中远距离、中等规模海上风电,该方案能大幅降低总体投资成本[3-4],是多电压等级全直流风电场技术发展的有益补充。
直流输出型风电机组是实现风场电能直流汇集的关键,它将交流发电机发出的交流电经AC/DC电力变换和升压后实现中压直流输出。根据发电机的类型和直流升压方式,直流输出型风电机组的拓扑可分为有变压器式和无变压器式。无变压器式直流输出型风电机组的关键是高变比AC/DC 变流器的实现,该方案对发电机绝缘提出更高要求[5-6]。考虑机组绝缘以及风电变流技术等因素,采用AC/DC 与DC/DC 级联变换的中压直流风电机组当下更具可行性。在交流变压器升压拓扑中,最典型的变流器结构是AC/DC 整流器和升压型DC/DC 变流器的级联。这种方案可以保留常规风电变流器的机侧变换器不变,无须改变其电路和控制方法[7]。该方案的技术关键是高变比升压DC/DC 变流器的实现方式,它要具备在发电机和直流电网之间提供电气隔离以及将电压升至中压的功能。一般地,隔离型DC/DC 变流器由逆变电路、中频变压器和整流电路构成。为了规避大功率中频隔离变压器在设计和制造方面存在技术瓶颈[8-9],结合二极管整流器大容量、低成本、高可靠等优势,文献[10]提出一种基于二极管整流器的直流输出型风电机组,该机组采用工频变压器,有利于大容量化实现。
多端直流系统的保护技术是另一关键问题,主要技术难点包括故障线路的可靠识别和快速隔离[11-12]。配置直流断路器是未来直流系统最为理想的故障隔离措施,然而对直流断路器的动作速度和切除容量提出了很高的要求[13-14]。在直流断路器成本高、工程应用尚不成熟的背景下,利用换流器自身动作实现直流故障电流的清除是另一种较为经济、有效的故障隔离方法[15-16]。直流故障保护的另一关键在于可靠识别故障线路,减小故障停电范围,提高直流系统供电可靠性,如何不依靠通信实现精准的故障定位也是当下研究热点[17-18]。
文献[10]所提直流输出型风电机组的直流输出侧无滤波电容器,通过变流器闭锁即可清除直流短路故障电流,用其构建中压直流汇集直接送出系统,有望省去直流断路器,进一步提升经济优势。与海上风电场经二极管集中整流送出系统相比[19-21],该系统将二极管分散布置于每台风电机组中,省去海上换流站。该系统在多机组网控制与故障保护方面的潜在优势有待进一步研究。
本文主要工作如下:1)研究分散式二极管整流器直流输出电流纹波交错控制,降低直流输电电流和电压纹波;2)基于状态空间建模和小信号分析,研究控制系统全功率段稳定性和稳定性优化提升措施;3)针对直流内网多种故障位置,研究无通信、无直流断路器故障定位与隔离方法。
1 系统拓扑与控制架构
基于二极管整流器的直流输出型风电机组,经负荷开关接入中压直流汇集网,无须升压直接通过中压直流海缆接入岸上换流站,岸上换流站采用模块化多电平换流器(MMC),系统拓扑结构如图1(a)所示。二极管整流的直流风电机组具有直流侧短路故障阻断能力,组成电网是否需要设置直流断路器取决于岸上MMC 的直流阻断能力,如采用半桥型MMC 换流器,需要在送出电缆的末端配置直流断路器。另一种创新的设想是在电缆末端设置一个用于限定电流单向流动的二极管半导体装置,目前尚无应用的案例。更加现实的方案是采用具有直流阻断能力的半桥-全桥混合型MMC,这种混合换流器已有成功运行的案例。本文以设置二极管单向电流限定装置为例,展开研究工作。与海上风电场经二极管集中整流送出系统相比,二极管整流器被分散布置到每台风电机组中。因此,将该系统命名为基于二极管分散整流的风电机组中压直流汇集直接送出并网系统。
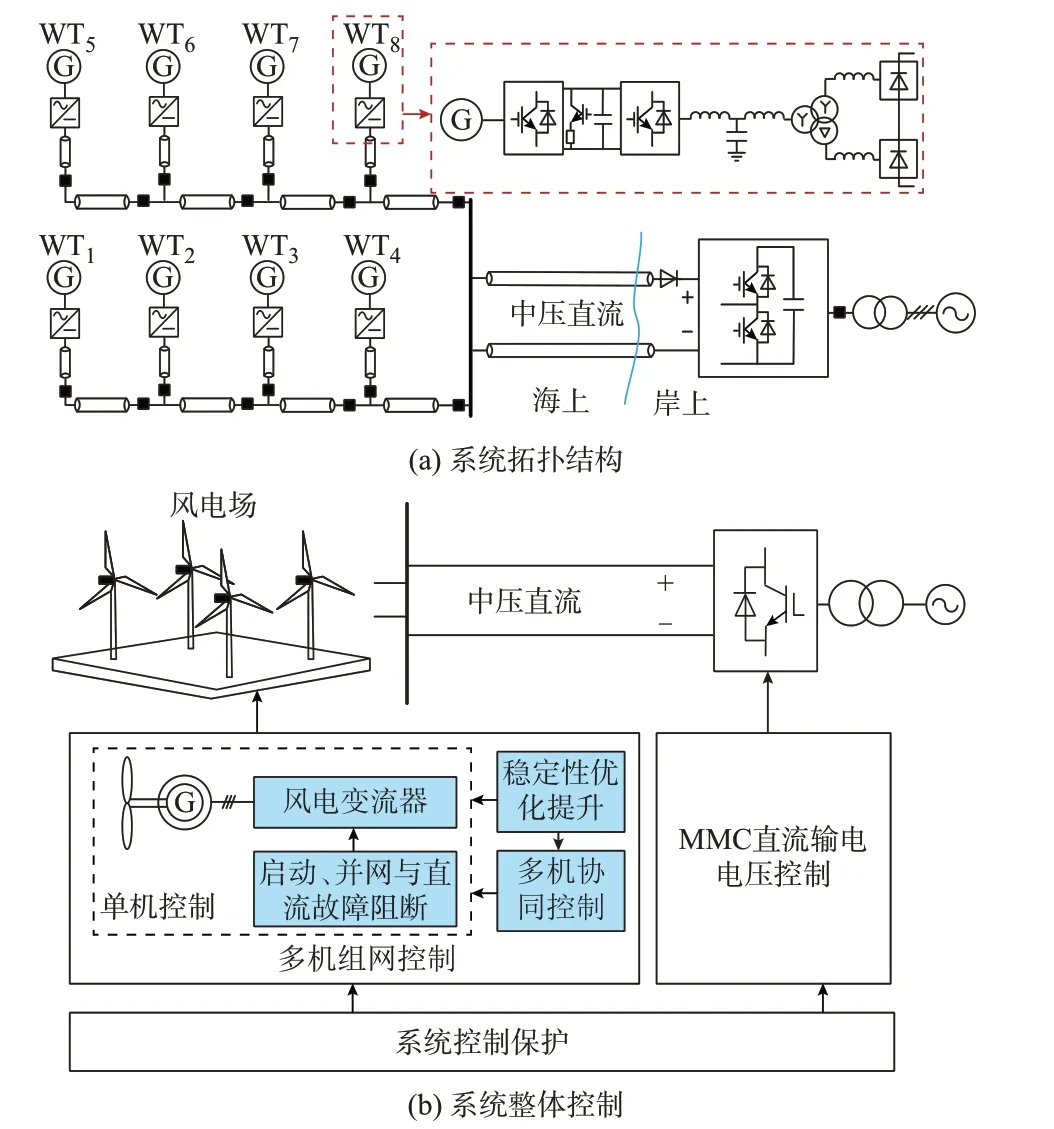
图1 基于二极管分散整流的风电中压直流汇集送出系统的拓扑与控制Fig.1 Topology and control of medium-voltage DC collection and transmission system for wind power based on distributed diode rectifiers
系统基本控制架构如图1(b)所示。图1(b)中,岸上MMC 采用常规跟网型控制策略,控制直流输电电压恒定。文献[10]提出的二极管整流型直流风电机组能实现单机启动、并网和直流侧短路故障阻断。多机协同控制环节实现输电电流纹波抑制;稳定性优化提升环节实现多机协同算法下的机组全功率段小信号稳定性提升;系统控制保护实现岸上电网故障穿越、直流汇集与送出线路的短路故障定位与隔离等,关于系统控制保护,本文主要探讨直流故障保护。
针对多机组网与保护,提出二极管整流型直流风电机组的网侧变换器综合控制框图,如图2 所示,机侧整流器控制与传统全功率风电机组保持一致。
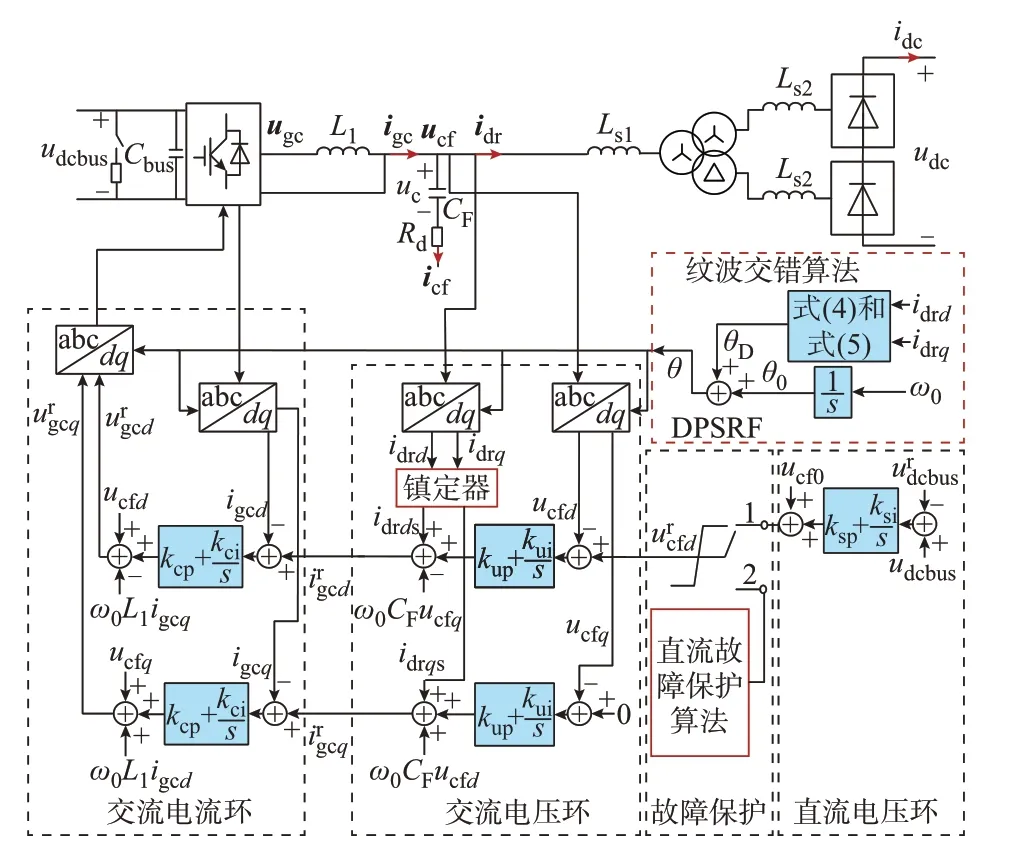
图2 直流机组网侧变换器综合控制框图Fig.2 Integrated control diagram of grid-side converter for wind turbines
图中:网侧变换器经LC 滤波器接入二极管整流器;Ls1、Ls2分别为整流变低压绕组漏感、高压绕组漏感;Cbus为逆变器直流侧电容;交流滤波电路由逆变电感L1、滤波电容CF以及阻尼电阻Rd构成;uc为滤波电容CF上的电压;ugc、igc、ucf、icf、idr分别为逆变电压、电流矢量、交流滤波电容支路电压、电流矢量和整流变压器一次侧电流矢量;udcbus表示直流母线电压;udc和idc分别为直流并网电压和电流;ucfd、igcd、idrd分别为ucf、igc、idr的d轴分量;ucfq、igcq、idrq分别为ucf、igc、idr的q轴分量;和分别为udcbus和ugc的d轴分量ugcd、ugcq、igcq、ucfd、igcd的参考值;idrqs、idrds分别为idrq、idrd经镇定得到的变量;ucf0为交流电压参考幅值的固定数值部分,设置低于二极管整流器的整流阈值;kcp和kci分别为逆变电流内环比例-积分(PI)控制器的比例、积分系数;kup和kui分别为交流电压环PI 控制器的比例、积分系数;ksp和ksi分别为直流电压环PI 控制器的比例、积分系数;ω0为固定角频率;θ0为ω0积分得到的角度,θ0叠加动态移相角θD得到动态移相参考坐标系(dynamic phase shifted reference frame,DPSRF)的参考角度θ。
网侧变换器的基本控制结构从内到外依次包括交流电流环、交流电压环和直流电压环,分别控制逆变电流、交流侧滤波电容电压和直流母线电压,基本控制原理参考文献[10],本文不再赘述。纹波交错算法输出控制系统参考坐标系,实现多台机组的分散式二极管整流器整流电压矢量和输出电流纹波的交错分布。交流电压环路的前馈通路中集成镇定环节,用于优化提升风电机组网侧变换器全功率段控制稳定性。直流短路故障发生后,故障保护模块的选择开关切换到2,通过机组扰动注入时序与继电保护逻辑配合,实现无通信系统、无直流断路器的直流短路故障定位、隔离。
2 分散式二极管整流器输出电流纹波交错控制
文献[10]提出的直流机组单机运行控制,当多机组网运行时,如果多台风电机组的二极管整流输出电流纹波同相叠加,会增大风场直流送出电流的脉动。可协同多机输出电流的纹波交错叠加,有效抑制风场送出电流的脉动。为此,本文将文献[10]采用的固定参考坐标系改进为图2 中的DPSRF。
十二脉波二极管整流器的直流侧电流纹波频率是交流输入电流频率的12 倍,如果能实现多机二极管整流器交流输入电流矢量在π/6 相位范围内的均匀移相,就可以实现多机二极管整流器直流输出电流纹波的交错分布。为此,通过控制将各机组二极管整流器输入电流矢量idr定向到移相参考坐标系(phase shifted reference frame,PSRF)的d轴上,实现二极管整流输入电流矢量的均匀移相。
均匀移相的PSRF 用式(1)表示。
式中:j为风电机组或对应二极管整流器的编号;NWT表示并网风电机组数量;θps为移相坐标系的参考角度。多机的θ0需要同步,后续阐述同步方式。
如果第j台机组中二极管整流器的输入电流矢量idrj定向到PSRF 的d轴,idrj对应的a 相电流idraj可采用式(2)表示。相应地,第j台机组二极管整流器的整流电压矢量ucfj对应的a 相电压ucfaj可用式(3)表示。
式中:idrj为idrj的幅值;ucfj为ucfj的幅值;φj为第j台机组中二极管整流器的基波功率因数角。
反之,如果分散式二极管整流器的整流电压矢量ucfj符合式(3),其交流输入电流矢量将自动定向到PSRF 的d轴上。由于机组网侧变换器采用二极管整流器输入电压的d轴定向控制[10],在分散式二极管整流器参数和功率完全相同的条件下,若将文献[10]中的固定参考坐标系改为PSRF 就能实现输出电流纹波交错。其原因如下:此条件下多机二极管整流器的输入电压均匀移相,二极管整流器实际功率因数一致,多机二极管整流器输入电流矢量同步偏移,但实际应用中,多机二极管整流器参数和功率存在差异。因此,需要根据二极管整流器的实时功率因数动态调整移相角,补偿上述差异引起的整流电流矢量间不一致偏移。基于上述考虑,在PSRF 的基础上进一步提出DPSRF,将其作为控制系统的参考坐标系,DPSRF 用式(4)描述。
式中:φjf=φj/(TPSs+1),时间常数为TPS的一阶滤波器用于抑制φj的扰动,φj的计算方法见式(5)。
式中:idrdj和idrqj分别为idrj的d、q轴分量。
分散式二极管整流器输出电流的纹波交错控制原理进一步如附录A 图A1 所示。图中:二极管整流器的编号为0 至NWT。以DPSRF 的第j个参考坐标系统为例,如果采用图2 所示控制算法,将第j个整流电压矢量ucfj定向在DPSRF 的d轴上,第j个整流变压器输入电流矢量idrj则会被定向在PSRF 的第j个d轴上,实现整流电流矢量的交错分布,电压、电流矢量关系如附录A 图A1 所示。
利用所提电流纹波交错控制,分散式二极管整流器的输入电流移相角度为π/(6NWT)。因此,分散式二极管整流器可以等效为12NWT脉波整流器。其中,NWT根据实际并网风电机组数量确定。当风场仅有两台风电机组并网时,两台机组的十二脉波二极管整流器输入电流移相π/12,并联等效为二十四脉波整流器;当3 台风电机组并网时,3 台十二脉波二极管整流器输入电流移相π/18,并联等效为三十六脉波整流器;以此类推,NWT台分散式二极管整流器并联等效为12NWT脉波整流器。如果不协同风电机组输出电流,分散式二极管整流器输出电流可能同相。此时,分布式二极管整流器等效为一个十二脉波二极管整流器。显然,相较于十二脉波二极管整流器,更多脉波数整流器的输出电流纹波较小,并且NWT越大,纹波抑制优势越明显。
电流纹波交错算法的实现关键在于确保多机DPSRF 中的θ0同步,本文考虑采用如下的工程实施方案:每台风电机组配置一套具有秒脉冲(PPS)输出功能的GPS 或北斗模块;由PPS 信号直接产生同步信号,该同步信号不会产生累计误差。考虑从天线安装位置到同步信号接收装置之间的传输延迟,该方案可以确保延迟时间在50 μs 以内,足够纹波交错算法的实施。注意:纹波交错算法只是系统优化运行算法,其有效运行与否不会影响系统的正常工作。即使控制系统的参考坐标系输出的角度达不到期望的最优角度,也不会影响系统的其他必要功能。
3 机组全功率段小信号稳定性分析与优化
本章将建立一种计及纹波交错算法动态移相角的直流机组网侧变流电路与控制系统数学模型,用于分析机组在不同功率输入下的稳定性。基于特征根分析辨识弱阻尼环节,并据此提出一种控制系统全局稳定性增强措施。
3.1 计及纹波交错算法动态移相角的机组网侧建模
首先,在PSRF 中建立风电机组网侧变流电路的d-q轴动态模型;接着,在DPSRF 中建立风电机组网侧控制环路的d-q轴动态模型;最后,通过旋转矩阵Trf将两者结合在一起,建立计及DPSRF 动态移相角的机组网侧变流电路与控制系统d-q模型,如图3 所示。该模型能体现纹波交错算法的动态移相角对控制系统的扰动作用。机侧功率pgen和直流母线电压参考值是模型输入。
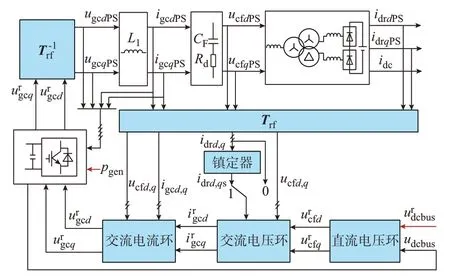
图3 计及DPSRF 的机组网侧变流电路与控制系统模型框图Fig.3 Block diagram of the model of the WT grid-side circuit and control system considering DPSRF
图3 中:旋转矩阵Trf的旋转角度取决于二极管整流器输出电流纹波交错控制算法中的动态移相角;下标dPS、qPS 分别表示相应变量在PSRF 中的d、q轴分量;ucfd,q为ucf的d、q轴分量;idrd,q和idrd,qs分别为idr的d、q轴和镇定后的分量;igcd,q为igc的d、q轴分量。
为了在PSRF 中建立二极管整流器的d-q轴动态模型,分别选取整流变压器输入电压矢量ucf和电流矢量idr在PSRF 中的d、q轴分量作为模型的输入信号和输出信号。整流变压器的输入侧电压矢量和电流矢量(ucf和idr)在PSRF 和DPSRF 下的投影关系见图4。图中:φf为PSRF 和DPSRF 之间的夹角,由式(4)决定;φ为二极管整流器的基波功率因数角;σ为ucf与PSRF 的d轴之间的夹角。
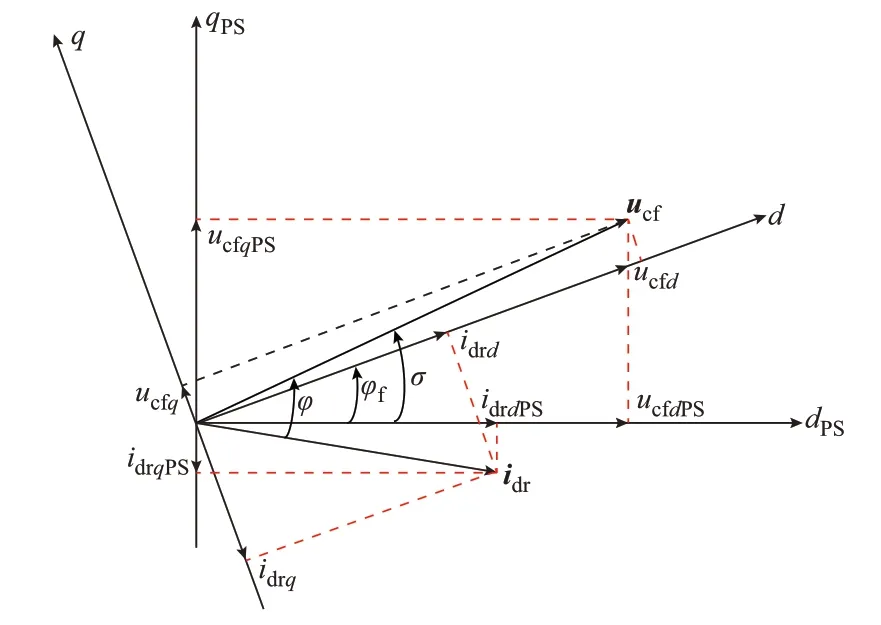
图4 PSRF 和DPSRF 下整流电压-电流矢量图Fig.4 Vectorgraph of rectified voltage-current in PSRF and DPSRF
考虑到受端换流站采用定直流电压控制,二极管整流器的直流侧可看作接恒压源。因此,二极管整流器输入-输出一阶动态模型见式(6)。
式中:nb为直流风电机组中六脉波二极管整流桥数量,由于本文采用十二脉波整流,nb为2;n为变压器比;为整流变压器低压绕组漏感Ls1和高压绕组漏感Ls2在高压侧的总等效漏感;ucf为ucf的幅值。
ucf可以用式(7)表示。
根据图4,idr的幅值idr与idr在PSRF 中的d、q分量(idrdPS,idrqPS)之间的关系可以用式(8)表示。
此外,idr的表达式如式(9)所示。
式中:μ表示二极管整流器的换相重叠角;ku由idr和idc的比值定义。
至此,式(6)所描述的微分方程和式(7)—式(9)所描述的代数方程一起构成了二极管整流器在PSRF 中的d-q轴动态模型。PSRF 下,含阻尼电阻Rd的滤波电容CF支路的d-q轴动态方程见式(10)。
滤波电感L1的动态方程如式(11)所示。
假设从风电机组机侧发出的有功功率为pgen,风电变流器直流母线电容Cbus的动态方程则可以表示为:
将图2 所示控制系统中的镇定器旁路,图3 中的开关选择到0。该条件下风电机组网侧变换器控制系统中的直流电压环、交流电压环、交流电流环可分别由式(13)—式(15)表示。
式中:igsd和igsq分别为交流电压环d轴和q轴PI 调节器中的积分项;ucsd为直流电压外环PI 调节器中的积分项;ugsd和ugsq分别为交流电流环d轴和q轴PI调节器中的积分项。
采用旋转矩阵Trf将PSRF 下的主电路动态模型和DPSRF 坐标系下的控制系统动态模型连接起来,矩阵Trf如下。
φf取决于式(4),将式(4)变形,得到其微分表达式如下。
在旋转矩阵Trf的作用下,PSRF 和DPSRF 两坐标系统中变量之间的关系可以描述如下。
最终,风电机组网侧电路的动态模型(式(6)—式(12)),镇定器旁路条件下风电机组网侧变换器控制系统的动态模型(式(13)—式(15)),以及由式(16)—式(18)所描述的坐标转换关系,三者共同构成镇定器禁用条件下风电机组直流并网系统的大信号模型。上述大信号模型的输入信号为风电机组机侧发电功率pgen和风电变流器直流母线电压的参考值udcbus;输出信号为系统的状态变量,取决于微分方程式(6)、式(10)—式(15)、式(17)等。
3.2 无镇定措施下稳定性分析
本节通过小信号模型研究镇定器旁路条件下风电机组网侧变换器控制系统的稳定性。为此,首先将图3 所示大信号模型中的开关选择到0;接着,在稳态工作点将其线性化得到小信号模型,通过小信号模型的特征值来进行稳定性分析。风电机组直流并网系统的小信号模型如下。
式中:Δx=[Δφf,Δucsd,Δigsd,Δigsq,Δugsd,Δugsq,Δudcbus,ΔigcdPS,ΔigcqPS,ΔucdPS,ΔucqPS,Δidc]T并且Δu=[Δpgen],Δ 表示相应变量的小信号分量;A和B分别为状态空间方程的状态矩阵和输入矩阵。
附录A 图A2 展示了不同有功输入条件下的系统特征值,分析模型参数见附录A 表A1。一共分析了50 个不同的功率点下的系统特征值,功率变化范围是0.02~1.0 p.u.。图A2 中箭头指向有功功率增长条件下的特征值运动方向。图A2 中所有特征值位于虚轴的左半平面,说明控制系统在所有功率点下都能稳定运行。随着有功功率的增加,系统阻尼提升。然而,当有功输入较小时,特征值λ5、λ6靠近虚轴,阻尼较弱,说明系统在轻载下的运行稳定性不强。附录A 表A2 展示了镇定器禁用条件下的参与因子分析结果,找到弱阻尼特征根的主导状态变量Δidc。
3.3 控制系统稳定性增强方法
本节通过前述弱阻尼状态变量对控制系统扰动路径进行分析,针对性给出镇定方法。式(14)所描述的交流电压环中存在与二极管整流器交流侧电流idr关联的前馈项。根据式(9)可知,二极管整流器交流侧电流idr与直流输出电流idc具有代数关系,而小信号模型中的状态变量Δidc受弱阻尼特征值λ5、λ6影响较大。因此,该前馈项可能将Δidc的弱阻尼扰动引入控制系统,降低控制系统稳定性。为了抑制该前馈项引入的扰动,采用一阶滤波器1/(Tstas+1)对其进行滤波(Tsta为滤波时间常数)。图3 中的镇定器即为该一阶滤波器,将开关置于1 时则使能该镇定器。镇定器使能条件下的交流电压环用式(20)表示。
进一步,建立镇定器使能条件下的风电机组直流并网系统的小信号模型如下。
式中:Δxsta=[Δφf,Δucsd,Δigsd,Δigsq,Δugsd,Δugsq,Δudcbus,ΔigcdPS,ΔigcqPS,ΔucdPS,ΔucqPS,Δidc,Δidrds,Δidrqs],Δu=[Δpgen];Asta和Bsta分别为状态空间方程的状态矩阵和输入矩阵。
接着,基于特征值评估镇定器使能条件下控制系统的小信号稳定性。附录A 图A3 展示了式(21)所描述小信号模型在不同有功功率输入条件下的特征值分布。与附录A 图A2 所示特征值分布相比,状态变量Δidc所对应的特征值整体向远离虚轴的方向移动,系统稳定性有效提升。
然后,对比镇定器使用前后系统最小阻尼比随有功输入变化的情况,评估镇定器对控制系统全局稳定性改善效果。附录A 图A4 描述了控制系统小信号模型的最小阻尼比与系统输入功率变化之间的关系。结果表明,当输入功率小于0.63 p.u.时,镇定器能显著改善系统稳定性。当输入功率较大时,系统最小阻尼比主要取决于附录A 图A2 和图A3 中的特征值λ3和λ4。对比发现镇定器的引入使得特征值λ3和λ4的阻尼略有所降低。这使得系统在高功率段的最小阻尼比有所降低,但仍具有较好的阻尼水平,并且输入功率越大,系统阻尼特性越好。值得注意的是,在风电机组实际运行过程中,半载和轻载工况占总运行时间较大比重,因此轻载运行稳定性极为重要。
4 直流汇集与送出线路的故障保护
本章针对塔筒电缆、直流汇集电缆、直流送出线路等不同位置线路的短路故障,制定基于机组扰动注入的故障定位策略,实现无通信依赖的直流内网故障定位与隔离。以岸上MMC 采用半桥拓扑,风场输电电缆末端配置二极管单相限流装置为例,系统中负荷开关和保护用电压、电流测量配置情况如图5 所示。图中:SP1至SP4表示风电机组塔筒电缆上负荷开关;SLP1至SLP4表示汇集电缆上负荷开关;iPk和uPk分别为机组开关的电流和电压检测量;iLPk和uLPk分别为线路开关的电流和电压检测量;k为开关编号。
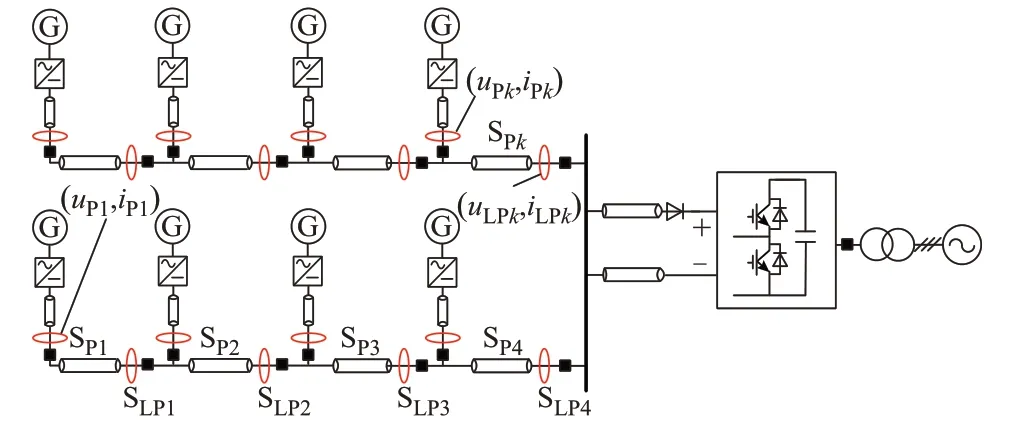
图5 继电保护系统电压、电流测量位置Fig.5 Voltage and current measurement position of relay protection system
考虑到电缆线路暂时性故障发生概率较低,为尽可能减少送电中断时间,按照非故障区域风电机组优先恢复、故障区域风电机组尽快恢复的方式,提出以下故障保护方案。以故障线路上的负荷开关作为分界点,划分故障区域与非故障区域,如附录A图A5 所示。故障发生后,定位故障点并快速隔离故障,位于非故障区域的风电机组优先恢复运行。若故障类型为暂时性故障,待故障消失后,故障区域风电机组再恢复运行。
为避免使用通信系统,制定了基于风电机组扰动注入的故障定位策略,配合继电保护逻辑实现故障定位与隔离。故障定位与隔离过程依次有:待跳闸开关选取、待跳闸开关跳闸、风电机组扰动注入、非故障线路开关重合闸等步骤,具体如下:1)直流短路发生后,整个直流场产生过流和欠压现象,风电机组的网侧变换器过流闭锁;负荷开关检测到反向过流和线路欠压后准备跳闸;2)故障电流衰减为0 后,待跳闸开关跳闸;3)负荷开关跳闸后,风电机组向故障线路注入电压或电流扰动;4)检测到电压扰动的负荷开关重合闸。综上,直流负荷开关的继电保护逻辑如附录A 图A6 所示。图中:idcmax和udcmin分别为过流和低压检测阈值,后者也是扰动电压检测阈值。
基于扰动注入的故障定位与隔离的原理如下:如果故障发生在某条馈线上,那么故障点与馈线汇集点之间的线路负荷开关会检测到电流反向和线路欠压现象,其余负荷开关则无法检测到反向电流。检测到反向电流的开关跳闸后,故障馈线上从馈线末端到故障点之间的机组仍然与故障点相连,其余机组则与故障点隔离。因此,在机组扰动注入控制下,故障区域风电机组向故障点注入电流扰动,其余风电机组向非故障线路注入电压扰动。检测到线路电压扰动的负荷开关重合闸后,非故障区域风电机组全部接入送出线路。如果故障发生在机组塔筒电缆上,故障所在机组的负荷开关跳闸,保护原理和前述馈线故障类似,不再赘述。如果故障发生在送出线路上,无负荷开关跳闸。
机组扰动注入方法为:机组正常运行时,风电机组的网侧变换器采用定直流母线电压控制,直流短路故障发生后,网侧变换器过流闭锁。闭锁信号持续一段时间,一直到直流负荷开关跳闸后,网侧变换器切换到故障电流控制模式。如果故障电流无法注入,则判定故障切除,网侧变换器切换回直流母线电压控制。如果故障电流注入成功,则判定故障未切除,考虑到暂时性故障可能,重新闭锁网侧变换器,并重复上述扰动注入步骤。累计注入3 次扰动后,若故障仍未切除,则准备停机。
综上,形成继电保护逻辑与风电机组扰动注入时序的配合方式如图6 所示。图中:tf表示故障时刻;tisc表示直流开关跳闸时刻;tci1、tci2、tci3分别表示风电机组第1 次、第2 次和第3 次扰动注入时刻;trcl表示直流开关重合闸时刻;trec表示暂时性故障恢复时刻;trth表示机组恢复运行时刻。
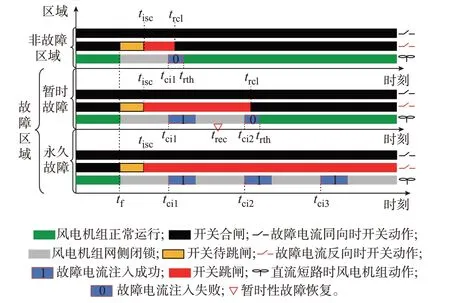
图6 继电保护与风电机组扰动注入时序配合Fig.6 Timing coordination between relay protection and wind turbine disturbance injection
接下来是机组扰动注入时序整定。由于机组网侧变换器的过流闭锁操作时间极短,并且直流风电机组无输出侧滤波电容器,故障电流衰减快,一般能在几十毫秒内衰减为0。考虑直流负荷开关的空载跳闸时间,本文将机组扰动注入时刻整定为故障发生后150 ms。150 ms 包括了故障电流衰减时间和负荷开关空载跳闸时间,如果负荷开关动作慢,则需要适当延长该整定时间。另外,计及继电保护系统扰动信号可靠检测,将扰动注入的持续时间整定为50 ms。因此,机组3 次扰动注入时刻分别整定为故障发生后150、350、550 ms,每次扰动注入持续时间为50 ms。按照上述整定时间,3 次扰动注入总时间为600 ms,小于常规机组规定的低电压穿越625 ms 时间,因此完成3 次扰动注入无需额外的机组卸荷能力。
综上,本章通过继电保护逻辑和风电机组扰动注入时序的配合,实现无直流断路器条件下,无须通信定位的直流汇集与送出线路故障保护。
5 仿真验证
在PSCAD 中按照图1(a)所示系统构建仿真模型,包含8 台8.0 MW 风电机组,仿真采用详细开关模型,仿真参数见附录A 表A1 和图A7 至图A9。仿真案例测试了输入功率阶跃变化下风电变流器的动态响应、直流输电系统的稳态特性、直流汇集线路故障保护。此外,通过平均值模型和开关详细模型的动态特性的对比,进一步验证了所提平均值模型的精确性。
5.1 并网系统功率阶跃响应
本仿真案例通过输入功率的两次阶跃变化测试风电变流系统动态特性,对比镇定器使用前后系统动态响应情况以及轻载稳定裕度。风电变流器初始功率为1.0 p.u.,在4 s 时阶跃到0.25 p.u.。接着,在4.1 s 时阶跃到0.05 p.u.。附录A 图A10 和图A11 分别为无镇定器和有镇定器条件下直流风电机组变流器功率阶跃响应波形。由图A10 和图A11 可知:不采用镇定器时,风电变流系统在功率阶跃过程中存在明显振荡,并且功率越小,振荡越难衰减,对应系统阻尼越小。使用镇定器后,系统在功率阶跃过程中不存在明显振荡,即使在轻载条件下也具有较好的动态特性,系统阻尼特性有效改善。上述结果与附录A 图A4 对镇定器使用前后系统稳定性的理论评估吻合。另外,本案例采用了平均值模型和详细开关两种模型,结果表明两种模型的时域响应结果在动态和稳态过程中均保持较好的一致性,这也证明了3.1 节和3.3 节建立的平均值模型的精确性。
5.2 直流输电系统稳态特性
本仿真案例将纹波交错算法使能前后系统的稳态特性进行对比,验证风电机组并网数量对纹波交错算法的影响。风电机组网侧变换器控制系统的参考角度分别由固定参考坐标系和动态移相参考坐标系产生。仿真中8 台风电机组并网功率依次从1.0 p.u.减少至0 p.u.,仿真结果如附录A 图A12 所示。仿真结果表明,风电机组并网数量越少,输电电压和电流纹波越小。并网风电机组数量越多,纹波交错算法在降低纹波幅值上的比较优势越明显,与第2 章原理分析一致。
5.3 直流汇集线路故障保护
本仿真案例针对馈线直流短路故障工况,对第4 章直流保护方法进行验证。仿真电路如图5 所示,开关SLP3所在汇集线路在3.5 s 时发生永久性短路故障,仿真结果如图7 所示。
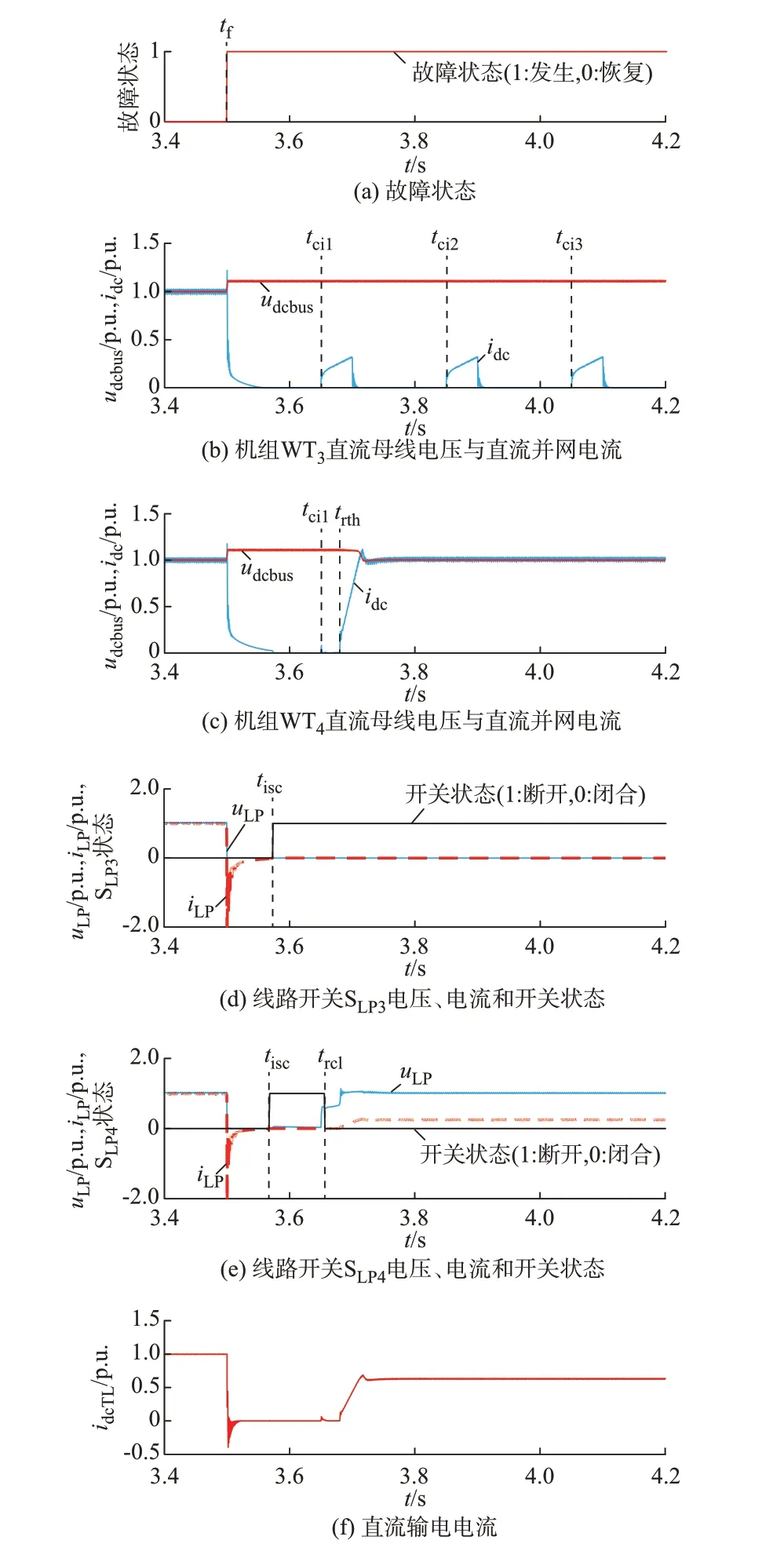
图7 直流内网永久性故障保护Fig.7 Permanent fault protection of DC internal network
图7(a)表示故障状态;图7(b)和(c)分别是机组WT3和WT4的波形,包括机组直流输出电流idc和风电变流器直流母线电压udcbus;图7(d)和(e)分别是负荷开关SLP3和SLP4的波形,包括开关所在线路的电压uLP、电流iLP以及开关状态;图7(f)是直流输电电流idcTL的波形。
故障发生前系统满载运行,馈线短路瞬间,直流汇集线路出现过流和欠压现象。直流送出线路电流在反向后迅速衰减为0,反向冲击电流幅值不超过0.5 p.u.。负荷开关SLP3和SLP4检测到反向故障电流和线路欠压信号,被选取为待跳闸开关,此时的系统状态如附录A 图A13(a)所示。图中:机组沿红色箭头方向对故障点注入故障电流,故障点与馈线汇集点之间线路电流反向,其余线路电流方向不变。因此,只有负荷开关SLP3和SLP4被选为待跳闸开关,用红色对号标识待跳闸开关。电缆、开关和风电变流器的运行状态用右上角的图例标识,其中,电缆用蓝色和黑色分别表示有压和欠压状态,负荷开关用红色和黑色表示开关打开和闭合,风电变流器的直流端口用红色短线和黑色短线分别表示直流升压变换器的闭锁和运行。
故障后极短时间内,风电机组的网侧变换器过流闭锁,负荷开关SLP3和SLP4所在线路故障电流在几十毫秒内衰减至0,上述负荷开关跳闸。图7 中跳闸时刻标记为tisc,此时系统状态如附录A 图A13(b)所示。图中:风电机组的网侧变换器闭锁,故障电流消失,SLP3和SLP4断开,其余开关保持闭合状态,汇集和送出电缆失电欠压。机组WT1、WT2和WT3与故障点保持连接,其余风电机组与故障隔离。
接下来是风电机组的扰动注入。第1 次扰动注入时刻为3.65 s,图7 中将该时刻标记为tci1。包括机组WT4等与故障点隔离的风电机组,给线路注入扰动电压,机组WT1、WT2和WT3则向故障点注入扰动电流。此时的系统状态如附录A 图A13(c)所示。图中:风电机组在非故障馈线和故障馈线汇集点到故障点之间的汇集线路上建立了扰动电压,其余线路保持欠压状态。
负荷开关SLP4检测到线路扰动电压信号,重新合闸,图7 中将重合闸时刻标记为trcl。成功在线路上建立扰动电压的机组判定故障切除,恢复运行;其余机组在3.85 s 和4.05 s 又注入两次持续50 ms 的扰动,但均无法建立线路扰动电压。因此,判定故障为永久性且无法切除,准备停机,此时的系统状态如附录A 图A13(d)所示。图中:负荷开关SLP3将故障线路切除,接入送出线路的风电机组恢复运行,其余机组准备停机。仿真结果表明,利用所制定直流故障保护方法,能有效实现直流汇集系统无通信故障定位和无直流断路器故障保护。
6 实验验证
在基于RT-LAB 实时仿真器和F28335 控制器的半实物仿真平台上搭建机组仿真模型,对镇定器禁用和使能条件下系统动态特性进行比较,实验平台如附录A 图A14 所示,机组参数见表A1,RTLAB 仿真步长为10 μs,F28335 控制器采样周期为50 μs。
实验中,机组功率从1.0 p.u.阶跃到0.25 p.u.,无镇定器和有镇定器条件下风电变流系统的实验波形比较如图8 所示。图中包括:二极管整流器交流侧a 相输入电流idra和输入电压ucfa、直流母线电压udcbus和二极管整流器直流输出电流idc。实验结果表明,针对机组输出功率阶跃变小过程,不采用镇定器时二极管输出电流存在明显振荡,说明机组轻载稳定裕度较小。而采用镇定器能有效改善系统动态特性,系统稳定性提升。实验结果与第3 章理论分析及5.1 节仿真结果吻合。
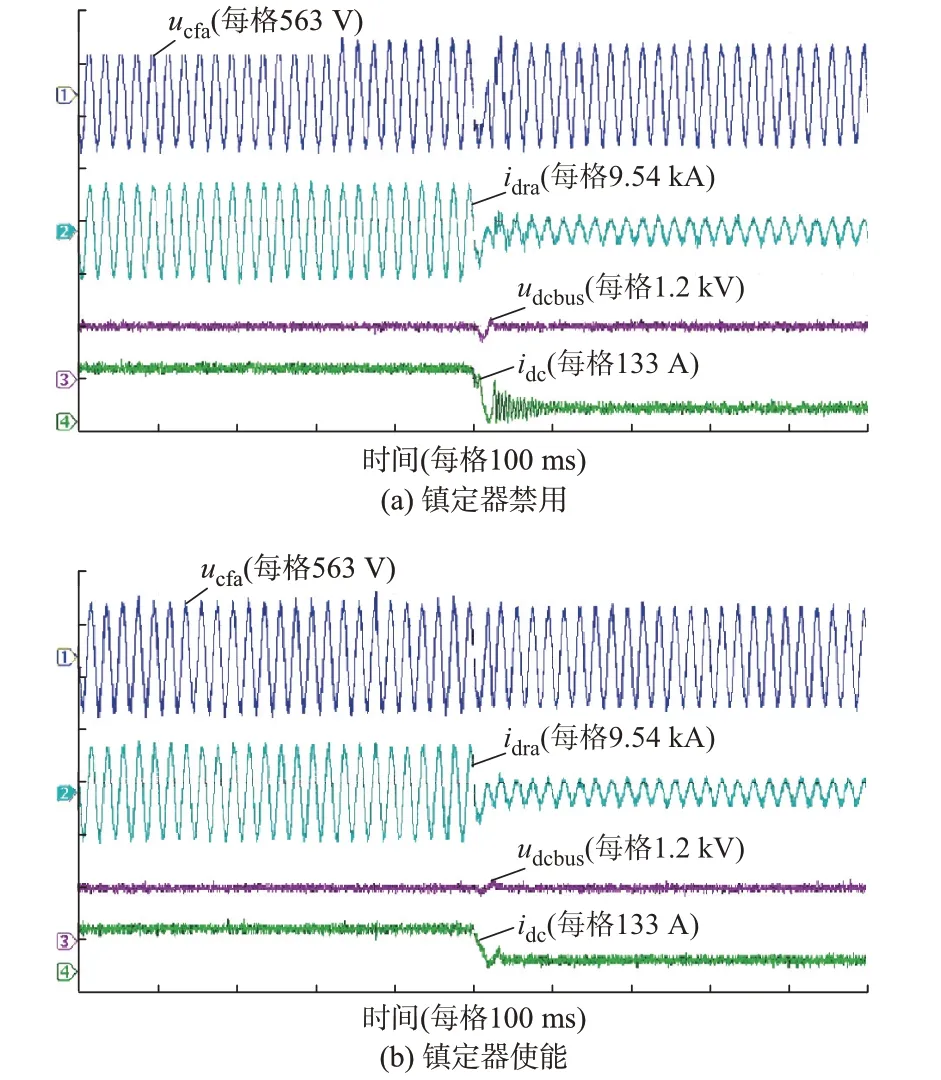
图8 镇定器禁用和使能条件下系统动态特性比较Fig.8 Comparison of dynamic characteristics of systems with disabled and enabled stabilizers
7 结语
本文提出一种基于二极管分散整流的风电机组中压直流汇集直接送出并网系统,研究其组网控制与保护,主要结论如下:
1)利用所提电流纹波交错控制,有效降低了直流输电电流和电压纹波,风电机组数量越多,算法优势越显著。
2)基于小信号状态空间建模和特征根分析,辨识弱阻尼状态变量及其在控制系统中关联的前馈项。在该前馈项中串联一阶滤波器能有效提升风电机组全功率段稳定性。
3)依靠继电保护逻辑与风电机组扰动注入时序配合,实现了直流短路故障定位与隔离,无须使用通信系统和直流断路器。最终,通过PSCAD 仿真和RT-LAB 硬件在环实验,验证了所提控制策略的有效性。
本文所研究系统的输电电压等级受限于风电机组的输出电压。未来,可结合基于直流变压器的海上换流站,进一步拓展为多电压等级全直流风电场,研究该系统的控制与保护。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
