球面坐标下基于语义分层的知识图谱补全方法
2024-02-18郭子溢林广艳谭火彬
郭子溢,朱 桐,林广艳,谭火彬
北京航空航天大学软件学院,北京 100191
知识图谱(knowledge graph,KG)概念的定义[1]随2012 年谷歌知识图谱[2]的发布而确立。知识图谱由描述事实(fact)的三元组(头实体,关系,尾实体)组成。目前学术界如WordNet[3]、Freebase[4]、YAGO[5]、Wikidata[6]、DBpedia[7]等开放知识图谱,为Q&A[8]和推荐系统[9]等上层应用提供底层数据支持。但现有知识图谱并不完善,缺少许多有效三元组,即语义含义在现实中成立,却不存在于知识图谱中的事实。为保证向上层应用提供更完善的服务,知识图谱补全(knowledge graph completion,KGC)便成为了知识图谱领域的一个主要研究方向。
该任务旨在根据图中已知的边的信息,对图中缺失的边进行预测,即链路预测任务。当前的主流思路是通过知识表示学习,将知识图谱中的实体和关系嵌入到连续低维的向量空间中进行运算,因此知识图谱补全任务方法也被称为知识图谱嵌入(knowledge graph embedding,KGE)。
目前主流的知识图谱嵌入模型类别大致可以分为:基于翻译的方法[10-14],基于张量分解的方法[15-19]和基于神经网络的方法[20-32]。现阶段基于翻译模型也衍生出了使用几何工具的拓展方法,包括RotatE[33]、HAKE[34]、Rotate3D[35]等。
但是大多上述现有知识图谱嵌入模型忽略了关系带来的语义层次信息。例如三元组〈苹果树,所属类别,植物〉,其中的尾实体“植物”属于更泛化的类别,其所处的语义层级显然高于“苹果树”,这种实体间的语义层次差异是客观存在的,对此类信息的丢失也会一定程度地影响最终结果。一般情况下,想要直接捕获这种差异信息比较困难,但是在知识图谱中,连结两个实体间的关系可以通过关系自身的语义信息,直观地将这种层次结构展现出来,例如对于一个未知的三元组〈A,所属类别,X〉,通过对关系“所属类别”语义的直接理解,不难判断未知实体A 属于未知实体X 的“子类”,因此如何通过对关系语义层面的建模,从而获取并充分利用实体间层次结构的差异信息便成为了关键问题。
对知识图谱中的语义分层现象进行建模是知识图谱补全的一种新方法,起源于2016 年提出的类型化知识表示学习(type-embodied knowledge representation learning,TKRL)[36]模型,其思想是利用实体的类型信息对语义分层现象进行建模。但并非所有数据集都包含实体类型数据,若数据集不直接存放此类信息,则需要通过维基百科进行额外的检索操作。文献[37-38] 通过在关系集合中划分关系的层次结构,再以聚类方式学习关系的语义层级,该方法弱化了更为重要的实体语义层级信息。HAKE 模型则是重新聚焦于实体的语义层级差异,通过极坐标系对这种差异信息进行建模,比TKRL 更加直观且简易,但HAKE 对关系语义部分的建模仍不够充分,模型使用的几何方法无法合理地建模逆关系。
本文提出一种在球面坐标系下基于语义分层信息的知识图谱补全(knowledge graph completion on semantic hierarchy in spherical coordinates,SpHKC)模型,旨在捕获关系在语义层面对实体语义层级的描述信息,提高了模型的直观性以及可解释性,丰富了嵌入的表达能力。SpHKC 模型继承了HAKE 模型的优势,可基于知识图谱原本的三元组信息进行训练,且不需要额外进行聚类操作。SpHKC 模型将关系视为从头实体到尾实体的移动,并且从“处于同一层级”和“处于不同层级”两方面考虑实体间的关系,具体讲,就是在球坐标系下,将实体所处的语义层级建模为该点位的极径,将关系的“移动”操作拆解为缩放和旋转:通过缩放操作控制实体的极径,对关系语义中蕴含的层次信息进行建模;通过对处于同一语义层级的实体进行旋转,对关系所反映出的不同实体语义之间的差异进行建模。实验表明,相较于目前主流方法,SpHKC 在当前大部分数据集上的性能指标都有一定提升,证明了方法的有效性。
1 基本原理
1.1 建模思路
实体的语义分层是知识图谱中客观存在的现象,实体所处的语义层级也属于实体自身的属性,在理论上通过获取实体语义层级信息可以更精确地对实体进行表示。一般情况下,获取实体的语义信息往往需要使用自然语言学习等方法进行大量的预训练,成本较高。但在知识图谱中,实体之间的语义层次差异能够通过实体之间的关系得到更为显式地表达。
如图1 所示,在三元组〈Dog,belong_to,Animal〉中,Animal 和Dog 在语义上的层级信息是它们各自的固有属性,但是这种语义层级的差异通过关系belong_to 直观地反映了出来,并且上层实体Organism 也通过另一种关系与Animal 相连,这种通过关系路径彼此连结的且有语义层次差异的实体共同组成了树状结构,在路径上越靠近根节点的实体越抽象,反之越靠近叶子节点的实体越具体。
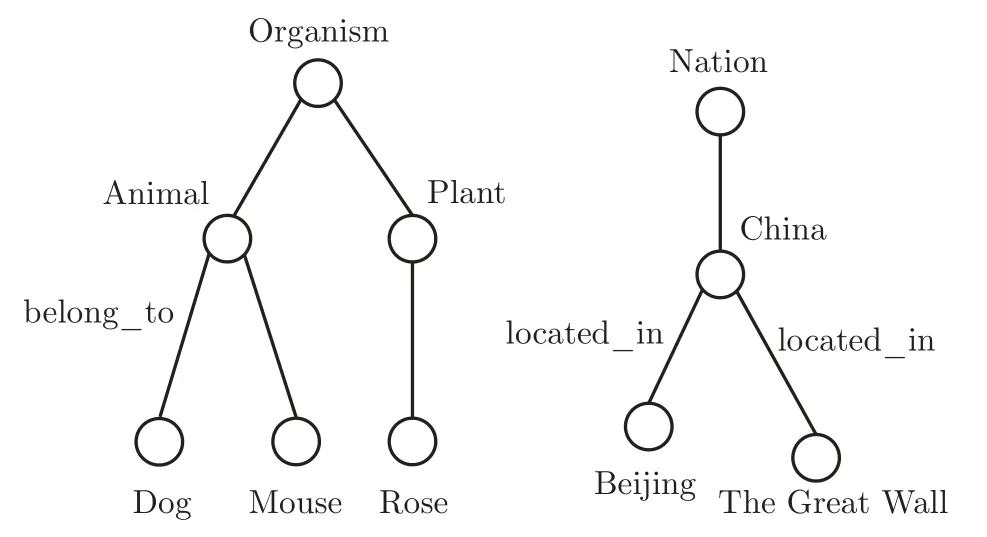
图1 知识图谱语义层次树状结构Figure 1 Tree structure of semantic hierarchy in knowledge graph
另外,若连结实体的关系不同,则头实体和尾实体所展现出来的语义层次差异也会变化,但是通过单个关系无法判断单个实体所处的语义层级。以图1 中另一个三元组〈Beijing,located_in,China〉为例,如果只观察关系belong_to 和located_in 的差别,则无法确定实体Animal、Dog、China 和Beijing 分别处于哪一语义层级,关系所展现出来的语义层次差异只是相对的概念,因此把关系视为从一个实体到另一个实体的移动来展现实体的语义层级差别,而不是通过对关系本身语义的学习去定性实体的语义层级,是本文的根本建模理念。
为了对上述语义层次的树状结构进行建模,我们将其映射到球坐标系中,如图2 所示。严格来说是将树结构的节点映射到球坐标系内围绕极点存在的无限个同心球面上,不同球面代表实体所处的不同语义层级,球面半径对应路径长度,半径越小,语义层级越高。

图2 语义树状结构到球面坐标系的映射Figure 2 Mapping from tree structure of semantic to spherical coordinate system
在球坐标系中,SpHKC 从两个方面考虑对实体和关系的建模,即处于同一层级的实体和处于不同层级的实体。对关系的建模则从这两部分入手。传统基于翻译的方法往往将关系视为从一个实体到另一个实体的“一次操作”,采用的方式是“平移”和“旋转”,本方法将关系所代表的移动操作拆分为两个主要部分:1)通过控制球面半径以表达实体语义结构层次差异的“缩放”操作;2)同一语义层级内通过控制实体点位三维角度以表达实体语义内容含义差异的“定位”操作,如图3 所示。

图3 关系在球面坐标系的建模Figure 3 Modeling of relation in spherical coordinate system
图3 中的h和t分别代表三元组〈h,r,t〉内头尾实体在球面坐标中的映射向量。在预测过程中,图3(a) 表示关系的定位操作,通过球面坐标中的极角rθ和方位角rφ调整头实体在球面的位置,使头实体与尾实体在语义含义层面趋近。图3(b) 表示关系的缩放操作,通过对球面坐标中极径rm的缩放,试图缩小头实体与尾实体在语义层次层面的差距。将两种操作视为整体,共同表示关系的移动操作,从而得到预测尾实体的嵌入t′。最后利用h和t′计算距离函数,对模型的预测效果进行打分。
1.2 球面坐标系及相关符号说明
本文引入球面坐标系对知识图谱中的语义分层现象进行建模,球面坐标系中各参数如图4 所示,每个点所处的空间方位用极径r、极角θ、方位角φ进行描述。
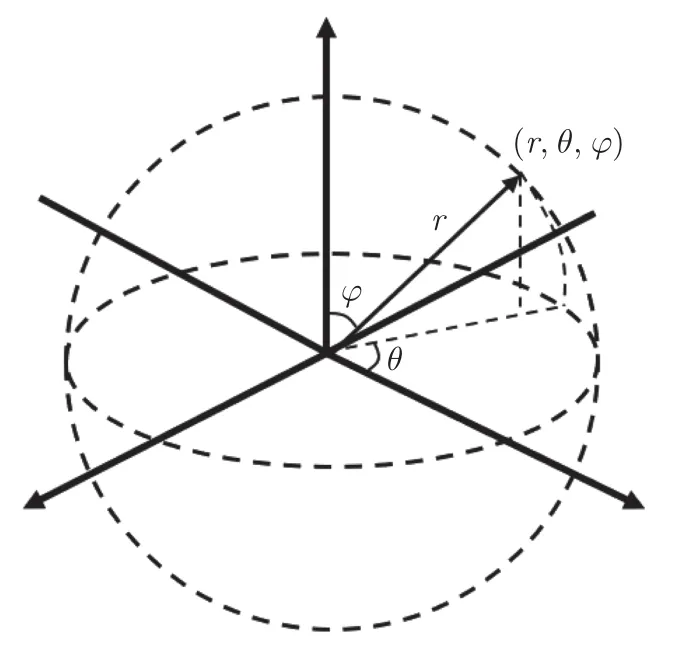
图4 球坐标系示意图Figure 4 Diagram of spherical coordinate system
由于关系需要通过控制上述3 个参数来描述两个实体间语义层次和语义含义之间的差异,因此对关系的建模将从极径部分rm、极角部分rθ、方位角部分rφ这3 个维度进行。同理,实体嵌入也分为hm、hθ和hφ,上述嵌入均为k维向量,公式为
式中:[h]i为向量h的第i个分量;向量运算“◦”表示哈达玛积,即两个向量的元素积。
2 方法
2.1 极径部分
该部分旨在对不同实体的语义层次差异信息进行建模,在极径维度上,关系将进行缩放操作,以表示实体在不同语义层级的跃迁。通过这种方式,每个实体在球坐标系的极径参数便可以表达实体的语义层级,即将hm和tm中的每一个分量[hm]i和[tm]i视为描述实体hm和tm语义层次的组成部分,即为极径;将rm中的每一个分量[rm]i视为在第i个分量上对头实体进行缩放操作。于是我们可以得到不同的头实体在同一条关系的作用下进行相同缩放的公式,为
式中:rm表示对头实体嵌入hm的每一个分量分别进行缩放操作。
进一步可以得到初步的极径部分距离函数,公式为
式中:hm和tm的每一个分量[hm]i和[tm]i的取值范围为实数域。这是因为通过模型的训练后,正样本的hm和tm计算出来的距离函数偏小,使[hm]i和[tm]i更倾向于享有相同的符号;而对于负样本,不同的符号会导致距离函数的计算结果明显偏大。于是通过符号的差异可以更方便地对三元组的存在性进行判断。rm的每一个分量[rm]i的取值范围为非零实数域,因为在球面坐标中约定极径不取负值,即不会对“向后”的距离进行测量。异符号是用于辅助区分负样本,因此在本方法中用于训练的关系数据不存在负样本,若[rm]i可以取到负值,则可能发生正样本头实体在正确关系的作用下靠近负样本的现象,这显然是不合理的。
但是上述对实体和关系的建模仍存在问题,从图1 可以看到,实体Beijing 和实体The Great Wall 均通过同一条关系located_in 与实体China 相连,但是很难认为Beijing 和The Great Wall 处于同一语义层级。由于知识图谱具有人为可修改性,管理者后续向其中添加三元组〈The Great Wall,located_in,Beijing〉也是合理的,因此在极径部分对关系建模时还需要进行补充,修改后的距离函数为
在原距离函数的基础上对关系嵌入额外添加了rmix部分,该部分融合头尾实体的信息之后进行训练,使模型结合了关系前后实体的信息从而对关系进行更为精确的建模。考虑到设计rmix的初衷是对头尾实体部分进行信息的补足,不能造成hm和tm符号的反转,因此[rmix]i的取值范围规定为[-[rm]i,1]。
2.2 极角部分
解决了对实体不同语义层级差异信息的建模问题后,即可利用极角部分对相同语义层级下不同实体的语义含义差别信息进行建模,例如三元组〈小明,朋友,小王〉。这部分思想更贴近传统的翻译模型,如RotatE,将关系rθ建模为实体hθ到实体tθ的旋转操作,公式为
由于是在球坐标系下进行建模的,因此对极角的相加实际上就表示旋转操作。另外,在球坐标系中约定极角的取值范围为[0,2π),故[hθ]i、[tθ]i和[rθ]i的取值范围均为[0,2π),于是极角的距离函数可以写为
式中:除以2 的目的是保证sin 函数内的自变量处于一个周期内。距离函数与HAKE 相同,由于相位角具有周期性特征,因此SpHKC 没有直接采用tθ与预测尾实体向量的差值作为计算结果的l2范数,而是使用了sin 函数进行得分的评估。
2.3 方位角部分
方位角和极角的变化共同构成了关系的定位操作。在球坐标系中,点在球面上的位置由两个角度参数共同控制,因此方位角部分是对极角部分建模的补充,强化了实体和关系嵌入的表达能力。与极角不同,方位角的取值范围一般为(-π/2,π/2],用来描述球面上的点“向上”或“向下”的俯仰操作,并且不能“向后”,因为如果一个点的方位角超过了这个范围,那么在球面上就会存在另一个与该点极角相差π 的点,与该点的方位角取值范围产生交集。从直观上讲,球面相比较平面多加了一个维度,也使得实体和关系的表达空间更加广阔。
该部分思路与极角部分的操作基本一致,将关系rφ建模为实体hφ到实体tφ的旋转操作,公式为
与球坐标系相同,[hφ]i、[tφ]i和[rφ]i的取值范围均为(-π/2,π/2]。方位角距离函数为
2.4 总距离函数与损失函数
将极径、极角以及方位角部分进行整合,可以得到SpHKC 模型的距离函数,公式为
式中:λ、µ为模型的超参数,用于控制各部分的权重占比。预测尾实体和真实尾实体之间的距离越小,模型的评估效果越好,因此得分函数可以表示为
模型使用基于负采样损失的损失函数进行模型的优化,并且采取自我对抗式负采样,损失函数为
式中:γ为误差边界,属于模型的超参数;σ为sigmoid 函数;表示第i个负样本在全部负样本中的可靠性比重,用于筛选明显不合理的负样本,公式为
式中:超参数α为平滑参数。
3 实验
3.1 数据集
实验使用的数据集为开源知识图谱WordNet 的子集WN18RR、Freebase 的子集FB15k-237 以及YAGO 的子集YAGO3-10。在知识图谱补全任务的实验中,早期使用的大多是WN18、FB15k 以及YAGO3 数据集,但是由于这些数据集存在测试集泄露问题,模型在这些数据集上的效果普遍虚高,因此目前大部分主流方法是在修正后的WN18RR、FB15k-237 以及YAGO3-10 数据集上进行实验。这3 个数据集的信息如表1 所示,可以看到它们在规模上存在一定差别,其中FB15k-237 和YAGO3-10 数据集的三元组较丰富。

表1 数据集统计信息Table 1 Statistics of datasets
3.2 实验超参数及其他配置
本文所提出模型采用的超参数由网格搜索得出,例如YAGO3-10 数据集上的超参数,如表2 所示。此外,采用Adam 算法对模型参数进行优化,并且在训练时学习率采用多段衰减,在当前训练步数进度到达总步数的1/2、1/4、1/8 时,分别将学习率衰减为原本的1/5、1/4、1/3。

表2 YAGO3-10 数据集超参数Table 2 Hyperparameters of dataset YAGO3-10
3.3 评价指标
链路预测任务的评价指标主要包括平均排名(mean rank,MR)、平均倒数排名(mean reciprocal ranking,MRR)、Hits@1、Hits@3 以及Hits@10 五种。上述指标的计算全部基于对正确三元组预测的排名rank,步骤如下:在对模型进行评估时,对于一个正确的三元组〈h,r,t〉,将其头实体或尾实体替换为任意一种其他的实体,假设数据集中共有n个实体,且仅替换尾实体,那么就会得到n-1 个新的三元组,其中i∈[1,n-1];然后对包含正确三元组在内的n个三元组通过得分函数计算其得分;最后将n个三元组按照得分降序排列,便可得到正确三元组〈h,r,t〉的排名rank。
利用模型对所有正确三元组进行预测并得到排名,最后取平均值得到MR 指标。计算公式为
式中:T为正确三元组的集合;|T| 为集合中元素的个数;ranki代表模型对第i个正确三元组预测的排名。MR 指标存在两个问题:1)因为MR 值越小,代表模型效果越好,这与直观理解相悖;2)MR 的计算结果取值范围过大,动辄上千,不方便进行比较。因此往往采用基于MR 的MRR 指标进行模型的评估。
通过对排名的倒数求平均得到指标MRR,它解决了上述MR 指标存在的两个问题,其计算公式为
Hits@n是指在链路预测任务中排名小于或等于n的三元组在正确三元组集合中的占比,具体计算公式为
式中:indicator(·) 为指示函数,表示若条件为真则函数值取1,否则取0;n通常取1、3 和10,即评价指标Hits@1、Hits@3 和Hits@10。Hits@n指标越大,表示模型越有效。
3.4 实验结果对比
为了验证本模型的有效性,分别在FB15k-237、WN18RR 以及YAGO3-10 数据集上进行实验,并且与目前主流的方法包括TransE、DistMult、ComplEx、ConvE、RotatE、Rotate3D以及HAKE 进行对比,如表3 所示。
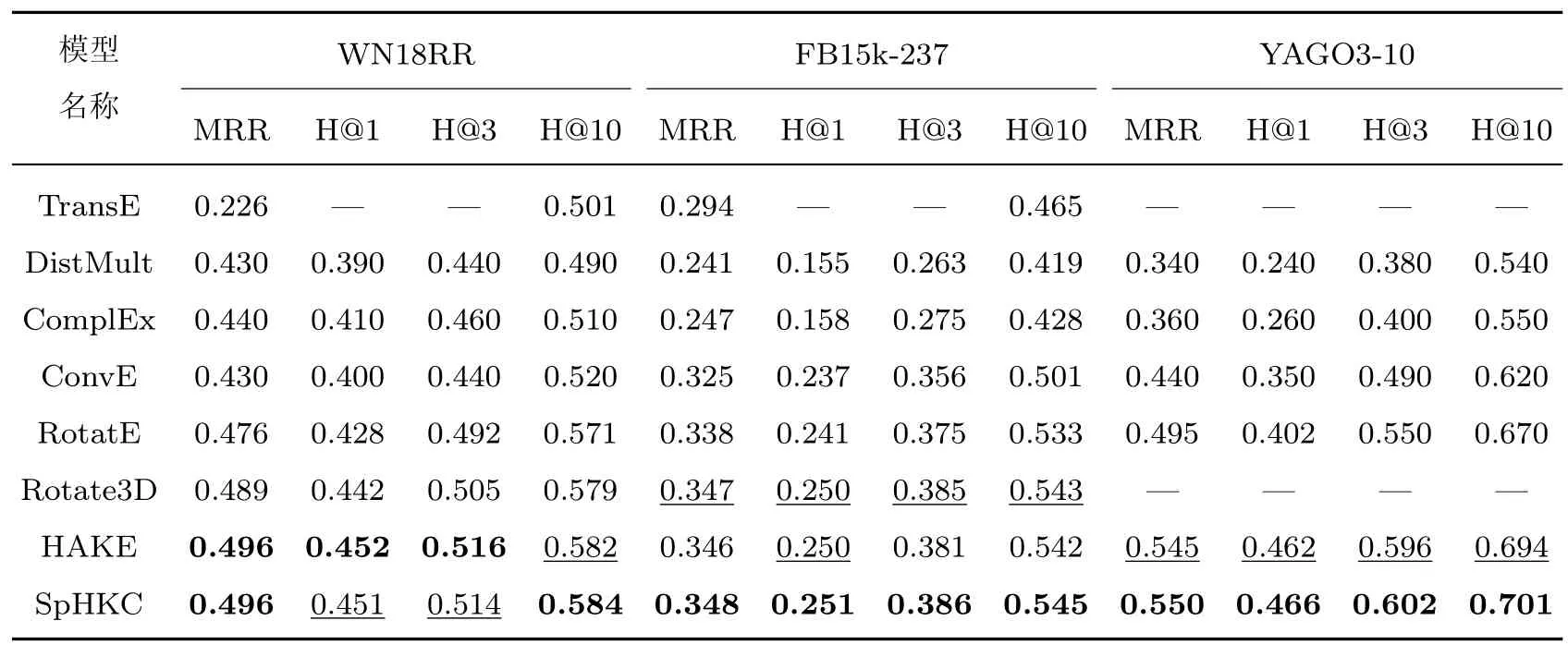
表3 SpHKC 与同类别SOTA 方法实验结果对比Table 3 Comparison of experimental results of SpHKC and relevant SOTA methods
表3 中的加粗项为每项指标的最高值,下划线项为次高值。最左侧所列出的方法按发表年份升序排列,其中TransE、DisMult 以及ComplEx 方法受限于早期思想的限制,对实体和关系的建模并不充分,因此性能指标相对于当今方法差距较大,后文不作讨论。作为神经网络方法的代表模型之一,ConvE 意味着知识图谱补全方法步入新阶段,其性能相对于先前模型有较大提升;RotatE 强化对关系模式的建模,因此其表达能力显著增强。上述两种方法均为各自方法类别的开山之作,后续的模型均基于它们进行了优化,取得了更好的效果。可以看到在不同的数据集上,Rotate3D、HAKE 以及本文的SpHKC 均在不同的指标分别取到最高和次高项,SpHKC 则是在每个数据集的各项指标上均取到最高或次高。
在WN18RR 数据集上,SpHKC 模型仅在MRR 和Hits@10 指标上取到最高,在Hits@1和Hits@3 指标上取到次高,而作为Baseline 参考的HAKE 模型在除Hits@10 外的其余指标取到最高,仅在Hits@10 取到次高,总体性能HAKE 优于SpHKC。在FB15k-237 数据集上,SpHKC 方法在各项指标均取到最高,并且在Hits@3 指标上相对HAKE 提升约1.3%,Rotate3D 模型则是在各项指标上均取到次高,而HAKE 仅在Hits@1 指标取到次高。可以看到,SpHKC 模型性能与Rotat3D 较为贴近,虽然提升较小,但整体稳定优于HAKE。在YAGO3-10 数据集上,SpHKC 全部取到最高,并且在4 项指标上相对次高的HAKE 模型分别提升0.9%、0.9%、1.0%和1.0%,提升幅度远大于在WN18RR 和FB15k-237 数据集上的结果。本文认为这种差异主要是由不同数据集之间关系数量和关系类型的差异所导致的,下面分析一下可能的原因。
在WN18RR 数据集上,考虑到WN18RR 数据集只包含11 种关系,关系类型相对较为简单,并且实体数量相比FB15k-237 也仅多了不到两倍。较小的数据集规模和关系种类使得模型在该数据集上往往不需要很强的表达能力便可得到相对较好的效果,因此无法发挥SpHKC对比HAKE 在三维层面扩展的优势,相对冗余的空间表达增加了模型复杂度,因此降低了模型性能。此外可以发现,SpHKC 与HAKE 的性能差异小于SpHKC 与Rotate3D 的性能差异,这是因为WordNet 数据集通过语义关系将同义词组组织成词汇网络,其中的语义关系包含单词概念层面的层级结构,而SpHKC 相比于Rotate3D 则是强化了对实体语义层次结构的学习,性能也整体领先,进而证明了对语义层次信息建模的重要性。
在FB15k-237 数据集上,SpHKC 的整体性能优于HAKE,其主要原因是FB15k-237 数据集的关系数量多,且类型相对复杂,既包括了“/award/award_category/category_of”这种明显表达了头尾实体间语义层次差异的关系,又包括诸如“/film/film/prequel”这种头尾实体属于同一类型,且近似无语义层次差异的关系。在对关系“/film/film/prequel”进行建模时,SpHKC 的三维空间给予了关系更丰富的表达,这也是Rotate3D 整体优于HAKE 的原因。另外可以发现,SpHKC 模型相比HAKE 模型在FB15k-237 数据集上的性能提升较小,这是由于FB15k-237 数据集的实体数量稀少,即使是在HAKE 的二维建模空间内,实体的嵌入需求也很容易得到满足,采用三维建模空间的SpHKC 能力没有得到充分的发挥。而和Rotate3D 模型对比,由于FB15k-237 数据集中实体的分层现象较少,因此SpHKC 模型的性能提升有限。
在YAGO3-10 数据集上,SpHKC 的性能则取得了较大幅度的提升。从数据集属性的角度进行分析,YAGO3-10 的关系种类包括37 种,虽然不及FB15k-237 的237 种,但也包含了明显表现实体间语义层次差异的关系imports,实体两侧无明显语义层次差异的对称关系hasNeighbor、非对称关系hasChild 以及可近似视为逆关系的worksAt 和isAffiliatedTo。关系种类较为丰富,对模型建模关系的能力有一定要求,并且YAGO3-10 数据集的实体数量约为WN18RR 的3 倍,达到了12.3 万,因此表达能力强大的模型在该数据集上往往会展现出更好的效果。可以看到,在WN18RR 和FB15k-237 数据集的MRR 指标上,SpHKC 模型相较于ConvE 模型的提升分别为15.3%和7.1%,而在YAGO3-10 上的提升达到了25%。综合以上几点,在对模型的实体和关系建模能力均有考察的情况下,SpHKC 在实体数量和关系种类数量两方面受到的限制得到了大大缓解,最终效果全面优于HAKE。
3.5 消融实验
除了上述SpHKC 与主流同类型方法在3 个数据集上的结果对比外,为了验证SpHKC方法3 个部分在建模时的有效性,本文进行了消融实验,如表4 所示。消融实验共进行4 次消除:消除极角和方位角部分,消除方位角部分,消除极角部分以及消除极径部分。表4 最左列为模型中保留的部分。
可以看到,无论是完全消除极径部分,还是完全消除角度部分,对模型的性能都会产生相当大的影响。若仅存在角度部分,则会丢失模型对语义层次信息的建模,对关系也仅仅是将其视为平面的旋转操作,在实验结果上也更接近类似思想的RotatE。而若仅存在极径部分,则模型只能对语义层次不同的实体进行建模,对处于同一层级的实体则完全无法区分,而在数据集中,处于相近语义层级的实体对占比仍较大,因此该部分实验得到的效果最差。
从实验结果来看,消除角度部分中的一个维度也会对模型的性能产生影响。若消除方位角部分,模型的思想则会变得贴近HAKE,结果上也较为一致;若消除极角部分,保留方位角,也是从三维模型退化为二维模型,但是受取值范围限制,导致单方位角模型的表达能力弱于单极角模型的表达能力。无论消除哪一个维度,模型还是结合了语义层次差异信息和语义含义差异信息,使得这两部分消融实验的整体结果仍优于前两个部分的消融实验结果。
总体来看,SpHKC 模型任一部分的缺失都会导致模型的最终结果受到负面影响,由此可以得出,模型的3 个建模部分之间是共同协调,彼此不可分割的。
3.6 数据集规模影响实验
从数据集规模上讲,FB15k-237 大于WN18RR,YAGO3-10 大于FB15k-237,而从主实验对比结果可以发现,相比HAKE 模型,SpHKC 模型在WN18RR、FB15k-237 以及YAGO3-10数据集上的性能指标提升是随着数据集规模的增大而增大的;为了验证这一想法,本文进行了数据集规模对HAKE 以及SpHKC 模型性能影响的实验。数据集选用规模最大,关系种类复杂且SpHKC 和HAKE 表现最好的YAGO3-10,对数据集规模的控制则是通过改变数据集中关系的数量来实现。在去除关系的过程中,保留三元组占比较大的关系,以避免数据集规模发生剧烈变化。实验结果如表5 所示。
可以看到,在关系数量为20 时,HAKE 模型的性能整体优于SpHKC 的,但是随着关系数量的增加以及数据集规模的增长,HAKE 对SpHKC 的指标值差距逐渐缩小,甚至在关系数量为30 的Hits@10 指标上SpHKC 超过了HAKE,最终在完整的YAGO3-10 数据集上,SpHKC 的性能整体优于HAKE。考虑到SpHKC 在三维空间下进行建模,相较于HAKE二维平面的建模方式,在表达空间上的优势通过数据集规模的增加而展现了出来,实验结果证实了上文的猜想。
3.7 融合图结构信息实验
为了探讨SpHKC 模型进一步拓展的可能性,本文试图将语义分层信息与图结构信息融合并进行了实验。目前,主流的基于图卷积神经网络的方法可以有效地对图结构信息进行建模,因此本文选用基于组合的多关系图卷积神经网络[39](composition-based multi-relational graph convolutional networks,CompGCN)模型作为参考方法。
由于图卷积神经网络相对较为复杂,并且本文的主体部分是对语义分层信息进行建模,而不在于对图网络结构进行改动,因此语义分层信息与图结构信息融合的方案设计了以下两种:
1)完成对实体语义分层信息的建模部分,通过模型训练得到包含语义层次信息的实体和关系嵌入,然后将得到的嵌入作为预训练词向量,用于初始化图卷积网络模型,以这种方式将语义信息和图结构信息通过图卷积网络模型融合。
2)考虑到图卷积神经网络模型为编码器-解码器结构,神经网络通常作为编码器部分,学习到实体和关系的嵌入,然后通过其他传统方法的得分函数进行得分评估。因此另一种融合方案是将SpHKC 的得分函数作为图卷积网络模型的解码器,使用图卷积网络算法一并进行训练,旨在将图结构信息融合进针对语义层次结构进行建模的模型中。
实验结果如表6 所示,表6 模型名称一列中SpHKC+GCN 代表基于预训练方法的实验方案,GCN+SpHKC 代表基于解码器修改的实验方案,GCN 统一指代CompGCN 方法,各项评估指标的最优结果均加粗处理。可以看到,对基于预训练方法的方案,其实验结果和原本的图卷积神经网络模型相比在各项指标上均存在小幅度的下降,而对基于解码器修改的方案,其实验结果和基于语义分层的模型相比总体上持平,仅在FB15k-237 数据集上的MRR和Hits@1 指标上有一定提升。考虑到CompGCN 模型在FB15k-237 数据集的这两项指标上的性能均明显优于SpHKC 模型,因此可以认为在SpHKC 模型的基础上前置图卷积网络的操作对基于语义分层模型在FB15k-237 数据集的这两项指标上起到了一定的优化作用。但是两种融合方案的总体实验结果不理想,仍需要给出进一步的解释。

表6 语义信息与图结构信息融合实验结果Table 6 Experimental results on the fusion of semantic hierarchy and graph structure
两种实验方案的初衷均是期望将知识图谱中的图结构信息与实体语义层级信息进行融合。在基于解码器修改的融合方案中,由于将得分函数修改为了SpHKC 模型的形式,因此实验结果理应与SpHKC 相近,并且在一定程度上有所提升。但是文献[40] 指出,图卷积网络模型实际并未对图结构信息进行充分建模,文章使用多种方法对图结构进行扰动,最终却都并没有影响到图卷积网络方法在链路预测任务上的效果。此后文献[40] 经过进一步探究发现,只要在图卷积操作的聚合过程中,模型能够成功区分具有不同语义的实体,便可提高知识图谱补全任务的性能。上述事实导致图卷积的模型在知识图谱领域的建模内容与本文主体方法重合,因此使用基于解码器修改的融合方案并没能实现语义层次信息和图结构信息的融合,也没能得到预想中的结果。
在基于预训练方法的融合方案中,上述两种模型的建模信息重复是效果下降的原因之一。另外虽然使用预训练词向量是较为常见的方法,但是由于语义分层模型建模方式的特殊性,该方法中图卷积神经网络学习到的嵌入在结构上并没有包含球面坐标系中的极径与角度参数部分,在这种情况下用于初始化的包含球面坐标系参数部分对应信息的预训练嵌入也就没能得到很好的利用。并且对于SpHKC 模型中嵌入取值范围的限制条件,在解码器的传统方法中并没有相关的约束,因此使用SpHKC 模型的输出嵌入作为CompGCN 模型的初始化内容,可能还会起到一定的副作用,从该角度可以对基于预训练方法的实验性能指标下降现象给出解释。
4 结语
本文提出了一种基于球坐标系的知识图谱补全方法,对知识图谱中客观存在的实体间语义分层信息进行建模。SpHKC 将三元组在语义层面构成的树结构映射到球坐标系中,使位于不同球面的实体处于不同的语义层级。SpHKC 将关系所代表的移动操作进行二次划分,对不同球面的实体采用极径方向的缩放操作以建模实体间的语义层次差异;对同一球面的实体先后采用极角和方位角的变化以建模实体间的语义含义差异,丰富实体语义信息的表达。同时SpHKC 的多维度操作也能更充分地对关系模式进行建模。实验表明,本文提出方法的各个部分均起到建模的作用,并且在关系数量较多的数据集上其表现略强于现有模型,在关系数量较少的数据集上其表现也优于大多数传统模型。
未来的模型改进工作可以尝试将语义层级信息融入到深层模型方法中,同时将知识图谱中的其他信息融入进来,在信息广度方面进行横向扩展。也可以考虑在更高维度或利用更先进的数学工具对模型进行优化,在建模深度方面进行纵向扩展。
