绝对式圆时栅偏心状态自诊断测量方法研究

陈 磊,于治成,许小虎,樊星辰,李佳豪

(1.重庆理工大学 机械检测与装备技术教育部工程研究中心, 重庆 400054;2.时栅传感及先进检测技术重庆市重点实验室, 重庆 400054;3.合肥工业大学 仪器科学与光电工程学院, 合肥 230009;4.中国通用技术集团国测时栅科技有限公司, 重庆 400039)

0 引言

随着现代工业中生产加工设备的自动化、智能化程度越来越高,角位移测量在航天、机械、光学、国防等领域得到了广泛应用[1-2],同时对其测量精度等参数指标提出了更高要求[3-4]。在角位移传感器实际应用时,因为安装偏心造成的测量误差不可忽视[5],直接决定了设备的性能。

圆光栅因其测量精度和分辨率高的优势[6],在相关领域得到广泛应用。但安装偏心同样也是圆光栅在工业现场面临的棘手问题之一[7-8],尤其是在需求高精度角位置反馈的设备中,由安装偏心引起的测量误差是非常显著的[9-10]。针对圆光栅安装偏心影响测量精度的问题,不少机构或高校在这方面做了大量研究。苏东风等[11]通过测头布置方式和数据处理两方面设计了四均布测头,有效减小了偏心对圆光栅测量精度的影响,测角精度达到0.33″。王笑一等[12]建立了双测头圆光栅偏心误差模型并采用误差修正的方法使测角误差达到了0.72″。冯超鹏等[13]采用双读数头的偏心参数自标定方法对圆光栅偏心误差进行补偿,使圆光栅的测量精度从0.046 4°提高到了0.003 7°。以上研究中采用多测头结构加误差修正或补偿的方法能有效减小圆光栅的安装偏心误差,但是测头的一致性和安装精度难以保证[14],传统的显微镜调节安装方式易受人为影响,安装时间较长。同时在空间受限的情况下布置额外的测头不仅会增加成本[15],在实现方式上也有困难。王文等[16]提出了一种基于模拟退火算法的角度传感器偏心参数辨识方法对传感器偏心参数进行辨识和修正。艾晨光等[7]采用圆光栅的2路测头信号合成李萨如图形来检测光栅的偏心,通过算法误差修正后测角误差从28.3″减小到了5.8″。王亚洲等[17]研究了一种图像式角位移测量的光栅偏心度监测系统,实现了对圆光栅的安装偏心调节,调节后的测角误差提高到了12.8″。以上研究中都对提高圆光栅的测角精度提供了有效的方法,但测角精度不够高,所用算法较复杂。

电场式圆时栅传感器是基于时空转换思想[18-19],通过构建匀速运动参考系,将空间位置信息与时间刻度关联,利用时间刻度更加精细的优点,从而实现高精度角位移测量。同样对于圆时栅传感器而言,安装同心度对于传感器的测量精度非常重要,安装偏心引入的测量误差会降低传感器的测量精度,因此提高转子与定子安装的同心度是保证圆时栅传感器测量精度的重要条件之一。目前,圆时栅以加工过程中传感片电极外圆和工装外圆同心作为安装调节基准,在安装过程中用显微镜和千分表来保证转轴和传感器的同心。但是,这种方式对制造精度和仪器精度要求较高,安装效率也较低。

为了提高圆时栅传感器的安装同心度,减小由安装偏心导致的1次谐波误差,从而提高传感器的测量精度,提出了一种绝对式圆时栅偏心状态自诊断测量方法。在前期绝对式圆时栅传感器的研究基础上,采用了一种多测头结构实现圆时栅偏心状态诊断,并制作了传感器样机。通过LabVIEW软件搭建了圆时栅偏心状态自诊断测量系统,设计了相关实验并进行了实验验证。实验结果表明,提出的自诊断测量方法显著提升了圆时栅传感器的安装同心度和测量精度,对于传感器的安装具有指导作用,为后续研究工作的展开提供了理论支撑。

1 电场式时栅测量原理

电场增量式圆时栅结构模型如图1所示。定子由扇弧形激励电极阵列组成,转子由差动结构的双正弦形感应电极阵列组成。每4个相邻激励电极构成1个对极,将N个对极的激励电极布置在圆的整周上,对极宽度为2π/N,定转子以一定的间隙正对平行安装。r是感应电极相对于转子中心的中心位置,Δr是形成感应电极正弦波的振幅。在定子激励电极上施加4路正交且激励幅值相等的正弦交流信号:Uc-=-Acos(ωt)、Us+=+Asin(ωt)、Uc+=+Acos(ωt)、Us-=-Asin(ωt)。其中,A为正弦激励信号的幅值,ω为正弦激励信号的频率,t为时间变量。

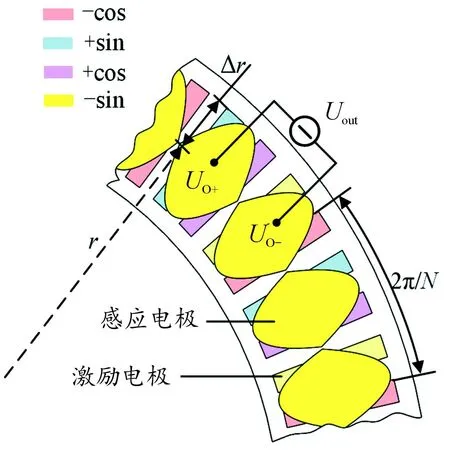
图1 电场增量式圆时栅结构模型图

根据电场式时栅测量原理,经过电场耦合后的单个感应电极输出信号Uo+可以表示为:

Uo+=Km[(ΔSc-·Uc-)+(ΔSs+·Us+)+
(ΔSc+·Uc+)+(ΔSs-·Us-)]

(1)

式中:Km为电场耦合系数;ΔSc-、ΔSs+、ΔSc+、ΔSs-分别为单个对极内4个激励电极与感应电极最大重叠面积。根据面积积分原理和式(1)可得到Uo+的表达式为:

Uo+=2KmArΔr{[1-cos(Nθ)]sin(ωt)+
[1+sin(Nθ)]cos(ωt)-
[1+cos(Nθ)]sin(ωt)-
[1-sin(Nθ)]cos(ωt)}=
K1sin(ωt-Nθ)

(2)

式中:K1=-4KmArΔr;θ为旋转角度。同理可以得到另一感应电极的输出信号Uo-。于是差动输出信号Uout可表示为:

Uout=Uo+-Uo-=2K1sin(ωt-Nθ)

(3)

最后将输出信号通过信号处理电路处理成方波信号后与同频参考信号进行比相,利用高频时钟插补将计数值转换为角位移值。

2 偏心自诊断测量方法

2.1 绝对定位原理

在增量式圆时栅结构的基础上,将N个对极和M个对极的增量式圆时栅角位移传感器进行组合[19],得到如图2所示的绝对式圆时栅传感器结构。

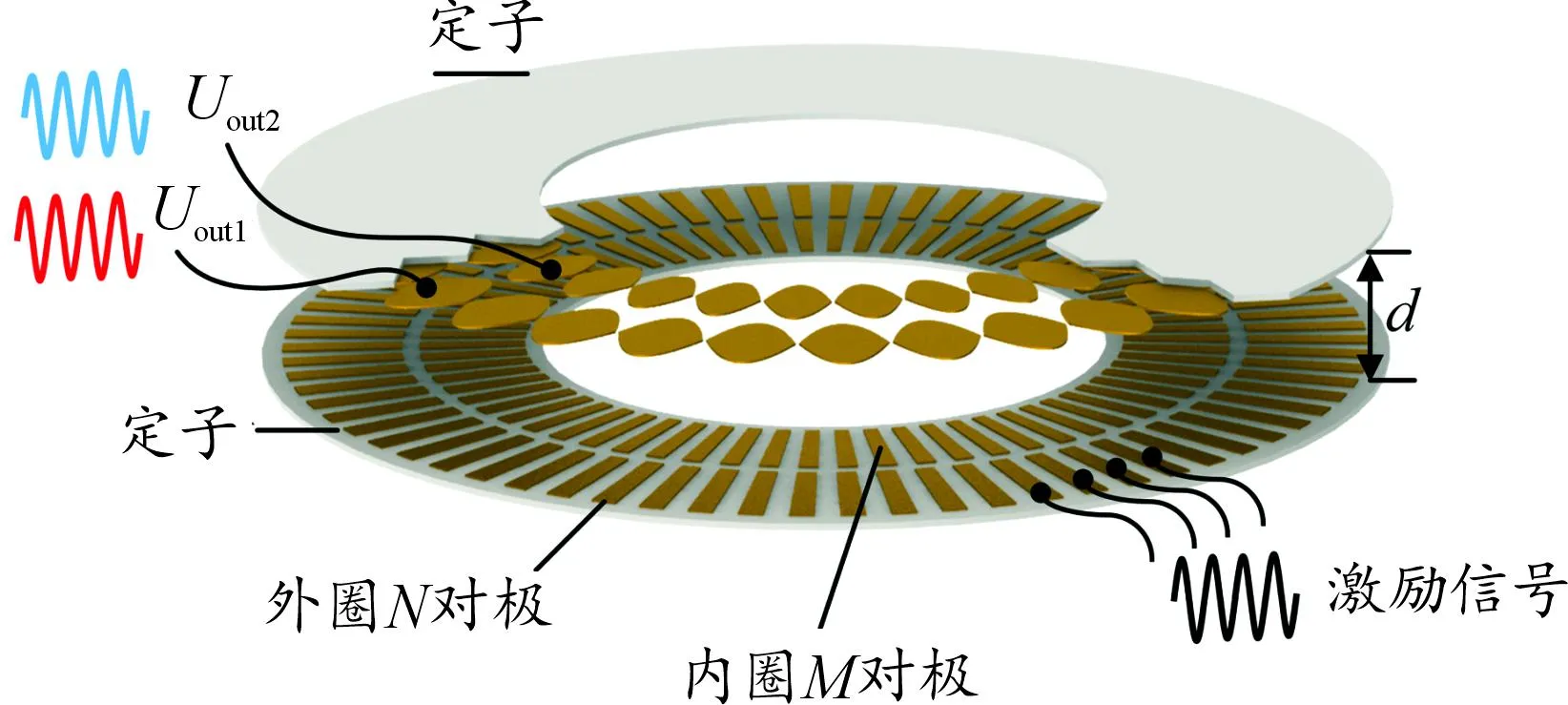
图2 绝对式圆时栅传感器结构图

经过电场耦合后由式(3)可得到转子外圈和内圈的输出信号表达式为:

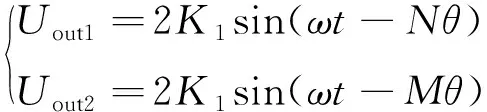
(4)

绝对定位原理如图3所示。r1和r2分别为转子外圈和内圈对应感应电极的运动路径,θa为当前待测角位移。外圈和内圈整周由不同对极数的单个对极角位移θp1和θp2组成,即θp1=2π/N、θp2=2π/M。因此,θa可表示为:

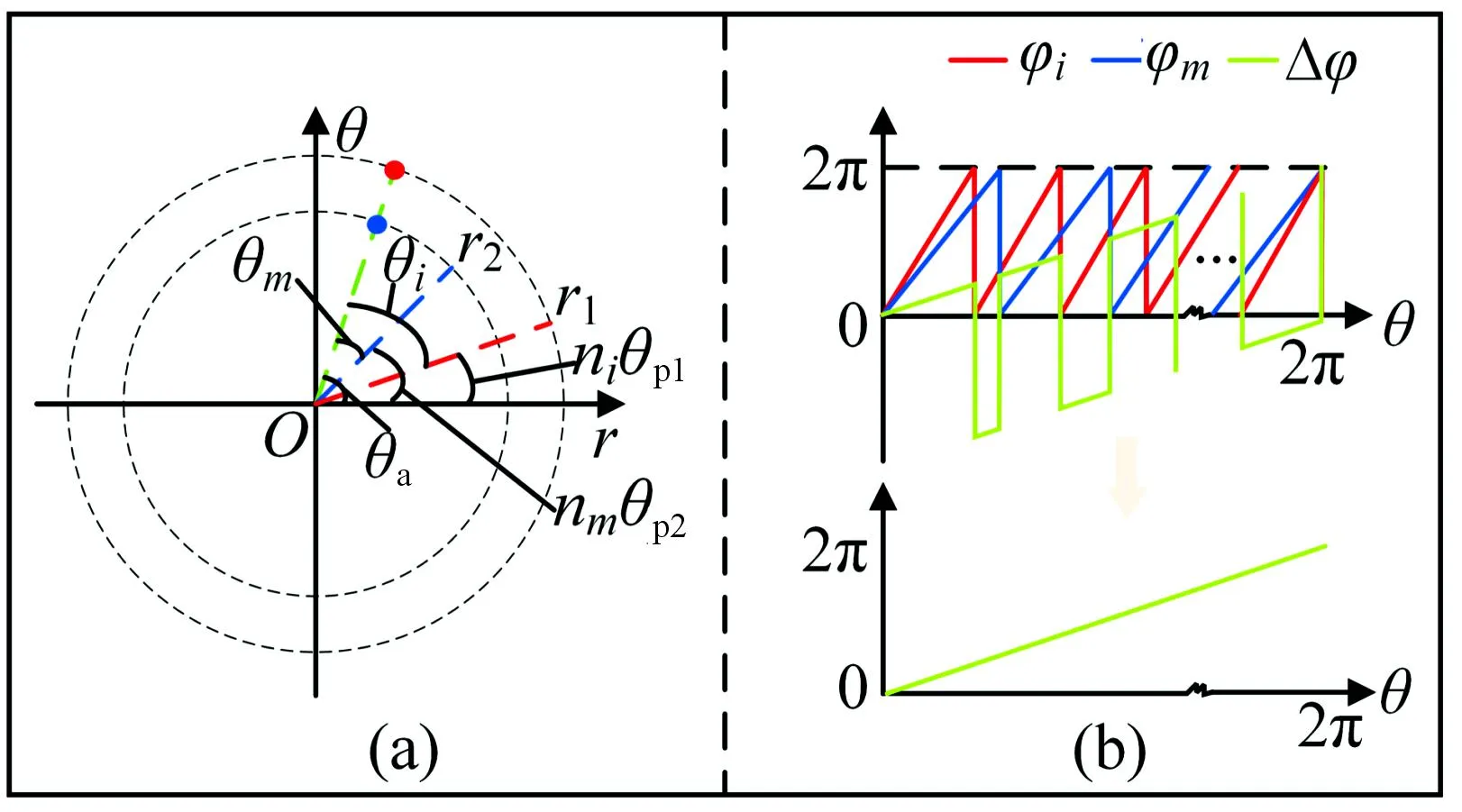
图3 绝对定位原理图

θa=niθp1+θi=nmθp2+θm

(5)

式中:ni和nm为当前位置外圈和内圈的最大整周期数,可通过传感器转子内外圈行波信号相位获得;θi和θm为周期内的残差值。niθp1和nmθp2作为粗测位移量,θi和θm作为当前周期内精测位移量。

将转子外圈输出信号与参考信号之间的相位差用φi表示,内圈行波信号与参考信号之间的相位差用φm表示,Δφ为φi与φm之差,相位差与角位移关系如图3(b)所示。

由图3可知,φi与φm从0到2π周期性变化,这种变化反映了传感器角位移也呈现周期性变化。Δφ与角位移的关系为分段线性不规则变化曲线。对Δφ作如下定义:

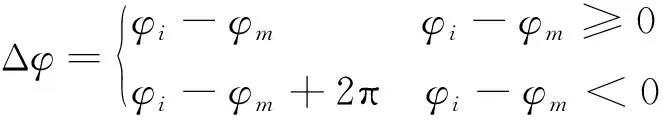
(6)

经过式(6)的转换,传感器内外圈行波信号的相位差就从0到2π呈线性变化,因此传感器空间上的位移变化量与感应信号时间变化是呈一一对应关系的。式(5)中周期数ni和nm的最大整数用取整函数表示为:

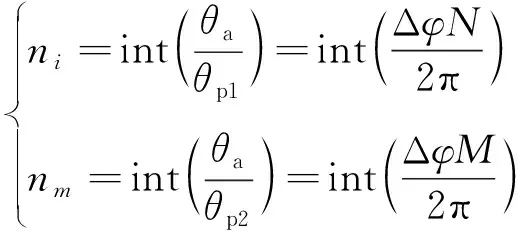
(7)

利用上述方法,就可对传感器任意一个当前所处位置的周期数进行判断,根据式(5)和式(7)得到绝对角位移值。

2.2 自诊断测量原理

图2所示的绝对式圆时栅传感器在安装时由于定转子之间不同心,转子上输出信号相位会发生偏移,从而带来安装偏心误差。为了实现传感器安装偏心自诊断,提高安装同心度,从而提高测量精度,在绝对式圆时栅结构基础上,根据传感器绝对定位原理,设计了多个测头的结构,利用传感器输出信号相位关系实现偏心状态自诊断。

圆时栅偏心自诊断测量结构如图4所示。将原来转子的外圈整周均分成A、B、C、D部分,4个部分分别在对径位置布置1个独立的测头。4个测头在一个平面上且均通过一次性加工得到,保证了测头的一致性和安装精度。最终外圈4个测头的输出信号只是幅值衰减,而相位保持不变。因此,转子内圈行波信号Uout2不变,根据式(4)可得到外圈A部分输出信号表达式为:

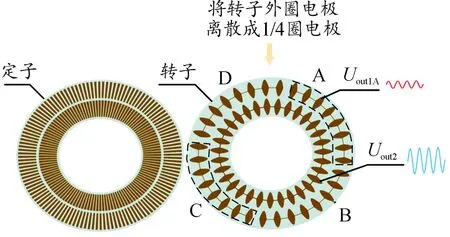
图4 圆时栅偏心自诊断测量结构图

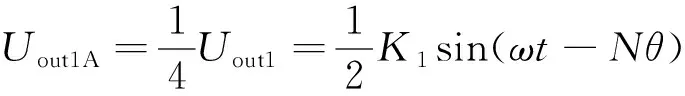
(8)

同理可得外圈其余部分行波信号Uout1B、Uout1C、Uout1D的表达式。

理想情况下,传感器转子与定子安装完全同心,根据绝对定位方法,由转子的外圈4个测头输出信号和内圈测头输出信号的相位信息求解得到的传感器绝对角位移是相同的。但当传感器转子与定子安装偏心时,外圈4个测头输出信号的相位会发生偏移。根据2.1小节中绝对定位原理绘制了如图5所示的偏心自诊断测量原理图。

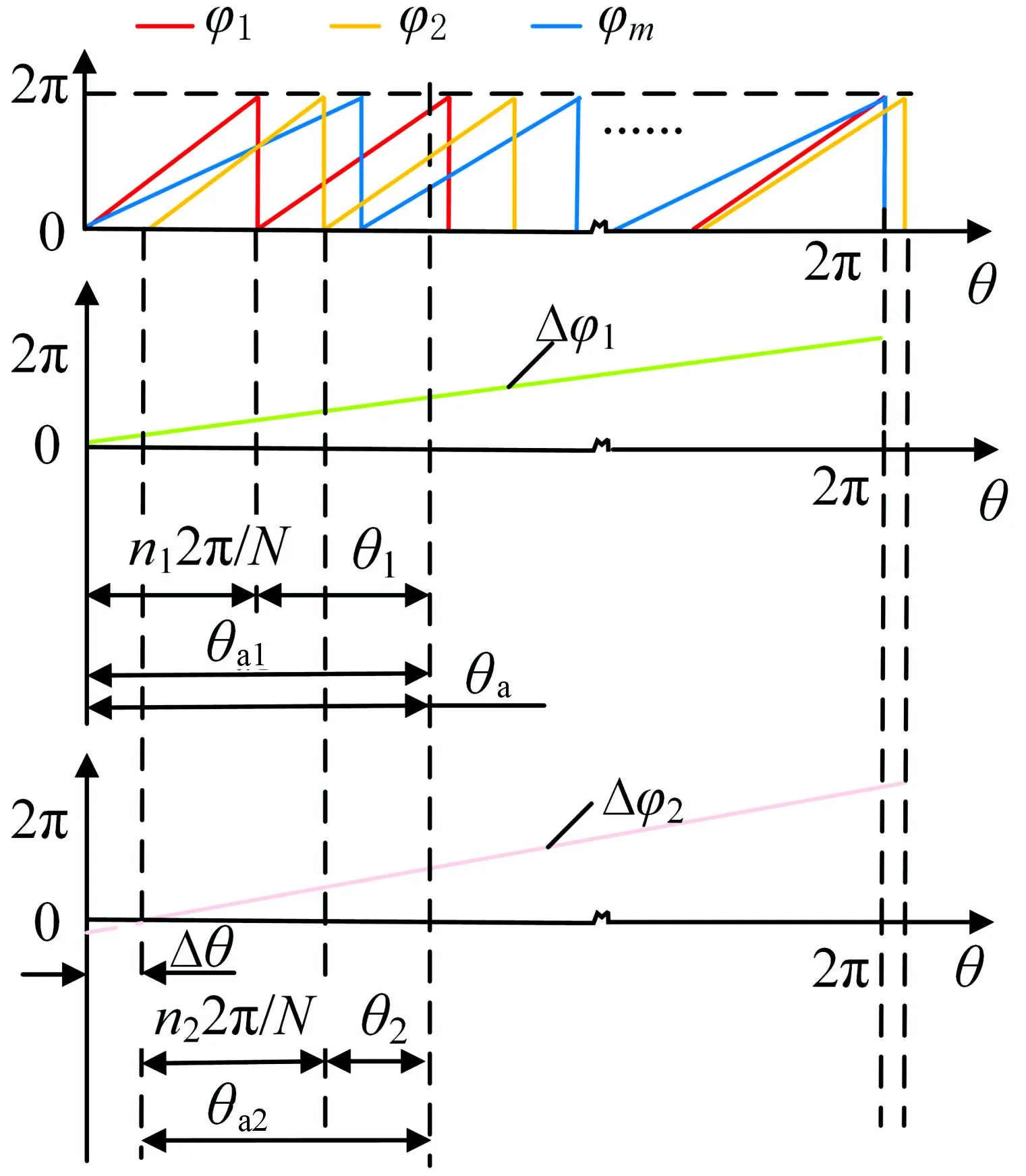
图5 偏心自诊断测量原理图

为了便于分析,图5中只给出了外圈2个测头的相位关系。其中,φ1表示外圈A测头输出信号与参考信号比相后的相位差,φ2表示B测头输出信号与参考信号比相后的相位差,φm表示内圈输出信号与参考信号比相后的相位差,Δφ1为φ1与φm之差,Δφ2为φ2与φm之差。以φ1为参考零点,由图5可知A测头在当前位置的待测角位移θa可表示为:

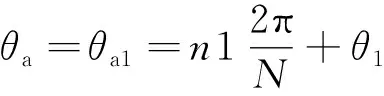
(9)

而当存在偏心状态时,B测头输出信号与参考信号比相后得到的φ2相比于参考零点发生偏移,经过式(6)处理后,得到Δφ2与θ的关系图,如图5所示。此时,B测头的角位移相对于参考零点偏移了Δθ,Δθ的大小与安装偏心程度成正比,则当前实际待测角位移θa可表示为:

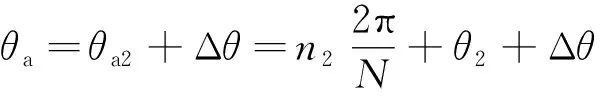
(10)

根据式(9)和式(10)可知,θa1≠θa2,因此A测头和B测头输出信号经过比相后得到的绝对位置是不相同的。于是,通过4个测头在偏心状态下的绝对位置差异便可实现传感器的安装偏心状态自诊断。

3 自诊断测量系统设计

为了实现传感器偏心状态自诊断测量,设计了自诊断测量系统。通过集成的时栅信号采集与处理电路对信号进行处理。信号处理基本流程图如图6所示。

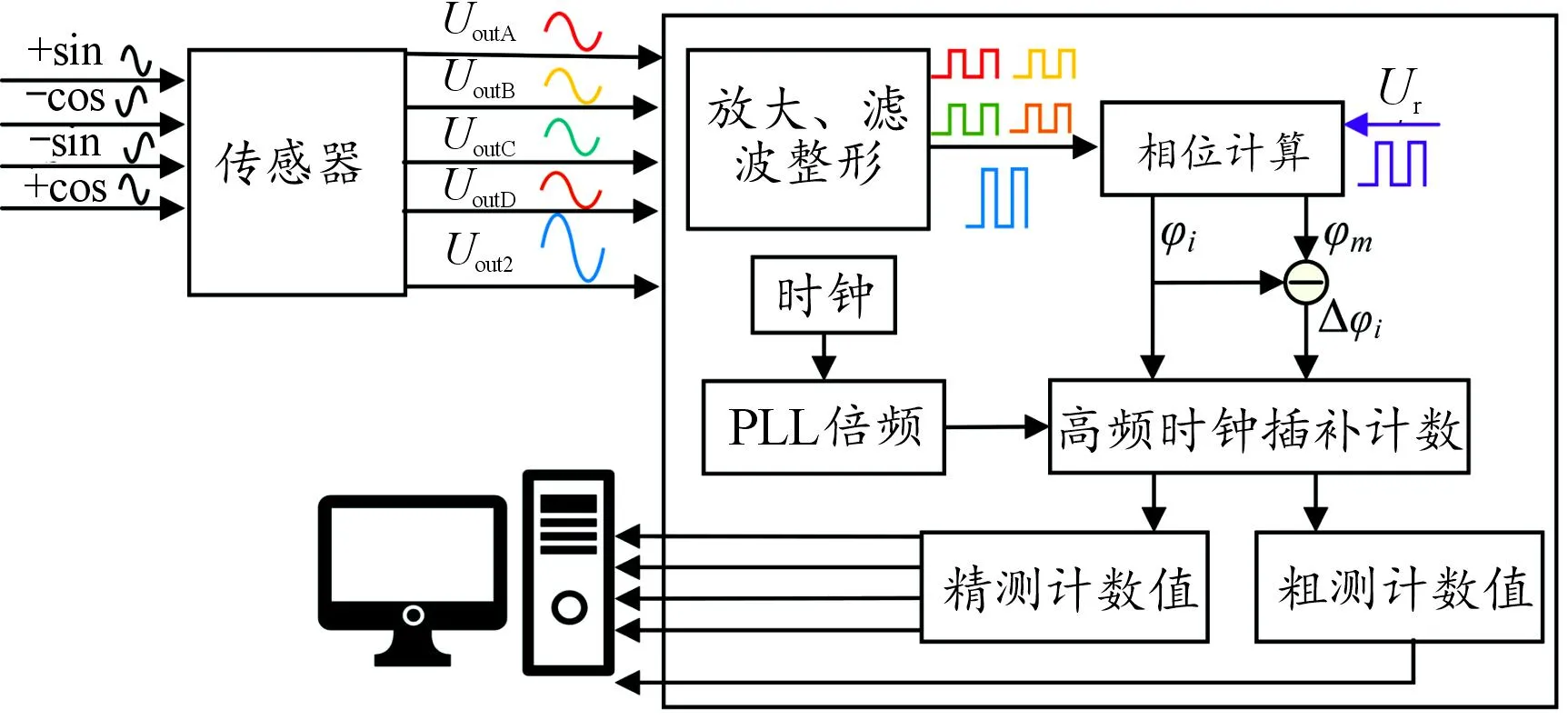
图6 信号处理流程图

首先将传感器耦合的内外圈信号处理整形成方波信号。然后与FPGA内的同频参考信号Ur比相后得到外圈4路信号相位差φi(i=1、2、3、4)、内圈信号相位差φm以及内外圈相位差的差值Δφi。最后利用FPGA内部数字锁相环(PLL)产生的高频时钟脉冲对相位差值进行插补计数,将得到的包含角位移信息的计数值通过串口实现与上位机的数据传输。

上位机采用LabVIEW软件搭建,实现相位信息计数值解码和算法分析[20],并将各项数据进行实时显示。上位机界面如图7所示,主要包括:① 测量模式选择区域(偏心诊断、绝对误差测试);② 4路测头角位移数值区域;③ 诊断标准值设定与指示区域;④ 偏差值显示区域;⑤ 采样数据界面;⑥ 指令操作区域。

图7 上位机界面图

将对径测头A、C(或B、D)读数值的偏差值Δθ与上位机设定的最大允许误差值θf进行对比,诊断偏心程度并通过指示灯颜色反映当前安装偏心状态。根据偏差值的大小不同,指示灯区域的颜色会呈现渐变显示。① 当Δθ<θf时,指示灯为绿色,表明安装处于相对同心的状态;② 当Δθ>θf时,指示灯为红色。程序设计流程图如图8所示。

图8 程序设计流程图

4 实验平台与测试结果

为了有效验证所提测量方法能实现传感器偏心状态下的自诊断,并保证实验结果的准确性,在保持温度为24 ℃、相对湿度为40%的千级超精密实验室内进行了实验验证,搭建了如图9所示的实验平台。该平台采用RPI公司的AP300型号的精密气浮转台作为传动系统,在整周范围内能实现±0.5"的定位精度。数据采集与信号处理电路集成于图9所示硬件电路中。采用印制电路板(printed circuit board,PCB)制造工艺制作了传感器样机。

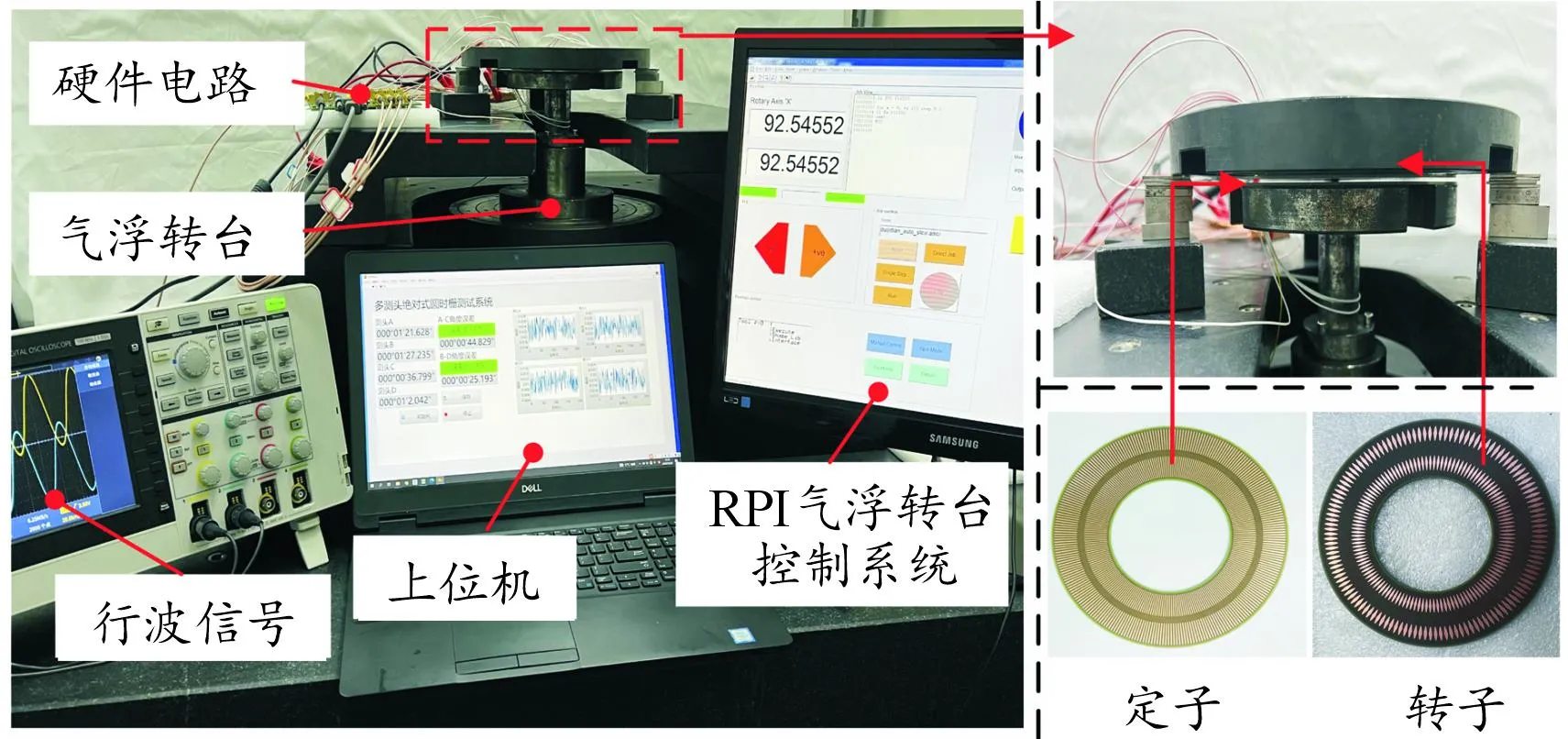
图9 实验平台

将转子安装于经过防震处理的大理石基座上,定子安装于精密气浮转台上,调整间隙为0.7 mm,利用配套的精密气浮转台控制系统控制转台转动,采用静态采样方式连续采集多个点进行传感器整周实验测试。

首先根据上位机诊断指示区域显示粗调,再根据偏差值进行微调,逐步调整传感器定转子处于相对同心的状态,对传感器整周以步长增量为7.2°来控制转台对传感器样机进行静态采样,采样点数为50。然后在转子对径位置布置4个千分表,以转子边缘为基准,沿1个偏心方向每次以0.02 mm逐步调整转子安装,使传感器安装处于偏心状态。以第1次安装作为0偏移量基准,记录测量结果误差峰峰值于表1中。根据测量误差绘制误差曲线,如图10(a)所示。

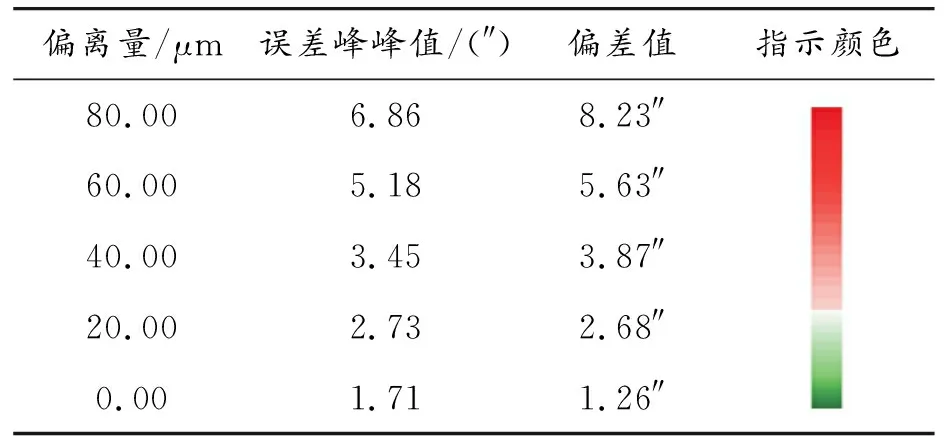
表1 测量误差峰峰值

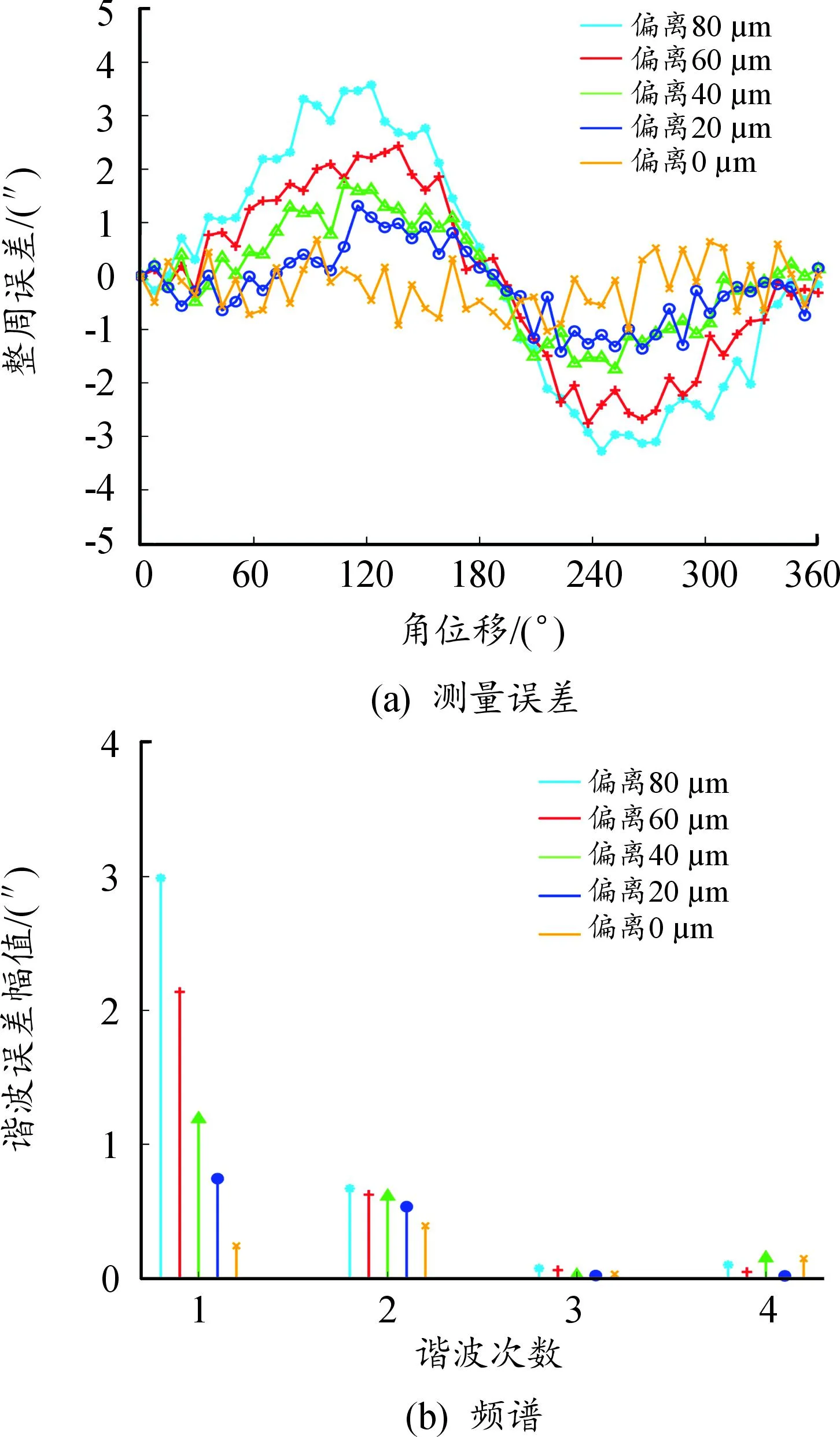
图10 测量误差曲线及频谱分析图

由表1和图10(a)可知,传感器转子相对于定子偏心程度越大,转子测头间的偏差值和测量误差峰峰值也越大,测量误差峰峰值与偏心量以及测头偏差值成正比,同时诊断指示区域颜色变化也反映了传感器偏心程度。在0～0.08 mm的偏移范围内,整周测量误差峰峰值分别为1.71″、2.73″、3.45″、5.18″、6.86″。通过傅里叶变换对上述测量数据进行频谱分析,频谱分析结果如图10(b)所示。

由图10(b)可知,偏心状态下整周误差以1次谐波误差为主,在0～0.08 mm的偏移范围内,1次谐波误差成分幅值分别为0.30″、0.82″、1.21″、2.15″、3.00″。经过自诊断指示逐步调整同心后,1次谐波误差相比于偏心状态明显减小。

由上述实验结果可知,偏心状态下整周测量误差包含较大的1次谐波误差成分。经过诊断指示逐步调整安装同心后,传感器整周测量精度相对偏心安装逐渐提高,最终调整后的整周测量误差精度为±1",1次谐波误差成分幅值大幅减小,传感器的测量精度得到了显著提高。

5 结论

提出了一种绝对式圆时栅偏心状态自诊断测量方法。该方法在绝对式圆时栅前期研究的基础上,采用多测头结构,通过偏心状态下外圈4个独立测头与内圈测头输出信号经过比相后所得绝对位移值不同实现了对传感器安装偏心状态的自诊断。搭建了基于LabVIEW的多测头圆时栅偏心状态自诊断测量系统,实现了对各测头输出信号以及绝对位置信息数据的处理。根据计算后的测头偏差值,实现了对安装偏心状态的诊断指示。通过实验验证了测量方法的可行性,结果表明,传感器调整后整周范围内测量误差精度为±1″,反映安装偏心的1次谐波误差成分幅值相比于未调整前大幅减小。后续将在现有的理论基础上对不同安装状态的自诊断方法展开研究,同时对现有测量系统进行扩容,将新的功能融入系统中,实现全方位、全状态的安装误差自诊断,并可结合软件程序的升级实现测量误差自补偿。