半挂汽车列车挂车转向PSO-LQR控制器设计

陆柯伟,徐晓美,秦勇杰,张 涌

(南京林业大学 汽车与交通工程学院, 南京 210037)

0 引言

半挂汽车列车因具有装载量大、运输成本低等特点,已成为公路运输的主要车型[1]。由于半挂汽车列车的牵引车与挂车通过牵引销铰接连接,因此整车纵向刚性较差。同时,由于挂车车轮不可转向,导致车辆在低速转弯时车轮轨迹与牵引车前轴车轮轨迹总存在偏差,增加了半挂汽车列车低速转弯的事故率。对此,国内外学者展开了关于半挂汽车列车低速转弯时挂车与牵引车前轴车轮轨迹偏差问题的研究。现有的解决方案主要包括主动改变挂车车轮转动方向和角度的主动转向系统[2-3]以及根据几何关系或力平衡控制挂车车轮转动的被动转向系统[4-5]。

近年来,随着控制技术的发展,挂车主动转向的研究得到了越来越多的关注。基于不同控制算法的主动转向控制系统陆续被提出,常用的控制算法包括PID控制、模糊控制、模型预测控制、线性二次调节理论(linear quadratic regulator,LQR)控制等。邵俊恺等[6]针对无人驾驶铰接式车辆设计了一种基于强化学习的自适应PID路径跟踪控制器,通过强化学习算法对PID参数进行在线自适应整定。邓召文等[7]设计了某重型半挂汽车列车牵引车的后轮主动转向模糊控制器和挂车车轮主动转向PID控制器,并仿真验证了控制器的有效性。Abroshan等[8]设计了模糊控制器和PID控制器控制车轮转向,以减小铰接车辆低速行驶的轨迹偏差。Guan等[9]基于模型预测控制为铰接车辆提出了一种综合路径和姿态控制的策略,以提高其横向稳定性。

比较而言,由于线性二次型最优控制LQR自身的优势,如能够利用较小的控制能量使系统状态变量维持在零值附近,可以对不稳定系统进行整定等[10],其在具有多自由度运动的汽车列车运动控制领域得到了更多的关注。Ni 等[11]设计了基于LQR的主动挂车转向系统,以提高多挂铰接重型车辆的低速机动性与高速稳定性。Kim等[12]基于LQR设计了半挂汽车列车的主动转向控制器,以最小化牵引车与挂车之间的质心侧偏角。Deng等[13]为提高铰接式重型车辆的方向性能,研究了三点预瞄驾驶员模型和LQR主动挂车转向控制策略。Deng等[14]基于LQR控制算法研究了牵引车和挂车后桥多轴转向的主动控制问题。显然,在LQR控制中状态量权重矩阵Q和控制能量权重矩阵R的选取直接影响控制效果。传统的依赖于专家经验的人为整定方式通常比较耗时,无法得到最优结果。对于此,近年来,研究人员开始采用一些进化算法对权重矩阵进行优化取值。孟宇等[15]提出一种基于预见信息的LQR控制策略,并应用遗传算法对状态量权重矩阵进行优化求解,从而实现了对铰接式车辆精确路径的跟踪控制。Qureshi等[16]设计了基于LQR的挂车主动转向控制器,并使用广义微分进化优化算法确定LQR控制器的加权矩阵。

鉴于上述研究现状,拟设计一种基于粒子群优化(particle swarm optimization,PSO)算法的挂车主动转向LQR控制器(简称为PSO-LQR控制器),基于PSO算法对状态量权重矩阵进行优化求解,以提高半挂汽车列车挂车车轮的轨迹跟踪精度。同时,探讨不同权重矩阵获取方式对挂车转向控制效果的影响程度。

1 模型构建

1.1 半挂汽车列车运动学模型

半挂汽车列车行驶时,牵引座承担半挂车的前部载荷,并且锁住牵引销带动半挂车移动。图1为牵引车以δ1f的前轮转角转向时牵引车与挂车各轮的运动关系。图1中,(X,Y)表示车辆位置的笛卡尔坐标系,X轴表示期望直线轨迹,Y轴表示距直线轨迹的偏差,称为轴线偏移距;P1为牵引车与挂车间的铰接点,其坐标为(x1,y1),P2为半挂车后轴的中点,其坐标为(x2,y2);x1和x2分别为铰接点和半挂车后轴中点对应于直线轨迹X轴上的坐标点;y1、y2分别为铰接点和半挂车后轴中点与X轴之间的偏差;O为牵引车转向圆的圆心,Q为牵引车转向轴中心点,OP1⊥P1Q;L1为牵引车前轴与铰接处的距离,L2为铰接处与挂车后轴间的距离;θ1为牵引车与半挂车间的铰接角度,θ2为半挂车相对于X轴的夹角,称之为半挂车位姿角;z1和z2分别为P1点和P2点的实际轨迹曲线。

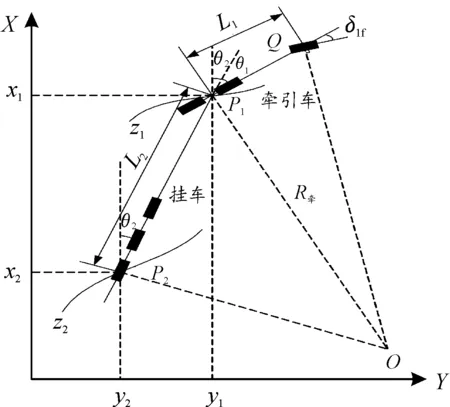
图1 半挂汽车列车的转向运动关系

为简化所要分析的半挂汽车列车模型,作如下假设:① 所述半挂汽车列车始终行驶在平坦路面上;② 牵引车以较低速度匀速行驶,驱动轮没有打滑;③ 连接牵引车和半挂车的鞍式牵引座位于P1处。基于上述假设,以及阿克曼原理可以得到半挂汽车列车低速转向运动的微分方程[17]:

d(θ1+θ2)/dz1=tanδ1f/L1

(1)

dθ2/dz1=tanθ1/L2

(2)

dy2/dz2=sinθ2

(3)

dx2/dz2=cosθ2

(4)

dz2/dz1=cosθ1

(5)

式(1)表示牵引车的运动规律;式(2)—式(4)表示半挂车的运动规律;式(5)表示牵引车与半挂车实际运动轨迹间的关系。

以x2表征上述牵引车与挂车的运动规律,坐标变换后的微分方程如式(6)所示。

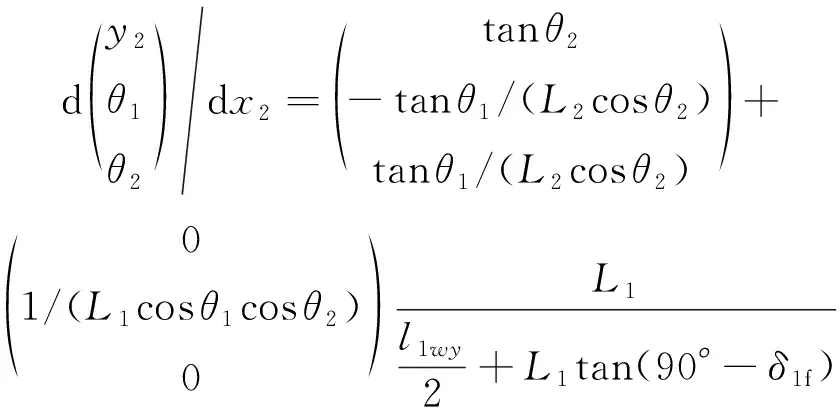
(6)

式中,l1wy为牵引车前轮轮距。

上述坐标变换关系可以写作:

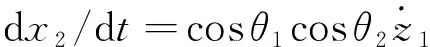
(7)

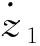
1.2 模型验证

为验证所构建的车辆模型的可靠性,利用TruckSim软件中的车辆模型对所建车辆模型进行运动关系验证。在TruckSim软件中选取3A Cab Over w/3A Euro Trailer 六轴半挂汽车列车作为标准参考模型,模型精度通过在稳态圆周路径下2种模型输出的挂车路径的一致性来体现。

国标GB1589—2016[18]对半挂汽车列车必须通过的通道圆作了定义,该通道圆外圆直径和内圆直径分别为25 m和10.6 m。考虑到半挂汽车列车的车宽为2.438 m,因此选择半径为11.5 m的稳态圆形路径作为模型验证的仿真路径。

在模型验证试验中,设置路面附着系数为0.85,半挂汽车列车以20 km/h的速度先沿直线路径行驶一段距离,然后逐渐进入圆形路径。2种车辆模型在圆形路径下的轨迹跟踪效果如图2所示。图2中,Tractor T和Trailer T分别表示TruckSim软件输出的牵引车和挂车运动轨迹,Tractor L和Trailer L分别表示由数学模型得到的牵引车和挂车运动轨迹。

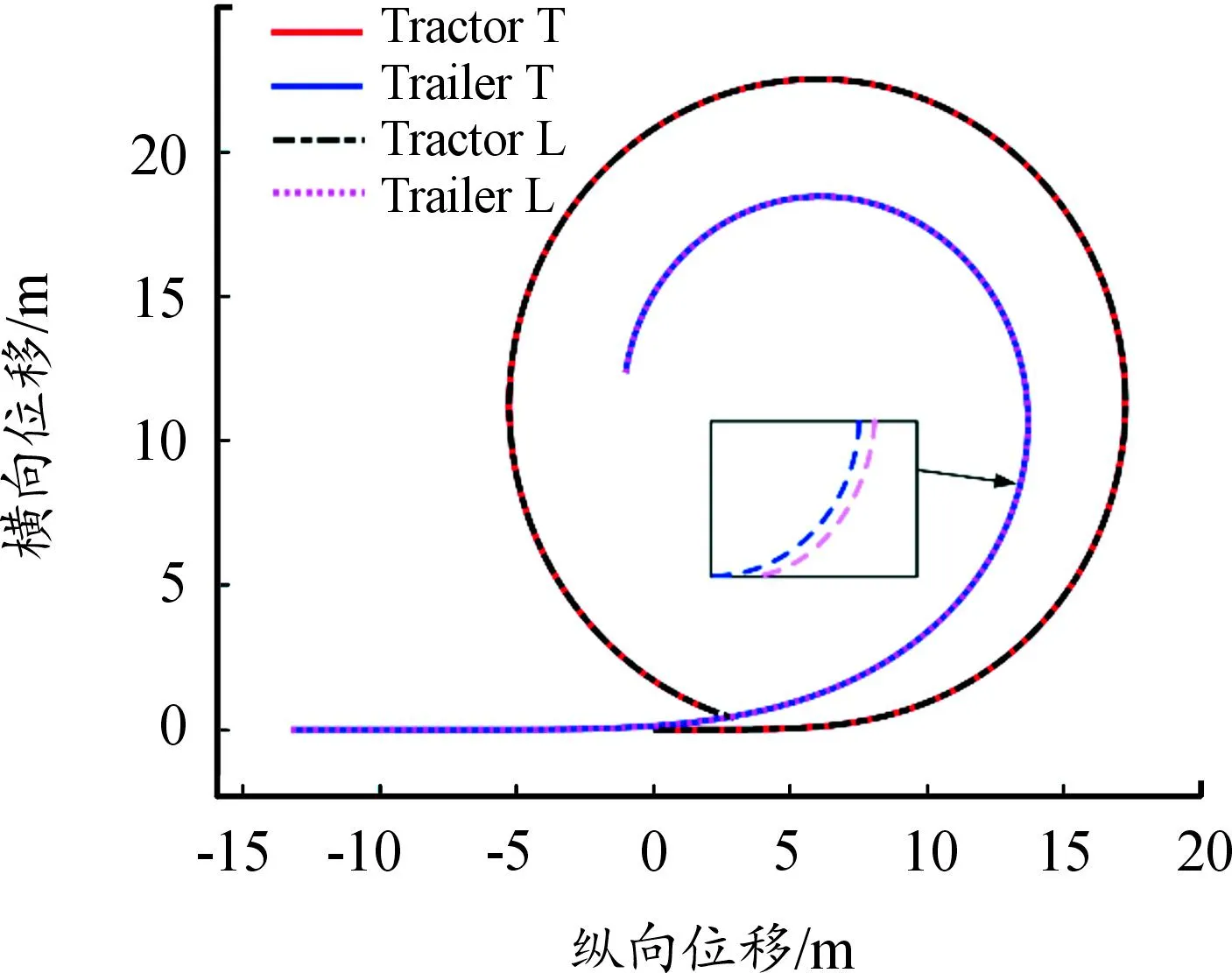
图2 2种模型输出的运动轨迹比较

由图2可以看出,当挂车达到稳定跟踪状态时,由数学模型输出的挂车轨迹与TruckSim软件中的挂车轨迹几乎完全重合,可见所建半挂汽车列车低速转向运动学模型具有较高的可靠度,可用于后续低速转向轨迹跟踪控制器的设计研究。

2 PSO-LQR控制器设计

2.1 转向控制状态方程

定义关于状态向量和控制向量的二次型性能指标为

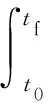
(8)

式中:Q为n×n维半正定(或正定)对称矩阵,R为m×m维正定矩阵,tf为系统运行时间。

最优控制规律中的反馈矩阵K需要求解黎卡提(Riccati)矩阵微分方程。Riccati方程描述为

ATP+PA-PBR-1BTP+Q=0

(9)

式中:P为待求解的未知矩阵;A、B为系统状态方程中的状态传递矩阵和控制系数矩阵,Q、R为二次型性能指标中的损失函数权重矩阵。

求解 Riccati方程中的P矩阵,反馈矩阵K可表示为

K=-R-1BTP

(10)

在低速工况下,选择牵引车与挂车轨迹的横向偏差和航向角偏差作为评价半挂汽车列车低速轨迹跟踪的性能指标,构建如式(11)所示的优化目标函数。

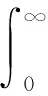
(11)

式中:ye和θe分别为牵引车与挂车间的横向偏差和航向角偏差;δ2r为挂车后轴车轮的转角控制输入;W1、W2、W3分别为半挂车的横向偏差、航向角偏差以及挂车后轴车轮转角输入的加权因子。

由式(8)可知,Q、R矩阵可表示为

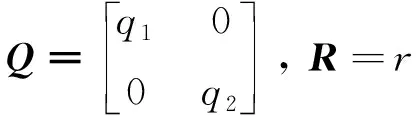
(12)

式中:q1、q2分别为横向偏差ye和航向角偏差θe的权重系数,r为挂车后轴车轮转角的权重系数。

通过设定合适的Q、R矩阵,求解Racctita方程可以得到反馈矩阵K。LQR轨迹跟踪控制器的最优控制律u*(t)可表示为

u*(t)=-Kx(t)=-k1*ye-k2*θe

(13)

2.2 权重矩阵参数范围分析

LQR轨迹跟踪控制器的跟踪效果受权重矩阵参数影响,确定其值通常需要通过人工设定参数并进行大量的试验分析。PSO算法可以通过设定合适的适应度函数,更好地搜索参数定义域范围之内的最优解。通过PSO算法可以对LQR轨迹跟踪控制器的权重矩阵参数进行批量化搜索[19]。

基于PSO设计的LQR控制器需要事先确定权重矩阵参数值的范围,在参数范围内搜索最佳个体。由于此系统是能控线性定常系统,当参考速度、预瞄距离不发生变化时,依据Matlab中的LQR求解器求解出的反馈矩阵K由Q、R矩阵参数决定。其中,Q矩阵中权重系数越大时,表示该状态变量在性能函数中越重要,对应的反馈矩阵K参数绝对值越大;R矩阵中的r表示对挂车后轮转角的约束系数,其值越大,控制约束越大,反馈矩阵K参数绝对值越小,δ2r的绝对值越小。因此,分析反馈矩阵K的参数随权重矩阵变化趋势,可以大致确定权重矩阵参数值的范围。在Matlab程序中通过设置不同Q、R矩阵及其参数值的变化,得到对应的反馈矩阵K的参数值,其结果如图3和图4所示。

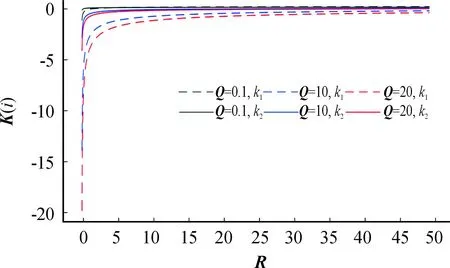
图3 K矩阵随R矩阵变化趋势

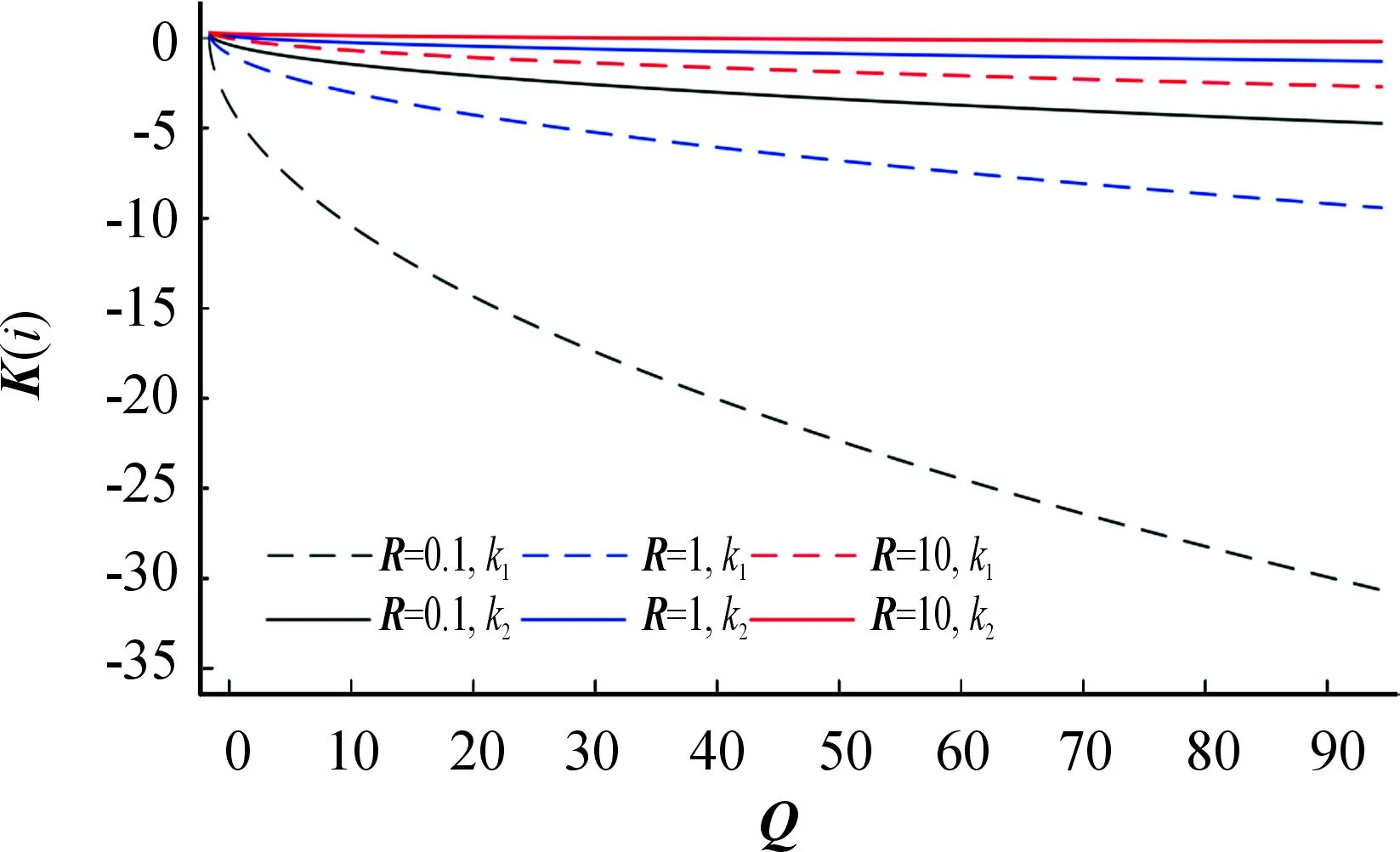
图4 K矩阵随Q矩阵变化趋势

由图3可知,k1、k2初始值的绝对值和稳定值的绝对值都随着Q矩阵参数增大而增大,当Q矩阵参数固定时,随着R增大反馈矩阵参数k1、k2的绝对值迅速减小并趋于稳定值。

图4显示,当R矩阵参数不变时,随着Q矩阵参数增大,反馈矩阵参数k1、k2绝对值逐渐增大,其中k1的变化速率大于k2。随着R对系统的约束能力增强,k1、k2绝对值整体呈现减小趋势,同时变化速率减小。

保持R不变,通过分析Q矩阵中q1、q2对反馈矩阵参数变化的影响可以发现,q1不变时,增大q2,k1的绝对值保持稳定基本不变,k2的绝对值变大;q2不变时,增大q1,k2的绝对值保持稳定基本不变,q1的绝对值变大。

根据式(13)可知,当反馈矩阵K参数绝对值较大时,将导致最优控制律u*(t)过大,半挂车出现陡转,因此反馈矩阵K参数值不能过大。经过权重参数对反馈矩阵参数的影响分析可知:当R∈[0.1,1]时,约束适当,能够较明显地体现出权重矩阵Q参数q1、q2变化对反馈矩阵K参数k1、k2值的影响;当q1∈[0.1,5.6],q2∈[0.1,10]时,k1、k2的值较为合适,挂车跟踪过程较为平稳。

2.3 权重参数搜索模型

在利用PSO对权重矩阵参数进行批量优化时,需要构建LQR轨迹跟踪控制器的Simulink模型和衡量控制效果的适应度函数。定义二次型性能指标为:

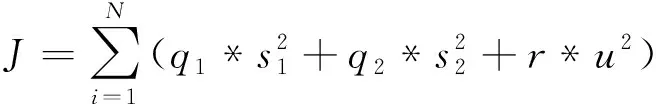
(14)

式中:s1为横向偏差,s2为航向角偏差,J为被控系统的综合指标。

通过判断二次性能指标值可以看出控制效果的好坏,J值越小表示控制效果越好,J值越大表示控制效果越差。ts表示达到稳定跟踪状态所需时间,即挂车与牵引车间的横向误差达到稳定所需的时间。半挂汽车列车的路径跟踪控制性能不仅由性能指标J体现,达到稳定跟踪状态所需时间ts的长短也是决定路径跟踪控制性能好坏的重要指标。所以综合考虑J和ts的值设计适应度函数。由于J和ts单位不同,因此需要对适应度函数进行相关处理。定义适应度函数为

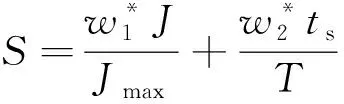
(15)

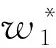
3 仿真试验

3.1 控制器仿真参数设置

半挂车低速轨迹跟踪LQR控制器中的权重矩阵R表示对挂车后轮转角的约束,为了减小PSO的寻优难度,将R设置为固定值,只要确保所设定的值能表现出对控制动作的约束性能即可[19]。

为实现Matlab中所搭建的车辆模型的闭环仿真,引入单点预瞄驾驶员模型[20],使半挂汽车列车牵引车前轴中心点沿着给定的路径行驶。利用PSO算法迭代寻优方法,得到权重矩阵Q参数定义域内的最优值q1与q2,进而求得反馈矩阵K的参数k1、k2。设置仿真步长Ts=0.1 s,预瞄距离为3 m,车辆行驶速度为20 km/h。PSO算法的初始化参数如表1所示。

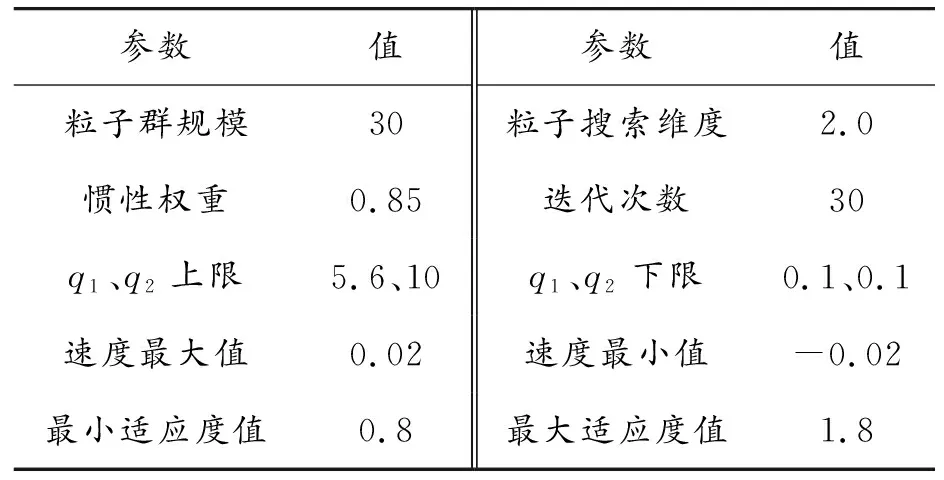
表1 初始化参数

为验证所设计的LQR轨迹跟踪控制器的有效性,在Matlab中对挂车具有转向控制功能的半挂汽车列车开展仿真试验。同时,为了验证基于PSO算法优化LQR控制器权重参数的有效性,选择基于PSO算法优化权重矩阵和人为整定的权重矩阵作为LQR控制器的Q权重矩阵,利用适应度函数计算出人为整定权重矩阵Q的适应度值,并根据适应度值的大小初步评估不同控制器的控制效果。基于上述对权重矩阵的分析,设定约束矩阵R分别为0.1和1,权重矩阵Q参数范围设置为q1∈[0.1,5.6]、q2∈[0.1,10],q1、q2为PSO算法中粒子群个体中的粒子。

3.2 R=0.1的仿真试验与结果分析

将控制约束矩阵R设为0.1,人为整定的权重矩阵Q=[2.569 0; 0 7.426],通过适应度函数可以求得权重矩阵适应度S=1.387。

PSO算法首先进行粒子初始化,并计算初始化粒子的适应度值,随后进行迭代寻优,寻找全局最优个体。优化结果显示,在30次迭代结束后,全局最优个体适应度值为0.996,对应的权重矩阵为[5.615 0; 0 2.305]。将人为整定的权重矩阵和适应度值,以及基于PSO初始化和最终搜索的结果进行比较,如表2所示。为方便表述,表中将全局最优个体简称为全局最优,将粒子初始化结果中适应度值最小的粒子简称为初始最佳,将粒子初始化结果中适应度值最大的粒子简称为初始最差。

表2 R=0.1时不同权重矩阵确定方式的结果对比

分析表2中各个适应度值可以预知:当R=0.1时,基于不同方式得到的权重矩阵Q优化后的挂车路径跟踪效果由好到差依次应为:全局最优>初始最佳>人为整定>初始最差。

为进一步验证基于PSO搜索最优权重矩阵的准确性,将表2中4组不同权重矩阵得到的反馈矩阵K作为LQR控制器的反馈矩阵,在单U形和匝道螺旋2种参考路径下开展仿真试验。

单U形参考路径由三段组成,刚开始是一段20 m长的直线路径,然后是半径为15 m的半圆弯道,最后依然是一段20 m长的直线路径。单U形路径的仿真结果如图5所示。图5(a)为不同Q矩阵下车辆跟踪单U形路径时,挂车运动轨迹与单U形参考路径的比较。图5(b)和图5(c)分别为不同Q矩阵下,挂车运动轨迹与参考路径间的跟踪误差与航向角误差。

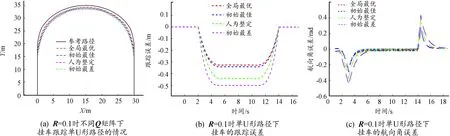
图5 R=0.1时单U形路径仿真结果

由图5可知,当R=0.1时,全局最优、初始最佳、人为整定和初始最差4种情况对应的挂车跟踪给定单U形路径的误差分别为0.325、0.340、0.440和0.495 m。全局最优个体对应的权重矩阵Q优化后的挂车路径跟踪误差相较于初始最差个体对应的优化权重矩阵Q的误差0.495减小了34.3%,相较于人为整定跟踪误差减小了26.1%,同时在全局最优矩阵条件下,挂车能够更快地进入稳定的跟踪状态。此外,相比于其他3种权重矩阵确定方式,全局最优个体对应的权重矩阵Q优化后的航向角能以最快的速度趋于稳定。

匝道螺旋路径由一段半径逐渐减小的曲线构成,最小处的半径为11.5 m。其仿真结果如图6所示。图6(a)为不同Q矩阵下车辆跟踪匝道螺旋路径时,挂车运动轨迹与匝道螺旋参考路径的比较。图6(b)为不同Q矩阵下,挂车运动轨迹与参考路径间的跟踪误差。

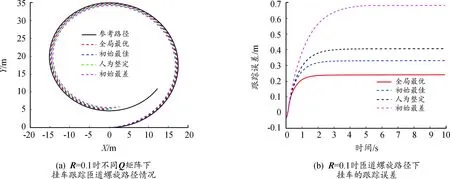
图6 R=0.1时匝道螺旋路径仿真结果

由图6可知,当R=0.1时,全局最优、初始最佳、人为整定和初始最差4种情况对应的挂车跟踪给定匝道螺旋路径的跟踪误差分别为0.239、0.329、0.405和0.68 m。全局最优个体对应的权重矩阵Q优化后的挂车路径跟踪误差相较于初始最差个体对应的优化权重矩阵Q的误差0.68减小了64.8%,相较于人为整定跟踪误差减小了40.9%,同时在全局最优矩阵条件下,挂车能够更快地进入稳定的跟踪状态。

3.3 R=1的仿真试验与结果分析

将控制约束矩阵R的值设为1,人为整定的权重矩阵Q=[2.569 0; 0 7.426],通过适应度函数可以求得权重矩阵适应度s=1.390。优化结果表明,在30次迭代结束后,全局最优个体适应度值为1.008,对应的权重矩阵为[5.601 0; 0 0.700]。将人为整定的权重矩阵和适应度值,以及基于PSO初始化和最终搜索的结果进行比较,如表3所示。分析表3中各个适应度值可以预知:当R=1时,基于不同方式得到的权重矩阵Q优化后的挂车路径跟踪效果,由好到差依次应为:全局最优>初始最佳>人为整定>初始最差。

表3 R=1时不同权重矩阵确定方式的结果对比

将表3中4组不同权重矩阵得到的反馈矩阵K作为LQR控制器的反馈矩阵,在单U形和匝道螺旋2种参考路径下开展仿真试验。

单U形路径下的仿真结果如图7所示。图7(a)为不同Q矩阵下挂车跟踪单U形路径时的运动轨迹与单U形参考路径的比较。图7(b)为不同Q矩阵下挂车运动轨迹与参考路径间的跟踪误差。

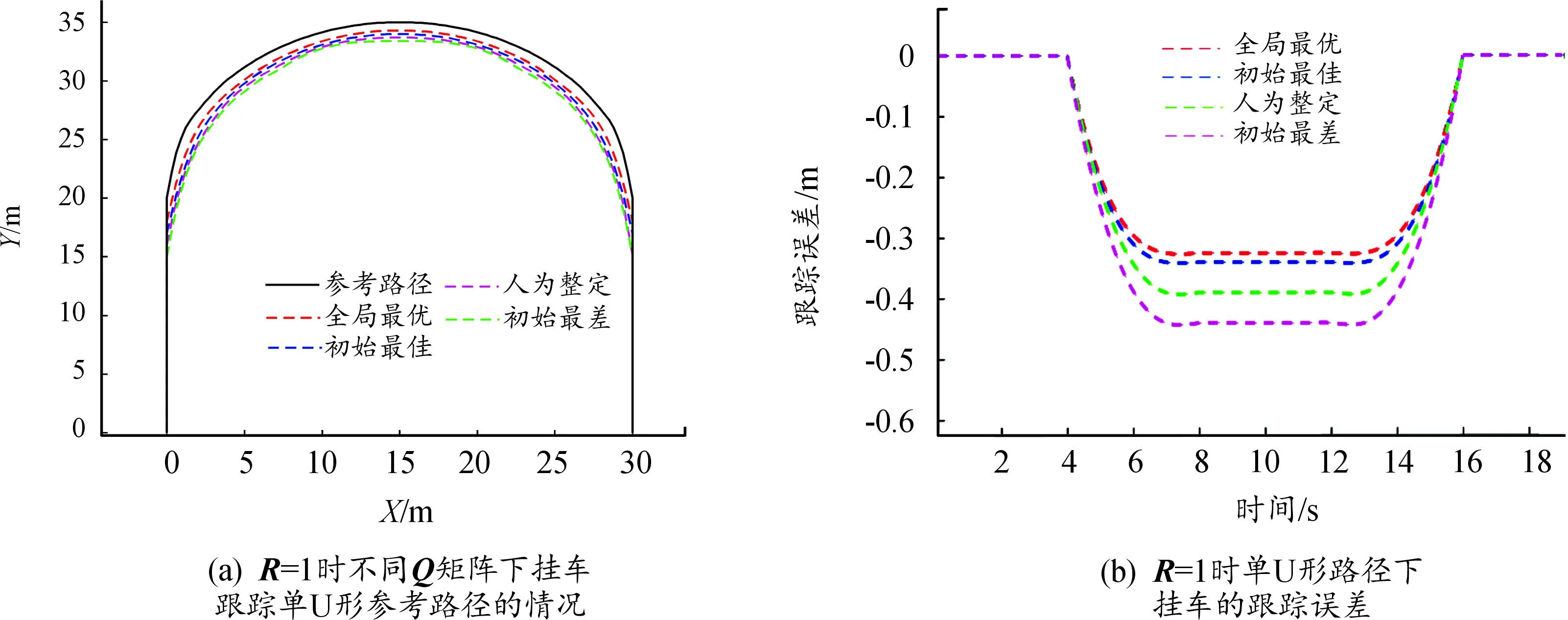
图7 R=1时单U形路径仿真结果

由图7可知,当R=1时,全局最优、初始最佳、人为整定和初始最差4种情况对应的挂车跟踪给定单U形路径的跟踪误差分别为0.319、0.339、0.396和0.473 m。全局最优个体对应的权重矩阵Q优化后的挂车路径跟踪误差相较于初始最差个体对应的优化权重矩阵Q的误差0.495减小了32.5%,相较于人为整定跟踪误差减小了19.4%,在全局最优矩阵条件下,挂车能够更快进入稳定跟踪状态。

匝道螺旋路径仿真结果如图8所示。图8(a)为车辆在不同权重矩阵Q下跟踪给定匝道螺旋参考路径时参考路径与挂车运动轨迹的比较,图8(b)为不同Q矩阵下参考路径与挂车轨迹间的跟踪误差。

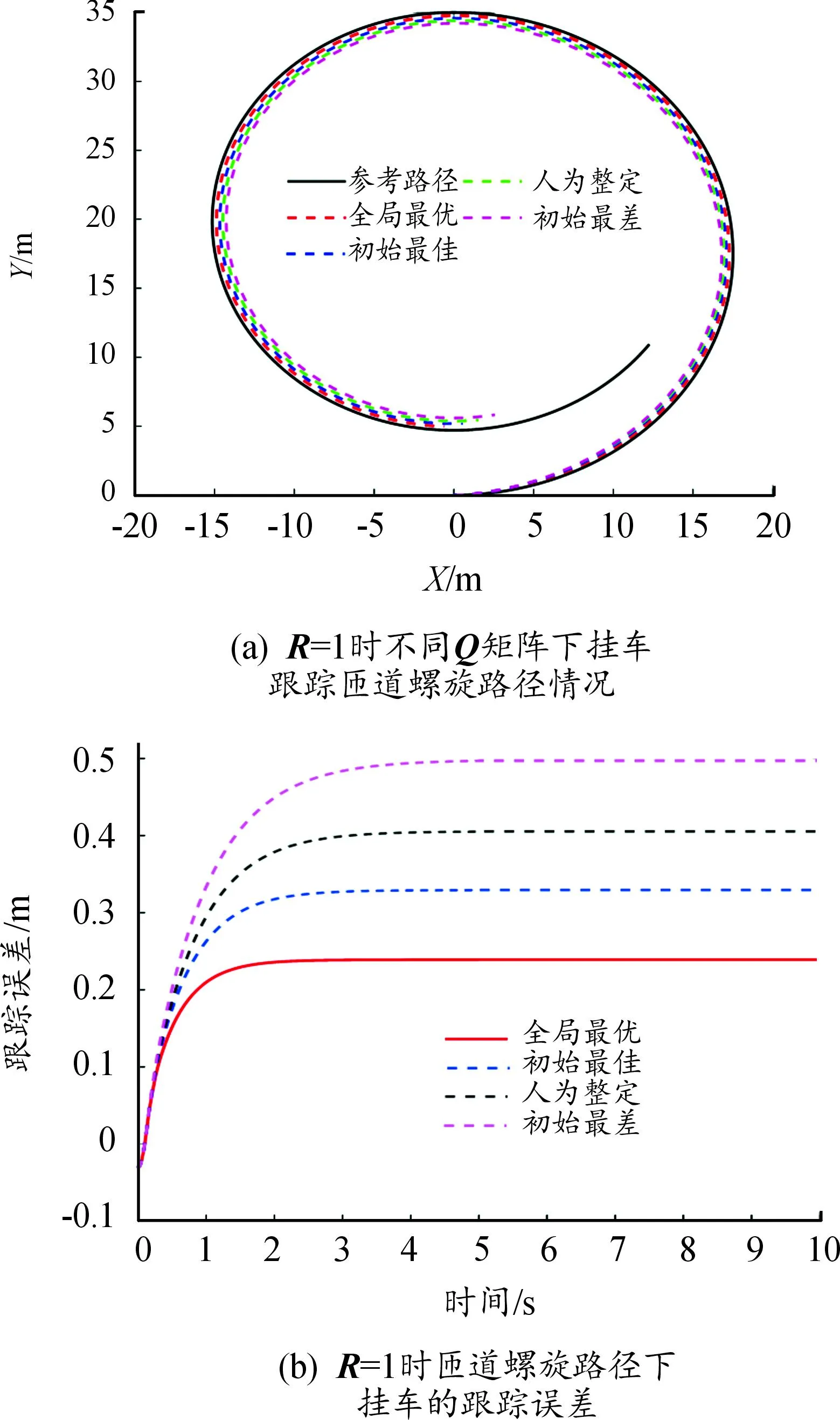
图8 R=1时匝道螺旋路径仿真结果

由图8可知,当R=1时,全局最优、初始最佳、人为整定和初始最差4种情况对应的挂车跟踪匝道螺旋路径的误差分别为0.224、0.315、0.396和0.497 m。全局最优个体对应的权重矩阵Q优化后的挂车路径跟踪误差相较于初始最差个体对应的优化权重矩阵Q的误差0.497减小54.9%,相较于人为整定跟踪误差减小43.4%,在全局最优矩阵条件下,挂车能够更快达到稳定的跟踪状态。

结合上述2种路径下的仿真试验结果可知,控制权重矩阵R分别为0.1和1时,全局最优个体对应的权重矩阵优化后的挂车跟踪误差最小,因此基于PSO-LQR设计的控制器可使挂车具有最佳的路径跟踪效果。权重矩阵R的增大使得挂车在2种路径下的跟踪误差都略有减小。相比于人为整定权重矩阵,基于PSO优化LQR权重矩阵可以显著提升工作效率,缩短车辆进入稳态跟踪的时间。

4 结论

针对半挂汽车列车低速转向挂车跟踪牵引车轨迹性能较差的问题,设计了一种基于粒子群优化算法的挂车主动转向LQR控制器,通过一系列仿真分析,得出以下主要研究结论:

1) 在权重矩阵R确定时,基于不同方式得到的权重矩阵Q优化后的挂车路径跟踪效果,由好到差依次为:全局最优>初始最佳>人为整定>初始最差,同时经PSO优化后的LQR控制器能使挂车更快地进入稳定跟踪状态,提高半挂汽车列车的低速转向安全性。

2) 当R取作0.1和1时,相较于人为整定方式得到的权重矩阵Q优化后的挂车路径跟踪误差,全局最优对应的挂车路径跟踪误差在U形路径下分别减小了26.1%和19.4%,在匝道螺旋路径下分别减小了40.9%和43.4%。也即,基于PSO优化LQR权重矩阵可以获得更为精确的挂车路径跟踪效果。此外,权重矩阵R增大,挂车在U形和匝道螺旋2种路径下的跟踪误差都略有减小。