基于流固耦合的轮胎花纹滑水性能研究

李 波,高陈诚,贝绍轶,刘 涛,林 棻,殷国栋

(1.江苏理工学院 汽车与交通工程学院, 江苏 常州 213001;2.通用装备研究所, 北京 102202;3.清华大学苏州汽车研究院, 江苏 苏州 215200;4.南京航空航天大学 能源与动力学院, 南京 210016;5.东南大学 机械工程学院, 南京 210096)

0 引言

作为车辆的基本组成部分之一,轮胎是车辆与道路接触并保持车辆动态的惟一有效部分。轮胎承载负荷,吸收冲击,对车辆安全有直接影响[1]。如今,轮胎的安全性越来越受到人们的关注。研究表明,全球交通事故案例中大约有1/5是发生在潮湿路面上[2-3]。轮胎在湿滑路面上高速行驶时,积水无法通过轮胎花纹沟槽排尽,楔形水膜区域的动水压力抵消了路面对轮胎的法向支持力,产生轮胎滑水现象,影响行车安全,应尽量避免。轮胎滑水现象的研究在道路交通安全方面有着重要的意义。随着高性能计算机的普及,通过有限元仿真研究轮胎滑水现象已经成为主流方法,国内外众多学者对此展开了深入的研究。

在纯流体仿真方面,董斌等[4]运用了大型有限元仿真软件Fluent,计算了不同工况下胎面所受的水流动压力和胎面接触区域的水流速度分布,并对比分析了不同花纹轮胎的滑水性能。此外,王国林等[5]采用计算流体力学的多相流(空气和水)仿真方法,用动水压力间接反映轮胎的滑水特性,并利用此方法预测轮胎的临界滑水速度。

近些年来,多物理场耦合的仿真技术发展迅速,采用双向流固耦合的仿真方法研究轮胎的滑水性能逐渐显现出优越性。双向流固耦合能实现轮胎和水膜数据的动态交互,提高仿真精度。臧孟炎等[6]建立了基于LS-DYNA软件的轮胎滑水模型,研究了不同水膜厚度下车辆临界滑水速度的变化以及轮胎滑水时水流流动的状态。Zeinab等[7]利用SPH方法研究了侧偏角、水深等影响因素对湿滑路面上轮胎侧偏特性的影响。而Jeong等[8]则提出了一种估算薄层水膜情况下路面摩擦因数的方法,解决了薄层水膜仿真计算难的问题。

通过上述国内外学者对轮胎滑水数值模拟的研究论述,不难发现:轮胎研究者已经通过仿真模拟取得了许多成果,指导轮胎的开发与生产,但在花纹结构优化对轮胎滑水性能的影响方面研究较少。

以某厂家提供的205/55 R16轮胎为例,基于Abaqus CEL流固耦合方法,建立轮胎滑水模型。通过优化欧拉区域提高计算的精度和效率,并分析不同充气压力和水膜厚度对轮胎临界滑水速度的影响。之后,通过2种方法优化轮胎花纹结构并对优化前后子模型和整个轮胎进行的滑水性能相关参数的对比分析,验证优化方法的合理性。

1 理论背景

1.1 轮胎的水滑机理

当车辆在湿滑路面上高速行驶时,水膜会被压缩向前移动,形成一个动态水压。这个水压会影响车轮与路面之间的力平衡,减小地面对轮胎的支持力,并导致车轮部分抬离地面。随着车速的增加,车轮和水的挤压作用不断增强,直到车轮彻底失去与地面的接触,产生“滑水现象”。滑水现象会导致车辆的制动和转向能力减弱,影响行车安全,因此需要避免。

在潮湿、湿滑的路面上行驶时,轮胎会遇到3个不同的区域:水膜区(A)、过渡区(B)和直接接触区(C),如图1所示[9]。水膜区是轮胎与路面之间最外层的区域。在这个区域,水分形成了一个薄水膜,覆盖在路面上。这个水膜阻碍了轮胎与路面之间的有效接触,降低了摩擦力。轮胎很难克服水膜产生的动水压力,因此附着力较弱。过渡区位于水膜区与直接接触区之间。当轮胎滑过水膜区时,水分会被挤压到过渡区域。在这个区域,轮胎与路面之间的接触逐渐增加,同时水分逐渐被排除。然而,过渡区的摩擦力仍然不足以提供充分的抓地力,轮胎仍然处于滑行状态。直接接触区是轮胎与路面之间的最内层区域,也是最关键的区域。在这个区域,轮胎与路面实际接触,并通过摩擦力提供牵引力和抓地力。然而,在湿滑路面上,水膜和过渡区的存在会影响直接接触区的附着力,使轮胎的抓地力降低,导致滑行风险增加[10]。

图1 轮胎滑水原理示意图

这3个区域的存在和特点在轮胎滑水过程中起着重要作用。水膜区和过渡区导致附着力降低,而直接接触区是提供抓地力的关键区域[11]。此外,轮胎花纹优化的目的是能够及时把A、B区域的水排出,降低滑水现象的出现概率,从而提高行车安全。

1.2 数值模拟方案选择

针对轮胎滑水有限元计算模型,目前主要有2种方法:一种是计算流体力学的CFD方法,另一种是建立的拉格朗日体和欧拉体耦合计算的CEL方法[12]。

对于前者,具有较强的流体分析能力,能较为透彻地分析楔形水膜的动压力、流体的速度场,代表软件有Fluent、STAR-CCM+等,但它在处理从结构出发的复杂非线性的耦合问题能力上还有一定欠缺。在捕捉轮胎与地面和水域接触区的变化复杂的花纹时,较为困难。此外,对于高速旋转的轮胎模型,流体区域动网格的处理难度以及计算量都相对较大。

对于后者,需求体现在结构和流体相互作用过程中,需要关注结构物的载荷和运动特性,而Abaqus计算高度非线性结构动力学问题非常成熟。但CEL相较于CFD方法,短板也很明显,虽然确实包括延伸到层流的黏性效应,但是不包括任何湍流效应,例如在模拟圆柱绕流时观察不到流动涡流和流动分离现象[13],如图2所示。但是在水流冲击轮胎的情况下,冲击持续时间短且高度瞬态,湍流效应对结构载荷不太重要,CEL非常适合。因此,综合考虑之下,选择目前主流的计算轮胎滑水的CEL方法。

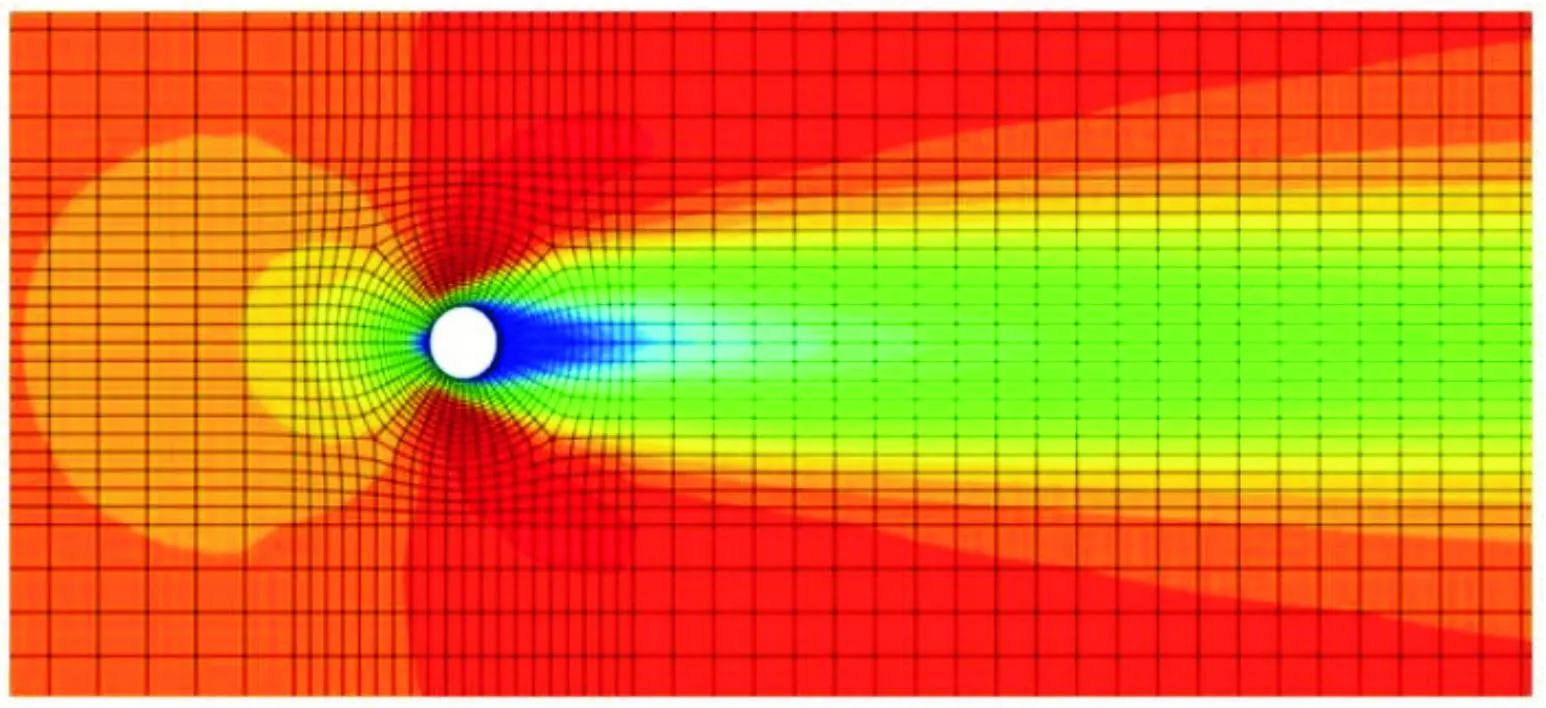
图2 CEL模拟圆柱绕流结果

1.3 轮胎滑水实验研究

Horne等[14]在1963年研究汽车在湿滑路面时水流的运动特征以及轮胎的力学性能,并推导出了具有普适性的NASA临界滑水速度经验公式。

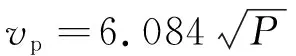
(1)

式中:vp为临界滑水速度;P为轮胎充气压力。

NASA滑水经验公式只推导出了临界滑水速度与轮胎充气压力的关系,但没能研究出水流特性以及轮胎结构特征对临界滑水速度的影响。Dunlap等[15]通过大量实验将水膜厚度和花纹结构等因素考虑进去,丰富了滑水经验公式。

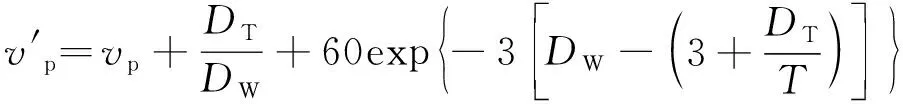
(2)

式中:v′p为预测临界滑水速度;DT为轮胎花纹深度;DW为水膜厚度;T为胎面宽度。

根据本文中轮胎模型可知,P=230 kPa,DT=8 mm,DW=10 mm,T=205 mm,代入式(2)中,计算v′p,为93.07 km/h。

2 有限元建模

2.1 轮胎有限元模型建立

子午线轮胎是由多种不同的材料构成的,包括胎体、钢丝帘子、芯体、胎面、胶条等部分,它们的不同组合方式和使用方法,可以根据轮胎的不同用途和特性来进行调整[16]。轮胎具有高度非线性的特点,因此,在建立轮胎模型时,需要以保证模拟精度为基础,对轮胎进行合理的简化,使其结构尽量简单,并节省计算时间。

以205/55 R16型号的轮胎为研究对象,通过AutoCAD中多段线工具,对轮胎截面实物图进行二维轮廓的描绘,如图3(a)所示。以dwg文件格式将轮廓线导入CATIA中,根据轮胎型号进行等比例缩放,将截面旋转成三维实体并对横向花纹进行设计,轮胎花纹选择滑水性能略优的垂直复杂花纹形式[17],轮胎三维模型如图3(b)所示。

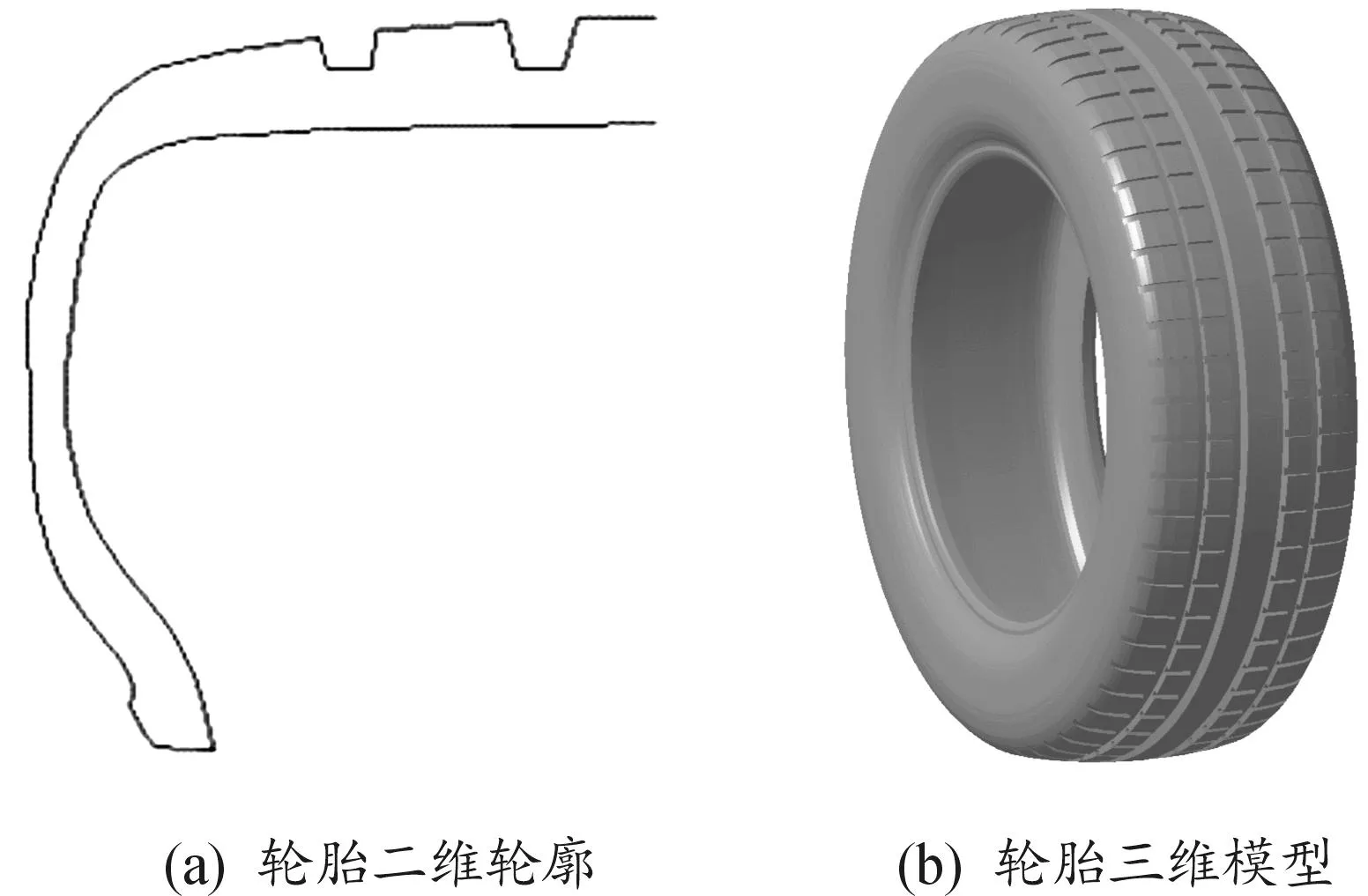
图3 轮胎二维轮廓和三维几何模型

通过HyperMesh进行网格划分。在绘制二维网格的基础上,通过扫掠生成轮胎模型的一个子部分的网格,如图4(a)所示,最后使用镜像和阵列生成如图4(b)所示整个轮胎网格。总体网格基本都是六面体结构化网格,质量较好,网格单元数量为52 560。

图4 轮胎网格模型

轮胎定义为均匀正交各向异性弹性材料,材料参数如表1所示。

表1 材料参数

2.2 轮胎静力学模型评估

在进行轮胎滑水仿真之前,静力学模型的评估和验证非常重要,因为轮胎流固耦合的求解需要依赖于轮胎静力学模型的求解结果。

轮胎静力学分析主要分为充气、强制位移和负载3个工况,具体工况设置如下:

1) 充气工况。约束轮胎与轮辋连接面的参考点的各方向自由度,轮胎内侧施加0.23 MPa压力。

2) 强制位移工况。施加轮胎与轮辋连接面的参考点垂直方向2 mm位移,使轮胎胎面与刚性路面完全接触,保证模型后续计算能够快速收敛。

3) 负载工况。释放轮胎与轮辋连接面的参考点垂直方向自由度,并在参考点上施加4 000 N的垂直载荷。

图5是轮胎位移仿真云图。从仿真结果来看,轮胎的最大位移为15.77 mm。

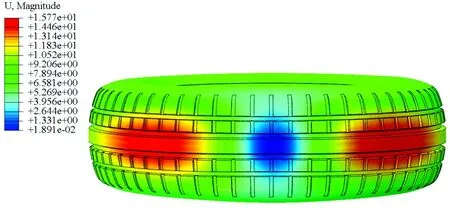
图5 轮胎位移仿真云图

通过改变轮胎充气压力以及垂直载荷的大小,得到不同胎压工况下的“载荷-径向变形”曲线,如图6所示。由图6可知,载荷与径向变形曲线近似呈线性关系,气压为0.23 MPa时的斜率即为轮胎在该工况下的垂直刚度253.65 N/mm。对比轮胎垂直刚度实验[18],实验数据为236.46 N/mm,相对误差在7.27%。由此可见,本文中所建立的轮胎有限元模型与实际情况相符,从而验证了该模型的可靠性。

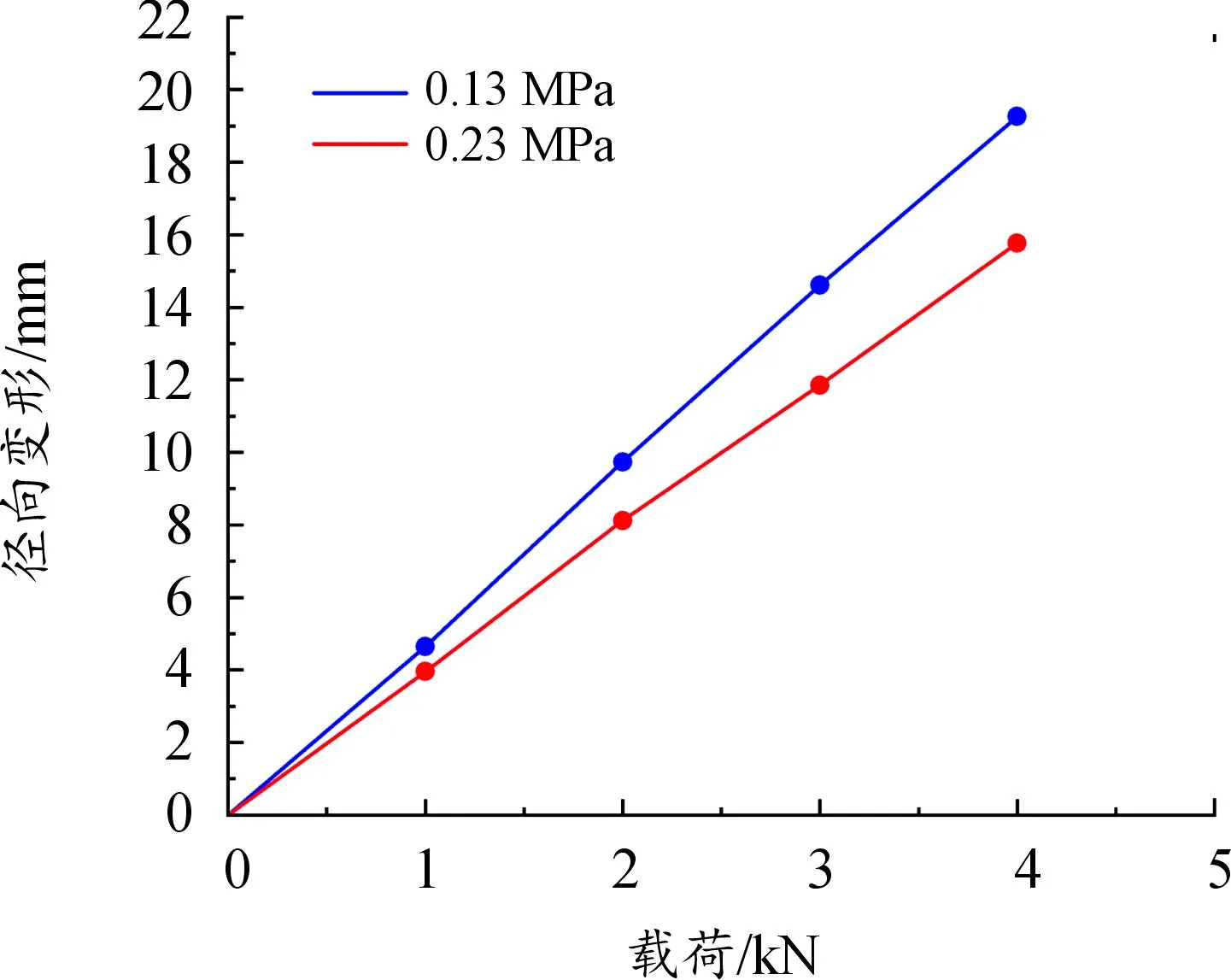
图6 不同胎压下的轮胎径向变形-载荷曲线

2.3 欧拉域的建立与优化

选用水流冲击轮胎模型进行轮胎滑水仿真,如图7所示为由泵水区域(蓝色)和空区域(灰色)组成的欧拉水/空气复合模型。整个欧拉域的长、宽、高分别为600、400、60 mm,水膜高度为10 mm。泵水区域设置体积分数为1,在初始状态下不能与轮胎产生接触,空区域体积分数为0。将整个欧拉域进行井字形切分处理,为后续的网格划分做准备。

图7 欧拉水/空气复合模型

根据水流的流动方向、流速分布以及水可能填充区域的范围[19],对模型的几何形状进行了如图8所示的优化。与优化前的模型相比,优化后的模型在后方两侧增加了60 mm高度的空间,用于捕捉轮胎滑水时后方的侧流,并删除了水流不可能流入的侧前方和正后方的部分计算区域。借助这些措施,优化后的模型将得到更加精确的计算结果,同时避免了计算时间的大幅增加。后文进行滑水仿真时均使用优化后的水/空气复合模型。

对欧拉域进行网格划分,要兼顾模型的计算精度和计算效率。目前CEL方法在计算过程中不能像传统CFD方法那样使用自适应网格来提高模型的计算精度和效率。因此,在欧拉域几何体上划分一个井字形,对轮胎与水流接触的区域以及轮胎后侧水流印迹集中的区域进行网格加密,其余区域网格适当粗化。最后,将轮胎、欧拉域以及刚性路面进行装配,如图9所示,轮胎和欧拉域网格单元质量均大于0.6。

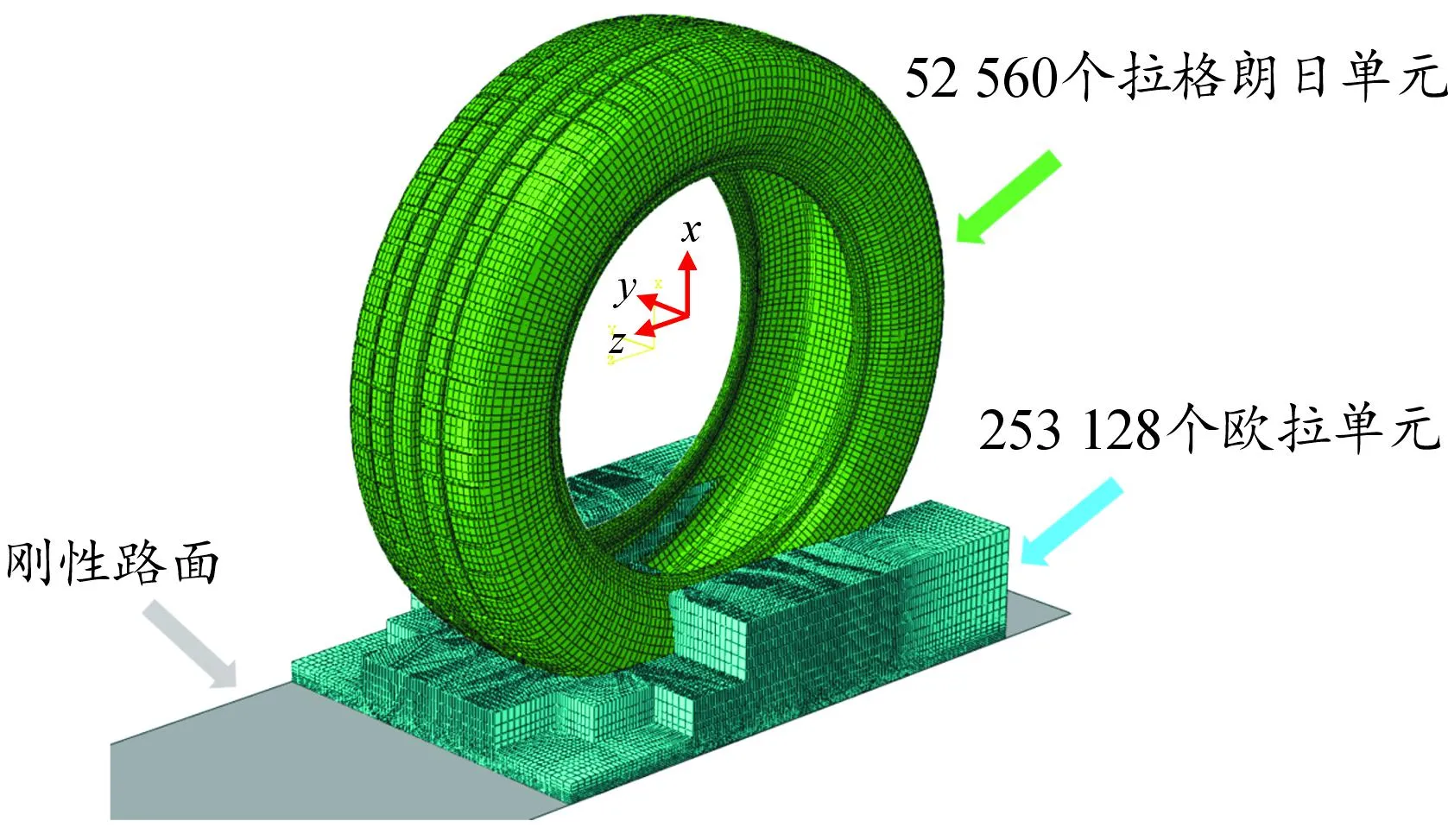
图9 轮胎滑水网格模型

2.4 流固耦合模型边界条件设置

模型的流固耦合计算采用隐式到显式的求解方法,将前文2.2轮胎充气压力为0.23 MPa、垂直载荷为4 000 N工况下的静力学分析结果传递到显示动力学模块,并在显示动力学模块中设置如下边界条件:

1) 轮胎。对轮胎内侧表面施加0.23 MPa的均布压力,同时释放胎体与轮辋连接处参考点垂直方向自由度,施加垂直向下的集中力,载荷大小为4 000 N。设置角速度,使轮胎在0.06 s内从0 km/h匀加速到120 km/h。

2) 路面。释放路面参考点沿水平方向的自由度,使路面在0.06 s内从0 km/h匀加速到120 km/h,固定剩余5个自由度。

3) 欧拉域。进行预定义场的设置:泵水区域体积分数为1,空区域体积分数为0。对泵水区域施加水平方向的速度,使水流在0.06 s内从0 km/h匀加速到120 km/h;限制欧拉域中水膜高度区域的侧面和底部的自由度,防止水流向两侧扩散,同时避免水流向下渗入路面。

3 结果与分析

3.1 水流印迹分析

轮胎在匀加速滑水时,在不同时刻,水流印迹将会有不同的特征,轮胎在车速不断增大的过程中经历了部分滑水和完全滑水两大阶段[20]。本节对部分滑水阶段再次细分,选取了4个具体参考意义车辆速度:20、60、98、120 km/h,分别代表初始接触、完全浸没、临界滑水和完全滑水4个阶段,如图10所示。

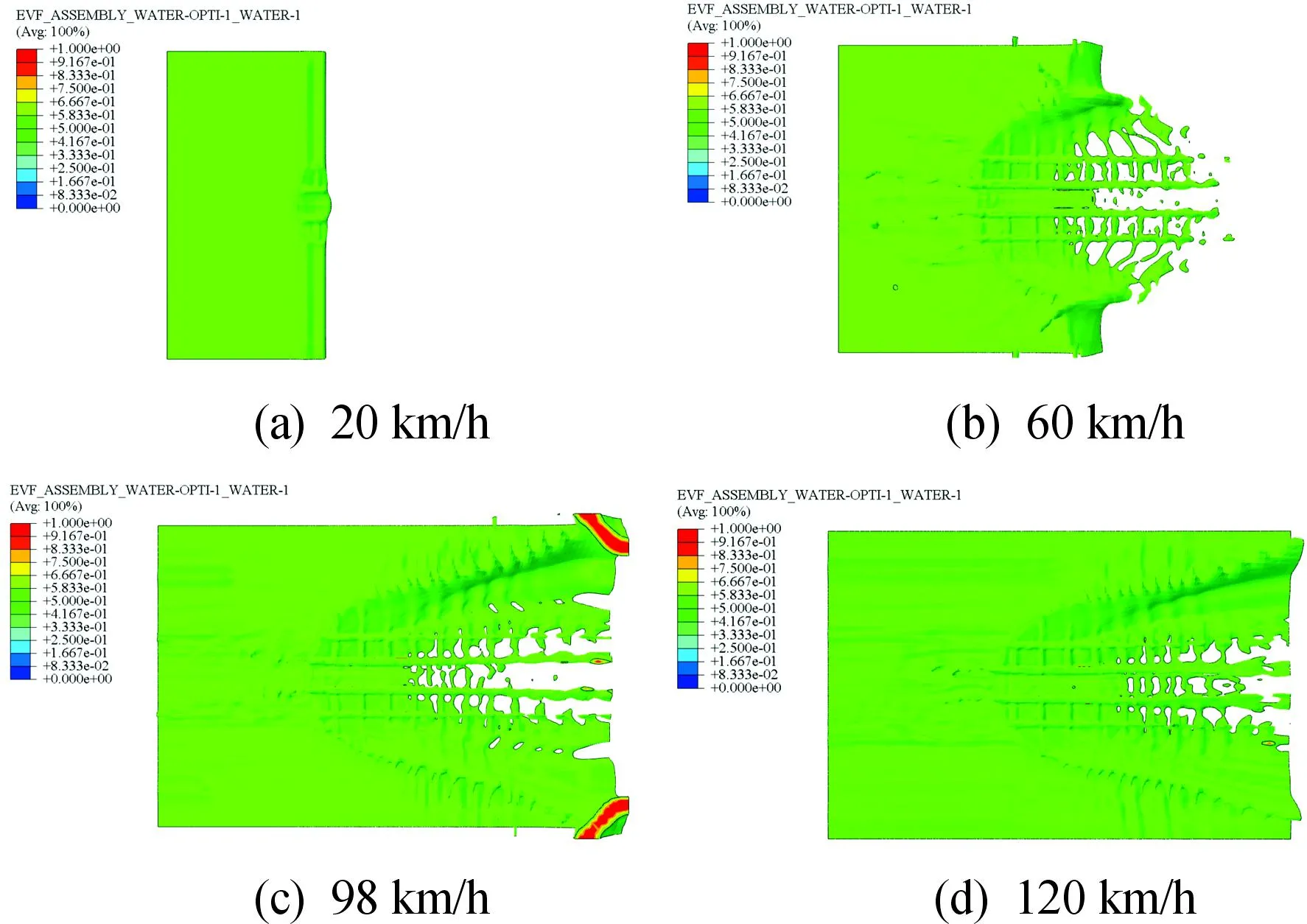
图10 不同速度下的轮胎滑水水流印迹云图

一开始,轮胎和水流没有接触。当水泵区域的水流向轮胎冲击时,轮胎和水流开始接触。从图10中可以看出,当速度达到20 km/h时,水流开始与轮胎前端接触,这时轮胎开始在潮湿的路面上滚动;当速度增加到60 km/h时,轮胎与路面接触区域完全处于欧拉流体模型中,水流被挤入纵向花纹、横向花纹,并沿花纹沟排出;随着水流速度的继续增大,胎冠前端与路面接触的楔形区域逐渐渗入积水,致使轮胎与地面的接触面积不断减小,当速度增加到98 km/h时,轮胎速度处于临界滑水速度附近,这一现象得到充分体现;随着速度的不断增加,路面对轮胎的法向支持力完全被水流的动水压力所代替,法向支持力降为0,导致轮胎被水膜抬起并与地面脱离接触,发生完全滑水现象,参考图示速度120 km/h时,轮胎底部被积水完全浸没,两侧飞溅水流向内收缩明显。

3.2 临界滑水速度验证

轮胎滑水时,轮胎负载与动水压力及路面法向支持力的合力相互平衡,因此,在负载一定的条件下,路面法向支持力能反映出轮胎滑水的状态。本文以路面上的参考点作为历史输出点,通过查看参考点垂直方向的受力情况推断出轮胎滑水状态。

图11是路面法向支持力和车辆加速时间的关系,其中前3.00 s是轮胎静力学工况,后0.06 s是轮胎加速滑水工况。从图11中可以发现,由于动水压力的作用,当车辆行驶速度增加时,路面对轮胎的支撑力变弱。经过计算,可以得出以下结论:当速度为20 km/h时,轮胎接触水膜,动态水压开始发挥作用;当速度为98.242 0 km/h时,轮胎处于临界滑水状态;当速度继续增加时,轮胎完全滑水,路面对轮胎的法向支持力始终为0 N。

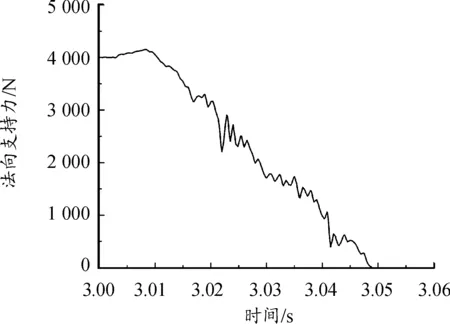
图11 轮胎-路面法向支持力与加速时间曲线

本次模拟得到的临界滑水速度98.24 km/h与1.3NASA经验公式计算得到的93.07 km/h相比,相对误差为5.55%,验证了本文中所建模型的可靠性。

3.3 水膜厚度的影响

在日常生活中,由于雨水的降落量、路面平整度以及排水效率的不同,导致路面上的积水情况也相应不同,进而使轮胎与水膜之间的厚度也各不相同。因此,研究水膜的厚度对于轮胎排水能力的影响具有重要的现实意义。在本节中,重点构建了欧拉模型,并设置了初始水膜厚度为6、8、10 mm的欧拉水域,其余轮胎滑水有限元模型的边界条件设置与前文2.4节一致。

图12是不同水膜厚度下路面法向支持力和车辆加速时间的关系曲线。由此可以看出,水膜厚度对轮胎滑水现象的发生影响很大。由图13可知,水膜厚度为6、8、10 mm的轮胎临界滑水速度分别为114.26、104.76、98.24 km/h,临界滑水速度与水膜厚度负相关。

图12 不同水膜厚度的支持力-加速时间曲线

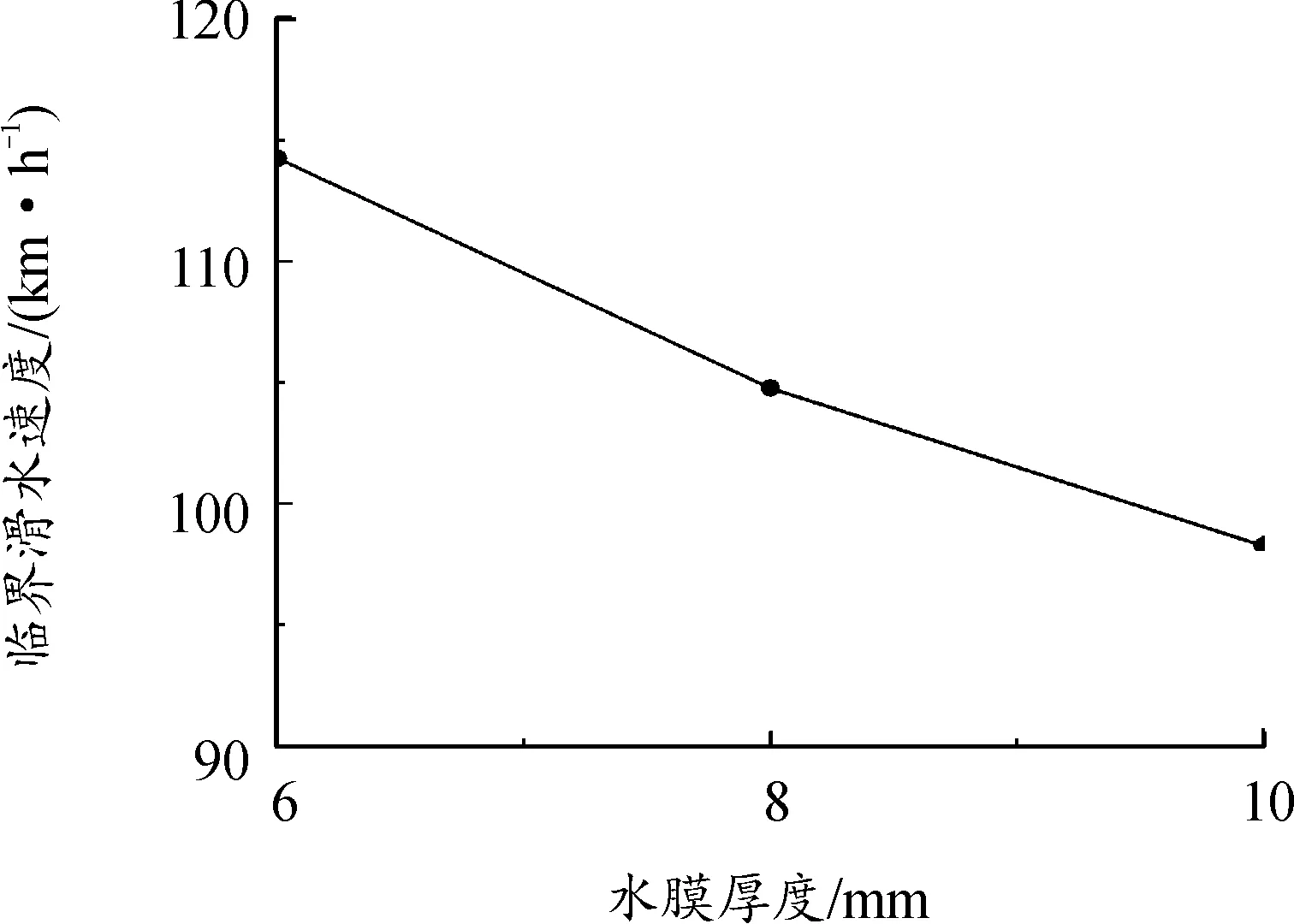
图13 不同水膜厚度的轮胎临界滑水速度

通过EVF斜视图分析车辆速度70 km/h时水膜厚度分别为6、8和10 mm的水流印迹,如图13、14所示。随着水膜厚度的增大,轮胎滑水时轮胎侧边形成的水浪变得更高,胎底积水也变得更多,轮胎自然更加容易完全脱离地面,产生安全风险。因此,在城市中建立一个良好的排水系统对降低因车辆轮胎滑水而导致的交通事故率至关重要。

3.4 充气压力的影响

由NASA经验公式可知,临界滑水速度主要依据轮胎充气压力,因此胎压是重要的滑水影响因素。选取充气压力为0.17、0.20、0.23、0.26 MPa的轮胎研究充气压力对轮胎滑水的影响,其余轮胎滑水有限元模型的边界条件设置与前文2.4节一致。

图15是不同胎压下路面法向支持力与车辆加速时间的关系曲线。随着车辆持续加速,路面对不同胎压轮胎的法向支持力差异越来越大,最终导致气压低的轮胎先发生滑水现象。由图16可知,充气压力为0.17、0.20、0.23、0.26 MPa的轮胎临界滑水速度分别为92.50、95.26、98.24、101.26 km/h,临界滑水速度与充气压力正相关。

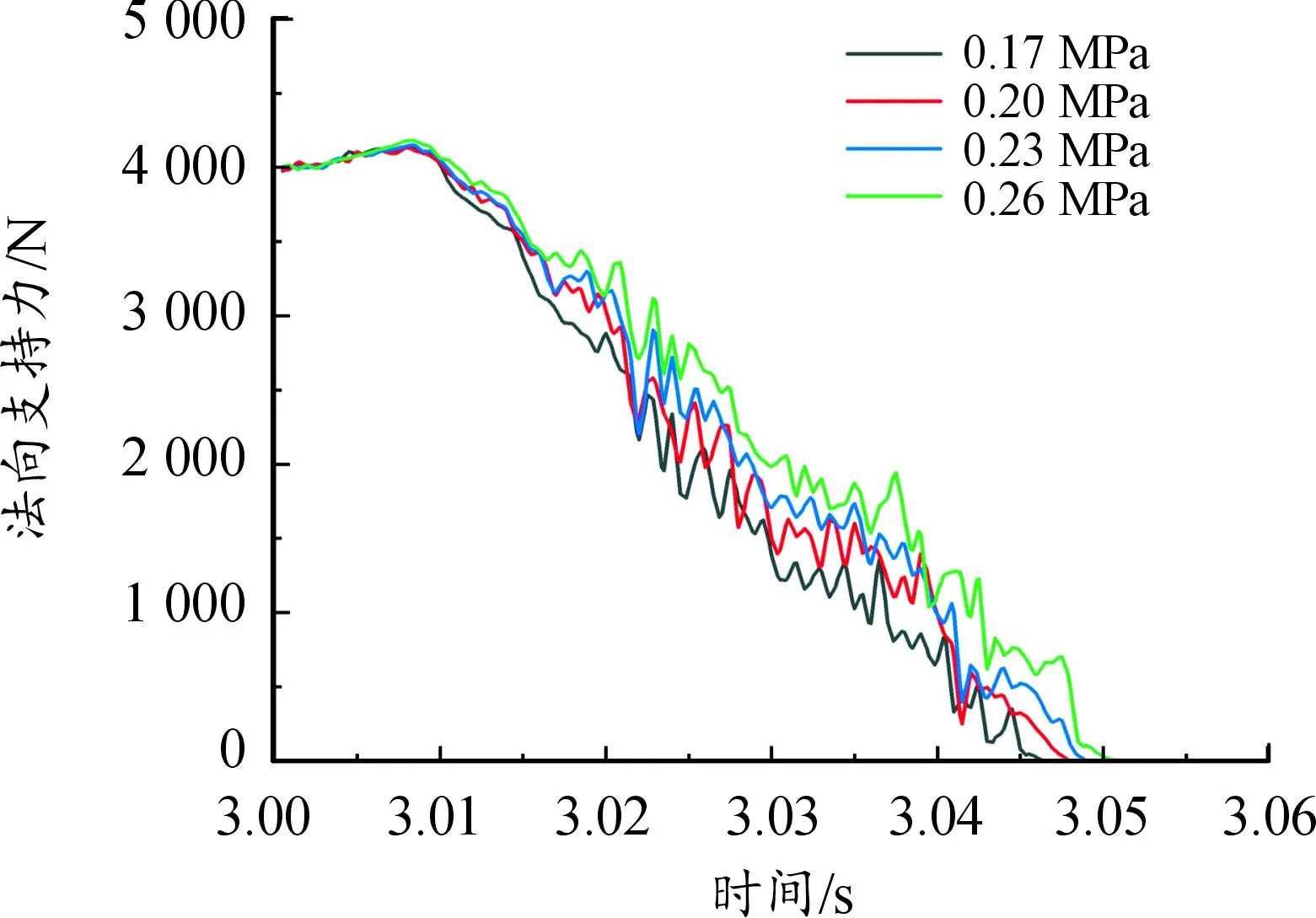
图15 不同充气压力的支持力-加速时间曲线

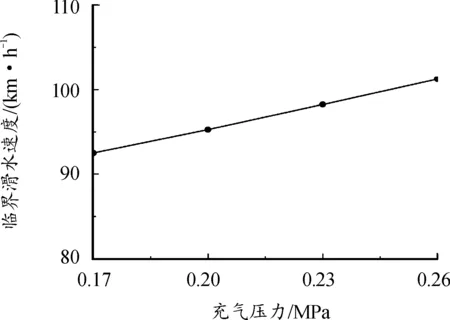
图16 不同充气压力的轮胎临界滑水速度

轮胎滑水的发生主要是因为胎冠前端与路面接触的楔形区域渗入的积水无法及时排尽而产生的动水压力导致的。图17是车辆行驶速度为70 km/h时不同胎压的水流印迹EVF仰视图。随着胎压降低,胎冠前端与路面接触的楔形区域面积增大,导致更多的积水停留在该区域而无法排尽,最终滑水现象提前出现。因此,在降水量大的雨季,应该定期检查胎压,并适当增大胎压,防止因胎压不足而造成的车辆滑水安全事故。

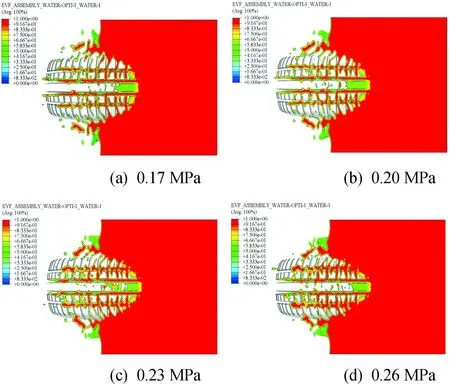
图17 不同充气压力的水流印迹仰视图

4 花纹结构优化

4.1 横向花纹优化

轮胎花纹的布置形式多种多样,然而再复杂的轮胎花纹布置形式都是由最简单的基本花纹组合而成。轮胎常见的基本花纹形式包括纵向花纹、横向花纹、V型花纹等[21],每种花纹的性能差异导致它们的使用场景的区别。对于单独的横向花纹轮胎而言,其滑水性能差,并且它在纵向平面上存在断开,当车辆高速行驶时,很容易发生侧滑现象,造成交通事故;对于纵向花纹轮胎,情况恰恰相反,它表现出纵向刚度较大,横向刚度相对较弱的情况,另外它的滑水性能好;对于V型基本花纹,它在横向和纵向刚度及滑水性能上相对均衡。因此,保留纵向花纹的基础上将滑水性能较差的横向花纹换成滑水性能较高的V型花纹,并保持V型方向顺应水流流向,这一方案理论上能够提升轮胎的滑水性能。

V型横向花纹结构优化的具体措施是将所有垂直横向花纹偏离水平线一定角度,形成V型横向花纹。花纹沟槽宽度、深度及其他结构性参数保持不变,偏离角度取20°,图18为优化前后横向花纹形式。

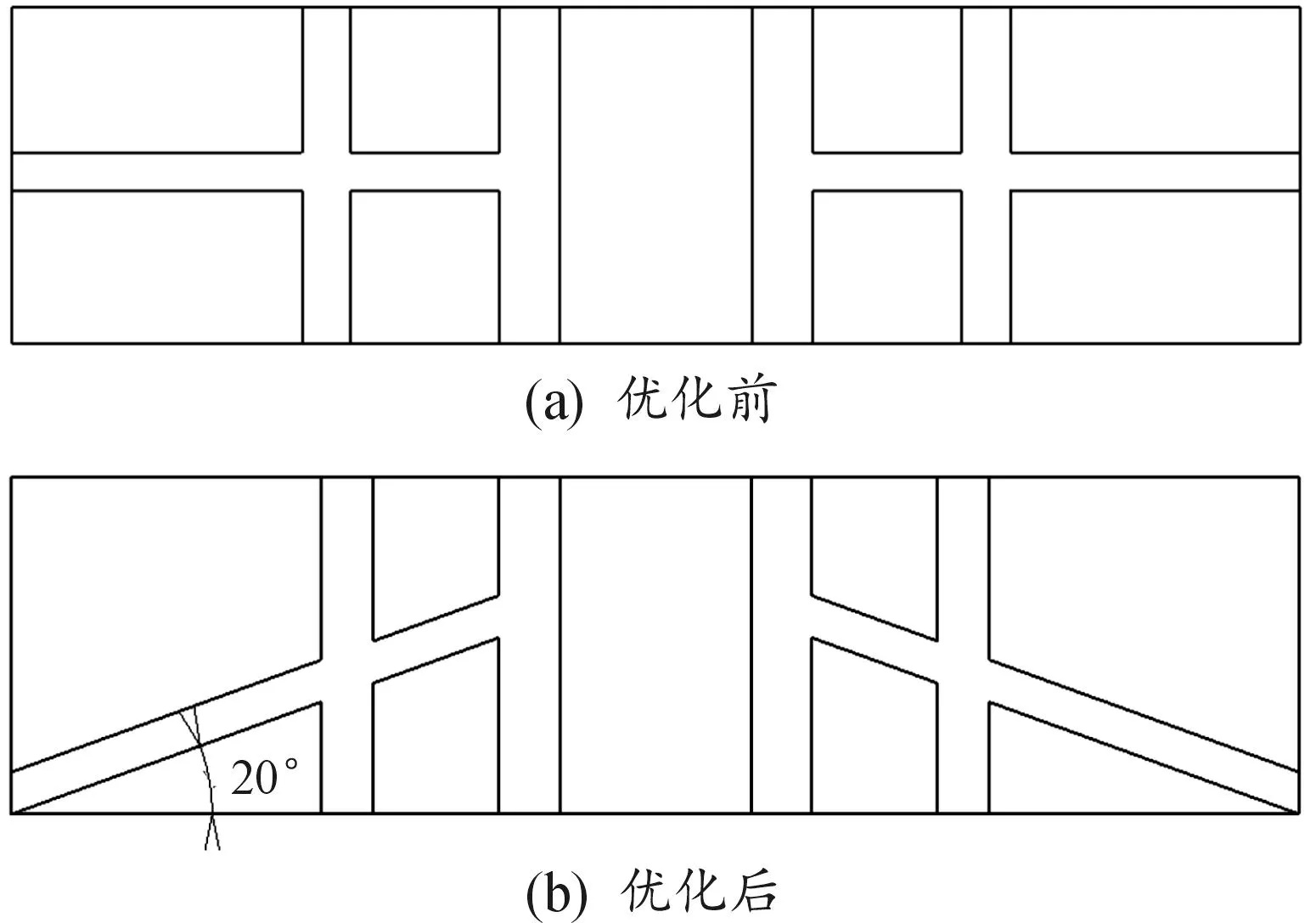
图18 优化前后横向花纹布置形式

4.2 局部花纹优化

本节在上一节V型横向花纹优化的基础上增加F1 Nose楔角结构,以求提升轮胎滑水性能。2000年,Seta等[22]提出了轮胎花纹块滑水性能局部优化方案,即在一个完整的花纹块上削去一个楔角,剩下的花纹块形状像F1赛车,因而命名为F1 Nose。本文中参考前人的设计思路,加以改进,在横向花纹的水流入口处上方位置设置楔角结构,如图19所示,楔角为边长7.5 mm的三角锥,一端顶点与横向花纹沟槽底部相连,以期最大限度地发挥这一结构特征的引流作用。

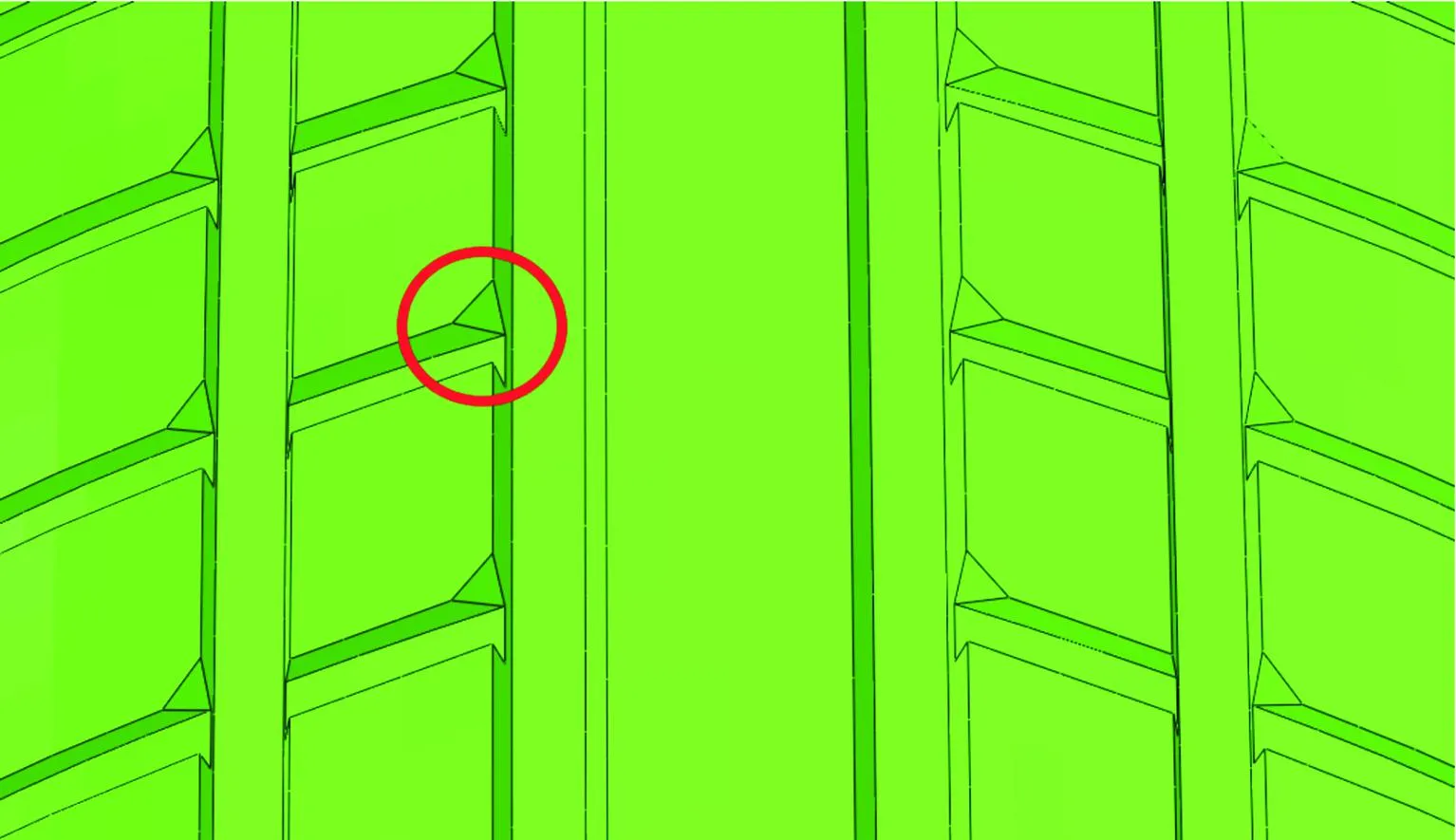
图19 带楔角结构的轮胎花纹

4.3 花纹子模型分析

由前文1.2节可知,CEL方法在纯流体计算方面能力较弱,很难较好地捕捉或展现局部细微的结构变化而导致的流场变化。因此,本节借助专业的CFD软件Fluent,兼顾滑水分析模型的合理性和计算效率,建立了3种不同方案的接地带有横向花纹的滑水分析子模型[23]。计算模型及边界条件如图20所示,除入口和出口外,其余壁面均为固定无滑移的wall面,中央纵沟水流在1 s内匀加速至19.44 m/s后匀速流动,胎肩处纵沟水流在1 s内匀加速至16.37 m/s后匀速流动,水流速度变化均通过udf来设置,所有压力出口静压均设置为101.325 kPa。

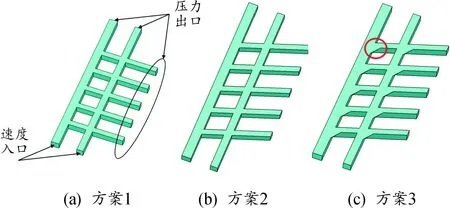
图20 不同方案子模型及边界条件

轮胎滑水时的动水压力是评价轮胎滑水性能的重要指标参数。在Fluent中提取子模型上表面的压力平均值即可间接获取具有参考意义的动水压力。表2为水流速度最大时横向花纹沟组合的方案设计及仿真结果,由表中可知动水压力大小:方案1>方案2>方案3。因此,V型结构及楔角结构的优化方案均合理。

表2 横向花纹设计方案及仿真结果

从表4中的动水压力仿真结果来看,楔角结构的优化对动水压力的削弱能力较强,因此针对这一局部特征,利用速度矢量图进行对比分析,如图21所示。

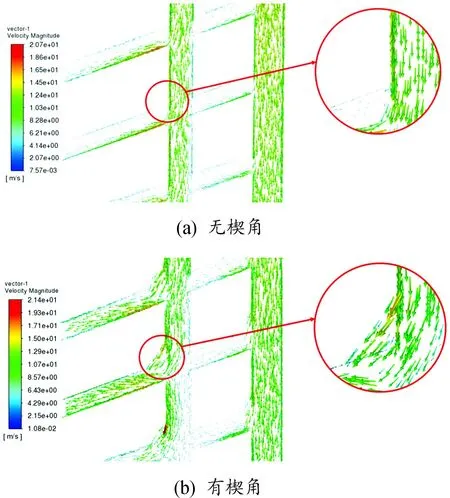
图21 有无楔角的子模型速度矢量图

从图21可以得知,通过楔角结构的增加,原本在纵向花纹沟槽中流动的水流被更多并更流畅地引入到V型横向花纹沟槽中,增大了V型横向花纹排水量,减小了壁面因水流集中而产生的压力,从而有效地减小动水压力,这就是楔角结构能够有效提高轮胎滑水性能的原因。

4.4 轮胎整体分析

将上一节方案3的子模型结构应用到完整的轮胎上,使用CATIA、HyperMesh和Abaqus联合建立花纹结构优化后的轮胎滑水有限元模型,如图22所示。

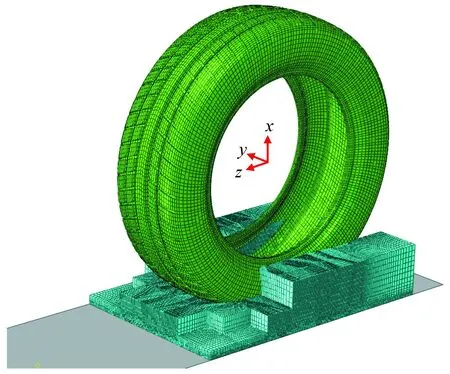
图22 花纹优化后的轮胎滑水模型

在充气压力为0.23 MPa、载荷为4 000 N、水膜厚度为10 mm的工况下,轮胎、欧拉域和刚性路面都会从0 km/h的初始速度开始加速,直到达到120 km/h的速度。

表3是优化前、后的有限元轮胎模型的临界滑水速度结果。从表3中可以得知,以方案3作为最终优化方案的轮胎模型,临界滑水速度达到了101.26 km/h,与初始方案相比,提升了3.07%。

表3 优化前后轮胎临界滑水速度

轮胎滑水时,胎面前端,尤其是楔形区域挤压水膜,使一部分水流从胎底流过,另一部分水流从轮面两侧排开。从图23车辆行驶速度70 km/h时的水流压力云图来看,楔形水膜区域压力明显高于其他位置。从云图左侧数值的对比结果可以看出,优化后的轮胎楔形水膜区域的压力分布更加均匀且最大值较小,这表明优化后的轮胎滑水时,花纹沟槽内水流流动更加通畅,轮胎滑水性能更加出众。

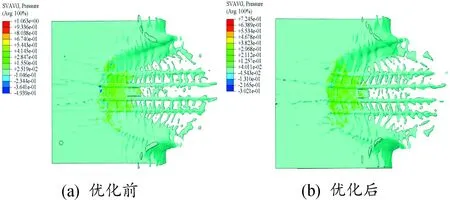
图23 花纹优化前后水流压力云图

5 结论

为了研究轮胎滑水性能并通过优化花纹结构提高这一性能指标,以205/55 R16轮胎为例,基于Abaqus CEL方法进行轮胎滑水流固耦合仿真分析,得到如下结论:

1) 轮胎匀加速滑水过程可以划分4个阶段:初始接触、完全浸没、临界滑水和完全滑水。

2) 根据仿真结果预测的临界滑水速度与NASA经验公式对比,相对误差为5.55%,在一定程度上可说明CEL流固耦合方法模拟轮胎滑水过程的可靠性。

3) 对比不同水膜厚度和充气压力的轮胎滑水仿真模型,得出轮胎的临界滑水速度随水膜厚度增大而减小,随充气压力的增大而增大的结论。

4) 通过引入V型横向花纹和增加F1 Nose结构优化轮胎花纹结构。对比分析子模型优化前、后结果,发现增加楔形结构能有效引导水流,增大横向花纹的排水量。对比分析整个轮胎优化前、后结果,发现优化后轮胎临界滑水速度提升3.07%,楔形水膜区域动水压力分布更均匀,在一定程度上说明了这种提高轮胎滑水性能的花纹优化方法的可行性。