基于加速度信号的轮胎滚动阻力估计算法
2024-02-05王子寒贝绍轶殷国栋
王子寒,李 波,2,贝绍轶,刘 涛,林 棻,殷国栋
(1.江苏理工学院 汽车与交通工程学院, 江苏 常州 213001;2.清华大学苏州汽车研究院, 江苏 苏州 215200;3.通用装备研究所, 北京 102202;4.南京航空航天大学 能源与动力学院, 南京 210016;5.东南大学 机械工程学院, 南京 210096)
0 引言
作为汽车与道路表面之间惟一的接触,轮胎的力学特性对汽车性能有直接影响,例如行驶稳定性、制动性、安全性和燃油经济性。汽车轮胎稳态滚动阻力是轮胎力学性能的重要组成部分,直接影响燃油消耗率、使用寿命和汽车操纵性能。低滚动阻力轮胎的研究对于降低传统燃油车的燃油消耗、减少二氧化碳排放,以及提升新能源汽车的续航里程方面都具有重要意义,已成为目前最受瞩目的课题之一,也是国内外相关企业和科研机构重要的研究方向[1-3]。
轮胎滚动阻力的实时获取对于提高汽车的燃油经济性尤为重要,但是滚动阻力是能量损失的等效力,无法直接获得。目前,国内外机构研究滚动阻力的方向多数是通过分析轮胎橡胶材料的黏弹滞后性与轮胎滚动变形的能量损耗之间的联系,如李波等[4]考虑材料的弹性迟滞特点,分析非线性弹性力和非线性阻尼力构建轮胎滚动阻力解析模型;或是基于室内台架与试验场地实车验证的工况数据与滚动阻力建立机器学习算法,如神经网络模型、Grover模型等[5-8];少数研究利用行驶数据对滚动阻力进行物理建模,但由于缺少轮胎本身随滚动阻力变化的参数,因此,对滚动阻力的估算精度不高,且易受环境因素的影响。
随着智能轮胎技术的出现,通过在轮胎上安装传感器对轮胎力学特性进行研究的方法受到广大关注。智能轮胎的传感器主要分为加速度传感器、光学传感器和应变传感器3种,其中基于微机电系统的加速度传感器近年来应用最为广泛[9-10],该类型的传感器不受温度变化的影响,且能随时间稳定地输出加速度信号,此外微电子机械系统(micro electro mechanical system,MEMS)加速度传感器还有质量轻、体积小等优势,可贴于轮胎内衬[11-12],既不损坏轮胎的整体物理结构,也不影响轮胎的行驶稳定性。
本文中提出了一种基于智能轮胎技术的轮胎滚动阻力估算算法,结合了车辆行驶参数和轮胎内衬中心轴线处的加速度数据对轮胎滚动阻力进行预估。相较于传统的物理模型,此模型利用轮胎滚动1周加速度信号的功率谱密度参数来描述轮胎变形前后的能量损耗,增加了模型对轮胎滚动阻力影响因素,并通过偏最小二乘回归拟合法筛选出与滚动阻力相关性更高的主成分,提升了模型对滚动阻力预测的精度。
1 轮胎稳态滚动阻力有限元建模
1.1 建模思路
轮胎是一种结构复杂的橡胶复合体,如图1所示,其组成构件包括胎面、胎侧、带束层、三角胶、冠带层、内衬层、帘布层和胎圈等。其中,胎面直接与地面接触,向轮胎提供路面的反作用力;帘布层是轮胎的受力骨架层,与带束层共同分担加载到轮胎的负荷,并保持外胎的形状和尺寸;胎圈固定在轮辋上,起到支撑和固定轮胎结构的作用。
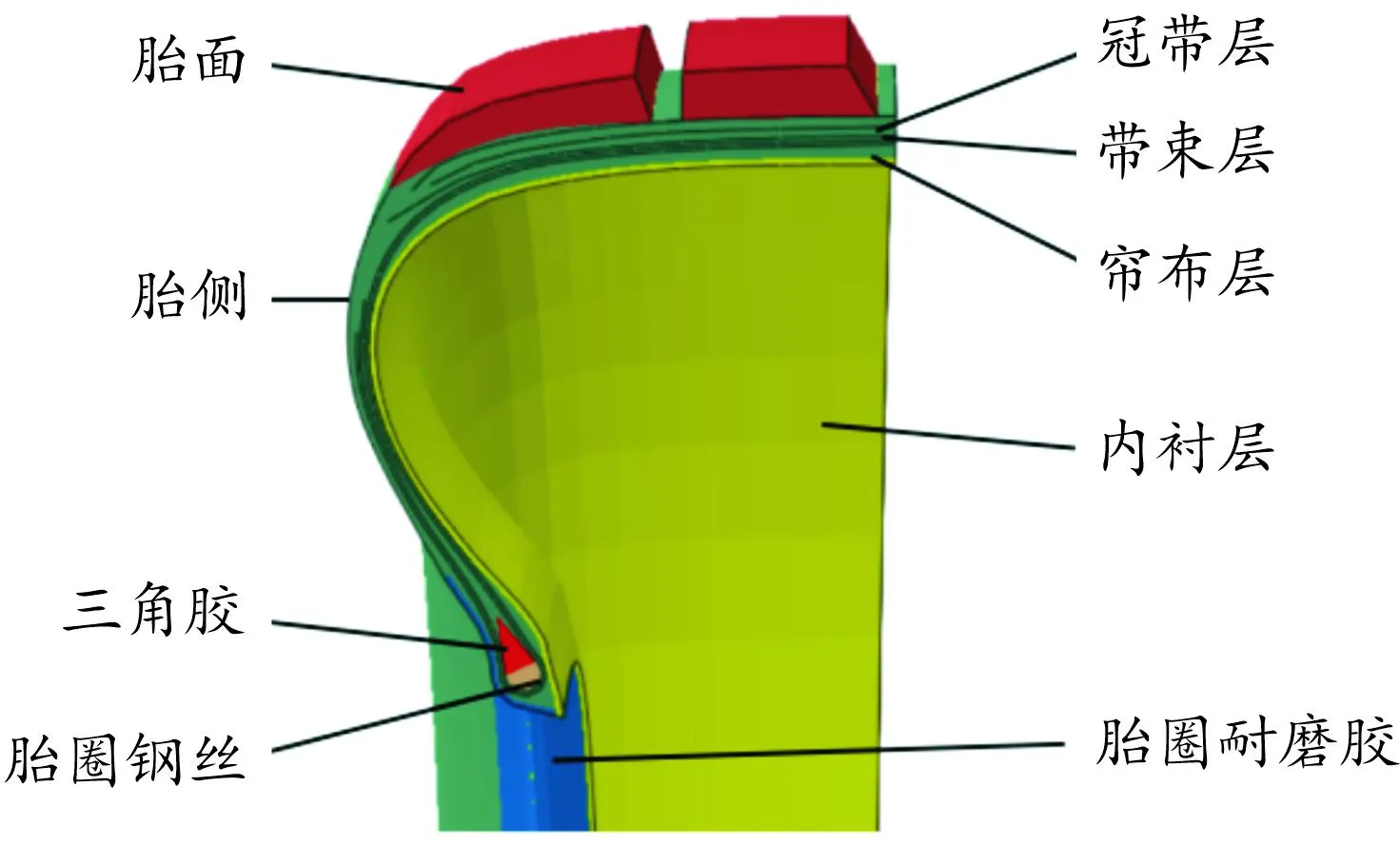
图1 轮胎有限元模型结构示意图
建立205/55/R16子午线轮胎有限元模型的流程是:通过轮胎各部分的材料分布图创建半二维对称截面轮胎模型,如图2(a)所示;将半二维对称截面模型围绕滚动轴线旋转360°,获得如图2(b)所示的轮胎半三维对称截面模型;将对称平面映射为一个完整的全三维轮胎模型,如图2(c)所示。
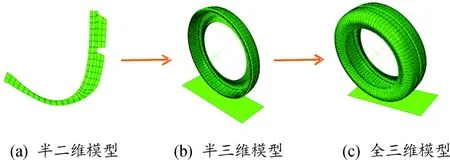
图2 205/55/R16子午线轮胎有限元模型的流程
1.2 模型优化
钢圈区域胶料较少,刚度高,对滚动阻力的贡献率仅为0.3%左右[13],所以建立有限元模型时简化了这部分,将图3红线所示钢圈边缘节点设为刚体约束。对于滚动阻力仿真来说,这种简化方式不仅不会影响最终计算结果,还可以大大提高网格的划分质量,缩短稳定时间增量内的计算时间。
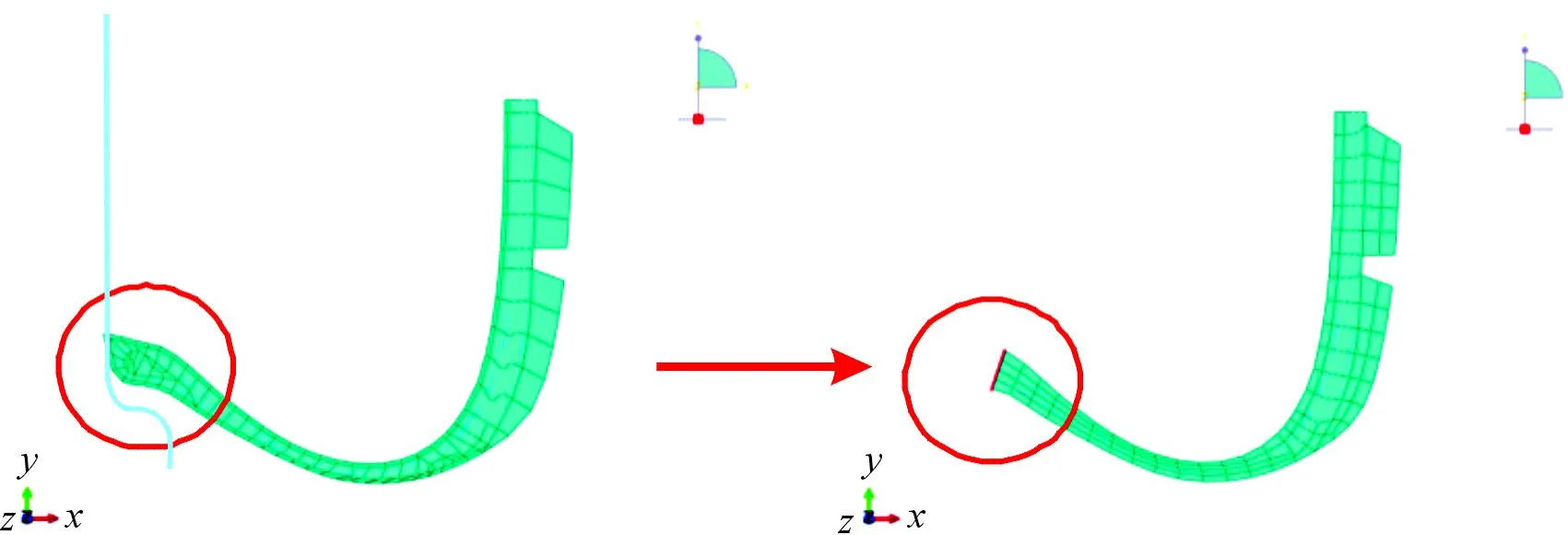
图3 钢圈区域建模优化
1.3 材料参数的获取
子午线轮胎的组成包含众多不同类型的橡胶材料,不同部件的材料属性也大不相同,对于轮胎有限元模型搭建的重中之重就是获取各橡胶材料的物理参数,因此,首先要选取合适的橡胶本构模型。常见的本构模型有Neo-Hookean模型、Yeoh模型、Mooney-Rivlin模型等,由于本次研究是为了获得轮胎滚动时产生的滚动阻力的变化情况,为了提高计算速度,选取材料参数简单且可描述变形范围较宽的Yeoh模型,通过单轴拉伸实验和资料查询[14]获得了表1所示不同胶料的Yeoh模型参数。
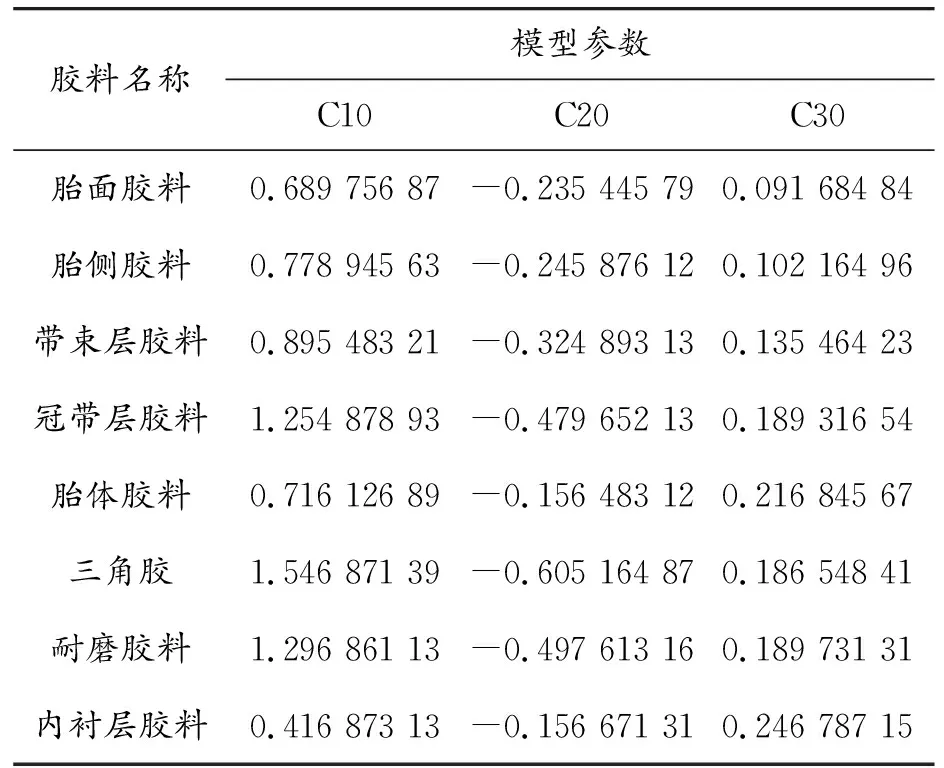
表1 不同胶料的Yeoh模型参数
1.4 轮胎稳态自由滚动状态有限元分析求解
据ISO28580轮胎滚动阻力试验标准所述,轮胎需达到稳态自由滚动状态时才可以对滚动阻力值进行测量,因此,为了符合测试标准,需要先获得轮胎的自由滚动状态。
在ABAQUS软件的轮胎有限元分析中,轮胎模型是否达到稳态自由滚动状态,取决于轮轴处施加的扭矩是否为零,只有当扭矩无限接近于零时,轮胎与地面接触点的反作用力可用于滚动阻力的计算。平衡扭矩与被称为牵引或制动的非零扭矩状况取决于车轮的滚动角速度和地面的线速度是否一致,而稳态滚动角速度事先是不知道。
通过使用用户子程序UAMP控制轮胎的角速度。UAMP子程序可以改变与角速度相关的振幅,作为车轴上扭矩的函数,直到实现自由滚动状态。该子程序采用梯度下降法获得轮胎的自由滚动速度。该分析包括2个步骤:在第一步中,路面设置成需要的速度,轮胎角速度被设置为与制动对应的值,即理论线速度与轮胎充气半径的比值。随后,子程序使用来自仿真的扭矩值来调整角速度的大小,直到扭矩大小低于指定的范围。本仿真设置扭矩阈值为30 N·mm。图4为UAMP子程序在胎压0.24 MPa、载荷4 920 N、车速80 km/h仿真工况下的迭代过程。由图4可以看出,轮胎稳态自由滚动角速度为74.22 rad/s。
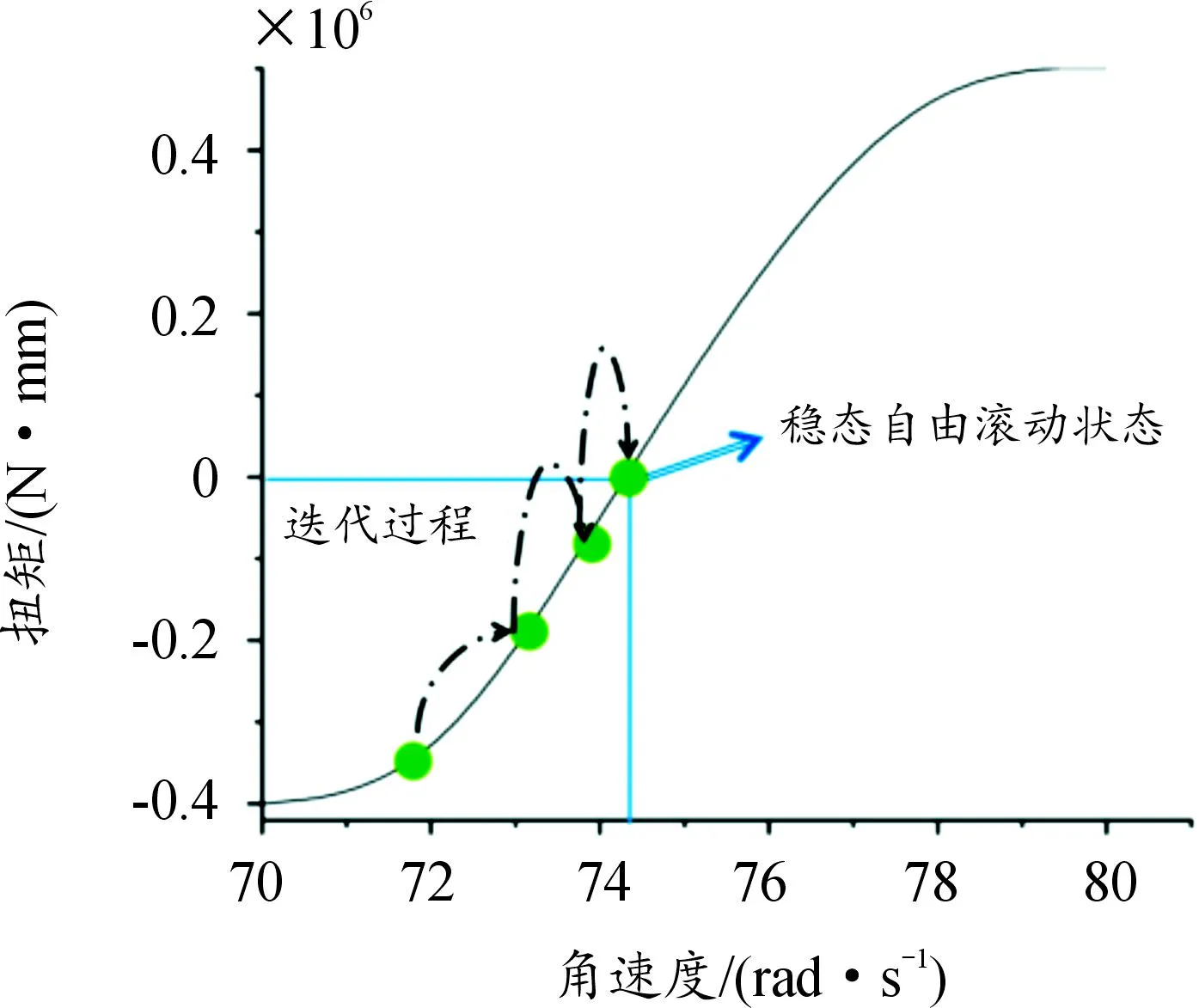
图4 UAMP子程序迭代过程
1.5 滚动阻力获取
轮胎滚动阻力产生的主要原因是轮胎橡胶材料内部的黏弹滞后特性,导致轮胎滚动时将一部分动能转换为热能消散掉,从而产生滚动阻力。
通过轮胎稳态自由滚动有限元求解,可以获得与地面线速度一致的轮胎角速度,即稳态自由滚动角速度。将获得的角速度施加到轮胎有限元模型上,此时轮胎无驱动力和制动力,但由于轮胎橡胶材料黏弹性的影响,路面对轮胎会产生一个反作用力,即为滚动阻力。
2 轮胎滚动阻力有限元模型验证
2.1 仿真结果验证
轮胎在稳态自由滚动状态下,与地面接地处断面单元的应力与应变分布如图5所示。
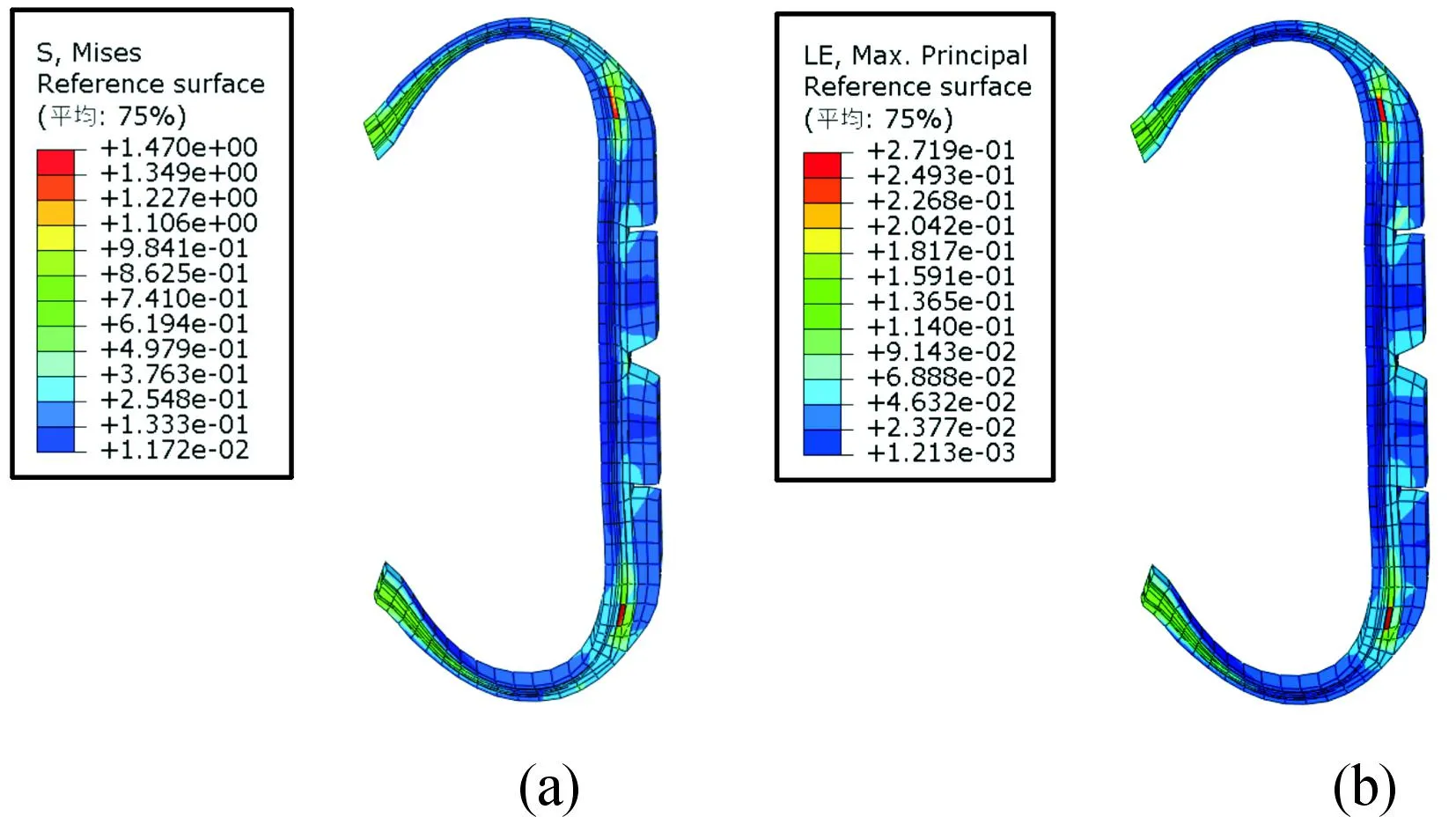
图5 轮胎接地截面单元应力与应变分布
由图5可以看出,轮胎在稳态自由滚动过程中应力和应变较高的区域均在轮胎与轮辋的接触处以及轮胎的轴肩处,而应力与应变较低的区域则处于轮胎胎侧以及胎面中心处。该分布规律与文献中所提及的情况相同[15],验证所作轮胎ABAQUS有限元模型的可靠性。
2.2 滚动阻力结果验证
载荷、速度和充气压力是轮胎行驶过程中最重要的3个变量因素,也是影响汽车各项性能的重要因素。因此,将载荷、速度和充气压力3种条件作为研究轮胎稳态滚动阻力特性的多工况条件进行模型验证。
2.2.1 基于载荷的滚动阻力验证
保持车速80 km/h,胎压2.4×105Pa为固定值不变,取不同载荷作为轮胎滚动阻力仿真参数,获得如图6载荷与滚动阻力关系曲线。由图6中曲线可以看出,滚动阻力与轮胎载荷正相关,这是由于随着轮胎载荷的增加,轮胎接地处材料的变形增大,材料的应力与应变值也随之增加,其产生的滞后能量损失越大,导致滚动阻力值越大。因此,图6中的滚动阻力仿真值随载荷的变化规律符合实际情况。

图6 轮胎载荷与滚动阻力关系
2.2.2 基于速度的滚动阻力验证
由于当行驶速度高于120 km/h时,轮胎会产生驻波现象,为研究正常行驶情况下滚动阻力的估计算法,选定20~100 km/h的速度区间作为模拟参数。图7为以205/55/R16子午线轮胎80%标准载荷(4 920 N)和额定胎压2.4×105Pa为固定模拟参数,不同车速与滚动阻力的仿真结果。可以发现,轮胎滚动阻力随着车速增大呈增加趋势,分析主要是由于轮胎滚动角速度增大导致轮胎的离心力也随之增大,轮胎的变形增大,与真实情况相符。

图7 车速与滚动阻力关系
2.2.3 基于胎压的滚动阻力验证
保持轮胎载荷4 920 N和车速80 km/h为固定仿真参数不变,对不同胎压下进行滚动阻力仿真,结果如图8所示。可以看到,仿真滚动阻力值与胎压之间呈现负相关趋势,这是由于轮胎在行驶过程中主要依靠股骨架材料和内部的气压承担整车的负荷,而充气压力的增大,增大了轮胎橡胶材料的刚度,使轮胎接地时的变形量减少,滚动阻力值也随之减小。因此,图8中滚动阻力仿真值随胎压的变化规律符合实际情况。
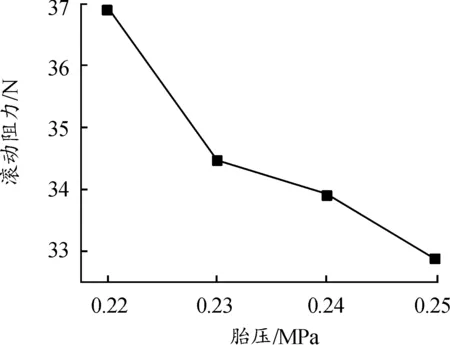
图8 胎压与滚动阻力关系
对比图中几种典型工况下滚动阻力仿真值的变化趋势与理论变化趋势,可以发现,在不同车速、胎压及载荷条件下对轮胎滚动阻力的仿真结果都符合文献描述的滚动阻力变化关系,因此,可以判断所作的205/55/R16子午线轮胎有限元模型具有可靠性。
3 加速度信号特征提取
3.1 轮胎滚动阻力与轮胎变形的关系
汽车在行驶过程中不可避免地会存在轮胎滚动阻力,如果汽车在较为柔软的路面上行驶,轮胎和路面都会有比较明显的变形,如果在较为硬的混凝土路面上行驶,轮胎变形得较多。无论在哪种路面,轮胎与地面接触的法向和切向接触面都会使轮胎发生变形,根据轮胎力学测量表示,轮胎加载过程中受力的曲线总是位于卸载过程中受力曲线的上方,如图9所示。这表明,要使轮胎产生相同状态的形变,加载过程的力要大于卸载过程的力。而图10的面积则表示轮胎形变所产生的能量,这个能量是加载和卸载过程中损失的能量,直接表现为轮胎的发热。
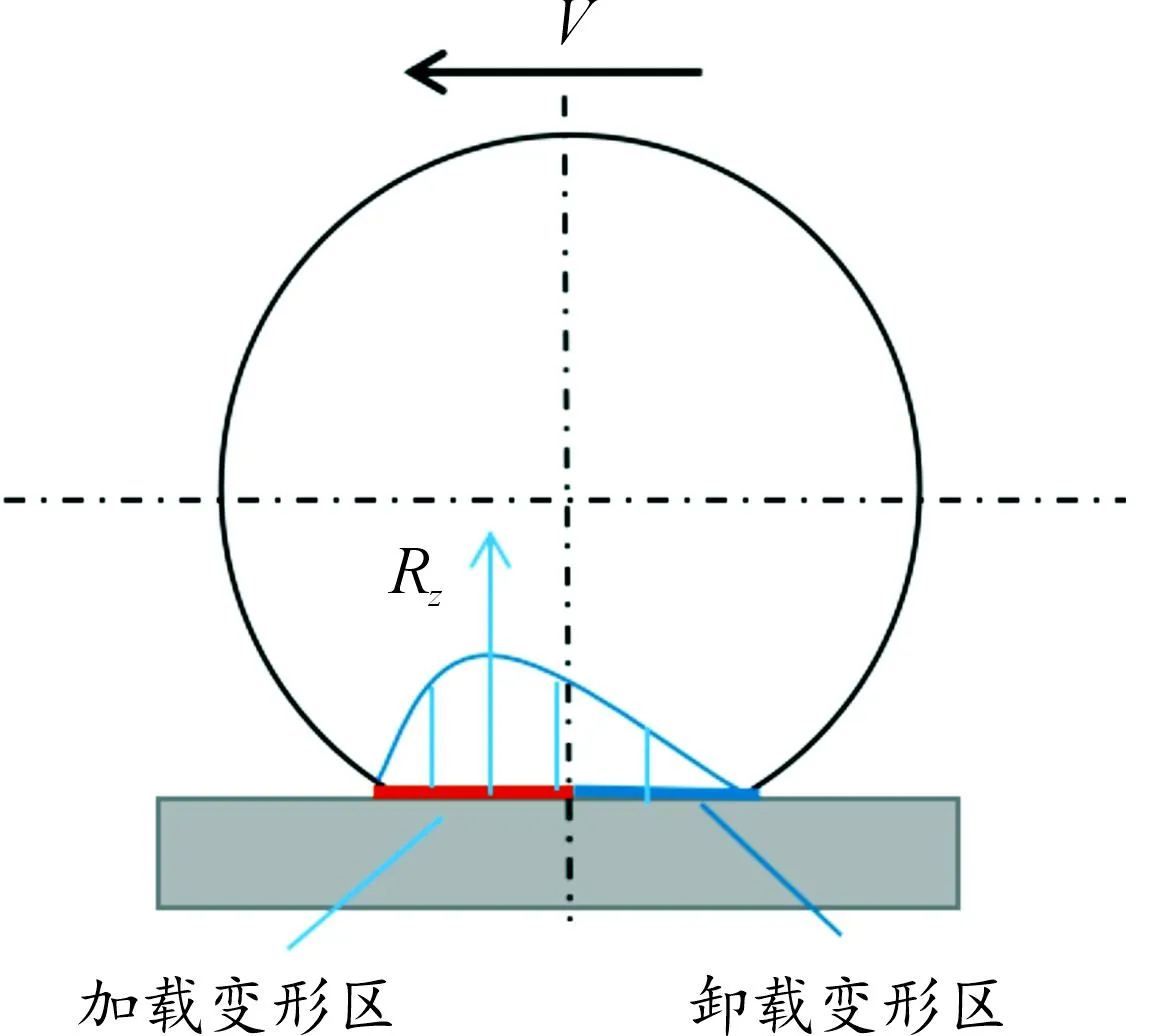
图9 轮胎变形受力
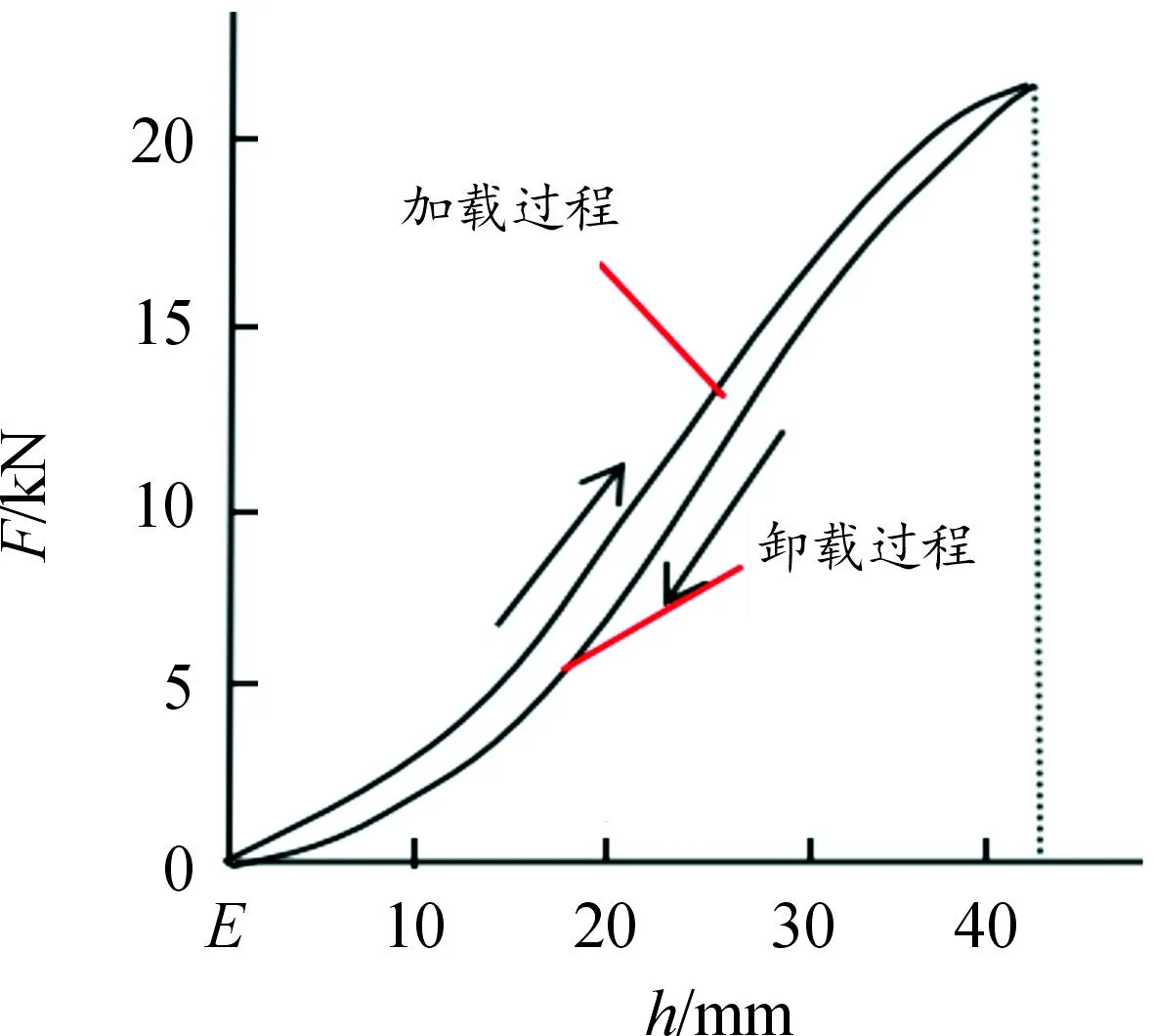
图10 轮胎变形能量损耗
3.2 加速度信号值获取
本模型采用混合欧拉-拉格朗日方法进行稳态传输分析,模拟轮胎与刚性表面之间的滚动和滑动接触。在此仿真模拟过程中,轮胎各单元和节点保持静止,轮胎各部分的材料在网格中围绕轮轴转动,以模拟轮胎滚动时的场景。所以想要获取轮胎内衬中心轴线处一点的加速度信号,需要如图11所示,选取轮胎内衬中心轴线处1圈的节点作节点集ACC,利用ABAQUS后处理功能输出整个节点集ACC的三轴加速度数据作为轮胎滚动1圈的加速度传感器信号。
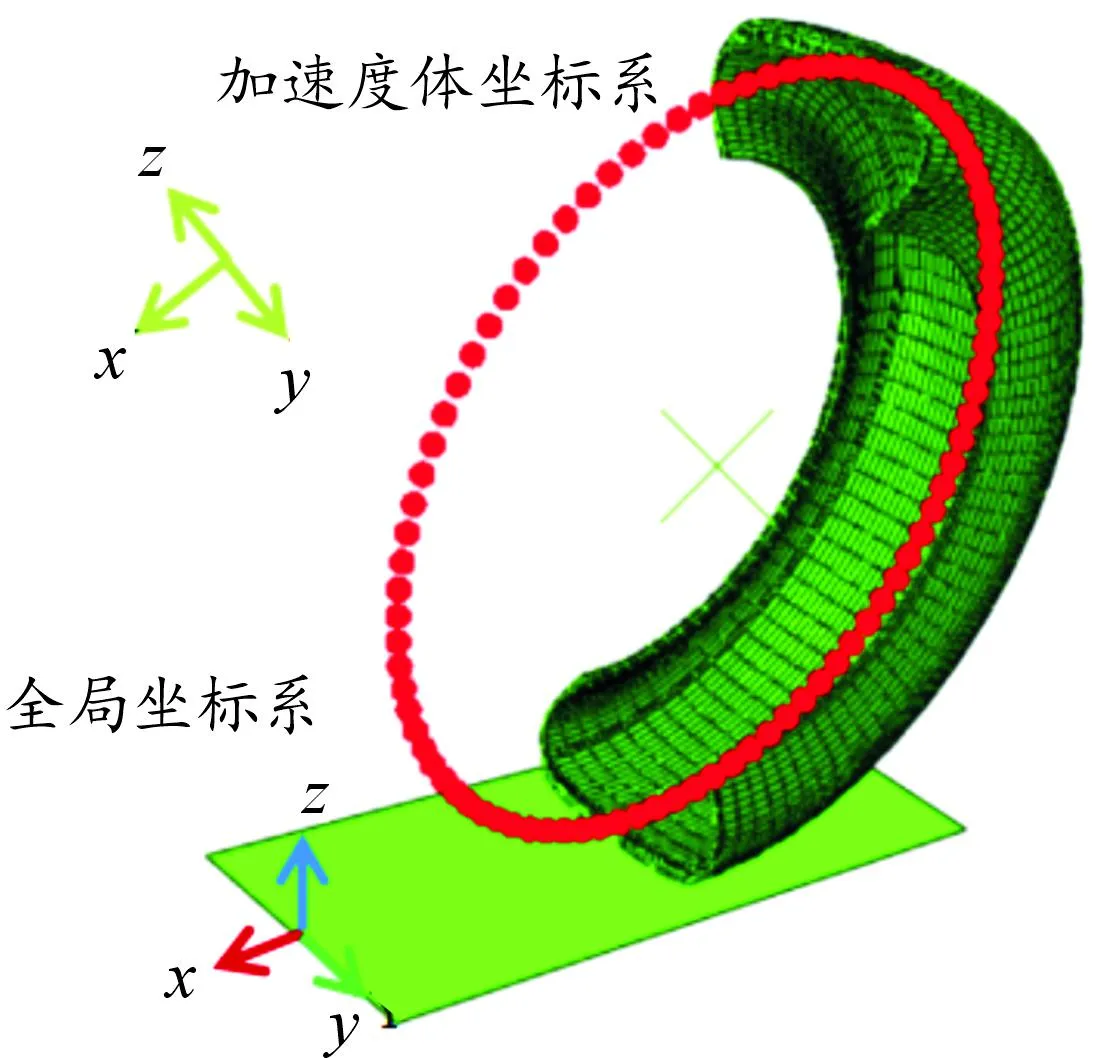
图11 加速度信号节点集
与现实情况不同的是,安装在轮胎内部的加速度传感器是以本身作为局部坐标系,而有限元仿真中取得各节点的加速度数据使用的是全局坐标系,即车身坐标系,因此在获取加速度数据时需要完成从车身坐标系到加速度体坐标系的转换。坐标转换的原理如下:
1) 选择中心线上的起始节点下一个节点的坐标
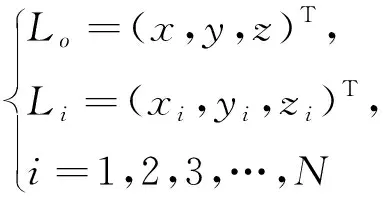
(1)
2) 计算在x、y、z方向上的单位向量
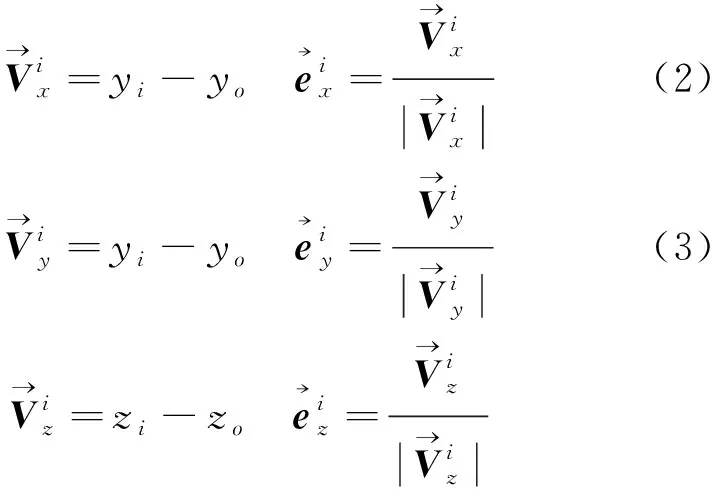
(4)
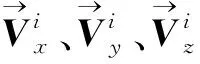
3) 加速度体坐标系
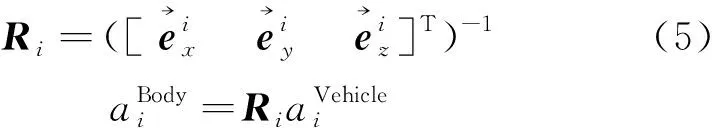
(6)
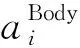
3.3 加速度信号分析和处理
由上文可知滚动阻力产生的机理、轮胎在滚动过程中的能量损失,而对加速度信号的时域分析只包含轮胎变形的积分速度和积分位移信息,无法表示出与能量相关的信息,所以需要对加速度信号进行频域分析。采用功率谱密度估计法[16-17](power spectral densities,PSD)对智能轮胎的加速度信号进行频域分析,通过信号的相关性估计出信号功率随频率的变化关系,相较于常用的快速傅里叶变换(fast fourier transform,FFT),该方法可以比较轮胎滚动过程中加载与卸载振动分量。
采用Yule-Walker分析法对功率谱密度进行估计,其方法的核心是从信号的自相关序列中计算出指定阶数AR模型的参数。Yule-Walker估计法可以通过求解描述自回归序列参数与其协方差函数之间关系的方程得到:

(7)
式中:r0,r1,…,rn-1为相关系数;a1,a2,…,an为自回归系数。
Yule-Walker法PSD估计的公式为
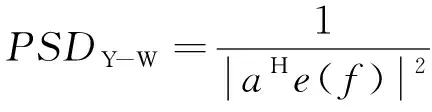
(8)
式中,e(f)为负数正弦曲线。
将纵向、侧向和径向加速度信号数据分别代入公式计算得其功率谱。图12显示了在载荷为4 920 N、胎压为2.4×105Pa、车速为80 km/h仿真条件下原始加速度信号。由图12中3个方向的加速度波动可以区分出轮胎中心轴线处接地前后的采样节点,由于本文中研究的滚动阻力主要与轮胎加载与卸载过程中的能量损失有关,因此选取图12黑框内采样节点30~60的加速度数据用作分析。图13显示了由Yule-Walker分析法得出的功率谱密度估计图,可以观察到加速度信号在单位频率下的能量分布特征。从图13中可以看出,纵向和径向的功率谱密度曲线分别有2处波峰,说明轮胎滚动过程中,纵向和径向加速度信号出现了2处高能量分布,可选取峰值作为特征参数,而侧向加速度的功率谱密度曲线没有明显的波峰,这是由于仿真所模拟的是轮胎稳态自由滚动工况,在此工况下轮胎在侧向几乎没有任何运动,对滚动阻力的影响也可忽略不计。所观察到的功率谱密度曲线特征与其他文献描述一致[18]。

图12 原始加速度信号
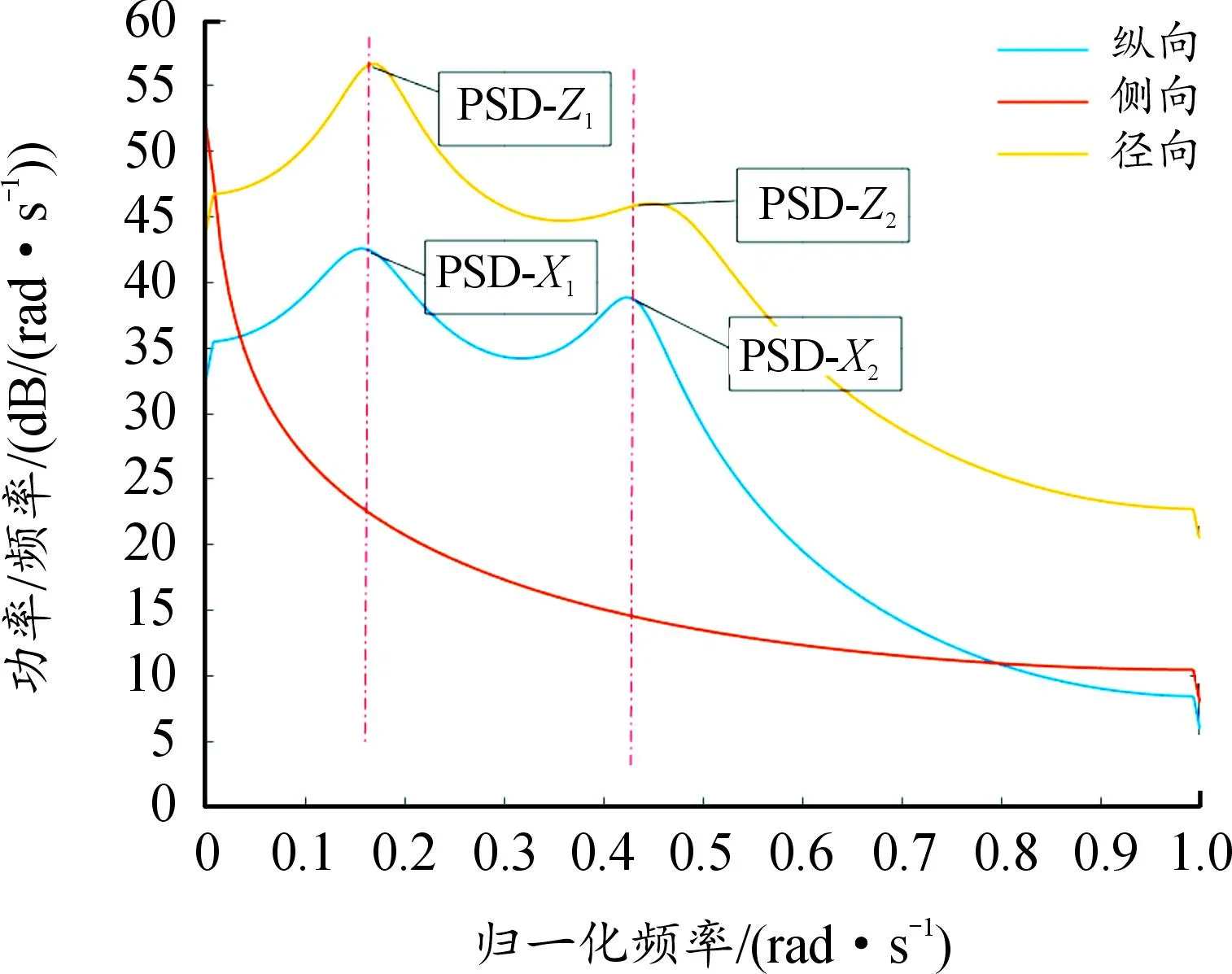
图13 Yule-Walker功率谱密度估计
整理轮胎滚动阻力估计分析的输入参数,将图13中纵向功率谱密度曲线的第1个波峰峰值记为PSD-X1,第2个波峰峰值记为PSD-X2;径向功率谱密度曲线的第1个波峰峰值记为PSD-Z1,第2个波峰峰值记为PSD-Z2;侧向加速度与滚动阻力相关性较低,且其功率谱密度没有规律可循,不计入滚动阻力分析的影响因素。将上述4个功率谱密度数据与行驶工况参数(载荷、胎压和车速)作为数据集的输入参数,滚动阻力与滚阻系数作为数据集的输出参数,用于后续的轮胎滚阻分析。
4 滚动阻力偏最小二乘回归算法
选取载荷、胎压、车速、PSD-X1、PSD-X2、PSD-Z1和PSD-Z2共7个特征为自变量,轮胎滚动阻力与滚阻系数为因变量,建立轮胎滚阻7特征物理模型。首先对滚动阻力参数进行相关性分析,将自变量与因变量统一放入一个增广矩阵中,获得每组数据之间的相关系数。各个参数之间的相关性如图14所示。可以看出,轮胎径向与垂向加速度信号的功率谱密度值与滚动阻力及滚阻系数的相关性最高,说明选取的智能轮胎参数能够很大程度地解释轮胎触地变形时损耗的热量。同时,发现车速与加速度参数之间有着很强的共线性,且轮胎压力对于滚动阻力估算影响明显低于其他几种工况条件,所以需要依据实际情况调整各参数的权重。
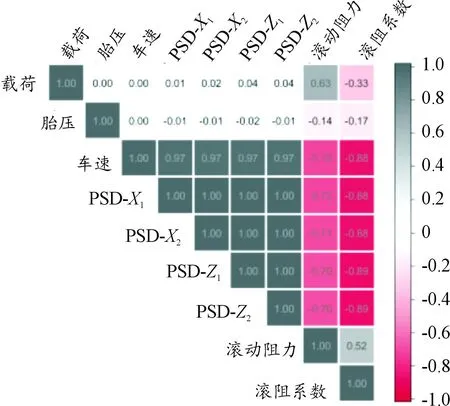
图14 输入输出各参数相关性
通过对上述轮胎滚动阻力相关参数进行相关性分析,可以发现变量间存在着明显的共线性,使用最小二乘准则下经典多元线性回归分析(MLR)无法达到理想的回归精度,而主成分分析(PCA)只考虑自变量的变异性,完全不考虑因变量,因此采用集主成分分析、典型相关分析和多元线性回归分析3种分析方法的优点于一身的偏最小二乘(PLS)回归方法[19-20]对轮胎滚动阻力进行回归分析。
为了保证回归算法的可靠性,需要对输入参数与滚动阻力参数数据进行标准化处理,其计算方式如下:

(9)
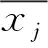
依据偏最小二乘回归分析法的算法原理,在Matlab中编写相应的计算程序,通过提取成分的贡献率确定要用的主成分个数,设置自变量和因变量提出成分的贡献率大于5%且累计贡献率小于95%为条件,最终计算获得主成分贡献的Pareto图,如图15和图16所示。
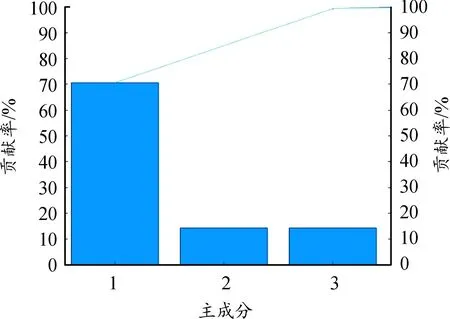
图15 主成分对自变量的贡献率
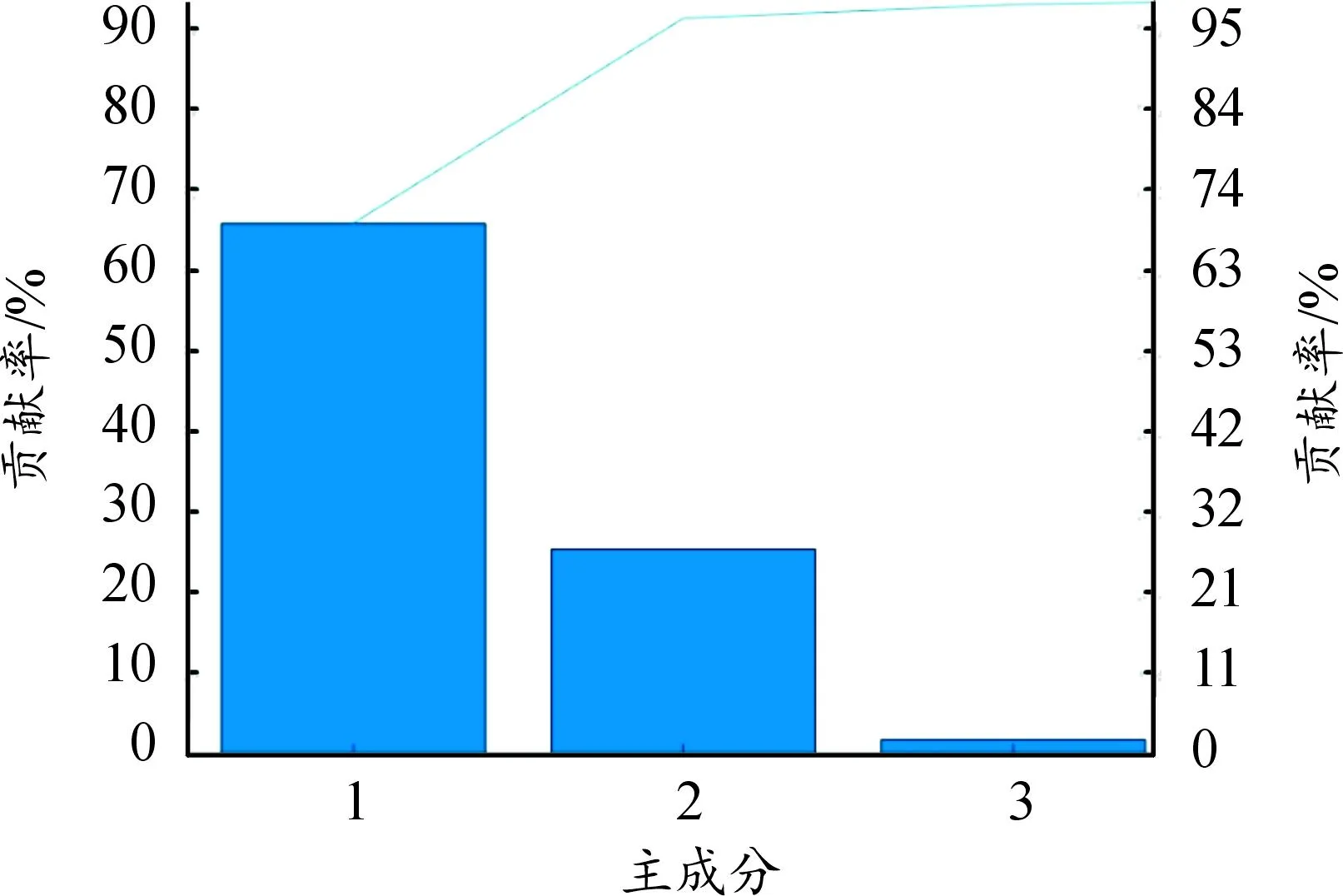
图16 主成分对因变量的贡献率
可以发现,提取的前3个主成分解释了输入参数98%的信息、输出参数97%的信息,能包括工况参数和加速度信号参数的绝大多数信息。计算所得的3对主成分和标准化处理的数据之间的关系式为
第1对成分:
u1=-0.006 088*x1+0.009 035*x2+
0.046 328*x3+0.046 229*x4+
0.045 987*x5+0.045 989*x6+
0.045 917*x7
(10)
v1=-3.200 231*y1-3.844495*y2
(11)
第2对成分:
u1=-0.228 732*x1+0.012 663*x2+
0.005 241*x3+0.001 739*x4+
0.000 484*x5-0.004 293*x6-
0.004 884*x7
(12)
v2=-2.472 622*y1+1.956187*y2
(13)
第3对成分:
u1=-0.013 522*x1-0.228 603*x2-
0.019 426*x3+0.004 595*x4+
0.008 812*x5+0.005 391*x6+
0.007 175*x7
(14)
v3=0.029 380*y1+0.096 003*y2
(15)
滚动阻力F与主成分之间的关系为
F=0.646 2*u1-0.148*u2-
0.169 9*u3
(16)
滚阻系数μ与主成分之间的关系为
μ=-0.313 8*u1-0.180 4*u2-
0.184 5*u3
(17)
将式(10)—式(15)代入到式(16)和式(17)中,可以获得标准化参数的偏最小二乘模型。对标准化参数进行逆变换,获得原始变量的偏最小二乘模型。
最后得出如下回归方程:
F=32.895 814+0.005 178*X1-
7.295 808*X2-0.014 801*X3-
0.037 032*X4-0.036 938*X5-
0.032 782*X6-0.032 919*X7
(18)
μ=14.496 886-0.000 453*X1-
1.603 217*X2-0.002 899*X3-
0.007 602*X4-0.007 786*X5-
0.007 940*X6-0.008 095*X7
(19)
式中:F为滚动阻力,μ为滚阻系数,X1—X7分别为载荷、胎压、车速、PSD-X1、PSD-X2、PSD-Z1和PSD-Z2数据。
滚动阻力的仿真值与拟合值结果如表2所示。由表2可见,其拟合的最大绝对误差为1.28,最大相对误差为3.70%,PLSR回归方程拟合精度较高,能够为同类型同工工况的轮胎提供实时的滚动阻力值估计。
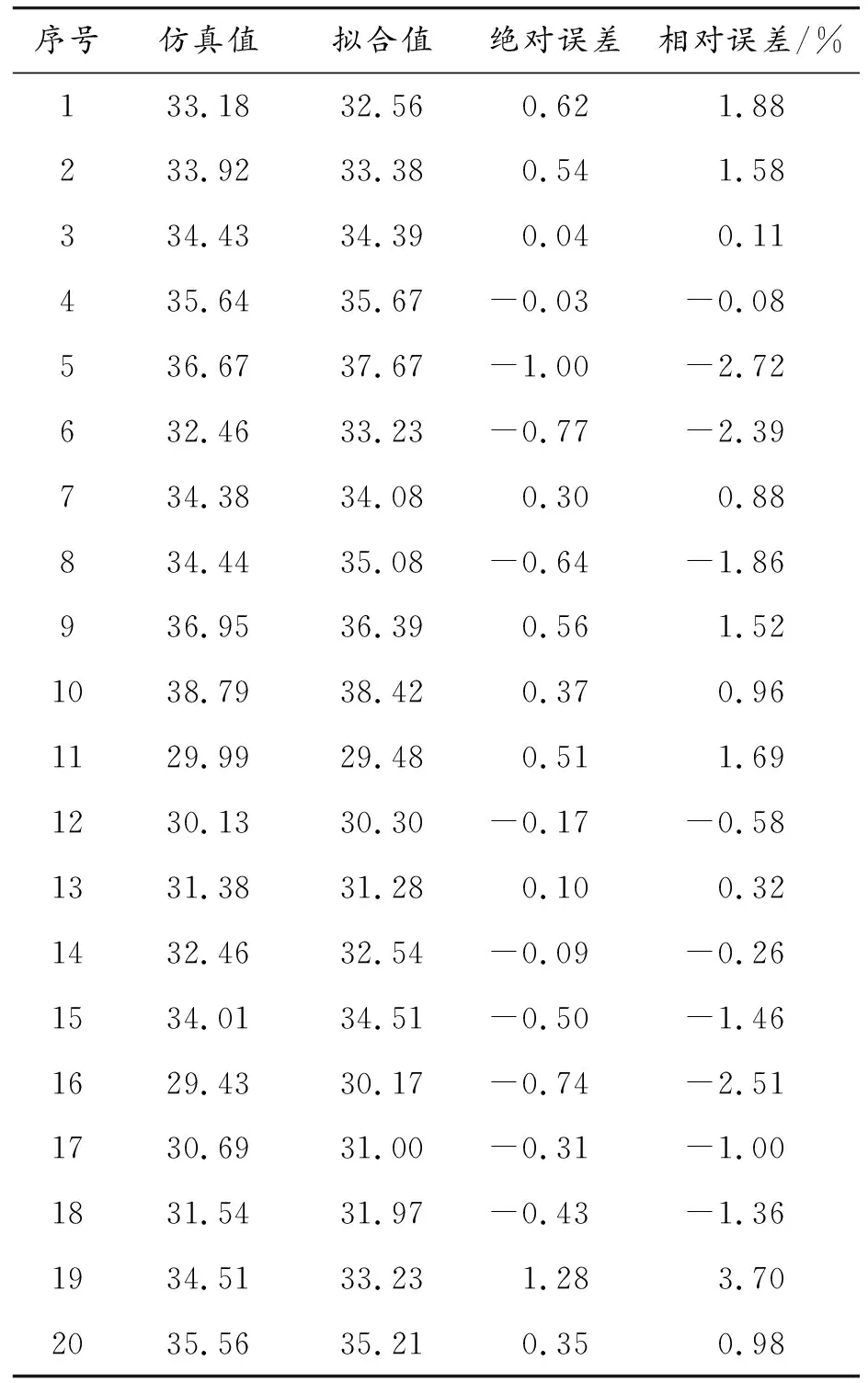
表2 滚动阻力PLSR回归方程拟合误差
轮胎滚阻系数的仿真值与拟合值结果如表3所示。由表3可见,其拟合的最大绝对误差为0.32,最大相对误差为3.95%,其平均误差要高于滚动阻力的拟合误差,但整体精度能够达到为同类型同工工况的轮胎提供实时的滚阻系数估计的标准。
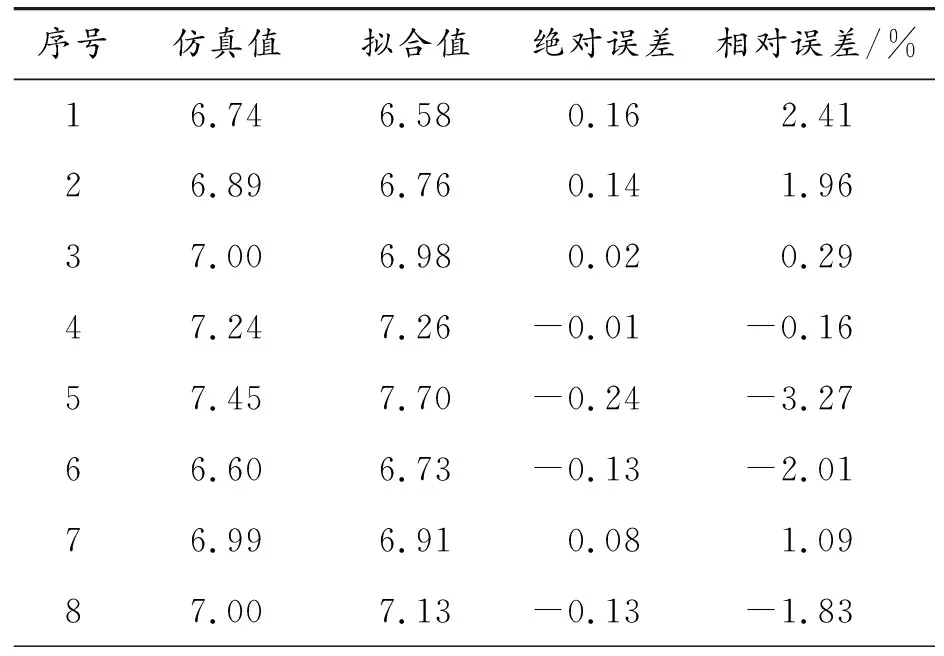
表3 滚阻系数PLSR回归方程拟合误差
为了验证基于加速度信号滚动阻力估计算法的优越性,使用相同的数据集拟合了基于行驶参数,即车速、负载和胎压的3特征模型。表4列出了3特征模型与7特征模型的估计结果对比。可以看出,7特征模型无论预测结果误差,还是拟合效果,都优于3特征模型,说明与传统的滚动阻力物理模型相比,基于智能轮胎的滚动阻力估计算法能够更精准地实现对轮胎滚动阻力的预估。
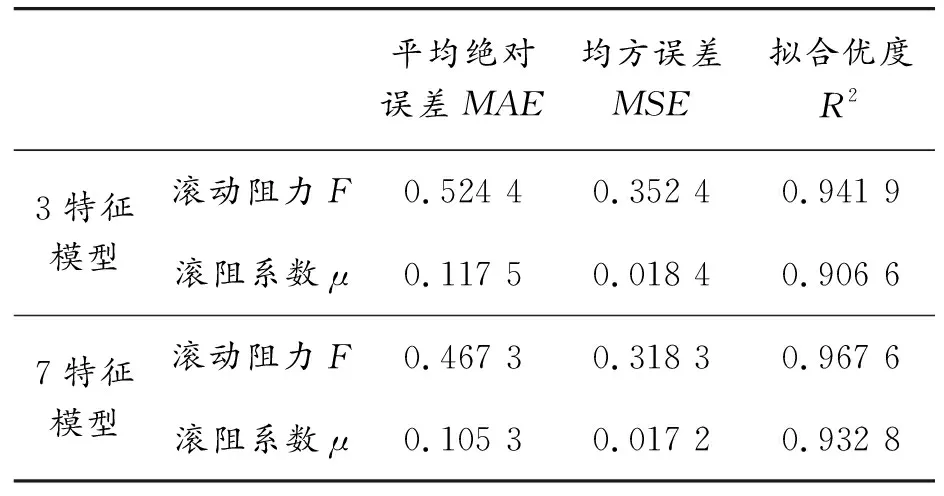
表4 回归模型性能参数
5 结论
1) 使用ABAQUS有限元仿真软件和智能轮胎技术分析轮胎内衬中心线一点加速度信号在轮胎接地变形过程中特征参数,构建了基于加速度信号的轮胎滚动阻力估计算法。
2) 分析三轴加速度信号功率谱密度波形特征,其纵向和径向波形有2个明显峰值,分别对应轮胎加载与卸载过程,而侧向波形没有可供参考的特征。
3) 含加速度信号特征参数的PLSR模型拟合结果优于与仅含工况参数的拟合结果,结合智能轮胎技术的滚动阻力物理模型能够提高对滚动阻力的估算精度。
