六自由度机械臂轨迹规划方法的研究
2024-02-03张博伦
张博伦, 于 涛
(辽宁工业大学机械工程与自动化学院, 辽宁锦州 121001)
0 引言
随着智能化时代到来,工业机器人的应用愈加广泛,轨迹规划是其中重要一环[1]。
轨迹规划是工业机器人的基础, 其性能对工业机器人工作效率、运动平稳性和能量消耗具有重大影响,如机器人在点动时末端抖动造成的机器人角加速度不连续、运动精度降低、轨迹偏移等问题,甚至由于冲击导致机械部件损坏[2-3]。
目前常见的轨迹规划方法主要有直线插补、 多项式曲线插补、S 型曲线插补、B 样条插补等方法[4]。 各种方法各有优劣,如B 样条插补方法的计算量大,多项式轨迹规划方法次数较高时容易出现龙格现象, 直线插补方法获得的轨迹曲线速度不连续, 带抛物线过渡的直线插补方法获得的轨迹曲线加速度不连续易产生抖震问题[5-6]。
本文以六自由度的UR10 机器人为研究对象,参考带抛物线过渡的线性插值轨迹规划方法提出一种新的轨迹规划方法,使其可以有效改善冲击对机械臂关节的影响,并通过MATLAB 进行仿真验证。
1 轨迹规划方法的分析与构造
1.1 对带抛物线过渡的线性插值轨迹规划的分析
在工业机器人的控制中, 为避免直接进行线性插值导致起终值点关节速度不连续,常使用抛物线进行过渡,可有效使直线插补轨迹规划获得连续速度[7]。 但是单纯使用抛物线过渡的轨迹规划方法同样导致关节加速度突变时对其产生一定冲击, 使得该方法在冲击影响不可忽视的场景下的适用性受到极大影响[8-9]。 如图1 所示为应用该方法对机械臂关节进行轨迹规划时关节角度与角加速度典型的曲线图[10]。
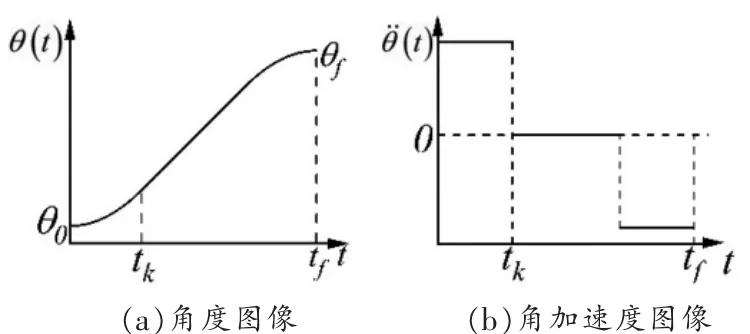
图1 带抛物线过渡的线性插值轨迹规划角度、角加速度图像
机械臂关节在tk时刻角加速度突变, 产生极大的角加加速度,对关节产生冲击。此时需要考虑冲击对机械臂运动及使用寿命等的影响, 判断该轨迹规划方法是否适用于机械臂当前的应用场景。
1.2 二三次多项式曲线混合过渡的构造
为降低带抛物线过渡的线性插值轨迹规划中冲击的影响, 可在其抛物线阶段与线性插值阶段过渡节点的邻域内增加一段三次多项式过渡, 使轨迹规划曲线在获得平滑的角度、角速度的同时,保证角加速度连续,进而削弱冲击造成的影响。该方案可被称为“带二三次多项式混合过渡的线性插值轨迹规划”,其角度、角速度、角加速度及角加加速度曲线如图2 所示。
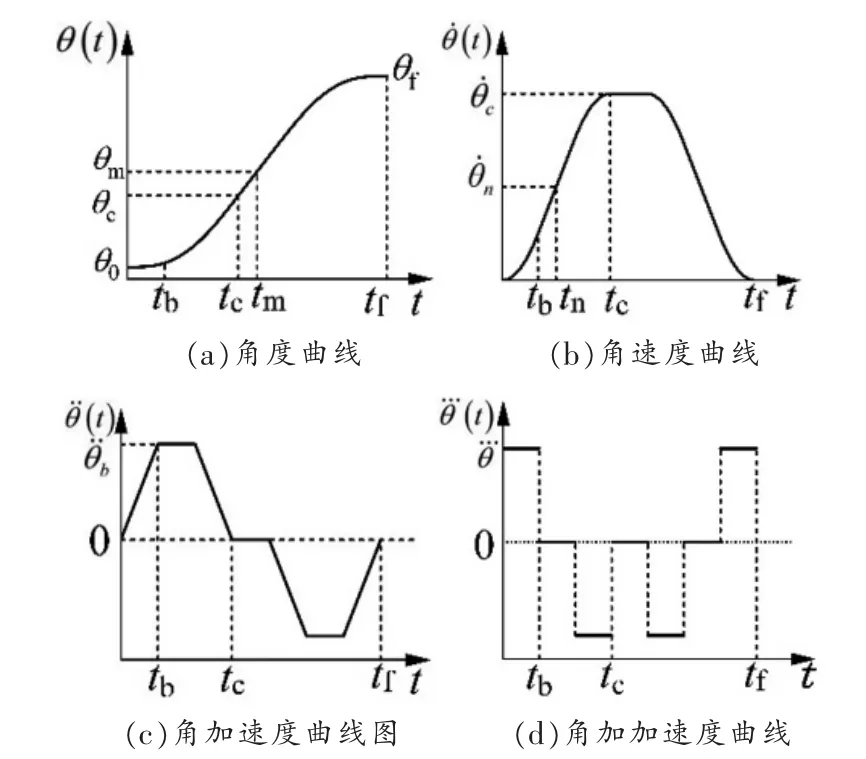
图2 带二三次多项式混合过渡的线性插值轨迹规划角度、角速度、角加速度及角加加速度示意图
图中tb时刻为三次多项式与二次多项式衔接时刻,tc时刻为二次多项式与线性插值衔接时刻。其中tm=tf/2,tn=tc/2。
根据tc时刻速度连续,有:
角度值θc:
将式(1)、式(2)与式(3)联立,且有θm=θf/2,得:
求解式(4)得
为保证tc≤tf/2,需满足:
此时tc必有实解。
为保证tb≤tc/2,需满足:
当式(6)取等时,线性段消失,路径完全由三次多项式与二次多项式构成。
当式(7)取等时,二次段消失,路径完全由三次多项式与线性段构成。
当tb=0,即加加速度无限大时,该轨迹规划方案退化为带抛物线过渡的线性插值轨迹规划。
2 推导轨迹方程
带二三次多项式混合过渡的线性插值轨迹规划可将轨迹方程分为七段,现用θ(1)~θ(7)对七段轨迹进行表示。其中tb在满足tb≤tf/4 的条件下适当选取,tc由式 (5)得出,在式(6)与式(7)所得出的上下限内选取,。
2.1 第一段曲线
当0≤t≤tb时,角加速度增大,轨迹曲线为三次多项式:
有边界约束条件:
将式(9)代入式(8)解得轨迹曲线系数:
2.2 第二段曲线
当tb≤t≤tc-tb时,角加速度保持,轨迹曲线为二次多项式:
为保证角度、速度与加速度连续,有约束条件:
将式(11)代入式(10)解得轨迹曲线系数:
2.3 第三段曲线
当tc-tb≤t≤tc时,角加速度降低,轨迹曲线为三次多项式:
为保证角度、速度与加速度连续,有约束条件:
将式(13)代入式(12)解得轨迹曲线系数:
2.4 第四段曲线
当tc≤t≤tf-tc时,该阶段为线性段,轨迹曲线为:
为保证角度与速度连续,有约束条件:
将式(15)代入式(14)解得轨迹参数:
2.5 第五段曲线
当tf-tc≤t≤tf-tc+tb时,角加速度增加,轨迹曲线为三次多项式:
为保证角度、速度与加速度连续,有约束条件:
将式(17)代入式(16)解得轨迹参数:
2.6 第六段曲线
当tf-tc+tb≤t≤tf-tb时,角加速度保持,轨迹曲线为二次多项式:
为保证角度、速度与加速度连续,有约束条件:
将式(19)代入式(18)解得轨迹参数
2.7 第七段曲线
当tf-tb≤t≤tf时有,角加速度降低,轨迹曲线为三次多项式:
为保证角度、速度与加速度连续,有约束条件:
将式(21)代入式(20)解得轨迹参数
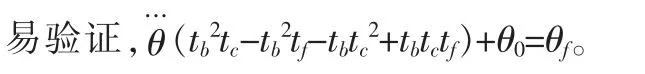
可得出,在七段轨迹中,关节产生的最大角速度:
最大角加速度:
3 在机械臂轨迹规划中的应用
本文选用丹麦优奥机器人公司生产的UR10 机器人为研究对象,其技术参数如下:有六个自由度,有效负载约10kg,有效工作半径为1300mm,所有关节的运动范围是±360°,均为旋转关节[11]。该机械臂各关节坐标系及D-H参数如图3 及表1 所示。

表1 UR10 机械臂D-H 参数表
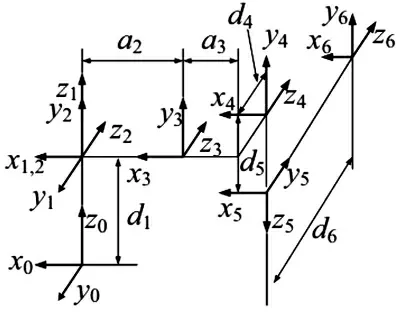
图3 UR10 的各关节坐标系
六个关节的启停时刻的角度如表2 所示。 时间设置为4s,指定启停时刻角速度、角加速度均为0,则针对机械臂关节分别应用带抛物线过渡的线性插值轨迹规划方法和二三次多项式混合过渡的线性插值轨迹规划方法针对关节角度与角加速度的仿真结果如图4 与图5 所示。各关节角度与角加速度分别用θ1~θ6、α1~α6表示,虚线部分为带抛物线过渡的线性插值轨迹规划方法,实线部分为本文方法。
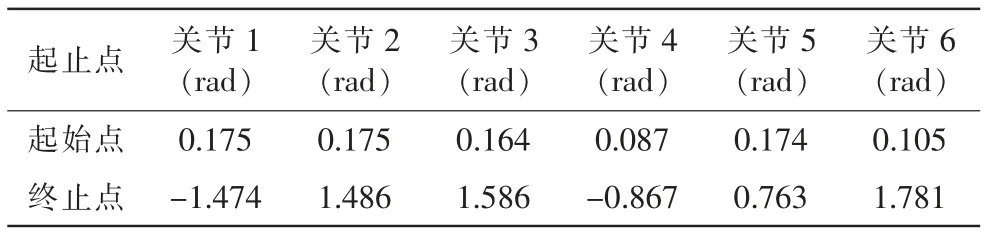
表2 关节启停时刻角度

图4 各关节角度变化曲线

图5 各关节加速度变化曲线
由图4 可知,两种方法在起始点和终止点间运行时间基本一致,且由初始值逐渐变化至终止值,轨迹规划均符合要求。
由图5 可知, 若采用带有抛物线过渡的线性插值方法, 在加速阶段与速度保持阶段的过渡时刻加速度会产生跳变,对机械臂关节造成较大冲击。本文方法则通过增加三次曲线过渡,使加速度连续变化,减弱了冲击对关节的影响。
4 结论
本文针对带有抛物线过渡的线性插值方法在抛物线段与线性段衔接时刻加速度产生跳变, 对关节产生过大冲击的问题, 提出了二三次多项式混合过渡的线性插值轨迹规划方法,并推导出了该方法的轨迹方程参数,给出了其相关参数的选取建议。 虽然本文给出方法相对带抛物线过渡的线性插值轨迹规划方法提升了轨迹方程的复杂度, 但是有效降低了轨迹规划中冲击对机械臂关节的影响,为轨迹规划方案的的创新提供了思路。
