锂离子电池模组自适应均衡阀值控制策略研究
2024-02-03姚琳娜罗仁宏王之丰
姚琳娜, 罗仁宏, 刘 瑛, 王之丰
(1.上海市工业技术学校, 上海200001; 2.武汉商贸职业学院现代工业技术学院, 湖北武汉 430000;3.中汽研汽车检验中心(常州)有限公司, 江苏常州 230000; 4.浙江省吉利汽车研究院有限公司, 浙江杭州 315336)
0 引言
随着新能源汽车、储能电站等领域的不断发展,电池模组将成百上千节动力电芯串并联组合起来, 然而在电池模组中,由于制造偏差、使用环境等因素的影响,电池之间的容量、内阻等参数会存在差异,容易导致电芯内部电阻、自放电率和容量等内部性能不一致性[1],进而影响电池组的性能和寿命[2-3]。 为了解决这一问题,电池均衡技术应运而生。
电池均衡技术主要有固定电阻式、开关电容式、变频器式和电感式等, 固定电阻式电池均衡结构简单且应用方便,但效率低且能量损失大;开关电容式电池均衡控制技术多用于低电压电池模组,控制相对简单,但均衡率较低[4-6];基于变换器式电池均衡能实现快速均衡且转化效率高,但其控制复杂且成本高[7];电感式电池均衡技术可以快速实现电池间电能的传输和均衡, 有效提高电池组的循环寿命和安全性能[8]。 因此,电感式电池均衡技术已经成为电池模组系统中不可或缺的一部分。
目前国内外学者对电池均衡控制系统进行大量研究,且多集中电池模组均衡阀值的设定上。 郭向伟等[9]通过修改设定阀值从而解决Buck-Boost 均衡电路中开关频繁通断问题,从而提高电池模组均衡效率; 谢伟[10]和ERDO ˘GAN[11]等人基于单电感串并联电池模组,设定一个固定启动阀值和一个固定停止阀值的均衡控制策略, 提高了该电池模组充放电均衡效率;吴铁洲[12]提出三阀值均衡控制策略,结果显示相比传统单阀值,可有效提高电池组均衡效率。 以上研究以电池模组设定阀值作为研究重点,在一定程度上改善了电池模组不一致性,提高均衡速率,但固定阀值无法根据电池模组工作状态进行自动调整,无法充分发挥出电池模组均衡潜力。基于上述分析,本次研究提出了一种锂离子电池模组自适应阀值电感式均衡控制策略,利用转移矩阵计算最佳转移路径,从而提升目标电池模组均衡效率。
1 电感式均衡控制原理
1.1 电感式均衡电路控制原理
电感式均衡控制原理是将较高SOC 值电池电量传输到电感中, 并通过电感将电量分配给较低SOC 值电池,从而达到均衡电池组目的。图1 为本次设计电感式均衡电路, 本电路由2 个续流二极管、2 个场效应管和1 个储能电感组成。PUMP2S 是Q1-B 的PWM 控制信号,通过驱动信号来控制MOSFET 管, 从而达到将电池电量转移到电池组正极或负极。整个均衡过程可以划分为三个阶段:储能阶段、释能阶段和结束阶段。

图1 电感式均衡模块电路图
1.2 储能阶段
当单体电池V2相对单体电池V1的SOC 过高时,PUMP2S 发出控制信号,C2 电容电压被拉低, 即与较低SOCV1单体电池的负极相连接,PUMP1N 无信号发出,N沟道Q1-A 不导通, 而P 沟道Q1-B 源极相对栅极电压Vsg高于其导通门限电压Vgsth,因而P 沟道Q1-B 导通,整个储能阶段等效电路见图2。

图2 储能阶段等效电路图
电感平均充电电流计算方程式:
式中:Ipeak—电感充电峰值电流;ton—导通时间;T—周期。
1.3 释能阶段
导通时间之后,P 沟道Q1-B 关断,N 沟道Q1-A 处于不导通状态。 当电感L1 感应电压高于Q1-A 续流二极管正偏电压时,其续流二极管导通,电感L1 将电能转移给较低SOC 单体电池,随着电感L1 电能转移,其整个释能阶段等效电路见图3。
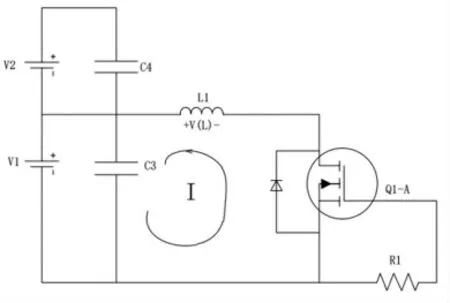
图3 释能阶段等效电路图
电感平均放电电流计算方程式:
式中:toff—截断时间。
1.4 结束阶段
当N 沟道Q1-A 的续流二极管两端电压差低于其正偏电压时,续流二极管立刻关断,从而停止电能转移,其结束阶段等效电路见图4。

图4 结束阶段等效电路图
当电流减小到不足以维持Q1-A续流二极管导通时,Q1-A 等效成输出电容,Q1-B 等效成续流二极管。 与此同时, 电感能量较少,这些能量被R3 消耗掉, 而L1 与R3组成欠阻尼震荡系统。
2 自适应均衡阀值控制逻辑求解
2.1 自适应均衡阀值求解
本次研究设置引入均衡阀值修正因子f 对设定阀值进行自适应优化,其阀值计算方程式如下:
式中:Sc—目标电芯单体SOC 值中点;f—均衡阀值修正因子, 其值根据电池模组工作工况进行取值;δ—均衡精度,一般取值为2%Sc。
对目标电池充放电特性进行拟合,得到一维方程式(3)。
式中:ai—多项式;i—电芯个数。
为了计算出电池均衡阀值修正因子f,设定e=|V'(Scen)|。对|V'(Q)〈1.5e|进行不等式求解。 得到修正因子见式(4):
式中:SII—II 区域起始SOC 值;l—II 区域电量范围长度值。
考虑到电芯单体差异性,对电池模组SOC 值进行修正,并在相邻区域边界处设置安全系数σ,从而提高电池模组均衡精确度。
式中:S*—修正后电池模组SOC 值;Si—各电芯SOC 值;SσII'—II′区起始SOC 值;SEII'—II′区截止SOC 值;
将式(5)代入式(4)中进行计算得到:
式中:l*为II′区域电量范围长度值。
为了确定电池均衡中心点Sc,求解|Δ(Sc)|的极小值,其计算方程式如式(7):
式中:δ 取值为2%Sc;η—能量转换效率。 Sc 在[Smin,Smax]内波动,对式(11)进行公式变换得到式(6)和式(7)。
式中:u—目标模组中有u 节电芯SOC 值超出设定均衡阀值;v—目标模组中有v 节电芯SOC 值低于设定均衡阀值。
从式中可以看出,Su(SC)和Sv(SC)在[Smin,Smax]区间内分别呈单调递减和单调递增变化。 在电池模组均衡初始时刻Su〉Sv,最终Su〈Sv,即△SC=|Su-Sv|在[Smin,Smax]区间内存在极值点|Δ(SC)|min。
2.2 自适应均衡阀值控制方法
考虑到单体电芯SOC 值通常在电池模组Savg左右,故以Savg为算法起点, 对单体电芯SC进行求解,h 为求解步长,其求解逻辑见图5。
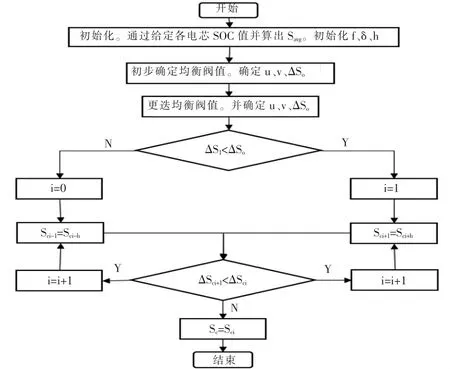
图5 电池模组均衡中心点求解逻辑图
确定SC后,建立电池模组均衡数学模型[13],其电量转移方程式将式(9)。
为了提高电池模组均衡速率, 应尽可能降低转移次数,即求解式(9)的稀疏度SPA(u*v)最小值,其求解方程见式(10)。
式中:tij—目标模组中高SOC 值单体电芯i 向低SOC 值单体电芯j 转移C 单位电量所需时间;T—脉冲信号周期;ΔS—周期内单体电芯之间转移电量。
3 仿真分析
3.1 锂离子等效模型
采用动态模型来模拟受控电压源串联电阻方式来等效电池充放电过程,利用商用软件MATLAB 来搭建锂离子等效模型 (见图6)。 电池充电电特性试验数值由零部件供应商提供(见图7)。

图6 锂离子电池充放电等效模型
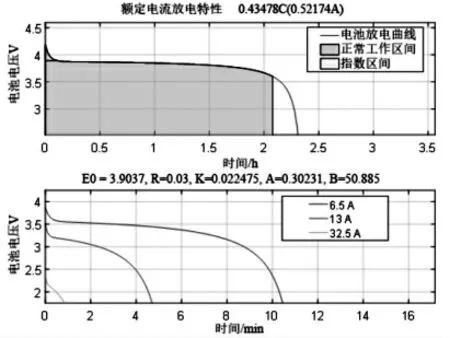
图7 充放电特性曲线
目标电池模组由5 节锂离子电池串联而组成, 单体电池额定容量为2.2Ah,电池额定电压为3.7V,充放电截止电压分别为4.2V 和2.7V,均衡电路中L=2Mh,充放电电流为1A,电池连接3 个示波器, 用于检测电池SOC 值、 充放电电压值和电流值。
将目标电池模组内电芯进行标记, 在固定均衡阀值和自适应均衡阀值控制策略下对目标电池模组进行充放电均衡性能对比仿真实验。
3.2 充电状态均衡仿真
图8 为固定均衡阀值和自适应均衡阀值控制策略下放电实验,从图8 可以看出,相比于固定均衡阀值控制策略,自适应均衡阀值控制策略下的高SOC 单体电池在开始时向低SOC 单体电池电量转移较快,有利于电池模组电量均衡。

图8 两种控制策略充电对比图
图9 为固定均衡阀值和自适应均衡阀值控制策略下放电实验,从图9 可以看出,相比于固定均衡阀值控制策略, 自适应均衡阀值控制策略下高SOC 单体电池与低SOC 单体电池之间进行电量均衡, 从而快速降低目标电池模组的不一致性。

图9 两种控制策略放电对比图
表1 为在固定均衡阀值控制策略和自适应均衡阀值控制策略下目标电池模组充放电SOC 值结果,固定均衡阀值控制策略下目标电池模组充放电SOC 极差值分别为4.5 和2.0,而自适应均衡阀值控制策略下目标电池模组充放电SOC 值分别为1.9 和0.4。

表1 仿真结果对比表
4 试验标定
图10 为目标电池模组均衡试验电路实物图,以PCB为载体搭建目标模组充放电均衡硬件电路, 作为实验测试平台,并基于MATLAB 进行DSP 控制器的软件开发,利用新威电池测试设备进行目标电池模组数据采集。本实验以5 节单体电芯为研究对象,电池初始值和试验工况同仿真试验。

图10 目标模组均衡电路实物图
进行目标电池模组进行自适应均衡阀值控制策略充放电试验,试验结果见表2。 从表中可以看出,实验值与仿真值误差较小,满足工程计算要求,验证了本次仿真计算的有效性。

表2 实验值与仿真值对比表
5 结论
本研究提出了一种锂离子电池模组自适应均衡阀值控制策略, 该方法在设计的电感式主动均衡电路上进行均衡阀值的整定,相比固定均衡阀值控制策略,该策略提高了电池模组的一致性,降低了单体电芯之间的差异性。通过仿真与实验相结合方法, 验证了该控制策略的可靠性,提高了目标电池模组的均衡能力。
