明渠非标准断面法测流水位流量关系的率定及影响因素分析

梁慧真,宗全利,2*,刘贞姬,谢炎,刘冬冬

(1. 石河子大学水利建筑工程学院,新疆 石河子832000; 2. 青岛农业大学资源与环境学院,山东 青岛266109)

灌区量水是实现灌区计划用水目标和节水农业的关键措施.为适应中国经济、社会等方面的发展,实现灌区量水设备现代化的要求显得尤为迫切.灌区量水设备正向着信息化和规范化方向发展.但目前,人工测流仍是灌区的常用量水方法,即使是自动化量水程度比较高的灌区也需要利用人工测流结果进行校核.仅依靠人工进行流量计算,测流效率较低且耗时耗力.若可以率定出精确的渠道断面水位流量关系曲线,测流人员只需观测固定断面水位就能快速推算出流量.中国新疆等西北干旱灌区灌溉渠系配套完善,引水和末级灌溉主要通过明渠渠系完成,灌区渠道常采用标准断面法、测水箱等方式量水,这2种量水方式均需要利用渠道断面水位流量关系进行测流.因此率定出精确的水位流量关系曲线对于新疆灌区量水工作来说十分必要.

在实际灌区量水过程中,利用标准断面法量水有时很难满足无冲刷或淤积及变动回水影响等要求[1],尤其对于渠系引水量较小且含沙量大的新疆等干旱区渠系,渠道淤积现象频繁,对量水影响较大,出现非标准断面量水.此外,非标准断面量水问题还包括:标准断面形成的稳定水位流量关系因受变动回水、泥沙冲淤、洪水涨落、水生植物、冬季结冰等因素影响而变为不稳定的水位流量关系.对此,刘焕芳[2]对稳定的和受泥沙冲淤、涨水退水等因素形成的不稳定的水位流量关系曲线的成因进行了分析.对于水位流量关系曲线的率定,李守义等[3]利用迭代法解决了多泥沙渠道水位流量关系的多曲线拟合问题.孙昭华等[4]对受回水影响的河道水位流量关系确定方法进行了研究.WANG等[5]提出了一种适合梯形渠道的水位流量关系优化方法.李应求等[6]基于Box-Cox变换模型对水位流量关系曲线进行了拟合.SINGH等[7]采用Tsallis熵来对水位流量曲线进行了推导;KASHANI等[8]利用智能算法建立了水位流量关系.KAVOUSIZADEH等[9]提出了一种适用于建立明渠水位流量关系的新方法.丁佩等[10]用综合校正法对受洪水涨落及回水变动综合影响的水位流量关系进行了研究.此外,也有学者就贝叶斯方法、遗传算法、神经网络等方法对水位流量关系进行研究并取得了相应的成果[11-13].

前人的研究大多是针对天然河道,而对干旱区灌溉渠道的研究相对较少,且较少考虑泥沙淤积、回水等因素对渠道水位流量关系的影响.新疆等西北干旱灌区,渠道来水含沙量大,若忽略泥沙淤积对测流的影响,将会对灌区量水的测流精度造成很大影响.

文中以新疆第三师某团场25处渠道量水断面为研究对象,对量水断面水位流量关系曲线进行率定和误差分析,并对影响流量拟合参数的因素进行分析,以期能够为灌区自动化量水提供率定依据,为当地灌区量水工作效率的提高及农业量水信息化的实现提供参考.

1 研究区概况

新疆第三师某团场地势平坦,灌溉面积1.512万hm2,地表水多年平均悬移质含沙量为4.26 kg/m3,泥沙含量较大,渠道流速在0.4 m/s左右.境内共有3条干渠(中干渠、四支干渠和八支干渠)向该团输水灌溉,另有支渠47条、斗渠241条.在该研究区共设计了25处测量点,均位于四支干渠和八支干渠及其支渠上,位于分水闸附近的测量点主要分布在分水闸后50～100 m处,在渠道供水时利用标准断面法量水.图1为新疆第三师某团场渠系分布图,主要渠系及测量点分布如图所示.研究区25处测量点所在渠道断面的各水力要素如表1所示,表中b为渠道底宽,m为边坡系数,i为水面比降,对于水位流量稳定的渠道断面,i为渠道坡降.

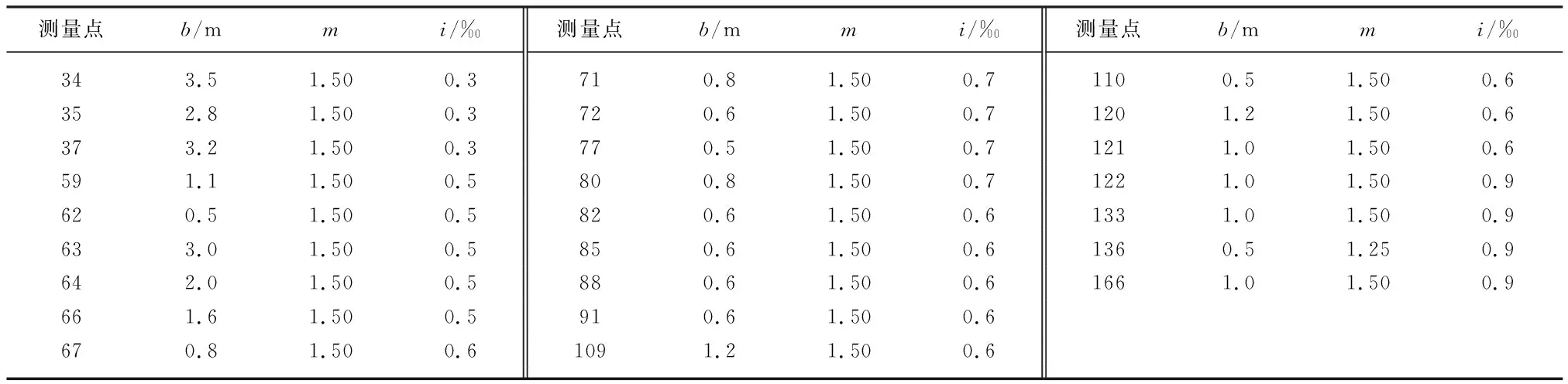
表1 渠道量水断面水力要Tab.1 Hydraulic elements of channel water measuring sections

图1 新疆第三师某团场渠系分布图Fig.1 Distribution map of channel system of regiment farm of the Third Division of Xinjiang

2 研究方法

2.1 测流原理与曲线检验方法

2.1.1标准断面法测流原理

标准断面法量水是利用稳定的渠道断面水位流量关系进行推流的一种灌区常用量水方法.渠道断面水位流量关系是否稳定与其过水断面的各水力要素有关,梯形明渠流量计算公式为

(1)

式中:Q为过水断面流量,m3/s;v为过水断面平均流速,m/s;A为过水断面面积,m2;H为过水断面水深,m;Ra为渠道粗糙系数.

对某一固定渠道而言,n,m,b,i为定值,因此流量Q可以表示为水深H的函数.渠道标准断面量水的水位流量关系式宜用幂函数[1]表示为

Q=KHμ,

(2)

式中:K为拟合系数;μ为拟合指数.

将实测流量值及其对应水位绘制成散点图,根据式(2),利用回归分析法拟合出拟合参数K和μ.如属于稳定的水位流量关系,可通过点带重心,绘出一条平滑连续的曲线,使数据点均匀地分布在曲线两侧,即得到量水断面的水位流量关系曲线.

2.1.2水位流量关系曲线检验方法

对于率定出的水位流量关系曲线,还应进行符号检验、适线检验和偏离数值检验,当3项检验结果均满足要求时,则可利用该水位流量关系曲线进行推流[14].

1) 符号检验

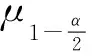
(3)

式中:μ为统计量;k为测点偏离曲线的正号或负号个数;n为测点总数.

2) 适线检验

将测点水位由低至高排序,从第2点开始统计偏离正负符号变换的次数,按式(4)计算μ值并与文献[14]中表5给定的显著性水平α的μ1-α比较,若满足μ<μ1-α则认为合理.

(4)

式中:k为变换符号次数,k<0.5(n-1)时进行检验,否则不进行此检验.

3) 偏离数值检验

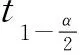
(5)

(6)

3 结果与分析

3.1 标准断面法测流的水位流量关系

图2为2021年3月测量点35和37处的水位流量测量结果.可以看出,这2处的水位流量点分布比较密集,均呈带状,且数据点不是依时间次序呈系统偏离,属于稳定的水位流量关系.根据式(2)得到2个断面的水位流量关系拟合结果为Q=2.854 7H2.071 4(R2=0.980 6),Q=3.104 4H1.838 7(R2=0.973 7).实测值与拟合值的相对误差最大值分别为5.49%和5.73%,表明所率定的水位流量关系曲线是稳定的.

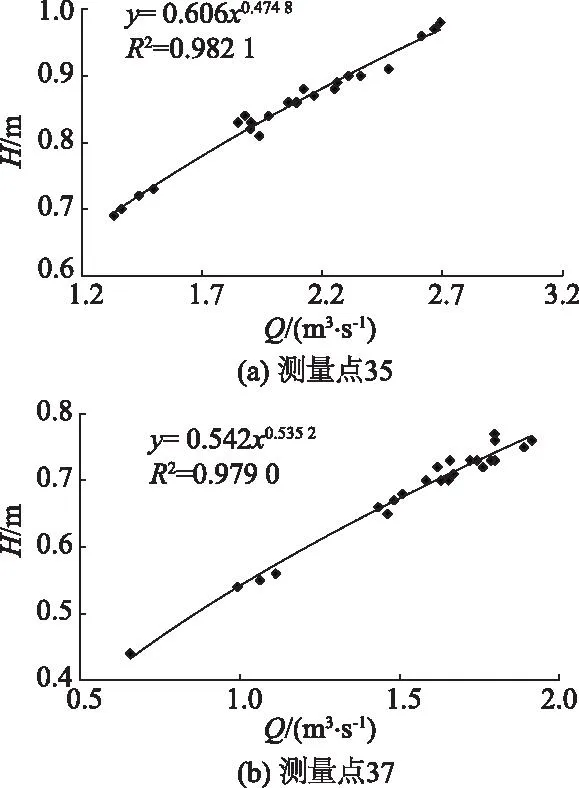
图2 稳定的水位流量关系曲线Fig.2 Stable stage-discharge relation curves

对25处测量点的水位流量关系曲线进行拟合,拟合结果如表2所示.从表中可以看出,有14处断面的水位流量关系曲线拟合方程的R2大于0.85,平均相对误差最小值为0.9%,最大值为6.4%,属于稳定的水位流量关系.说明该部分测流断面选取比较合理,没有受到泥沙淤积或回水等因素的影响.但仍有11处测量点的水位流量关系不稳定,其测流断面属于非标准断面,需进行特殊的分析.

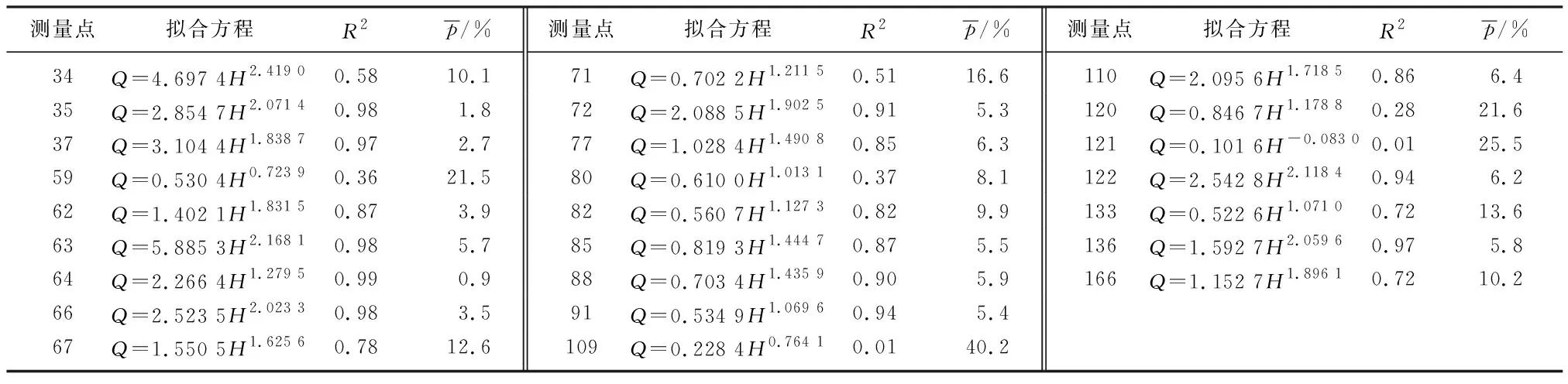
表2 水位流量关系曲线拟合及相对误差计算结果Tab.2 Stage-discharge relation curve fitting and relative error calculation results

3.2 非标准断面法测流的水位流量关系

3.2.1受变动回水影响的水位流量关系

以测量点71和109为例,测量点71所在渠道内无泥沙淤积等因素影响,但断面流量较小,测流时下游闸门开度较小,对水流形成阻碍,使水流出现回流现象;测量点109所在渠道底部有较少量泥沙,无回水等因素影响,水流流速几乎为0,测流时下游闸门处于关闭状态,下游水位不断抬高,导致水流出现回水现象.图3—5分别为测量点71和109的水位流量、水位流速和水位面积关系曲线图.

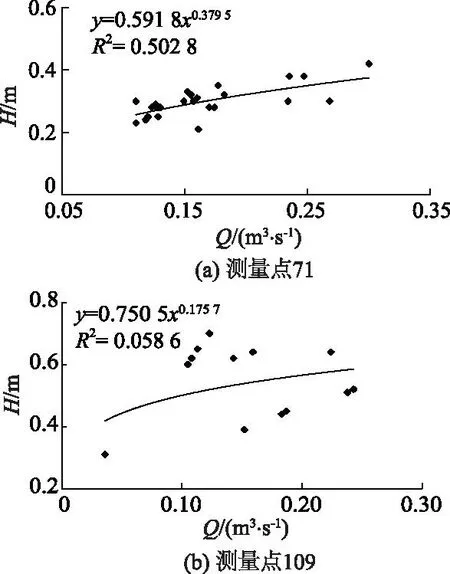
图3 水位流量关系Fig.3 Stage-discharge relation

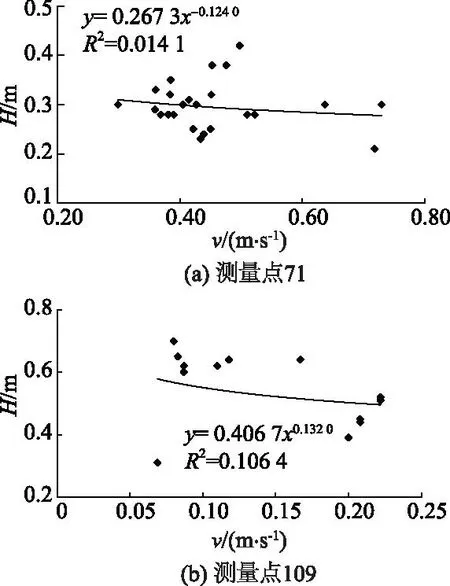
图4 水位流速关系Fig.4 Stage-velocity relation

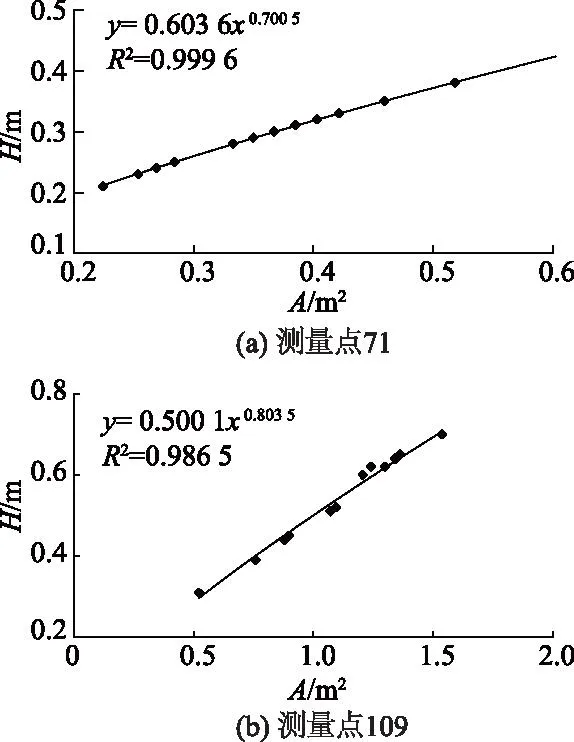
图5 水位面积关系Fig.5 Stage-area relation

从图3—5可以看出,受回水影响的水位流量关系、水位流速关系的数据点分布比较散乱,而水位面积关系数据点则密集地分布在一条带上.这主要是因为渠道水流受到下游渠道闸门开度等因素影响,下游水位发生变化,使测流断面受下游回水的顶托,导致该测流断面的水面比降发生变化,从而引起了测流断面流速和流量的变化.同水位下比降大的水位流量(流速)关系点偏向曲线右侧,比降小的水位流量(流速)关系点偏向左侧,所以水位流量关系曲线和水位流速关系曲线的数据点呈散乱分布.水面比降越大,流速和流量越大;比降越小,流速和流量越小.

根据实测结果,25处测量点中有5处断面为受变动回水影响不稳定的水位流量关系,说明实际渠系水量分配的调度运行对流量测量有较大影响.测流应尽可能在渠道运行调度稳定一段时间,下游水位的涨落不再影响测流断面水位后进行,从而可有效避免变动回水引起的不稳定水位流量关系.

3.2.2受淤积影响的水位流量关系

由于研究区地势平坦,纵坡在0.3‰～0.9‰,渠道流速大多约0.4 m/s,加之地表水多年平均悬移质含沙量为4.26 kg/m3,泥沙含量很大,造成渠道淤积明显.如测量点59所在渠道坡降较小,水流速度较慢,渠道内无变动回水、洪水涨落及水生植物等因素影响.根据2021年3月28日现场观测结果,渠道淤积厚度达32 cm,淤积较为严重,渠道两侧堆积了大量人工清理出的泥沙.

图6为测量点59水位相关曲线.

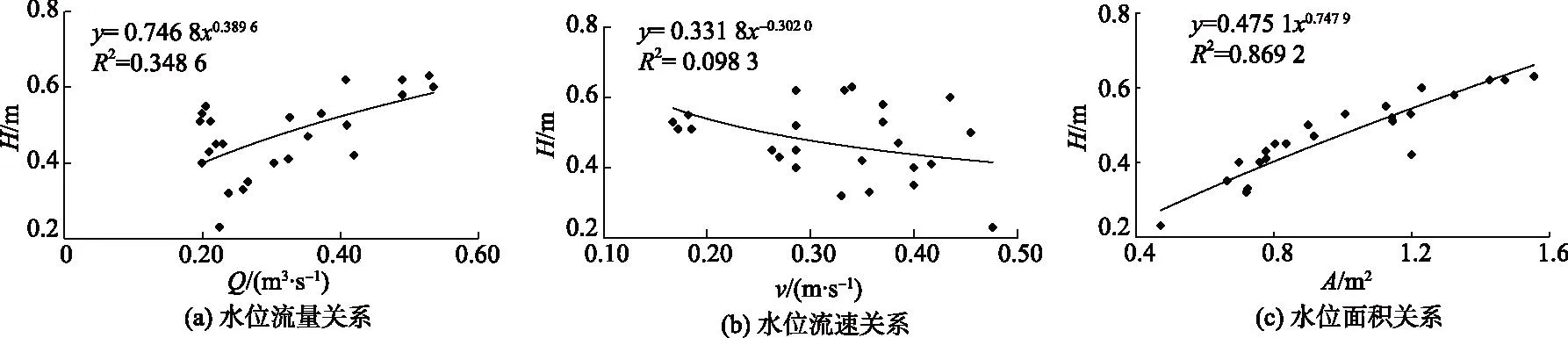
图6 测量点59水位相关曲线Fig.6 Correlation curve of stage at measuring point 59

从图6可以看出,受淤积影响的水位与流量、流速、面积关系曲线的数据点分布较散乱,但流速、面积与流量的变化不是相应的,流速、面积与流量的关系没有呈现一定规律性.根据实测结果,25处测量点中有6处为受淤积影响的不稳定水位流量关系,说明渠道淤积对流量测量有一定影响.当淤积达到一定厚度(如测量点59的32 cm),则会形成明显的不稳定水位流量关系,从而影响测流结果.因此,在实际应用过程中,当断面仅受冲淤影响有冲淤变化,但在冲淤前后仍可保持稳定时,可以在冲刷或淤积前后,分时段确定不同的水位流量关系.

3.3 不同水位流量关系检验结果及误差分析

3.3.1稳定水位流量关系检验结果及误差分析

以测量点35为例,根据已率定的水位流量关系(如图2a所示),对其进行误差和三项检验计算.检验结果及误差计算如表3所示,表中Q实和Q计分别为实测和计算流量.经过计算,所率定测量点的水位流量关系曲线的三项检验均能通过检验,相对误差最大值为5.49%,精度满足要求,可用于流量推算.

表3 稳定水位流量关系检验结果及误差统计(测点35)Tab.3 Test results and error statistics of stable stage-discharge relation (measuring point 35)

3.3.2不稳定的水位流量关系检验结果及误差分析

4 讨 论

从式(1)中可以看出,流量与渠道粗糙系数、边坡系数、底宽、坡降和水深有关.由于所率定出的稳定水位流量关系曲线的渠道均为混凝土衬砌,施工工艺基本相同,渠道粗糙系数和边坡系数基本相同.因此,主要分析渠道底宽、坡降对流量拟合参数K和μ的影响.

4.1 渠道底宽对流量拟合参数的影响

选取研究区中渠道粗糙系数、边坡系数相同的渠道断面,比较其底宽对流量拟合参数的影响.结果如图7所示.

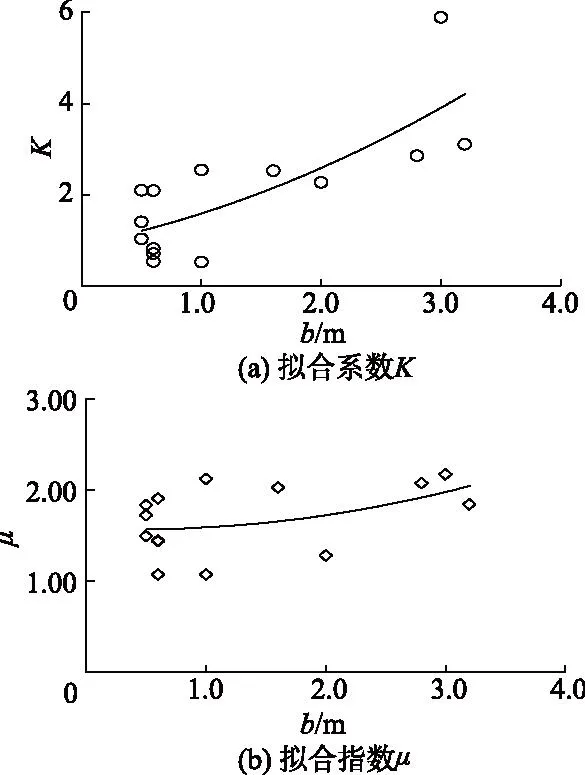
图7 不同底宽渠道的流量拟合参数Fig.7 Flow fitting parameters for channels with different bottom widths

在渠道粗糙系数、坡降、施工工艺基本相同的情况下,渠道量水断面流量拟合参数与渠道底宽呈正相关关系.在底宽一定时,流量拟合参数还与渠道坡降有关.在同一渠道底宽下,选取坡降不同的若干渠道,因此在图7中同一底宽下会对应若干拟合参数;相同底宽情况下,渠道坡降越大,拟合参数也越大.

4.2 渠道比降对流量拟合参数的影响

选择研究区中粗糙系数、边坡系数、底宽相同的渠道,比较其坡降对流量拟合参数的影响,结果如图8所示.随着渠道坡降的增加,其流量拟合公式的拟合参数逐渐减小,即渠道量水断面流量拟合参数与渠道坡降呈负相关关系.在同一渠道坡降下,选取底宽不同的若干渠道,所以在同一坡降下会对应若干拟合参数.文中的渠道位于干旱灌区的新疆南疆地区,泥沙含量较大,与以往研究的渠道运行条件有所不同;其次研究共选取了14处不同渠道测量点且每个坡降均选取了若干个渠道参数,而现有研究中的渠道坡降资料较少,这进一步证明文中结果的可靠性.

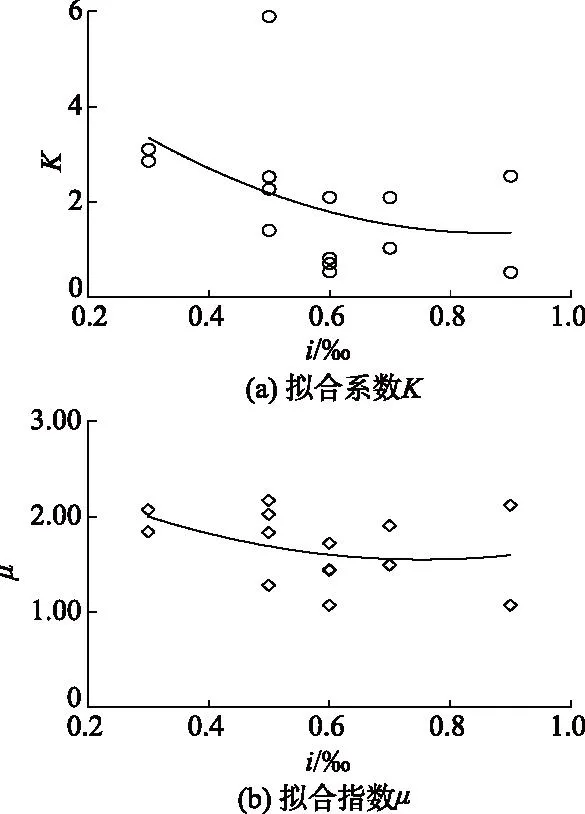
图8 不同坡降渠道的流量拟合参数Fig.8 Flow fitting parameters of channels with diffe-rent slopes

5 结 论

1) 在渠系引水量较小且含沙量大的新疆等干旱区明渠中,非标准断面法测流占有较大比率.对于受回水影响的断面测流时,应尽可能在渠道运行调度稳定一段时间,下游水位的涨落不再影响测流断面水位后进行;当测流断面仅受冲淤影响有冲淤变化,但在冲淤前后仍保持稳定时,可以在淤积前后,分时段确定不同的水位流量关系.

2) 水位流量关系的流量拟合参数受渠道粗糙系数、边坡系数、底宽和坡降等因素影响.在渠道粗糙系数、边坡系数及坡降相同的条件下,流量拟合参数与渠道底宽总体呈正相关关系;在渠道粗糙系数、边坡系数及底宽相同的条件下,流量拟合参数与渠道坡降总体呈负相关关系.

3) 在实际应用中,率定出量水断面精准的水位流量关系曲线能够提高量水工作效率,并能够为后续灌区自动化量水设备测流准确性的校核提供重要参考依据.