大型水利工程梯级泵站短期优化调度方案
2024-02-02杜梦盈张召李谷涵雷晓辉
杜梦盈,张召,李谷涵,雷晓辉
(1. 江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013; 2. 中国水利水电科学研究院,北京 100038)
梯级泵站采用多级低扬程泵站以串联的方式抬升水位,克服地势影响以实现长距离输水任务,可有效解决水资源时空分布不均的问题.但梯级泵站的运行需要消耗大量能源,为进一步贯彻党的二十大报告“积极稳妥推进碳达峰碳中和”决策部署,落实《“十四五”公共机构节约能源资源工作规划》指示,探究梯级泵站节能降耗策略势在必行.梯级泵站的输水过程较为复杂,调度方案制定需考虑渠道安全、运行成本、水量要求等因素[1],是一个涉及多变量多复杂工况的非线性问题,如何求解满足调度需求的各时段内泵站开机数量、各机组开机流量、叶片转角、电动机转速[2-4]等节能降耗的运行方案是国内外相关学者重点关注的问题.
赵方玲[5]、李梦轩[6]分别进行了不同水利工程的梯级泵站系统优化问题研究.何臻等[7]以不同工况下梯级泵站输水系统效率最高为优化目标,研究了管渠结合的输水区域各级泵站扬程分配方案.作为连接上下游泵站的输水元件,渠道的水力损失也会引起泵站扬程变化,AMBROAIO等[8]分析了管道连接的泵站输水系统水力损失引起的扬程变化情况.宋淑馨[9]对梯级泵站的不同输水工况进行仿真模拟,研究了明渠渠道间水力损失与上游水位、下游流量之间的关系.对于大型明渠调水工程,渠道长度远远大于输水断面的宽度和深度,输水过程可概化为一维质点运动问题[10].LEI等[11]、WEI等[12]使用卡尔曼滤波方法进一步提升了泵站系统水动力模拟的精度.ZHANG等[13]将泵站特性曲线耦合进一维水动力模型中,模拟密云梯级泵站输水过程,并提出甩站运行方式以实现经济运行的目的.张焱炜等[14]基于分解协调法建立了梯级泵站能耗优化模型和日运行电费优化模型,并利用修正的Morris筛选法对模型进行了局部敏感性分析.吴帮等[15]通过克隆免疫算子和疫苗接种算子优化粒子群算法提高了梯级泵站优化算法的搜索范围和精度.王阳等[16]采用人工蜂群算法求解供水泵站最优运行方案,取得较好应用效果.上述针对梯级泵站优化运行相关研究主要是集中在不同工况下稳态的经济扬程分配方案求解,但对于短时间内的动态水位调整过程研究鲜见文献报道.
文中针对梯级泵站短期调度的经济节能问题,考虑水位动态调整过程,以整个调度期内泵站产生的运行电费为优化目标,并耦合考虑实时水位的梯级扬程优化模型计算结果为水位目标,构建梯级泵站短期优化调度模型,求解更经济节能的梯级泵站运行方案,以期为大型水利工程低碳调度提供技术支撑.
1 梯级泵站扬程优化分配模型
泵站机组在运行过程中受水源水位波动、用户需水量增减等影响,扬程会发生变化,易偏离高效区运行.为解决上述问题,构建梯级泵站群扬程优化分配模型,采用优化算法求解出在一定的梯级净扬程下,输水系统运行效率最优时的各级泵站扬程分配方案是必要的.已有研究较少考虑泵站扬程非稳态调整过程,扬程分配结果可作为梯级泵站扬程长期调整目标,但短期内处于稳定运行状态的梯级泵站能够调整的渠池水位幅度有限,即稳态的扬程优化结果并不适用于短期调度.因此,应根据泵站短期内调整渠池水位阈值以及泵站实时水位确定优化空间,进一步得到可在短期调度内实现的扬程调整方案.
水位调整幅度受工程实际及渠池地形参数的影响,通过构建水动力模型可模拟计算水位变化.对于第i个渠池(第i级和第i+1级泵站之间的渠池)选用流量-流量边界,通过恒定流计算得到调度期内第i级泵站以设计流量运行、第i+1级泵站关机状态下的水位涨幅,并作为水位调整阈值.
渠池水位约束条件为
Zi,out-Hth,i,out≤Z′i,out≤Zi,out+Hth,i,out,
(1)
Zi+1,in-Hth,i+1,in≤Z′i+1,in≤Zi+1,in+Hth,i+1,in,
(2)
式中:Z′i,out为优化后第i级泵站站后水位;Zi,out为当前时刻第i级泵站站后水位;Z′i+1,in为优化后第i+1级泵站站前水位;Zi+1,in为当前时刻第i+1级泵站站前水位;Hth,i,out为第i级泵站站后水位调整阈值;Hth,i+1,in为第i+1级泵站站前水位调整阈值.
不同输水工况下河渠的水头损失也存在差异,选用流量-水位边界分析不同工况下的水头损失,通过拟合关系曲线为优化模型提供支撑,即
hw,i=F(Qi,Zi+1,in),
(3)
式中:hw,i为第i个渠池的水力损失;Qi为第i级泵站的流量.
第i级泵站和第i+1级泵站水位满足以下关系:
Z′i+1,in+hw,i=Z′i,out.
(4)
2 梯级泵站短期优化调度模型
文中包含了考虑实时水位的扬程优化分配和梯级短期优化调度2个过程,2个模型输入同样的水位边界及目标流量要求.首先通过考虑实时水位的扬程优化分配模型得到短期内可实现的扬程分配方案,并将其作为目标水位传至梯级泵站短期优化调度模型,从而生成经济性调度方案.
2.1 渠道水位变化过程计算
传统水动力模型依托圣维南方程组求解的方式较为复杂,直接代入优化模型进行渠道水位变化过程的模拟会大幅降低优化速度,且泵站流量进行较大调整时极易导致水位和流量模拟值远远偏离实际值.为贴合实际输水过程、提高模型运算速度,采用渠道蓄量关系模拟调度期间渠道水位的动态变化过程.
渠道内的蓄量变化主要来源于相邻泵站抽水流量不匹配,忽略水量扰动的影响,则第i—(i+1)时段内渠道的蓄量计算公式为
(5)

采用LH-OAT全局敏感性分析模型,分析得到上游流量和下游水位参数对于河道蓄量的敏感性系数为2.4,2.9,即上游流量和下游水位为渠道蓄量的高敏感因子,通过恒定流水动力模拟得到不同上游流量、下游水位工况下的渠道蓄量值,并基于最小二乘法进行曲线拟合得到稳定输水工况下的蓄量与水位、流量之间的函数关系式.将式(5)与式(6)联立可得第i时段下的渠道蓄量,经过式(7)推得第i时段下的下游水位,并根据式(3),(4)推求上游水位,循环此过程即可推演调度期内渠道上下游水位变化过程.
(6)
(7)

2.2 优化模型
2.2.1目标函数
为实现运行节能降耗,以调度期内整个输水系统能耗最低为目标函数,但实际调度过程中不同时间段内的用电收费标准可能并不相同,为满足经济运行的调度需求及增强模型通用性,以整个输水系统用电费用最低作为优化目标,即
(8)
式中:Qj,i为i时段第j座泵站的流量;Hj,i为第i时段第j座泵站的扬程;ηj,i为第i时段第j座泵站的效率,可根据水泵理论特性曲线换算得到;Pi为第i时段的电费单价;输水系统共有n座泵站,调度期分为m个时段.
输水泵站长时间低效运行会缩短设备使用寿命,因此水泵机组保持高效运行也是维持可持续性发展的必要保障之一[17].上述模型提供短期内可实现的梯级泵站输水系统运行效率最高的扬程分配方案,将其分配结果作为目标水位,以调控后的水位距目标水位最小作为第2个目标函数,即
min |Zk-Zk,target|,
(9)
式中:Zk为调控后的特征水位;Zk,target为其对应的目标水位.
2.2.2约束条件
首先满足调水量约束.完全按照调水量要求进行调水会因约束过于严格而导致问题无可行解,故本模型以实际输水量大于调水任务量但不超过规定的误差上限作为约束.由于输水系统最终目的是为用户提供一定量的用水,以梯级泵站群最后一级泵站流量计算实际输水量.
(10)
式中:Qn,i为最后一级泵站在第i时段内的流量;Vplan为调水任务量;Vact为实际输水量;Vth为调水量允许的误差上限.
水泵机组的流量、扬程、进水池出水池水位约束分别为
Qmin≤Q≤Qmax,
(11)
Hmin≤H≤Hmax,
(12)
Zmin≤Z≤Zmax,
(13)
式中:Qmin,Qmax分别为单台机组流量允许的最小值、最大值;Hmin,Hmax分别为机组扬程的最小值、最大值;Zmin,Zmax分别为机组进水池或出水池水位允许的最小值、最大值.
考虑实际工程配置及调度需求,对可用机组台数进行限制,即
0≤N≤Nmax,
(14)
式中:Nmax为当前泵站可用机组台数的上限.
泵站可调节时段约束为
tadj∈{Talow1,Talow2,...},
(15)
式中:tadj为泵站调整时刻;Talow1,Talow2为泵站允许调节时段.
考虑泵站调整操作时长,以及减少频繁调节造成的机组损耗,对相邻2次调控时间间隔进行约束,即
tadj,k-tadj,k-1≥Tadj,th,
(16)
式中:tadj,k,tadj,k-1分别为泵站第k,k-1次调控时刻;Tadj,th为相邻2次调控的最短时间间隔.
2.3 优化算法
粒子群优化算法具有搜索能力强、通用性好、收敛速度快等特点,被广泛应用于工程优化问题的求解.因此,文中采用粒子群优化算法进行模型求解,并将考虑实时水位的梯级扬程优化分配结果作为水位目标削弱PSO算法在求解过程中陷入局部最优的程度.随机生成满足问题决策变量边界的种群粒子的初始值,在每一次的迭代过程中,计算种群最优值,引导下一代粒子沿着更优的方向进行搜寻,直至找寻到最优解.上述2个优化目标的可行解之间相互影响作用,为更好求得合适的可行解,分别赋予不同权重并叠加为一个复合目标函数,即最终的目标函数为
(17)
式中:w1,w2为2个单个目标函数对应的权重,其数值大小决定了最终优化结果偏向于更经济还是更节能.图1和图2分别为考虑实时水位的扬程优化分配模型和梯级短期优化调度模型的求解流程.

图1 考虑实时水位的扬程优化分配模型求解流程Fig.1 Solution process of head optimization allocation model considering real-time water level

图2 梯级短期优化调度模型求解流程Fig.2 Solution process of short-term optimal schedu-ling of cascade pumping stations
3 应用实例
3.1 工程介绍
南水北调东线工程从长江下游扬州市江都区抽引长江水,沿线通过13座梯级泵站逐级提水北上,总扬程65 m,有效解决沿线和山东半岛用水问题,提高沿线易涝地区的排涝能力,并在需要时提供农业和生态环境用水.徐洪河为南水北调东线江苏境内工程参与最多的输水河道,其河道上4座泵站的总运行台时占境内所有泵站总运行台时60%以上,能源消耗大,输水费用成本高,充分证明了在调水期间进行经济性优化调度的重要性.
徐洪河道的4座泵站逐级往上分别为泗洪站、睢宁二站、沙集站、邳州站,其中睢宁二站和沙集站并联运行,但4座泵站分别由不同单位管辖,文中研究所涉及的输水时段中,沙集站未参与实际调度,其余3座泵站均实行0.616 4元/(kW·h)的电费标准.据调度管理要求,徐洪河的调控时段为每日7:00—17:00,且相邻2次泵站的调控间隔时长不小于8 h.各泵站的设计参数如表1所示,表中M为泵站装机台数,qi为各泵站单机设计流量,li为各泵站进水池水位,l′i为各泵站出水池水位.

表1 徐洪河各泵站参数Tab.1 Parameters of pumping stations in Xuhong River
该梯级泵站通过徐洪河输水线路连通洪泽湖和骆马湖,即针对短期调度,泗洪站进水侧以及末级邳州站的出水侧水位均可认为是稳定的水位边界.
3.2 结果分析
根据建立的梯级短期优化调度模型,对徐洪河的梯级泵站进行优化调度方案的生成.东线工程自投入使用以来积累了大量的运行数据,为更好地说明和验证模型效果,选取多个时段的实际工况输入调度模型生成经济性优化调度方案,并与实际运行数据进行对比分析.
3.2.1水位推求结果精度分析
调度期内渠道动态水位的计算结果影响调度模型的优化方向,计算结果精度越高,优化调度方案越满足实际需求.选取徐洪河线泗洪站、睢宁二站、邳州站2022年某2天的实际运行数据进行模拟精度的分析.根据此时间段内的梯级边界水位序列及各泵站流量序列采用上述方法,推求各泵站进水池、出水池水位变化过程,并与实际的水位序列进行对比.
各泵站水位变化过程如图3所示,可以看出,通过蓄量关系和水力损失函数推求得到的水位过程相对平稳,忽略由于仪器设备造成的监测数据波动,模拟的水位变化趋势基本贴合泵站实际水位调整过程.
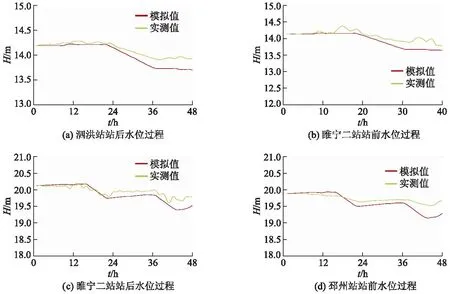
图3 各泵站水位变化过程Fig.3 Water level change process of each pumping station
表2为各泵站不同位置水位的模拟值与实测值对比,表中Za为水位平均值,Ez为误差.可以看出,各泵站水位模拟值与实测值的误差均在10 cm左右.因此,使用该方法可较好模拟河道水位变化过程,且仅采用数个高次多项式即可推演出水位过程,相对于需求解偏微分方程组的传统水动力模型而言,该方法计算速度更快、计算结果更稳定,作为梯级泵站短期优化调度模型大大加快了整体优化速度.
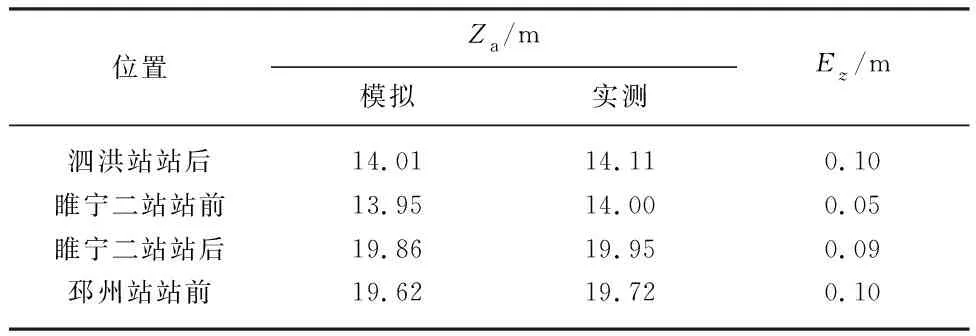
表2 水位对比Tab.2 Comparison of simulated and measured water levels
3.2.2优化效果对比分析
针对短期调度,调控频次过多会缩短机组的使用寿命以及引起非电费成本的增加,但调控次数过少也难以计算得到满足调度需求的方案,因此文中以每座泵站至多调控2次为例进行研究,其中第一次调控时刻为调度期初始时刻.并以1 h为单个时段时长,调水量容许的误差上限为5万m3,取综合优化目标的权重系数w1,w2分别为1,10.
使用扬程分配结果作为优化调度模型的目标水位,一方面达到扬程调整的目的,另一方面期望能够保证调控后水位的稳定.以下表3所列工况作为河道初始运行工况,以48 h为调度期,计算调水平均流量在43~63 m3/s内对应的经济性调度方案,表中M′为可运行机组台数.为便于比较,将总费用转换为单位体积调水费用,并分析引入目标水位对调度方案产生的影响.
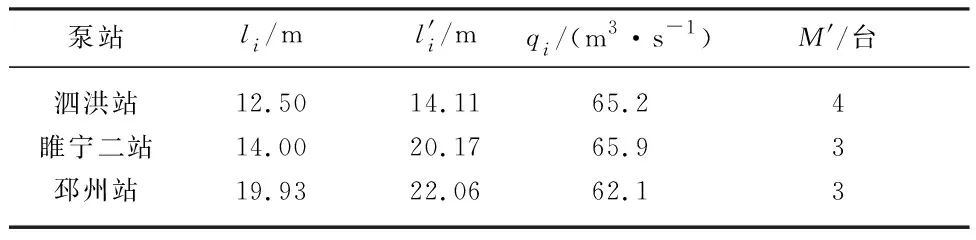
表3 初始工况Tab.3 Initial operating condition
图4为优化效果对比,图中纵坐标Fc为单位提水电费,横坐标Vd为调水量.可以看出:调出单位体积水量所需电费成本随调水体积增大呈减小趋势,且以考虑实时水位的梯级扬程优化分配方案作为目标水位得到的梯级优化方案单位提水电费整体上比不进行目标水位约束的费用要低;当调水任务为810~850万m3,900~950万m3,980~1 050万m3时,加入目标水位的调度方案节省费用的效果更加显著,最高可相对节省约30元/万m3,平均相对节省约4.7元/万m3.

图4 优化效果对比Fig.4 Comparison of optimization effect
由于徐洪河梯级各泵站全天收费标准相同,梯级输水系统效率最高点即为调水电费最低点,即扬程优化分配模型的结果进一步引导优化模型朝整体最优的方向进行寻优,且在一定程度上可削弱梯级优化调度模型陷入局部最优的程度.采用耦合梯级扬程分配模型的梯级优化调度方案具有效果更好的节能效果.
3.2.3实际工况结果对比


表4 目标水位Tab.4 Water level target
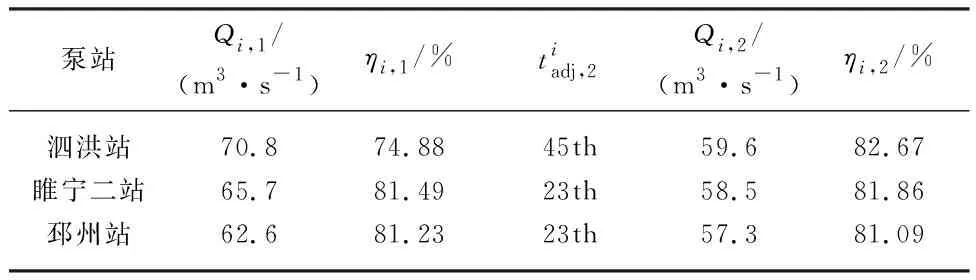
表5 优化调度方案Tab.5 Optimal scheduling scheme
4 结 论
1) 针对梯级泵站开展短期内经济性调度方案的研究,利用水量平衡方法耦合流量、水位、蓄量及水力损失函数关系式替代一维水动力模型,动态模拟渠道水情变化过程,并以更适合短期内调整的扬程优化分配结果作为目标水位,考虑水位动态调整过程中产生的电费,构建梯级短期优化调度模型.
2) 无分时段电价差异的梯级输水系统效率最高点即为调水电费最低点,将考虑实时水位的梯级扬程优化分配方案作为目标水位输入至梯级短期优化调度模型中,削弱了由于优化算法本身导致优化结果陷入局部最优的程度.
3) 验证结果表明,用水量平衡方法模拟出的水位值与实际值的平均误差在10 cm左右,模拟速度更快且更稳定;增加目标水位的优化方案平均可节省4.7元/万m3费用,且更易保证调控后水位的稳定,所构建的梯级短期优化调度模型可有效降低梯级输水系统6.7%的单位运行费用.
