顾及时空特征的参考作物蒸散量集成学习估算

刘傲,赵东保*,魏义长,肖炼

(1. 华北水利水电大学测绘与地理信息学院,河南 郑州 450046; 2. 自然资源部四川基础地理信息中心,四川 成都 610041)

参考作物蒸散量(reference crop evapotranspiration,ET0)是田间水量平衡法中计算作物需水量的关键参数,也是反映土壤水分供应能力的重要指标.随着道尔顿蒸发定律的提出,学者们构建了多种ET0经验估算公式,如Penman-Monteith公式、Blaney-Criddle公式、Thornthwaite公式、Hargreaves-Samani公式与Priestley-Taylor公式[1-3].这些公式皆是基于ET0与气象要素在特定的地理条件上的关系发展而来[4],在不同的气候区这种关系可能会发生改变.例如,Penman-Monteith公式在寒冷半干旱与热带草原气候区域精度较差[5],Hargreaves-Samani公式在气候湿润的区域精度欠佳[6].并且,丘陵等复杂地形上的ET0也会受到坡度、坡向等地形因子的影响,在这类地理条件复杂的区域,将经验公式与地形因子相结合,可获得更精准的估算结果[7].但空间要素、气象要素与ET0之间关系十分复杂,使用数学模型去描述这种非线性关系仍具有局限性.

计算机硬件的提升与机器学习技术的发展为描述复杂的非线性关系提供了一种新的解决思路.许多研究[8-9]均表明,相比经验公式,机器学习方法得出的ET0估算结果与实测值更相近.现有研究大多是通过对比寻求ET0估算精度更好的单一模型,但单一模型只能发现气候要素与ET0之间的部分关系,在地形复杂、气候多变的区域泛化能力欠缺.近些年集成学习技术的飞速发展,为ET0的估算带来了新的解决方案.多个机器学习模型进行组合构建新模型即为集成学习技术,大致可分为Bagging,Boosting与Stacking模型.其中,Boosting模型与随机森林等Bagging模型已被证实能有效提升ET0的估算精度[10-11].与这两者相比,尽管Stacking模型在ET0估算研究中起步较晚,但也取得了初步成效,WU等[12]基于Stacking模型估算中国不同气候区的ET0,指出Stacking模型可以显著提升ET0估算精度;FAN等[13]发现在改变ET0估算区域时,Stacking模型的性能变异性最低.但上述研究在使用Stacking模型估算ET0时仅考虑了气象要素,这会导致模型在地理条件复杂的地区性能下降.

四川省是中国地形最为复杂的省份,最高峰与最低点落差近7 000 m,气候差异明显[14],结合空间特征去分析ET0与气候要素之间的关系会更加可靠.另外,气候要素在时序上也有一定的规律[15],可结合时序特征对ET0估算结果进行修正.因此,文中在顾及时空特征的情况下构建Stacking模型,对四川省气候要素与ET0之间的关系进行模拟,并综合评价在考虑不同特征时,Stacking模型与其他机器学习模型的估算精度,最终确定最佳输入特征及模型,为四川省区域灌溉决策、农业水资源管理提供一定的理论依据.

1 方法与资料

1.1 研究区概况

四川省是中国重要的农业区,虽然四川省水资源总量丰富,但时空分布不均,形成季节性和区域性缺水.四川省各气象站点分布如图1所示,图中h为海拔.

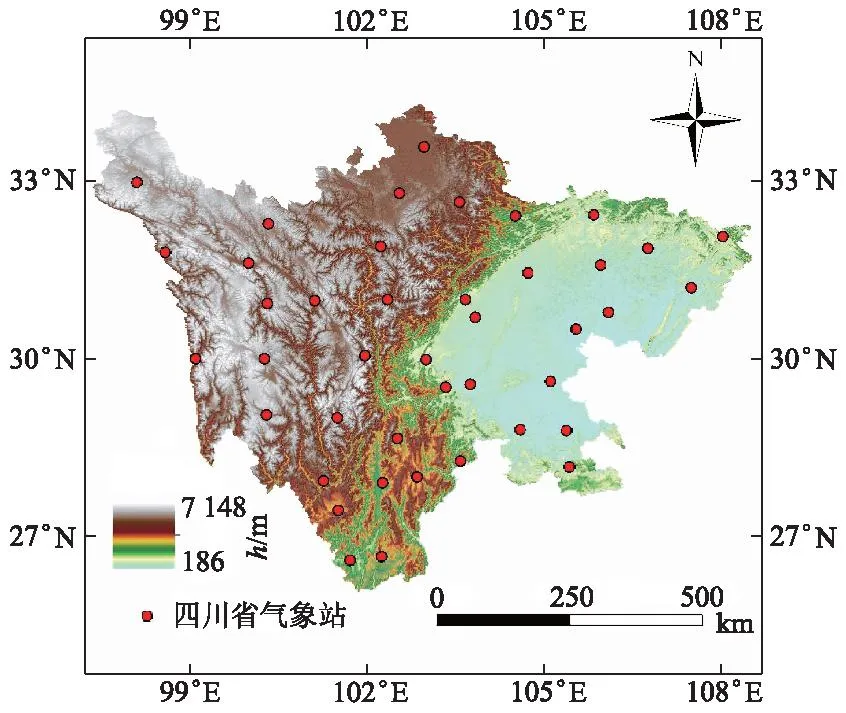
图1 四川省数字高程模型及气象站位置Fig.1 Digital elevation model and weather station location in Sichuan Province

1.2 数据说明

研究所用气象数据均来自国家气象数据中心,使用四川省52个国家基本站1981—2010年的逐日气象数据.研究所用(digital elevation model, DEM)数据分辨率为30 m,来源于中国科学院计算机网络信息中心地理空间数据云平台.坡度和坡向数据皆基于DEM数据提取而来.

1.3 时空自相关分析方法

1.3.1空间自相关

空间自相关是衡量观测数据在空间中是否聚集的标准,能反映研究区域上相邻站点ET0的平均关联程度.文中采用全局莫兰指数I表示ET0空间自相关系数.标准差倍数Z用来检验空间自相关是否存在.置信水平为95%时,如果Z>1.96,可认为I值通过检验.

(1)

(2)

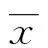
1.3.2时间自相关

时间自相关是衡量时间序列中不同时段的观测数据间的相关性,能反映研究区域ET0在时间上的变化规律.

(3)

1.4 ET0经验公式估算方法

彭曼公式(FAO 56 Penman-Monteith)常被用作ET0估算方法精度检验[17].其公式为

(4)

式中:Rn为作物表面净辐射,MJ/(m2·d);G为土壤热通量,MJ/(m2·d);γ为干湿球湿度计常数,kPa/℃;Tmean为距地面高2 m处日平均气温;u2为距地面高2 m处风速,m/s;es为饱和水汽压,kPa;ea为实际水汽压,kPa;Δ为饱和水汽压与温度曲线的斜率,kPa/℃.

1.5 精度评定

采用决定系数(R2)、平均绝对值误差(MAE)和均方误差(MSE)来评价所有方法的ET0估算精度.R2为模型估算值与实测值的拟合度,MSE为估算值中误差较大值的偏离程度.MAE和MSE越趋于0,R2越趋于1,说明该模型估算精度越高.

(5)

(6)

(7)

式中:ypredi为ET0估算值;yi为ET0实测值;l为验证数据样本数量;i为样本序数,i=1,2,3,…,l;yavg为所有验证数据ET0实测值的平均值.

2 Stacking模型ET0估算方法

Stacking模型一般为2层结构.第1层为基模型,在给定的训练集上进行训练,将输出结果作为新的特征供第2层的元模型学习,得到最终的估算结果.相比Bagging与Boosting模型,Stacking模型的精度与泛化能力更高[18].

XGBoost,LightGBM,GBDT、极限树与随机森林均为较流行的集成学习模型,围绕这些学习模型构建Stacking模型,以获取更高的精度与泛化能力.顾及时空特征的Stacking模型ET0估算方法构建过程如下:

1) 对研究对象四川省ET0分别进行空间与时间上的自相关分析,当研究结果呈正相关关系时,可引入时空特征,与1981—2010年四川省气象数据组成原始数据集.

2) 确定Stacking模型的基模型与元模型.

3) 对原始数据集构建特征工程.由于气象观测仪器会出现损坏与维护等情况,气象数据中会包含异常值,需对气象数据进行清洗.此外,初始选用的时空与气象特征数据并非都有益于提升ET0估算精度,需对这些特征进行评估,从而剔除无用特征.将处理过的数据集作为构建Stacking模型所用数据集.

4) 将数据集按需划分为训练集与测试集.在引入空间特征的情况下,应按照地理位置划分数据集去检验模型精度.

5) 将训练集划分为训练集1与测试集1,利用五折交叉验证训练Stacking基模型.具体过程如图2所示.

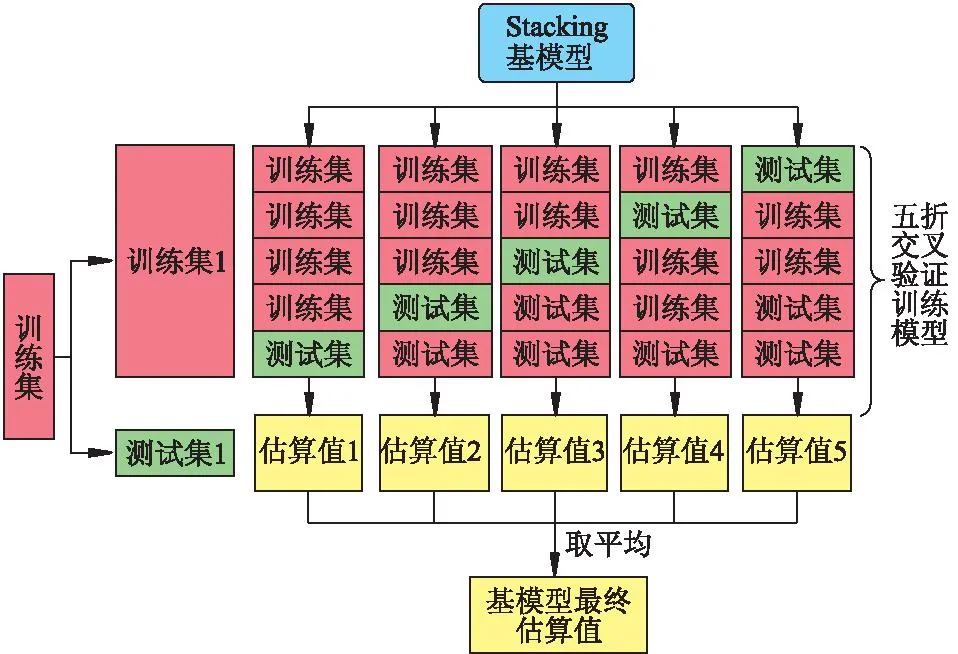
图2 Stacking基模型构建过程Fig.2 Stacking base model construction process

6) 对剩余所有基模型重复步骤5的操作,并将每个基模型对ET0的估算值都视作元模型的一个特征进行建模.

7) 使用Stacking模型对最初划分的测试集进行ET0估算,并对其进行精度评价.

3 试验结果与分析

首先得到本研究区域ET0空间和时序特征自相关分析结果,考察ET0随空间和时序的变化情况.之后根据基模型与特征的选取结果构建模型,进而得到顾及时空特征的Stacking模型的试验结果和精度分析情况.

3.1 研究区ET0时空自相关

3.1.1研究区ET0空间自相关分析结果

基于2006年四川省各气象站点月均ET0进行空间自相关分析如表1所示.

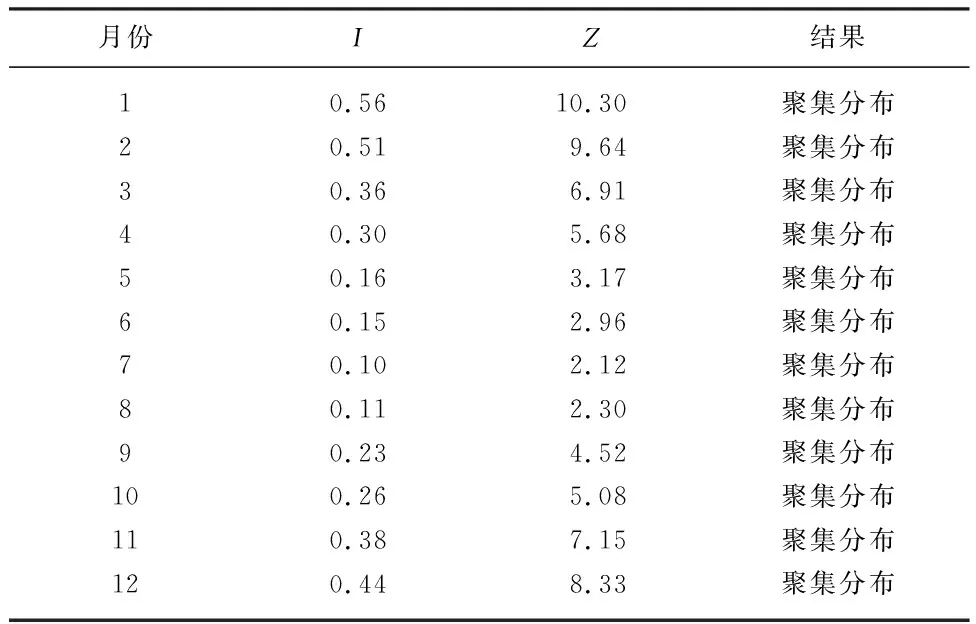
表1 2006年四川省月均ET0全局莫兰指数ITab.1 Monthly average ET0 global Moran index I in Sichuan Province in 2006

由表1可知,1—12月I值均大于0,且Z值皆大于1.96.说明在置信水平为95%的情况下,四川省ET0呈现空间正相关关系.因此,将空间特征用于模型构建,具体选用经度、纬度、海拔、坡度、坡向这5项空间特征.

3.1.2研究区ET0时间自相关

基于四川省台站号为56038气象站1981—2010年逐日ET0进行时间自相关分析.图3为ET0随时间的变化图,由图可知,ET0始终在0～6 mm/d以年为单位上下波动,说明该时序数据为明显的平稳序列.这意味着四川省历史ET0具备代表性与可延续性,在未来一段时期内仍遵循历史变化趋势.并且,平稳序列有助于模型准确捕捉数据的潜在趋势,提升模型的稳定性与准确性.

图3 ET0随时间变化图Fig.3 ET0 changes with time

图4为ET0时间自相关系数随时间间隔k变化图,由图可知,当k值在365,730 d等年的倍数周围时,ACF趋于1.0,说明ET0具有以年为单位的周期性.根据分析结果,将时序特征用于构建模型,具体选用年份、日序及历史的3天共5项时序特征.

图4 ET0时间自相关系数随时间间隔k变化图Fig.4 ET0 time autocorrelation coefficient changes with time interval k

3.2 Stacking模型的基模型选择与特征筛选

3.2.1Stacking模型的基模型选择

将台站号为56038的气象站1981—2010年逐日ET0作为数据集,基于随机森林、极限树、GBDT,XGBoost,LightGBM创建不同的基模型组合来构建Stacking模型.

表2为不同基模型组合的精度评定与时间成本,表中t1为训练时间.当基模型为随机森林与极限树2个Bagging模型时,训练时间成本为25 916 ms.当基模型为GBDT, XGBoost, LightGBM这3个Boosting模型时,训练时间成本为6 018 ms,仅为前者的1/4.可见,不同基模型的训练时长主要取决于基模型类型,并非基模型数量越多,时间成本就越高.基模型数量增多虽有助于提升精度,但过多的基模型意味着过高的训练时间成本,且精度的提升也有限.当基模型组合为5个时(随机森林、极限树、GBDT,XGBoost,LightGBM),比基模型组合为2个(随机森林,极限树)的时间成本约增加了22%,但MSE和MAE减少了约12%和5%.当在5个基模型上又添加强模型Adaboost时,其各项精度评定指标仅略微增加,但训练时间成本更高,故文中采用随机森林、极限树、GBDT,XGBoost,LightGBM等5个模型的组合作为最终的基模型.

表2 不同基模型组合的精度评定与时间成本Tab.2 Accuracy estimation and time cost of different base model combinations

3.2.2数据集特征筛选

数据集中用来估算ET0的初始特征为最大温度Tmax、最小温度Tmin、日序Rd、日照时长N、平均温度Tmean、相对湿度RH、气压p、纬度φ1、海拔h、经度φ2、坡向A、平均风速ua、最大风速umax、坡度C、年份ta以及前3天的ET0,该值分别用ET(t-1),ET(t-2),ET(t-3)表示.但是这些特征并非都有助于提升ET0估算精度,故需要对这些特征进行筛选.文中基于XGBoost评估这些特征的重要度排序如图5所示.图中D为特征的重要度.

XGBoost的基模型为决策树,能够根据结构分数的增益情况计算出选择哪个特征作为分割点,每个特征的重要度就是其在所有树中出现的次数之和.重要度相对较高的特征会被更多地用于模型中构建决策树.之后通过递归特征消除算法(recursive feature elimination, RFE)消除噪声特征,即按照特征重要度从大到小排名,每次增加一个特征,反复构建随机森林模型.选用决定系数R2作为模型的评价分数,当评价分数开始下降时,即可将新增特征视为噪声.

图6为RFE特征筛选.图中R2为模型评价分数.由图可知,模型评价分数R2从添加平均风速ua后开始下降,并在之后一直保持下降趋势.从模型角度考虑,在四川省地区,平均风速ua、最大风速umax、坡度C、年份ta这些特征并不能帮助提升模型性能,故剔除这些特征.

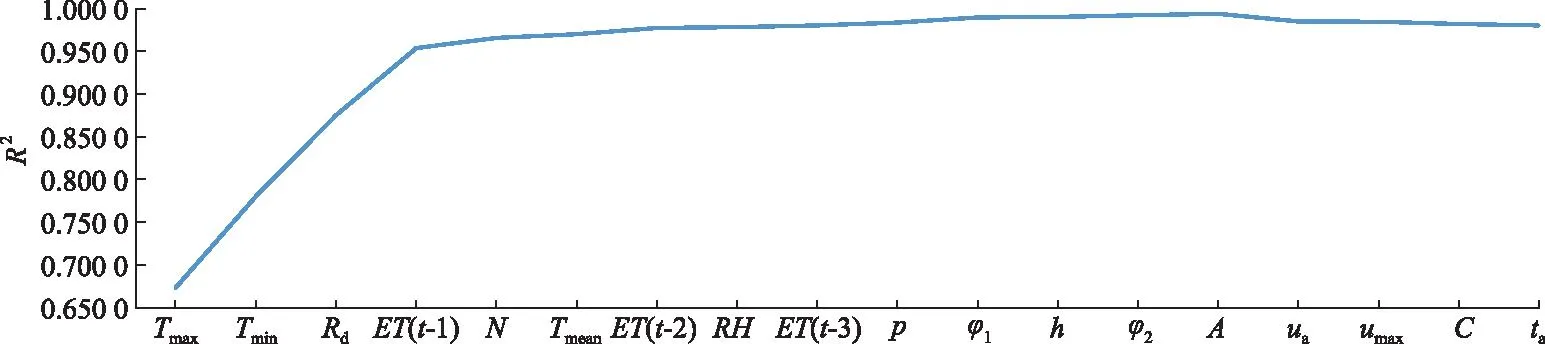
图6 RFE特征筛选Fig.6 RFE characteristics screening

3.3 Stacking模型ET0估算精度验证和分析

分别验证空间和时间特征对Stacking模型的ET0估算精度改善情况.首先,在气象特征与时序特征的基础上引入空间特征,分别训练顾及空间特征模型和没有顾及空间特征模型,并对四川省52个站点进行五折交叉精度验证;其次,在气象特征与空间特征的基础上引入时间特征,将四川省1981—2010年的逐日ET0数据集按照8∶2分成训练集与测试集,分别训练顾及时序特征模型和没有顾及时序特征模型,并探讨时序特征对模型性能的改善效果;最后,在顾及时空特征的情况下,将Stacking模型与经验模型以及各种基模型(随机森林、极限树、LightGBM,XGBoost)进行全面的精度对比,以验证文中模型的各方面性能.

3.3.1空间特征对ET0估算的影响

图7为顾及空间特征模型与没有顾及空间特征模型精度对比.如图所示,顾及空间特征的模型在训练集上的R2与测试集几乎一致,平均MSE与MAE分别降低了68%和46%,而没有顾及空间特征的模型在训练集上的平均R2相较于测试集提升了4%,平均MSE与MAE分别下降了92%和73%.没有顾及空间特征的模型与顾及空间特征的模型在训练集上精度无明显变化,相较于没有顾及空间特征的模型,顾及空间特征的模型在测试集上平均R2提升了3%,平均MSE降低了76%,平均MAE降低了51%.基模型中,XGBoost与LightGBM在加入了空间特征后精度提升最为明显,其中,XGBoost的R2提升了5%,MSE和MAE分别降低了85%和62%;LightGBM的R2提升了4%,MSE和MAE分别降低了84%和59%.

四川省各气象要素存在极强的空间异质性.在缺少空间特征的情况下,模型无法准确地描述四川省ET0与各特征之间内在关系,使得模型泛化能力受限,在测试集的精度大幅降低.相比于Bagging模型,XGBoost与LightGBM这类Boosting模型往往偏差更低,但在训练过程中也更容易过拟合,导致模型在测试集的精度明显低于训练集.而在加入空间特征后,XGBoost与LightGBM在测试集的精度与训练集相比无明显下降,说明顾及空间特征可改善XGBoost与LightGBM的过拟合问题,从而提升了Stacking模型的性能.

3.3.2时序特征对ET0估算的影响

图8为顾及时序特征模型与没有顾及时序特征模型精度对比.由图可知,所有模型在测试集的精度和训练集相比皆无明显降低.

图8 顾及时序特征模型与没有顾及时序特征模型精度对比Fig.8 Comparison of accuracy of models that take into account temporal characteristics and models that do not take into account temporal characteristics

在测试集中,相较于没有顾及时序特征的模型,顾及时序特征的模型的平均R2提升了4%,平均MSE与MAE降低了92%和72%.其中,在引入时序特征后,GBDT的R2提升了5%,MSE与MAE分别降低了94%和75%;XGBoost的R2提升了4%,MSE与MAE分别降低了93%和74%;LightGBM的R2提升了4%,MSE与MAE分别降低了93%和75%,精度提升程度高;随机森林在引入时序特征后的R2提升了3%,MSE与MAE分别降低了85%和62%,精度提升程度最小.

在引入时序特征后,所有模型在训练集和测试集上的精度都得到了明显提升.说明时序特征可协助模型挖掘四川省地区ET0周期性变化规律,从而提升四川省地区ET0的估算精度.其中,LightGBM,XGBoost与GBDT精度提升程度显著高于随机森林与极限树,这得益于Boosting这类模型在训练过程中会不断调整未能充分利用时序特征的基模型权重.而Bagging模型的每个基模型都是独立的,训练过程中无法自主调整每个基模型的权重,使得利用时序特征程度不同的基模型对整个Bagging模型的贡献都相同,降低了时序特征带来的收益.

3.3.3Stacking与其基模型及经验模型精度对比

将1981—2005年四川省逐日气象数据作为训练集,顾及时空特征构建Stacking模型.将2006—2010年数据作为测试集,Stacking模型与其各个基模型与彭曼公式ET0估算精度对比如表3所示.

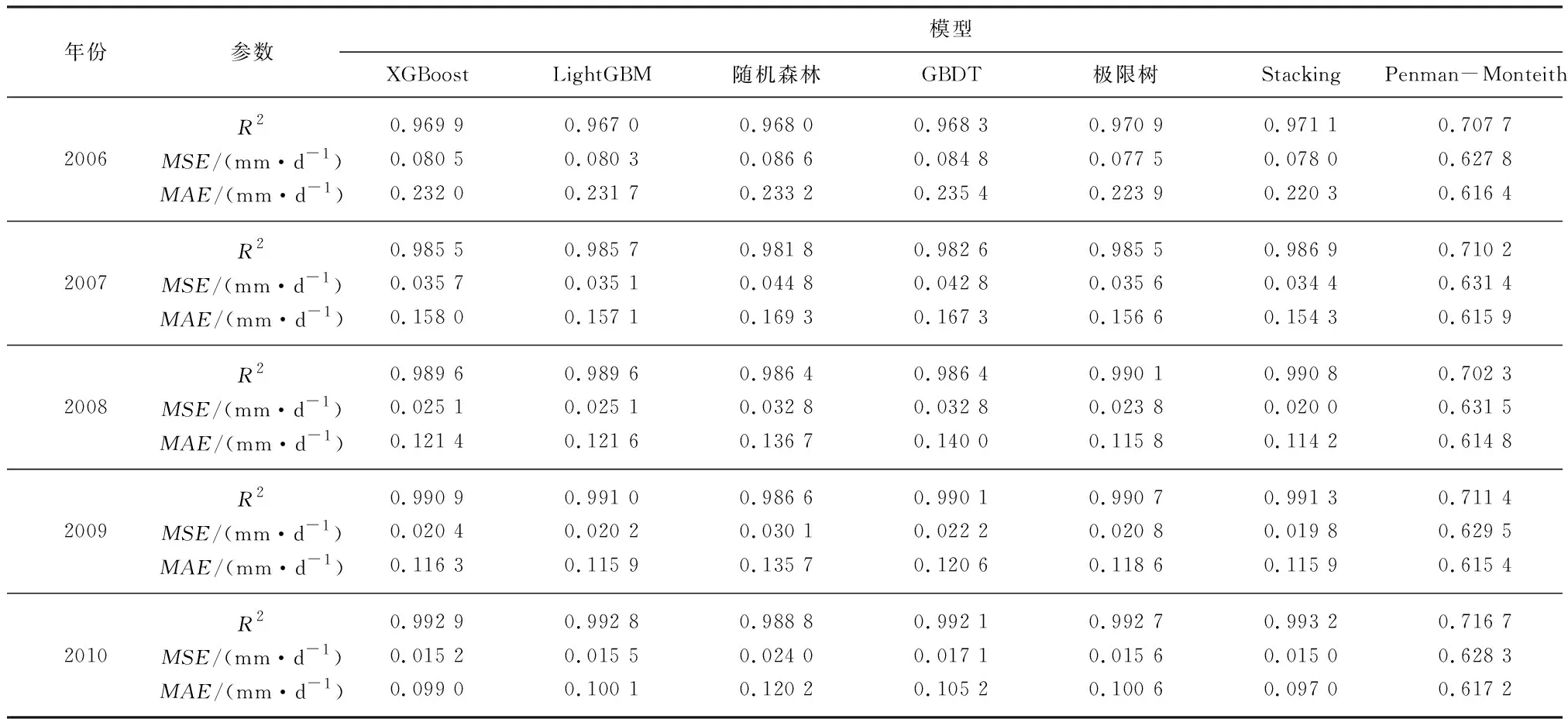
表3 Stacking及其基模型与彭曼公式ET0估算精度对比Tab.3 Comparison of estimation accuracy between Stacking and its base model with the Penman-Monteith formula ET0

由表3可知,Stacking模型的平均R2相较于彭曼公式提升了39%,平均MSE和MAE分别降低了95%和77%.Stacking模型精度显著优于彭曼公式,一方面由于彭曼公式作为一种经验公式,具备一定的地域性,但Stacking模型同时结合时空特征与气象特征可探索出更通用的ET0估算方法.另一方面由于ET0与气象特征之间存在着复杂的非线性关系,很难使用数学模型准确地描述他们之间内在联系.文中则采用多种机器学习模型集成的方式,可适应不同的数据特征,从而更好地处理非线性关系,以此提升ET0估算精度.此外,在精度验证中,2006—2010年逐年精度最优基模型分别为极限树,LightGBM,极限树,LightGBM,XGBoost,但Stacking模型在逐年精度验证中皆优于其各个基模型,并有着较小的误差波动范围,说明模型同时具备较高的精度与稳定性.在逐年验证中,Stacking模型精度并未随着年份的递增而下降,说明其在时间上也具备较高的泛化能力.

4 结 论

文中以四川省52个气象站点为研究对象,揭示了四川省ET0值的时空分布变异情况,提出了顾及时空特征的Stacking模型ET0估算方法,并将其与经验模型彭曼公式以及各个基模型包括XGBoost,LightGBM、随机森林、GBDT、极限树等进行了全面的精度对比和验证.得出主要结论如下:

四川省ET0在空间与时间上的分布都具有明显的自相关性.时空特征的引入,可显著提升模型在整个四川省地区的泛化能力与估算精度.在顾及时空特征的情况下,Stacking模型精度显著优于彭曼公式.此外,虽然文中所用数据较老,但是模型精度在2006—2010年的逐年验证中并未出现随时间推移而下降的情况,说明其具备较好的泛化能力,对当前时段也有一定的参考意义.综上所述,顾及时空特征的Stacking模型可有效提升ET0,并给其他地理条件复杂的地区ET0估算方法提供一定的参考价值.