泵站-水库原水调水系统经济运行方式优化
2024-02-02高中阳张召司乔瑞薛萍雷晓辉李月强杜梦盈
高中阳,张召,司乔瑞,薛萍,雷晓辉*,李月强,杜梦盈
(1. 江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013; 2. 中国水利水电科学研究院,北京 100038;3. 河海大学计算机与信息学院,江苏 南京 210098; 4. 河海大学水利水电学院,江苏 南京 210098)
调水工程在解决中国的水资源空间分配不均上发挥了关键作用.其中,泵站作为调水工程中主要的动力来源,用电量占整个供水系统电耗的95%以上,因此在输水过程中会产生巨大的能源消耗[1].随着数字孪生建设的不断推进,泵站调度方式由人工经验主导逐渐转变为智能化控制,可通过建模计算和机器学习算法求解等方式生成科学合理的调度方案.
由于变频调速泵具有效率高、体积小、维护简单、调速范围宽、精度高、能无级调速且自动化水平高等一系列突出的优点而在城市供水工程中采用较多.同时,调节水泵转速是拓宽水泵高效区和降低泵站运行能耗的一种有效途径[2].利用计算机技术科学制定水泵高效区运行下的调水方案是保证受水区安全性和经济性运行的基础.城市的供水方案往往取决于输水工程不同时空阶段下的用水需求.当前运行方式较多根据水位进行经验调控,较少考虑扬程、分时电价和调控次数等因素的影响,因此,存在一定的经济性优化调度空间.
近年来,国内外一些专家学者针对泵站优化调度进行了多方面研究.桑国庆等[3]以日运行费用最小为目标,构建了优化模型,采用基于区间离散的动态规划法进行求解,优化后费用降低10.43%.GONG等[4]发现日最小提水费用对应的单位提水费用较定角恒速运行下的日最小单位提水费用可节省4.85%~5.37%.随着人工智能算法的发展,有学者将泵站经济运行研究与遗传算法[5-6]、蚁群算法[7]、粒子群算法[8]和人工神经网络[9]等人工智能算法进行融合,解决了多维度下的求解问题.其中,遗传算法因可对多个局部最优解进行比较,整体收敛性较强,便于获取全局最优解,在泵站优化调度领域应用较多.李娜等[10]针对泵站优化调度,提出了改进适应度函数的遗传算法,优化得出泵站能耗比传统遗传算法和经验运行方案分别低1.77%和8.07%.
为实现国家“双碳”目标及节能减排战略,文中开展相关城市供水系统泵站工程的经济运行研究.以泵站-水库原水调水系统泵站输水方式为例,综合考虑泵站输水管道的水力损失、分时电价和调水总量等约束,以单位提水费用最低为目标函数,构建泵站经济运行模型,并分析周期调水总量和单位提水费用之间的关系,寻求更符合实际的优化运行方案,为降低工程运行成本提供科学依据.
1 泵站扬程计算
在泵站-水库原水调水系统中,由于城市土地资源和建筑的限制,一般采用管道输水.因此在泵站设计中,水泵扬程主要消耗在2方面:一方面是将水提升至水塔中(即净扬程);另一方面用来克服管道的水头损失.在实际运行过程中,由于水源来水量和上下游水位的变化,水泵装置的总扬程也会发生变化.此外,城市供水泵站安全要求较高,为了便于自动化运行和管理,机组多采用自灌式充水,故可根据泵站出口实测流量数据对水泵装置的总扬程进行计算.
由经典的管道满流理论可知,满流时管道的水力损失由沿程水力损失和局部水力损失组成.管道输水过程中沿程水力损失通常采用基于满流的达西-威斯巴赫方程[11]计算,即
(1)
式中:Δhf为输水管道的沿程水力损失,m;λ为水力摩擦系数,可根据雷诺数和管道粗糙度查穆迪图确定;L为输水管道长度,m;D为输水管道直径,m;v为管道内水流平均速度,m/s;g为重力加速度,m/s2.
输水管道的局部水力损失Δhl可根据局部损失系数δ和流速水头求得,即
(2)
输水管道的总水头损失Δh为
(3)
运行过程中,水泵装置总扬程为
H=h+hf_pipeline+hl_pipeline+hf_inside+hl_inside,
(4)
式中:H为泵站提水过程中总扬程,m;h为水泵装置净扬程,m;hf_pipeline和hl_pipeline分别为泵站提水过程中出水管道中沿程水头损失和局部水头损失,m;hf_inside和hl_inside分别为泵站提水过程中泵房内管道沿程水头损失和局部水头损失,m.
2 泵站经济运行模型
基于泵站-原水调水系统的经济运行需要泵站内各机组流量及时段内调水流量相互协调,并综合考虑管道水力损失和分时电价等因素的影响.因此,构建泵站机组流量优化分配模型,确定泵站内部最优开机组合及机组流量,基于此构建经济运行模型并采用遗传算法进行求解.
2.1 泵站机组流量优化分配模型
由于不同水泵机组组合下流量可行域范围存在交叉,导致泵站不同流量-扬程工况下开机台数组合也存在多个解,因此需要通过优化算法进行寻优求解.在泵站系统稳定运行阶段,调水流量和净扬程已知情况下,构建泵站机组流量优化分配模型,采用遗传算法求解站内各水泵机组流量的最优分配组合.
1) 目标函数
模型以泵站系统运行效率最高为优化目标,计算式为
(5)
式中:ηst为总泵机组效率,%;Qst为泵站的提水流量,m3/s;Qi为第i台机组的提水流量,m3/s;ηi为第i台机组的效率,%.
其中,泵站内第i台机组的抽水装置效率为
ηi=ηpumpAssemηtransηmotorηf,
(6)
式中:ηpumpAssem为水泵装置效率[12-13],%;ηtrans为传动装置效率(电动机和水泵直连情况下取“1”),%;ηmotor为电动机效率,%;ηf为变频效率(变频调节取0.96),%.
离心泵在固定转速下其效率和扬程H分别为
ηpumpAssem=a1Q3+a2Q2+a3Q+a4,
(7)
H=b1Q3+b2Q2+b3Q+b4,
(8)
式中:a1,a2,a3,a4,b1,b2,b3,b4为系数.
当水泵转速可调节时,在转速范围内根据效率-流量-扬程的关系可将效率和扬程表示为
ηpumpAssem=p00+p10Q+p10H+p20Q2+p11QH+p02H2+p30Q3+p21Q2H+p12QH2+p03H3,
(9)
H=k00+k10Q+k01n+k20Q2+k11Qn+k02n2,
(10)
式中:n为水泵转速,r/min;pab,kab均为系数,其中a,b分别为第一个元素和第二个元素的次方根.
2) 决策变量
采用泵站内各水泵机组的提水流量Qi为决策变量,以“0.1”为计算步长,通过泵站机组流量优化分配模型,计算泵站流量-扬程可行域内所有工况点的流量最优分配方案,为泵站经济运行模型提供支撑.
3) 约束条件
流量约束为
(11)
式中:Qi,min和Qi,max分别为泵站第i台机组可运行最小和最大流量,m3/s.
转速约束:80%ne≤n≤100%ne,其中ne为额定转速,亳州加压泵站采用高压变频电动机,水泵机组转速可以在一定范围内进行调整.
2.2 泵站经济运行模型
在满足调度期内水量任务及各种约束条件的前提下,以调度期内泵站提水费用最小为优化目标,构建泵站优化调度模型.并利用遗传算法,对泵站各个机组的运行流量及开机状态进行优化,求解过程中考虑分时电价和输水管道流速等影响因素,计算泵站整体最优调度运行参数,得出最优运行方案.
2.2.1目标函数
以调度期限内泵站单位提水费用最小为目标函数,则目标函数为
(12)
(13)
式中:Ftotal为泵站调度期最小运行成本,元;C为单位提水费用,元/104m3;N为站内机组台数;m为调度期内时段数;Ej为第j时段下的能源单价,元/(kW·h);Tj为第j时段调度期时间长度,h;Hi为泵站第i台机组的扬程,m;ρ为水的密度, kg/m3;g为重力加速度,m/s2;ηij为泵站在第j时段下第i台机组的运行效率,%.
2.2.2约束条件
1) 扬程约束
泵站运行过程中各水泵机组应满足泵站最低提水需求,即满足进口水位最低、出口水位最高时的水位差约束,且满足泵站机组在高效区间运行需求.文中泵站内各机组并联,因此需满足以下条件,即
(14)
式中:Hq和Hk分别为泵站站内第q台机组和第k台机组的进出口水位差,m;Δh为水泵管道水头损失,m.
2) 水量约束
泵站调度运行过程中需满足时段水量需求,因此需满足以下条件,即
(15)
式中:W为调度期内目标提水量,m3;φ为调度期限内允许多提水量(该值一般设置为目标提水量的0.1%),m3.
3) 流量约束
泵站调度运行过程中需考虑单泵流量需求,因此需满足流量约束条件同式(11).
4) 分时电价约束
分时电价指按系统运行状况,将一天24 h划分为若干个时段t1,每个时段按系统运行的平均边际成本收取电费.泵站调度运行过程中,需考虑当地电价结构,文中研究区域分时电价结构如图1所示,图中P为分时电价.
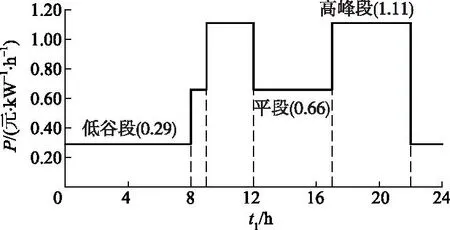
图1 分时电价时段分布Fig.1 Time-of-use electricity price period distribution
2.3 遗传算法
遗传算法求解过程的本质是以生物进化机组为基础实现全局优化搜索,可从群体角度进行最优解搜索,比单一方向搜索寻优能力更强,可针对多个局部最优解进行比较,整体收敛性较强,便于获取全局最优解.
遗传算法相较于其他寻优算法,在处理复杂性和非线性的数学优化问题时具有一定的优越性.采用遗传算法求解跟传统的爬山算法相比,遗传算法能够跳出局部最优而找到全局最优点[14].且遗传算法允许使用非常复杂的适应度函数(或者叫做目标函数),并对变量的变化范围加以限制.其主要思路是先确定泵站可运行工况的集合并对其编码,随机生成一系列的流量组合(在遗传算法中称之为个体),判断不同工况下的泵站效率系数(在遗传算法中称之为适应度),保留效率系数较高的流量组合,并据此生成新的流量组合.之后再重复这个过程,直至满足停止条件.遗传算法的计算步骤具体包括6个部分:编码、适应度函数、遗传算子、种群的初始化、评价群体和约束条件的处理.
遗传算法的流程图如下所示:
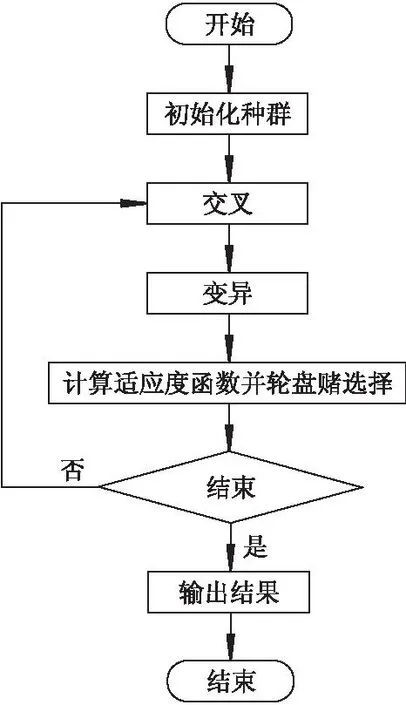
图2 算法流程图Fig.2 Algorithm flowchart
3 应用实例
3.1 工程概况
亳州城市供水工程由亳州加压泵站、供水管道和亳州调蓄水库组成,是安徽省引江济淮一期工程城市供水规划之一.亳州加压泵站加压后通过供水管道(单管)沿龙凤新河右岸北上,输水至亳州调蓄水库.亳州泵站布置如图3所示.

图3 泵站布置图Fig.3 Layout of pumping station
亳州加压泵站总设计输水流量为5.00 m3/s,设计扬程为48.62 m(泵站扬程由净扬程和损失扬程组成),布置4台(3用1备)卧式双吸离心泵,额定转速980 r/min,通过传动装置耦合电动机设备,配套高压变频电动机额定功率为1 120 kW,变频器电压为10 kV,容量为1 500 kVA.亳州加压泵站供水管道末端为亳州调蓄水库,水库起到贮水池作用,水库正常蓄水位为36.60 m,当水库水位淹没供水管道时为管道满流状态,泵站基本参数中进水池设计水位(西淝河侧)为27.35 m,出水池设计水位(调蓄水库侧)为35.60 m,水泵设计净扬程为8.55 m,水泵设计最高和最低净扬程分别为9.10和0.35 m,水泵单机设计流量为1.703 m,水泵最小转速、额定转速和最大转速分别为735,980和1 100 r/min,电动机额定功率为1 120 kW.供水管道基本参数:管道公称直径为DN2000,管道数量为1,管道长度为31.44 km,设计工况下沿程和局部水头损失分别为31.39 m和3.24 m.调蓄水库基本参数中设计蓄水位为35.60 m,总库容为4.93×106m3,调蓄库容为4.60×106m3.
3.2 历史运行成本分析
结合泵站工程设计参数,从历史运行工况中,选取工程设计提水扬程下的不同开机流量组合方式,得出不同工况的单位提水成本费用分析如表1所示,表中Nk为开机台数.
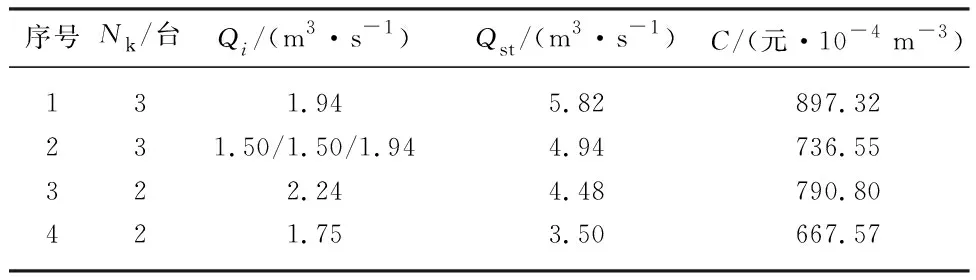
表1 历史运行方案成本分析Tab.1 Cost analysis of historical operating plans
由表1可知,因为实际工况和调度需求的变化,使得调度人员改变开机状况引起水泵流量、总扬程和频率的不同,最终导致能耗也随之变化,且在不考虑分时电价的影响下,最高与最低运行单位提水费用相差229.75元/104m3.
3.3 管道水力损失计算
提水泵站扬程由水泵垂直高度的水头差、管路损耗和出水口压力组成.输水管道的糙率系数采用工程设计报告中的0.012 5.各部分扬程计算公式为
hf_pipeline=0.129 6Q2,
(16)
hl_pipeline=1.255 6Q2,
(17)
(18)
hf_inside=0.032 27Q2.
(19)
3.4 流量优化分配方案
根据亳州加压泵站机组特性曲线和泵站设计扬程范围(泵站最高设计扬程:55.00 m;最低设计扬程:36.00 m)推算出单台水泵机组运行流量为0~2.27 m3/s,为避免输水流量较小产生汽化现象,取水泵设计流量的30%为最小运行流量.由此可得亳州加压泵站运行流量为0.51~6.61 m3/s(1台水泵机组流量可行域为0.51~2.27 m3/s;2台水泵机组流量可行域为1.02~4.34 m3/s;3台水泵机组流量可行域为1.53~6.61 m3/s).
在不考虑时间因素影响的情况下,以泵站系统运行效率最高为优化目标,利用泵站机组流量优化分配模型,考虑亳州加压泵站实际工程约束(运行流量为1.53~5.96 m3/s),以流量0.01 m3/s,扬程 0.10 m为计算步长,并根据历史运行数据,对泵站系统设计范围内全工况的机组流量分配进行优化计算,全工况内流量扬程的最优开机台数如图4所示.

图4 泵站全工况内流量扬程的最优开机台数Fig.4 Optimal number of starting pumps for flow head under all working conditions of the pumping station
选取3个亳州加压泵站历史运行典型工况,并将其与优化分配方案进行对比,如表2所示.泵站内水泵机组管路损失不同导致扬程不同,但优化后的流量分配方案机组之间流量依旧相似(偏差不超过0.10 m3/s),符合等微增率原则(管路损失差别影响可忽略).同时,优化后流量分配方案泵站效率比优化前分别提高4.9%,2.8%,7.9%.
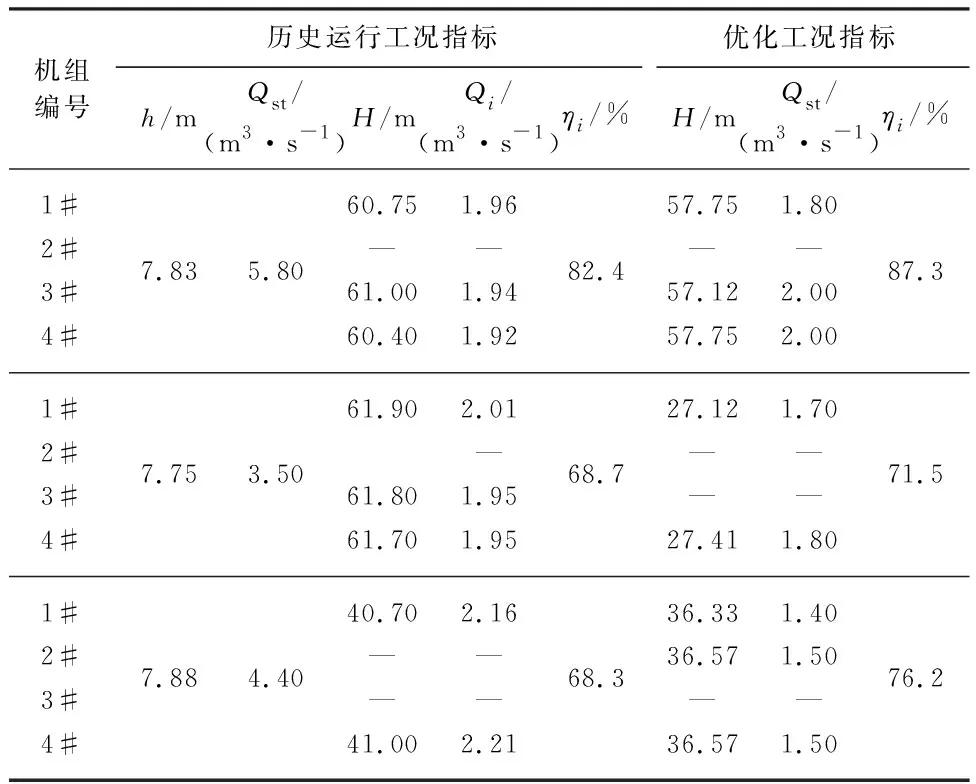
表2 实际工况流量优化分配对比Tab.2 Comparison of optimal flow distribution under actual working conditions
3.5 经济运行结果及分析
泵站机组流量优化分配模型主要是对泵站系统某一时刻状态的优化,不受时间影响.实际工程中,受时间和提水扬程不断变化的影响,需对调水量进行时间上的优化分配.因此,文中基于泵站机组流量优化分配模型的结果,将时间因素即分时电价结构考虑在内,继续构建泵站经济运行模型.
3.5.1实际工况优化结果
对亳州加压泵站历史监测数据进行整理分析发现:① 历史调度运行持续时间多为48 h左右;② 在历史调度期内,泵站转速调整小于等于1次.基于以上2点,考虑不同时段扬程和电价变化情况,从亳州加压泵站历史运行数据中选取3个工况点进行分析,调度运行时长均取48 h,转速调整次数设置为1,累计调水量分别为71.15×104m3,100.92×104m3和92.86×104m3.
所选工况点净扬程h随时间序列t的变化如图5所示,在所属调度期内,工况1泵站提水净扬程最大为7.88 m,最小为7.81 m,平均值为7.85 m,标准差为0.02 m,扬程变化较为平缓.扬程变化过程如图5所示.因此,为方便计算,下文净扬程均取调度期内平均值计算.以上述工况为例,实际运行方案同经济运行方案对比结果见表3.模型计算方案电费成本分别降低了11.93%,16.62%,11.68%.2021年11个月输水量为3 577.36×104m3,耗电费用271.18万元,以选取3个工况点优化后的成本平均降低13.40%进行计算,优化后成本可节约36.34万元.效益十分可观.由此可见,所构建的泵站经济运行模型可有效降低系统运行费用.
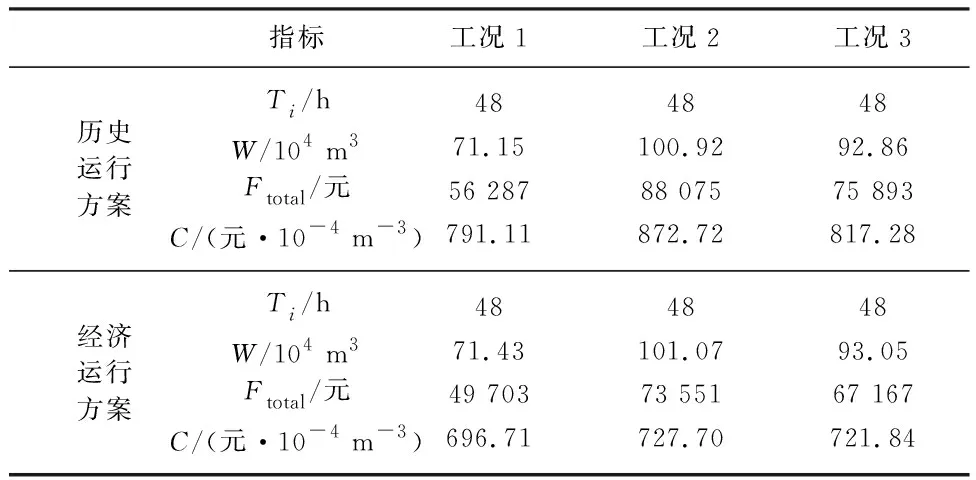
表3 实际工况经济运行结果对比Tab.3 Comparison of economic operation results under actual working conditions
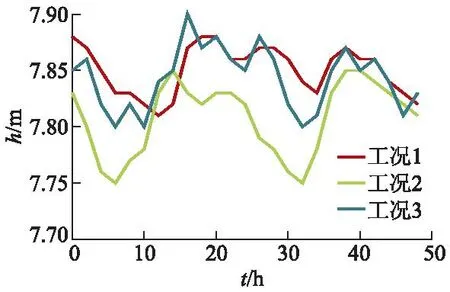
图5 历史工况点净扬程变化Fig.5 Change in net head at historical operating conditions
3.5.2周期输水量与最小运行费用关系分析
综合考虑亳州调蓄水库调蓄能力以及维持城市生态和景观需求,按照正常水位维持在35.35 m左右时,根据水位-库容关系,其调蓄量约为92.00×104m3.对历史运行数据分析得到历史工况下泵站提水流量最小值和最大值分别为3.47 m3/s和5.94 m3/s,在48 h内对应输水总量分别为59.96×104m3和102.67×104m3.因此,以48 h为1个调度周期,以最大和最小输水量为边界条件,为使实时调度模型优化结果与实际工程运行更为相似,设置优化机组调整次数为1,计算相同调度期内不同输水总量与单位提水费用的关系如图6所示.由图可知,当调水量为75.50×104m3时,单位提水费用最低为662.4元/104m3.
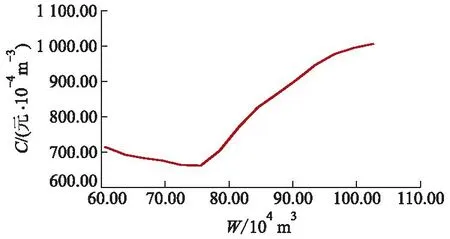
图6 周期输水量与最小运行费用关系Fig.6 Relationship between periodic water delivery volume and minimum operating costs
由图6可知,优化后的单位提水费用随提水量的增加呈先减少后增加的趋势,产生该现象的原因如下:由分时电价定义可知,当提水量为定值时,若使单位提水费用最低,则需在谷电时输送更多水量.考虑实际运行工况中每个调度周期机组调整次数为1次,对图1分时电价时段分布进行分析得出第一阶段运行时长应大于8.0 h或大于32.0 h.
对所有提水方案中两阶段泵站运行效率和运行阶段耗时进行统计,统计结果如表4和图7所示.图中t2为机组运行时长.
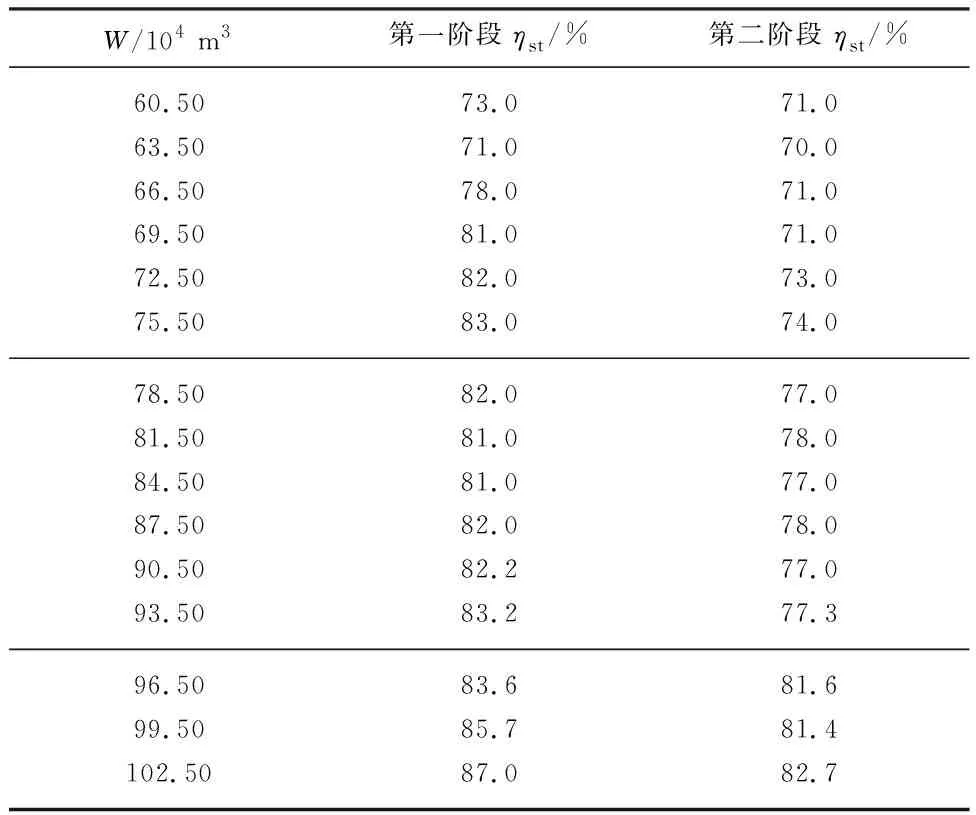
表4 优化调度方案阶段运行效率表Tab.4 Optimization schedule operation efficiency table
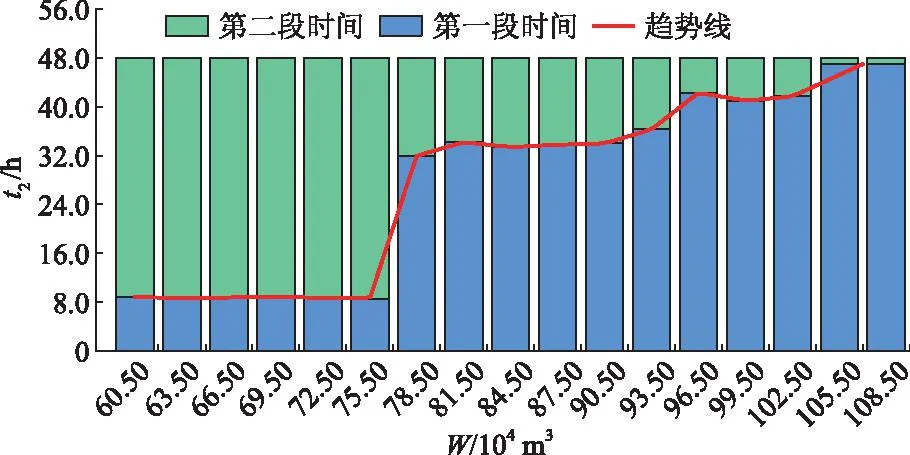
图7 调度期阶段提水耗时Fig.7 Time consumption for water lifting during the scheduling period
对表4中数据进行分析,当调度期内提水量在60.50×104~75.50×104m3时,第一阶段运行效率分别为73.0%,71.0%,78.0%,81.0%,82.0%和83.0%,整体呈上升趋势.第二阶段运行效率分别为71.0%,70.0%,71.0%,71.0%,73.0%和74.0%,平均值为71.5%,标准差为1.22%,效率变化不明显.由图7可知,机组在该提水范围内第一阶段运行时长分别为8.8,8.7,8.7,8.9,8.7,8.6 h,标准差为0.09 h,时间变化较小.由此,可推断出提水量在该范围内时,第一阶段泵站运行效率升高使得单位提水费用降低.
当调度期提水量为78.50×104~93.50×104m3时,第一、二阶段平均运行效率分别为82.1%和76.8%,标准差分别为0.86%和1.71%.观察图7可知,机组在该范围内第一阶段运行时长分别为32.0,34.2,33.4,33.8,34.0,36.3 h,随着提水量增加,第一阶段运行时长整体呈上升趋势,结合图1可知,该调水区间影响单位提水费用升高的原因是第一阶段运行时间增加,即在第一阶段运行过程中使用峰电价时间增加.
当调度期提水量在96.50×104~102.50×104m3时,第一阶段机组运行效率分别为83.6%,85.7%和87.0%,随着提水量增加,泵站运行效率呈逐步上升趋势;第二阶段泵站运行效率分别为81.6%,81.4%和82.7%,随着提水量增加,泵站运行效率变化相对平稳.第一阶段运行时长分别是41.0,41.7和42.3 h,随着提水量增加,第一阶段运行时长呈上升趋势,且在超过41.0 h后逐渐进入峰电时段,综上所述,该阶段泵站单位提水费用提高受泵站运行时长和运行效率的影响.
4 结 论
针对泵站-水库原水调水系统中泵站能耗较高的问题,以泵站运行效率最高为优化目标,构建了机组流量分配模型,在输水工程运行流量确定的基础上,利用流量优化分配模型,生成机组优化分配方案,提高水泵装置抽水效率.在此研究基础上考虑时间维度中分时电价对流量分配的影响,构建泵站经济运行模型,得到主要结论如下:
1) 经过机组流量分配后,泵站运行的平均效率明显提升,以文中典型工况为例,优化后工作效率较优化前分别提升了4.9%,2.8%,7.9%.
2) 通过泵站经济运行模型优化后,单位提水费用明显降低,以文中典型工况为例,根据选取工况进行优化,经模型计算后单位提水费用较实际工况分别降低了11.93%,16.62%,11.68%.
3)在周期调水过程中,由于分时电价的存在,在1个调水周期内,随着调水量的增加,单位提水费用呈先减少后增加的趋势,分析其原因为受阶段运行时长和运行效率的影响.对1个周期调水量进行离散优化,得出在调水量为75.50×104m3时,单位提水费用最低为662.4元/104m3.
