裂隙影响下的微润灌水分运移和分布规律

2024-02-02齐伟和玉璞纪仁婧麦紫君王策江晓星

排灌机械工程学报 2024年2期

齐伟,和玉璞,纪仁婧,麦紫君,王策,江晓星

(1. 南京水利科学研究院,江苏南京 210029;2. 河海大学农业科学与工程学院,江苏南京 211100; 3. 南京江宁湖熟街道水务站,江苏南京 211121)

微润灌是由中国率先研发、提出并逐步应用的一种高效节水灌溉技术.该技术核心部件是微润管,系统运行时管多埋在地下,管内水分在管内水压力和管外土壤基质势的作用下从管壁孔隙缓慢渗出,然后在土壤基质势作用下向周围扩散从而向作物根区供水[1].微润管出流速率可根据土壤质量含水量自行调节,实现了自动、连续、适时和适量灌溉.与传统灌溉技术相比,微润灌具有节水效果明显、灌水均匀度高和运行成本低等特点[2],是一种有广阔应用前景的节水灌溉技术.

微润灌水分运移规律的研究可为其灌溉制度的制定和进一步推广应用提供理论依据.近些年来国内外学者通过室内入渗试验、大田观测试验和模型模拟等方法对微润灌水分运移规律开展了较多研究,主要集中在微润管出流特性、微润灌水分运移分布特征及其影响因素等方面[3-5].薛万来等[6]研究了压力水头对微润灌水分运动特性的影响,结果表明,累积入渗量、湿润锋运移距离和入渗后土壤平均质量含水率与压力水头均呈正相关,湿润锋运移速率初期较快,后期减缓,此外微润管在土壤中的出流量明显大于空气出流量.牛文全等[5]研究表明,微润管埋深对湿润体形状有显著影响,主要表现为湿润锋水平运移距离和宽深比随埋深增大而减小,垂直运移距离随埋深增大而小幅增加,累积入渗量与埋深呈负相关,土壤湿润均匀系数与埋深呈正相关.KANDA等[7]探究了灌溉水质对微润管出流特性的影响,结果表明,用含杂质的水灌溉会降低微润管出流速率,且含悬浮性杂质水大于含可溶性杂质水的影响.DIRWAI等[8]研究了管外蒸发强度对微润管出流速率的影响规律,发现管外蒸发强度越大,微润管出流速率越快.

农田土壤在干湿冻融交替、根系延展与腐烂及动物活动等因素的影响下普遍存在大孔隙结构[9].土壤干缩开裂形成的裂隙是一种常见的大孔隙[10].干缩裂隙多在土壤表层发育,但也可发育至五六十厘米深度[11].裂隙的存在改变了土壤结构和水力特性,从而对水分溶质运移造成影响.有研究表明,裂隙可导致优先流现象[12],在农田中可导致深层渗漏[13].也有研究发现,裂隙的存在切断了土壤基质和毛管的连续性,严重阻碍了水分的横向运移[14].目前,对裂隙及其影响效应的研究已成为农业、土壤、水文等学科领域共同关注的热点之一[15].微润灌作为一种高度依赖土壤基质势驱动入渗的地下灌溉方式,其水分运移特征势必受土壤大孔隙结构尤其是裂隙的影响.因此,文中通过室内微润灌水分入渗试验,研究不同发育形式的裂隙对微润灌水分运移和分布规律的影响,以期为微润灌优化设计和科学管理提供理论参考.

1 材料与方法

1.1 供试土壤

试验在河海大学江宁校区节水园开展.供试土壤取自园内稻麦轮作试验大田0～20 cm土层.在田间将土壤收集后碾碎并通过2 mm孔径的筛网,后置于阴凉通风处风干备用(土壤水分质量比约为0.04 g/g).土壤黏粒[0,0.002) mm、粉粒[0.002,0.02) mm、砂粒[0.02,2) mm质量分数分别为21.1%, 56.2%和22.7%.根据国际制土壤质地分类标准(ISSS),供试土壤质地为粉砂质黏壤土.回填后土壤水分饱和体积比为0.502 cm3/cm3,田间持水体积比为0.467 cm3/cm3,有机碳质量比为11.7 g/kg.

1.2 入渗试验

研究试验装置与文献[16]的研究中类似,主要由有机玻璃土箱、微润灌溉系统和数据采集系统组成.土箱采用1 cm厚透明有机玻璃板制作而成,规格为长40 cm×宽40 cm×高60 cm.土箱后面板按上下左右间距5 cm的布局打有直径1 cm的土壤体积含水率测量孔,前后面板打有直径2 cm的对称微润管安装孔.土箱底部打有排水孔,并铺设5 cm厚的砾石层,从而构成排水系统.将风干土按1.25 g/cm3干容重分层回填至土箱内,填土高度为50 cm,分5层回填,每层回填高度为10 cm,单层回填后平整上表面,轻微压实至设定容重,然后对表面进行打毛处理,以保证层与层之间的水力连续性.微润管、橡胶管和马氏瓶组成简易微润灌溉系统.微润管产自深圳微润灌溉技术有限公司,为第三代管,四折痕双层结构,水平铺设于土箱中,埋深为20 cm.微润管通过橡胶管与马氏瓶连接.调节马氏瓶高度,将微润管内压力水头控制在100 cm.通过预试验发现,入渗120 h时湿润锋接近土箱边缘,因此,限于土箱几何尺寸影响,将试验各处理总入渗时间设置为120 h.试验过程中采集湿润体、入渗量和含水率数据,采用数码相机拍照记录湿润体变化,拍照时间按照先密后疏原则,并同时记录相应时刻马氏瓶内液面高度以推算入渗量.入渗结束采用TDR(时域反射仪)快速测量土壤剖面含水率,在30 min内完成测量,忽略水分再分布的影响.

试验处理如表1所示,表中J为裂隙间距,S为裂隙深度.C1—C6为不同处理,CK为无裂隙处理.

表1 试验处理Tab.1 Experimental treatments cm

根据节水园试验大田内土壤裂隙发育情况和试验装置有机玻璃土箱几何尺寸情况设置裂隙间距和深度,间距设6和8 cm这2个水平(对应裂隙条数分别为5和3条),深度设5,10和15 cm这3个水平,共6组处理,设空白对照(无裂隙),各处理重复3次.为精准控制裂隙发育形式以便对比分析,采用人造裂隙的方式,将金属筛网制成顶部宽度为1 cm的楔状裂隙,在填土过程中根据设定高度和位置嵌入土中,筛网材质的人造裂隙可较好地模拟天然裂隙的透水透气性.试验装置和裂隙布置情况如图1所示.为了简便,示意图仅展示了10 cm裂隙深度下2种裂隙间距的布置情况.

图1 试验装置和裂隙布置示意图(单位:cm)Fig.1 Schematic diagram of experimental setup and crack layout (unit: cm)

1.3 图像处理

湿润体图像采用Photoshop和MATLAB软件处理.首先采用Photoshop进行图像裁剪,截取试样区域(宽40 cm×高50 cm),图像分辨率设置为1 600 pixel×2 000 pixel.试样湿润区域和干燥区域颜色对比明显,因此采用“快速选择工具”选中湿润区域并填充为白色,选中干燥区域填充为黑色,实现区域分割,并将图像转化为灰度图像.将分割后的灰度图像导入MATLAB软件,通过自编程序,将灰度图像转化为二值图像,并计算各方向的湿润锋运移距离,其中向上和向下运移距离为该方向上距离微润管中心的最大距离,水平运移距离为向左和向右2个方向上距离微润管中心最大距离的平均值.

1.4 数据分析

试验数据采用Microsoft Excel 2019记录和整理.数据分析均取3组重复平均值,使用IBM SPSS Statistics 20.0软件,以裂隙间距和裂隙深度作为主效应因素进行方差分析,采用最小显著性差异检验进行多重比较(显著性水平P<0.05),最后采用Origin软件制图.

采用分散度指标描述微润灌湿润体形态规则度[17].几何图形的分散度定义为

(1)

式中:D为图形分散度;C为湿润锋周长;A为湿润体面积.几何形态越不规则,分散度则越高.在常见的几何图形中,圆形的分散度最小,为4π.

采用幂函数对湿润锋运移距离变化进行拟合,即

L=atb,

(2)

式中:L为湿润锋运移距离,下文L1,L2,L3分别为湿润锋向上、向下和水平运移距离;a为湿润锋扩散系数;b为湿润锋扩散指数;t为入渗时间.

采用克里斯琴森均匀系数计算入渗结束时土壤剖面水分分布均匀度,计算公式为

(3)

2 结果与分析

2.1 入渗特征

图2为不同处理微润灌累积入渗量Q随入渗时间t的变化关系.由图可以看出,各处理下的累积入渗量变化趋势基本一致,均呈一条直线.同时可以看出,各处理之间及与CK之间的差异均较小.入渗前期,各处理之间累积入渗量几乎重合,入渗结束时,CK和C1—C6处理的最终累积入渗量分别为10 000.8,9 785.2,10 211.2,10 403.5,10 234.2,10 421.5,10 542.1 mL,处理间相对差异小于10%,通过方差分析发现,各处理的最终累积入渗量之间差异不具有统计学意义(P>0.05).综合上述分析发现,不同裂隙间距和深度对微润灌的水分入渗速率无明显影响.

图2 不同处理累积入渗量随时间变化Fig.2 Variation of cumulative infiltration amount related to infiltration time for different treatments

2.2 湿润体形态特征

2.2.1形态演变过程

图3为不同处理微润灌土壤湿润体(截面)随入渗时间(3,24,48,96,120 h)的演变情况.无裂隙时,不同时刻的湿润体呈近似圆形,随入渗时间的增加,湿润锋不断向外扩展.观察有裂隙处理组发现,当裂隙深度为5 cm时(C1,C4处理),入渗结束时湿润锋未到达裂隙区域,因而湿润体形态与CK处理类似,也呈近似圆形.当裂隙深度为10 cm时(C2,C5处理),入渗96 h时湿润锋已到达裂隙区域,湿润锋不再以同心圆方式向外扩展,与裂隙相遇后水分水平运动受到一定抑制,竖直向上运动得到一定加强,相邻裂隙之间湿润体呈近似矩形分布.这一现象在裂隙深度为15 cm时表现得更加明显,C3和C6处理中湿润锋到达裂隙区域时间更早,C3处理中湿润锋约在第48 h到达裂隙区域,C6处理中约在第24 h到达裂隙区域.

图3 不同处理微润灌湿润体形态演变Fig.3 Evolution of wetting body morphology under different treatments of moistube irrigation

可以观察到,入渗结束时,C3处理中湿润体呈墨水瓶状,上部为近似矩形,下部为近似椭圆形,C6处理中湿润体上部为多个矩形,靠近中间的裂隙之间矩形长度明显大于位于边缘裂隙之间的矩形长度,湿润体下部也接近椭圆形.综上可以得出,裂隙对微润灌水分运动的影响发生在湿润锋与裂隙相遇之后,裂隙会一定程度上抑制附近区域水分水平方向的运移,而促进水分上移,从而影响湿润体形态.

2.2.2形态规则度

由上可知,裂隙的存在改变了微润灌湿润体形态,使湿润体呈现不规则形状.对所有处理不同时刻的湿润体分散度D进行统计,得出其随入渗时间变化趋势如图4所示.

图4 不同处理湿润体分散度随时间变化Fig.4 Variation of dispersity of wetting body related to infiltration time for different treatments

由图可知,所有处理中入渗起始阶段湿润体分散度值较为接近,均在13.0～14.0,随入渗时间增加各处理之间差异逐渐增大.CK处理中湿润体分散度随入渗时间变化不大,一直稳定在13.7左右.当裂隙深度为5 cm时,入渗结束时湿润锋未到达裂隙区域,裂隙对湿润锋运移基本无影响,因此C1和C4处理中湿润体分散度随时间变化幅度也较小,分散度值约为14.0.当裂隙深度为10 cm及以上时,裂隙对湿润锋运移的影响较为明显.C2—C6处理中湿润体分散度均随入渗时间的推移而快速增加,其中,C2和C5处理的变化趋势较为接近,C3和C6处理的变化趋势较为接近,这说明随入渗时间推移,裂隙深度越大,湿润体分散度增加幅度也越大.入渗结束时,C2和C5处理湿润体分散度约为16.0,C3和C6处理湿润体分散度高于18.0.

表2为不同处理入渗结束时湿润体分散度、湿润锋运移距离、水分分布均匀度方差分析结果.由表可知,裂隙深度和裂隙间距无交互效应,裂隙间距对入渗结束时刻湿润体分散度影响不具有统计学意义(P>0.05),而裂隙深度对其影响具有统计学意义(P<0.01).

表2 湿润体分散度、湿润锋运移距离、水分分布均匀度方差分析Tab.2 Analysis of variance for dispersity of wetting body, advancing distance of wetting front and uniformity of soil water distribution

图5为不同裂隙深度对入渗结束时湿润体分散度的影响.裂隙深度为5 cm时,湿润体分散度与CK相比差异不具有统计学意义(P>0.05);裂隙深度为10 cm时,湿润体分散度与CK相比差异具有统计学意义(P<0.05),增加了约18.3%;裂隙深度为15 cm时,湿润体分散度与CK相比差异具有统计学意义(P<0.05),增加了约34.5%.

注:图中不同小写字母表示不同处理间差异具有统计学意义(P<0.05),下同图5 不同裂隙深度处理下湿润体分散度比较Fig.5 Comparison of dispersity of wetting body among treatments of different crack depth

2.2.3湿润锋运移距离

图6为不同处理微润灌湿润锋运移距离L随时间的变化情况.

图6 不同处理湿润锋运移距离随时间变化Fig.6 Variation of wetting distance related to infiltration time for different treatments

由图6可以看出,各处理湿润锋运移距离随时间的变化趋势基本一致,呈先快后慢的变化趋势.在入渗开始阶段,湿润锋运移速率较快.入渗10 h后湿润锋运移速率开始减缓,且各方向运移距离逐渐出现差异,具体表现为竖直向上的运移距离小于竖直向下和水平方向的运移距离,且随入渗时间增加差异不断增大.这主要是由于在入渗前期土壤体积含水率较低,土壤基质势较大,水分运动主要受基质势驱动,各方向驱动力差异不大,因此各方向湿润锋运移距离接近.而随着入渗时间增加,土壤体积含水率升高,基质势减小,重力势影响越来越大,在重力势影响下水分向上运移速率逐渐小于水平和向下方向,因此运移距离也表现为竖直向上方向相对较小.

由图6还可以看出,所有处理中湿润锋各方向运移距离与入渗时间均符合幂函数关系,拟合决定系数为0.984～0.999.各处理间扩散系数和扩散指数无明显规律,扩散系数为1.599～2.947,扩散指数为0.396～0.525.

由表2可以看出,裂隙深度和裂隙间距在湿润锋向上、向下和水平方向最终运移距离上不存在交互效应,且对湿润锋向下运移距离和水平方向运移距离的影响均不具有统计学意义(P>0.05),但裂隙深度对湿润锋向上运移距离的影响具有统计学意义(P<0.01).图7为不同裂隙深度处理湿润锋最终向上运移距离L1比较.

图7 不同裂隙深度处理湿润锋最终向上运移距离比较Fig.7 Comparison of final advancing distance of upward wetting front among treatments of diffe-rent crack depth

由图7可以看出,裂隙深度为5 cm和10 cm时,湿润锋最终向上运移距离与CK差异不具有统计学意义(P>0.05);而裂隙深度为15 cm时,湿润锋最终向上运移距离与CK差异具有统计学意义(P<0.05),其运移距离较CK约增加12.9%,这表明当微润灌裂隙深度达到一定值时,水分向上运移距离将会明显增加.

2.3 水分分布特征

2.3.1含水率分布

图8为不同处理入渗结束时土壤中水分分布情况.图中l为土壤宽度;h为土壤深度;θ为土壤水分体积比.

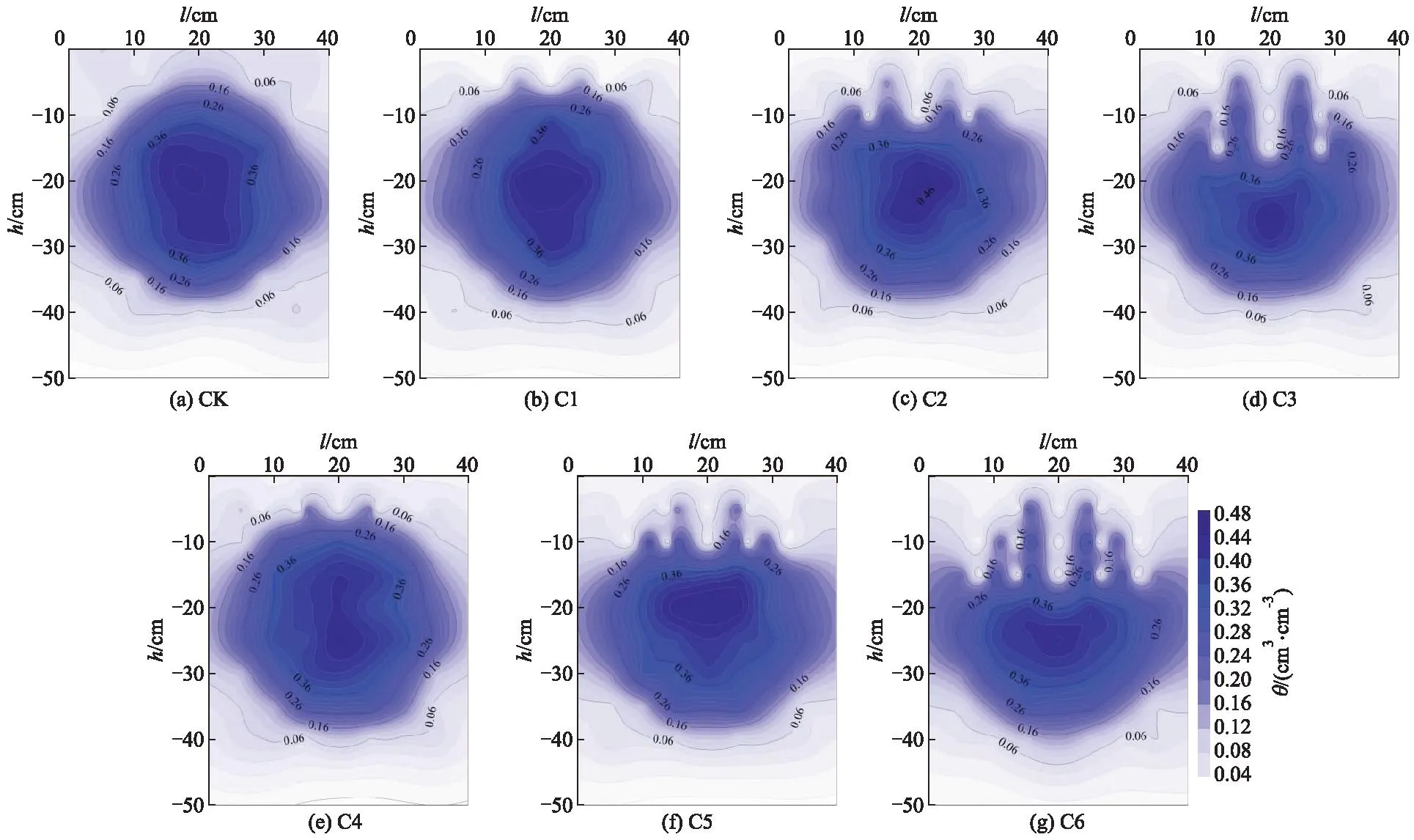
图8 不同处理入渗结束时刻土壤水分分布Fig.8 Soil water distribution at end of infiltration for different treatments

由图8可知,微润灌后水分主要集中在微润管周围.在各组处理中,越靠近微润管,土壤水分体积比越高,各处理中微润管附近的土壤水分体积比约为0.40～0.48 cm3/cm3.在以微润管为圆心半径大约7 cm的圆形范围内,土壤水分体积比都高于0.36 cm3/cm3,当距离微润管10 cm及以上时,土壤水分体积比基本低于0.26 cm3/cm3.比较不同处理之间水分分布特征,可以发现水分分布与湿润体形态类似,当土壤中无裂隙或裂隙深度较浅时,水分分布区域呈近似椭圆状.随着裂隙深度的增大和裂隙间距的减小,水分分布范围呈现出明显的不规则性,在C2,C3,C5和C6处理中,土壤上层20 cm中的水分分布都表现为明显的指状特征.

2.3.2分布均匀度

水分分布均匀度反映了灌水均匀性,而灌水均匀性很大程度上决定了灌溉质量[18].表2结果表明,裂隙深度和裂隙间距在水分分布均匀度上不存在交互效应,裂隙间距对水分分布均匀度影响不具有统计学意义(P>0.05),而裂隙深度对其影响具有统计学意义(P<0.01).图9为不同裂隙深度处理入渗结束时刻土壤水分分布均匀度.可以看出,裂隙深度为5 cm时水分分布均匀度与CK差异较小,均在40.0%左右.当裂隙深度达到10 cm及以上时,水分分布均匀度与CK差异具有统计学意义(P<0.05).裂隙深度为10 cm时水分分布均匀度显著降低了约15.2%,裂隙深度为15 cm时水分分布均匀度显著降低了约27.5%.

图9 不同裂隙深度处理入渗结束时刻水分分布均匀度比较Fig.9 Comparison of uniformity of soil water distribution at end of infiltration among treatments of different crack depth

3 讨论

在含有不同发育形式裂隙的土壤中,微润灌水分入渗速率差异不大(见图2),即微润管出流速率基本一致.这主要是因为裂隙的存在未明显影响微润管周围的土壤水势.由图8可以看出,各处理中管附近土壤体积含水率较为接近.微润灌水分入渗过程中,管内和管外具有水势差,管中水则在水势差的驱动下进入土壤.当管附近土壤体积含水率相互接近时,管内外水势差也较为接近,因而微润管出流速率基本一致,可认为裂隙对微润灌水分入渗速率基本无影响.

裂隙对微润灌水分运移路径有明显影响.图10为均质土和开裂土水分运移示意图.由于微润管出流缓慢,土壤内未形成饱和区,故可忽略压力势影响,进入土壤后的水分主要靠土壤基质势作用运移,不断向湿润体四周扩散.在均质土中,湿润锋处土壤基质势ψ1高于湿润锋外圈土壤基质势ψ2,从t1时刻至t2时刻,在水势差的驱动下,水分基本呈同心圆式扩散.相比之下,在含裂隙土壤中,裂隙切断了土壤基质和毛管的连续性,产生毛管阻隔效应.当湿润锋扩展到裂隙边缘处时,裂隙区与大气接触,可看作基质势为0,因此靠近裂隙的湿润锋处土壤水势低于裂隙区土壤水势,水分不再从湿润锋处往外圈扩散,在裂隙毛管阻隔效应下,水分的扩散被直接切断,原本应往外圈扩散的水分沿着裂隙临水侧边缘向上方运动,使裂隙临水侧水分增多,而背水侧水分减少,湿润体形状不规则程度增加,同时水分分布均匀度降低,当裂隙间距较小时,湿润体在裂隙之间的形状接近矩形,土壤水分分布呈指状特征.

图10 微润灌下均质土和开裂土中水分运移示意图Fig.10 Schematic diagram of water movement in homogeneous soil and cracked soil under moistube irrigation

裂隙深度对微润灌水分运移分布起决定性作用.微润灌作为一种地下灌溉方式,水分自微润管渗出后逐渐向四周以近似圆形或椭圆形扩散,湿润锋与裂隙的相遇时间和裂隙深度密切相关,裂隙深度的增加明显缩短湿润锋与裂隙相遇时间,水分运移受裂隙影响的时间提前,受影响程度也相应增大.深裂隙的存在可明显增大局部水分上移量和上移速率,当裂隙深度为15 cm时湿润锋向上运移距离显著增加(见图7).从图3也可看出,裂隙或裂隙较浅的处理中湿润锋向上尚未到达土壤表面,而C6处理中湿润锋向上已基本到达土壤表面.由此不难推测,当土壤蒸发强度较大时,深裂隙将增大土壤表层无效蒸发,降低微润灌水分利用效率.此外,考虑微润灌大田应用,若采用一管控制2行作物的管道布置方式,深裂隙将显著降低裂隙背水侧区域供水强度,减少该区域水分入渗量,延缓水分运移到达时间,将对作物根系吸水造成不利影响.因此,在易开裂土壤中应用微润灌时,应当采取有效措施如翻耕、秸秆添加等控制裂隙发育,减小裂隙深度.本次试验和得出的结论是基于室内人造裂隙且无作物的情况,在实际大田中气候条件、土壤性质和作物根系等均会影响裂隙发育特征[19],致使裂隙对微润灌水分运移及分布的影响规律发生变化,所以还需在大田尺度下进一步研究,综合考虑多方面因素,以消除或最小化土壤裂隙对微润灌的不利影响.