非晶合金结构演变影响玻璃形成能力的分子动力学研究

史天姿, 龙志林, 张新瑞

(湘潭大学 土木工程学院, 湘潭 411105)

1 引 言

非晶合金又称金属玻璃，由于没有晶体合金中诸如位错等结构缺陷从而表现出超高强度、韧性、弹性极限等优异的力学性能因此受到广泛关注[1]. 然而，玻璃转变的本质(包括玻璃结构和玻璃转变行为)是长期以来困扰凝聚态物理和材料科学领域的一个重大难题，非晶合金作为从原子尺度研究该类问题的极佳物理模型，肩上背负着沉重的使命[2]. 宏观无序的非晶结构中存在有序特征，非晶合金中已被证明有短程序(SRO)和中程序(MRO)且与非晶的诸多性质如玻璃形成能力(GFA)有重要联系[3-8]. 然而，由于非晶制备的困难以及实验观测手段的限制，非晶在玻璃转变过程中的微观结构演化过程至今没有一个清晰的图像. 分子动力学(MD)模拟是弥补这些不足的重要手段.

采用MD方法分析液态金属和金属玻璃的微观结构和玻璃转变行为迄今已取得诸多重要进展[9-15]. 如Park等[9]在非晶体系微观结构与宏观性能关系的研究中发现，原子堆积密度与非晶固体的弹性模量、强度和塑性密切相关，由Voronoi多面体定义的各种原子团簇构成了非晶的SRO，并对非晶固体的力学性能有决定性影响. Cheng等[10]利用CuZr体系证明了二十面体团簇是金属过冷液体非Arrhenius动力学降速的微观起源，从结构动力学角度解释了非晶依赖成分的力学性质以及其强度与玻璃转变温度之间的关系. Sha等[11]在模拟CuZr体系的玻璃转变过程中发现大量以Cu原子为中心的类二十面体团簇可使体系的堆积方式更为致密，从而提高体系的GFA. Li等[12]在MRO尺度通过X-Ray衍射实验揭示了CuZr非晶以二十面体团簇构成弦状主干并以类液结构填充剩余空间的堆积方式并与经典MD模拟结果一致. Wei等[13]在CuZrAl三元体系的MD模拟中发现Al元素的含量对体系团簇种类和数量的分布有显著影响，从而在该体系GFA中扮演关键角色.

然而，上述研究主要关注的二十面体团簇随Cu含量变化较大，在其他不含Cu元素的体系中几乎监测不到，表明该参数用于描述非晶结构特征并不具有广泛代表性，需要引进新的结构参数. 且上述研究大都致力于多元非晶体系的模拟，但合金中含有多个组元使得对非晶GFA、玻璃转变等基础问题的研究和计算机模拟分析变得十分复杂，因此，开发和研究二元块体非晶合金具有重要意义. 作为典型的二元非晶态材料，Ni-Zr系可在相当宽的成份范围(20-70 at%Zr)内形成非晶态从而引起人们很大兴趣. 最近的研究发现，Ni-Zr非晶合金的屈服强度随材料尺寸的降低而增加，当薄膜厚度低于360 nm时，拉伸过程中不出现剪切带，具有非常大的塑性，甚至能达到15%的断裂应变[15]，是研究尺寸效应和非晶增韧的绝佳模型. Ti-Al合金具有低密度、高比强度、抗高温、抗氧化、耐腐蚀等特殊性能，是航空航天和高温应用领域具有吸引力的材料，且该合金具有很强的结晶性，是研究非晶晶化行为的良好模型[16，17].

本文利用MD手段，模拟了Ti75Al25、Ni50Zr50和Cu50Zr50三种典型并极具对比性的二元非晶合金模型的玻璃转变过程，并引进更具广泛性的新结构参数‘局部五次对称性(LFFS)’研究了非晶由SRO连接至MRO再至长程无序的动力学演化过程，并由此解释了三种非晶合金宏观力学性质迥异的原子结构层面原因.

2 模拟计算的条件和方法

利用开源的大规模原子分子并行程序LAMMPS模拟了Ti75Al25和Ni50Zr50非晶合金的玻璃转变过程. 表1列举了模拟过程中两种非晶的不同参数设置，考虑到原子间的多体相互作用，Ti75Al25合金原子间相互作用势选用Mishin[18]拟合第一性原理数据得到的金属合金镶嵌原子势(EAM)，Ni50Zr50合金原子间相互作用势选用Sheng等[19]拟合得到的EAM势. 如图1所示，Ti75Al25(Ni50Zr50)模拟在含有4000(32000)个原子50×50×50 Å3(72×72×72 Å3)的模拟盒子中进行，其中Ti(Ni)和Al(Zr)的原子数分别为3000(16000)和1000(16000)个. 冷却过程中采用等压等温系综并利用Nose-Hoover算法控制温度和压强，边界条件采用立方周期性边界条件，时间步长设定为2 fs.

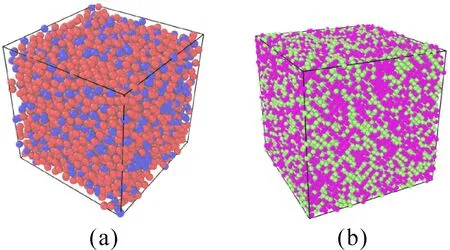
图1 分子动力学结构模型示意图 (a)Ti75Al25，红色原子为Ti，蓝色原子为Al；(b)Ni50Zr50，紫色原子为Ni，绿色原子为ZrFig. 1 The schematics of molecular dynamics structure models：(a)Ti75Al25，the red atoms are Ti，blue atoms are Al；(b)Ni50Zr50，the purple atoms are Ni，green atoms are Zr.

表1 两种非晶合金的分子动力学模拟参数设置

首先，根据最小势能原理，系统处于稳态时的能量最小. 如图2可见，让系统在2000 K温度下弛豫100 ps (20 ps)后体系原子处于稳定状态，即得到热力学平衡的非晶合金熔融液态结构，可以开始模拟玻璃转变. 随后，分别以Q1=0.5×1013Ks-1，Q2=0.5×1012Ks-1(Q3=1.0×1013Ks-1，Q4=1.0×1012Ks-1)的冷却速率快速降温至300 K，并保温20 ps得到系统的微观结构，每隔1000步记录一次系统的位置信息. 最后，运用微观结构可视化分析程序 Ovito 分析其微观结构特征.

图2 平均原子势能随驰豫时间的变化图 (a)Ti75Al25；(b)Ni50Zr50Fig. 2 Plots of average atomic potential energy with relaxation time：(a)Ti75Al25；(b)Ni50Zr50.

3 模拟计算结果与讨论

在金属液体冷却过程中，通常采用平均原子体积(体系总体积与所含原子数N的比)描述体系密度的变化情况. 图3显示出Ti75Al25和Ni50Zr50合金在不同冷却速率下平均原子体积随温度的变化情况. 由图3(a)可以发现，Ti75Al25合金在Q1冷却速率下，平均原子体积随着温度的降低缓慢且连续地减少；而在Q2冷却速率下，体系平均原子体积在1000 K左右发生突变，表明此时Ti75Al25合金结构发生重大变化，即由无序的液态结构形成有序的晶态结构. 根据Abraham对形成玻璃系统的模拟研究表明：冷却过程中，如果平均原子体积与温度曲线的斜率发生突变，说明形成晶体结构. 结合图3(a)可以确定Ti75Al25合金发生玻璃转变的温度大约为1000 K. 同理，由图3(b)可知，Ni50Zr50合金在Q3和Q4两种冷却速率下均形成了非晶结构.Q1与Q2、Q3与Q4均只相差一个数量级，但两种合金却表现出完全不同的玻璃转变行为，这表明Ni50Zr50合金的GFA胜于Ti75Al25合金至少一个量级，Ti75Al25合金十分容易发生晶化，目前的实验手段很难获得稳定的Ti75Al25非晶合金.

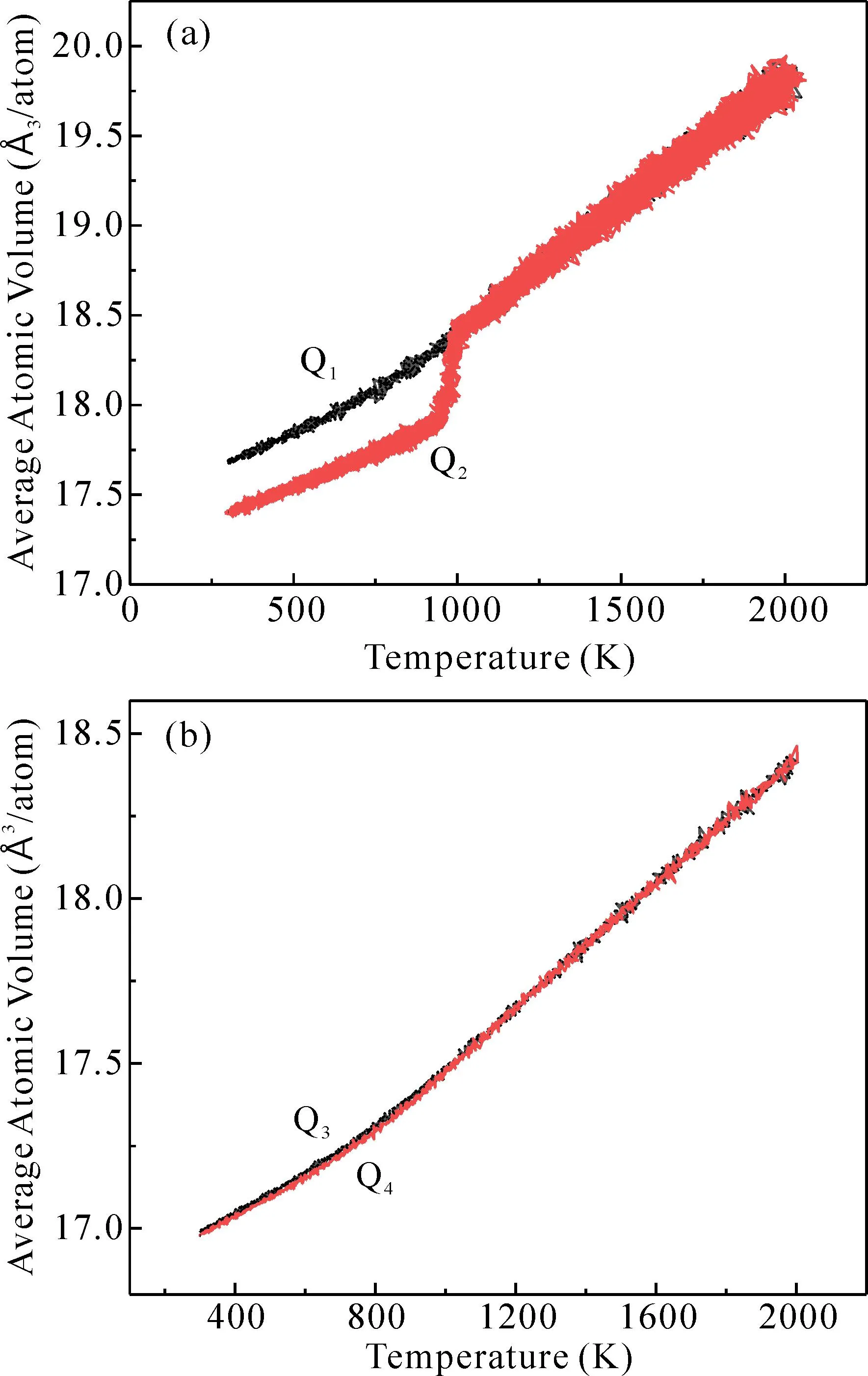
图3 平均原子体积在不同冷却速率下随温度的变化关系图 (a)Ti75Al25；(b)Ni50Zr50Fig. 3 Plots of average atomic volume with temperature at different cooling rates：(a)Ti75Al25；(b)Ni50Zr50.

双体分布函数(RDF)g(r)描述的是在原点处存在粒子的情况下在距离r处找到粒子的概率，它本质上是粒子间距离的直方图，通过粒子的数密度(即粒子总数除以模拟盒子体积)进行归一化，是MD模拟中表示微观结构的一个重要方法.α和β原子的偏双体分布函数定义如下

(1)

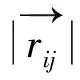
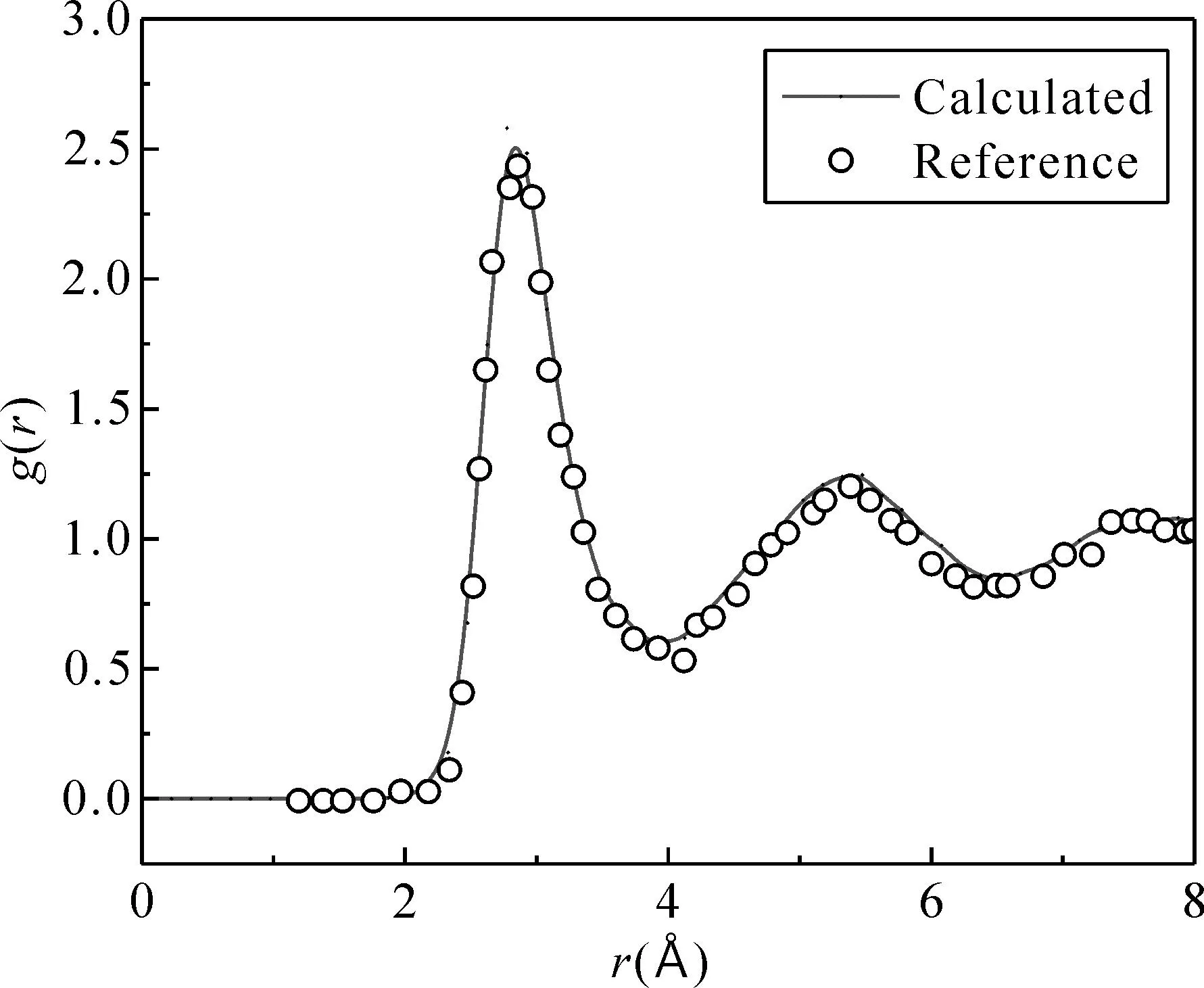
图4 本文计算得到的Ti75Al25合金在2000 K时的RDF与参考文献[17]的对比曲线Fig. 4 The calculated RDF of Ti75Al25 at temperature 2000 K with the available data.

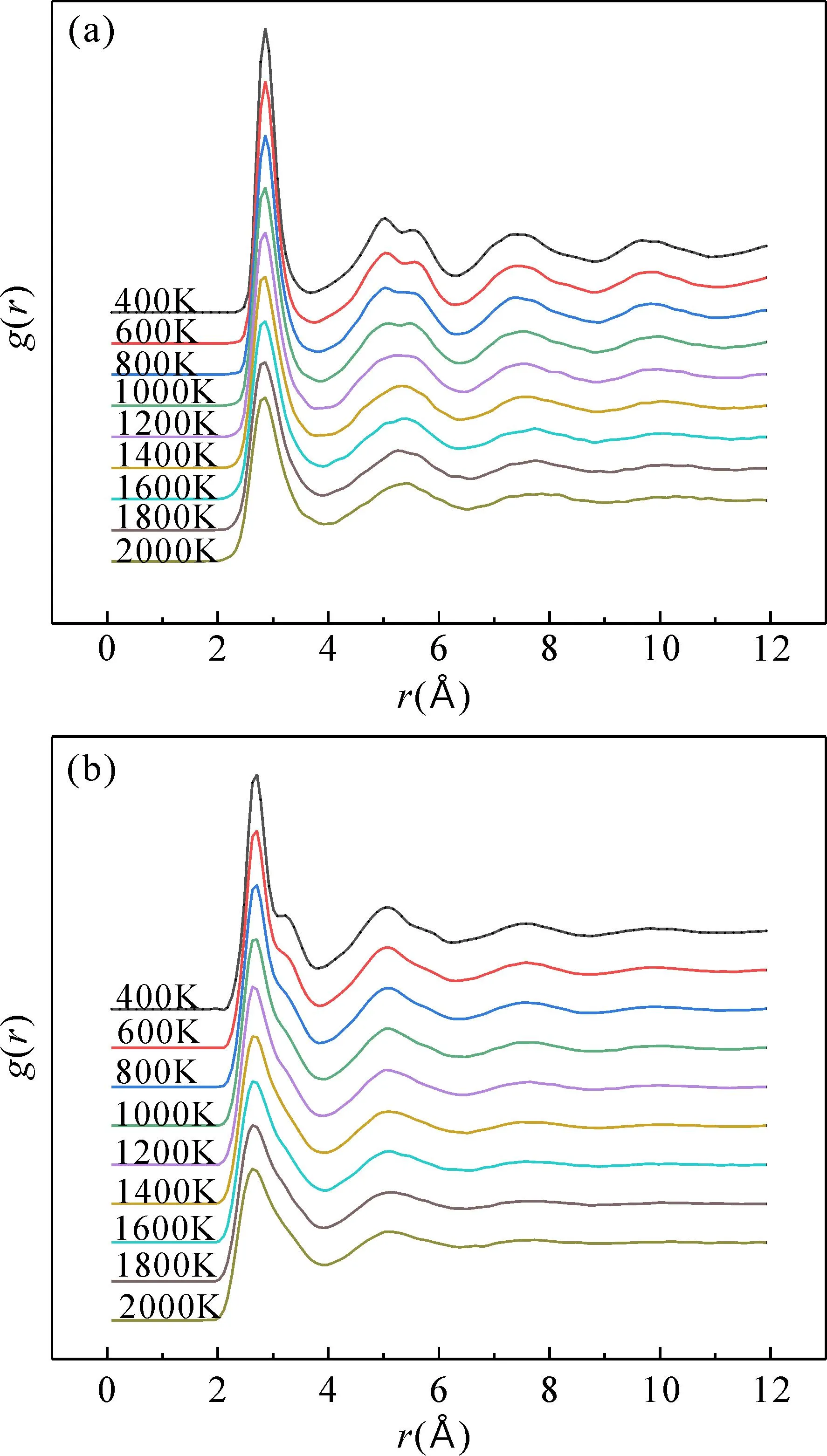
图5 2000～400 K温度范围每隔200 K的双体分布函数曲线集 (a)Q1冷却速率下的Ti75Al25合金；(b)Q3冷却速率下的Ni50Zr50合金Fig. 5 The radial pair distribution function curve sets of temperature range from 2000 to 400 K at intervals of 200 K：(a)Ti75Al25 alloy of Q1 cooling rate；(b)Ni50Zr50 alloy of Q3 cooling rate.

图6给出了300 K下MD模拟得到的非晶合金样品的偏双体分布函数. 无论Ti75Al25(图6a)还是Ni50Zr50(图6b)的偏双体分布函数均展现出了第二峰劈裂的特性，表明MD模拟所得样品均处于非晶态. Ti75Al25非晶的三个偏双体分布函数中，Ti-Al和Ti-Ti曲线基本重合且第一峰强度最大，表明Ti原子吸引Ti原子和Al原子的能力均较强并倾向于排列在第一近邻的位置上；铝原子之间吸引力较弱，也排在第一近邻位置上. 然而，Ni50Zr50非晶的三个偏双体分布函数的第一峰强度均较大，Ni-Ni曲线第一峰位置最近，Zr-Zr曲线第一峰位置最远，但均没有超过4 Å，这表明Ni和Zr原子间均表现为引力并依次排列在第一近邻位置，增加了体系的SRO. 同时，以上分析表明偏径向分布函数的分散度在一定程度上也可以反映出金属玻璃的GFA.

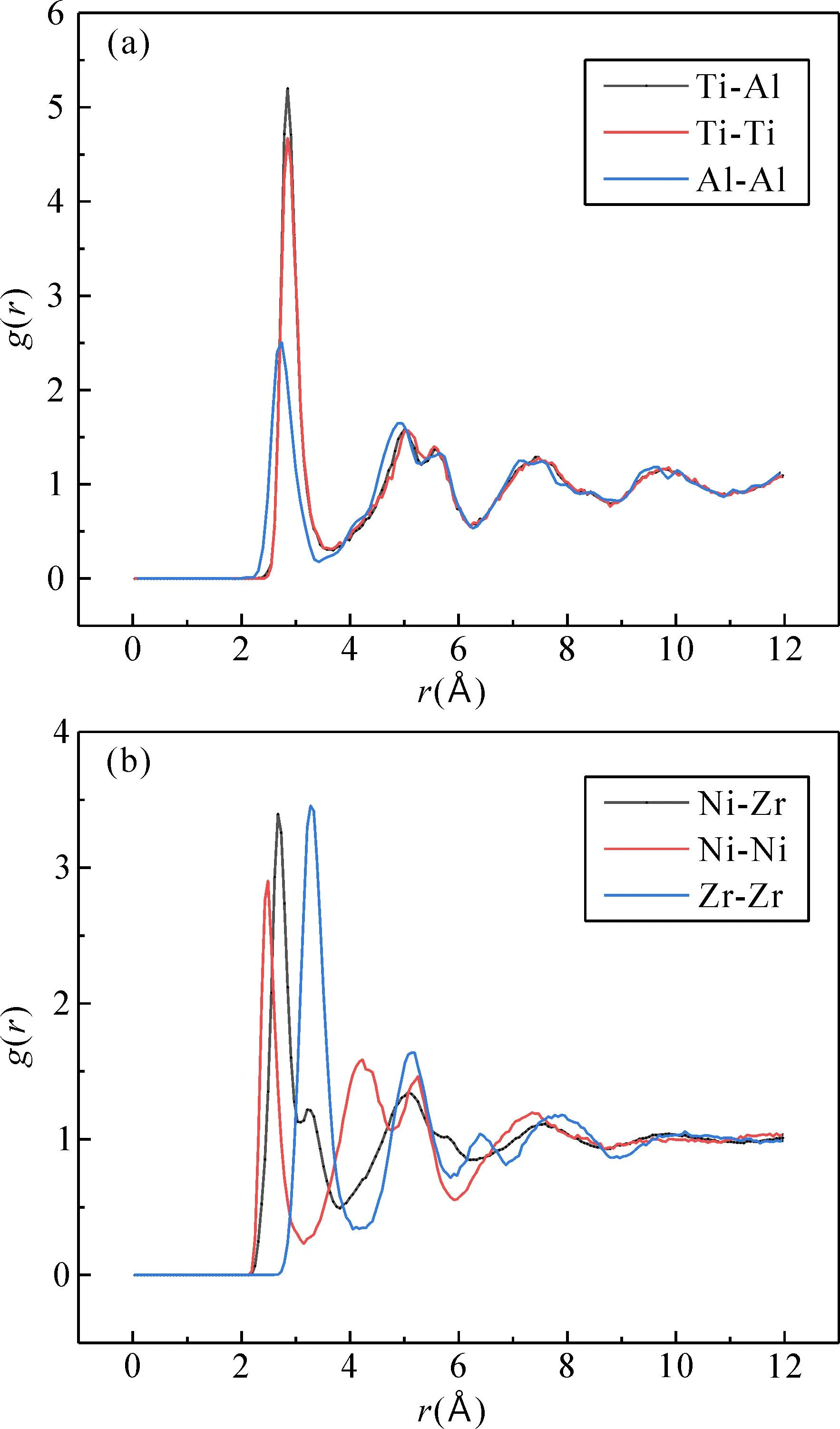
图6 300 K温度下的偏双体分布函数 (a)Ti75Al25；(b)Ni50Zr50Fig. 6 The partial radial pair distribution function curves at 300 K：(a)Ti75Al25；(b)Ni50Zr50

研究表明，金属玻璃中的二十面体团簇能够抑制晶体序的形核与长大，从而对GFA有显著影响，一般情况下二十面体团簇含量越高GFA越强[20]. 为进一步研究原子团簇中起主要作用的Zr-centered团簇，需控制单一变量，对Ni50Zr50非晶中的Ni原子用Cu原子进行等比例替换，在相同模拟条件下(冷却速率为Q3)，选用LAMMPS自附的Cu-Zr EAM势，进行了Cu50Zr50非晶的玻璃转变模拟. 采用 Voronoi 多面体指数分析法对三种模型中二十面体及类二十面体团簇的种类和数量进行了Voronoi指数标定. 某一原子的Voronoi多面体定义为该原子与其近邻各原子间连线的垂直平分面所围成的包含该原子的具有最小面积的多面体. Voronoi指数是用多面体中具有k(k=3，4，5，6 …)边的面数nk表征一个Voronoi多面体. 例如二十面体的Voronoi指数为<0，0，12，0>. 表2列举了在300 K模拟温度下，本文监测的二十面体及类二十面体团簇的Voronoi指数及其含量. 由表2中数据可以发现，除了Cu50Zr50非晶，其余两个模型的二十面体团簇数量几乎检测不到，即使在CuxZr100-x非晶体系中团簇<0，0，12，0>的数量也会随Cu含量的减少而显著降低[21]，这表明二十面体团簇数量作为联系非晶性能的结构参数有其局限之处.

表2 三种非晶在300 K温度下d5≥0.46的Voronoi指数及其含量(%)

局部五次对称性(LFFS)作为一个能够广泛地描述非晶合金体系结构特征的新结构参量近年来被提出[21，22]. LFFS被定义为Voronoi多面体类型i中五边形的面所占的百分比，即

(2)

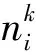
(3)

其中，Pi为Voronoi多面体类型i的含量. 图7显示了Ti75Al25、Ni50Zr50、Cu50Zr50非晶MD模型体系中的LFFS分布，可以看出这些多面体团簇不是随机分布在空间中的，其形状类似于高斯分布，LFFS高的团簇倾向于连接在一起，这也在一定程度上表明非晶结构的不均匀特征. 此外 Ti75Al25非晶(WTi75Al25≈15.526)的LFFS分布最为靠前，表明其包含的二十面体及类二十面体团簇数量较少，而Ni50Zr50非晶(WNi50Zr50≈20.347)和Cu50Zr50非晶(WCu50Zr50≈21.415)的LFFS分布较为靠后，且LFFS较强的团簇(如<0，0，12，0>，<0，1，10，2>)能够通过和它们自身，以及一些较大的Zr原子团簇相互连接，降低整个体系的动力学行为，从而增加系统的GFA. 另一方面，以Zr原子为中心具有较高LFFS的团簇(如<0，1，10，5>，<0，2，8，6>， <0，2，8，1>等)能够把类二十面体结构其它多面体团簇在一起形成链，从而密排满整个空间，起稳定整个非晶系统的作用. 值得注意的是，Ni50Zr50非晶的LFFS分布主要集中在d5= 0.6附近的中段位置，对应于其纳米尺度下塑性变形能力强的宏观力学性质，可做出微观结构层面的解释，即塑性变形更倾向于发生在局部五次对称性较低的区域，这些区域拥有较高的平移对称性和较低的势垒，能够容纳更多塑性变形量. LFFS分布再次表明，Ti75Al25，Ni50Zr50， Cu50Zr50三种非晶的GFA依次减小，这也与上述分析一致.

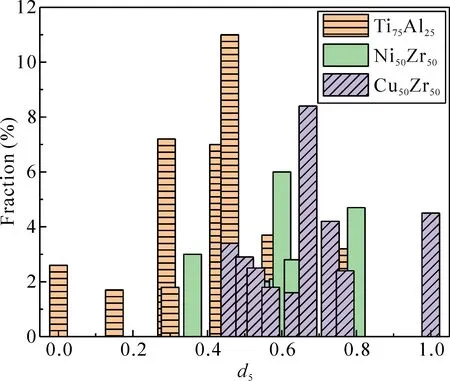
图7 三种非晶合金模型在300 K温度下的局部五次对称性分布图Fig.7 Local quintuple symmetry distributions of three metallic glass models at 300 K.

研究了准静态情况下非晶团簇的LFFS分布并验证了二十面体团簇连接填充理论后，为进一步探索其玻璃转变过程中微观结构演化的动力学行为，对表2中监测的Voronoi团簇类型的数量进行随时间的动态标定. 图8为Ti75Al25、Ni50Zr50、Cu50Zr50三种非晶合金模型在玻璃转变过程中团簇种类和数量随温度的变化情况，LFFS依图例由上到下依次减少. 可以看出，n5= 6，8，10，12的Voronoi多面体构成了非晶玻璃转变过程中的主要团簇，且随着温度的降低，各Voronoi团簇的数量均呈上升趋势，表明短程有序性的逐步增强. 图8(a)为Ti75Al25非晶的团簇变化情况. 可以发现Ti75Al25体系的LFFS较弱，团簇<0，3，6，4>在整个玻璃转变过程中都占据着含量最高的地位，且随温度降低增长较快，而LFFS较高的团簇<0，2，8，4>，<0，1，10，2>增长较为平缓，且在玻璃转变温度1000 K附近出现拐点，对比Cu50Zr50非晶的图8(c)呈现出不同的略微下降的趋势. 这表明Ti75Al25模型在玻璃转变温度附近LFFS高的团簇会向LFFS低的团簇结构转化，从而导致体系的GFA降低，倾向于发生晶化行为. 图8(b)Ni50Zr50非晶的团簇变化情况，可以看出其LFFS高的团簇种类和含量显著增多，其中团簇<0，3，6，0>， <0，3，6，1>含量最高且随温度降低上升得尤为迅速，团簇<0，3，6，2>随温度变化得较为平缓，保留了熔融液态的结构特征. 值得注意的是，与之前团簇连续稳定增长变化的方式不同，团簇<0，2，8，6>，<0，1，10，5>，<0，1，10，6>起初几乎监测不到，在温度降至玻璃转变温度850 K附近突然大量出现，是非晶玻璃转变过程中自组织临界行为的原子团簇结构体现，更多LFFS高的团簇的涌现也表明非晶结构的形成. 图8(c)为Cu50Zr50非晶的团簇变化情况. 对比图8(b)，团簇<0，2，8，1>，<0，2，8，6>和<0，1，10，5>在Cu50Zr50非晶合金中依然存在，表明其存在不受Cu原子含量影响，为Zr-centered团簇. 而团簇<0，2，8，2>和<0，0，12，0>含量非常高且独立与另两种模型存在，表明它们可能是Cu-centered团簇. 值得注意的是，二十面体团簇在Cu50Zr50非晶合金中的增长趋势尤为不同，当温度降至1300 K时开始出现并迅速增加，增长速率为所有团簇中最快，并在玻璃转变温度750 K附近出现拐点，一些LFFS高的类二十面体团簇(如<0，1，10，4>，<0，1，10，5>，<0，2，8，6>)也在这一温度段开始出现，表明二十面体团簇含量变化与CuZr体系的玻璃转变行为和GFA有密切联系，而一些比较大的Zr-centered团簇在玻璃转变过程中也扮演了重要角色，它们与周围类二十面体团簇连接从而填充整个空间，不断降低系统的动能和熵，从而起到稳定整个系统的作用.

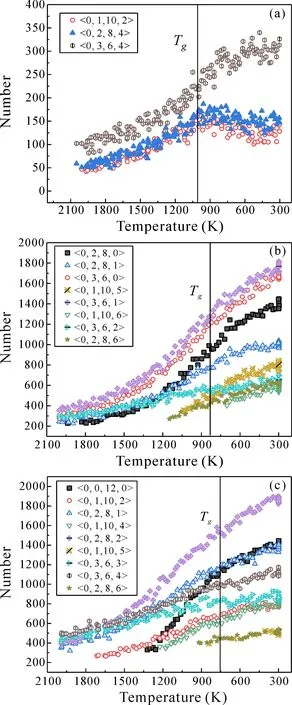
图8 三种非晶合金模型在玻璃转变过程中团簇数量随温度的变化情况 (a)Ti75Al25，冷却速率为Q1；(b)Ni50Zr50；(c)Cu50Zr50，冷却速率为Q3.Fig. 8 The numbers of clusters vary with temperature during glass transition in three metallic glass models：(a)Ti75Al25，the cooling rate is Q1；(b)Ni50Zr50；(c)Cu50Zr50，the cooling rate is Q3.

4 结 论

本文利用分子动力学方法，在微观结构层面通过分析平均原子体积、双体分布函数等结构参数以及Vonoroi多面体团簇在300 K准静态情况下的局部五次对称性分布和整个温度区间的涨落，研究了Ti75Al25，Ni50Zr50和Cu50Zr50三种非晶合金模型的玻璃转变行为，解释了三种非晶合金宏观力学性质迥异的微观结构层面原因，得到以下结论：

1)Ti75Al25非晶合金的局部五次对称性分布始终较弱，且在玻璃转变温度附近局部五次对称性高的团簇会向局部五次对称性低的团簇类型转化，因此无法形成稳定的链密排空间，导致体系稳定性差，易发生晶化行为.

2)Ni50Zr50非晶合金纳米尺度塑性变形能力强的原子结构层面原因是由于其局部五次对称性分布不高且集中，这些原子团簇具有较高的平移对称性和较低的势垒，因此能容纳更多的塑性变形量；其双体分布函数曲线的第一峰在整个冷却过程中发生了不同于一般非晶合金的劈裂现象，表明其有序性在短程尺度上较强，局部五次对称性弱，因此塑性变形能力强.

3)Cu50Zr50非晶合金具有非常强的玻璃形成能力是因为其二十面体团簇含量高并在玻璃转变温度附近急剧上升，某些特定原子团簇类型十分依赖于样品元素并在玻璃转变过程中起主要作用，其中以Zr原子为中心体积较大的团簇可以与周围的类二十面体团簇连接，从而增加系统的玻璃形成能力.

4)n5= 6，8，10，12的Voronoi多面体构成了三种非晶体系玻璃转变过程中的主要团簇集合且数量随温度降低而增多；团簇的种类和数量会在玻璃转变温度附近出现激增和拐点，是非晶合金玻璃转变过程中自组织临界行为在原子团簇结构层面的体现，蕴含着丰富的动力学现象.