基于带参数单步块方法的电力系统暂态稳定性数值计算方法

林沁庭，王 永，郝跃东，吴秀海，张 磊，靳生鹏

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.国网上海市电力公司特高压换流站分公司，上海 201314；3.国网青海省电力公司超高压公司，青海西宁 810008）

0 引言

电力系统暂态稳定性的数值计算方法众多，但基本上可以归纳为显式分离求解法（Partitioned Explicit Method，PE）和隐式联立求解法（Simultaneous Implicit Method，SI）两大类[1]。其中，隐式联立求解法由于不存在交接误差，而被广泛采用[1]。

但是，隐式联立求解法存在的问题是采用严格的Newton 法在联立求解过程需要多次形成雅克比矩阵并对其进行三角分解，计算速度较慢。众所周知，隐式梯形积分法因具有A-稳定性且计算精度为二阶而被广泛用于电力系统暂态稳定性分析中。为此，有必要寻找一种新的具有良好数值稳定性的隐式积分法，并结合与数值积分算法相适应的高效线性方程组求解方法，则在一定程度上可以满足暂态稳定性计算的实时性要求。

隐式数值积分法可大致分为2 类[2]: 第一类是Runge-Kutta 方法，该方法使用较少；第二类是线性多步法，常用于求解微分方程初值问题，包括向后差分方法（Backward Differentiation Formulae，BDF）方法和Adams 方法。除了这2 类方法，还有1 种在隐式线性多步法的基础上扩展出的被称为边界值方法的第三类方法。然而，隐式线性多步法存在着Dahlquist 限制，在现阶段众多学者还无法克服这个问题，因此在求解刚性微分方程问题上受到限制。学者L.Lopez 在基于线性二步法的基础上，成功地构造出了二步边界值方法[3]（Boundary Value Methods，BVM）。随后，L.Brugnano 等学者在前人研究的基础上提出了一系列BVM 方法，包括广义BDF 方法（Generalized BDF，GBDF）、广义Adams 方法和扩展的隐式梯形积分法（Extended Trapezoidal Rules，ETRs）。BVM 方法不存在任何阶障碍，具有良好的数值稳定性，因此被广泛应用于求解微分动力系统[4]。

本文将带参数二步边界值方法用于电力系统暂态稳定性计算，并根据单步块格式的基本原理得到二步边界值方法的新的计算格式，减小了牛顿迭代的方程组的维数，提高了计算的效率。首先，在二步边界值方法的计算格式的基础上分析了其数值稳定性。其次，为降低离散后方程组的维数并提高计算效率，采用了单步块格式，并推导了基于带参数多步块方法的电力系统暂态稳定性计算公式。最后利用典型算例系统，并与电力系统分析综合程序（Power System Analysis Software Package，PSASP）软件作对比测试。数值结果表明，文中方法在计算精度、通用性和数值稳定性上效果明显，取得了较好的结果，可用于快速判别大扰动后发电机转子首次摇摆的稳定性。

1 边界值方法

1.1 计算格式

首先需要解决一阶常微分方程组的初值问题，其标准形式为[5]：

式中：t为时间变量；y0为状态变量在t=0 s 时刻的数值；y为系统状态变量所构成的n维向量，y=(y1y2…yn)T∈Rn，Rn为状态变量y是n维实数域内的列向量；y′为状态变量y的一阶导数；函数f(t,y(t))为关于t和状态变量y(t)的变量；T为待求解问题中t的取值区间的右端点。

式（1）可改写成关于t的函数：

考虑带参数β的二步二阶边界值方法[3]离散格式求解式（2），此时式（2）可以离散为：

式中：M为对时间区间划分的网格个数；m为式（3）中代数方程的个数；h为时间步长，有h≡tm+1-tm=T/M；fm为函数f(t)在t=tm=m∙h时的函数值，即fm=f(tm)；ym为状态变量y(t) 在t=tm=mh时的数值。

考虑另外一种带实数参数α的二步三阶边界值方法[3]对式（2）进行数值积分，有：

联立求解式（3）或式（4），需要补充2 个关于状态变量的边界值方程。对于式（2）来说，仅只有首端边值是提前给定的。为此，需要在式（3）或式（4）的两端添加二阶隐式梯形数值积分公式[3]：

式中：fM为函数f(t)在t=tM=Mh时的函数值，即fM=f(tM)；yM为状态变量y(t)在t=tM=M∙h时的数值。

1.2 算法的数值稳定性分析

为验证二步边界值方法的数值稳定性，采用的检验方程[2]：

式中：λ为实部为负数的虚数。

采用单步法以固定步长求解式（6），令变量ξ=λh，构造以ξ为变量的带参数二步边界值方法特征多项式，结合数值算法的稳定性定义[1]，L.Lopez详细证明了关于带参数二步边界值方法稳定性的结论[3]：

1）当β≤1时，对于具有（1，1）边界条件的式（3）是二阶、01，1-稳定及A1，1-稳定的数值积分方法。当参数β取值[-2，-6]时的稳定域见图1 所示。图1中稳定域定义为封闭曲线以外的区域。

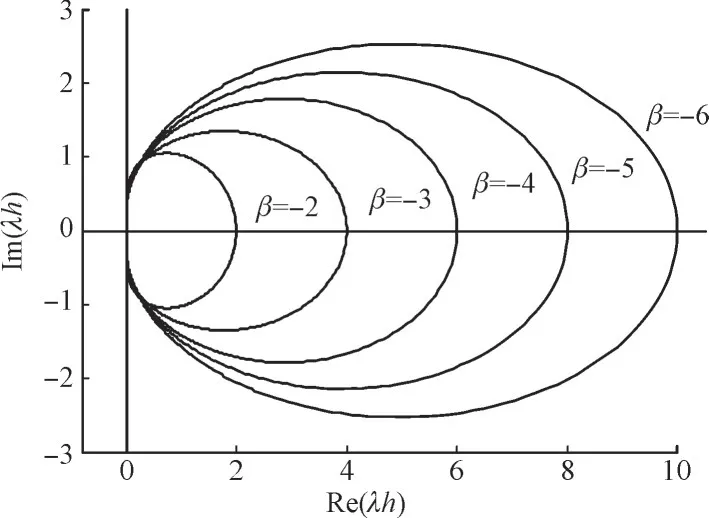
图1 二步二阶边界值方法的稳定域Fig.1 Stability region of two-step two-order boundary value method

2）当α∈(-∞,-1]⋃(1,+∞)时，具有（1，1）边界条件的式（4）是三阶、01，1-稳定及A1，1-稳定的数值积分方法。当参数α取值[-9，15]时的稳定域见图2所示。图2 中稳定域定义为封闭曲线以外的区域。

图2 二步三阶边界值方法的稳定域Fig.2 Stability region of two-step three-order boundary value method

2 带参数单步块方法用于暂态稳定性计算的分析流程

电力系统暂态过程可用微分-代数方程组描述为：

式中：x为状态变量；u为网络节点电压；Y为电力网络的节点导纳矩阵；g为系统网络节点的注入电流函数。

为对电力系统暂态稳定性进行实时在线分析，采用经典暂态稳定性计算模型：

式中：下标i表示第i台发电机；Pei为电磁功率；Pmi为机械功率；Mi为惯性常数；ωi为转速；δi为转角。

Pei(δi)的表达式为：

式中：Cij，Dij均为常量；i，j均为常量，下标i，j表示待研究电力系统中第i台发电机节点与其它网络节点j之间拓扑连接关系。

为了方便分析各发电机间的相对转子角和角速度，采用惯性中心（Center of Inertia，COI）参考坐标系[12]。首先，定义系统惯性中心下的等值转子角δCOI和等值角速度ωCOI为：

式中：MT为待分析电力系统中总的发电机惯性时间常数，。

定义COI 坐标系下的发电机转子角θi和角速度φi为：

得到COI 坐标系下的发电机转子运动方程：

式中：PCOI为惯性中心转子运动方程的总功率差额。

Pei(θi)的表达式同式（9）。

重新定义：

式中：z(y,u)为由COI 坐标系下的发电机转子角和角速度以及网络节点电压表示的状态变量y的一阶导函数。

式（12）可简记为：

式中：为状态变量y的一阶导数；Rm×1为状态变量y取值为m维实数域，且m=2n为系统状态变量y的维数。

按照二步二阶边界值方法（参数β=-2）离散计算式（16），式（5）作为附加方法，如图3 所示。

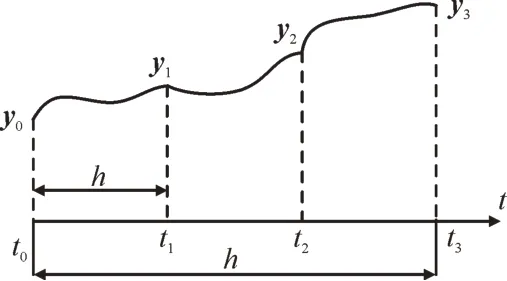
图3 s级单步块格式的内在时间并行性Fig.3 Intrinsic time parallelism of s-level single step block format

s=3 表示将二步边界值方法转为为单步块方法后的级数，h为二步边界值方法的计算步长，为二步边界值方法求解过程中内点的计算步长，h=s且h=t3-t0。此外，若令tk=t0，tk+1=t3则在时间区间[tk,tk+1]内将s个时刻处状态变量按列采用该方法求解式（16），并仿照隐式Runge-Kutta 方法的计算格式表示如下：

当s=3 时，且有相当于时间区间[tk,tk+1]内在s个时间点上同时求解才能得到yk+1，因而具有较好的内在时间并行性。根据式（17）和式（18）可以得到Butcher 表格形式，即，c，和bT均为二步边界值方法相关的系数矩阵，其中的表达式如下：

同理，采用二步三阶块边界值方法（Block Boundary Value Methods，BBVM）（参数α=-3）离散计算式（16），隐式梯形积分公式（5）作为附加方法，则按照式（17）-式（18）的有如下的系数矩阵：

通过式（17）—式（20），可以看出此时的2 步块边界值方法可以看作是一种单步块方法，不妨定义新的计算过程的中间变量如式（21）所示：

式中：y，w，Z，d和q均为新的计算过程的中间变量。

则将式（18）和式（7）中的网络方程联立求解可得：

式中：g为系统网络节点的注入电流函数；=-yk；Im为m维的单位矩阵；⊗为矩阵或向量的直积。

定义牛顿迭代法过程新变量为：

记Δg构成新的向量ΔG为：

则利用牛顿法联立求解式（22）可得：

按照式（25）的排列方式，式（24）中雅克比矩阵中各分块矩阵J11，J12，J21和J22的表达式参见文献[12]。

本文采用广义极小残余方法（Generalized Minimal Residual，GMRES）[12]求解方程（25），并采用预处理矩阵提高算法的收敛性。

3 算例分析

算例采用IEEE 145 节点系统，发电机模型采用经典模型[13]，负荷采用恒阻抗模型[14-20]。故障设定为在7 号母线处发生三相短路。在故障发生0.1 s 后切除，整体积分时间为1.50 s。由于104 号母线与7号母线距离最近[21-24]，具体的网络拓扑图参考文献[21]，本文主要分析比较104 号母线上的发电机功角的计算结果误差曲线。数值计算中以步长取h=0.001 s 时的PSASP 软件[18]计算结果（数值方法为隐式梯形积分法，其中θ表示发电机之间相对功角，φ表示发电机之间相对角速度）[8-11]为基准，跟踪观察本文方法（s级单步块边界值方法BBVM）和同阶Runge-Kutta 方法的数值计算误差曲线。牛顿法的收敛精度（无量纲）设置为ε=1×10-5。

图4 和图5 分别为h等于0.06 s，0.1 s 时的误差曲线。如图4 和图5 所示，本文方法即使采用60倍或10 倍于隐式梯形积分法的计算步长仍可与PSASP 计算结果保持一致（误差控制在0.1 之内）。此外，与同阶的Runge-Kutta 方法相比，保持计算步长不变，本文方法的计算精度更高。

图4 步长h=0.06 s 时的误差曲线Fig.4 Error curves when h is 0.06 s

图5 步长h=0.1 s 时的误差曲线Fig.5 Error curves for when h is 0.1 s

对于部分比较靠近故障7 号母线的发电机的相对转子角的摇摆曲线，如第20，24，26，28 和36台发电机组的功角θ20，θ24，θ26，θ28和θ36变化曲线如图6 和图7 所示。可以看出故障发生后到0.1 s后故障被切除后的1.5 s 内，各发电机的相对转子角均未超过180°，这表明系统在首次摇摆时是暂态稳定的。

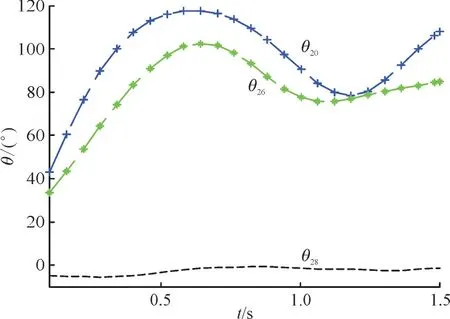
图6 步长h=0.06 s 时的二步二阶块BVM计算的相对功角曲线Fig.6 Relative power angle curves for generators computed by two-step two-order BVM when h is 0.06 s

图7 步长h=0.06 s 时的二步三阶块BVM计算的相对功角曲线Fig.7 Relative power angle curves for generators computed by two-step three-order BVM when h is 0.06 s

对于部分比较靠近故障7 号母线的发电机机组的相对角速度曲线，如第20，24 和36 台发电机组的转子角速度φ20，φ24和φ36变化曲线如图8 所示。可以看出当第20 台发电机相对于COI 在减速时，第24 台发电机则相对于COI 在加速。这说明在故障扰动下，发电机转子运动具有分群特性[25-28]。

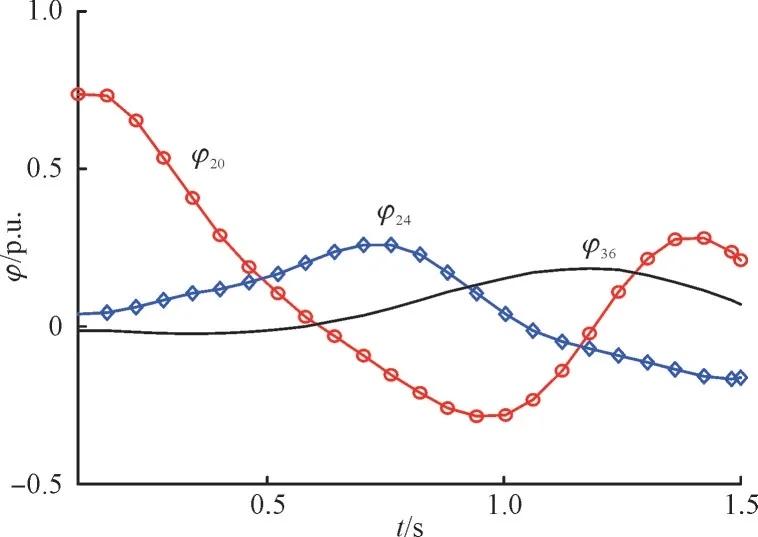
图8 步长h=0.06 s 时的二步三阶块BVM计算的相对角速度曲线Fig.8 Relative angular velocity curves for generators computed by two-step three-order BVM when h is 0.06 s

4 结论

本文将带参数的二步块边界值方法巧妙地用于电力系统暂态稳定性数值计算中。带参数二步边界值方法具有二到三阶精度，且是A-稳定的单步块方法。针对二步块边界值方法差分离散后经牛顿法得到的代数方程组是一个高维的分块矩阵，采用广义极小残余方法求解方程经单步块方法离散后的代数方程组，并采用预处理矩阵提高算法的收敛性。相对于隐式梯形法及同阶的Runge-Kutta 法而言，本文在计算效率及精度上具有明显优势。通过IEEE145 节点算例系统仿真表明：本文方法可以快速求解电力系统暂态稳定性，对于机组首次摇摆时的暂态稳定性可以准确判别。此外，文中所提算法可方便实现暂态稳定性的并行计算，相关成果可以进一步推广至其它类似的计算领域。