基于威布尔分布的智能电表时钟电池可靠性分析

2024-01-28王伟峰叶方彬陈徐笛

智慧电力 2024年1期

王伟峰，叶方彬，陈徐笛，杨杰，李璟，蔡慧，郑迪

（1.国网浙江省电力有限公司，浙江杭州 310014；2.中国计量大学机电工程学院，浙江杭州 310018；3.浙江华云信息科技有限公司，浙江杭州 310000）

0 引言

随着智能电表覆盖率的不断提高，智能电表的管控要求也越来越高[1]。智能电表的时钟作为承担电表重要功能的部件，其质量关系到智能电表是否可以正常工作。据不完全统计，在浙江省智能电表的实验室检定结果中，故障原因为时钟电池欠压的智能电表占比高达52%[2]。时钟电池欠压故障高发使得时钟电池的可靠性成为电表质量监管工作中无法忽视的关键点。时钟电池欠压会导致电能表费率切换错误，系统召测时间错误，数据冻结功能异常等影响电表正常计量的问题[3-4]，损害了电能交易的公平与公正，造成智能电表的查证维修成本增加。

目前，针对智能电表的时钟电池的研究主要围绕其故障原因，故障影响以及如何提高时钟电池寿命进行。文献[5]从硬件、软件、电网选型等角度提出了目前较为可行的电池欠压故障问题解决方案。文献[6]电化学反应为基础，通过数据模拟，建立了脉冲电压与剩余电量的数学模型。文献[7]从硬件、软件、生产工艺、质量体系等多角度对电表时钟可能发生的故障提出了预防及解决方案。

对智能电表进行可靠性预测可以很大程度提高其工作效率。文献[8]通过应力加速法综合应用加速试验理论、加速模型和算法，制定了加速寿命试验（Accelerated Life Test，ALT）方案，确定了影响电能表寿命的关键参数。但缺少对正常工况下的卡扣断裂数据的分析比较，无法推断其寿命分布参数是否完全一致。文献[9]通过元器件应力法排列出了对电表寿命可靠性影响较大的元器件，但是元器件应力法的缺点在于太过于依赖可靠性手册。这可能由于手册数据更新不及时等原因导致得到的预计结果与实际结果存在较大的差异。文献[10]研究了定时截尾数据下智能电表的可靠性模型优选、融合现场数据和ALT 数据的可靠性评估，可用于指导智能电表的轮换与检修工作。但受数据记录的影响，部分智能电表存在安装时间、故障时间记录不全的问题；而且备选模型均为简单模型，但智能电表的故障是多种故障模式共同作用引起的。

现有研究大多是在实验室环境下完成电能表的加速试验，缺少对电能表中时钟电池的寿命可靠性研究，且没有从安装到失效的大批量实际数据。对于大规模现场运行的电能表基本未提出如何确定其时钟电池可靠性的具体方案，缺乏现场实际应用性。针对这一研究空缺，本文以用电信息采集系统召测的智能电表时钟电池欠压数据为基础，建立威布尔分布下的智能电表时钟电池模块的可靠性分布模型，并提出量化智能电表时钟电池质量的评价指标。所做研究适用于以智能电表批次为单位进行智能电表可靠性预测，为智能电表运行状态监测提供有力支撑。

1 智能电表时钟电池状态

目前，智能电表生产中主要采用容量1.2 Ah，电压3.65 V 的ER14250 锂-亚硫酰氯电池作为电表的时钟电池。根据国家电网公司要求，智能电表的时钟电池在电能表寿命周期内无需更换，断电后可维持内部时钟正确工作时间累计不少于5 年。随着运行年限加长，电池质量、电池钝化、电池自放电、外围电路漏电等都可能引起电池电压损失，导致时钟电池欠压[11]。而一旦时钟电池处于欠压状态，将无法进行自我恢复，电池无法正常工作，影响电能表的可靠性[12]。

DT/L 645-2007《多功能电能表通信协议》[13]中，电表运行状态字1 记录了智能电表时钟电池的电压状态，如表1 所示。Bit0—Bit15 表示电表的时钟电池、停电抄表电池、功率方向和系统状态等信息，其中“保留”表示该Bit 位没有被明确定义或者使用。

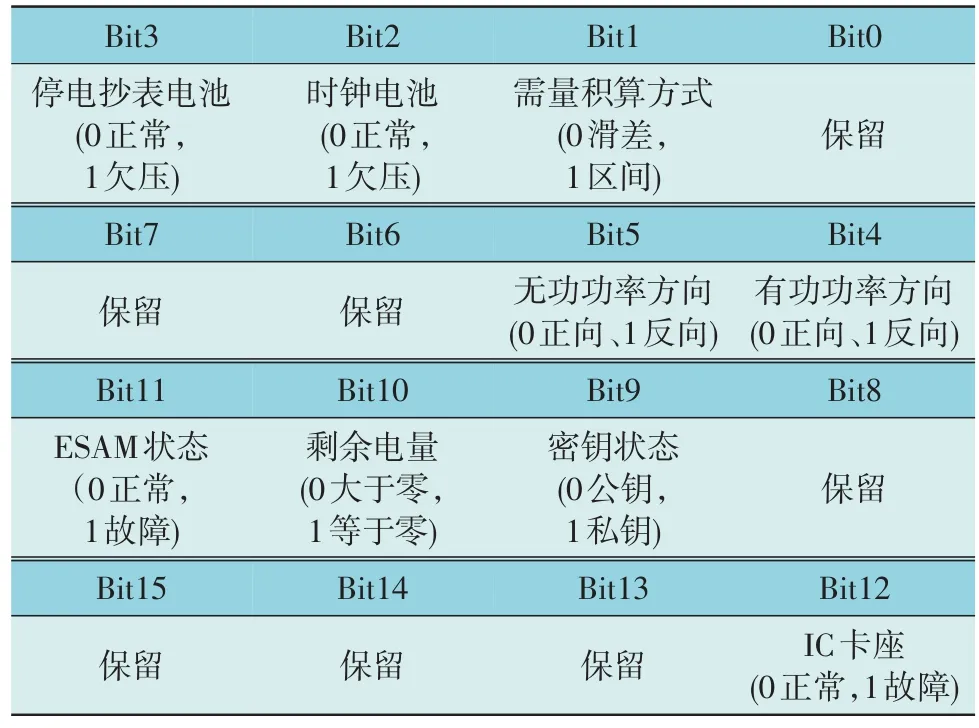
表1 电能表运行状态字1Table 1 Operation status word 1 of electric energy meter

2 时钟电池可靠性

可靠性是产品在规定的条件下、在规定的时间内完成规定的功能的能力。产品泛指任何系统、设备和元器件，包括智能电表的时钟电池。可通过可靠度、不可靠度、失效密度、失效率等来评价产品的可靠性[14]。

在评价智能电表可靠度性能的时候，常见方法有威布尔分布、机器学习的神经网络和决策树等方法，根据现有文献结论，各方法优缺点和预测精度比较如表2 所示。经过综合分析，本文选用威布尔分布方法作为本文智能电表时钟电池可靠性分析的方法。

表2 3种算法的优缺点及算法复杂度对比Table 2 Comparison of advantages＆disadvantages and complexity between three algorithms

2.1 威布尔分布下的可靠性

威布尔分布对各种数据的拟合能力强，适用性高，广泛应用于可靠性工程，尤其适用于机电类产品的磨损累计失效的分布形式。在做变换后，指数、正态分布[21]都可作为威布尔分布的简化，因此威布尔分布能有效描述电子类产品的失效分布[22-23]。

智能电表的时钟电池作为典型的电子产品元器件可以采用威布尔分布作为其可靠性预测的分布模型。

威布尔分布下的可靠度函数R(t)为：

式中：t为时间；m为形状参数；η为尺度参数。

与可靠度函数相对应的是不可靠度函数，又称为失效概率函数F（t），两者之间存在的关系为：

威布尔分布下，失效密度f（t）如式（3）所示。

失效率函数λ(t)由失效密度和可靠度函数相除得到：

2.2 时钟电池可靠性参数计算

由于同一批次电能表采用的电子元器件相同，加工工艺相同，可以近似认为其质量水平相近[24]。因此，文章认为同一批次的智能电表时钟电池遵循同一可靠度分布函数。文章通过威布尔分布确定时钟电池的可靠性，其关键是要通过实际数据获取威布尔分布下的2 个关键参数即m（无量纲）和η（无量纲）。

2.2.1 数据来源

DT/L 645-2007《多功能电能表通信协议》中，电能表运行状态字中的Bit2 位存储了时钟电池欠压信息，0 代表正常，1 代表欠压。目前，国家电网公司通过主站召测的方式每月进行4 次时钟电池欠压数据的召测。因此，文章以用电信息采集系统的召测结果作为可靠性参数的计算来源。

2.2.2 参数计算

用电信息采集系统的召测结果可以明确智能电表时钟电池发生欠压的时间。通过对实际批次的智能电表数据进行累计分布统计，可以得到该批次智能电表时钟电池的实际不可靠度F（t），如式（5）所示。

式中：u为自智能电表安装开始的月份序号；Nu为第u月发生时钟电池欠压的智能电表数量；N为该批次智能电表总数量。

通过取对数将式（1）和式（2）变形为：

将式（6）变形为线性方程：

式中：A（无量纲）为线性回归方程的斜率；B（无量纲）为线性回归方程的纵截距。

由式（7）可知，威布尔分布下时钟电池的可靠度计算过程可等效为对时钟电池的实际不可靠度进行处理后通过线性回归求取参数的过程。将式（5）中各月份计算得到的不可靠度F（t）代入式（7），得到多组（X，Y）数据点。根据式（7）可以计算得出威布尔分布的m和η。最后，将参数代入式（1）即可绘制该批次的智能电表时钟电池在威布尔分布下的可靠度函数分布图。

可靠度函数表示了以批次为单位的智能电表时钟电池的质量，随着智能电表运行时间的增长，时钟电池的可靠度逐渐下降。威布尔分布的m和η决定了时钟电池可靠度的下降趋势，但是仅比较以上2 个参数无法直观反映智能电表的时钟电池质量。为了量化比较各个批次的智能电表时钟电池质量差异，以可靠度函数与坐标轴围成的面积SR（无量纲）作为时钟电池质量评价的指标，并根据黎曼积分定义得到其计算过程，如式（8）所示。

式中：a为划定的积分区域上限；n为积分中的区间分割数量；i为分割后的子区间序号。

3 现场运行智能电表的时钟电池可靠性计算

3.1 时钟电池数据

在实验室条件下进行可靠性试验时，往往利用加速试验的方法，加快产品退化过程，以期尽快获取数据[25]。然而，文章目的是对实际运行智能电表时钟电池进行状态评估，因此选用了运行时间较长的某批次智能电表数据作为实例。批次I 共含24 079个智能电表，该批次的电能表安装时间为2013 年8月。表3 所示为按月统计的批次I 的智能电表出现时钟电池欠压字段召测为1 的电表数量与平均运行时长信息。需要注意的是，由于时钟电池的欠压状态无法自我恢复[26]，因此忽略历史数据中已经出现时钟电池欠压的电表的后续召测结果。

表3 批次I智能电表时钟电池故障数量与运行时长历史数据Table 3 The number of clock battery faults in smart meter of batch I and its running time history data 个

3.2 可靠性计算

根据批次I 的智能电表历史数据，通过式（5）可以获取该批次的智能电表实际的不可靠度F（t）。由该批次自安装起的实验室检定结果数据按月进行不可靠度的计算，可以得到F（t）的变化趋势，如图1所示。

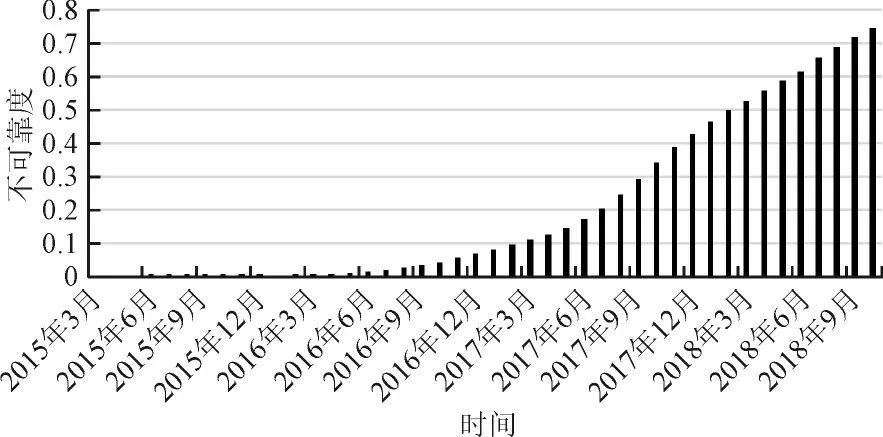
图1 批次I时钟电池不可靠度变化趋势Fig.1 Change trend in unreliability of clock battery of batch I

根据2.2.2 节提出的威布尔分布下时钟电池的可靠度计算方法，通过式（7）得到多组（X，Y）散点坐标，通过Matlab 进行线性回归计算，得到回归方程如图2 所示。图2 中X，Y均无量纲。

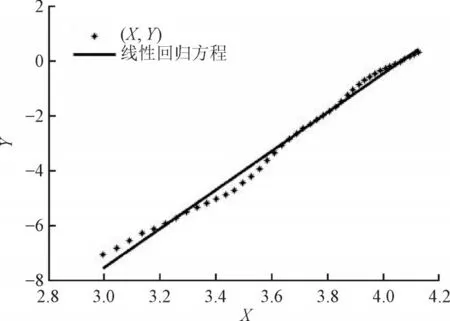
图2 批次I线性回归方程Fig.2 Linear regression equation for smart meter of batch I

通过拟合可得线性回归方程斜率A为7.068，纵截距B为-28.73。根据式（7）可得该批次的智能电表时钟电池在威布尔分布下的可靠度函数，m为7.068，η为58.253 2，其可靠度及不可靠度函数如图3 所示。

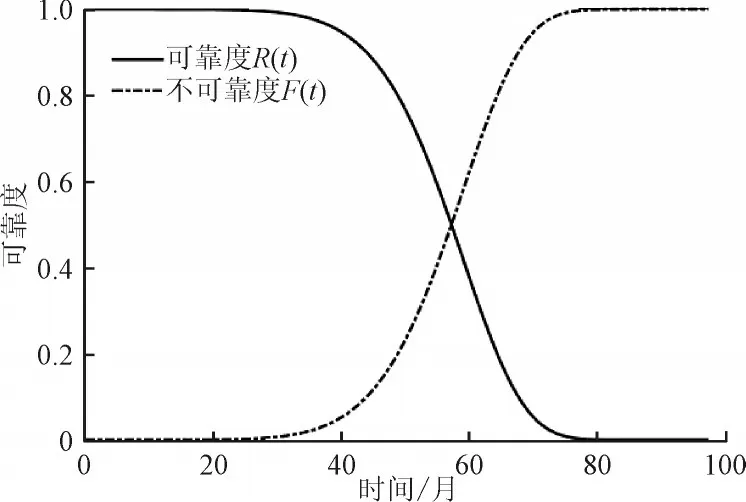
图3 批次I时钟电池可靠度与不可靠度函数Fig.3 Reliability and unreliability function of clock battery of batch I

在对4 个批次进行可靠度预测时，批次III 存在首个数据点与相邻数据点偏离较大的现象，线性回归方程系数出现偏差，最终导致预测结果误差率偏高。因此，提出根据首个数据点（x1，y1）与第二个数据（x2，y2）比值的大小，来判断是否要去除首个数据点，以此达到提高预测准确度。若比值大于5 或者小于0.2，则认为首个数据点偏离过大，去除首个数据点。

3.3 可靠性验证

选取批次I 中2015 年3 月到2018 年3 月的智能电表历史数据，通过式（5）获取该批次在威布尔分布下的可靠度函数。并根据所预测2018 年4 月到2018 年10 月的可靠度，计算得出对应月份的时钟电池欠压电表数量，并与实际数据进行对比，得到预测累计数量与实际故障累计数量误差率，结果如表4 所示。

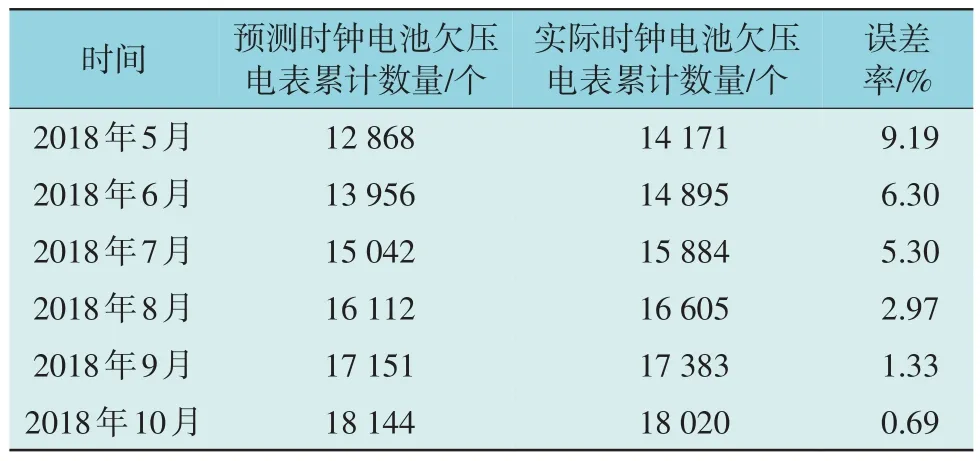
表4 批次I智能电表时钟电池预测故障数量误差率Table 4 Error rate in predicting the number of clock battery faults in smart meter of batch I

根据表4 结果可得，批次I 在2018 年5 月至2018 年10 月的预测误差率在0.69%～9.19%之间，表明了该模型具有较高的精确度。

表5 为4 批次智能电表时钟电池预测误差率。由表5 可得，4 个批次中批次II 的误差率相比较高，这可能与该电表批次的原始数据有关，其余3个批次的误差率都较低，预测结果与实际数据相近，证明该模型具有一般适用性与较高的准确率。

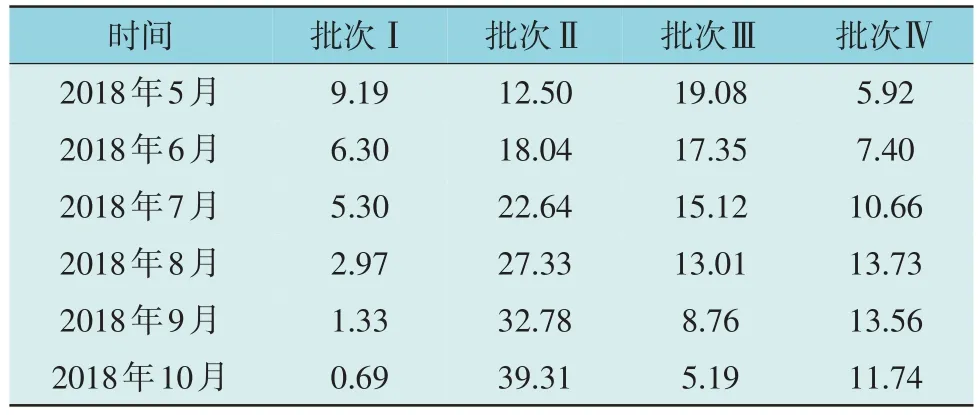
表5 4批次智能电表时钟电池预测误差率Table 5 Prediction error rate of clock battery of four batches of smart meters %

3.4 时钟电池质量评价

按照文中所述方法分别对其它3 个智能电表批次II，III，IV 进行时钟电池可靠性分析，得到4 个批次的时钟电池可靠度分布函数如图4 所示。其中批次II 为2013 年6 月安装，该批次共有4 987 个智能电表；批次III 为2013 年10 月安装，该批次共有9 738 个智能电表；批次IV 为2013 年7 月安装，该批次共有16 041 个智能电表。

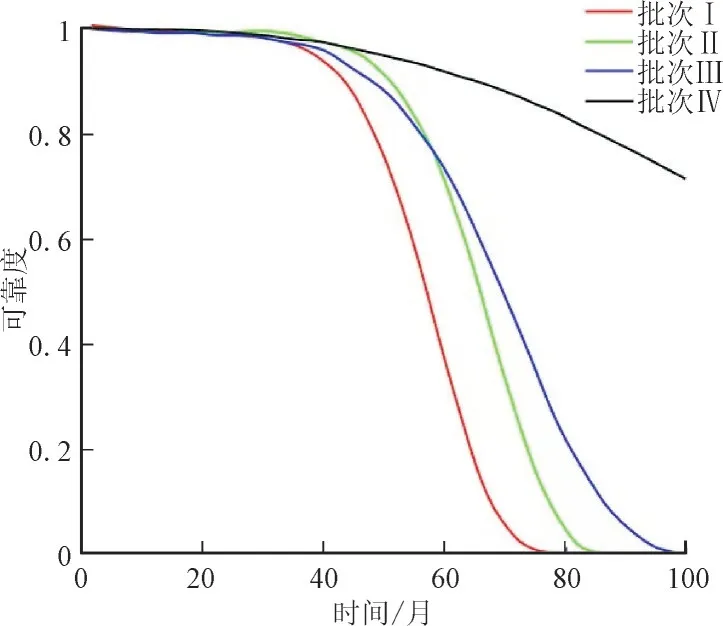
图4 4个批次的时钟电池可靠度分布函数Fig.4 Reliability distribution function of four batches of clock battery

从4 个批次的时钟电池可靠度函数中观察发现，批次I 的时钟电池可靠度下降最快，时钟电池质量最差。批次II，III，IV 的时钟电池可靠度下降趋势随依次减缓，批次IV 的时钟电池质量最高。各批次的时钟电池可靠度呈现出的特征为在安装后的较长时间内保持稳定，然后在一段时间内迅速下降，大量失效，最后缓缓趋向于0。

批次I，II，III，IV 的时钟电池质量量化评价指标SR计算分别为56.36，65.16，68.91 和91.74，与观察结果一致。

因此，对各批次智能电表的时钟电池，可以依据文章所述方法进行时钟电池质量的量化评价，筛选出优秀的智能电表厂商进行采购，提高智能电表的使用寿命。同时，根据智能电表的可靠度函数变化趋势，为即将大批量失效的智能电表批次提前制定更换计划。